A&A 380, 186-189 (2001)
DOI: 10.1051/0004-6361:20011358
Apparent radii of neutron stars
and equation of state of dense matter
P. Haensel
N. Copernicus Astronomical Center, Polish
Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
Received 20 July 2001 / Accepted 20 September 2001
Abstract
Apparent (radiation) radius of neutron star,
 ,
depends on the star gravitational mass
in quite a different way than the standard coordinate
radius in the Schwarzschild metric, R.
We show that, for a broad set of equations
of state of dense matter,
,
depends on the star gravitational mass
in quite a different way than the standard coordinate
radius in the Schwarzschild metric, R.
We show that, for a broad set of equations
of state of dense matter,
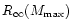 for the configurations with maximum allowable masses
is very close to
the absolute lower bound on
for the configurations with maximum allowable masses
is very close to
the absolute lower bound on  at fixed
M,
resulting from the very definition of
at fixed
M,
resulting from the very definition of
 .
Also, the value of
.
Also, the value of  at given M,
corresponding to the
maximum compactness (minimum R) of neutron star consistent with
general relativity and condition
at given M,
corresponding to the
maximum compactness (minimum R) of neutron star consistent with
general relativity and condition
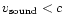 ,
is only 0.6% higher than this absolute
lower bound.
Theoretical predictions for
,
is only 0.6% higher than this absolute
lower bound.
Theoretical predictions for  are compared with
existing observational estimates of the apparent radii of
neutron stars.
are compared with
existing observational estimates of the apparent radii of
neutron stars.
Key words: dense matter - equation
of state - stars: neutron - stars
Measuring the spectrum of
radiation from neutron star surface (or, more
precisely, atmospheres), combined with knowledge
of distance,
enables one, assuming spherical symmetry,
to determine total luminosity,
effective surface temperature, and neutron star
radius. Recently, such studies have been carried out
for Geminga (Golden & Shearer 1999) and RX J185635-3754
(Walter 2001); distance from these isolated neutron stars
was obtained from measuring of the annual parallax.
Very recently, Chandra observations of X-ray sources
in the globular clusters (whose distance is known
with relatively good precision) were proposed
(and applied) to calculate
the radius of a neutron star in quiescence (Rutledge et al. 2001).
Neutron star are relativistic objects, and for masses
above solar mass their radii may be only 1.5-2 times larger
than the gravitational (Schwarzschild) radius
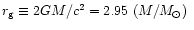 km.
Therefore, because of a sizable spacetime curvature
close to neutron star, one has to distinguish between
the "true'' or "coordinate'' radius, R, which is the radial
coordinate of the stellar surface in the Schwarzschild
metric, and the "apparent radius'' (sometimes called
"radiation radius''),
km.
Therefore, because of a sizable spacetime curvature
close to neutron star, one has to distinguish between
the "true'' or "coordinate'' radius, R, which is the radial
coordinate of the stellar surface in the Schwarzschild
metric, and the "apparent radius'' (sometimes called
"radiation radius''),  ,
as determined by a distant observer
studying radiation from neutron star surface.
,
as determined by a distant observer
studying radiation from neutron star surface.
In the present letter we calculate dependence of  on neutron star mass for a broad set of equations of state
of dense matter. We discuss properties
of the theoretical
on neutron star mass for a broad set of equations of state
of dense matter. We discuss properties
of the theoretical
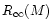 curves,
and finally we confront theoretical calculations
with recent observational
estimates of apparent radii of neutron stars.
curves,
and finally we confront theoretical calculations
with recent observational
estimates of apparent radii of neutron stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3021F1.eps}\end{figure}](/articles/aa/full/2001/46/aah3021/Timg9.gif) |
Figure 1:
Neutron star radius R versus gravitational mass M,
for seven EOS of baryonic matter, labeled by
numbers 1-7. 1: BPAL12 of Bombaci
et al. (1995); 2: EoSN1H1 of Balberg et al. (1999);
3: FPS of Pandharipande & Ravenhall (1989); 4: Baldo
et al. (1997); 5: Douchin & Haensel (2000);
6: EoSN1 of Balberg et al. (1999); 7:
EoSN2 of Balberg et al. (1999). Dotted line
corresponds to strange stars built of self-bound
quark matter (SQ1, Haensel et al. 1986). Long dashes: hybrid
neutron stars of dense matter with a mixed baryon-quark phase,
EOS from Table 9.1 of Glendenning (1997).
Long dashes-dot line: EOS with first-order phase transition
to a pure kaon-condensed matter (Kubis 2001). Doubly hatched
area is prohibited by general relativity and
corresponds to
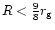 .
Singly
hatched area is excluded by general relativity
combined with condition .
Singly
hatched area is excluded by general relativity
combined with condition
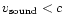 .
In the
case of stars built of baryonic matter, configurations
with maximum allowable mass is indicated by a filled circle,
and in the case of strange stars,
built of
self-bound quark matter - by an open circle.
Shaded vertical band corresponds to the range of precisely
measured
masses of binary radio pulsars. .
In the
case of stars built of baryonic matter, configurations
with maximum allowable mass is indicated by a filled circle,
and in the case of strange stars,
built of
self-bound quark matter - by an open circle.
Shaded vertical band corresponds to the range of precisely
measured
masses of binary radio pulsars.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3021F2.eps}\end{figure}](/articles/aa/full/2001/46/aah3021/Timg10.gif) |
Figure 2:
Apparent radius of neutron star,  ,
versus gravitational mass, M. Notation as
in Fig. 1. Thick long-dash - dot straight line corresponds to
minimum ,
versus gravitational mass, M. Notation as
in Fig. 1. Thick long-dash - dot straight line corresponds to
minimum  at a given M.
at a given M.
|
| Open with DEXTER |
The effective surface temperature, 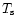 ,
at the
neutron star surface, is related to total photon
luminosity,
,
at the
neutron star surface, is related to total photon
luminosity, 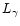 ,
by
,
by
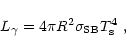 |
(1) |
where all quantities are measured by a local observer on
neutron star surface. Spherical symmetry is assumed.
A distant observer ("at infinity'')
will measure "apparent luminosity''
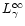 ,
"apparent effective temperature''
,
"apparent effective temperature''
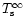 ,
and
"apparent radius''
,
and
"apparent radius''  ,
related to quantities
appearing in Eq. (1) by (Thorne 1977)
0pt
,
related to quantities
appearing in Eq. (1) by (Thorne 1977)
0pt
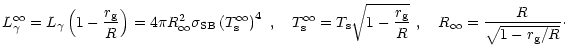 |
|
|
(2) |
As we will show, dependence of  on neutron star mass differs
considerably from R(M); the difference, which reflects spacetime
curvature near neutron star, increases with increasing M, and becomes
quite large at the maximum allowable mass,
on neutron star mass differs
considerably from R(M); the difference, which reflects spacetime
curvature near neutron star, increases with increasing M, and becomes
quite large at the maximum allowable mass,
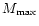 .
The curves R(M) and
.
The curves R(M) and
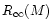 ,
calculated for a broad
set of equations of state (EOS) of dense matter, are presented
in Figs. 1 and 2, respectively. One notices, that for
moderately stiff and stiff equations of state (
,
calculated for a broad
set of equations of state (EOS) of dense matter, are presented
in Figs. 1 and 2, respectively. One notices, that for
moderately stiff and stiff equations of state (
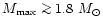 )
without a strong softening at highest densities,
for
)
without a strong softening at highest densities,
for
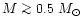 the apparent radius
the apparent radius
 increases with increasing M (except
for a tiny region close to
increases with increasing M (except
for a tiny region close to
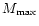 ), in contrast to
R(M), which decreases in the same mass interval.
), in contrast to
R(M), which decreases in the same mass interval.
In Fig. 1, straight lines, marking upper boundaries of the
hatched regions of the R-M plane, result from quite
general physical conditions imposed on the configurations
of hydrostatic equilibrium in general relativity.
The lower boundary results from the condition that pressure
within an equilibrium configuration should be finite,
and can be expressed as
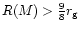 (Buchdahl 1959; general proof can be found in Weinberg 1972).
This condition can rewritten as
(Buchdahl 1959; general proof can be found in Weinberg 1972).
This condition can rewritten as
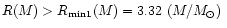 km.
A stronger condition is obtained if we additionally
require that sound speed within the star should
be subluminal:
km.
A stronger condition is obtained if we additionally
require that sound speed within the star should
be subluminal:
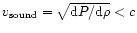 (such a condition is necessary,
but not sufficient (Olson 2000), to respect
causality in a fluid medium).
The condition
(such a condition is necessary,
but not sufficient (Olson 2000), to respect
causality in a fluid medium).
The condition
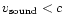 implies a lower
bound on R at a given M (Lindblom 1983; Haensel & Zdunik
1989; Lattimer et al. 1990; Glendenning 1992; Haensel et al. 1999; Glendenning 2000).
In what follows, we will use numerical values of the
absolute lower bound
implies a lower
bound on R at a given M (Lindblom 1983; Haensel & Zdunik
1989; Lattimer et al. 1990; Glendenning 1992; Haensel et al. 1999; Glendenning 2000).
In what follows, we will use numerical values of the
absolute lower bound
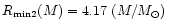 km, as calculated
in Haensel et al. (1999); the older values obtained in
(Lattimer et al. 1990; Glendenning 1992) are slightly higher,
because of the assumed presence of an outer envelope (crust)
in neutron star models, while the value deduced from (Lindblom
1983) is not very precise (see Haensel et al. 1999).
km, as calculated
in Haensel et al. (1999); the older values obtained in
(Lattimer et al. 1990; Glendenning 1992) are slightly higher,
because of the assumed presence of an outer envelope (crust)
in neutron star models, while the value deduced from (Lindblom
1983) is not very precise (see Haensel et al. 1999).
A strict lower bound on
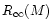 results from the
very definition of
results from the
very definition of  (Lattimer & Prakash 2001).
Namely, the definition of
(Lattimer & Prakash 2001).
Namely, the definition of  implies
implies
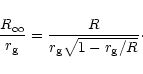 |
(3) |
The right-hand-side of the above equation is a function of
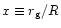 only.
It diverges to
only.
It diverges to  at x
=0 and at x=1. At fixed M, it has a single minimum
at x=2/3. Therefore, minimum value of
at x
=0 and at x=1. At fixed M, it has a single minimum
at x=2/3. Therefore, minimum value of
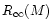 is
is
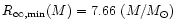 km
(Lattimer & Prakash 2001).
Let us notice, that this limiting
km
(Lattimer & Prakash 2001).
Let us notice, that this limiting
 for an "apparently
most compact'' neutron star is very close to
(but a little smaller than)
that for a maximum compactness x=0.7081consistent with
for an "apparently
most compact'' neutron star is very close to
(but a little smaller than)
that for a maximum compactness x=0.7081consistent with
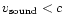 ,
given by
,
given by
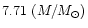 km. However, at
any M the difference is only 0.6%, and therefore in
practice smallest R at a fixed M, consistent with
km. However, at
any M the difference is only 0.6%, and therefore in
practice smallest R at a fixed M, consistent with
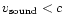 ,
can be considered as corresponding to
smallest
,
can be considered as corresponding to
smallest
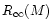 ,
and vice versa.
,
and vice versa.
This result can be easily understood, because
x=0.7081 is only by 0.05 higher than 2/3 corresponding
to the minimum of  .
Therefore, relative difference
between
.
Therefore, relative difference
between
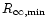 and the value corresponding
to minimum value of R at given M (assuming
and the value corresponding
to minimum value of R at given M (assuming
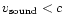 ), can be estimated as
), can be estimated as
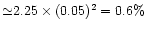 ,
which is
consistent with our exact result.
,
which is
consistent with our exact result.
While the subluminal (
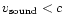 )
upper bound on x at
given M is slightly larger than 2/3, the actual maximum
values of x for various EOS, which are reached
at
)
upper bound on x at
given M is slightly larger than 2/3, the actual maximum
values of x for various EOS, which are reached
at
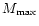 for these EOS, are lower than 2/3. However,
if we restrict to medium stiff and stiff EOS, with
for these EOS, are lower than 2/3. However,
if we restrict to medium stiff and stiff EOS, with
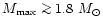 ,
then
,
then
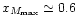 ,
which is only 0.06 lower than 2/3. We may therefore
expect, that for these EOS, which actually constitute majority
of models in Figs. 1, 2,
,
which is only 0.06 lower than 2/3. We may therefore
expect, that for these EOS, which actually constitute majority
of models in Figs. 1, 2,
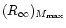 will be only
will be only
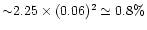 larger than
larger than
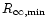 .
This explains, why for these EOS the
points at
.
This explains, why for these EOS the
points at
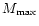 are so close to the
are so close to the
 line in Fig. 2.
line in Fig. 2.
As shown by Lattimer & Prakash (2001), one expects that
for any baryonic
baryonic EOS,
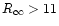 km,
independently of neutron star mass. Our Fig. 2 confirms
this "practical lower bound'' on
km,
independently of neutron star mass. Our Fig. 2 confirms
this "practical lower bound'' on  .
On the contrary, there is
no lower limit on
.
On the contrary, there is
no lower limit on  for bare strange stars, whose
size can be as small as hundred fermis. For strange stars covered
with a layer of normal matter, minimum radius is reached at
for bare strange stars, whose
size can be as small as hundred fermis. For strange stars covered
with a layer of normal matter, minimum radius is reached at
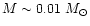 ,
and for a maximally thick crust it is
about 5-6 km (see, e.g., Glendenning 1997).
,
and for a maximally thick crust it is
about 5-6 km (see, e.g., Glendenning 1997).
In what follows we will briefly review observational determination
of apparent radius of neutron star. We will restrict to cases,
which seem to us most promising. In all cases, what one determines
is actually
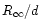 ,
where d is neutron star distance.
Therefore, independent knowledge of d is mandatory to calculate
,
where d is neutron star distance.
Therefore, independent knowledge of d is mandatory to calculate
 from observational data. Generally, after fitting
the spectrum of photons emitted from neutron star, one tries
to get the interval
from observational data. Generally, after fitting
the spectrum of photons emitted from neutron star, one tries
to get the interval
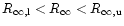 ,
to which the value
,
to which the value  belongs at not less than 90% confidence level.
An EOS is considered to be ruled out,
if no point on its
belongs at not less than 90% confidence level.
An EOS is considered to be ruled out,
if no point on its
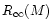 curve
can satify this condition. In practice, the condition reduces
to
curve
can satify this condition. In practice, the condition reduces
to
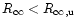 .
Generally, conclusions
from the application of this criterion should be taken with
a grain of salt, because of the difficulty in estimating
of the error in the photon spectrum fitting.
At the
.
Generally, conclusions
from the application of this criterion should be taken with
a grain of salt, because of the difficulty in estimating
of the error in the photon spectrum fitting.
At the 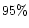 confidence level,
results of Golden & Shearer (1999) imply
confidence level,
results of Golden & Shearer (1999) imply
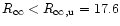 km assuming the H atmosphere, and
km assuming the H atmosphere, and
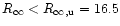 km
for the black body thermal spectrum (which turns out to be
practically indistinguishable from the
Fe/Si model atmosphere spectrum). Therefore,
the value of the upper bound
on the apparent radius of Geminga
is, fortunately,
not very sensitive to the assumed atmospheric model.
km
for the black body thermal spectrum (which turns out to be
practically indistinguishable from the
Fe/Si model atmosphere spectrum). Therefore,
the value of the upper bound
on the apparent radius of Geminga
is, fortunately,
not very sensitive to the assumed atmospheric model.
As for this writing, the case of RX J185635-3754 (Walter 2001, and references
therein), is much less clear.
Using atmosphere model of the photon spectrum, one deduces
from numbers quoted in Walter (2001) the upper bound
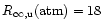 km
at the
km
at the 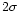 confidence level. However,
if one uses the black body spectrum model, assuming
spherical symmetry, one gets
an abnormally small upper bound,
confidence level. However,
if one uses the black body spectrum model, assuming
spherical symmetry, one gets
an abnormally small upper bound,
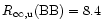 km (Walter 2001; notice
that we use results at the
km (Walter 2001; notice
that we use results at the 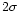 confidence level).
Clearly, these results are very preliminary, and we have still to wait
for more reliable and less model dependent determinations of
confidence level).
Clearly, these results are very preliminary, and we have still to wait
for more reliable and less model dependent determinations of  for this isolated neutron star.
for this isolated neutron star.
Very recently, Rutledge et al. (2001) proposed a method
of measuring  of neutron stars, observed as
X-ray transients in globular clusters.
As an example, they
studied
transcient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139,
fitting photon spectrum with the
H-atmosphere model. They
obtained, at
of neutron stars, observed as
X-ray transients in globular clusters.
As an example, they
studied
transcient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139,
fitting photon spectrum with the
H-atmosphere model. They
obtained, at 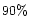 confidence level,
confidence level,
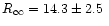 km (assuming 10% uncertainty
in the distance to NGC 5139), which results
in
km (assuming 10% uncertainty
in the distance to NGC 5139), which results
in
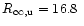 km.
The advantage of the proposed method stems from the fact,
that for neutron stars located in globular clusters both
the distance and interstellar hydrogen column density
are rather well known.
They are mostly related to accreting neutron stars, observed as
X-ray bursters (see, e.g., Titarchuk 1994; Haberl & Titarchuk 1995;
Burderi & King 1998; Psaltis & Chakrabarty 1999; Li et al.
1999a; Li et al. 1999b, and references therein). One has to
mention a strong model dependence of theoretical analyses, and frequent
neglect (Burderi & King 1998;
Psaltis & Chakrabarty 1999; Li et al.
1999a; Li et al. 1999b)
of the space-time curvature effects, which are
actually crucial
for the difference between R and
km.
The advantage of the proposed method stems from the fact,
that for neutron stars located in globular clusters both
the distance and interstellar hydrogen column density
are rather well known.
They are mostly related to accreting neutron stars, observed as
X-ray bursters (see, e.g., Titarchuk 1994; Haberl & Titarchuk 1995;
Burderi & King 1998; Psaltis & Chakrabarty 1999; Li et al.
1999a; Li et al. 1999b, and references therein). One has to
mention a strong model dependence of theoretical analyses, and frequent
neglect (Burderi & King 1998;
Psaltis & Chakrabarty 1999; Li et al.
1999a; Li et al. 1999b)
of the space-time curvature effects, which are
actually crucial
for the difference between R and  .
As one can see in Fig. 2,
the upper bounds
.
As one can see in Fig. 2,
the upper bounds
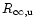 on the apparent radius of Geminga
are consistent with theoretical
predictions for
on the apparent radius of Geminga
are consistent with theoretical
predictions for
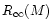 ,
based on
considered baryonic EOS of dense matter,
provided the neutron star
mass is above
,
based on
considered baryonic EOS of dense matter,
provided the neutron star
mass is above
 .
.
The value of the upper bound
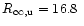 km,
obtained by Rutledge et al. (2001) for the
transient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139, is consistent with neutron star
km,
obtained by Rutledge et al. (2001) for the
transient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139, is consistent with neutron star
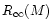 curves
in Fig. 2,
provided
curves
in Fig. 2,
provided
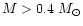 .
In the case of stiffest EOS
(with
.
In the case of stiffest EOS
(with
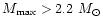 ), the value of
), the value of
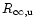 rules out high-mass neutron stars
with
rules out high-mass neutron stars
with
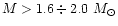 .
.
As for this writing, attempts to estimate the apparent
radius of RX J185635-3754 (Walter 2001)
are very model dependent.
Nevertheless, we are tempted to
make a following
comment.
Had we accepted the estimate
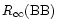 for
RX J185635-3754,
this object could be but a low-mass strange star. In order
to produce thermal photon spectrum, this low-mass strange star should
have been covered with a layer of normal matter, because a bare quark surface
would be a too weak photon emitter (Chmaj et al. 1991; Usov 2001).
One can only hope that more precise measurement of the photon spectrum
for this isolated neutron star will liberate us from such basic
ambiguities.
for
RX J185635-3754,
this object could be but a low-mass strange star. In order
to produce thermal photon spectrum, this low-mass strange star should
have been covered with a layer of normal matter, because a bare quark surface
would be a too weak photon emitter (Chmaj et al. 1991; Usov 2001).
One can only hope that more precise measurement of the photon spectrum
for this isolated neutron star will liberate us from such basic
ambiguities.
Detection of photons emitted from the surface of isolated neutron stars of known
distance can result in determination of the apparent neutron star radius,
 .
Due to significant space-time curvature, dependence of
.
Due to significant space-time curvature, dependence of  on
on stellar mass is quite different from that of the standard "coordinate'' radius
R. The very definition of
on
on stellar mass is quite different from that of the standard "coordinate'' radius
R. The very definition of  implies a lower bound, obtained
by Lattimer & Prakash (2001), of
implies a lower bound, obtained
by Lattimer & Prakash (2001), of
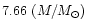 km.
At any M, this lower limit is very close
to the value of
km.
At any M, this lower limit is very close
to the value of  corresponding to the minimum R, calculated under
the condition of subluminal sound. Simultaneously, the actual
values of
corresponding to the minimum R, calculated under
the condition of subluminal sound. Simultaneously, the actual
values of  calculated at the maximum allowable mass are also close to this limit. For
moderately stiff and stiff EOS with
calculated at the maximum allowable mass are also close to this limit. For
moderately stiff and stiff EOS with
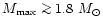 ,
the actual
value of
,
the actual
value of
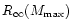 is less than one percent higher than the absolute
lower bound on
is less than one percent higher than the absolute
lower bound on  at this value of stellar mass.
at this value of stellar mass.
Most reliable observational estimates of  ,
obtained
for Geminga and transient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139,
lead to upper bounds on
,
obtained
for Geminga and transient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139,
lead to upper bounds on  ,
which are consistent with all considered baryonic EOS, provided the mass
of neutron star is above
,
which are consistent with all considered baryonic EOS, provided the mass
of neutron star is above
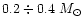 .
.
Acknowledgements
I am grateful to J. L. Zdunik for the reading of the manuscript and for
helpful remarks. I am also grateful to A. Potekhin for his precious help in
the preparation of figures.
This research
was partially supported by the KBN grant No. 5P03D.020.20.
-
Balberg, S., Lichtenstadt, I., & Cook, G. B. 1999,
ApJS, 121, 515
In the text
NASA ADS
-
Baldo, M., Bombaci, I., & Burgio, G. F. 1997, A&A, 328, 279
In the text
-
Bombaci, I. 1995, in Perspectives on Theoretical Nuclear Physics, ed. I. Bombaci, A.
Bonaccorso, A. Fabrocini, et al., 223
In the text
-
Bondi, H. 1964, Proc. Roy. Soc. A, 281, 39
-
Buchdahl, H. A. 1959,
Phys. Rev., 116, 1027
In the text
NASA ADS
-
Burderi, L., & King, A. R. 1998,
ApJ, 505, L135
In the text
NASA ADS
-
Caraveo, P. A., Bignami, G. F., Mignani, R., & Taff, L. G. 1996,
ApJ, 461, L91
NASA ADS
-
Chmaj, T., Haensel, P., & S
 ominski, 1991, Nucl. Phys. B, 24B, 40
In the text
ominski, 1991, Nucl. Phys. B, 24B, 40
In the text
-
Douchin, F., P., & Haensel, P. 2000, Phys. Lett. B, 485, 107
In the text
NASA ADS
-
Glendenning, N. K. 1992,
Phys. Rev. D, 46, 4161
In the text
NASA ADS
-
Glendenning, N. K. 2000,
Phys. Rev. Lett., 85, 1150
In the text
NASA ADS
-
Glendenning, N. K. 1997, Compact Stars: Nuclear Physics, Particle Physics
and General Relativity (Springer, New York)
In the text
-
Golden, A., & Shearer, A. 1999,
A&A, 342, L5
In the text
NASA ADS
-
Haberl, F., & Titarchuk, L. 1995,
A&A, 299, 414
In the text
NASA ADS
-
Haensel, P., Zdunik, J. L., & Schaeffer, R. 1986,
A&A, 160, 121
In the text
NASA ADS
-
Haensel, P., & Zdunik, J. L. 1989,
Nature, 340, 617
In the text
NASA ADS
-
Haensel, P., Lasota, J. P., & Zdunik, J. L. 1999,
A&A, 344, 151
In the text
NASA ADS
-
Kubis, S. 2001, Ph.D. Thesis, Jagellonian University (unpublished)
In the text
-
Lampton, M., Lieu, R., Schmitt, J. H. M. M., et al. 1997, ApJS, 108, 545
NASA ADS
-
Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426
In the text
NASA ADS
-
Li, X.-D., Bombaci, I., Dey, M., Dey, J., & van den Heuvel, E. P. J. 1999a,
Phys. Rev. Lett., 83, 3776
In the text
NASA ADS
-
Li, X.-D., Ray, S., Dey, J., Dey, M., & Bombaci, I. 1999b,
ApJ, 527, L51
In the text
NASA ADS
-
Lindblom, L. 1984, ApJ, 278, 364
NASA ADS
-
Olson, T. S. 2001, Phys. Rev. C, 63, 015802
-
Pandharipande, V. R., & Ravenhall, D. G. 1989, in Proc. NATO Advanced Research Workshop
on nuclear matter and heavy ion collisions, Les Houches, 1989,
ed. M. Soyeur et al. (Plenum, New York, 1989), 103
In the text
-
Psaltis, D., & Chakrabarty, D. 1999,
ApJ, 521, 332
In the text
NASA ADS
-
Rutledge, R. E., Bildsten, L., Brown, E. F., Pavlov, G. G., & Zavlin, V. E.,
ApJ, submitted [astro-ph/0105405]
In the text
-
Thorne, K. S. 1977,
ApJ, 212, 825
In the text
NASA ADS
-
Titarchuk, L. 1994,
ApJ, 429, 340
In the text
NASA ADS
-
Usov, V. V. 2001, ApJ, 550, L179
In the text
NASA ADS
-
Walter, F. M., Wolk, S. J., & Neuhäuser, R. 1996, Nature, 379, 233
NASA ADS
-
Walter, F. M., & Matthews, L. D. 1997, Nature, 389, 358
NASA ADS
-
Walter, F. M., & An, P. 1998, BAAS, 192, 50.04
-
Walter, F. M., An, P., Lattimer, J., & Prakash, M. 2000, in Highly Energetic Physical Processes and Mechanisms for Emission
from Astrophysical Plasmas, ed. P. C. H. Martens, S. Tsuruta, & M. A. Weber
(ASP Conf. Ser., San Francisco, ASP), IAU Symp., 195, 437
-
Walter, F. M. 2001, ApJ, 549, 433
In the text
NASA ADS
-
Weinberg, S. 1972, Gravitation and Cosmology: Principles and Applications
of the General Theory of Relativity (John Wiley & Sons, New York), Sect. 11.6
In the text
Copyright ESO 2001
![]() ,
depends on the star gravitational mass
in quite a different way than the standard coordinate
radius in the Schwarzschild metric, R.
We show that, for a broad set of equations
of state of dense matter,
,
depends on the star gravitational mass
in quite a different way than the standard coordinate
radius in the Schwarzschild metric, R.
We show that, for a broad set of equations
of state of dense matter,
![]() for the configurations with maximum allowable masses
is very close to
the absolute lower bound on
for the configurations with maximum allowable masses
is very close to
the absolute lower bound on ![]() at fixed
M,
resulting from the very definition of
at fixed
M,
resulting from the very definition of
![]() .
Also, the value of
.
Also, the value of ![]() at given M,
corresponding to the
maximum compactness (minimum R) of neutron star consistent with
general relativity and condition
at given M,
corresponding to the
maximum compactness (minimum R) of neutron star consistent with
general relativity and condition
![]() ,
is only 0.6% higher than this absolute
lower bound.
Theoretical predictions for
,
is only 0.6% higher than this absolute
lower bound.
Theoretical predictions for ![]() are compared with
existing observational estimates of the apparent radii of
neutron stars.
are compared with
existing observational estimates of the apparent radii of
neutron stars.
![]() km.
Therefore, because of a sizable spacetime curvature
close to neutron star, one has to distinguish between
the "true'' or "coordinate'' radius, R, which is the radial
coordinate of the stellar surface in the Schwarzschild
metric, and the "apparent radius'' (sometimes called
"radiation radius''),
km.
Therefore, because of a sizable spacetime curvature
close to neutron star, one has to distinguish between
the "true'' or "coordinate'' radius, R, which is the radial
coordinate of the stellar surface in the Schwarzschild
metric, and the "apparent radius'' (sometimes called
"radiation radius''), ![]() ,
as determined by a distant observer
studying radiation from neutron star surface.
,
as determined by a distant observer
studying radiation from neutron star surface.
![]() on neutron star mass for a broad set of equations of state
of dense matter. We discuss properties
of the theoretical
on neutron star mass for a broad set of equations of state
of dense matter. We discuss properties
of the theoretical
![]() curves,
and finally we confront theoretical calculations
with recent observational
estimates of apparent radii of neutron stars.
curves,
and finally we confront theoretical calculations
with recent observational
estimates of apparent radii of neutron stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3021F1.eps}\end{figure}](/articles/aa/full/2001/46/aah3021/Timg9.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3021F2.eps}\end{figure}](/articles/aa/full/2001/46/aah3021/Timg10.gif)
![]() (Buchdahl 1959; general proof can be found in Weinberg 1972).
This condition can rewritten as
(Buchdahl 1959; general proof can be found in Weinberg 1972).
This condition can rewritten as
![]() km.
A stronger condition is obtained if we additionally
require that sound speed within the star should
be subluminal:
km.
A stronger condition is obtained if we additionally
require that sound speed within the star should
be subluminal:
![]() (such a condition is necessary,
but not sufficient (Olson 2000), to respect
causality in a fluid medium).
The condition
(such a condition is necessary,
but not sufficient (Olson 2000), to respect
causality in a fluid medium).
The condition
![]() implies a lower
bound on R at a given M (Lindblom 1983; Haensel & Zdunik
1989; Lattimer et al. 1990; Glendenning 1992; Haensel et al. 1999; Glendenning 2000).
In what follows, we will use numerical values of the
absolute lower bound
implies a lower
bound on R at a given M (Lindblom 1983; Haensel & Zdunik
1989; Lattimer et al. 1990; Glendenning 1992; Haensel et al. 1999; Glendenning 2000).
In what follows, we will use numerical values of the
absolute lower bound
![]() km, as calculated
in Haensel et al. (1999); the older values obtained in
(Lattimer et al. 1990; Glendenning 1992) are slightly higher,
because of the assumed presence of an outer envelope (crust)
in neutron star models, while the value deduced from (Lindblom
1983) is not very precise (see Haensel et al. 1999).
km, as calculated
in Haensel et al. (1999); the older values obtained in
(Lattimer et al. 1990; Glendenning 1992) are slightly higher,
because of the assumed presence of an outer envelope (crust)
in neutron star models, while the value deduced from (Lindblom
1983) is not very precise (see Haensel et al. 1999).
![]() results from the
very definition of
results from the
very definition of ![]() (Lattimer & Prakash 2001).
Namely, the definition of
(Lattimer & Prakash 2001).
Namely, the definition of ![]() implies
implies
![]() .
Therefore, relative difference
between
.
Therefore, relative difference
between
![]() and the value corresponding
to minimum value of R at given M (assuming
and the value corresponding
to minimum value of R at given M (assuming
![]() ), can be estimated as
), can be estimated as
![]() ,
which is
consistent with our exact result.
,
which is
consistent with our exact result.
![]() )
upper bound on x at
given M is slightly larger than 2/3, the actual maximum
values of x for various EOS, which are reached
at
)
upper bound on x at
given M is slightly larger than 2/3, the actual maximum
values of x for various EOS, which are reached
at
![]() for these EOS, are lower than 2/3. However,
if we restrict to medium stiff and stiff EOS, with
for these EOS, are lower than 2/3. However,
if we restrict to medium stiff and stiff EOS, with
![]() ,
then
,
then
![]() ,
which is only 0.06 lower than 2/3. We may therefore
expect, that for these EOS, which actually constitute majority
of models in Figs. 1, 2,
,
which is only 0.06 lower than 2/3. We may therefore
expect, that for these EOS, which actually constitute majority
of models in Figs. 1, 2,
![]() will be only
will be only
![]() larger than
larger than
![]() .
This explains, why for these EOS the
points at
.
This explains, why for these EOS the
points at
![]() are so close to the
are so close to the
![]() line in Fig. 2.
line in Fig. 2.
![]() km,
independently of neutron star mass. Our Fig. 2 confirms
this "practical lower bound'' on
km,
independently of neutron star mass. Our Fig. 2 confirms
this "practical lower bound'' on ![]() .
On the contrary, there is
no lower limit on
.
On the contrary, there is
no lower limit on ![]() for bare strange stars, whose
size can be as small as hundred fermis. For strange stars covered
with a layer of normal matter, minimum radius is reached at
for bare strange stars, whose
size can be as small as hundred fermis. For strange stars covered
with a layer of normal matter, minimum radius is reached at
![]() ,
and for a maximally thick crust it is
about 5-6 km (see, e.g., Glendenning 1997).
,
and for a maximally thick crust it is
about 5-6 km (see, e.g., Glendenning 1997).
![]() km
at the
km
at the ![]() confidence level. However,
if one uses the black body spectrum model, assuming
spherical symmetry, one gets
an abnormally small upper bound,
confidence level. However,
if one uses the black body spectrum model, assuming
spherical symmetry, one gets
an abnormally small upper bound,
![]() km (Walter 2001; notice
that we use results at the
km (Walter 2001; notice
that we use results at the ![]() confidence level).
Clearly, these results are very preliminary, and we have still to wait
for more reliable and less model dependent determinations of
confidence level).
Clearly, these results are very preliminary, and we have still to wait
for more reliable and less model dependent determinations of ![]() for this isolated neutron star.
for this isolated neutron star.
![]() km,
obtained by Rutledge et al. (2001) for the
transient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139, is consistent with neutron star
km,
obtained by Rutledge et al. (2001) for the
transient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139, is consistent with neutron star
![]() curves
in Fig. 2,
provided
curves
in Fig. 2,
provided
![]() .
In the case of stiffest EOS
(with
.
In the case of stiffest EOS
(with
![]() ), the value of
), the value of
![]() rules out high-mass neutron stars
with
rules out high-mass neutron stars
with
![]() .
.
![]() for
RX J185635-3754,
this object could be but a low-mass strange star. In order
to produce thermal photon spectrum, this low-mass strange star should
have been covered with a layer of normal matter, because a bare quark surface
would be a too weak photon emitter (Chmaj et al. 1991; Usov 2001).
One can only hope that more precise measurement of the photon spectrum
for this isolated neutron star will liberate us from such basic
ambiguities.
for
RX J185635-3754,
this object could be but a low-mass strange star. In order
to produce thermal photon spectrum, this low-mass strange star should
have been covered with a layer of normal matter, because a bare quark surface
would be a too weak photon emitter (Chmaj et al. 1991; Usov 2001).
One can only hope that more precise measurement of the photon spectrum
for this isolated neutron star will liberate us from such basic
ambiguities.
![]() ,
obtained
for Geminga and transient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139,
lead to upper bounds on
,
obtained
for Geminga and transient X-ray source
CXOU 132619.7-472910.8 in
NGC 5139,
lead to upper bounds on ![]() ,
which are consistent with all considered baryonic EOS, provided the mass
of neutron star is above
,
which are consistent with all considered baryonic EOS, provided the mass
of neutron star is above
![]() .
.