A&A 380, 359-372 (2001)
DOI: 10.1051/0004-6361:20011388

Search for non-helical disc dynamos in simulations

R. Arlt1 - A. Brandenburg2,3


1 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
2 - NORDITA, Blegdamsvej 17, 2100 Copenhagen Ø, Denmark
3 - Department of Mathematics, University of Newcastle upon Tyne, NE1 7RU, UK

Received 2 July 2001 / Accepted 1 October 2001

Abstract
The origin of large scale magnetic fields in accretion discs is investigated. Using global three-dimensional simulations of accretion disc turbulence, a recent suggestion of Vishniac & Cho (2001, ApJ 550, 752) is re-examined, according to which large scale fields in accretion discs could be understood without explicitly invoking the usual helicity effect. Particular emphasis is placed on a certain correlation between vorticity and azimuthal velocity gradient which has been predicted to drive large scale dynamo action, independent of the presence or absence of kinetic helicity. In the global disc simulations two types of behaviours are found: those which do show this type of velocity correlation and those which do not. The former ones are typically also the cases where the resistivity is larger. The latter ones show signs typical of dynamo action based on the usual helicity effect. In the idealized simulations without rotation and just shear the above correlation is found to be particularly strong. In both cases there is, as expected, a systematic flux of magnetic helicity through the midplane. However, very little magnetic helicity leaves the domain through the top and bottom boundaries. The idealized simulations reveal that much of this systematic flux comes from the rotational component of the helicity flux and does not contribute to its divergence.

Key words: MHD - turbulence


1 Introduction

A number of different simulations have now established the possibility to generating strong large scale magnetic fields from turbulent motions (Glatzmaier & Roberts 1995; Brandenburg et al. 1995; Ziegler & Rüdiger 2000; Brandenburg 2001, hereafter referred to as B2001). Although most of these simulations were devised to explain magnetism in real astrophysical bodies, it remains debatable whether or not the mechanisms that are at work in those simulations are also those that are responsible for the generation of large scale fields in astrophysical bodies. Up to modestly high magnetic Reynolds numbers, currently accessible to simulations, the by far strongest large scale dynamo effect is based on kinetic helicity of the flow. This effect is described in standard text books (e.g. Moffatt 1978; Krause & Rädler 1980), and is closely related to the inverse cascade of magnetic helicity (Frisch et al. 1975; Pouquet et al. 1976). The reason why one may suspect problems with such mechanisms in astrophysical settings is that they tend to produce large scale magnetic fields that are helical and that, owing to magnetic helicity conservation, such helical fields can only be built up slowly on a resistive time scale (B2001). Of course, shear (or differential rotation) contributes strongly to the dynamo and enhances the growth rate and final field strength, but this reduces the resistively limited saturation time of the dynamo only by a factor of 10-100 for the Sun (Brandenburg et al. 2001, hereafter referred to as BBS2001), or perhaps somewhat more for accretion discs. Typical growth times will still be of the order of $10^6\,{\rm yr}$. Open boundaries also tend to reduce the time scale, but this is typically at the expense of lowering the final field strength (Brandenburg & Dobler 2001, hereafter referred to as BD2001).

The "helicity problem'' was originally identified in attempts to understand the "catastrophic'' magnetic feedback on turbulent transport coefficients such as turbulent diffusivity (Cattaneo & Vainshtein 1991) and the alpha-effect (Vainshtein & Cattaneo 1992; Cattaneo & Hughes 1996). Although the original arguments did not invoke magnetic helicity, subsequent work by Bhattacharjee & Yuan (1995) and Gruzinov & Diamond (1995) related the quenching to helicity conservation. Furthermore, models using the proposed quenching formulae reproduce the field evolution in the simulations and those predicted by magnetic helicity conservation extremely well (B2001, Fig. 21). Blackman & Field (2000) pointed out that catastrophic quenching of the $\alpha$-effect is peculiar to flows in periodic domains where there is no loss of magnetic helicity. It is important to emphasise that the helicity problem applies to the non-kinematic stage of dynamo activity, without explicitly invoking the concept of $\alpha$-effect dynamos.

A possible way out of the helicity problem is to produce large scale fields without invoking kinetic helicity of the flow. That helicity is not crucial for large scale dynamo action was already known since the work of Gilbert et al. (1988), who found that flows that only lack parity invariance are already capable of producing large scale dynamo action via an $\alpha$-effect. The problem has been investigated further in a recent paper by Zheligovsky et al. (2001), who found that even parity invariant flows are capable of large-scale dynamo action. In that case the dynamo works not via an $\alpha$-effect, but through a negative turbulent magnetic diffusivity effect. A related issue was brought up by Vishniac & Cho (2001, hereafter referred to as VC2001) in an attempt to produce large scale non-helical dynamo action that would survive in the large magnetic Reynolds number limit. Their mechanism requires the presence of a certain correlation between the azimuthal component of the vorticity and the azimuthal gradient of the vertical velocity. If that is the case they predict the presence of a strong vertical magnetic helicity current upwards. This could then drive a field-aligned electromotive force that is proportional to the divergence of this magnetic helicity current. This form of the electromotive force would conserve magnetic helicity and was first proposed by Bhattacharjee & Hameiri (1986).

The purpose of the present paper is to assess the viability and properties of the mechanism proposed by VC2001 using numerical simulations. The required correlation between the azimuthal derivative of the vertical velocity and the azimuthal component of the vorticity is expected to occur in the presence of shear. It should thus be especially important in accretion discs. We therefore begin by determining the presence of such a correlation using global simulations of accretion discs (Sect. 2).

However, in order to isolate the proposed effect from the ordinary helicity effect, which is always present because of rotation, we have also carried out some idealized simulations of forced turbulence with shear, but no rotation. The latter is expected to promote the correlation anticipated by VC2001, but would not lead to kinetic helicity in the flow. Of course, real systems do rotate and have therefore also kinetic helicity. However, at small and modestly large magnetic Reynolds numbers the dynamo effect based on kinetic helicity is so much more powerful than other mechanisms that it is necessary to suppress it artificially if one wants to study it in isolation. This will be done in Sect. 3.

For both the global disc simulations as well as the idealized model we also determine the resulting helicity fluxes, which turn out to be small and fluctuating about zero, however. We conclude in Sect. 4 with summarizing remarks and speculations concerning the viability of conventional helicity-driven dynamos.

   
2 A global disc simulation

2.1 Description of the model

In order to study the possibility of dynamo action of the form envisaged by VC2001 we use the recent global hydromagnetic accretion disc simulation by Arlt & Rüdiger (2001). Unlike earlier global MHD disc simulations by Armitage (1998) and Hawley (2000), the radial extent does here not cover the entire disc, so inflow and outflow boundary conditions have to be applied in the radial direction. A possible advantage of this is that a larger spatial resolution per unit length is now possible. Like Armitage (1998), Arlt & Rüdiger (2001) also use the ZEUS-3D code which, in turn, is very similar to the code used by Hawley (2000). A version of ZEUS that is close to the one used by Arlt & Rüdiger is described by Stone & Norman (1992a,b) and Stone et al. (1992). The equations that are being solved are

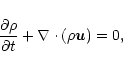\begin{displaymath}\frac{\partial\rho}{\partial t}+\nabla\cdot(\rho {\vec u})=0, \end{displaymath} (1)


 \begin{displaymath}\frac{\partial{\rho \vec u}}{\partial t}+\nabla\cdot(\rho{\ve... ...ec u}) =-\nabla p-\rho \nabla\Phi+{\vec J}\times {\vec B}+..., \end{displaymath} (2)


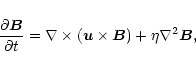\begin{displaymath}\frac{\partial {\vec B}}{\partial t}=\nabla\times({\vec u} \times {\vec B}) +\eta\nabla^2\vec B, \end{displaymath} (3)

where $\rho$, ${\vec u}$, and ${\vec B}$ are density, velocity, and magnetic field, respectively; p is the pressure, $\Phi$ is the gravitational potential (solely from a central mass $M_\ast$), ${\vec J}=\vec{\nabla}\times{\vec B}/\mu_0$ is the current density, $\mu_0$ is the vacuum permeability, and $\eta $ is a constant magnetic diffusivity as implemented by D. Elstner, Potsdam. The dots on the right hand side of Eq. (2) indicate the presence of numerical viscosity for removing energy at small scales. No energy equation appears as we deal with an isothermal model where $p=c_{\rm s}^2\rho$. The sound speed, $c_{\rm s}$, is 7% of the Keplerian orbital velocity in the middle of the simulated ring. Cylindrical polar coordinates, $(r,\phi,z)$, are used and the entire azimuthal range from $\phi =0$ to $2\pi$is considered. The model covers vertically the range from z=-1 to +1which corresponds to 1.5-3 pressure scale heights, depending on the value of r.

In most of the models we apply closed boundary conditions for the flow on the z-boundaries, with the magnetic field penetrating the boundaries at right angles. One of the models (Model IX; see below) uses open boundaries in the z-direction. The inner radial boundary is open in all models; the mass flux is monitored on the inner boundary and fed back into the domain on the outer radial boundary with either a homogeneous or a Gaussian infall pattern for the density. The maximum infall velocity is constant in time and over zand is either 10-2 or 10-3 of the sound speed. The $\phi $-direction has periodic boundaries.

The initial configuration contains a relaxed disk with a slow outflow on the inner boundary due to numerical viscosity. The density scale height varies between $H_\rho=0.33$ and 0.66 between the radii r=4 and 6. In the absence of magnetic fields the system is hydrodynamically stable; this was verified numerically for up to 30 orbits without producing any visible changes at the end of the simulation. The magnetic field imposed to this configuration is merely a vertical Bz field with zero net flux through the vertical surfaces.

Table 1 summarizes the global runs used for this analysis. The same numbering of the models as in Arlt & Rüdiger (2001) is used. Two of the simulations are new on this list: Model Va is a repetition of the configuration of Model V, but with an initial magnetic field of mixed parity. The parity of the Bz field was zero at the beginning as was the parity of the emerging $B_\phi$ field. All other models start with an initial field parity of -1 (antisymmetry). Model IX is similar to Model V, but uses outflow boundary conditions for the vertical direction instead of closed boundaries. In Table 1 the magnetic diffusivity $\eta $ is also given for all runs. Since the considerations presented here were made after the actual production runs had been performed, only a limited number of fully three-dimensional snapshots were available, which is the reason for a relatively coarse sampling.


 

 
Table 1: Global simulations used for the analysis. The duration $t_{\rm end}$ of each run is given in orbits. The infall velocities are given in units of the sound speed $c_{\rm s}$. Symmetries refer to the type of initial Bz fields. The kinetic energy is based on the poloidal velocities only and is an average over the last two orbits.
Run Grid (z, r, $\phi $) Radial boundary condition r-range $T_{\rm orb}$ $t_{\rm end}$ Init. parity $\eta $
II $31\times61\times351$ homogeneous accretion $u_{\rm in}=-0.001c_{\rm s}$ 4.0-6.0 0.159 14.7 antisym. 0.001
III $31\times61\times351$ homogeneous accretion $u_{\rm in}=-0.01c_{\rm s}$ 4.0-6.0 0.159 9.7 antisym. 0.001
VIII $31\times61\times351$ homogeneous accretion $u_{\rm in}=-0.001c_{\rm s}$ 3.0-7.0 0.103 22.4 antisym. 0.001
V $31\times61\times351$ Gaussian accretion $u_{\rm in}=-0.001c_{\rm s}$ 4.0-6.0 0.159 18.4 antisym. 0.01
Va $31\times61\times351$ Gaussian accretion $u_{\rm in}=-0.001c_{\rm s}$ 4.0-6.0 0.159 12.4 mixed 0.01
VI $31\times61\times351$ Gaussian accretion $u_{\rm in}=-0.01c_{\rm s}$ 4.0-6.0 0.159 16.1 antisym. 0.01
IX $31\times61\times351$ Gaussian accretion $u_{\rm in}=-0.01c_{\rm s}$, z open 4.0-6.0 0.159 16.9 antisym. 0.01


2.2 The Vishniac-Cho correlation

In the theory of VC2001 large scale magnetic field generation is possible when there is a finite value of the correlation

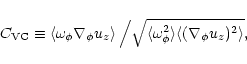\begin{displaymath}C_{\rm VC}\equiv\left\langle\omega_\phi\nabla_\phi u_z\right\... ...\langle\omega_\phi^2\rangle\langle(\nabla_\phi u_z)^2\rangle}, \end{displaymath} (4)

where $\nabla_\phi\equiv r^{-1}\partial_\phi$, and $\vec\omega={\rm curl} \, {}\vec u$ is the vorticity. We begin by showing $C_{\rm VC}$ as time series; see Fig. 1. The temporal averages of these time series (excluding the initial five snapshots of each of the runs which correspond to a lapse of 2 to 4 orbits) are listed in Table 2. We found that the simulations can tentatively be divided into two groups: the first group comprises the low-$\eta $ models showing decreasing correlations (left column of Fig. 1), the other group has modestly large values of $\eta $ and is characterized by a non-vanishing $C_{\rm VC}$ that is on the average about 5 to 10 times larger than in the low-$\eta $ cases (right column of Fig. 1).

A scatter plot of $\nabla _\phi u_z$ versus $\omega _\phi $ is shown in Fig. 2 for the data of a snapshot from Model V, which has the largest (negative) correlation. The plot contains points in the $(z,\phi)$ plane at r=5which is in the middle of the computational domain. The plot looks rather noisy, but one sees nevertheless a slight negative correlation.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{h2980f1.ps}\end{figure} Figure 1: Correlation of $\nabla _\phi u_z$ versus $\omega _\phi $in global disc simulation; here of Models II and III (left), as well as Models V and Va (right).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{h2980f2.ps}\end{figure} Figure 2: Scatter plot of $\nabla _\phi u_z$ with $\omega _\phi $for a snapshot of Model V at $t=14.8\,T_{\rm orb}$. The straight line gives the least square fit, which has a correlation coefficient of $C_{\rm VC}=-0.13$ in this example.
Open with DEXTER

2.3 Resulting magnetic field configurations

We first discuss the overall field structure. Horizontal slices of the field at z=-0.39are shown for Models VIII (less resistive) and V (more resistive) in Figs. 3 and 4, respectively. The former figure exhibits a spiral pattern whilst the latter is rather dominated by intermediate scale structures or eddies, which is probably directly a consequence of the larger magnetic diffusivity in that case.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{h2980f3.ps}\end{figure} Figure 3: Projection of magnetic field vectors in a horizontal slice at z=-0.39of Model VIII after 19.9 orbits.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{h2980f4.ps}\end{figure} Figure 4: Projection of magnetic field vectors in a horizontal slice at z=-0.39of Model V after 17.6 orbits.
Open with DEXTER

Next we derive a number of averaged quantities from the simulations. Throughout this section we denote azimuthal averages by an overbar, e.g. $\overline{\vec{B}}=\int\vec{B}\,{\rm d} {}\phi/2\pi$. In Fig. 5 are shown the energies contained in the large scale field, $M_{\rm mean}=\int\overline{\vec{B}}{}^2{\rm d} {}V/(2\mu_0)$, and the energies of the remaining fluctuations, $M_{\rm fluct}=\int\vec{b}{}^2{\rm d} {}V/(2\mu_0)$, where $\vec{b}=\vec{B}-\overline{\vec{B}}$. Like in Fig. 1, the temporal evolution behaviours separate into the same two groups: the low-$\eta $ (less resistive) runs which show significant energies in the large scale field, and models with larger $\eta $ that are more resistive, but better able to generate fluctuation energies of at least 50% of the large scale energy. We note that there is one model (Model IX, not shown) where at the end the energy of magnetic fluctuations exceeds the large scale magnetic energy. The fact that the energy of the mean field is typically larger than that of the fluctuating field is somewhat surprising. A possible reason could be that the memory of the initial mean field has not yet been lost. It is also possible, however, that it is because of the global geometry and the shear that a strong large scale field is more easily established when the magnetic Reynolds number is large.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{h2980f5.ps}\end{figure} Figure 5: Comparison of energies in the large scale ($\phi $-averaged) magnetic field (solid lines) and the small-scale magnetic field (dotted lines) for Models II and III (left), as well as Models V and Va (right). Note that the fluctuations are larger in the cases where $\eta $ is larger.
Open with DEXTER

Another distinction between the two groups of runs is given by the magnetic Taylor microscale, $\lambda _{\rm M}$, which we define here via $\lambda_{\rm M}^2=\langle\vec{B}^2\rangle/\langle\mu_0^2\vec{J}^2\rangle$. In Fig. 6 we show the value of $\lambda _{\rm M}$for the same four models as in Fig. 1. The quantity $2\pi\lambda_{\rm M}$ characterized the typical thickness of flux structures. Its significance is that in runs with dynamo action $\lambda _{\rm M}$ tends to increase with time until it reaches saturation (e.g. Brandenburg et al. 1996). Conversely, when the field is amplified just by field compression the value of $\lambda _{\rm M}$ decreases somewhat with time. This is what happened in the more resistive runs ($\eta=0.01$). These were actually the runs that did show evidence for a finite Vishniac-Cho correlation. In contrast, the less resistive runs ( $\eta=0.001$) do not show any such trend.

A useful quantity for assessing the importance of helicity in the large scale field is to look at the nondimensional quantity

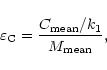\begin{displaymath}\varepsilon_{\rm C}={C_{\rm mean}/k_1\over M_{\rm mean}}, \end{displaymath} (5)

where $C_{\rm mean}=\int\overline{\vec{J}}\cdot\overline{\vec{B}}\,{\rm d} {}V$is the current helicity of the mean field. In BD2001 the value of $\varepsilon\rm _C$ was found to be of order unity (between 1-2) for the models with a halo. In Fig. 7 we show the value of $\varepsilon\rm _C$for the global accretion disc runs. The less resistive models show negative current helicity whilst the more resistive ones show vanishing or positive current helicity toward the end of the run. In any case, the values of $\vert\varepsilon\rm _C\vert$ are smaller compared with the models studied in BD2001 where $\vert\varepsilon_{\rm C}\vert={\cal O}(1)$. This is not surprising, because in BD2001 the kinetic helicity was close to the maximum value, which would be an unrealistic assumption for any astrophysical body.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{h2980f6.ps}\end{figure} Figure 6: Comparison of the magnetic Taylor microscale $\lambda _{\rm M}$ for Models II and III (left), as well as V and Va (right).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{h2980f7.ps}\end{figure} Figure 7: Evolution of the nondimensional large-scale current helicity parameter (upper disc plane) for Models II and III (left), as well as Models V and Va (right).
Open with DEXTER

We now discuss the sign of $\varepsilon_{\rm C}$. In BD2001 the sign of the kinetic helicity was positive, and so was the sign of the small scale current helicity. The sign of the large scale current helicity is typically opposite, i.e. negative in that case. In the present case, where we consider the upper disc plane, the kinetic helicity is negative, so we would expect a positive value of $\varepsilon_{\rm C}$, which is not what we find (except for one of the more resistive cases, Model Va). However, the unusual sign of $\overline{\vec{J}}\cdot\overline{\vec{B}}$ is primarily related to an unusual sign of the effective $\alpha$ found in the present simulations. This is because in the steady state the energy-generating effect, $\alpha\overline{\vec{B}}^2$, must balance turbulent diffusion, $\eta_{\rm T}\overline{\vec{J}}\cdot\overline{\vec{B}}$. Therefore the sign of $\alpha$ must coincide with the sign of $\overline{\vec{J}}\cdot\overline{\vec{B}}$. In discs, however, the sign of $\alpha$ is negative (in the upper disc plane), so $\overline{\vec{J}}\cdot\overline{\vec{B}}$ must also be negative, and hence $\varepsilon_{\rm C}$ is negative, as observed. The perhaps most convincing explanation for the negative $\alpha$ is that intense parts of a flux tube contract (to maintain pressure balance along field lines), but are also most buoyant. If this contraction is stronger than the expansion associated with the rise into a less dense medium, $\alpha$ will be negative (Brandenburg 1998, see also Rüdiger & Pipin 2000).

We shall now return to the question of whether there is any evidence for the presence of a dynamo effect as envisaged by VC2001. We therefore need to look at the possibility of magnetic helicity fluxes through the domain.


 

 
Table 2: Results after the magnetic field was switched on. All values are temporal averages excluding the first five snapshots (about 2 to 4 orbital periods). The first group of models (II, III, and VIII) comprises less resistive runs, whilst the second group (Models V, Va, VI, and IX) refers to the more resistive ones.
Run $u_{\rm rms}$ $E_{\rm kin}$ $2\eta C_{\rm mean}/(\mu_0 u_{\rm rms}E_{\rm kin})$ $2\eta C_{\rm fluc}/(\mu_0 u_{\rm rms} E_{\rm kin})$ $Q_{\rm mean}/$ slope $C_{\rm VC}$
      North South North South $(\mu_0 u_{\rm rms} E_{\rm kin})$    
II 3.7 $3.6\times 10^5$ $-7.8\times10^{-6}$ $+1.5\times10^{-6}$ $-5.0\times10^{-6}$ $+5.6\times10^{-6}$ +0.00006 -0.0024 -0.012
III 7.5 $6.9\times 10^5$ $-4.0\times10^{-6}$ $+9.3\times10^{-7}$ $-2.9\times10^{-6}$ $+2.3\times10^{-6}$ +0.00007 -0.0005 +0.003
VIII 7.6 $4.9\times 10^5$ $-5.4\times10^{-7}$ $+3.5\times10^{-7}$ $-2.8\times10^{-6}$ $+3.5\times10^{-6}$ +0.00029 -0.0018 -0.005
V 3.8 $1.4\times 10^6$ $-2.2\times10^{-5}$ $+3.9\times10^{-5}$ $-2.0\times10^{-7}$ $+1.1\times10^{-5}$ -0.00013 -0.0086 -0.050
Va 5.3 $3.9\times 10^5$ $+6.9\times10^{-5}$ $+6.6\times10^{-5}$ $+2.4\times10^{-4}$ $-2.6\times10^{-5}$ -0.00038 -0.0096 -0.086
VI 4.0 $1.7\times 10^6$ $-5.0\times10^{-5}$ $+3.3\times10^{-5}$ $-5.0\times10^{-6}$ $+2.1\times10^{-6}$ -0.00157 $-0.012\phantom{0}$ -0.060
IX 2.9 $2.9\times 10^5$ $-1.9\times10^{-4}$ $+1.6\times10^{-4}$ $-1.4\times10^{-4}$ $+1.9\times10^{-4}$ +0.00007 -0.0053 -0.047


2.4 Magnetic helicity flux

In VC2001 it was argued that, although the overall magnetic helicity is small, there could still be a significant (spatially constant) flux of magnetic helicity vertically through the domain. The numerical procedures for evaluating gauge invariant magnetic helicity and magnetic helicity flux in cylindrical geometry with open boundaries in the r and zdirections are not yet available. However, for the present purpose most important is the contribution from the large scales. If we adopt horizontal averages (over r and $\phi $), the mean fields are one-dimensional and the mean magnetic vector potential can be obtained simply by integration. The corresponding magnetic helicity and magnetic helicity fluxes of the mean field can then be calculated quite easily (see the appendix of BD2001). In Fig. 8 we plot, for the four models, the magnetic helicity flux, $Q_{\rm mean}=Q_{\rm mean}^{(2)}-Q_{\rm mean}^{(1)}$, out of the domain through the two boundaries at z=z1 and z2. Here, $Q_{\rm mean}^{(1)}$ and $Q_{\rm mean}^{(2)}$ denote the upward helicity fluxes at z=z1and z2, respectively; see Appendix A.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2980f8.ps}\end{figure} Figure 8: Estimates of the magnetic helicity flux $Q_{\rm mean}$ out through the vertical boundaries. The dotted lines give the zero value.
Open with DEXTER

The mean outward flux, expressed in "dynamical'' units, $\mu_0 u_{\rm rms} E_{\rm kin}$, is small ( ${\sim}10^{-4}$). A small outward flux was also found in the case of helical turbulence (BD2001). Furthermore, the signs tend to be different in the cases where $\eta $ is small ( $Q_{\rm mean}>0$ for $\eta=10^{-3}$) and where it is larger ( $Q_{\rm mean}<0$ for $\eta=10^{-2}$). It is doubtful that this result indicates any significant departure from zero, because the magnetic helicity on the two sides about the midplane of the disc are expected to be different. Thus, equal losses or gains on the two surfaces (z=z1 and z2) should result in zero net magnetic helicity flux. It is therefore now necessary to determine the mean upward fluxes of magnetic helicity on the two sides, $Q_{\rm mean}^{(2)}$ and $Q_{\rm mean}^{(1)}$. Its average is denoted by $Q_{\rm mean}^{\rm (up)}={\textstyle{1\over2}}[Q_{\rm mean}^{(2)}+Q_{\rm mean}^{(1)}]$. If there is indeed a systematic upwards flux through the two boundaries, this quantity should be finite and positive. As expected, this quantity turns out to be small. In order to check whether this is the result of some cancellation, we need to consider the magnetic helicity fluxes in smaller sub-volumes.

A difficulty associated with calculating magnetic helicity and magnetic helicity fluxes separately in two sub-volumes (e.g., above and below the midplane) is that we want to make sure that the sum of the two is equal to the total magnetic helicity calculated earlier. This will be the case provided the magnetic helicity in each sub-domain is calculated using the same gauge that also made the helicity of the full domain gauge invariant. This then also allows one to calculate the integrated magnetic helicity fluxes out of each sub-domain. The corresponding formulae are given in Appendix B.

It turns out that the helicity fluxes out of each sub-volume are actually large but of opposite sign. This means that there is actually a large magnetic helicity flux through the midplane, but not through the upper and lower boundaries. Having fixed the gauge such that $\int\overline{\vec{A}}\cdot\overline{\vec{B}}\,{\rm d} {}z$ is equal to the helicity of BD2001 for the full domain, we can also calculate the local magnetic helicity fluxes. We denote these by $Q_{\rm mean}^{\rm (mid)}$ (if evaluated at the midplane), or by $Q_{\rm mean}^{(z)}$ (if calculated for all values of z). In Fig. 9 we plot $Q_{\rm mean}^{\rm (mid)}$ and compare with the averaged boundary fluxes $Q_{\rm mean}^{\rm (up)}$. It turns out that $Q_{\rm mean}^{\rm (mid)}$ is indeed mostly positive, as predicted by VC2001, but this flux is not sustained all the way to the boundaries: $Q_{\rm mean}^{\rm (up)}$ is virtually zero by comparison. An exception is Run Va, where $Q_{\rm mean}^{\rm (mid)}$shows large variations about zero and $Q_{\rm mean}^{\rm (up)}$ begins to deviate systematically from zero. (We recall that this is the run where the initial field had mixed parity.)


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{h2980f9.ps} \end{figure} Figure 9: Estimates of the integrated magnetic helicity fluxes at the midplane, $Q_{\rm mean}^{\rm (mid)}$, (solid line) and on the boundaries, $Q_{\rm mean}^{\rm (up)}$ (dotted line).
Open with DEXTER

In order to see whether the magnetic helicity flux at the midplane is typical of the entire interior of the simulation domain, we plot in Fig. 10 the vertical distribution of the magnetic helicity flux, which was derived from horizontal averages of field and flow and then averaged in time (again excluding the first 2 to 4 orbits). Figure 10 shows that a positive (i.e. upwards) flux of magnetic helicity is indeed typical of the interior of the entire domain, and that it vanishes only near the boundaries. Thus the boundaries seem to play an important role, which may of course be unrealistic. We note, however, even Model IX with open boundaries does show a rapid drop of magnetic helicity flux near the z-boundaries. Clearly, an abrupt change of this flux implies generation and destruction of magnetic helicity near the vertical boundaries.

To summarize the global disc simulations, the correlation anticipated by VC2001 is present, provided the magnetic diffusivity is not too small. If the magnetic diffusivity is smaller, the magnetic field tends to be stronger and can become more important and may hence be able to suppress this correlation. Nevertheless, these are also the cases which show most clearly a systematic magnetic helicity flux within the simulation domain, even though it is unable to leave or enter it through the boundaries. It is difficult to say whether the effect of VC2001 was really responsible for the field generation found in the disc simulations. We recall that in the present simulations there is also some evidence for a $\alpha$-effect, although it is based on a rather noisy correlation between the turbulent electromotive force and the mean field; see Arlt & Rüdiger (2001). In the following section we isolate the VC-effect by studying a more idealized model with no net helicity. This model also allows for longer runs and therefore clearer statistics.

   
3 An idealized model with shear and stratification, but no rotation nor helicity

In order to study the effect proposed by VC2001 in isolation we need to suppress artificially the ordinary dynamo effect due to kinetic helicity of the flow. Following VC2001 the crucial factor that is necessary for causing the anticipated correlation is shear, but not rotation. To check this we have used a simulation of externally driven turbulence with zero net helicity. This is done by using the forcing function of B2001, but with helicity whose sign changes randomly. In addition, the model is supplemented by the effects of sinusoidal shear (as in BBS2001) and vertical stratification with a conducting halo above a turbulent layer (as in BD2001).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2980f10.ps} \end{figure} Figure 10: Vertical distribution of the estimates of the upward magnetic helicity flux $Q_{\rm mean}^{\rm (up)}$ through planes at various locations z (negative sign means downward). The values at each zare averages over time, excluding the first five snapshots of the simulations.
Open with DEXTER

3.1 Description of the model

We solve the isothermal compressible MHD equations for the logarithmic density $\ln\rho$, the velocity $\mbox{\boldmath$u$ } {}$, and the magnetic vector potential $\vec{A}$,

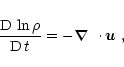\begin{displaymath}{{\rm D} \, {}\ln\rho\over{\rm D} \, {}t}=-\mbox{\boldmath$\nabla$ } {}\cdot\mbox{\boldmath$u$ } {}, \end{displaymath} (6)


 \begin{displaymath}{{\rm D} \, {}\mbox{\boldmath$u$ } {}\over{\rm D} \, {}t}=-c_... ...la$ } {}\cdot\mbox{\boldmath$u$ } {})+\mbox{\boldmath$f$ } {}, \end{displaymath} (7)


 \begin{displaymath}{\partial\vec{A}\over\partial t}=\mbox{\boldmath$u$ } {}\time... ...\mu_0\mbox{\boldmath$J$ } {}-\mbox{\boldmath$\nabla$ } {}\phi, \end{displaymath} (8)

where ${\rm D}/{\rm D}t=\partial/\partial t+\mbox{\boldmath$u$ } {}\cdot\mbox{\boldmath$\nabla$ } {}$ is the advective derivative, $\mbox{\boldmath$B$ } {}=\mbox{\boldmath$\nabla$ } {}\times\vec{A}$ is the magnetic field, and

\begin{displaymath}\mbox{\boldmath$f$ } {}=\mbox{\boldmath$f$ } {}_{\rm turb}+\mbox{\boldmath$f$ } {}_{\rm shear}+\mbox{\boldmath$g$ } {} \end{displaymath} (9)

is the sum of a random forcing function, $\mbox{\boldmath$f$ } {}_{\rm turb}$ (specified in B2001), a sinusoidal shear profile, $\mbox{\boldmath$f$ } {}_{\rm shear}=S_0(\mu/\rho)\hat{\mbox{\boldmath$y$ }} {}\sin x$, and a periodic gravity potential, $\mbox{\boldmath$g$ } {}={\textstyle{1\over2}}g_0\hat{\mbox{\boldmath$z$ }} {}\sin(z/2)$. In all calculations we assume the gauge $\phi =0$ (vanishing electrostatic potential), but for some of the analysis we also adopt the gauge $\mbox{\boldmath$\nabla$ } {}\cdot\vec{A}=0$. Instead of the dynamical viscosity $\mu$ ( $=\mbox{const.}$) we will in the following refer to $\nu\equiv~\mu/\rho_0$, where $\rho_0$ is the mean density in the domain ( $\rho_0=~\mbox{const.}$ owing to mass conservation).

We use nondimensional units where $c_{\rm s}=k_1=\rho_0=\mu_0=1$. Here, $c_{\rm s}=\mbox{const}$ is the isothermal sound speed, k1 the smallest wavenumber of the two horizontal directions (so its size is $2\pi$ in the horizontal direction). The vertical extent of the domain is $4\pi$. Periodic boundary conditions are adopted in all three directions. The wavenumber of the forcing is $k=k_{\rm f}=5$. As in BBS2001 the forcing amplitude is f0=0.01 and the nominal shear is $S_0\equiv\vert\partial u_y/\partial x\vert _{\max}=1$. This means that the resulting shear velocity (in the absence of magnetic stresses) is then also of order unity, i.e. close to the speed of sound, and the turbulent rms velocity is about a hundred times smaller. As in BD2001, the gravitational potential varies sinusoidally in z with an amplitude g0=0.5, so the density contrast is $\Delta\ln\rho\approx1$. The main parameter that is varied in the models considered below is the magnetic diffusivity $\eta $, which is in the range $(1...5)\times10^{-4}$.


 

 
Table 3: Summary of the main properties of various runs. The kinetic energy, $E_{\rm kin}$, is based on the poloidal flow only, whilst $E_{\rm kin}^{\rm (tot)}$refers to the total kinetic energy (including the shear motion). In Runs A-C the resolution is $60^2\times 120$ meshpoints and in Run C2 it is $120^2\times 240$ meshpoints. The magnetic energies in Run C2 are only lower limits, because the field has not reached final saturation yet.
Run $\nu$ $\eta $ $E_{\rm kin}$ $E_{\rm kin}^{\rm (tot)}$ $M_{\rm fluct}$ $M_{\rm mean}$
A 0.01 $5\times10^{-4}$ 0.0030 2.2 0.005 0.002
B 0.01 $2\times10^{-4}$ 0.0030 0.7 0.018 0.002
C 0.01 10-4 0.0035 0.23 0.013 0.001
C2 0.005 10-4 0.005 0.35 >0.012 >0.0004


Once the magnetic field becomes strong the shear motion becomes reduced significantly due to magnetic forces. We define the total kinetic energy (per unit surface) as $E_{\rm kin}^{\rm (tot)}={\textstyle{1\over2}}\int_{z_1}^{z_2} {\overline{\rho\vec{u}^2}}{\rm d} {}z$, where $z_1=-\pi$ and $z_2=\pi$ are the boundaries between halo and disc plane. (This expression for $E_{\rm kin}^{\rm (tot)}$ includes the energy contained in the shear, in contrast to $E_{\rm kin}$ which does not.) When the field is still weak we have $E_{\rm kin}^{\rm (tot)}\approx2.4$, but once the field is strong this value gets significantly reduced by magnetic stresses; see Table 3. One should keep this in mind when comparing the magnetic energies for the different runs. In the following we use rms values of velocity and magnetic field for normalization purposes; these quantities are defined in terms of $E_{\rm kin}$ and M via $u_{\rm rms}=\sqrt{2E_{\rm kin}/(\langle \rho\rangle L_z)}$and $B_{\rm rms}=\sqrt{2M/L_z}$, respectively.

3.2 The Vishniac-Cho correlation

In Fig. 11 we plot the resulting correlation between $\nabla _y u_z$( $\equiv\partial u_z/\partial y$) and $\omega _y$ for a particular snapshot at the end of Run A. The anticipated effect is relatively well pronounced - much more than in the global disc simulations. As expected (see VC2001), its sign changes where the local shear, $S=\partial u_y/\partial x$, is reversed. This supports the validity of the basic result of VC2001 that such a correlation exists owing to the presence of shear.

It turns out that the Vishniac-Cho correlation is in fact the most significant correlation coefficient that changes sign when shear changes sign. In Appendix C we have calculated, for this flow, all 81 correlation coefficients of $\langle u_{i,j}u_{k,l}\rangle$. The Vishniac-Cho correlation is given by the sum of $\langle u_{x,z}u_{z,y}\rangle$ and $-\langle u_{z,x}u_{z,y}\rangle$. These two terms are indeed the most important ones. We note that the correlators $\langle u_{i,j}u_{j,i}\rangle$ (for $i\neq j$) are also relatively large, but they do not change sign when the sign of the shear changes.

Next, we need to check whether this flow is capable of dynamo action and whether large scale fields can be generated. If so, then this effect should be associated with a significant vertical transport of magnetic helicity (VC2001). Whether or not such a flux really helps the dynamo needs of course to be seen.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2980f11.ps}\end{figure} Figure 11: Scatter plot showing the correlation between $\nabla _y u_z$ and $\omega _y$ for a snapshot taken at a late time of the run with $\eta =5\times 10^{-4}$. In this example the correlation coefficients are -0.66 (for $x=-\pi $, where S<0) and +0.55 (for x=0, where S>0).
Open with DEXTER

3.3 Dynamo action

In this model we find dynamo action provided the magnetic Reynolds number is large enough. In Table 3 we give various parameters for the models considered. In Run A where $\eta =5\times 10^{-4}$ (the value used in BBS2001) the dynamo growth rate, $\lambda\equiv{\rm d} {}\ln B_{\rm rms}/{\rm d} {}t$, is about $\lambda =0.0012$. This is much less than in the case with helical forcing where $\lambda=0.015$. As in B2001 and BBS2001 the initial field strengths are about 10-6. Thus, in the present case the saturation time is about $\lambda^{-1}\ln10^6\approx10^4$, compared to about 103 in BBS2001. For $\eta =10^{-4}$ (Run C) the growth rate is about five times larger (0.0053) and the resulting saturation time correspondingly shorter. The field is concentrated at small scales and shows some loop-like pattern within the turbulent layer; see Fig. 12. In Fig. 13 we plot the evolution of magnetic energies of the mean and fluctuating field components within the turbulent zone, $\vert z\vert\le\pi$. Here, mean fields are defined with respect to averaging in the toroidal direction. Large scale magnetic fields are not present in the bulk of the turbulent layer, but can be seen in the halo, especially at later times.


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{h2980f12.ps}\end{figure} Figure 12: Vertical slice of By (left) and its y-average (right) for Run C2. The boundaries between halo and disc plane are indicated by white lines. The resolution of this run is $120^2\times 240$ meshpoints and t=810, corresponding to $\lambda t=4.3$. Dark and light shades indicate negative and positive values, respectively.
Open with DEXTER

In Run A where $\eta =5\times 10^{-4}$ there is significant magnetic energy in the mean magnetic field (upper panel of Fig. 13), but this mean field diminishes and the fluctuating field gains in strength as the magnetic diffusivity is lowered to $\eta =10^{-4}$ (Run C).


  \begin{figure} \par\includegraphics[width=7cm,clip]{h2980f13.ps}\end{figure} Figure 13: Normalized magnetic energies in the mean and fluctuating components for Runs A and C. Time is given in units of the inverse growth rate ( $\lambda =0.0012$ for Run A and $\lambda =0.0053$ for Run C).
Open with DEXTER

Next we look at the evolution of magnetic and current helicities;

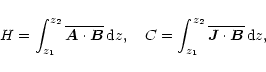\begin{displaymath}H=\int_{z_1}^{z_2}\overline{\vec{A}\cdot\vec{B}}\,{\rm d} {}z... ...C=\int_{z_1}^{z_2}\overline{\vec{J}\cdot\vec{B}}\,{\rm d} {}z, \end{displaymath} (10)

where z1 and z2 are the boundaries of the turbulent subdomain. In the present case, $z_1=-\pi$ and $z_2=+\pi$, as indicated by white lines in Fig. 12. Overbars denote horizontal averaging, so the helicities are really volume integrals, but they are normalized by the horizontal surface area. The definition of H depends on the gauge, but by extrapolating the field onto a periodic domain using potential fields one can define a gauge independent magnetic helicity (Berger & Field 1984). This is also the one used in this paper. The gauge independent magnetic helicity of the mean-field is particularly important and requires special care due to the fact that our vector and gauge potentials are periodic in the horizontal directions; see BD2001[*] for details.

As expected, because there is no net helicity in the forcing of the flow, there are also no net magnetic and current helicities in the fields; see Fig. 14. The fluctuations of magnetic helicity are generally weak, but the contributions from the mean and fluctuating fields are comparable. For the current helicity there is a clear dominance of the small scale fields over the large scale fields. This is explained by the fact that the current helicity has two k-factors more than the magnetic helicity and hence the ratio of small scale to large scale contributions are larger by a factor $(k_{\rm f}/k_1)^2$ for current helicity relative to magnetic helicity.


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{h2980f14.ps}\end{figure} Figure 14: Magnetic and current helicities in the mean and fluctuating components for the run with $\eta =10^{-4}$. H and C are given in units of $\mu _0\rho _0 u_{\rm rms}^2 L_z/k_1$ and $\rho _0 u_{\rm rms}^2 L_z k_1^2$, respectively.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{h2980f15.ps}\end{figure} Figure 15: Magnetic helicity flux density in Coulomb gauge (upper panel) compared with that in the $\phi =0$ gauge (lower panel). The local flux density has been averaged in y and in t (between $\lambda t=32$ and 42). Run C.
Open with DEXTER

3.4 Magnetic helicity flux

Vishniac & Cho (2001) pointed out that the $\phi =0$ gauge in Eq. (8) is not suited for analysing local helicity flux densities. We recall that the procedures of Berger & Field (1984) and BD2001 only apply to helicities in a given volume and the corresponding helicity fluxes through its bounding surface. Magnetic helicity densities and the corresponding flux densities are only possible to define in a given gauge.

In the following we denote by $\vec{A}_{\rm c}$ the magnetic vector potential in the Coulomb gauge, whilst $\vec{A}$ still refers to the vector potential in the $\phi =0$ gauge. The conversion between the two is given by $\vec{A}_{\rm c}=\vec{A}-\vec{A}_0$, where $\vec{A}_0=\langle \vec{A}\rangle+\mbox{\boldmath$\nabla$ } {}\psi$and $\nabla^2\psi=\mbox{\boldmath$\nabla$ } {}\cdot\vec{A}$. In the following we use the notation $\vec{A}_0=\mbox{\boldmath$\nabla$ } {}(\nabla^{-2}\mbox{\boldmath$\nabla$ } {}\cdot\vec{A})$.

In the $\phi =0$ gauge the magnetic helicity flux density is simply $\mbox{\boldmath$E$ } {}\times\vec{A}$, but when converted into the Coulomb gauge it becomes (see Appendix D)

 \begin{displaymath}\mbox{\boldmath$J$ } {}_{\rm H}^{\rm Cou}= (\mbox{\boldmath$E... ...ox{\boldmath$\nabla$ } {}\times[2\phi(\vec{A}-\vec{A}_0)]\cdot \end{displaymath} (11)

The second part does not contribute to the divergence of the magnetic helicity flux. In Fig. 15 we plot the first part, denoted by $\mbox{\boldmath$J$ } {}_{\rm H,1st}^{\rm Cou}(\mbox{fluct})$. The suffix "(fluct)'' indicates that we have only included the contribution from the fluctuating components of $\vec{A}$ and $\mbox{\boldmath$E$ } {}$ and then averaged over y and t. This term was used extensively by VC2001. We also compare with the helicity flux in the $\phi =0$ gauge, $\mbox{\boldmath$J$ } {}_{\rm H}^{\phi=0}(\mbox{fluct})$. It is striking that the two are quite different; $\mbox{\boldmath$J$ } {}_{\rm H,1st}^{\rm Cou}(\mbox{fluct})$ shows a systematic circulation pattern with noise where shear is weak, i.e. near $x=\pm\pi/2$. Such a circulation patter is absent in $\mbox{\boldmath$J$ } {}_{\rm H}^{\phi=0}(\mbox{fluct})$.

There may be additional solenoidal contributions also from $\mbox{\boldmath$J$ } {}_{\rm H,1st}^{\rm Cou}$. In general we may split $\mbox{\boldmath$J$ } {}_{\rm H}^{\rm Cou}$ into an irrotational and a solenoidal part,

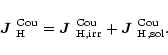\begin{displaymath}\mbox{\boldmath$J$ } {}_{\rm H}^{\rm Cou}= \mbox{\boldmath$J$... ...,irr}^{\rm Cou}+\mbox{\boldmath$J$ } {}_{\rm H,sol}^{\rm Cou}. \end{displaymath} (12)

It turns out that $\mbox{\boldmath$J$ } {}_{\rm H,1st}^{\rm Cou}$ has still a noticeable solenoidal (i.e. rotational) contribution. In particular, it is interesting to note that $\mbox{\boldmath$J$ } {}_{\rm H,1st}^{\rm Cou}$has a systematic flux through the middle of the domain with an orientation that agrees with that predicted by VC2001 (upward where S>0and downward where S<0). At x=0 (i.e. the position where shear is maximum), the solenoidal part of the averaged magnetic helicity flux is about 200 times larger than its irrotational part. The profiles of the time averaged vertical magnetic helicity flux density at x=0 is plotted in Fig. 16 as functions of z for different gauges. Clearly, the relevant irrotational part of the magnetic helicity flux does not have a systematic component.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{h2980f16.ps}\end{figure} Figure 16: Time averaged vertical magnetic helicity flux density at x=0 as a function of z in different gauges. $J_{\rm H}^{\phi =0}$ refers to the $\phi =0$ gauge and $J_{\rm H}^{\rm Cou}$ refers to the Coulomb gauge. $J_{\rm H,irr}^{\rm Cou}$ refers to the irrotational part and $J_{\rm H,1st}^{\rm Cou}$ refers to the first part in Eq. (11). Like in Fig. 15, only the contributions from the fluctuating components of $\vec{A}$ and $\mbox{\boldmath$E$ } {}$are included. Run C.
Open with DEXTER

In order to assess the possibility of dynamo action we plot in Fig. 17 vertical profiles of the divergence of the helicity flux density, in units of $u_{\rm rms}B^2_{\rm rms}$. This non-dimensional quantity is reminiscent of a local dynamo number, $\alpha_{\rm BH}/(k_1\eta_{\rm T})\approx(k_{\rm f}/k_1) (\alpha_{\rm BH}/u_{\rm rms})$, where

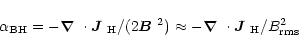\begin{displaymath}\alpha_{\rm BH}=-\mbox{\boldmath$\nabla$ } {}\cdot\mbox{\bold... ...\nabla$ } {}\cdot\mbox{\boldmath$J$ } {}_{\rm H}/B^2_{\rm rms} \end{displaymath} (13)

has been introduced for the $\alpha$ effect of Bhattacharjee & Hameiri (1986) and $k_{\rm f}\eta_{\rm T}\approx u_{\rm rms}$ for the turbulent magnetic diffusivity, $\eta_{\rm T}$. Our results (Fig. 17) suggest that the local dynamo number is fluctuating in space and that its rms value is somewhat larger when the magnetic Reynolds number is larger (cf. lower panel). The fact that $\alpha_{\rm BH}$ fluctuates in space (and probably also in time) is not necessarily bad; such an "incoherent'' $\alpha$ may still, together with shear and turbulent diffusion, contribute to producing large scale fields (Vishniac & Brandenburg 1997).

Figure 17 shows that the non-dimensional measure of the $\alpha_{\rm BH}$ fluctuates around $\pm0.01$. This value should be compared with the critical value of $\alpha/(\eta_{\rm T}k_1)\equiv C_\alpha$ above which dynamo action is possible. We define the dynamo number as ${\cal D}=C_\alpha C_{\rm S}$, where $C_{\rm S}=S/(\eta_{\rm T}k_1^2)$. With $S\approx S_0=1$ and $\eta_{\rm T}k_1=u_{\rm rms}k_1/k_{\rm f}=0.005$we have $C\rm _S=~200$, and since the critical dynamo number is around 2 (BBS2001) we have 0.01, which agrees with the estimate above (cf. Fig. 17). However, this estimate has been too optimistic in several ways: the actual value of S is smaller than S0and the incoherent $\alpha$ effect dynamo will be less efficient. This may explain why the Vishniac-Cho effect does not seem to operate in the present simulations, but it may become more important at higher magnetic Reynolds numbers.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{h2980f17.ps}\end{figure} Figure 17: Divergence of the mean helicity flux, normalized to make it similar to a local dynamo number. As in Figs. 15 and 16, only the contributions from the fluctuating components of $\vec{A}$ and  $\mbox{\boldmath$E$ } {}$are included in the calculation of the y and t averaged magnetic helicity flux. Run C.
Open with DEXTER

   
4 Conclusions

In this paper we have re-examined the recent suggestion by VC2001 that large scale dynamo action can result from velocity correlations involving higher derivatives. We found this effect to be present both in global accretion disc simulations as well as in models of forced turbulence with no rotation and just shear. Nevertheless, it does not seem to produce large scale dynamo action in the parameter regime considered here. In particular, we find no signs of any net vertical flux of magnetic helicity through the domain. This was thought to be an important property of the model suggested by VC2001.

Of course, the range of parameters considered in the present work is limited, and the degree of stratification is relatively weak. Nevertheless, the anticipated velocity correlations are strongly present and yet there are no signs of large scale dynamo action. As the magnetic Reynolds number is increased, the anticipated velocity correlations that are necessary to drive non-helical large scale dynamo action become smaller, making this new mechanism an unlikely candidate for explaining the field found in accretion disc simulations. Although we cannot exclude the possibility of different behaviour at larger magnetic Reynolds number or in more realistic representations of accretion discs, it is clear that the anticipated effect will not be easily detectable. This is quite important given the fact that large scale dynamo action owing to the helicity effect is so much stronger than nonhelical dynamo action. Thus, if one is to find the effect anticipated by VC2001 it will be quite important to isolate it from the much stronger helicity-driven dynamo effect.

Some concluding speculations regarding the viability of helicity-driven dynamo action in astrophysical settings are now in order. At large magnetic Reynolds numbers dynamo action will always generate strong magnetic fields within a short period of time. What the helicity constraint does is to prevent the formation of large scale helical patterns in a time less than a certain fraction of the magnetic diffusion time. It does not exclude however the formation of large scale patterns where the magnetic helicity cancels to zero. This would however require an exchange of magnetic helicity between various sub-domains. This does unfortunately not come automatically, as the simulations of BD2001 have shown. However, for the sun the relevant resistive time scales are estimated to be around or less than 106 years. On the one hand this is long enough for large scale dynamo to be well established at the present time. On the other hand, it would suggest that the time scale for the solar cycle must essentially be controlled by non-resistive effects. One idea that deserved further attention is the possibility that the dynamo wave corresponds to actual fluid motions within the solar convection zone, such that the magnetic helicity within a Lagrangian fluid patch remains to be conserved. Since this would correspond to a systematic flux of magnetic helicity, this mechanism would be similar to that of VC2001. Here, however, the magnetic helicity flux would not be self-driven, but driven externally, e.g. by the meridional circulation. A number of recent investigations have shown that meridional circulation would be capable of reversing the sense of the dynamo wave driven by the $\alpha\Omega$-dynamo (Durney 1995; Choudhuri et al. 1995; Küker et al. 2001). This is similar to the possibility discussed above where the dynamo wave itself drives the meridional circulation.

As far as discs is concerned, the long resistive time scale is perhaps not a problem, because the possibility of strong outflows always shortens the saturation time scales, albeit at the expense of lowering the final saturation field strengths (see BD2001). The final solution to the problem may require more realistic global simulations with explicit resistivities, combined with suitable analytic approaches to enable one to extrapolate to astrophysical conditions.

Acknowledgements
We thank Wolfgang Dobler, Kandu Subramanian and Ethan Vishniac for interesting discussions and comments on the manuscript. Use of the PPARC supported supercomputers in St Andrews and Leicester (UKAFF) is acknowledged. We thank the John v. Neumann-Institut for Computing at the Forschungszentrum Jülich, Germany, for using the T90 computer. R.A. acknowledges the kind support by the Deutsche Forschungsgemeinschaft and the hospitality of Nordita, where much of this work has been carried out.

   
Appendix A: A gauge in which magnetic helicity and magnetic helicity flux are automatically gauge invariant

The purpose of this appendix is to show that there is a particular gauge for the vector potential of the one-dimensional mean field such that $\int\overline{\vec{A}}\cdot\overline{\vec{B}}\,{\rm d} {}z$ is automatically gauge invariant. This allows us then to define a local helicity flux such that its integral over a closed surface (top and bottom of a slab) equals the gauge invariant integrated helicity flux of BD2001.

The evolution equation of the mean (one-dimensional) magnetic vector potential is

 \begin{displaymath}\dot{\overline{\vec{A}}}=-(\overline{\vec{E}}-\overline{\vec{E}}_0), \end{displaymath} (A.1)

where $\vec{E}=\eta\mu_0\vec{J}-\vec{u}\times\vec{B}$ is the electric field, $\overline{\vec{E}}_0=\overline{\vec{E}}_0(t)$ is an integration constant, and $\overline{\vec{A}}$ and $\overline{\vec{E}}$ depend only on z and t. From Eq. (A.1) follows the evolution equation for the magnetic helicity density,

 \begin{displaymath}{\partial\over\partial t}({\overline{\vec{A}}}\cdot{\overline... ...rline{\vec{A}}}] =-2\overline{\vec{E}}\cdot\overline{\vec{B}}. \end{displaymath} (A.2)

In BD2001 the gauge independent magnetic helicity of the mean field was found to be

 \begin{displaymath}H_{\rm mean}=\int_{z_1}^{z_2} \overline{\vec{A}}\cdot\overlin... ...\vec{z}}\cdot(\overline{\vec{A}}_1\times\overline{\vec{A}}_2), \end{displaymath} (A.3)

where $\overline{\vec{A}}_1$ and $\overline{\vec{A}}_2$ are the values of $\overline{\vec{A}}$ at z=z1 and z2, respectively. At the initial time one can always subtract a constant from $\overline{\vec{A}}$ such that the second term vanishes. This constant turns out to be the average of $\overline{\vec{A}}_1$ and $\overline{\vec{A}}_2$, so we replace initially

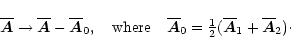\begin{displaymath}\overline{\vec{A}}\rightarrow\overline{\vec{A}}-\overline{\ve... ...tyle{1\over2}}(\overline{\vec{A}}_1+\overline{\vec{A}}_2)\cdot \end{displaymath} (A.4)

Next we choose $\overline{\vec{E}}_0$ such that $\overline{\vec{A}}_1+\overline{\vec{A}}_2$ remains zero at all later times. This yields

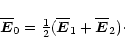\begin{displaymath}\overline{\vec{E}}_0={\textstyle{1\over2}}(\overline{\vec{E}}_1+\overline{\vec{E}}_2)\cdot \end{displaymath} (A.5)

We can then express the two integrated fluxes on z2 as

\begin{displaymath}Q_{\rm mean}^{(2)}=\hat{\vec{z}}\cdot[ (\overline{\vec{E}}_2+... ...over2}}\overline{\vec{E}}_1)\times{\overline{\vec{A}}}_2]\cdot \end{displaymath} (A.6)

Using the fact that $\overline{\vec{A}}_1+\overline{\vec{A}}_2=0$ we can write

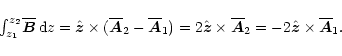\begin{displaymath}{\textstyle\int_{z_1}^{z_2}}\overline{\vec{B}}\,{\rm d} {}z =... ...verline{\vec{A}}_2 =-2\hat{\vec{z}}\times\overline{\vec{A}}_1. \end{displaymath} (A.7)

This allows us to express $Q_{\rm mean}^{(2)}$ as

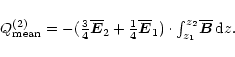\begin{displaymath}Q_{\rm mean}^{(2)}=-({\textstyle{3\over4}}\overline{\vec{E}}_... ...ot{\textstyle\int_{z_1}^{z_2}}\overline{\vec{B}}\,{\rm d} {}z. \end{displaymath} (A.8)

At z=z1 we count the flux as negative when helicity leaves the domain in the downward direction, so

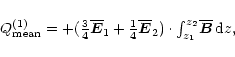\begin{displaymath}Q_{\rm mean}^{(1)}=+({\textstyle{3\over4}}\overline{\vec{E}}_... ...ot{\textstyle\int_{z_1}^{z_2}}\overline{\vec{B}}\,{\rm d} {}z, \end{displaymath} (A.9)

with $Q_{\rm mean}=Q_{\rm mean}^{(2)}-Q_{\rm mean}^{(1)}$ being the gauge invariant magnetic helicity flux of BD2001. The average upward flux of mean magnetic helicity on the two boundaries is

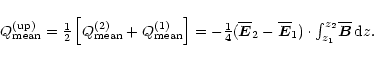\begin{displaymath}Q_{\rm mean}^{\rm (up)} ={\textstyle{1\over2}}\left[Q_{\rm me... ...{\textstyle\int_{z_1}^{z_2}}\overline{\vec{B}}\,{\rm d} {}z.\; \end{displaymath} (A.10)

   
Appendix B: Magnetic helicity in sub-domains

In a periodic domain the sum of the magnetic helicities of any two sub-domains is equal to the magnetic helicity of the entire (periodic) domain. In the non-periodic case this is not the case if the gauge invariant magnetic helicity of BD2001 is used also for the sub-domains. We therefore calculate the magnetic helicity of sub-domains by using the gauge discussed in Appendix A, so the magnetic helicity between the points $z_{\it a}$ and $z_{\it b}$ is then

 \begin{displaymath}H_{\rm mean}^{\it (ab)}=\int_{z_{\it a}}^{z_{\it b}} (\overli... ...}}-\overline{\vec{A}}_0) \cdot\overline{\vec{B}}\,{\rm d} {}z, \end{displaymath} (B.1)

where $\overline{\vec{A}}_0={\textstyle{1\over2}}(\overline{\vec{A}}_1+ \overline{\vec{A}}_2)$ is independent of the values of $z_{\it a}$ and $z_{\it b}$. For $z_{\it a}=z_1$ and $z_{\it b}=z_2$we recover Eq. (A.3), and the sum of the magnetic helicities of sub-domains agrees with the magnetic helicity of the whole domain from z1 to z2.

Similar to Eq. (A.2), we can now derive an evolution equation for $(\overline{\vec{A}}-\overline{\vec{A}}_0)\cdot\overline{\vec{B}}$. The flux term is then like in Eq. (A.2), but with $\overline{\vec{A}}$being replaced by $\overline{\vec{A}}-\overline{\vec{A}}_0$. The magnetic helicity flux out of an individual sub-domain is then $Q_{\rm mean}^{\it (ab)} =Q_{\rm mean}^{\it (b)}-Q_{\rm mean}^{\it (a)}$, where

 \begin{displaymath}Q_{\rm mean}^{(\alpha)}=\hat{\vec{z}}\cdot[ (\overline{\vec{E... ...{\vec{A}}}_{\alpha}-{\overline{\vec{A}}}_0)], \quad\alpha=a,b. \end{displaymath} (B.2)

Again, the sum of net helicity fluxes out of sub-domains equals the gauge invariant net helicity fluxes, $Q_{\rm mean}$, of the full domain. This formula can be applied to value of $z_\alpha$, in particular to the equator. In that case one obtains the horizontally averaged magnetic helicity flux through the surface $z_\alpha=0$.

   
Appendix C: Velocity gradient correlation tensor

In order to check that the Vishniac-Cho correlation is the dominant correlation among the different components of the velocity gradient matrix, we define the correlation coefficient

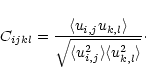\begin{displaymath}C_{ijkl}={\langle u_{i,j}u_{k,l}\rangle\over\sqrt{\langle u_{i,j}^2\rangle\langle u_{k,l}^2\rangle}}\cdot \end{displaymath} (C.1)

We denote by $C^{(\pm)}_{ijkl}$ the values of Cijkl evaluated in those sub-domains where the sign of shear is locally positive or negative, respectively. We separate the coefficients that are symmetric and antisymmetric with respect to changing the sign of shear. Hence, we calculate

\begin{displaymath}C^{(S)}_{ijkl}={\textstyle{1\over2}}[C^{(+)}_{ijkl}+C^{(-)}_{... ...}_{ijkl}={\textstyle{1\over2}}[C^{(+)}_{ijkl}-C^{(-)}_{ijkl}], \end{displaymath} (C.2)

whose values are shown in Tables C.1 and C.2, respectively.


 

 
Table C.1: The coefficients C(S)ijkl, arranged in blocks where k increases downward and l increases to the right. Within each block i increases downward and j increases to the right. In bold are given the values that are largest by magnitude, but different from unity.
  l=1     l=2     l=3  
1.00 0.04 -0.09 0.04 1.00 -0.14 -0.09 -0.14 1.00
0.02 -0.01 -0.01 -0.26 -0.03 0.03 -0.03 0.01 0.03
0.01 0.05 -0.23 0.10 0.10 -0.02 -0.54 -0.01 0.04
0.02 -0.26 -0.03 -0.01 -0.03 0.01 -0.01 0.03 0.03
1.00 -0.00 -0.03 -0.00 1.00 -0.01 -0.03 -0.01 1.00
-0.03 0.02 -0.04 0.00 0.07 -0.07 -0.03 -0.60 0.06
0.01 0.10 -0.54 0.05 0.10 -0.01 -0.23 -0.02 0.04
-0.03 0.00 -0.03 0.02 0.07 -0.60 -0.04 -0.07 0.06
1.00 -0.00 -0.03 -0.00 1.00 -0.13 -0.03 -0.13 1.00



 

 
Table C.2: Like Table C.1, but for the coefficients C(A)ijkl which have an antisymmetric dependence on shear. The components that enter the Vishniac-Cho correlation are shown in bold; these are also the coefficients with the largest magnitude in this table.
  l=1     l=2     l=3  
0.00 -0.16 -0.01 -0.16 0.00 -0.06 -0.01 -0.06 0.00
-0.01 0.00 0.00 0.01 -0.17 0.09 0.00 0.02 -0.13
-0.15 -0.02 0.00 -0.03 -0.04 0.21 0.01 0.28 -0.07
-0.01 0.01 0.00 0.00 -0.17 0.02 0.00 0.09 -0.13
0.00 -0.04 0.11 -0.04 0.00 -0.01 0.11 -0.01 0.00
0.01 0.03 0.10 0.00 0.03 -0.00 0.05 -0.02 0.01
-0.15 -0.03 0.01 -0.02 -0.04 0.28 0.00 0.21 -0.07
0.01 0.00 0.05 0.03 0.03 -0.02 0.10 -0.00 0.01
0.00 -0.51 0.10 -0.51 0.00 0.00 0.10 0.00 0.00


In Table C.1 the largest contributions come from C(S)xyyx=-0.26, C(S)yzzy=-0.60, and C(S)zxxz=-0.54. In Table C.2 the largest contributions come from C(A)xzzy=+0.28 and C(A)zxzy=-0.51. These are also the coefficients that are important in the Vishniac-Cho correlation.

   
Appendix D: Coulomb-gauged helicity flux

In the $\phi =0$ gauge we have $\dot{\vec{A}}=-\mbox{\boldmath$E$ } {}$. In that gauge, the evolution of the magnetic helicity density is given by

 \begin{displaymath}{\partial\over\partial t}(\vec{A}\cdot\mbox{\boldmath$B$ } {}... ...ec{A}) =-2\mbox{\boldmath$E$ } {}\cdot\mbox{\boldmath$B$ } {}. \end{displaymath} (D.1)

Note that the term on the right hand side of this equation is gauge-invariant, but the terms on the left hand side are not. In the Coulomb gauge we have $\mbox{\boldmath$\nabla$ } {}\cdot\vec{A}_{\rm C}=0$, where $\vec{A}_{\rm C}\equiv\vec{A}-\vec{A}_0$. In order to maintain $\mbox{\boldmath$\nabla$ } {}\cdot\vec{A}_{\rm C}=0$ for all times, we have to add the term $-\mbox{\boldmath$\nabla$ } {}\phi\equiv\mbox{\boldmath$E$ } {}_0=\mbox{\boldmat... ...abla$ } {}(\nabla^{-2}\mbox{\boldmath$\nabla$ } {}\cdot\mbox{\boldmath$E$ } {})$ to the right hand side of the uncurled induction equation,

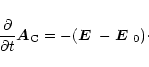\begin{displaymath}{\partial\over\partial t}\vec{A}_{\rm C}=-(\mbox{\boldmath$E$ } {}-\mbox{\boldmath$E$ } {}_0)\cdot \end{displaymath} (D.2)

In this gauge the evolution equation for the helicity density becomes

 \begin{displaymath}{\partial\over\partial t}(\vec{A}_{\rm C}\cdot\mbox{\boldmath... ...$ } {}-\mbox{\boldmath$E$ } {}_0)\cdot\mbox{\boldmath$B$ } {}. \end{displaymath} (D.3)

Unlike Eq. (D.1), the right hand side of Eq. (D.3) is gauge dependent owing to the extra term $2\mbox{\boldmath$E$ } {}_0\cdot\mbox{\boldmath$B$ } {}$. However, because of $\mbox{\boldmath$\nabla$ } {}\cdot\mbox{\boldmath$B$ } {}=0$, we can write this as the divergence of another contribution to the helicity flux density,

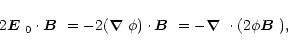\begin{displaymath}2\mbox{\boldmath$E$ } {}_0\cdot\mbox{\boldmath$B$ } {}=-2(\mb... ...box{\boldmath$\nabla$ } {}\cdot(2\phi\mbox{\boldmath$B$ } {}), \end{displaymath} (D.4)

which should be included in the expression for the Coulomb gauged helicity flux density,

 \begin{displaymath}\mbox{\boldmath$J$ } {}_{\rm H}^{\rm Cou}=(\mbox{\boldmath$E$... ...} {}_0)\times(\vec{A}-\vec{A}_0)+2\phi\mbox{\boldmath$B$ } {}, \end{displaymath} (D.5)

so Eq. (D.3) becomes

 \begin{displaymath}{\partial\over\partial t}(\vec{A}_{\rm C}\cdot\mbox{\boldmath... ...rm Cou}=-2\mbox{\boldmath$E$ } {}\cdot\mbox{\boldmath$B$ } {}. \end{displaymath} (D.6)

Now the right hand sides of Eqs. (D.1) and (D.6) agree and are gauge-invariant. Note, however, that

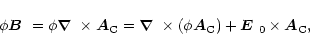\begin{displaymath}\phi\mbox{\boldmath$B$ } {}=\phi\mbox{\boldmath$\nabla$ } {}\... ...ec{A}_{\rm C})+\mbox{\boldmath$E$ } {}_0\times\vec{A}_{\rm C}, \end{displaymath} (D.7)

so Eq. (D.5) can also be written as

\begin{displaymath}\mbox{\boldmath$J$ } {}_{\rm H}^{\rm Cou}= (\mbox{\boldmath$E... ...+\mbox{\boldmath$\nabla$ } {}\times[2\phi(\vec{A}-\vec{A}_0)], \end{displaymath} (D.8)

which is identical to Eq. (11).

References

 
Copyright ESO 2001