5 Discussion

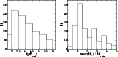
Figure 3: Final sample characteristics: Left: the histogram of the logarithm of outer subsystem period; Right: the distribution of the mass of the most massive star in the system.

Figure 4: Left: the distribution of the projected separation ratio $a_{\rm out}/a_{\rm in}$; Right: thick lines: the cumulative distribution $F(e_{\rm crit})$ of critical eccentricities computed for stability limit $a_{\rm out}(1\!-\!e_{\rm crit})/a_{\rm in}$ equal to 3 (solid line) and 5 (dashed line). Thin lines: scaled twice respective ( differential) linear distributions of e with rejection: $f(e)\!=\!2e(1\!-\!F(e))$.

Some characteristics of the final sample are shown in Fig. 3. As expected, the shortest periods are most frequent, although the periods as long as ${\sim} 10^5$ yr are present (for nearby systems). The median period is 6100 yr. Having a characteristic separation of ${\sim}10\hbox{$^{\prime\prime}$ }$ and best-represented first epoch of 1835, the system with such a period gives a motion of ${\sim}1.4\hbox{$^{\prime\prime}$ }$ in 155 years. As we see, there is nothing mysterious about detecting the orbital motion at such long periods.

The constraint accepted for maximal stellar mass in the system seems reasonable: there are few cases of $M^*_{\rm max}\!>\!4~M_{\odot}$. So, our study is restricted to low-to-intermediate mass stars.

The difference of our $\gamma$-angle distribution from a uniform one is clearly seen. It is unlikely that this result is heavily distorted by selection. The errors of the measurements of the position angle are at least not larger than in separation (Pannunzio et al. 1988) so the excess of values near $90\hbox{$^\circ$ }$ is hard to explain in this way. Both our and BDS92's samples refer roughly to the same range of periods but, apparently, differ in fraction of highly elongated orbits.

For visual orbits, a bell-shaped distribution of eccentricity was obtained by Ruymaekers (1999). Nevertheless, the author notices (after Harrington 1977b) that in orbit computation the quality of inclined or eccentric orbits is strongly degraded and that probably for this reason good high-e orbits are rare. It is obviously not the case for objects in our sample with periods longer than 500-1000 years. Since the position changes are mostly very small compared to the separation, the systems with large eccentricities are not discriminated to be discovered or measured.

Still keeping in mind the possibility of some selection in the MSC itself, we nevertheless suggest that eccentric long-period orbits among outer subsystems in multiple stars are rare. Apart from some possible unaccounted systematic errors in observations, two explanations can be advanced for our finding.

Dynamical instability.

Our systems are all hierarchical: they have the size of the outer subsystem at least several times wider than that of inner subsystems (Fig. 4). To check whether the dynamical instability factor is responsible for "damping'' of high eccentricities in our f(e), we can apply the crude criterion of stability for the ratio of the outer subsystem periastron distance $R_{\rm p}^{\rm out}$ to the size of an inner orbit $a_{\rm in}$:

$$\frac{R_{\rm p}^{\rm out}}{a_{\rm in}} \approx \frac{\rho_{\rm out}(1-e_{\rm out})}{\rho_{\rm in}} > C$$

where C is about 3-5 and, in principle, is a weak function of eccentricity $e_{\rm out}$ and mass ratio $q_{\rm out}$ (Harrington 1977a). In high-order (N>3) multiples, $a_{\rm in}$stands for the size of the widest subsystem (Mardling & Aarseth 2001, p. 414). Here we suppose that, statistically, the semi-major axis a of an orbit is close to the observed projected separation $\rho$.

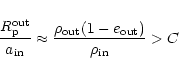
For a given C, we can derive some critical value of the eccentricity $e_{\rm crit}$ for each our system which would "make'' it marginally stable. The cumulative distributions F of these $e_{\rm crit}$ are shown in Fig. 4 (right). If we assume that the universal $f(e)\!=\!2e$ distribution applies to all multiple systems and that the highest eccentricities are eliminated by instability, then the modified distribution can be modeled as $f(e)=2e \cdot [1-F(e)]$, where F(e) is the cumulative distribution of critical eccentricities (thin lines in the same figure).

We reran our Monte-Carlo simulations with the modified f(e), noticing the weak sensitivity of this f(e) to the value of C. As expected, the resulting $f(\gamma )$ is a bit closer to the observed one (thick grey line in Fig. 2), but still far from it.

 

 

Table 1: Angle $\gamma$ for objects of an output sample. Columns are: WDS-designation of the object; outer subsystem identification as given in MSC; second epoch separation and position angle; angle $\gamma$ and its error; motion $\delta \hbox {$^{\prime \prime }$ }=\Delta \mu (T_2 - T_1)$ between two epochs; note symbols (see bottom of the table). Values $\gamma$ and $\delta$ are corrected for the motion in the subsystems, if it is significant.

WDS	SYS	$\rho_2\hbox{$^{\prime\prime}$ }$	$\theta_2\hbox{$^\circ$ }$	$\gamma\hbox{$^\circ$ }$	$\epsilon_{\gamma}\hbox{$^\circ$ }$	$\delta\hbox{$^{\prime\prime}$ }$	note	WDS	SYS	$\rho_2\hbox{$^{\prime\prime}$ }$	$\theta_2\hbox{$^\circ$ }$	$\gamma\hbox{$^\circ$ }$	$\epsilon_{\gamma}\hbox{$^\circ$ }$	$\delta\hbox{$^{\prime\prime}$ }$	note
00057+4549	AF	328.0	254	215	24	1.6	cO	07185-5721	AB	2.4	254	97	13	0.6	w
00108-5729	AB	3.2	183	108	16	0.3		07204-5219	AB	9.2	26	128	5	1.6
00134+2659	AC	18.0	225	0	24	0.6	wX	07359+4302	AB	2.1	88	32	14	0.3
00150+0849	AB	11.5	148	264	18	0.5		07378-0236	AC	1.4	303	31	6	0.6	1
00174+0853	BC	4.0	235	195	14	0.3	1	07354-7417	AB	1.9	125	109	6	0.8
00219-2300	AB	6.1	26	93	10	0.7	2	08047+4717	AC	5.9	214	303	15	0.2	m
00321-0511	AC	2.6	190	283	6	1.0	1	08044+1217	AC	5.0	213	99	4	2.3	w1
00335-5520	AC	6.8	245	235	22	0.3	1O	08065-0915	AB	30.6	327	132	22	0.4	mx
00345-0433	AC	19.7	45	194	24	0.5	1O	08198-7131	AB	64.8	58	263	11	1.6
00360+2959	AB	6.2	23	299	4	1.5		08267+2432	AB	5.7	50	104	5	1.2
00393+3052	AB	28.7	298	327	24	1.0	w	08368+7443	AB	1.5	234	191	13	0.3
00493-2124	AC	11.0	299	342	13	0.1	mX	08555-0758	AB	4.1	3	130	8	0.7
01041+2635	AB	0.8	244	5	23	0.1		09125-4337	AB	2.8	282	270	20	0.3
01137+0735	AB	22.9	63	216	19	0.9	x	09205-0933	AB	229.1	211	262	11	2.2
01158-6853	AC	319.3	310	106	9	3.3	2O	09272-0913	AC	10.5	176	174	24	0.3	1
01230-1258	AB	40.5	313	216	13	0.2	mo	09354+3958	AB	25.0	149	72	24	0.6
01409+4952	AC	6.1	282	34	26	0.2		10311-2411	AB	1.9	67	352	24	0.2
01413+2545	AB	10.5	31	197	12	0.8	w	10350+0839	AB	2.2	157	217	15	0.3
01493+4754	AC	20.8	178	303	26	0.5	wO	10401+1914	AC	6.4	355	49	29	0.3	O
01551+2847	AC	5.7	163	272	17	0.4	1O	10409-3545	AB	0.6	48	236	23	0.2
01590-2255	AB	8.6	303	301	24	0.3		10435+4612	AB	288.0	88	267	11	1.7
01586-5332	AB	2.3	103	306	17	0.3		10443-7052	AB	62.7	75	250	21	1.0	x
02128+7941	AB	55.6	277	263	12	1.4		10575-1105	AC	4.5	8	91	13	0.5	1
02124+3018	AB	3.9	70	274	8	0.7		11047-0413	AB	11.6	221	60	5	2.0	2
02110-3540	AC	13.6	41	236	18	1.0	O	11170-0708	AB	1.0	210	229	16	0.4	w
02128-0224	AB	16.6	234	57	6	1.9		11366+5608	AB	6.1	166	326	6	0.9
02280-5808	AC	17.6	299	264	26	0.3	O	11387+4507	AB	9.2	250	238	3	3.1
02370+2439	AB	38.2	275	127	25	0.7		12143+1149	AB	1.7	16	359	16	0.4
02411+1848	AC	65.5	242	61	12	0.4	m	12413-1301	AB	5.3	312	99	5	1.2
02529+5300	AC	1.6	312	73	10	0.5	1	12492+8325	AB	21.5	326	130	16	0.8
02583-4018	AB	8.3	90	93	7	1.1		12563+5406	AB	3.8	281	313	8	0.7
03158+5057	AB	1.5	102	5	4	0.9		13066-6434	AB	0.5	234	154	13	0.3
03302+5922	AB	2.6	70	120	20	0.4	X	13123-5955	AC	1.9	7	84	7	0.7	1*
03480+6840	AB	17.1	14	272	12	0.9	2*	13145-2417	AC	12.5	332	282	22	0.5	1
03470+4126	AB	7.3	54	139	3	2.1		13196+3507	AB	17.6	129	90	5	2.9
03566+5042	AB	75.3	31	270	22	0.8		13258+4430	AC	2.6	205	79	6	1.2	w
04226+2538	AB	19.4	25	263	28	0.5		13328-1746	AB	1.2	26	326	12	0.3
04436-0848	AB	9.3	318	316	27	0.3		13437-4204	AC	0.9	72	40	24	0.2	1
04475+4324	AC	1.4	24	270	14	0.4	1	14135+5147	AB	13.5	236	339	8	1.0
04563+5206	AC	4.6	114	341	7	0.7	1	14158+1018	AC	3.9	148	312	7	0.7	1
05012+3430	AB	1.7	229	339	19	0.2		14182-2731	AC	3.3	111	284	17	0.3	1x
05017+2640	AC	78.4	160	248	26	0.8	1	14234+0827	AB	6.3	194	85	7	0.9
05098+2802	AB	11.5	28	181	26	0.3	2*	14375+4743	AC	78.8	117	100	15	1.2
05133+0252	AB	6.9	63	223	25	0.3		14426+1929	AC	135.0	309	90	11	1.5	1
05154+3241	AC	14.2	225	213	18	0.5		14497+4843	AB	2.8	45	173	4	0.9
05239-0052	AB	2.9	160	338	2	1.6	2	15185-4753	BC	22.7	129	317	18	0.6	O
05248-5219	AC	38.1	288	96	25	0.7	1	15245+3723	AB	108.1	171	103	15	1.4	2
05301+2933	AC	15.1	352	148	15	0.0	mO	15290-2852	AC	9.5	9	66	12	0.7	c1
05364+2200	AB	4.0	272	76	3	1.6		15332-2429	AB	9.1	301	106	14	0.6	2
05508-3945	AC	3.7	197	306	19	0.3	1	15387-0847	AB	11.8	189	103	15	0.6
06047-4505	AC	196.2	321	271	6	3.0	O	15382+3615	AC	15.0	86	142	29	0.2	*Oo
06200+2826	AC	2.9	263	95	7	0.8	1	16035-5747	AC	11.0	243	299	7	1.7	w
06298-5014	AC	12.0	312	221	5	2.0	3	16086-3906	AC	44.2	184	93	20	0.9	x
06462+5927	AC	8.7	309	99	13	0.0	mO	16235+3321	AC	1.0	35	264	13	0.4
06423-3824	AB	7.9	277	166	11	0.1	m	16242+3702	AB	8.3	341	250	10	0.8
06482+5542	BA	4.6	77	219	23	0.2		16238+6142	AB	1.0	352	296	24	0.3	X
07031+5410	AB	9.0	66	152	13	0.1	m	16362+5255	AC	90.2	193	81	15	1.1	O
07040-4337	AC	184.9	335	79	10	2.1	O	16579+4722	AC	112.5	262	92	18	1.5	O
07148-1529	AC	15.7	2	277	28	0.4	1O	17130-5836	AB	3.1	322	279	18	0.3
07171-1202	AC	15.9	242	48	22	0.5	1	17153-2636	AC	732.8	74	83	9	5.8
07201+2159	AB	5.8	220	129	3	2.7	w	17131+5408	AC	88.5	233	98	8	2.4

 

Table 1: continued.

WDS	SYS	$\rho_2\hbox{$^{\prime\prime}$ }$	$\theta_2\hbox{$^\circ$ }$	$\gamma\hbox{$^\circ$ }$	$\epsilon_{\gamma}\hbox{$^\circ$ }$	$\delta\hbox{$^{\prime\prime}$ }$	note	WDS	SYS	$\rho_2\hbox{$^{\prime\prime}$ }$	$\theta_2\hbox{$^\circ$ }$	$\gamma\hbox{$^\circ$ }$	$\epsilon_{\gamma}\hbox{$^\circ$ }$	$\delta\hbox{$^{\prime\prime}$ }$	note
17190-3459	AC	32.0	138	66	4	5.5	w1	20078+0924	AB	3.3	340	201	3	1.4
17237+3709	AB	4.1	318	75	8	1.0	X	20205-2912	AC	27.2	321	71	11	0.1	m
17322+5511	AB	62.0	311	82	26	0.7		20210-1447	AB	205.2	267	94	24	1.0	Xx
17350+6153	AP	737.4	160	267	2	15.0	c	20203+3924	AC	3.4	282	279	8	0.7	1
17465+2743	AB	33.8	247	48	4	5.5	w	20587-7025	AB	6.8	113	117	13	0.5	2
17460+3919	AB	7.9	349	9	29	0.2		20591+0418	AC	10.6	68	260	5	1.7	1
17592-3656	AB	7.5	103	328	7	0.9		21022-4300	AB	57.4	73	88	27	0.6
18028+7547	AC	22.9	274	258	11	1.9	w	21041-0549	AB	2.4	195	139	13	0.4
18002+8000	AB	19.0	232	168	7	1.7		21094-7310	AC	7.2	123	235	5	1.8	w
18118+3327	AC	0.7	218	57	23	0.2		21047+0332	AB	3.4	173	108	4	1.5
18178+4351	AC	1.8	164	269	16	0.4	1O	21086+3012	AB	3.4	305	258	9	0.6
18238+5139	AB	2.6	205	95	23	0.2		21135+0713	AD	184.1	172	100	8	2.8	c1
18272+0012	AB	3.8	319	97	15	0.4	1X	21148+3803	AQ	89.9	184	264	21	1.0	wO
18239+5848	AC	88.9	20	95	29	1.0	O	21221+1948	AB	36.2	311	96	26	0.7
18338+1744	AC	1.8	275	166	10	0.5	1x	21223+5734	AP	83.7	192	189	15	0.0	mO
18497-7300	AB	1.9	271	56	8	0.5		22024-1658	AB	3.9	246	66	16	0.3
18455+0530	AB	2.5	119	62	8	0.6	2	22038+6438	AB	7.9	276	323	2	2.6
18448+3736	AD	43.7	150	90	27	0.6		21582+8252	AB	13.8	67	272	7	1.4
18465-0058	AB	12.7	121	164	13	0.6		22375+2356	AC	5.8	194	64	28	0.2	O
19021+5216	AB	5.2	299	311	12	0.5	2	22388-2037	AB	24.5	351	311	4	4.4	w
19037+5727	AB	10.6	57	42	13	0.2	m	22361+7253	AD	42.2	137	91	20	0.9	c
19091+3436	AB	16.1	262	134	6	1.7		22397-2820	AB	86.5	159	76	10	0.2	m
19083+5520	AC	6.5	30	262	9	0.8	1	23069-4331	AC	159.3	292	267	19	0.7	O
19313-0207	AB	1.3	63	298	29	0.1		23100+4758	AB	15.6	256	62	8	1.2
19407-1618	AC	45.6	42	87	26	0.7		23175+1652	AB	2.2	26	228	16	0.3	o
20014+1045	AB	3.8	354	167	5	1.0		23191-1328	AB	12.6	351	125	6	1.5

Notes:
``c'': first epoch $\rho$, $\theta$ are taken from CCDM rather than from WDS;
``w'': second epoch position is taken from WDS (no Hipparcos or Tycho identifications);
``*'': one of the alternative Hipparcos solutions is accepted;
``1'',``2'' or ``3'': Hipparcos or Tycho photocenter positions are computed for primary, secondary or both subsystems of the object, respectively;
``m'': Tycho-II proper motion difference is used to compute $\gamma$instead of $\rho$, $\theta$-change;
``O'',``o'': position parameters are corrected for orbital motion in primary, secondary subsystems of the object;
``X'',``x'': uncertainty from unpredictable motion in primary, secondary subsystem is taken into account in $\epsilon_\gamma$.

Figure 5: Distributions $f(\gamma )$ for two halves of the sample: with $a_{\rm out}/a_{\rm in}$ less than 44 (dashed line) and more than 44 (solid line). Deviations of $f(\gamma )$ from flat are characterized by $\chi^2\!\approx\!29$ and $\chi^2 \approx~15$, respectively; this tendency is expected from stability constraints.

Alternatively, we can try to look for the variation of $f(\gamma )$among the subsamples with different $a_{\rm out}/a_{\rm in}$. The output sample was thus divided in two halves by the ratio $a_{\rm out}/a_{\rm in}$(the median ratio is $\approx$44). We find that, indeed, the significance of the deviation of $f(\gamma )$ from the uniform one decreases for a "stable'' half-sample of objects ( $a_{\rm out}/a_{\rm in}\!>\!44$; see Fig. 5): the ${\sim}90\hbox{$^\circ$ }$ bins are redistributed into $150\hbox{$^\circ$ }$- $180\hbox{$^\circ$ }$bin. Nevertheless, evidently, the dynamical stability constraint alone is unable to account for the observed $f(\gamma )$.

Angular momentum transfer.

The outer subsystem may receive angular momentum and get circularized via the torques from the gaseous material in the system and those from the inner binary (see Artymowicz & Lubow 1996; Reipurth 2000; Mardling & Aarseth 2001 and references therein). This process may take place at the earliest stages of the formation of the system. In general, it is characterized by the outward transfer of the angular momentum which makes the inner system more eccentric and the outer more circular. Thus the outer system may become nearly circular, having a degree of hierarchy far above that demanded by pure dynamical stability constraints.

At the current stage, we cannot reach more definitive conclusions about the shape and origin of f(e) for orbits in multiple stars. Larger samples of systems with precisely measured relative proper motions will give a better input information. In this respect, the launch of the GAIA mission of ESA seems to be most promising.

Acknowledgements

Part of this work was supported by the Fellowship of the Belgian Services Fédéraux des Affaires Scientifiques, Techniques and Culturelles, which provided the possibility for the author to work at the Royal Observatory of Belgium. I'm grateful to Dr. A. Tokovinin for his support and encouraging through the progress of this work and to E. van Dessel and Th. Nakos for remarks on the text.
This research made extensive use of Simbad database operated at CDS, Strasbourg, France and of the Digital Sky Survey produced at the Space Telescope Science Institute, USA.