3 Angle $\gamma$ and the role of subsystems

The vectors of the outer component relative motion (modulus $\delta$and the angle $\gamma$) were computed as follows:

$$\delta^2 = \rho_1^2+\rho_2^2-2\rho_1\rho_2 \cos{\Delta \theta}$$

$$\tan{\gamma} = \frac{\rho_2\sin{\Delta \theta}} {\rho_2\cos{\Delta \theta} - \rho_1},$$

where $\Delta \theta=\theta_2-\theta_1$ and indices 1 and 2 refer to the first and second epoch observations, respectively. The angle $\gamma$ refers hereby to the second epoch. The errors of $\delta$ and $\gamma$ come mostly from the uncertainty of the WDS-position which is poorly defined for visual observations. Nevertheless, we adopt the error model based on the works of Douglass (1992) and Pannunzio et al. (1988). The error in separation $\epsilon_{\rho}$grows linearly from $\pm 0\hbox{$.\!\!^{\prime\prime}$ }07$ to $\pm 0\hbox{$.\!\!^{\prime\prime}$ }3$ in the $0\hbox{$^{\prime\prime}$ }$- $30\hbox{$^{\prime\prime}$ }$ range of $\rho$. The transversal error $\rho\epsilon_{\theta}$ grows from a 0.5 to 1.0 fraction of this value in the same range. For systems wider than $30\hbox{$^{\prime\prime}$ }$, the error of $\theta$ is dominated by the $\pm 0.5\hbox{$^\circ$ }$ round-off error of the published WDS catalogue data.

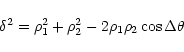
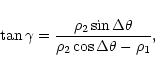
In a hierarchical multiple star, the outer companion orbits around the center of mass of stars which constitute the inner hierarchical levels. This means that the body "A'' (and/or "B'') in Fig. 1 is in fact the gravity center of inner sub-systems. Meanwhile, the measurements are made having as a reference point either the photocenter or even one of the companions of an inner subsystem (if it is resolved). This reference point also shifts at the sky due to the orbital motion in the inner subsystem. A correction of the position parameters is needed to convert the observed parameters $\rho$, $\theta$ into $\rho_0$, $\theta_0$, latter referring already to the position of the gravity center of the inner subsystem.

This correction was applied in case of the known orbital motion in the inner subsystem. Otherwise, an estimate of the unknown photocenter motion in inner sub-systems was incorporated into the error assessment of the calculated $\gamma$. This procedure removed from the sample the systems in which an apparent motion of the outer companion reflects mainly the orbital motion in the inner subsystem.

The final values of the relative motion modulus $\delta$ were checked to be consistent with the expected orbital motion velocities. A few $\delta$appear unreally large and mostly result from uncertainty of a position angle. Nevertheless, respective dynamical parallaxes

$$DP = 0\hbox{$.\!\!^{\prime\prime}$ }418 \left[ \frac{\rho}{{\... ...\left(\frac{\delta}{\Delta(\rm Epoch)}\right)^2 \right]^{1/3}$$

(Russell & Moore 1940) statistically resemble the MSC parallax estimates $\pi$: median ratio $DP/\pi$ is 1.15; 10%- and 90%-percentiles of this ratio are 0.67 and 3.0.

The values of the $\gamma$-angle corrected for motion in the inner subsystems are given in Table 1. In total, 174 systems are presented for which all the corrections still allow to determine $\gamma$ with a precision better than $\pm30\hbox{$^\circ$ }$. The note column provides the information on the used sources of data and on the applied corrections for the calculation of $\gamma$.

The relative proper motions derived by us suffer to some extent from round-off errors in WDS data for the first epoch positions. In contrast to our approach, Brosche & Sinachopoulos (1988, 1989) used original observational data to compute the relative motions instead of somehow generalized values in WDS. Nevertheless, the fifteen objects which are common to both studies show the good agreement of the derived angles $\gamma$ given our $\gamma$-errors $\epsilon_\gamma$:

$$\left<\vert\gamma_{\rm BS}-\gamma\vert~/~\epsilon_\gamma\right>\approx1.0.$$

It is worth to note that the usage of precise second-epoch parameters removes some biasing of angles $\gamma$ caused by the round-off errors (this bias would be noticeable if only the WDS data were used).