1 - Institut für Astronomie, Universität Wien, Türkenschanzstr.17, 1180 Vienna, Austria
2 - Department of Experimental Physics and Astronomical Observatory, University of Szeged, Hungary

Abstract
We discuss the possibilities of investigating the semiregular and irregular light change found in evolved late type giant stars with photometric and visually obtained (amateur) data. Period analysis has been done on light curve data from both sources for a sample of semiregular variables. The results are compared to test the ability of visual data to show the frequency contents present in these variables. We find that both sources of data complete each other, as fitting the fine structure visible only in the photometric data needs long-term visual monitoring to guarantee the uniqueness of the fit.

Key words: stars: variables: general - stars: late-type - stars: AGB and post-AGB - methods: observational - techniques: photometric

As a result, only for a small number of AGB stars have good lightcurves been obtained with high photometric accuracy (see, e.g., Percy et al. 1989; Cristian et al. 1995; Percy et al. 1996; Lebzelter 1999; Kiss & Skiff 2001; Percy et al. 2001). Our knowledge of the light change of these variables is mainly based on the one hand on the analysis of large archives of photographic plates obtained during the first half of the 20th century (e.g. Houk 1963; Lebzelter et al. 1995), and on the other hand on the observations of a large number of amateur astronomers who contribute their measurements to public access databases (e.g. AAVSO, AFOEV, VSOLJ, BAA/VSS, HAA/VSS - see Kiss et al. 1999, 2000 for recent applications).

Due to small irregularities in the light change of all types of variables on the AGB, predictions of the phase and even of fundamental parameters like cycle length or amplitude are not possible over several light cycles. Therefore, amateur data have been the only available source in the past years, whenever the current characteristics of a star's light change was needed.

However, the vast majority of the amateur data are not obtained with a CCD or a photomultiplier, but are visual estimates of the current brightness of a star, and are therefore of limited accuracy. Recently, robotic photometric telescopes have become a new source of highly accurate photometric data of AGB variables providing also the necessary time coverage in a comfortable way. Nevertheless, these robotic telescopes can monitor only a small fraction of the large number of AGB variables. Furthermore, with a few exceptions (e.g. Percy et al.2001), only a relatively small number of light cycles have been measured with automatic telescopes up to now. Therefore, visual data are still a highly important source of information on the light change of these stars.

In this context we note that recent surveys looking for gravitational lenses (e.g. MACHO) provided photometric light curves with a good time coverage for a large number of red variables in the Magellanic Clouds and the Galactic Bulge. This sample allows one to investigate a variety of common aspects of different groups of variables (Wood 2000), but does not help to correlate the light change with other observations that can only be obtained for objects that are much closer.

But how reliable and useable are the light curves obtained by visual estimates of amateur astronomers? Our paper aims to investigate this question by a comparison of the light curve obtained by a robotic telescope using a photomultiplier as detector and the light curve derived from databases of visual observations for a sample of semiregular variables.

2 Data

2.1 APT observations

The sample of stars used here is part of a program to monitor semiregular and irregular variables over a long time initiated by one of us (TL). The aim was to study the light and colour variations of SRVs and to provide phase estimation for stars observed spectroscopically. A more detailed description of the whole project can be found in Lebzelter (1999). First results for individual stars have been presented elsewhere (Kerschbaum et al. 2001).

Stars are observed on average every second night. The brightness of the program stars is measured relative to two comparison stars. For the latter, absolute photometry has been obtained which was found to be in excellent agreement with the photometry given in the Hipparcos catalogue. The photometric accuracy is typically better than 0 $.\!\!^{\rm m}$ 02. Observations are done in Johnson V and $I_{\rm C}$ filters. Due to the bad weather season in Arizona the telescope is not operated from July to mid-September.

The selection of late-type variables for observation with the APT has been driven by the technical constraints of the configuration used. The finding algorithm of the telescope cannot handle stars that are weaker than about 12.5 to 13 mag and the brightness of the star has to be known as accurately as $\pm$ 1.5 mag. Due to the second constraint for observing miras with the APT the input file would have to be updated several times during a light cycle (based on at least some phase information of the star!). As the large amplitude variability of miras is well monitored by amateur astronomers, we did not want to invest this additional effort. Therefore we have not observed miras with the APT thus far. As a further selection criterion the summer shutdown was relevant in excluding stars visible almost exclusively during that time.

For the present paper we selected those objects for which at least 100 data points have been obtained. Our sample consists of 26 semiregular and irregular variables with a moderate amplitude in V up to 2.5 mag. Their list is presented in Table 1 (left column).

2.2 Visual observations

Table 1: The list of programme stars with the basic properties of the analysed datasets.
Name IRAS name APT: from...to number visual: from...to number number of points/bins

(JD-2400000) of points (JD-2400000) of points simultaneous points

EP Aqr 21439-0226 50714-51847 161 51371-51860 19 17

CI Boo 14200+2935 51219-51986 184 51262-51426 8 8

RV Boo 14371+3245 51219-51986 188 39293-51972 1119 205 1.3

RV Cam 04265+5718 50473-51981 312 51271-51832 16 15

CW Cnc 09057+1325 51529-51986 107 - - -

U Del 20431+1754 50519-51874 283 21129-51999 9762 2107 7.8

TX Dra 16342+6034 51219-51952 139 25501-52000 7624 814 5.6

BR Eri 03463-0710 50714-51908 250 46357-51983 36 7

g Her 16269+4159 50520-51981 287 20313-52000 15 279 2513 8.6

X Her 16011+4722 50400-51986 331 19667-52000 8468 1746 5.9

EY Hya 08437+0149 51530-51986 92 47552-47653 8 0

FZ Hya 08189+0507 50485-51986 342 51562 1 1

FK Hya 08220-0821 50465-51986 365 - - -

AF Leo 11252+1525 51530-51986 65 51273 1 0

SX Leo 11010-0256 50468-51986 330 45054-51999 166 103

FZ Lib 15166-0857 50473-51986 368 51306 1 1

o¹ Ori 04497+1410 51148-51957 169 51598-51599 2 2

UW Peg 22156+0228 50714-51894 204 51468 1 1

AC Pup 08204-1545 50489-51985 366 - - 0

TT UMa 09013+6029 50465-51985 407 - - 0

Y UMa 12380+5607 50465-51986 398 19842-51982 1977 661 2.2

AZ UMa 11445+4344 50464-51985 436 - - 0

V UMi 13377+7433 51218-51729 74 20246-52000 6293 478 4.7

BK Vir 12277+0441 51530-51986 117 51262-51902 19 9

RT Vir 13001+0527 50465-51986 291 45100-51719 134 57

RW Vir 12046-0629 50465-51986 412 23887-51718 54 43

**Table 1:** The list of programme stars with the basic properties of the analysed datasets.
Name	IRAS name	APT: from...to	number	visual: from...to	number	number of	points/bins
		(JD-2400000)	of points	(JD-2400000)	of points	simultaneous points
EP Aqr	21439-0226	50714-51847	161	51371-51860	19	17
CI Boo	14200+2935	51219-51986	184	51262-51426	8	8
RV Boo	14371+3245	51219-51986	188	39293-51972	1119	205	1.3
RV Cam	04265+5718	50473-51981	312	51271-51832	16	15
CW Cnc	09057+1325	51529-51986	107	-	-	-
U Del	20431+1754	50519-51874	283	21129-51999	9762	2107	7.8
TX Dra	16342+6034	51219-51952	139	25501-52000	7624	814	5.6
BR Eri	03463-0710	50714-51908	250	46357-51983	36	7
g Her	16269+4159	50520-51981	287	20313-52000	15 279	2513	8.6
X Her	16011+4722	50400-51986	331	19667-52000	8468	1746	5.9
EY Hya	08437+0149	51530-51986	92	47552-47653	8	0
FZ Hya	08189+0507	50485-51986	342	51562	1	1
FK Hya	08220-0821	50465-51986	365	-	-	-
AF Leo	11252+1525	51530-51986	65	51273	1	0
SX Leo	11010-0256	50468-51986	330	45054-51999	166	103
FZ Lib	15166-0857	50473-51986	368	51306	1	1
o¹ Ori	04497+1410	51148-51957	169	51598-51599	2	2
UW Peg	22156+0228	50714-51894	204	51468	1	1
AC Pup	08204-1545	50489-51985	366	-	-	0
TT UMa	09013+6029	50465-51985	407	-	-	0
Y UMa	12380+5607	50465-51986	398	19842-51982	1977	661	2.2
AZ UMa	11445+4344	50464-51985	436	-	-	0
V UMi	13377+7433	51218-51729	74	20246-52000	6293	478	4.7
BK Vir	12277+0441	51530-51986	117	51262-51902	19	9
RT Vir	13001+0527	50465-51986	291	45100-51719	134	57
RW Vir	12046-0629	50465-51986	412	23887-51718	54	43

The total number of visual (amateur) observations, taken from the publicly available database of the Association Française des Observateurs d'Étoiles Variables (AFOEV), for the stars in the APT sample is given in Table 1. Obviously, less than half of the APT variables have well-observed visual light curves. Very little additional data exist in the similar database of the Variable Star Observers' League in Japan (VSOLJ) and the AAVSO International Database. The latter was judged from the quick-look at their light curves (see http://www.aavso.org/adata/curvegenerator.shtml). Therefore, we decided to use only AFOEV data for the best-observed SRVs. The lack of visual data for the majority of stars is mainly due to their low amplitudes: some stars are totally neglected by the amateur organizations, because it is assumed that their light changes are extremely difficult or even impossible to detect visually. It is interesting to note that none of the stars classified as irregular variables in the GCVS (CI Boo, CW Cnc, FZ Hya, FK Hya, FZ Lib, AC Pup, TT UMa, AZ UMa and RW Vir) has been observed frequently. In our list there are 7 variables with well-defined and more or less continuous visual light curves, their names are typeset in boldface in Table 1. These stars formed the basis of our comparative analysis.

Before the comparison with the APT data, two steps were performed in the data handling. The first one takes 5-day means of the original light curves. The bin length was chosen to be the same for all of the stars. This way a homogeneous sample could be formed. In practice, different bins might be used, only the amplitude decrease due to the too long bins should be avoided. In our case, the 5-day long bins resulted in calculating mean points from 2 to 9 (typically 5-6) individual estimates. The standard deviation of these averages ranged from 0 $.\!\!^{\rm m}$ 1-0 $.\!\!^{\rm m}$ 3. The second step takes another binned light curve, but here we used a Gaussian weight-function. It means that potentially a much wider region of the light curve affects the individual mean data points. Our experience showed that only a slight Gaussian smoothing is required to get "good'' data, in practice we never used a wider (FWHM) Gaussian than $0.8 \times {\rm bin}$ length (in our case, 4 days). A good example is shown in Fig. 1, where the original light curve is compared with the averaged and smoothed one. We note that the whole procedure was also shown for RY Dra in Kiss et al. (1999) for illustrative purposes only.

3 Comparison

The first comparison addresses the determination of the mean brightness and cycle-to-cycle variations of the amplitudes. For this, we plot all analysed APT and visual data in common graphs in Fig. 2.

Two important general remarks can be drawn based on the direct comparison. First of all, there are systematic shifts between the curves which can be attributed to the red colours of the variables. It is well-known that visual photometric estimates suffer from a quite strong colour-dependent systematic shift. Several transformation equations have been derived between $m_{\rm vis}$ and Johnson V data, from which one of the most easily usable is that of Stanton (1981) and Zissell (1998):

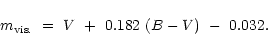
But this difference might have a severe impact on light curve data for mira variables. Miras can show B-V variations of more than 0 $.\!\!^{\rm m}$ 5. Using the formula of Stanton this would have only a rather small effect. The difference between using the amplitude from visual data directly and a colour-corrected amplitude would be of the order of 0 $.\!\!^{\rm m}$ 1, i.e. just about two percent of the typical V amplitude. However, as our comparison for the SRVs shows, the Stanton formula does not give the correct shift for late type stars. Therefore we compare in Fig. 3 the photometric V light curve of the mira R Hya obtained by Celis (1977) with visual data which have been treated the same way as the semiregular variables described above. A shift between the visual and the photometric data of about 0 $.\!\!^{\rm m}$ 5 can be clearly seen. But obviously there is no difference in the shape of the variation or in the amplitude. The same result was reached for two other miras, o Cet and S Vir. Therefore, although the conversion formula between photometric and visual data needs to be revised, this has no significant effect on the lightcurve data derived from visual observations.

Note that the shift may also be affected by the selection of comparison stars. Both photometric and visual magnitudes are measured relative to comparison stars, which are, however, typically not identical for the two data sets. It has to be expected that a difference in colour between the comparison stars of the two data sets has an effect on the observed brightness shift. For the visual data we do not know which comparison stars have been used. From our experience we have to assume that not all observers used the same comparison stars. Therefore we cannot study this effect in more detail with the data sets available.

The second remark is that visual data define very similar light curves to the APT data. The cycle-to-cycle changes are well reproduced by both datasets and even the amplitudes of individual cycles are similar. The light extrema can be easily estimated in both sets and consequently, the mean amplitude can be derived with good agreement. Some underestimate caused by the averaging is unavoidable, but in most cases the differences do not exceed 0 $.\!\!^{\rm m}$ 1.

The similarity of the light curves can be quantified by determining and comparing the frequency content of the corresponding datasets. This is also a very important point considering the pulsation of these variables. For this purpose, we have performed standard Fourier-analyses with Period98 (Sperl 1998) of the APT and visual light curves separately. For illustration we present in Figure 4 a typical Fourier spectrum of an APT light curve. The resulting periods were also compared with the results of period analyses of long-term (70-90 years) visual data by Kiss et al. (1999).

We plot the APT and visual data with the finally adopted multicomponent harmonic fits in Fig. 5. The uncertainties of the periods given can be estimated from the half width at half maximum of the peak in the Fourier power spectrum. This quantity is inversely proportional to the length of the data set. We list the corresponding value together with the periods used for each star below. The results on the individual objects can be listed as follows:

RV Boo: the frequency analysis of APT data yielded to the following results (periods and amplitudes are given):

P₁: 228 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 33	P₂: 97 $.\!\!^{\rm d}$ 8, A₂: 0 $.\!\!^{\rm m}$ 16
P₃: 86 $.\!\!^{\rm d}$ 8, A₃: 0 $.\!\!^{\rm m}$ 05	P₄: 63 $.\!\!^{\rm d}$ 1, A₄: 0 $.\!\!^{\rm m}$ 05.

P₁: 210 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 18	P₂: 144 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 13
P₃: 60 $.\!\!^{\rm d}$ 6, A₃: 0 $.\!\!^{\rm m}$ 06

$\Delta f =$ 0.00075 c/d. GCVS lists 137 $^{\rm d}$ , while Kiss et al. (1999) gave a single period of 144 $^{\rm d}$ with 0 $.\!\!^{\rm m}$ 09. The individual cycles of APT data also support a c.c. 150 $^{\rm d}$ period, but a "blind'' frequency analysis does not reveal this period. Keeping in mind the full length of data, P₁(APT)-P₁(vis.) and P₄(APT)-P₃(vis.) are in good agreement.

P₁: 1190 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 32	P₂: 630 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 13
P₃: 205 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 12	P₄: 174 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 10
P₅: 83 $.\!\!^{\rm d}$ 2, A₅: 0 $.\!\!^{\rm m}$ 06	P₆: 53 $.\!\!^{\rm d}$ 6, A₆: 0 $.\!\!^{\rm m}$ 05.

The analysis of the visual light curves results in:

P₁: 1220 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 30	P₂: 560 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 12
P₃: 322 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 07	P₄: 139 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 05
P₅: 208 $^{\rm d}$ , A₅: 0 $.\!\!^{\rm m}$ 05	P₆: 114 $^{\rm d}$ , A₆: 0 $.\!\!^{\rm m}$ 04
P₇: 82 $^{\rm d}$ , A₇: 0 $.\!\!^{\rm m}$ 04

$\Delta f =$ 0.00048 c/d. GCVS: 110 $^{\rm d}$ , Kiss et al. (1999): 1146 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 21, 580 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 05. The long period (1200 $^{\rm d}$ ) is well-defined, the second one at $\sim$ 600 $^{\rm d}$ is also, while some components can be well identified in both datasets (200+ days, 83 $^{\rm d}$ ). Most components are due to the quite irregular change of the mean brightness. Visual data also support the GCVS period at 110 $^{\rm d}$ , but with low significance. The main problem is that the frequency content is highly variable in time, therefore, only some sort of mean cycle length can be derived.

P₁: 74 $.\!\!^{\rm d}$ 3, A₁: 0 $.\!\!^{\rm m}$ 19	P₂: 232 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 08
P₃: 46 $.\!\!^{\rm d}$ 3, A₃: 0 $.\!\!^{\rm m}$ 06.

The analysis of the visual light curves results in:

P₁: 127 $^{\rm d}$ , A₁:0 $.\!\!^{\rm m}$ 11	P₂: 145 $^{\rm d}$ , A₂:0 $.\!\!^{\rm m}$ 08
P₃: 85 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 08	P₄: 9560 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 09
P₅: 239 $^{\rm d}$ , A₅: 0 $.\!\!^{\rm m}$ 05	P₆: 53 $.\!\!^{\rm d}$ 3, A₆: 0 $.\!\!^{\rm m}$ 05

$\Delta f =$ 0.00091 c/d. GCVS: 78 $^{\rm d}$ , Kiss et al. (1999): 706 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 10, 137 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 06, 77 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 07. However, we have shown that this star is the best example of repetitive mode change (and the last one occurred in early 2000, just as was predicted in Kiss et al. 1999), thus the only meaningful result is that simultaneous visual data reveal a similar set of frequencies (75-80 $^{\rm d}$ , 230+ days, 50 $^{\rm d}$ ). We have to note that this case is the worst one in the whole comparison, however, the APT coverage is quite scanty. Still it can be seen that the visual data do not match the APT data as well as for the other objects.

P₁: 90 $.\!\!^{\rm d}$ 7, A₁: 0 $.\!\!^{\rm m}$ 08	P₂: 306 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 12
P₃: 935 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 09	P₄: 69 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 06.

P₁: 1100 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 07	P₂: 88 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 06
P₃: 62 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 04	P₄: 384 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 04

$\Delta f =$ 0.00044 c/d. GCVS: 89 $^{\rm d}$ , Kiss et al. (1999): 887 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 20, 90 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 07. Obviously, the numbers can be associated unambiguously. The long period (1000 $^{\rm d}$ ) is well revealed considering the full length of analyzed datasets. 90 $^{\rm d}$ and 60+ days are also in agreement. Some uncertainty is present in the 300+ days period. But generally, both datasets define the same set of periods.

P₁: 101 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 19	P₂: 165 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 19
P₃: 395 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 12	P₄: 155 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 09.

P₁: 101 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 14	P₂: 175 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 15
P₃: 133 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 11	P₄: 194 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 11
P₅: 620 $^{\rm d}$ , A₅: 0 $.\!\!^{\rm m}$ 07	P₆: 385 $^{\rm d}$ , A₆: 0 $.\!\!^{\rm m}$ 06

$\Delta f =$ 0.00045 c/d. GCVS: 95 $^{\rm d}$ , Kiss et al. (1999): 178 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 05, 102 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 03. Again, there are remarkable similarities. The main periodicity at 101 $^{\rm d}$ is very well revealed by both sets. At longer periods some differences exist, but their actual values (10-20 days) corresponds to only a few percent relative uncertainty.

P₁: 161 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 29	P₂: 537 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 10
P₃: 153 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 07	P₄: 82 $.\!\!^{\rm d}$ 2, A₄: 0 $.\!\!^{\rm m}$ 13
P₅: 199 $^{\rm d}$ , A₅: 0 $.\!\!^{\rm m}$ 09	P₆: 71 $.\!\!^{\rm d}$ 6, A₆: 0 $.\!\!^{\rm m}$ 03.

P₁: 310 $^{\rm d}$ , A₁: 0 $.\!\!^{\rm m}$ 16	P₂: 585 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 11
P₃: 205 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 07	P₄: 1065 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 06
P₅: 83 d, A₅: 0 $.\!\!^{\rm m}$ 04.

$\Delta f =$ 0.00043 c/d. GCVS: 168 $^{\rm d}$ , Kiss et al. (1999): 324 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 16, 315 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 09, 164 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 06. This star is a very interesting case. Due to the bad sampling, APT data give an alias period, therefore, here the visual data yield much better results compared with the long term dataset by Kiss et al. (1999). The short, 82 $^{\rm d}$ period can be the harmonic of the 160+ days period. Obviously, such a short time span causes ambiguous results. We note that the result may also be affected by the significant difference between visual and APT data at the maximum around JD 2451200.

P₁: 72 $.\!\!^{\rm d}$ 5, A₁: 0 $.\!\!^{\rm m}$ 40	P₂: 794 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 27
P₃: 65 $.\!\!^{\rm d}$ 9, A₃: 0 $.\!\!^{\rm m}$ 11	P₄: 124 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 06.

P₁: 71 $.\!\!^{\rm d}$ 9, A₁: 0 $.\!\!^{\rm m}$ 28	P₂: 670 $^{\rm d}$ , A₂: 0 $.\!\!^{\rm m}$ 22
P₃: 64 $^{\rm d}$ , A₃: 0 $.\!\!^{\rm m}$ 11	P₄: 132 $^{\rm d}$ , A₄: 0 $.\!\!^{\rm m}$ 09

$\Delta f =$ 0.00089 c/d. GCVS: 72 $^{\rm d}$ , Kiss et al. (1999): 737 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 06, 126 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 04, 73 $^{\rm d}$ 0 $.\!\!^{\rm m}$ 06. Considering that the time span is barely 600 days, even the recovery of the long period is quite good. The remaining numbers do not need detailed discussion, their agreement is simply excellent.

4 Discussion

There are several important aspects which follow from the above discussed comparisons. As expected from a simple comparison of the plots, visual data are a reliable source used to estimate the main variability period and amplitude of a SRV. The amplitude may depend on the applied averaging method, i.e. the binning length has to be choosen with care. In practice, one has to take a look at the original data and estimate an approximate "cycle length''. Then the binning length should not exceed $\sim$ 10% of the estimated characteristic time-scale of variation.

Another important point is the number of independent visual estimates per bin. The best agreement is found in those cases when there were at least 4-5 points per bin in average. Reaching the optimal mean light curve may need some slight tuning of the binning length.

It follows also from the visual comparison that variations with an amplitude of less than 0 $.\!\!^{\rm m}$ 1 can be hardly detected in the visual data. As such variations obviously occur in the APT data, we conclude that the total light change of SRVs is more complex than visual data can reveal. Similar limitations are raised when studying light variations of large-amplitude Mira stars. Although visual light curves of Mira variables are extensively used to describe long-term behaviour (e.g. Mennessier et al. 1997), short-term and small-amplitude irregularities were not discovered until the analysis of Hipparcos epoch photometry revealed the presence of such rapid light changes (de Laverny et al. 1998).

The period analyses of simultaneous APT and visual light curves revealed that it is extremely difficult to fit the light change of SRVs accurately (at least in form of multicomponent harmonic fits). There are two stars (g Her and Y UMa) in our sample for which data have been analysed independently by Kerschbaum et al. (2001). It is interesting (and illustrative) to compare their results with ours. In g Her Kerschbaum et al. found the following periods: 89 $^{\rm d}$ (this is the strongest), 74 $^{\rm d}$ , 103 $^{\rm d}$ , 1239 $^{\rm d}$ . From these values, two are in agreement with our findings, two are not. In Y UMa, Kerschbaum et al. give 331 $^{\rm d}$ , 166 $^{\rm d}$ (2f), 260 $^{\rm d}$ , 358 $^{\rm d}$ , 725 $^{\rm d}$ , in which 166 $^{\rm d}$ and 260 $^{\rm d}$ are the strongest. Obviously, our description differs essentially, though the fits look equally good in both cases. We tried to quantify the quality of the fit by calculating O-C values for the fit by Kerschbaum et al. and our fit. The mean absolute differences are given in Table 2. The corresponding value for the fit of the visual data has been added for comparison.

Table 2: Comparison of observed and calculated light curves. The average of the absolute differences between observed and calculated values is given.
g Her Y UMa

aver. $\sigma$ aver. $\sigma$

APT $_{\rm this\ paper}$ 0 $.\!\!^{\rm m}$ 05 0 $.\!\!^{\rm m}$ 04 0 $.\!\!^{\rm m}$ 02 0 $.\!\!^{\rm m}$ 02

APT $_{\rm Kerschbaum\ et\ al.\ (2001)}$ 0 $.\!\!^{\rm m}$ 04 0 $.\!\!^{\rm m}$ 03 0 $.\!\!^{\rm m}$ 03 0 $.\!\!^{\rm m}$ 03

visual $_{\rm this\ paper}$ 0 $.\!\!^{\rm m}$ 06 0 $.\!\!^{\rm m}$ 05 0 $.\!\!^{\rm m}$ 07 0 $.\!\!^{\rm m}$ 05

**Table 2:** Comparison of observed and calculated light curves. The average of the absolute differences between observed and calculated values is given.
	g Her	Y UMa
	aver.	$\sigma$	aver.	$\sigma$
APT $_{\rm this\ paper}$	0 $.\!\!^{\rm m}$ 05	0 $.\!\!^{\rm m}$ 04	0 $.\!\!^{\rm m}$ 02	0 $.\!\!^{\rm m}$ 02
APT $_{\rm Kerschbaum\ et\ al.\ (2001)}$	0 $.\!\!^{\rm m}$ 04	0 $.\!\!^{\rm m}$ 03	0 $.\!\!^{\rm m}$ 03	0 $.\!\!^{\rm m}$ 03
visual $_{\rm this\ paper}$	0 $.\!\!^{\rm m}$ 06	0 $.\!\!^{\rm m}$ 05	0 $.\!\!^{\rm m}$ 07	0 $.\!\!^{\rm m}$ 05

Taking into account the partly irregular light change of these stars the resulting differences between the data and the fit is in all cases less than 10% of the observed light amplitude. The slightly larger differences found for the visual data can be understood as due to the lower accuracy in the observational data. Comparing the numbers for the APT data in Table 2 we think that one cannot really quantify which fit is better. This means that a uniqueness of the solution is not guaranteed and this again becomes more visible in the APT data than in the visual data. This is a critical point for a possible combination of APT and visual data. The latter can provide important input as to what the star is doing during the observational holes in the APT data. This should help to limit the number of possible solutions.

The periods given in this paper for the individual stars have been derived in an attempt to produce a good fit to the light curve. This does not mean that they are all really excited in the stars. Some periods may be artefacts needed to get good fits. To get an idea of this effect we split the APT light curve of gHer into two equal halves and made a Fourier analysis on each half. The first half gives 92, 265, 62 and 428 days as the strongest peaks, while the second half leads to periods of 696, 83, 93 and 41 days. The main period of about 90 days is present in both halves. Beside that, a long and a short period is visible in both data sets as well, but the derived periods are clearly different. This example illustrates the problem one is confronted with when trying to accurately determine the period(s) of a semiregular variable.

When comparing APT analyses with longer visual data series, we noticed the following interesting result: 3-4 years of accurate APT data reveal the frequency content at similar precision as 15-20 years of visual data. This has very important consequences for stars with a highly variable period pattern. One can follow more adequately the possible mode changes, which can occur quite regularly (see, e.g. the case of TX Dra - Kiss et al. 1999, or W Cyg and AF Cyg - Kiss et al. 2000).

5 Conclusions

The variability behaviour of SRVs is interesting for several reasons, which favour different approaches for the monitoring of the light change:

a) Defining the variability class of a variable star. As the separation is still done mainly into SRVs and Miras, both photoelectric and (amateur) visual data provide the necessary information to classify a star. Irregular variables, if they really exist, may be difficult to detect with both sources of data. A combination may help.

b) Determining of the period for any kind of correlation with other stellar properties: both datasets provide a very similar "main'' period in most cases. A critical question may be: what is the main period of the star?

c) Determining the number and periods of excited modes in SRVs, for instance, to derive the origin of the pulsation, explain the irregularities, etc.: in this case our comparison shows that the APT data reveal more details. These, however, may need continuous visual data to achieve a better and more definitive result concerning the uniqueness of the solution and therefore the identification of the true excited periods. The fact that stars classified as irregular variables are obviously much less frequently observed by amateur astronomers than semiregular variables may be a hint that the irregular variables are not a separate variability class but are insufficiently observed SRVs. This would be in agreement with several other investigations of these stars (Lebzelter et al. 1995; Kerschbaum et al. 1996, 2001).

d) Detection of long-term variations that may also have different reasons than pulsation: APT datasets are still rather short. They may only allow one to get a very rough impression of the long time change. The long time series of visual data are here clearly an advantage.

e) Detect mode changes: as these occur also on timescales typically longer than the currently existing APT data series, visual data are more suitable for this task. Predicted mode changes can possibly be studied in detail by APT data.

As a result we find that investigations of SRV light curves need both sources of data to achieve the best results. The limitations of using only one source have to be kept in mind whenever addressing one of the questions discussed above.

The amount of data provided by automatic photometric telescopes is increasing steadily. To gain more detailed insight into the light change of these variables it may become important to establish a common database for APT data to make them available to the scientific community, similar to the databases provided by amateur organisations.

Monitoring of LPVs with an automatic telescope.

II: A comparison of APT data and visual observations

1 Introduction