A&A 380, 123-129 (2001)
DOI: 10.1051/0004-6361:20011439
An accelerated jet in DA193?
W. H. Wang 1,2 - X. Y. Hong 1,2 - D. R. Jiang 1,2 - T. Venturi 3 - Y. J. Chen 1,2 - T. An 1,2
1 - Shanghai Astronomical Observatory, Chinese Academy of
Sciences, Shanghai 200030, PR China
2 - National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, PR China
3 - Institutor di Radioastronomia del CNR, Via P. Gobetti 101,
40129 Bologna, Italy
Received 14 August 2001 / Accepted 10 October 2001
Abstract
We present four epoch images with milliarcsecond resolution,
from VLBI (Very Long Baseline
Interferometry) observations of the quasar DA193
(J0555+3948) at 5GHz. The model-fitting results show that the
source is resolved with a core-jet structure. A proper motion of
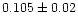 mas yr-1 of the jet component was
estimated, which corresponds to an apparent velocity of
mas yr-1 of the jet component was
estimated, which corresponds to an apparent velocity of
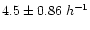 c at its redshift of z=2.365. Estimates of the
Doppler factor and of the brightness temperature confirm that this
source is considerably boosted towards the line of sight. The
velocity is about 4 times larger than previous estimates, which
may indicate (1) that the jet component is being accelerated, possibly
due to a bending jet aligned close to the line of sight;
or (2) that there are two different components ejected in two flares.
The possibility that multiple ejection of short-lived components is
taking place in the core region of DA193 is also presented.
Throughout this paper, the
values q0=0.5, H0=100 kms-1Mpc-1 will be used.
c at its redshift of z=2.365. Estimates of the
Doppler factor and of the brightness temperature confirm that this
source is considerably boosted towards the line of sight. The
velocity is about 4 times larger than previous estimates, which
may indicate (1) that the jet component is being accelerated, possibly
due to a bending jet aligned close to the line of sight;
or (2) that there are two different components ejected in two flares.
The possibility that multiple ejection of short-lived components is
taking place in the core region of DA193 is also presented.
Throughout this paper, the
values q0=0.5, H0=100 kms-1Mpc-1 will be used.
Key words: galaxies: jets - galaxies: quasars: general - galaxies: quasars: individual: DA193
The study of compact radio sources with Very Long Baseline
Interferometry (VLBI) has revealed some intrinsic properties of
active galactic nuclei (AGN) (Pearson 1989; Cohen & Kellermann
1995; Hirabayashi et al. 2000).
The phenomenon of apparent superluminal motion, predicted by
theory and found by the VLBI observations, has been explained in
terms of relativistic bulk motion along (or very close to) the
line of sight of the emitting plasma in AGN (Blandford 1987; Pearson & Zensus 1987).
DA193 (RAJ2000 = 05 55
55 30.806
30.806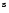 ,
DECJ2000 = 39
,
DECJ2000 = 39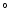 48
48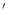 49.16
49.16
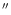 )
is identified with an 18th magnitude low-polarization
quasar at z=2.365 (Wills & Wills 1976). It is one of the
most compact radio sources known to date, both on the arcsecond
(Dallacasa et al. 1995; Stanghellini et al.
1990) and milliarcsecond (see for instance Fey et al. 1996) scale, and is characterised by a classical
homogeneous synchrotron self-absorption spectrum, with a turnover
at 5 GHz (Spangler et al. 1983). For this reason
it was classified as a GHz-peaked spectrum source (GPS) by O'Dea
et al. (1991). Because of its strong and compact nature,
DA193 has been observed with VLBI since the early 1980s
at several frequencies. At the resolution of the order of the
milliarcsecond (typical of global VLBI observations at frequencies
)
is identified with an 18th magnitude low-polarization
quasar at z=2.365 (Wills & Wills 1976). It is one of the
most compact radio sources known to date, both on the arcsecond
(Dallacasa et al. 1995; Stanghellini et al.
1990) and milliarcsecond (see for instance Fey et al. 1996) scale, and is characterised by a classical
homogeneous synchrotron self-absorption spectrum, with a turnover
at 5 GHz (Spangler et al. 1983). For this reason
it was classified as a GHz-peaked spectrum source (GPS) by O'Dea
et al. (1991). Because of its strong and compact nature,
DA193 has been observed with VLBI since the early 1980s
at several frequencies. At the resolution of the order of the
milliarcsecond (typical of global VLBI observations at frequencies
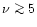 GHz) the source is only slightly resolved,
and can be interpreted as the sum of a strong dominant compact
component and a weaker one in PA ranging from
GHz) the source is only slightly resolved,
and can be interpreted as the sum of a strong dominant compact
component and a weaker one in PA ranging from
 to
to
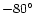 depending on the frequency and on the array (see for
example Spangler et al. 1983, 4.99 GHz observations
carried out in August 1981; Charlot 1990, 2.3 GHz
and 8.4 GHz observations carried out in May 1985;
multiepoch observations at 2.3 GHz and 8.4 GHz in Fey et al.
1996); multiepoch observations at 5 GHz in Hong et al. (1999).
depending on the frequency and on the array (see for
example Spangler et al. 1983, 4.99 GHz observations
carried out in August 1981; Charlot 1990, 2.3 GHz
and 8.4 GHz observations carried out in May 1985;
multiepoch observations at 2.3 GHz and 8.4 GHz in Fey et al.
1996); multiepoch observations at 5 GHz in Hong et al. (1999).
On the basis of 8 GHz multiepoch observations (1981.5, 1985.37,
and 1994.9), Bajkova et al. (1996) proposed a proper
motion of
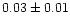 masyr-1. This is in agreement with
an analysis carried out at 5 GHz by Hong et al. (1999), and
with more recent 43 GHz VLBA imaging presented in Lister et al.
(1998), whose submilliarcsecond scale resolution revealed a
more complex structure than previously observed. In particular,
beyond the extension in PA
masyr-1. This is in agreement with
an analysis carried out at 5 GHz by Hong et al. (1999), and
with more recent 43 GHz VLBA imaging presented in Lister et al.
(1998), whose submilliarcsecond scale resolution revealed a
more complex structure than previously observed. In particular,
beyond the extension in PA
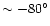 with respect to
the most compact component, another feature is visible, in PA
with respect to
the most compact component, another feature is visible, in PA
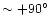 .
It is not yet clear if this component is a
counterjet or the true core.
.
It is not yet clear if this component is a
counterjet or the true core.
DA193 is one of the most common calibrator sources used
in astronomic and geodetic VLBI observations, therefore a thorough
knowledge of its radio morphology and variations is essential for
its proper use as calibrator. A wealth of data in a wide
range of radio wavelengths and resolutions is available for this
source, and this allows us to carry out this crucial investigation.
In this paper we present four epoch VLBI images at 5 GHz, from 1996 to
1997, and estimate the proper motion of the jet components based
on model-fitting results. The physical parameters of
DA193, such as the equipartition Doppler factor,
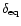 ,
the Lorentz factor
,
the Lorentz factor 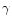 ,
the brightness
temperature,
,
the brightness
temperature, 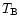 and the angle to the line of sight
and the angle to the line of sight 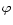 are
also estimated.
are
also estimated.
5 GHz VLBI observations of radio loud blazars, in a search for
superluminal motion, were carried out with the European VLBI
Network (EVN) on 17 June 1996 (Zhou et al. 2000), 18
February 1997 (Chen & Zhang 1999), 7 June 1997 and 7
November 1997 (Hong et al. 2001) in snapshot mode.
DA193 was used as a calibrator in all four experiments,
and it was observed about 4-6 times, in scans of 13 min each.
The resolution is typically 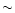 1 mas and the rms
1 mas and the rms 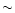 7 mJy
b-1 in the observations. The antennas involved in each epoch
and their characteristics are listed in Table 1. An
example of u-v coverage (epoch 1997.9) is given in
Fig. 1.
7 mJy
b-1 in the observations. The antennas involved in each epoch
and their characteristics are listed in Table 1. An
example of u-v coverage (epoch 1997.9) is given in
Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1813f2.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg35.gif) |
Figure 2:
The
VLBI image of DA193 at 5 GHz at Jun. 1996 Image
peak: 3.2 Jy b-1. Contours: 0.02 Jy b
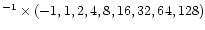 .
Beam FWHM: .
Beam FWHM:
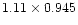 (mas)
at (mas)
at
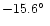 .
rms: 6 mJy b-1. .
rms: 6 mJy b-1. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1813f3.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg36.gif) |
Figure 3:
The
VLBI image of DA193 at 5 GHz at Feb. 1997 Image
peak: 3.65 Jy b-1. Contours: 0.02 Jy b
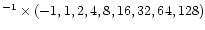 .
Beam FWHM: .
Beam FWHM:
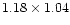 (mas) at
(mas) at
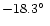 .
rms: 7 mJy b-1. .
rms: 7 mJy b-1. |
| Open with DEXTER |
All the data were obtained with the MK III mode B recording system (28
MHz bandwidth). The correlation was performed in Bonn with
the Max-Planck-Institute für Radioastronomie MK III
correlator with a 4 s integration time.
Data post-processing, including editing and amplitude calibration,
were performed using the NRAO AIPS package (Cotton 1995;
Diamond 1995). The hybrid images were produced by means
of the package DIFMAP (Shepherd et al. 1994). A
point-source model was used as an initial step for iterative
self-calibration procedure for all epochs. The source was
initially cleaned and phase self-calibrated using uniform
weighting in the (u,v) plane, then we switched to natural
weighting to decrease the noise level in the image plane.
The VLBI images obtained at the various epochs are displayed in
Figs. 2 to 5.
As clear from the images displayed, the source is slightly resolved by
our observations at all epochs.
By superresolving our images with the DIFMAP package, we have
indication that it is a core-jet structure consisting of two
components aligned in
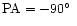 .
The two components are
labelled C1, C2 (see Figs. 2 to 5). This is
consistent with the previous images and models available in the
literature. We estimated the separations between the two
components and their flux densities in each image by fitting a
point-circle and Gaussian component model to our data using the
MODELFIT program in the DIFMAP package. On the basis of mutil-band
observations, the spectrum of C1 is the flattest, so we assume
that C1 is the core of DA193.
.
The two components are
labelled C1, C2 (see Figs. 2 to 5). This is
consistent with the previous images and models available in the
literature. We estimated the separations between the two
components and their flux densities in each image by fitting a
point-circle and Gaussian component model to our data using the
MODELFIT program in the DIFMAP package. On the basis of mutil-band
observations, the spectrum of C1 is the flattest, so we assume
that C1 is the core of DA193.
The model-fitting results are listed in Table 2, where
we also list the models available in the literature at the same frequency
from 1987 to 1995.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1813f4.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg38.gif) |
Figure 4:
The
VLBI image of DA193 at 5 GHz at Jun. 1997 Image
peak: 3.45 Jy b-1. Contours: 0.02 Jy b
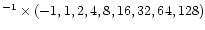 .
Beam FWHM: .
Beam FWHM:
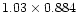 (mas)
at
(mas)
at
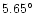 .
rms: 7 mJy b-1. .
rms: 7 mJy b-1. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1813f5.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg39.gif) |
Figure 5:
The
VLBI image of DA193 at 5 GHz at Nov 1997 Image
peak: 3.67 Jy b-1. Contours: 0.02 Jy b
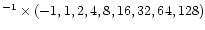 .
Beam FWHM: .
Beam FWHM:
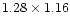 (mas) at
(mas) at
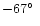 .
rms: 7 mJy b-1. .
rms: 7 mJy b-1. |
| Open with DEXTER |
Columns in Table 2 are as follows: Col. 1 is the
observation epoch; Col. 2 is the component label; Col. 3 gives the
flux density of each component; Cols. 4 and 5 list the distance and
position angle of each component with respect to the strongest
one; Cols. 6, 7 and 8 refer to the parameters of the Gaussian
model: the width at half maximum, the axis ratio and the
orientation of the individual component, respectively; Col. 9 is
notes. The uncertainties of the parameters are estimated with the
formulae given by Fomalont (1999):
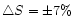 ,
,
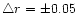 mas,
mas,
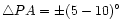 ,
,
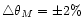 .
In Fig. 6 we plot the
separation between the two components C1 and C2 vs. epoch for each
epoch reported in Table 2. The core is always assumed
to be stationary, so the relative proper motion of the jet can be
estimated. We note that at epoch 1981.61 the jet component C2
is brighter than the core C1.
.
In Fig. 6 we plot the
separation between the two components C1 and C2 vs. epoch for each
epoch reported in Table 2. The core is always assumed
to be stationary, so the relative proper motion of the jet can be
estimated. We note that at epoch 1981.61 the jet component C2
is brighter than the core C1.
From Fig. 6 two different proper motions can be derived.
The proper motion derived on the basis of the first four epochs
(from 1981.61 to 1995.83), is
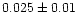 masyr-1, i.e.
masyr-1, i.e.
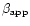 = 1.1, consistent with the result of Bajkova et al.
(1996) at 8 GHz. Such a value is reported in Fig. 6 with
a long-dashed line. On the basis of the five epochs from 1995 to
1997, a higher proper motion, with
= 1.1, consistent with the result of Bajkova et al.
(1996) at 8 GHz. Such a value is reported in Fig. 6 with
a long-dashed line. On the basis of the five epochs from 1995 to
1997, a higher proper motion, with
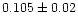 masyr-1,
can be estimated (full line in Fig. 6), which
corresponds to an apparent velocity of
masyr-1,
can be estimated (full line in Fig. 6), which
corresponds to an apparent velocity of
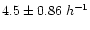 c.
c.
If we assume that equipartition holds in the source, it is possible
to estimate the Doppler factor
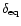 (Readhead 1994):
(Readhead 1994):
![$\displaystyle \delta_{\rm eq}=[[10^3 F(\alpha)]^{34}\{[1-(1+z)^{-1/2}]/2h\}^{-2...
...\theta^{-34}_{\rm d}(\nu_{\rm op}\times 10^3)^{-(2\alpha+35)}]^{1/(13-2\alpha)}$](/articles/aa/full/2001/46/aa1813/img45.gif) |
|
|
(1) |
where 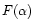 is given by Scott & Readhead (1977),
and
is given by Scott & Readhead (1977),
and 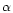 (assumed to be -0.75) is the spectral index of the
radio emission. In particular,
(assumed to be -0.75) is the spectral index of the
radio emission. In particular,
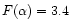 ;
z is the
redshift, h is the Hubble constant in units of H0=100 kms-1 Mpc-1 and
;
z is the
redshift, h is the Hubble constant in units of H0=100 kms-1 Mpc-1 and
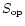 is the observed peak flux
density in Jy at the observed frequency
is the observed peak flux
density in Jy at the observed frequency
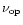 in GHz.
The angular diameter
in GHz.
The angular diameter
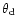 (in mas) of the core component
is greater than the observed angular diameter. Marscher
(1987) suggested a correction for this by using
(in mas) of the core component
is greater than the observed angular diameter. Marscher
(1987) suggested a correction for this by using
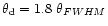 .
We computed the equipartition
Doppler factors of DA193 assuming h=1,
.
We computed the equipartition
Doppler factors of DA193 assuming h=1,
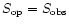 ,
and
,
and
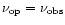 ,
where
,
where
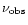 is
the frequency of our observations and
is
the frequency of our observations and
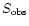 is the flux
density we derived.
is the flux
density we derived.
In the relativistic beaming model,
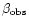 is related to the
true velocity
is related to the
true velocity 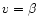 c, and the angle to the line of sight
c, and the angle to the line of sight
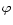 (Pearson & Zensus 1987),
(Pearson & Zensus 1987),
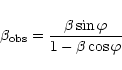 |
(2) |
and the Doppler factor can be written as
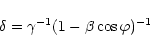 |
(3) |
where
![$\gamma=1/\sqrt[2]{1-\beta^2}$](/articles/aa/full/2001/46/aa1813/img61.gif) .
.
On the basis of the above equations, the Lorentz factor 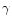 and the angle to the line of sight
and the angle to the line of sight 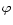 can be computed
(Ghisellini et al. 1993):
can be computed
(Ghisellini et al. 1993):
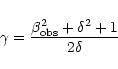 |
(4) |
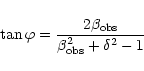 |
(5) |
where
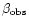 is a known superluminal velocity and
is a known superluminal velocity and 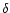 was assumed to be
was assumed to be
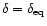 .
.
The brightness temperature 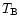 is given (Ghisellini et al. 1993) by
is given (Ghisellini et al. 1993) by
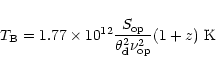 |
(6) |
where the observable quantities have the same units as in Eq. (1).
The physical parameters at each epoch are listed in
Table 3. We can see that DA193 has
properties of typical superluminal objects, i.e. high Doppler
boosting and small viewing angle. In addition, the observed
brightness temperature 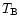 always exceeds the inverse Compton limit
(Kellermann & Pauliny-Toth 1969).
always exceeds the inverse Compton limit
(Kellermann & Pauliny-Toth 1969).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms1813f7.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg67.gif) |
Figure 7:
Dependence of the apparent speed of the superluminal jet
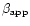 on the angle of the line of sight
on the angle of the line of sight 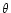 and
intrinsic flow velocity
and
intrinsic flow velocity 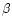 .
The dashed lines show the loci on
which the component is constrained by the superluminal speed, .
The dashed lines show the loci on
which the component is constrained by the superluminal speed,
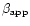 ,
for 4.4 and 1.1. The horizontal dotted lines show
the Lorentz factor ,
for 4.4 and 1.1. The horizontal dotted lines show
the Lorentz factor 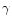 corresponding to
corresponding to 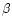 .
The full
lines are loci of constant Doppler factor .
The full
lines are loci of constant Doppler factor 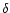 . . |
| Open with DEXTER |
Table 2:
VLBI component properties.
| epoch |
Comp |
S |
r |
PA |
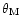 |
Ratio |
pa |
Notes |
| |
|
(Jy) |
(mas) |
(
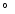 ) ) |
(mas) |
|
(
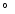 ) ) |
|
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
| 1981.61 |
C1 |
1.7 |
|
|
0.3 |
0.5 |
|
1 |
| |
C2 |
3.0 |
0.37 |
|
0.88 |
1.0 |
|
|
| 1985.37 |
C1 |
3.0 |
|
|
0.73 |
0.79 |
-57.87 |
2 |
| |
C2 |
1.3 |
0.52 |
-75.0 |
|
|
|
|
| 1994.52 |
C1 |
4.07 |
0.0 |
0.0 |
0.44 |
0.80 |
-83 |
3 |
| |
C2 |
1.19 |
0.70 |
-74 |
0.67 |
1.0 |
|
|
| 1995.83 |
C1 |
4.14 |
0.0 |
0.0 |
0.62 |
0.99 |
89.20 |
4 |
| |
C2 |
1.24 |
0.75 |
-87.29 |
0.41 |
0.79 |
85.21 |
|
| 1996.46 |
C1 |
4.23 |
0.0 |
0.0 |
0.73 |
0.79 |
-57.87 |
5 |
| |
C2 |
0.98 |
0.78 |
-90.56 |
1.58 |
0.46 |
-22.49 |
|
| 1997.13 |
C1 |
4.92 |
0.0 |
0.0 |
0.75 |
0.67 |
-75.9 |
5 |
| |
C2 |
0.53 |
0.90 |
-94.3 |
2.61 |
1.0 |
41.2 |
|
| 1997.43 |
C1 |
4.92 |
0.0 |
0.0 |
0.80 |
0.69 |
82.92 |
5 |
| |
C2 |
1.33 |
0.89 |
-75.25 |
1.52 |
0.40 |
42.98 |
|
| 1997.85 |
C1 |
4.69 |
0.0 |
0.0 |
0.74 |
0.81 |
-59.56 |
5 |
| |
C2 |
0.32 |
0.97 |
-89.01 |
1.65 |
0.27 |
-8.46 |
|
Notes. - (1) Spangler et al. (
1983); (2) Charlot
(
1990); (3) Fey et al. (
1996); (4) Hong et al.
(
1999); (5) this paper.
The inferred proper motion suggests DA193 as a
superluminal quasar. The proper motion derived from this paper is
at least 4 times larger than that estimated on the basis of the data
available in the literature. Two possibilities can be taken into
account:
- (i)
- the jet component accelerates after epoch
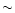 1995;
1995;
- (ii)
- we track two different knots, each emitted during two
different outbursts.
(i) If the jet component is the same, our results suggest
that it is being accelerated. This could be due to an increase of
the Lorentz factor 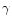 ,
or to a change in the viewing angle,
possibly associated with a change in the jet trajectory. The
viewing angle should change by
,
or to a change in the viewing angle,
possibly associated with a change in the jet trajectory. The
viewing angle should change by 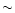
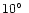 to explain the
increase in the proper motion. Alternatively, if the viewing angle
is the same at each epoch, then an intrinsic acceleration is
necessary to explain the observations (see Fig. 7).
We note that the proper motion we derived minimizes the Lorentz
factor
to explain the
increase in the proper motion. Alternatively, if the viewing angle
is the same at each epoch, then an intrinsic acceleration is
necessary to explain the observations (see Fig. 7).
We note that the proper motion we derived minimizes the Lorentz
factor 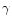 for a viewing angle
for a viewing angle
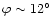 ,
in reasonable agreement with the values derived in Sect. 4
on the basis of equipartition arguments.
,
in reasonable agreement with the values derived in Sect. 4
on the basis of equipartition arguments.
![\begin{figure}
\par\includegraphics[angle=-90,width=12.9cm,clip]{ms1813f8.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg72.gif) |
Figure 8:
The total flux densities vary with epochs at 4.8, 8.0 and
14.5 GHz The data are archived from the University of
Michigan Radio Astronomy Observatory. |
| Open with DEXTER |
Comparison of the previous analysis carried out by Hong et al.
(1999) with the result presented in this paper shows that
the Lorentz factor 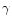 did not change considerably from epoch to
epoch; therefore we favour the hypothesis that the observed
increase of
did not change considerably from epoch to
epoch; therefore we favour the hypothesis that the observed
increase of
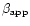 is due to projection effects.
is due to projection effects.
Bent jets are very common on the VLBI scales of compact radio
sources, so a change of trajectory in the inner region of DA193
is not implausible. Unfortunately, the very compact nature of this
source both on the arcsecond and milliarcsecond scale makes it
difficult to search for other signatures of the possible bending
in its morphology.
(ii) A second possibility is that we track a new
component after epoch  1995, characterised by higher
apparent speed. If we extrapolate the trajectory shown in
Fig. 6, we find that the birth of this component could
be located between 1989 and 1990. In an attempt to find a
signature of this new component in the radio flux variability, in
Fig. 8 we plotted the lightcurve of DA193 from
1975 to 1999 at 4.8, 8.0 and 14.5 GHz, extracting the data
from the database of the University of Michigan Radio Astronomy
Observatory (UMRAO). It is clear that the flux density gradually
rises from
1995, characterised by higher
apparent speed. If we extrapolate the trajectory shown in
Fig. 6, we find that the birth of this component could
be located between 1989 and 1990. In an attempt to find a
signature of this new component in the radio flux variability, in
Fig. 8 we plotted the lightcurve of DA193 from
1975 to 1999 at 4.8, 8.0 and 14.5 GHz, extracting the data
from the database of the University of Michigan Radio Astronomy
Observatory (UMRAO). It is clear that the flux density gradually
rises from  1987 at all frequencies, reaching a maximum
first at 14.5 GHz and 8.4 GHz around
1987 at all frequencies, reaching a maximum
first at 14.5 GHz and 8.4 GHz around  1990-1991, which
propagates to 5 GHZ with a delay of a few months.
The data are suggestive of a connection between the birth of a new component
and a total flux density outburst, but the evidence is not compelling.
1990-1991, which
propagates to 5 GHZ with a delay of a few months.
The data are suggestive of a connection between the birth of a new component
and a total flux density outburst, but the evidence is not compelling.
Inspection of Table 2 and Fig. 6 suggests a third,
alternative explanation. We note that component C2 may not be the
same one from epoch 1996.46 to epoch 1997.85. The flux density of
C2 decreases from 0.98 Jy (in 1996.46) to 0.53 Jy in 1997.13, then
it brightens again to 1.33 Jy in the following epoch, to decrease
by  a factor of 4 in 1997.85. Such strong variability in a
jet component is difficult to explain in simple terms. One
possibility is that the jet component, labelled C2 in all epochs,
is very short-lived, and fades away within a few months. In this
framework, component C2 in epoch 1997.43 would be a new ejection,
along the same path already traced by the previous component. This
possibility is supported by Fig. 6. We note that the position of
C2 did not change from 1997.13 to 1997.43 (see also Table
2), to speed up again in the following epoch. The
separation of C1 and C2 for the four epochs presented in this
paper could actually be fitted by two different lines, parallel to
each other, giving support to our idea of recurrent ejection of
superluminal short-lived components. It is possible to modelfit
the image with three components in epoch 1997.13 because the new
component should be visible here. Since the source DA193
is compact and the resolution is only
a factor of 4 in 1997.85. Such strong variability in a
jet component is difficult to explain in simple terms. One
possibility is that the jet component, labelled C2 in all epochs,
is very short-lived, and fades away within a few months. In this
framework, component C2 in epoch 1997.43 would be a new ejection,
along the same path already traced by the previous component. This
possibility is supported by Fig. 6. We note that the position of
C2 did not change from 1997.13 to 1997.43 (see also Table
2), to speed up again in the following epoch. The
separation of C1 and C2 for the four epochs presented in this
paper could actually be fitted by two different lines, parallel to
each other, giving support to our idea of recurrent ejection of
superluminal short-lived components. It is possible to modelfit
the image with three components in epoch 1997.13 because the new
component should be visible here. Since the source DA193
is compact and the resolution is only
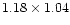 mas, it
is unlikely that three components give an equally good fitting.
mas, it
is unlikely that three components give an equally good fitting.
Given the very compact nature of DA193, it is crucial to
observe the source at submilliarcsecond resolution.
To this end, either 5 GHz Space VLBI observations or 43 GHz ground VLBI
observations are necessary tools to clarify the nature of
this source, and its nuclear properties.
Acknowledgements
The authors wish to thank Dr. Daniele Dallacasa for critical
reading of the manuscript and for his insightful suggestions. The
authors are grateful to the staff of EVN and the Hartebeesthoek
observatory for support of the observing projects. The European
VLBI Network is a joint facility of European and Chinese radio
astronomy institutes funded by their national research councils.
The research was supported by the National Science Foundation
(19973103), the Pan Deng Plan of China, and NKBRSF G19990754.
This work has made use of NASA's Astrophysics Data System Abstract
Service. The research has made use of data from the University of Michigan
Radio Astronomy Observatory, which is supported by funds from the
University of Michigan.
- Bajkova, A. T., Pyatunina, T. B., & Finkelstein, A. M. 1996, Commun. Inst. Appl. Astron, No. 87
In the text
- Blandford, R. D. 1987, in Superluminal Radio Sources,
ed. J. A. Zensus, & T. J. Pearson (Cambridge University Press, New York), 310
In the text
- Charlot, P. 1990, A&A, 229, 51
In the text
NASA ADS
- Chen, Yong-Jun, & Zhang, Fu-Jun 1999, Ch. A&A, 23, 299
In the text
- Cohen, M. I., & Kellerman, K. I. (editors) 1995, Quasars
and Active Galactic Nuclei: High Resolution and Radio Imaging
(Publi. of the National Academy of Sciences), Conf. Proc., 92
In the text
- Cotton, W. D. 1995, in Very Long Baseline Interferometry and the VLBA, ed. J. A. Zensus, P. J. Diamond, & P. J. Napier, ASP Conf. Ser., 82, 189
In the text
- Dallacasa, D., Fanti, C., Fanti, R., et al. 1995, A&A, 295, 27
In the text
NASA ADS
- Diamond, P. J. 1995, in
Very Long Baseline Interferometry and the VLBA, ed. J. A. Zensus, P. J. Diamond, & P. J. Napier, ASP Conf. Ser., 82, 227
In the text
- Fey, A. L., Clegg, A. W., & Fomalont, E. B. 1996, ApJS, 105, 299
In the text
NASA ADS
- Fomalont, E. B. 1999, in Synthesis Imaging
in Radio Astronomy II, ed. G. B. Taylor, C. L. Carilli, & R. A. Perley, 301
In the text
- Ghisellini, G., Padovani, P., Celotti, A., et al.
1993, ApJ, 407, 65
In the text
NASA ADS
- Hirabayashi, H., Pedwards, P. G., & Murphy, D. W. (editors) 2000,
Astrophycial Phenonema Revealed by Space VLBI, proceedings of the
VSOP Symp., Published by the Institute of Space and
Astronautical Science
In the text
- Hong, X. Y., Venturi, T., Wan, T. S., et al. 1999, A&AS, 134, 201
In the text
NASA ADS
- Hong, X. Y., Jiang, D. R., Schilizzi, R. T., et al. 2001,
in Galaxies and their constituents at the highest angular resolutions,
IAU Symp., 205, ed. R. T. Schilizzi, S. N. Vogel, F. Paresce, et al., ASP Conf. Ser. Publication Committee: A. V. Filipenko, G. Marcy, R. Norris, et al., 116
In the text
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1969, ApJ, 155, L71
In the text
NASA ADS
- Lister, M. L., Marscher, A. P., & Gear, W. K. 1998, ApJ, 504, 702
In the text
NASA ADS
- Marscher, A. P. 1987, in Superluminal Radio Sources,
ed. J. A. Zensus, & T. J. Pearson (Cambridge University Press, New York), 208
In the text
- O'Dea, C. P., Baum, S. A., & Stanghellini C. 1991, ApJ, 380, 66
NASA ADS
- Pearson, T. J., & Zensus, J. A. 1987, in Superluminal Radio Sources, ed. J. A. Zensus, & T. J. Person (Cambridge University Press, New York), 1
In the text
- Pearson, T. J. 1989, in Parsec-Scale Radio Jets, ed. J. A. Zensus, & T. J. Person (Cambridge University Press, New York), 1
In the text
- Readhead, A. C. S. 1994, ApJ, 426, 51
In the text
NASA ADS
- Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, BAAS, 26, 987
In the text
- Spangler, S. R., Mutel, R. L., & Bension, J. M. 1983, ApJ, 271, 44
In the text
NASA ADS
- Stanghellini, C., Baum, S. A., Dea, C. P., et al. 1990, A&A, 233, 379
In the text
NASA ADS
- Scott, M. A., & Readhead, A. C. S. 1977, MNRAS, 180, 539
In the text
NASA ADS
- Venturi, T., Pearson, T. J., Barthel, P. D., et al. 1993, A&A, 271, 65
NASA ADS
- Wills, D., & Wills, B. J. 1976, ApJS, 31, 143
In the text
NASA ADS
- Zhou, J. F., Jiang, D. R., Hong, X. Y., & Venturi, T. 2000,
in Proceedings of the 5th EVN Symposium, ed. J. E. Conway, A. G. Polatidis,
R. S. Booth, & Y. M. Philström, Publ. Onsala Space Observatory,
Chalmers technical University, Göteborg, Sweden, 31
In the text
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[angle=-90,width=10.3cm,clip]{ms1813f1.eps}
\end{figure}](/articles/aa/full/2001/46/aa1813/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1813f2.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1813f3.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg36.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1813f4.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg38.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1813f5.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg39.gif)
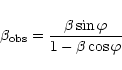
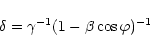
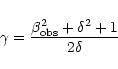
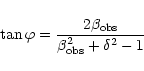
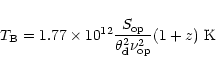
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms1813f6.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg66.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms1813f7.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg67.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=12.9cm,clip]{ms1813f8.eps}\end{figure}](/articles/aa/full/2001/46/aa1813/Timg72.gif)