3 The model

   
3.1 The gas velocity field

The velocity field was taken from data supplied by E. Athanassoula, corresponding to Model 001 shown in Fig. 2 of A92. This model is two-dimensional, with $\vec{u}=(u_x(x,y), u_y(x,y), 0)$in Cartesian coordinates (x,y,z). The gas velocity and density fields are steady in the frame rotating with the bar (the corotating frame). The stellar bar extends approximately between the ends of the dust lanes (shown as a light shade in Fig. 2). We reproduce in Fig. 2 the velocity field in this frame rotating in a clockwise sense with angular velocity of about $34\,{\rm km\,s^{-1}}\,{\rm kpc}^{-1}$, placing the corotation radius at about $r=r_{\rm c}\approx6\,{\rm kpc}$. The streaming velocities relative to the rotating frame are as large as $100\,{\rm km\,s^{-1}}$ near the shock fronts, which are slightly offset from the major axis of the bar. Regions where the sheared velocity is comparable with the rotational velocity are widespread in the bar region. A shock near the dust lanes is just resolved in the data. The region in which the velocities are available is $16\,{\rm kpc}$ across.

The magnetic fields obtained using this velocity field will be compared with observations of NGC 1097 where the corotation radius is $r_{\rm c}\approx12\,{\rm kpc}$ (assuming a distance to NGC 1097 of 17 Mpc); the length scales are therefore renormalized correspondingly before any comparison is made. However, when discussing the computational results in Sect. 4 we retain the original length scale of A92 with corotation at $6\,{\rm kpc}$. Since the model of A92 refers to a generic barred galaxy rather than to the galaxy NGC 1097 specifically, our comparison with observations can only be qualitative.

   
3.2 The dynamo model

The basic dynamo model, as applied to galaxies with strong noncircular motions, is described in Moss et al. (1999a); it uses the "no-z'' approximation (Moss 1995), replacing derivatives perpendicular to the galactic midplane (z-direction) with inverse powers of h, the disc semi-thickness. This is in some ways consistent with the two-dimensional flow model of A92. The mean field dynamo equations are solved for the magnetic field components in the directions orthogonal to z. (B_z is given in principle by the condition $\nabla\cdot\vec{B}= {0}$.) The resulting magnetic field can be thought of as an approximation to the field in the mid-plane, or to represent values averaged vertically over the disc.

We made one significant amendment to the model. Phillips (2001) has showed that the dynamo growth rates in the "no-z'' model can be made to agree more closely with those of the asymptotic analysis (e.g. Ruzmaikin et al. 1988) by including a correction factor of $\pi^2/4$into the terms representing diffusion in the vertical direction, and so we also included these factors. Thus the local marginal dynamo numbers for our models can now be expected to be fairly directly comparable to standard values of about 10.

The large velocity shear present in barred galaxies resulted in unsatisfactory numerical behaviour of the numerical algorithm previously employed (e.g. Moss et al. 1998, 1999a; Moss 1995), and so a new version in Cartesian coordinates was written, using a second order Runge-Kutta method for time-stepping, and second-order accurate space discretisation. This code solves the "no-z'' dynamo equations in the frame corotating with the bar. The earlier calculations were carried out using the $\alpha\omega$ formulation, but now we allow for the regeneration of both meridional and azimuthal regular magnetic field by interstellar turbulence (the $\alpha^2\omega$ dynamo). The dynamo equation has the form

$$% \frac{\partial \vec{B}}{\partial t}=\nabla\times(\vec{u}\ti... ...}{+}\alpha\vec{B}){-} \nabla{\times}(\eta\nabla\times\vec{B}),$$ (1)

where $\vec u$ is the regular velocity field described in Sect. 3.1, $\alpha$ parameterizes the dynamo action of the interstellar turbulence, and $\eta$ is the turbulent magnetic diffusivity (see, e.g., Ruzmaikin et al. 1988; Beck et al. 1996). In Eq. (1), we ignore any vertical (z-wise) variation of $\eta$, but allow a variation in the disc plane. (In principle we might, in the spirit of the no-z approximation, have approximated the effects of a halo diffusivity larger than that in the disc by an estimate of the form $\partial\eta/\partial z \sim \eta(x,y)/h$.) The equation is solved in a cylindrical region with radius $8\,{\rm kpc}$. We allow for nonlinear dynamo effects leading to the saturation of the magnetic field growth by adopting

$$% \alpha=\alpha_0\frac{\tilde\alpha(\vec{r})}{1+\xi\vec{B}^2/4\pi\rho (\vec{r})v_{\rm t}^2},$$ (2)

where $\alpha_0$ (a typical amplitude of $\alpha$) is a constant, $\tilde\alpha(\vec{r})$ is the normalized background value, and $\rho$ and $v_{\rm t}$ are the gas density and turbulent velocity. We are thus assuming that the large-scale magnetic field significantly reduces the $\alpha$-effect when its energy density approaches that of the turbulence; $\xi$ is a constant, introduced to suggest some of the uncertainty about the details of this feedback. When estimating field strength from our models we set $\xi=1$, but this fundamental uncertainty should be kept in mind. (Indeed, it is quite possible that, rather than being a constant, $\xi$ could depend on local conditions.) We assume that $v_{\rm t}=10\,{\rm km\,s^{-1}}$, and $\rho$ is taken from the same gas dynamical model of A92 as the velocity field $\vec u$. It is often assumed that $\alpha\propto\omega$ with $\omega$ the angular velocity of rotation. We first consider models with $\alpha$ constant apart from quenching effects, i.e. $\widetilde\alpha(\vec{r})=1$, and then put $\widetilde\alpha(\vec{r})=\omega(r)/\omega(r_\omega)$, where we arbitrarily choose $r_\omega=0.3~R$, and $R=8\,{\rm kpc}$. (Note that $\omega(r_\omega)/\Omega_0\approx 0.22$ where the unit angular velocity $\Omega_0$ is introduced in Sect. 3.3.) We choose this normalization so as to have the dimensionless quantities of order unity in the outer parts of the galaxy.

We can estimate the z-averaged vertical field in the disc, by using the condition $\nabla\cdot\vec{B}= {0}$, and estimating $\partial B_z/\partial z$ by B_z/h. This vertical magnetic field (not shown in Fig. 4 and other similar figures), is small on average, being about 10 times weaker than the average horizontal field. However, the vertical field is significant in regions with pronounced structure in the horizontal field (e.g. the shock front and the central region) where it can be comparable to the horizontal field.

Note that the dynamo equations with the quadratic nonlinearity (2) allow the transformation $\vec{B}\to-\vec{B}$; therefore the magnetic field vectors in the figures shown below can be reversed.

Equation (1) is nondimensionalized in terms of length R, the characteristic disc radius, and the magnetic diffusion time across the galactic disc, $h^2/\eta_0$ with h the disc scale height and $\eta_0$ a typical value of $\eta$. Magnetic field is measured in units of $B_0=\sqrt{4\pi\rho_0 v_{\rm t}^2/\xi}$(corresponding to equipartition between the turbulent and magnetic energies), where $\rho_0$ is the maximum density. The induction effects arising from turbulence and large-scale motions are quantified by dimensionless dynamo numbers

$$R_\alpha=\frac{\alpha_0 h}{\eta_0}\;, \quad R_\omega=\frac{\Omega_0 h^2}{\eta_0}\;,$$

where subscript zero denotes a characteristic value of the corresponding variable. From here onwards we refer only to dimensionless quantities, unless explicitly stated otherwise.

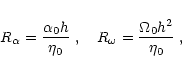
Although we are studying an $\alpha^2\omega$ dynamo characterized by two separate dimensionless parameters $R_\alpha$ and $R_\omega$, it is still useful to consider the dynamo number $D=-R_\alpha R_\omega$ as a crude measure of the dynamo intensity. $R_\omega$ is positive here because it is defined in terms of a typical angular velocity $\Omega_0 > 0$. In the standard asymptotic analysis for galactic dynamos (see Sect. VI.4 in Ruzmaikin et al. 1988), D is defined in terms of $r{\rm d}\omega/{\rm d}r$, which is negative. Thus we have introduced a minus sign into our definition of D so that, consistent with Ruzmaikin et al., the standard galactic dynamo has D<0. Our results are primarily a function of D (for given $f_\alpha$, $f_\eta$, see Eq. (5)) being quite insensitive to the relative values of $R_\alpha$ and $R_\omega$ in the parameter range considered; this indicates that rotational velocity shear dominates in the production of the azimuthal magnetic field (i.e. we have approximately an $\alpha\omega$ dynamo). The dynamo can maintain the regular magnetic field if $\vert D\vert\geq D_{{\rm cr}}$, where $D_{{\rm cr}}$ is a critical dynamo number, which depends weakly on details of the model (Sect. VI.4 in Ruzmaikin et al. 1988); as a rough estimate, $D_{{\rm cr}}\simeq8$ in the simple model discussed in Sect. 4.1. This marginal value (obtained with the velocity field of A92) is close to that found for a calculation using only the axisymmetric part of the azimuthal velocities.

The computational domain formally is $-1\leq x,y \leq +1$, but we solve only in the region $r = (x^2+y^2)^{1/2} \leq 1$, with boundary conditions B_x, B_y=0 at r=1. Field amplitudes are found to be small near the boundaries of the domain in most cases considered, and so the boundary conditions remain self-consistent throughout the simulations. The region r>1is ignored; formally $\vec{B}=0$ there. Our choice is conservative, being arguably the least favourable for dynamo action; for example dynamo action occurring outside $r=8\,{\rm kpc}$ could feed field into the region, interior to this radius, where the equations are solved.

Our standard computational grid has 160 mesh lines in both the x- and y-directions, uniformly distributed over $-1 \leq x,y \leq 1$; we made a trial integration on a finer grid, finding insignificant differences in our results.

   
3.3 Units

We choose the size of the formal computational domain to be 16kpc, consistent with that of A92. Thus $R=8\,{\rm kpc}$, and we choose $h=0.4\,{\rm kpc}$, although the overall nature of the solutions is relatively insensitive to the latter choice: h appears in the dimensionless control parameters $R_\alpha$ and $R_\omega$, and the overall field strength depends on their product D. With $\Omega_0=150\,{\rm km\,s^{-1}}\,{\rm kpc}^{-1}$ (of order the value in the inner $1\,{\rm kpc}$ radius), we have $R_\omega\approx 72/\eta_{26}$, where $\eta_{26}=\eta_0/10^{26}\,{\rm cm}^2\,{\rm s}^{-1}$ and, if $\alpha_0$ is a few kms^-1, then $R_\alpha$ will be of order unity. We assume that $v_t=10\,{\rm km\,s^{-1}}$ everywhere, so that, with $\rho_0\approx 3.5\times 10^{-24}\,{\rm g}\,{\rm cm^{-3}}$, the unit magnetic field strength is $B_0=6.6\times 10^{-6}\,\xi^{-1/2}\,{\rm G}$.

Neither $v_{\rm t}$ nor $c_{\rm s}$ are well known from observations of barred galaxies. However, Englmaier & Gerhard (1997) found that sound speeds less than about $20\,{\rm km\,s^{-1}}$ are necessary to produce shocks shifted away from the bar axis. We note in this connection that random velocities of molecular clouds in the central regions of NGC 1097 are as high as $35\,{\rm km\,s^{-1}}$ (Gerin et al. 1988), i.e. 3-4 times larger than the turbulent velocities at larger distances from the centre. A similar central enhancement in the velocity dispersion of molecular gas has been detected in NGC 3504 (Kenney et al. 1993). We take $v_{\rm t}=10\,{\rm km\,s^{-1}}$ as a uniform background value, but the turbulent intensity is assumed to be enhanced in the shock fronts and in the central region as described in Sect. 3.4.

A representative value of the turbulent magnetic diffusivity is $\eta_0\simeq\frac{1}{3}v_{\rm t}l\simeq10^{26}\,{\rm cm}^2\,{\rm s}^{-1}$ for $v_{\rm t}=10\,{\rm km\,s^{-1}}$, where $l\simeq100$pc is the turbulent scale. A convenient estimate of $\alpha$ is (Sect. V.4 in Ruzmaikin et al. 1988)

 

$$\alpha \simeq \min{\left(\displaystyle\frac{l^2\Omega}{h},v_{\rm t}\right)}$$ (3)

$$\min{\left[0.5\,{\rm km\,s^{-1}}\,\left(\displaystyle\frac{\Omega}{20\,{\rm km\,s^{-1}}\,{\rm kpc}^{-1}}\right),10\,{\rm km\,s^{-1}}\right]},$$ = (4)

where we neglect possible local enhancements of turbulent velocity beyond $10\,{\rm km\,s^{-1}}$. With the above values of l, h and $\Omega_0$, we obtain $\alpha_0\simeq4\,{\rm km\,s^{-1}}$. Thus, our representative values of the dynamo coefficients are $R_\alpha=5$ and $R_\omega=70$. Since Eq. (3) is just an order of magnitude estimate, we consider that a variation of a factor 3 in the dynamo coefficients is quite acceptable.

   
3.4 Enhancement of turbulence by shear

Figure 3: Contours of $\eta /\eta _0-1$ with $f_\eta =3$ in Eq. (5) with $\vec u$ from A92, as used in Sect. 4.2. The 5 contour levels are equally spaced with a range from 0.10 to 0.90. As in Fig. 2, the frame radius is 1.7 times the corotation radius.

We allow for the possibility that both $\eta$ and $\alpha$ may be enhanced where shear flow instabilities are likely to occur, by writing

$$% \alpha=\alpha_0\left(1 + f_\alpha\frac{S}{S_{\rm max}}\righ... ...=\eta_0(\vec{r})\left(1 + f_\eta \frac{S}{S_{\rm max}}\right),$$ (5)

where $f_\alpha$ and $f_\eta$ are constants and $S=\vert\partial u_x/\partial y\vert + \vert\partial u_y/\partial x\vert$, ${\bf u}=(u_x,u_y)$and $S_{\rm max}$ is the maximum value of S. For given values of $R_\alpha$, $R_\omega$ and/or D, the local dynamo action is weakened if $f_\eta > 0$, and enhanced if $f_\alpha > 0$. Contours of $\eta /\eta _0-1$ with $f_\eta =3$ are shown in Fig. 3; our models have magnetic diffusivity enhanced in the dust lanes and in the innermost 1-2kpc.

The effects of varying $\alpha$ and $\eta$ cannot be disentangled completely since it is the ratio $\alpha/\eta^2$ that affects magnetic fields generated by an $\alpha\omega$ dynamo. Therefore, the result of enhanced $\alpha$ can be reproduced, quite closely, by reducing $\eta$ instead. Thus, in order to keep the models as simple as possible, we preferred to take $f_\alpha =0$ in most simulations. Furthermore, with S defined after Eq. (5), the turbulent transport coefficients $\alpha$ and $\eta$ with $f_\alpha,f_\eta\neq0$ would be enhanced even in rigidly rotating regions. The most important result of this is that $\eta$ can be unrealistically large in the central parts of the disc in models discussed below. A perhaps more physically meaningful prescription could be $S=\vert\partial u_x/\partial y+\omega\vert + \vert\partial u_y/\partial x-\omega\vert$. However, the effect of the latter refinement is reduced when working in the rotating frame and, moreover, it would plausibly be similar to that of reducing $f_\eta$. So we leave this refinement for future, more advanced models. A trial calculation showed that the effect is small when and $\alpha_0$ is constant.

We suggest that the enhancement of the turbulent diffusivity in the shear flow (the dust lane) is due to the development of flow instabilities. The enhancement will be sufficient to reduce the contrast in the magnetic field if the turbulent diffusion time is shorter than the advection time across the dust lane width: $d^2/\eta < d/c_{\rm s}$ with $d\simeq0.5\,{\rm kpc}$ in NGC 1530 (Regan et al. 1995, 1997) and we have assumed that the transverse velocity immediately behind the shock is equal to the speed of sound $c_{\rm s} \simeq10\,{\rm km\,s^{-1}}$ (e.g. Roberts et al. 1979; Englmaier & Gerhard 1997). This yields $\eta>1.5\times10^{27}\,{\rm cm}^2\,{\rm s}^{-1}$ for the turbulent magnetic diffusivity within the dust lanes, so $\eta$ would have to be increased about tenfold from the background value $\eta_0$, in order to reduce the field contrast.

The Kelvin-Helmholtz instability is an obvious candidate for turbulence amplification in the dust lanes (see Townsend 1976 or Terry 2000 for a recent discussion of turbulence in shear flows and Ryu et al. 2000 and Brüggen & Hillebrandt 2001 for a discussion of mixing enhancement by the instability). The growth rate of the instability in a piecewise continuous flow is given by

$$\gamma_{\rm KH}=\frac{U}{2d} K \left[2K^{-1}-1-2K^{-2}\frac{\sinh{K}}{\exp{K}}\right]^{1/2},$$

where K=kd with k the wavenumber in the direction of the shear flow, $d\simeq0.5\,{\rm kpc}$ is the transverse width of the sheared region and $U\simeq100$ kms^-1 is the velocity difference across it. The growth rate has a maximum, $\gamma_{\rm max}\approx0.1U/d$, for $K\approx0.8$. The resulting enhancement in the turbulent velocity can be estimated as $v_{\rm t}\simeq v_{\rm t0}\exp(\gamma_{\rm max}d/c_{\rm s})$, where $v_{\rm t0}\simeq c_{\rm s}\simeq10\,{\rm km\,s^{-1}}$is the turbulent velocity upstream of the dust lane, and we have assumed that the transverse velocity immediately after the shock is equal to the speed of sound, so the residence time of the matter in the unstable region is given by $d/c_{\rm s}$. This yields $\gamma_{\rm max}d/c_{\rm s}\simeq1$, so the turbulent velocity in the dust lane is expected to be 2-3 times larger than the upstream value of  $10\,{\rm km\,s^{-1}}$. The most unstable mode has a scale of $l=2\pi d/0.8\approx4\,{\rm kpc}$. The resulting enhancement in the turbulent diffusivity $\eta\simeq\frac{1}{3}v_{\rm t}l$can be as large as by a factor of 100, but this enhancement will be limited by the fact that only a part of the flow produced by the instability will be randomized, and simultaneously the effective value of l will be reduced. Arguably, a better estimate of $\eta$ resulting from the instability is $\eta\simeq\frac{1}{3}v_{\rm t}^2\gamma_{\rm max}^{-1}\simeq3v_{\rm t0}d \simeq15v_{\rm t0}l$, implying enhancement by a factor of 50. The above estimates are upper limits, referring to the maximum rather than the mean enhancement. The enhancement of $\eta$used in our models ranges up to a factor of $f_\eta+1=6$, and the case $f_\eta =3$ is illustrated in Fig. 3.

A magnetic field parallel to the shear velocity can suppress the Kelvin-Helmholtz instability if $V_{\rm A}>U$ (Chandrasekhar 1981), but this inequality is not satisfied in our case.

Apart from the Kelvin-Helmholtz instability, enhanced small-scale three-dimensional motions can arise from local perturbations to the gravitational field as discussed by Otmianowska-Mazur et al. (2001).

Figure 4: Vectors of the horizontal magnetic field for the model with $R_\alpha =0.3$, $R_\omega =36$, $f_\alpha =f_\eta =0$. The circumscribing circle has radius 8 kpc. Shades of grey show gas density, with lighter shades corresponding to higher values. The magnetic field vectors have been rescaled by $\vec{B}\to\vec{B}/B^n$ with n=0.3, to improve the visibility of the field vectors in regions with small B. Panel a) shows the field vectors over the entire computational domain, whereas in b) the inner region has been omitted, in order to show the structure in the outer regions of the disc.