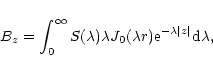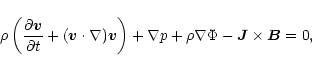 |
(1) |
A&A 379, 1170-1175 (2001)
DOI: 10.1051/0004-6361:20011367
M. A. S. G. Jørgensen1 - R. Ouyed2 - M. Christensen1
1 - University of Copenhagen, Astronomical Observatory, Juliane
Maries Vej 30, 2100 Copenhagen Ø, Denmark
2 -
Nordic Institute for Theoretical Physics, Blegdamsvej 17, 2100
Copenhagen Ø, Denmark
Received 27 June 2001 / Accepted 21 September 2001
Abstract
We solve, and provide analytical expressions, for current-free magnetic
configurations in the context of initial setups of 3-dimensional
simulations of astrophysical jets involving
an accretion disk corona in hydrostatic balance around
a central object. These configurations which thread through
the accretion disk and its corona preserve the initial hydrostatic state.
This work sets stage for future 3-dimensional jet simulations
(including disk rotation and mass-load) where
launching, acceleration and collimation mechanisms
can be investigated.
Key words: MHD - stars: winds - outflows
The most successful model of astrophysical jets is that of magneto-hydrodynamic (MHD) driven winds (Blandford & Payne 1982). In this model, the magnetic field is predicted to launch, accelerate and efficiently collimate the jet. The advent of MHD codes over the last decade allowed us to study the details of this model through the use of time-dependent MHD simulations and confirm the importance of the magnetic field. One point that has been emphasized in many of these simulations is the importance of properly setting up the initial state. A numerically stable initial setup makes the simulation tractable and allows contact with theory. Here, we are particularly interested in simulations as presented in Ouyed & Pudritz (1997a, OPI) and Ouyed & Pudritz (1997b, OPII) focusing on the technical aspect of the initial state.
The initial conditions as defined in OPI and OPII
correspond to a central object (a proto-star)
surrounded by a Keplerian disk and an overlying corona in
hydrostatic equilibrium. The disk has fixed properties and provides the
boundary conditions for the outflow.
The time evolution of the initial state is
partly depicted by the momentum equation (using the standard nomenclature),
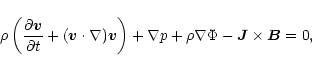 |
(1) |
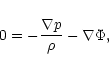 |
(2) |
Force-free configurations
are characterized by
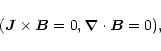 |
(3) |
Using relation
(4) and the fact that the magnetic field is
divergence free we arrive at:
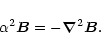 |
(5) |
| B | = | ||
| R | = | ||
| = | |||
| Z | = | (6) |
| = | 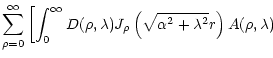 |
||
Here,
![]() is a necessary and sufficient condition to
guaranty the existence of a scalar field (
is a necessary and sufficient condition to
guaranty the existence of a scalar field (![]() )
with the property,
)
with the property,
![]() .
As can be seen in Appendix A this
greatly simplifies our task of finding the initial configurations.
We investigate two kind of current-free magnetic fields, with and without
toroidal component (
.
As can be seen in Appendix A this
greatly simplifies our task of finding the initial configurations.
We investigate two kind of current-free magnetic fields, with and without
toroidal component (![]() ).
).
Here we do not demand that the toroidal field is zero in the corona. We use
the following boundary condition:
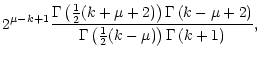 |
|
| (8) |
In the current-free initial setup the differential
equation for the scalar field of the magnetic field (![]() )
reduces to
the Laplace equation (since
)
reduces to
the Laplace equation (since
![]() ):
):
We examined configurations for 2
different values of ![]() (the radial dependence of the magnetic field);
an open (
(the radial dependence of the magnetic field);
an open (![]() )
and a closed
(
)
and a closed
(![]() )
configuration. The
closed configuration has the same radial
dependence as a dipole field, which is expected (in first approximation)
around stars however ours is strictly a solution of the
disk boundary condition. The open
configuration is the 3-D analogue/extension of the open configuration
used in OPI.
We implemented these 2 configurations
in our initial setup and let them evolve in time after applying
a small perturbation to the density.
No mass injection and no disk rotation were set,
and
)
configuration. The
closed configuration has the same radial
dependence as a dipole field, which is expected (in first approximation)
around stars however ours is strictly a solution of the
disk boundary condition. The open
configuration is the 3-D analogue/extension of the open configuration
used in OPI.
We implemented these 2 configurations
in our initial setup and let them evolve in time after applying
a small perturbation to the density.
No mass injection and no disk rotation were set,
and
![]() in the corona (z > 0.0).
For the simulations we used the time-explicit
Eulerian MHD-code ZEUS3D (Stone & Norman 1992).
in the corona (z > 0.0).
For the simulations we used the time-explicit
Eulerian MHD-code ZEUS3D (Stone & Norman 1992).
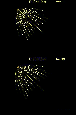 |
Figure 1:
Current-free solutions (
|
| Open with DEXTER | |
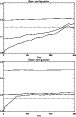 |
Figure 2:
Current-free solutions (
|
| Open with DEXTER | |
Cartesian coordinates, (x,y,z), are used for all simulations.
While being the natural system to use to avoid any directional biases, it does
introduce some of its own problems not encountered in the 2-D cylindrically
symmetric simulations. We refer
the interested reader to OPC for the technical
reasons underlying the choice of Cartesian coordinates for such simulations.
The disc is taken to lie along the x-y plane, and the disc axis
corresponds to the z-axis. In units of the inside radius of the disc,
![]() ,
the simulated region has dimensions
(-15:+15, -15:+15,
0:+60), and is divided into
(95, 95, 120) uniform rectangular zones.
,
the simulated region has dimensions
(-15:+15, -15:+15,
0:+60), and is divided into
(95, 95, 120) uniform rectangular zones.
 |
Figure 3:
Current-free solutions (
|
| Open with DEXTER | |
Figure 1 shows the magnetic field lines for the open
configuration at time ![]() (in units
of inner Kepler period) and at time
(in units
of inner Kepler period) and at time
![]() .
The magnetic configuration changes only slightly in time and the generated
currents are negligible.
This is further demonstrated in Fig. 2 (top panel) where
we show the time evolution of the maximum values
for velocity, density and magnetic field strength.
The induced velocity and slight variations in the
magnetic field topology are signature of Alfvén waves which
as expected have no dynamical effects on the coronal material.
The solution stays force-free up to
.
The magnetic configuration changes only slightly in time and the generated
currents are negligible.
This is further demonstrated in Fig. 2 (top panel) where
we show the time evolution of the maximum values
for velocity, density and magnetic field strength.
The induced velocity and slight variations in the
magnetic field topology are signature of Alfvén waves which
as expected have no dynamical effects on the coronal material.
The solution stays force-free up to
![]() and no motion/jet is generated - as can
further be checked from the movies of the simulations (at
http://www.fys.ku.dk/~svart/Jets/).
The closed configuration (lower panel in Fig. 2) is also
stable in time although
the induced errors are 20% larger than in the open case (Fig. 3).
Here as well the initial hydrostatic balance
is preserved up to
and no motion/jet is generated - as can
further be checked from the movies of the simulations (at
http://www.fys.ku.dk/~svart/Jets/).
The closed configuration (lower panel in Fig. 2) is also
stable in time although
the induced errors are 20% larger than in the open case (Fig. 3).
Here as well the initial hydrostatic balance
is preserved up to ![]() .
.
The simulations described above are easily implemented
numerically and if it is left unperturbed, the corona will remain in perfect
numerical balance to within machine round-off errors.
In any case, when disk rotation and mass-load are taken into account,
the small perturbations are quickly and completely washed out by the jet
dynamics (
![]() ). The complete set of simulations
with and without disk rotation and mass-loading can be
visualized and compared at http://www.fys.ku.dk/~svart/Jets/.
). The complete set of simulations
with and without disk rotation and mass-loading can be
visualized and compared at http://www.fys.ku.dk/~svart/Jets/.
We developed a tool, named JETSET, that generates initial states as described above. The JETSET main frame is shown in Fig. 4. Once the grid dimensions, the physical scales and the appropriate coronal and disk parameters have been specified, JETSET performs a Newton-Raphson method to find the correct density distribution while the corresponding magnetic field configuration is computed using the approach described in previous sections. The resulting Data (density, specific energies, velocity, and magnetic field) describing the initial setup is stored in an HDF (Hierarchical Data Format) file which can then be read by the user's code (such as ZEUS). The magnetic field lines can be visualized (see Fig. 4) as well as the density distribution around the central object (see Fig. 5). JETSET is available (down-loadable) at http://www.nordita.dk/~ouyed/JETTOOLS/. Included in the package are README and HELP files.
In this paper, we solved analytically for force-free solutions of magnetic configurations which can be implemented in 3-D simulations of astrophysical jets (disk winds). These configurations which thread the accretion disk and the corona, we showed, do not perturb the initial hydrostatic balance and are stable in time. While idealistic (developed for ease of implementation and computation), they constitute the first stage towards testing the effects of different magnetic configurations on the simulated jets in 3-D. Realistic configurations ought to reproduce basic features of astrophysical jets, such as their cylindrical shape, their knotty structure, and their stability.
![\begin{figure}
\par\includegraphics[angle=270,width=18cm]{h3158f4.eps}\end{figure}](/articles/aa/full/2001/45/aah3158/Timg67.gif) |
Figure 4:
JETSET TOOL: JETSET sets initial states for astrophysical
jet simulations in 3-D.
The initial set up consists of a corona in hydrostatic
balance around a central object with current-free magnetic fields threading
through the corona and the underlying accretion disk (fixed boundary).
JETSET solves for the correct density distribution around
the central object and the appropriate current-free magnetic field configuration
once the two parameters, k and |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.7cm]{h3158f5a.eps} \includegraphics[angle=270,width=7.7cm]{h3158f5b.eps} \end{figure}](/articles/aa/full/2001/45/aah3158/Timg68.gif) |
Figure 5:
JETSET TOOL - Density contours
as generated by JETSET for a single pressure
component corona with
|
| Open with DEXTER | |
Acknowledgements
We thank R. E. Pudritz and C. Rogers for helpful discussions.
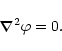 |
(A.1) |
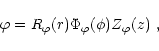 |
(A.2) |
We now look at the
![]() component:
component:
Equation above is simply a Fourier expansion in the toroidal
dependence of the magnetic field. The integrals before the trigonometric
functions are the Fourier coefficients; so we may write:
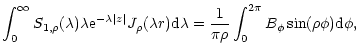 |
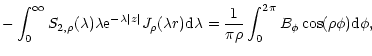 |
Finally, note that the simplest magnetic
configuration possible is given by
![]() which gives us the boundary condition investigated in this paper
which gives us the boundary condition investigated in this paper
![]() (including the k=0 case with
no toroidal dependence); b is a scaling factor.
(including the k=0 case with
no toroidal dependence); b is a scaling factor.
The corresponding scalar field is obtained by cancelling the
![]() dependence in (A.3). The components Brand Bz are then direct derivative of
dependence in (A.3). The components Brand Bz are then direct derivative of ![]() .
For example,
one can show that
.
For example,
one can show that