A&A 379, 872-877 (2001)
DOI: 10.1051/0004-6361:20011229
Microlensing planets in M 22: Free-floating or bound?
R. de la Fuente Marcos
-
C. de la Fuente Marcos
Universidad Complutense de Madrid, Ciudad Universitaria,
28040 Madrid, Spain
Received 9 July 2001 / Accepted 31 August 2001
Abstract
We use detailed numerical simulations and theoretical
estimates to show that, if confirmed, the unusually brief
microlensing events observed by Sahu et al. (2001) in the
field of the globular cluster M 22 might be explained as a
result of microlensing by a population of clustered MACHOs,
a dark cluster or RAMBO, not associated with the globular
cluster. If real, this dark cluster would be located
between M 22 and the Galactic bulge and could include at
least 106 substellar members with a typical size of
1-3 pc. Bound planets in wide or/and eccentric orbits are
also able to reproduce the observed microlensing behaviour,
but only if multiplanet systems (including large
Kuiper-belt-like objects) are abundant, although, our
calculations argue against the latter scenario as the
ionization rate in M 22 is very high. Dynamically ejected or
lone planets are, in principle, incompatible with the
observational findings as they either escape their parent
cluster in a relatively short time-scale after ejection or
segregate toward the outskirts of the cluster. We discuss
additional implications of the dark cluster scenario,
including the existence of a population of RAMBOs toward
the Galactic bulge.
Key words: celestial mechanics - stellar dynamics - dark matter -
Galaxy: globular clusters: individual: NGC 6656 -
globular clusters: general -
gravitational lensing -
planetary systems
Gravitational microlensing occurs when the gravitational field
of a massive object (the lens), located close to the observer's
line-of-sight, bends the light from a distant object (the source)
to generate two or more unresolved images. For a point mass event,
the two images are not identical, they have different areas and
opposite parities. Although the gravitational microlensing effect
conserves surface brightness it alters the flux of the unresolved images
as the relative positions of the lens, the source, and the observer
change. These variations in flux translate into a measurable
increase of the photometric magnitude (magnification). The effect
does not depend on the photometric color used in the observations.
Microlensing was proposed in 1986 by Paczynski as a method to
detect compact baryonic dark matter in the halo of our Galaxy, but
before the first events were discovered, Mao and Paczynski (1991)
had already noted that is might be possible to detect planetary
companions of the primary microlenses.
Stars or sub-stellar objects in globular clusters can act either as
sources to detect MACHOS (Massive Astrophysical Compact Halo Objects)
located along the line-of-sight or as lenses for more distant background
stars (Jetzer et al. 1998). Under normal conditions, the probability of
detecting microlensing events is very small but observing a globular
cluster projected against the star-rich Galactic bulge increases this
probability by a significant amount. Monitoring the bulge stars for
variability may then help to detect dim or dark objects within the star
cluster. Using this technique, Sahu et al. (2001) (hereafter SM22) have
recently presented evidence for the existence of free-floating
planetary-mass objects in M 22. They have detected six microlensing
events that are completely unresolved in time. If these events indeed
represent gravitational microlensing, the upper limit to the mass of the
lens is less than 80
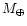 (Saturn mass is about 95). They
interpret that these objects must be either free-floating, or at least
several AUs from any stellar-mass objects, although they favour the
free-floating hypothesis. If real, the total contribution of these
free-floating planets to the mass of M 22 is estimated by these authors
to be of the order of 10%.
(Saturn mass is about 95). They
interpret that these objects must be either free-floating, or at least
several AUs from any stellar-mass objects, although they favour the
free-floating hypothesis. If real, the total contribution of these
free-floating planets to the mass of M 22 is estimated by these authors
to be of the order of 10%.
M 22 (NGC 6656) is an unusual star cluster with a diameter of about 18 pc
and ranking fourth in brightness among globulars, this heavily
reddened metal-poor globular cluster is 12 Gyr old (Davidge &
Harris 1996). Its binary fraction is 0.01-0.03 depending on the
eccentricity as opposed to 0.12, the binary fraction for nearby,
solar-type stars having similar mass ratios and periods
(Cote et al. 1996). M 22 has a binary ionization rate as high as
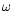 Centauri and very likely all its soft (long period)
binaries have been disrupted by stellar encounters.
Centauri and very likely all its soft (long period)
binaries have been disrupted by stellar encounters.
In this paper, we investigate how bound planets can induce single
lens gravitational microlensing in star clusters. In Sect. 2, we present
relevant results from numerical simulations. Different scenarios
able to explain the SM22 findings are introduced in Sect. 3 as well as
relevant microlensing theory. Section 4 is a discussion.
Here, we present partial results from a systematic long-term
project aimed to study planetary dynamics in star clusters. Full details
and results of our calculations will be presented elsewhere. Partial
results from this program can be found in de la Fuente Marcos and de la
Fuente Marcos (1997, 1998, 2000, 2001a,b).
In this paper, we
will only provide the data required to support our interpretation of the
results from SM22. Calculations have been carried out using a version of
Sverre Aarseth's NBODY5 code (Aarseth 1994). This code includes
the effect of the Galactic tidal field and the mass loss due to stellar
evolution (Eggleton et al. 1989). Most of the models consider a realistic
mass spectrum (Scalo 1986) in the range [0.08, 15.0] 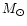 .
Spherical symmetry and constant star density or Plummer models are
assumed for generating initial positions, with the ratio of the total
kinetic and potential energy fixed to 0.25 (0.5 for virial equilibrium).
Our choice of the initial ratio of kinetic to potential energy produces
an initial contraction of the cluster and simulates violent relaxation.
Several models (N = 1000 particles) include both
a significant primordial binary fraction and realistic orbital elements
for this binary population. The N in our models ranges from 100 to 10000.
Although globular clusters are significantly more populated, our
present results are consistent with very preliminary partial results from
our models with
.
Spherical symmetry and constant star density or Plummer models are
assumed for generating initial positions, with the ratio of the total
kinetic and potential energy fixed to 0.25 (0.5 for virial equilibrium).
Our choice of the initial ratio of kinetic to potential energy produces
an initial contraction of the cluster and simulates violent relaxation.
Several models (N = 1000 particles) include both
a significant primordial binary fraction and realistic orbital elements
for this binary population. The N in our models ranges from 100 to 10000.
Although globular clusters are significantly more populated, our
present results are consistent with very preliminary partial results from
our models with
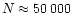 and also with results from other
authors (Laughlin & Adams 1998, 2000;
Adams & Laughlin 2001;
Smith & Bonnell 2001; Bonnell et al. 2001),
therefore we will apply them
to globular clusters through this paper. Instead of computing the
evolution of several cluster models with different populations and sizes
we consider samples of models (10 or more for each N) only differing
in the value of the seed
number for generating initial conditions. For example, in one of our
samples we choose an open cluster with N = 1000 objects (40% binaries,
60% planetary systems) and a half-mass radius of about 0.9 pc. We select
40% primordial binaries as a plausible binary percentage for typical
galactic clusters, with semi-major axis in the range 51.6-309.4 AU. For
simplicity, the planetary systems studied in this research consist of
one giant planet and its host star. Our giant planet populations have
semi-major axes in the range [0.5, 60] AU, masses uniformly distributed
in the range 0.1-8
and also with results from other
authors (Laughlin & Adams 1998, 2000;
Adams & Laughlin 2001;
Smith & Bonnell 2001; Bonnell et al. 2001),
therefore we will apply them
to globular clusters through this paper. Instead of computing the
evolution of several cluster models with different populations and sizes
we consider samples of models (10 or more for each N) only differing
in the value of the seed
number for generating initial conditions. For example, in one of our
samples we choose an open cluster with N = 1000 objects (40% binaries,
60% planetary systems) and a half-mass radius of about 0.9 pc. We select
40% primordial binaries as a plausible binary percentage for typical
galactic clusters, with semi-major axis in the range 51.6-309.4 AU. For
simplicity, the planetary systems studied in this research consist of
one giant planet and its host star. Our giant planet populations have
semi-major axes in the range [0.5, 60] AU, masses uniformly distributed
in the range 0.1-8 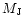 (
(
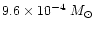 ), and an
initial eccentricity of 0.010. Pericentre, nodes, and inclinations for
both, planetary systems and binaries, as well as the eccentricities of
the binaries, are chosen from a random (thermalized) distribution.
), and an
initial eccentricity of 0.010. Pericentre, nodes, and inclinations for
both, planetary systems and binaries, as well as the eccentricities of
the binaries, are chosen from a random (thermalized) distribution.
Our calculations show that a significant fraction of the planetary
systems suffer modification of their primordial orbital elements as a
result of complex gravitational interactions with binaries, single stars,
and/or other planetary systems. Eccentricity modification is, by far,
the most common event. Modification of the semi-major axis is not so
frequent and just in a few cases an interaction results in a decrease of
the orbital size. Most of the times, the semi-major axis changes as a
result not only of external perturbations but also because of mass loss
from the parent star. The more massive the planet, the higher the
probability of being involved in an orbital modification event.
Before presenting different scenarios able to induce planetary
microlensing we introduce some relevant equations from the gravitational
microlensing theory. Following Gaudi & Sackett (2000), let us consider
a single lens, in this case the time-variable flux observed from a
microlensed star is
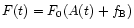 ,
where F0 is the
unlensed flux of the star,
,
where F0 is the
unlensed flux of the star, 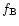 is the ratio of any unresolved, unlensed
background light to F0 (the "blend fraction"), and A(t) is the
magnification. The magnification for a single lens is given by
is the ratio of any unresolved, unlensed
background light to F0 (the "blend fraction"), and A(t) is the
magnification. The magnification for a single lens is given by
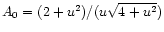 ,
where u is the instantaneous angular separation of the source and
the lens in units of the angular Einstein ring radius
,
where u is the instantaneous angular separation of the source and
the lens in units of the angular Einstein ring radius
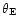 of the lens that can be written as
of the lens that can be written as
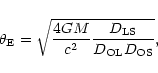 |
(1) |
where G is the gravitational constant, M is the mass of the lens,
c is the speed of light, and
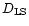 ,
,
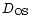 ,
,
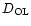 are the
lens-source, observer-source, and observer-lens distances, respectively.
For a lens in M 22 and a source in the Galactic bulge,
are the
lens-source, observer-source, and observer-lens distances, respectively.
For a lens in M 22 and a source in the Galactic bulge,
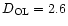 kpc
and
kpc
and
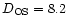 kpc, therefore
kpc, therefore
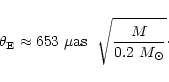 |
(2) |
In principle, if u > 1.5, the magnification is not large enough to
be measurable, although it depends strongly on the photometric errors.
The characteristic timescale of one of these events is given by the
Einstein time,
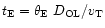 ,
where
,
where 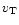 is the
transverse velocity of the lens relative to the observer-source
line-of-sight. This timescale increases as
is the
transverse velocity of the lens relative to the observer-source
line-of-sight. This timescale increases as 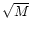 ,
therefore the smaller the
lens the shorter the duration of the microlensing event. If the lens is
not a single object but it has a companion, the formalism for binary
lenses should be used. The flux is still expressed by the same equation,
but the magnification can no longer be calculated analytically and
numerical techniques are required (Witt 1990).
The minimum separation between a planet and its host star (in units
of
,
therefore the smaller the
lens the shorter the duration of the microlensing event. If the lens is
not a single object but it has a companion, the formalism for binary
lenses should be used. The flux is still expressed by the same equation,
but the magnification can no longer be calculated analytically and
numerical techniques are required (Witt 1990).
The minimum separation between a planet and its host star (in units
of
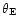 )
for which planets can be discovered using microlensing
is about 0.8. For planetary separations roughly between 0.8 and 1.5,
the microlensing signature corresponds to a binary lens. For larger
values of the separation, the planet generally acts as an independent
lens. The angular separation given by Eq. (2) is equivalent
to the spatial distance
)
for which planets can be discovered using microlensing
is about 0.8. For planetary separations roughly between 0.8 and 1.5,
the microlensing signature corresponds to a binary lens. For larger
values of the separation, the planet generally acts as an independent
lens. The angular separation given by Eq. (2) is equivalent
to the spatial distance
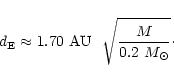 |
(3) |
In order to obtain isolated short-duration events corresponding to
planetary-class single-lens microlensing, the instantaneous separation
between the planet and its host star must be larger than 1.5 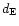 .
This magnitude is plotted in Fig. 1, therefore virtually
any planetary system (in M 22) with a separation between planet and
host star wider than about 7 AU (upper limit for massive primary) will
induce a single lens microlensing event in exactly the same way a
lone planet does. As an example and from the figure, if the primary
has a mass of 0.3
.
This magnitude is plotted in Fig. 1, therefore virtually
any planetary system (in M 22) with a separation between planet and
host star wider than about 7 AU (upper limit for massive primary) will
induce a single lens microlensing event in exactly the same way a
lone planet does. As an example and from the figure, if the primary
has a mass of 0.3 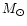 ,
the minimum distance for single lens
is 3.1 AU at the 95% confidence level. For this hypothetical system any
planet farther from the central star may induce single lens microlensing.
More rigorous arguments using the full binary lens formalism give
essentially the same results. Let us consider several configurations
able to produce planetary-class single lens microlensing.
,
the minimum distance for single lens
is 3.1 AU at the 95% confidence level. For this hypothetical system any
planet farther from the central star may induce single lens microlensing.
More rigorous arguments using the full binary lens formalism give
essentially the same results. Let us consider several configurations
able to produce planetary-class single lens microlensing.
![\begin{figure}
\par\includegraphics[width=7.9cm,height=8.6cm,angle=-90,clip]{h3102f1.ps} \end{figure}](/articles/aa/full/2001/45/aah3102/Timg23.gif) |
Figure 1:
Einstein ring radius of the lens multiplied by
1.5 as a function of the stellar mass for M 22.
A bound planet with separation from its host
star below the curve would induce double lens
behaviour with contributions of both objects, planet
and host star, clearly visible on the light curve.
Above the curve, single lens behaviour is expected. |
| Open with DEXTER |
SM22 interpret that their unresolved microlensing events have
been probably induced by a free-floating planetary-mass population
located at the cluster core. However, existence of standalone
planets poses some theoretical challenges. Star clusters tend to
energy equipartition among stars of different mass. As a result of
this process, the heavier stars will tend to slow down and sink
toward the center of the cluster. Globular clusters are very old,
therefore mass segregation has already been well established
through the entire cluster. As an example from our calculations, for
a
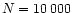 model and after about 500 Myr mass segregation gives
an average mass of about 1
model and after about 500 Myr mass segregation gives
an average mass of about 1 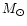 for the cluster core and
about 0.5
for the cluster core and
about 0.5 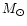 for the halo, and these values remain rather
constant during the evolution of the model.
Therefore, if they form, low-mass substellar objects
should be a minority in the cluster core. On the other hand,
standalone planets cannot be formed by accretion, therefore
protostellar collapse and fragmentation is currently the
only other alternative. Boss (2001) has shown that if the magnetic
field tension effects are important, collapse and fragmentation of
molecular clouds might be able to produce self-gravitating objects
with Jovian (not Saturn or smaller) masses although this author
terms the resulting objects as sub-brown dwarfs not planets.
However, it seems that, regardless of whether the planets were
formed via collapse or were formed via accretion and subsequently
ionized, they would still not survive in the core of the cluster.
Free-floating planets have recently been identified in Orion
(Lucas & Roche 2000; Zapatero Osorio et al. 2000) but their
origin remains controversial as they can be escapees or even actual
brown dwarfs.
for the halo, and these values remain rather
constant during the evolution of the model.
Therefore, if they form, low-mass substellar objects
should be a minority in the cluster core. On the other hand,
standalone planets cannot be formed by accretion, therefore
protostellar collapse and fragmentation is currently the
only other alternative. Boss (2001) has shown that if the magnetic
field tension effects are important, collapse and fragmentation of
molecular clouds might be able to produce self-gravitating objects
with Jovian (not Saturn or smaller) masses although this author
terms the resulting objects as sub-brown dwarfs not planets.
However, it seems that, regardless of whether the planets were
formed via collapse or were formed via accretion and subsequently
ionized, they would still not survive in the core of the cluster.
Free-floating planets have recently been identified in Orion
(Lucas & Roche 2000; Zapatero Osorio et al. 2000) but their
origin remains controversial as they can be escapees or even actual
brown dwarfs.
Dynamic or supernova driven ejection of planets is possible
in star clusters (de la Fuente Marcos & de la Fuente Marcos
1998) but the fraction of runaway planets is less than a few
percent for the entire cluster, much smaller than the figure
suggested by SM22. However, if the analysis is restricted to
the core of a globular cluster which is a very high star density
region this number rises to about 50%, although ejected planets
have very high characteristic velocities with the smaller planets
escaping faster. The actual percentage depends on the semi-major
axis: if it is <3 AU the ejection rate is 1% but it is almost
100% if the semiaxis is >15 AU. On the other hand, in our
models more than 70% of planetary escapees have a velocity
<25 kms-1 with an upper limit for the remaining fraction
of about 200 kms-1. Fast or super-fast planetary escapees are always
the result of strong multibody interactions inside the cluster core.
Although for the core of M 22 the escape velocity is in the range
26-31 kms-1, ejections from the core are the result of strong close
encounters with characteristic velocities much higher than the
escape velocity. Therefore, it is very unlikely to be able to
detect several of these events just by chance unless they are
ejected planets moving almost parallel to the line-of-sight. In
that case, the number of detected events might be consistent with the
expected fraction of runaways from the cluster core. In this
scenario, the detected objects would be moving toward us and likely
located between M 22 and the Earth as they were ejected long ago.
One can argue that this is practically impossible if the
ejection is isotropic, as the fraction of planets moving sufficiently
close to our line-of-sight would be incredibly tiny; however,
ejections are only isotropical if they are the result of close
encounters (likely at the cluster core). If planetary objects escape
from the cluster as a result of evaporation (gradual increase in
kinetic energy due to distant encounters) then they escape through
the Lagrangian points, L1 and L2. If we consider lone planets
formed by collapse, this is a plausible scenario only if a Lagrangian
point is along our line-of-sight. However and although the lack of
precise three-dimensional information makes it difficult to
estimate, it is not very likely that one of the Lagrangian points
might be projected toward the cluster core as the cluster is not
observed against the Galactic Center.
Low eccentricity, distant sub-Saturnian planets similar to the
gas giants (Uranus and Neptune) in our own Solar System are also
able to generate microlensing events like the ones described in SM22.
However, the probability of getting them involved in microlensing
events is only significant if these planets are abundant (several
per host star). On the other hand, Edgeworth-Kuiper-belt-like
structures including Earth-sized objects in large numbers may also
be able to induce brief microlensing events. In fact and from a
strictly intuitive point of view, the relatively high number of
planetary-class detections (6) as compared to a single
classical (stellar) event argues in favor of a multiplanet
scenario. However, low eccentricity primordial planetary orbits
are very unlikely in a highly ionizing environment like M 22, at
least in the cluster core. As pointed out before, planetary systems
wider than 10-15 AU are catastrophically disrupted and due to mass
segregation the most massive stars, and likely less favorable for
planetary-class microlensing (Fig. 1), are dominant
in the core and therefore the optical depth for bound planetary
microlensing at the cluster core is not very significant.
On the other hand, it is also possible that the detected objects are
projected against the core but they are actually part of the halo
of M 22 where the star density is low enough to allow for relatively
primordial, unperturbed (likely multiplanet) systems. Our results
suggest that the percentage of planetary systems disrupted in the
halo of a typical star cluster is very negligible, and the fraction
that experiences significant variation (>10%) in the orbital
elements is a few percent and mainly connected with stellar evolution
not dynamical interactions. If that is the case, the number of
multiplanet systems similar to our Solar System in M 22, and likely
in other globulars, could be much higher than expected. It is
possible to argue against this latter scenario claiming that the
optical depth (or probability) to lensing for the halo of M 22 is
negligible. However, this could not be the case if we consider
planetary objects instead of stars. Let us assume that the membership
of M 22 is 106, simulations suggest that for rich star clusters the
core includes about 10% of the cluster total population, therefore
we have about 105 core stars (or planets if we assume that they
exist) able to contribute to microlensing. As pointed out before,
the actual number of planets available for single lens microlensing
could be just a small fraction of that number, as low as a few
percent. However, we are observing through the cluster halo. If we
assume that the volume of the cluster is about 103 the core volume
and the core population is 10% of the total population, then the
cluster average star density is about 1/100 the core density. On the
other hand, if we consider that the HST observed a region of radius
1 pc (core radius) and that the radius of M 22 is about 18 pc, then
the number of halo stars included in an imaginary cylinder of radius
1 pc and length 36 pc could be estimated by considering that the
average mass ratio between core and cluster is 1.5. This number is
about 30% the core population or 30000 stars, most of them
low-mass. If we assume an average of 4 giant planets per star we
found about 120000 objects available for microlensing. It implies
that the optical depth to planetary companions in the halo of M 22
relative to its core is at least a factor 100 higher. Therefore, our
simplified calculation suggests that, as regards single lens planetary
microlensing, the halo of M 22 is dominant.
The probability P or optical depth for a microlensing event
is given by
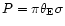 ,
where
,
where 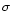 is the
surface density of objects. Therefore, the probability for a
core-induced classical (stellar) microlensing
event is
is the
surface density of objects. Therefore, the probability for a
core-induced classical (stellar) microlensing
event is
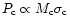 ,
where
,
where 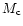 is the average
mass for stars in the core, and
is the average
mass for stars in the core, and
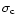 is the surface density
of stars toward the cluster core. In addition, the probability
for a halo-induced planetary microlensing event will be
is the surface density
of stars toward the cluster core. In addition, the probability
for a halo-induced planetary microlensing event will be
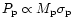 ,
with
,
with 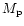 the
average mass for planets
in the halo and
the
average mass for planets
in the halo and
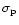 the surface density of planets toward
the cluster halo; this can be calculated by using
the surface density of planets toward
the cluster halo; this can be calculated by using
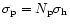 ,
where
,
where 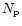 is the number of planets per halo star
and
is the number of planets per halo star
and
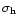 is the surface density of stars toward the cluster
halo. To estimate the actual number of planets per star we may use
is the surface density of stars toward the cluster
halo. To estimate the actual number of planets per star we may use
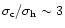 and
and
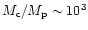 .
On the other
hand, if as suggested by the observations the proportion of available
planets/stars for microlensing is 6 to 1 then the average number of
planetary-size companions per halo star could be as high as
20000 if we consider sub-Saturnian objects or about 2000000 if
the lenses are Earth-sized. In any case, the results of this
quantitative analysis makes it difficult to attribute the observed
events to planetary objects in M 22 unless planets in globular
clusters (or the early Universe for that matter) formed in a
fundamentally different manner than planets in the Galactic disk.
.
On the other
hand, if as suggested by the observations the proportion of available
planets/stars for microlensing is 6 to 1 then the average number of
planetary-size companions per halo star could be as high as
20000 if we consider sub-Saturnian objects or about 2000000 if
the lenses are Earth-sized. In any case, the results of this
quantitative analysis makes it difficult to attribute the observed
events to planetary objects in M 22 unless planets in globular
clusters (or the early Universe for that matter) formed in a
fundamentally different manner than planets in the Galactic disk.
If the objects detected by SM22 are actually located in the core
of M 22, low-eccentricity primordial planetary orbits are very
unlikely if the initial semi-major axis is larger than about 0.5 AU,
as they should be, otherwise a double lens microlensing event must
be recorded, Fig. 1. Our numerical results show that
within the cluster lifetime and for high star density environments
(103-104 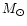 /pc-3) like the core of M 22 about
50% of systems are disrupted with the remaining fraction being
characterized by high eccentricities (e > 0.3). A large fraction
of planets in very elongated orbits increases the probability of
single lens microlensing but not very significantly due to random
orientations.
/pc-3) like the core of M 22 about
50% of systems are disrupted with the remaining fraction being
characterized by high eccentricities (e > 0.3). A large fraction
of planets in very elongated orbits increases the probability of
single lens microlensing but not very significantly due to random
orientations.
Finally, the events reported by SM22 may have been induced
by non-M 22-related substellar objects located along the
line-of-sight. Although current Massive Astrophysical Compact
Halo Objects (MACHOs) observational results toward the
Large Magellanic Cloud (LMC) exclude brown dwarfs as the
primary constituent of the halo (Alcock et al. 1998), any
hypothetical population of free-floating halo (single or
binary) brown dwarfs should have been born elsewhere, namely
in massive dark clusters or Robust Associations of Massive
Baryonic Objects (RAMBOs) (Moore & Silk 1995). The dynamics
of these objects must be quite different from that of typical
star clusters. With a very narrow mass range, the evaporation
of these RAMBOs should be very slow as predicted by the
evolution of mono-component cluster models (de la Fuente Marcos
1995). These very long-lived objects may exist in large numbers.
On the other hand, the microlensing rate is
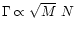 ,
where M is the mass of the lens and N the
number of available lensing objects. SM22 found a single stellar
microlensing event (very likely M 22-related) and six unresolved
events. If they are indeed due to substellar objects in the field
they must be clustered and a naive estimate suggests that the
dark cluster population must be at least 100 times larger than the
core population of M 22, with the same apparent diameter. It means
that the dark cluster might include
107-108 members with a
total mass of
,
where M is the mass of the lens and N the
number of available lensing objects. SM22 found a single stellar
microlensing event (very likely M 22-related) and six unresolved
events. If they are indeed due to substellar objects in the field
they must be clustered and a naive estimate suggests that the
dark cluster population must be at least 100 times larger than the
core population of M 22, with the same apparent diameter. It means
that the dark cluster might include
107-108 members with a
total mass of
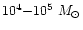 .
In principle, the object
could be located in front of or behind M 22. For the same duration
(upper limit, 0.8 days), the lens is more massive if the dark
cluster is near the Galactic bulge and if its transverse velocity
relative to the observer-source line-of-sight is higher. In any case
the objects are well below 13 Jovian masses. The existence of a
clustered thick disk-like component of dark matter in the Milky Way
has been suggested by Sanchez-Salcedo (1997, 1999)
and Kerins (1997).
Although one can argue that the most likely explanation of the
brief events toward M 22 is simply that they are not due to
microlensing but, for example, to stellar variability, we will not
include this conclusion in our discussion. Rather than consider
astrophysical explanations as stellar variability, we will focus
our discussion, assuming that the events are due to microlensing,
on the astrodynamical (or kinematical) explanations. Our analysis
suggests that, if stellar variability is excluded, only two scenarios
are able to explain the unresolved microlensing events observed toward
M 22: a cluster halo very rich in multiplanet systems (but Solar
System-like) or a chance alignement with a dark cluster or RAMBO. The
upper limit for the mass of the substellar lenses found by SM22 is about
80 times that of Earth. In the first scenario, as microlensing detection
is totally by chance it means that the distribution of masses of
the planetary-mass population in M 22 peaks around that value with a
very likely negligible fraction of planets above it. However, in the
Galactic disk the fraction of substellar objects with Jovian (or
higher) masses is not negligible. If the objects are indeed bound,
most planetary systems in M 22 are dominated by planets of about
Saturn's mass. Preferential formation of low-mass giant planets
in globular clusters can be explained as a result of poor metallicity
and shorter lifetime of protoplanetary disks. In any case, planetary
formation in the early Universe seems to be rather different from
current one with super-Jupiters being more numerous now. On the other
hand, as SM22 detected only one classical (stellar) microlensing
event but six unexpectedly brief events it means that M 22 is rather
rich in planetary-mass objects. As pointed out before, a planet in
a low-eccentricity, short semi-major axis orbit will induce a
double lens behaviour with both objects (planet & host star)
contributing to the magnification. On the other hand, a planet
in a wide but not eccentric orbit will be able to induce a photometric
behaviour like the one observed by SM22 but these objects are unlikely
in the core of a globular cluster. If the lenses are located at the
cluster halo the relatively high rate of detections suggests that
multiplanet systems are very common in globular clusters and that
giant planets in wide orbits are dominant as in our own planetary system.
.
In principle, the object
could be located in front of or behind M 22. For the same duration
(upper limit, 0.8 days), the lens is more massive if the dark
cluster is near the Galactic bulge and if its transverse velocity
relative to the observer-source line-of-sight is higher. In any case
the objects are well below 13 Jovian masses. The existence of a
clustered thick disk-like component of dark matter in the Milky Way
has been suggested by Sanchez-Salcedo (1997, 1999)
and Kerins (1997).
Although one can argue that the most likely explanation of the
brief events toward M 22 is simply that they are not due to
microlensing but, for example, to stellar variability, we will not
include this conclusion in our discussion. Rather than consider
astrophysical explanations as stellar variability, we will focus
our discussion, assuming that the events are due to microlensing,
on the astrodynamical (or kinematical) explanations. Our analysis
suggests that, if stellar variability is excluded, only two scenarios
are able to explain the unresolved microlensing events observed toward
M 22: a cluster halo very rich in multiplanet systems (but Solar
System-like) or a chance alignement with a dark cluster or RAMBO. The
upper limit for the mass of the substellar lenses found by SM22 is about
80 times that of Earth. In the first scenario, as microlensing detection
is totally by chance it means that the distribution of masses of
the planetary-mass population in M 22 peaks around that value with a
very likely negligible fraction of planets above it. However, in the
Galactic disk the fraction of substellar objects with Jovian (or
higher) masses is not negligible. If the objects are indeed bound,
most planetary systems in M 22 are dominated by planets of about
Saturn's mass. Preferential formation of low-mass giant planets
in globular clusters can be explained as a result of poor metallicity
and shorter lifetime of protoplanetary disks. In any case, planetary
formation in the early Universe seems to be rather different from
current one with super-Jupiters being more numerous now. On the other
hand, as SM22 detected only one classical (stellar) microlensing
event but six unexpectedly brief events it means that M 22 is rather
rich in planetary-mass objects. As pointed out before, a planet in
a low-eccentricity, short semi-major axis orbit will induce a
double lens behaviour with both objects (planet & host star)
contributing to the magnification. On the other hand, a planet
in a wide but not eccentric orbit will be able to induce a photometric
behaviour like the one observed by SM22 but these objects are unlikely
in the core of a globular cluster. If the lenses are located at the
cluster halo the relatively high rate of detections suggests that
multiplanet systems are very common in globular clusters and that
giant planets in wide orbits are dominant as in our own planetary system.
The dark cluster scenario is also able to explain the observations.
The only problem posed by this explanation is the mass of the
cluster members. From the Einstein time equation, the upper limit
for the mass of the lenses is a few Jovian masses. From a strictly
theoretical point of view it is difficult to explain how such an
object can form. On the other hand, the mass of the dark cluster
might span the range
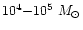 .
This is consistent with
primordial (pre-Galactic) origin of MACHO clusters as cosmological
considerations of the minimum Jeans mass suggest a typical pre-Galactic
mass scale of
.
This is consistent with
primordial (pre-Galactic) origin of MACHO clusters as cosmological
considerations of the minimum Jeans mass suggest a typical pre-Galactic
mass scale of
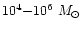 .
If there exist many more
of these dark clusters, the microlensing statistics would be
essentially unchanged from the unclustered case (Metcalf & Silk 1996),
therefore it would be a really serendipitous discovery. This is
consistent with the lack of an analogous population of events toward
the LMC (Alcock et al. 1998).
.
If there exist many more
of these dark clusters, the microlensing statistics would be
essentially unchanged from the unclustered case (Metcalf & Silk 1996),
therefore it would be a really serendipitous discovery. This is
consistent with the lack of an analogous population of events toward
the LMC (Alcock et al. 1998).
In this paper we have presented several plausible alternatives to the
free-floating planets interpretation of the microlensing events
observed by SM22. Our analysis is not meant to provide a unique or
complete model either to explain microlensing in M 22 or in any other
star cluster. Instead we simply point out different but compatible
scenarios able to generate the same photometric signatures as detected
by SM22. Our analysis can be easily tested by surveying low ionization
rate globular clusters like M 71, M 4, or NGC 3201 in which, if they form,
a fraction of low eccentricity, short semi-major axis planetary systems
is likely to survive and be able to contribute to (binary) microlensing.
If the observation of other clusters is not successful in finding
microlensing events then the dark cluster scenario is the only plausible
scenario. In addition, a comparison between microlensing data from core
and off-core observations of M 22 may also help to clarify this matter,
and follow-up HST observations can shed new light on this tentative
discovery.
Acknowledgements
We thank Dr. S. J. Aarseth for providing his computer code and
Dr. K. C. Sahu for some remarks on his results. The authors thank the
Department of Astrophysics of Universidad Complutense de Madrid
(UCM) for allotting excellent computing facilities. We also thank
the referee, Scott Gaudi, for his rapid and very helpful report.
Part of the calculations were performed on the SGI Origin 2000 of the
"Centro de Supercomputación Complutense'' through the UCM project
"Dinámica Estelar y Sistemas Planetarios'' (CIP 454). In preparation
of this paper, we made use of the ASTRO-PH e-print server and the NASA
Astrophysics Data System.
- Aarseth, S. J. 1994,
in Galactic Dynamics and N-body Simulations,
ed. G. Contopoulos, N. K. Spyrou, & L. Vlahos
(Springer Verlag, Berlin), 277
In the text
- Adams, F. C., & Laughlin, G. 2001,
Icarus, 150, 151
In the text
NASA ADS
- Alcock, C., Allsman, R. A., Alves, D., et al. 1998,
ApJ, 499, L9
In the text
NASA ADS
- Bonnell, I. A., Smith, K. W., Davis, M. B., & Horne, K. 2001,
MNRAS, 322, 859
In the text
NASA ADS
- Boss, A. P. 2001,
ApJ, 551, L167
In the text
NASA ADS
- Cote, P., Pryor, C., McClure, R. D., Fletcher, J. M., &
Hesser, J. E. 1996,
AJ, 112, 574
In the text
NASA ADS
- Davidge, T. J., & Harris, W. E. 1996,
ApJ, 462, 255
In the text
NASA ADS
- Eggleton, P. P., Fitchett, M. J., & Tout, C. A. 1989,
ApJ, 347, 998
In the text
NASA ADS
- de la Fuente Marcos, R. 1995,
A&A, 301, 407
In the text
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 1997,
A&A, 326, L21
In the text
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 1998,
NewA, 4, 21
In the text
NASA ADS
- de la Fuente Marcos, R., & de la Fuente Marcos, C. 2000,
in Stellar Clusters and Associations: Convection, Rotation, and
Dynamos, ed. R. Pallavicini, G. Micela, & S. Sciortino
(San Francisco), ASP Conf. Ser., 198, 183
In the text
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2001a,
A&A, 371, 1097
In the text
NASA ADS
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2001b,
in Modes of Star Formation and the Origin of Field Populations,
ed. E. Grebel, & W. Brandner
(San Francisco), ASP Conf. Ser., in press
- Gaudi, D. S., & Sackett, P. D. 2000,
ApJ, 528, 56
In the text
NASA ADS
- Jetzer, P., Straessle, M., & Wandeler, U. 1998,
A&A, 336, 411
In the text
NASA ADS
- Kerins, E. J. 1997,
A&A, 322, 709
In the text
NASA ADS
- Laughlin, G., & Adams, F. C. 1998,
ApJ, 508, L171
In the text
NASA ADS
- Laughlin, G., & Adams, F. C. 2000,
Icarus, 145, 614
In the text
NASA ADS
- Lucas, P. W., & Roche, P. F. 2000,
MNRAS, 314, 858
In the text
NASA ADS
- Mao, S., & Paczynski, B. 1991,
ApJ, 374, 37
In the text
- Metcalf, R. B., & Silk, J. 1996,
ApJ 464, 218
In the text
NASA ADS
- Moore, B., & Silk, J. 1995,
ApJ, 442, L5
In the text
NASA ADS
- Paczynski, B. 1986,
ApJ, 304, 1
NASA ADS
- Sahu, K. C., Casertano, S., Livio, M., et al. (SM22) 2001,
Nature, 411, 1022
In the text
NASA ADS
- Sánchez-Salcedo, F. J. 1997,
ApJ, 487, L61
In the text
NASA ADS
- Sánchez-Salcedo, F. J. 1999,
MNRAS, 303, 755
In the text
NASA ADS
- Scalo, M. J. 1986,
Fundam. Cosmic. Phys., 11, 1
In the text
- Smith, K. W., & Bonnell, I. A. 2001,
MNRAS, 322, L1
In the text
NASA ADS
- Witt, H. J. 1990,
A&A, 236, 311
In the text
NASA ADS
- Zapatero Osorio, M. R., Béjar, V. J. S., Martín, E. L.,
et al. 2000, Science, 290, 103
In the text
NASA ADS
Copyright ESO 2001
![]() (Saturn mass is about 95). They
interpret that these objects must be either free-floating, or at least
several AUs from any stellar-mass objects, although they favour the
free-floating hypothesis. If real, the total contribution of these
free-floating planets to the mass of M 22 is estimated by these authors
to be of the order of 10%.
(Saturn mass is about 95). They
interpret that these objects must be either free-floating, or at least
several AUs from any stellar-mass objects, although they favour the
free-floating hypothesis. If real, the total contribution of these
free-floating planets to the mass of M 22 is estimated by these authors
to be of the order of 10%.
![]() Centauri and very likely all its soft (long period)
binaries have been disrupted by stellar encounters.
Centauri and very likely all its soft (long period)
binaries have been disrupted by stellar encounters.
![\begin{figure}
\par\includegraphics[width=7.9cm,height=8.6cm,angle=-90,clip]{h3102f1.ps} \end{figure}](/articles/aa/full/2001/45/aah3102/Timg23.gif)
![]() ,
where
,
where ![]() is the
surface density of objects. Therefore, the probability for a
core-induced classical (stellar) microlensing
event is
is the
surface density of objects. Therefore, the probability for a
core-induced classical (stellar) microlensing
event is
![]() ,
where
,
where ![]() is the average
mass for stars in the core, and
is the average
mass for stars in the core, and
![]() is the surface density
of stars toward the cluster core. In addition, the probability
for a halo-induced planetary microlensing event will be
is the surface density
of stars toward the cluster core. In addition, the probability
for a halo-induced planetary microlensing event will be
![]() ,
with
,
with ![]() the
average mass for planets
in the halo and
the
average mass for planets
in the halo and
![]() the surface density of planets toward
the cluster halo; this can be calculated by using
the surface density of planets toward
the cluster halo; this can be calculated by using
![]() ,
where
,
where ![]() is the number of planets per halo star
and
is the number of planets per halo star
and
![]() is the surface density of stars toward the cluster
halo. To estimate the actual number of planets per star we may use
is the surface density of stars toward the cluster
halo. To estimate the actual number of planets per star we may use
![]() and
and
![]() .
On the other
hand, if as suggested by the observations the proportion of available
planets/stars for microlensing is 6 to 1 then the average number of
planetary-size companions per halo star could be as high as
20000 if we consider sub-Saturnian objects or about 2000000 if
the lenses are Earth-sized. In any case, the results of this
quantitative analysis makes it difficult to attribute the observed
events to planetary objects in M 22 unless planets in globular
clusters (or the early Universe for that matter) formed in a
fundamentally different manner than planets in the Galactic disk.
.
On the other
hand, if as suggested by the observations the proportion of available
planets/stars for microlensing is 6 to 1 then the average number of
planetary-size companions per halo star could be as high as
20000 if we consider sub-Saturnian objects or about 2000000 if
the lenses are Earth-sized. In any case, the results of this
quantitative analysis makes it difficult to attribute the observed
events to planetary objects in M 22 unless planets in globular
clusters (or the early Universe for that matter) formed in a
fundamentally different manner than planets in the Galactic disk.
![]() .
This is consistent with
primordial (pre-Galactic) origin of MACHO clusters as cosmological
considerations of the minimum Jeans mass suggest a typical pre-Galactic
mass scale of
.
This is consistent with
primordial (pre-Galactic) origin of MACHO clusters as cosmological
considerations of the minimum Jeans mass suggest a typical pre-Galactic
mass scale of
![]() .
If there exist many more
of these dark clusters, the microlensing statistics would be
essentially unchanged from the unclustered case (Metcalf & Silk 1996),
therefore it would be a really serendipitous discovery. This is
consistent with the lack of an analogous population of events toward
the LMC (Alcock et al. 1998).
.
If there exist many more
of these dark clusters, the microlensing statistics would be
essentially unchanged from the unclustered case (Metcalf & Silk 1996),
therefore it would be a really serendipitous discovery. This is
consistent with the lack of an analogous population of events toward
the LMC (Alcock et al. 1998).