A&A 379, L44-L47 (2001)
DOI: 10.1051/0004-6361:20011487

Another bar in the Bulge

C. Alard1,2


1 - Institut d'Astrophysique de Paris, 98bis boulevard Arago, 75014 Paris, France
2 - Observatoire de Paris, 77 avenue Denfert Rochereau, 75014 Paris, France

Received 12 September 2001 / Accepted 22 October 2001

Abstract
A map of the projected density of the old stellar population of the Galactic Bulge region is reconstructed using 2MASS data. By making a combination of the H and K photometric bands, it is possible to overcome the effect of reddening, and thus penetrate the inner structure of the Galactic Bulge. The main structure in the map corresponds to the well documented peanut shaped bar which is formed by the inner parts of the Galactic disk as a result of dynamical instabilities. As suggested by numerical simulations, the projected Z profile of the bar, has an almost exponential shape. After subtracting the exponential profile associated with the bar, a large residual appear near the Galactic Center. This residual is elongated and asymmetrical, which suggest a bar structure. Thus we arrive at the conclusion that in addition to the main bar a smaller bar with a different orientation may exist in the central region of the Milky Way. This finding makes the Milky Way very similar to a large number of barred spiral Galaxies which show as well a smaller bar in their central regions.

Key words: Galaxy: bulge - Galaxy: structure


1 Introduction

The recent release by the 2MASS collaboration of a catalogue of point sources covering a large fraction of the sky is of great interest for the study of the Galactic Structure. Since the 2MASS infrared magnitudes by 2MASS are insensitive to extinction, these data are an ideal tool to probe the structure of the Galaxy within a few degrees from its center. The study of the Galactic Bulge in low extinction windows situated at larger distances from the center revealed that the Bulge was flattened and asymmetric. This elongated bulge with marked tri-axial structure is usually called the "bar''. The major axis of the bar is pointing towards the first Galactic quadrant. The presence of the bar is very noticeable in the stellar component. Stanek (1994) detected an offset in magnitude for clump giants on different sides of the bar. A similar asymmetry is visible in the COBE image of the Bulge region taken in the near infrared (Dwek et al. 1995). But the bar is also quite visible in the pattern speed of the gas (Binney et al. 1991). The nature of the Bar/Bulge system and its formation process are not completely clear. Spiral Galaxies like the Milky way have exponential bulges (Carollo et al. 2001; Mollenhoff & Heidt 2000; Van der Marel 2000), since exponential bulges can be formed easily has a result of disk instability in the central regions, we may infer that the exponential bulges are formed by a dynamical perturbation of the central disk. This bar structure seems to dominate the central region of our Galaxy, but a fundamental question is to know whether other components do exist at smaller scales. One may expect to find some parts of the bulge that were not formed dynamically from disk stars, but from a distinct stellar population. This population should be dominant in the central degree, and should be detectable using the 2MASS data.

2 Data analysis

2.1 Basic processing

The 2MASS catalogues corresponding to the range $\vert b_{\rm II}\vert<10$ and $\vert l_{\rm II}\vert<15$ were obtained from the 2MASS public release. In this release the coverage of this coordinate range is not complete ( ${\simeq} 60\%$), but is sufficient for studies of Galactic structure. The first step is to select the sources with sufficient quality (read_flag>1). Using this criterion there are about 30 millions stars in the region of interest. Within this area there are a number of regions which are affected by the presence of bright stars and their diffraction spikes. It is easy to identify these areas since the star counts in the neighborhood are much lower than average. By making star counts in a box of 0.15 sq degree all over the frame, we obtain an image where the regions occupied by bright stars appear as dark patches. In case the counts in a box are less than 10, the relevant pixel in the image is considered to belong to a dark patch. Even in the lower density regions, the mean star counts are about 10 times larger, thus our cut-off does not induce any artifact. To remove any contamination from the dark spots to the nearby pixels, all the pixels belonging to a $3\times 3$ mesh were also flagged.

2.2 Canceling the effect of extinction

By combining 2 photometric bands it is easy to derive a magnitude that is independent of reddening. For instance using H and K, we can derive the apparent magnitude $m_{\rm e}$:

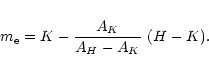
\begin{eqnarray*}m_{\rm e} = K - \frac{A_K}{A_H-A_K} \ (H-K). \end{eqnarray*}


Following Rieke & Lebofsky (1985) we take:

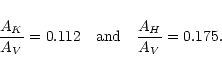
\begin{eqnarray*}\frac{A_K}{A_V} = 0.112 \ \ \ {\rm and} \ \ \ \frac{A_H}{A_V} = 0.175 . \end{eqnarray*}


Leading finally to:
$\displaystyle m_{\rm e} = K - C_K \ (H-K) \qquad {\rm with{:}} \ C_K=1.77.$     (1)

Note that since the reddening law in the infrared is unique (Cardelli et al. 1989), the definition given in Eq. (1) is valid for any line of sight, and not only for the particular area probed by Rieke & Lebofski (1985). Thus in this band the cumulative counts of the stars brighter than some cut-off in magnitude $M_{\rm C}$ will be independent of the reddening (provided that $M_{\rm C}$ is brighter than the observational limiting magnitude). Considering that the limiting magnitude in the H band is about 16 and that the maximum extinction is about $A_V \simeq 30$, we infer that the cut-off should be brighter than H=11. Since the color of the tip of the upper giant branch is $H-K \simeq 0.5$ we obtain finally in the $m_{\rm e}$ band, $M_{\rm C} \simeq 9.6$. For security we will adopt the very conservative bright upper cut-off in magnitude $M_{\rm C} = 9$.
  \begin{figure} \par\includegraphics[width=7.5cm,clip]{Fig1.eps} \end{figure} Figure 1: Here we present the polynomial smoothing of 2 sections of the projected density taken at constant longitude. Note that the profile deviates from an exponential near the Galactic Center.
Open with DEXTER

2.3 Reconstructing density maps of the bulge region

There is one major difficulty in producing a map of the Bulge region: the coverage is not complete and additionally there are holes due to the bright stars. However provided that we assume that the Galaxy is symmetrical about its plane, it is possible to fill most of the gaps. In order to smooth and fill the smaller data gaps which remain, we use the fact that the density profile at constant longitude is almost exponential (see Fig. 1). This property suggests that the profile can be represented by a polynomial function. Numerical experiments shows that it is not significant to increase the degree of the polynomial beyond 5 to represent the data. To increase the numerical stability of the fit we will use a strip of 9 columns centered around the column of interest. This procedure is carried out for each column in the image. A filtered image is constructed by replacing each column in the original image by the polynomial solution. Some example of polynomial fitting of the columns are given in Fig. 1. This procedure has a good ability to fill or extrapolate small data gaps, and has an excellent numerical stability. Once we have reconstructed this image of the star counts in the Bulge region, we apply a final wavelet smoothing procedure in order to balance the smoothing at all scales. This final smoothing is interesting because the polynomial reconstruction is one dimensional, and thus is biased in one direction, on a particular scale. The Wavelet decomposition is obtained by applying iteratively the Spline filter to the image and the smoothed images (Starck & Murtagh 1994). To estimate the statistical cuts to apply in the wavelet decomposition we generate Monte-Carlo images with counts approaching our own image. In the final reconstruction of the smoothed image we use 4$\sigma$ cuts. One final concern is the possible effect of small uncertainties in the determination of CK (typically a few %). This can be investigated by reconstructing the density with small variations of CK. The comparison with the initial map shows that the density variations induced by such changes in the value of CK are about the amplitude of the noise, and thus do not affect the final result.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{Fig2.ps} \end{figure} Figure 2: Map of the Galactic Bar region reconstructed using a polynomial fitting method and wavelet smoothing. Note that the star counts are systematically higher at positive longitude for |b|>2. Contours values: (max,min)=(60000,400) stars/sq deg.
Open with DEXTER

2.4 Analysis of the projected density

We have already noticed that the Z profile of the projected density is almost exponential. This exponential profile is also present in numerical simulations of peanut shaped bars. Combes et al. (1990) showed that a disk with a small bulge near its center forms a peanut shaped bar with a nearly exponential projected Z profile (see in particular Fig. 4 in Combes 1990). Thus if we subtract the exponential contribution which corresponds to the bar-disk system, the remaining density may reveal another component. The contribution of the bar will be estimated by fitting an exponential to each column of the image (which corresponds to the projected Z profile). This procedure is more flexible than trying to subtract a bar model. There are still many uncertainties concerning the structure of the Galactic bar, thus the subtraction of a bar model may give ambiguous results. By fitting an exponential profile, we make no particular assumption about the shape of the bar, other than a general assumption on the Z profile at equilibrium which is justified by numerical simulations. To implement the fit of the exponential profile, we perform a robust fitting of a straight line to the log of density (by minimizing the sum of absolute deviations). Once the exponential contribution has been subtracted, a very significant residual appears in the central region ($R<2^\circ$). The contours of this residual are smooth and elongated along the Galactic plane. This component shows also a very significant asymmetry in longitude. The amplitude of this asymmetry is close to 15%, which is about 7 sigmas according to Poisson statistics. There are also some residuals along the Galactic plane in general. But their amplitude is about 10 times smaller, they do not have smooth structure, and their scale is much smaller. These residuals are probably due to the presence of young stars in the HII regions.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{Fig3.ps} \end{figure} Figure 3: Contours of the residual density after subtracting the main component. Note that the asymmetry is in the opposite direction of the large scale Galactic Bar. Contours values: (max,min)=(38000,400) stars/sq deg.
Open with DEXTER

3 Discussion

There are some intrinsic difficulties in the interpretation of the former results, we see a residual component after subtracting a main component. But this result is based on the assumption that the bar has a projected density profile in the Z direction which is exponential. Even if this assumption is supported by numerical simulations, it might just be that the projected density of the bar is not exponential. But in this case, why do we observe an asymmetry in an opposite direction to the bar? Two possible sources of bias are: the residual extinction, and the steepness of the density profile near the center (Blitz & Spergel 1991). In principle the extinction should have no effect in the $m_{\rm E}$ band, but it is possible that for observational reasons the limiting magnitude in 2MASS is somewhat brighter than expected, which would result in an indirect extinction effect. These biases can be investigated by using numerical simulations. To build a numerical model we need to integrate the convolution product of the luminosity function $\phi$ with the density distribution $\rho$. The integration domain in the space of the magnitudes will be modulated by the extinction AV. For the luminosity function we will adopt the model of Wainscoat et al. (1992). The density distribution will be built using a truncated exponential disk (Lopez-Corredoira et al. 2001) and a triaxial bar model with a power law profile. This bar model has an inclination of 20 deg with respect to the line of sight, and axis ratio: $\frac{x_0}{y_0} \simeq 3$ and $\frac{z_0}{y_0} \simeq 0.7$ (Dwek et al. 1995). And finally the extinction map of the whole area was built from our 2MASS data by using a method presented by Schultheis et al. (2000). Let's start with the case of residual extinction effects: the counts were generated using the aforementioned procedure, Poisson noise was simulated, and finally the whole process of polynomial reconstruction, smoothing and exponential subtraction was applied. This procedure was undertaken for different observational limiting magnitudes, starting from our default value (no extinction cut-off). To summarize the results, the longitude profile of the residual density has been represented for the different limiting magnitude (Fig. 4).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{Fig4.ps} \end{figure} Figure 4: The marginal distribution in longitude of simulated profiles for different limiting magnitude (default: thin line, 1 mag brighter than default: dashed line, 1.5 mag brighter: dotted dashed line). The last profile is the observational profile (thick line). All profiles have been normalized so that the sum of the profile is unity.
Open with DEXTER

The comparison of these results with the observational profile shows unambiguously that the effect of extinction is in the opposite direction to the observed asymmetry. Furthermore, it is interesting to notice the steep edge of the observational profile, which is similar on both side of the diagram. The profile variations produced by extinction are not similar on both edges, and are hardly so steep. Concerning the effect of the steepness of the inner bar profile, even if a steep bar profile, may produce an asymmetry opposite to the bar, it is not possible reproduce the amplitude of the asymmetry even if the density profile behaves like: R-7. A steeper density profile appears unphysical. These results are not very dependent upon the luminosity function. Power law luminosity functions gives the same result. The best explanation is to consider the presence of another component in the inner Galaxy. A small bar with a steeply dropping density near its edge can reproduce the observed asymmetry. This finding is not surprising, the discovery of small substructure in the central region of barred spiral Galaxies is very common (Erwin & Sparke 1999; Fiedli et al. 1996; Friedli 1996; Shaw et al. 1995). This small bar structure was not found in previous studies for 2 fundamental reasons, the former data set lacked either the depth or the resolution. The 2MASS H band is deep and insensitive to extinction, and furthermore the 30 millions stars available result in an excellent spatial resolution.

References

 

Copyright ESO 2001