A&A 379, 893-904 (2001)
DOI: 10.1051/0004-6361:20011376

HS 0705+6700: A new eclipsing sdB binary[*],[*]

H. Drechsel1 - U. Heber1 - R. Napiwotzki1 - R. Østensen2,3 - J.-E. Solheim3 - F. Johannessen3 - S. L. Schuh4 - J. Deetjen4 - S. Zola5


1 - Dr. Remeis-Sternwarte Bamberg, Astronomisches Institut der Universität Erlangen-Nürnberg,
Sternwartstraße 7, 96049 Bamberg, Germany
2 - Isaac Newton Group of Telescopes, 37800 Santa Cruz de La Palma, Canary Islands, Spain
3 - University of Tromsø, Department of Physics, 9037 Tromsø, Norway
4 - Institut für Astronomie und Astrophysik, Universität Tübingen, Waldhäuser Straße 64,
72076 Tübingen, Germany
5 - Astronomical Observatory of the Jagiellonian University, ul. Orla 171, 30-244 Cracow, Poland

Received 14 August 2001 / Accepted 26 September 2001

Abstract
We report the discovery of an eclipsing binary - HS 0705+6700 - being an sdB star with a faint companion. From its light curve the orbital period of 8263.87 s, the mass ratio of the system q = 0.28, the inclination of 84 $\hbox{$.\!\!^\circ$ }4$ and other system parameters are derived. The companion does not contribute to the optical light of the system except through a strong reflection effect. The semi-amplitude of the radial velocity curve K1 = 85.8 kms-1 and a mass function of f(m) = 0.00626 $M_{\odot}$ are determined. A spectroscopic analysis of the blue spectra results in $T_{\rm eff} = 28\,800$ K, $\log~g = 5.40$, and $\log (n_{\rm He}/n_{\rm H}) = -2.68$. These characteristics are typical for sdB stars, as is its mass of 0.48 $M_{\odot}$. According to its mass (0.13 $M_{\odot}$) and radius (0.19 $R_{\odot}$), the companion is an M dwarf. The primary is in a core helium burning phase of evolution, and the system must have gone through a common envelope stage when the primary was near the tip of the red giant branch.

Key words: stars: subdwarfs - binaries: eclipsing - binaries: spectroscopic - stars: early-type - stars: fundamental parameters - stars: individual: HS 0705+6700


1 Introduction

Subluminous B stars (sdB) dominate the populations of faint blue stars of our own Galaxy and are found in both the old disk and in halo populations, e.g. as stars forming the blue tails to the horizontal branches of globular clusters (Ferraro et al. 1997).

In the context of galaxy evolution, sdB stars are important because they are sufficiently common to be the dominant source for the "UV upturn phenomenon'' observed in elliptical galaxies and galaxy bulges (Brown et al. 1997, 2000a; Greggio & Renzini 1990, 1999). They might also be used as age indicators for elliptical galaxies (Brown et al. 2000b).

However, important questions remain regarding the evolutionary paths and the appropriate timescales. There is general consensus that the sdB stars can be identified with models for Extreme Horizontal Branch (EHB) stars (Heber 1986; Saffer et al. 1994). Like all HB stars they are core helium burning objects. However, their internal structure differs from typical HB stars, because their hydrogen envelope is very thin (<1% by mass) and therefore inert. As a consequence EHB stars evolve directly to the white dwarf cooling sequence, thus avoiding a second red giant phase (Dorman et al. 1993).

The discovery of multi-mode, short-period ( P = 2-10 min) pulsators among sdB stars (see O'Donoghue et al. 1999 for a review) has opened a new possibility of probing their interiors using seismological tools. Recently, Brassard et al. (2001) were able to derive the mass and hydrogen envelope mass of the pulsating sdB star PG 0014+067 by asteroseismology. Their results (total mass $M = 0.49 \pm 0.019$ $M_{\odot}$ and envelope mass $\log (M_{\rm env}/\mbox{~$M_{\odot}$ }) = -4.3 \pm 0.22$) are in excellent agreement with the predictions by evolution theory.

Considerable evidence is accumulating that many sdB stars reside in close binaries (Maxted et al. 2001a; Saffer et al. 2001). Therefore mass transfer should play an important role in the evolution of such binary systems. Detailed investigations of sdB binaries, in particular eclipsing systems, are crucial to determine their masses. However, only two such eclipsing binaries, HW Vir (Menzies & Marang 1986) and PG 1336-018 (Kilkenny et al. 1998) are currently known, which consist of an sdB star and an optically invisible M dwarf companion. Here we report the discovery of a third such system - HS 0705+6700.

HS 0705+6700 was selected from a list of candidates drawn from the Hamburg Schmidt survey (Hagen et al. 1995). Follow-up spectroscopy (Heber et al. 1999; Edelmann et al. 2001b) revealed that its effective temperature lies in the domain predicted for the pulsational instability. Therefore, HS 0705+6700 was included in a photometric monitoring programme at the Nordic Optical Telescope (see Østensen et al. 2001a, 2001b) in order to search for pulsations. Indeed, the star turned out to be variable, but not on the time and flux scale expected for pulsations. The onset of a primary eclipse event shortly after the start of the observations brought the observed brightness down by about a magnitude. This made it evident that HS 0705+6700 must be an eclipsing binary. This was confirmed in the following night when both primary and secondary minima were monitored.

   
2 Observations

   
2.1 Photometry

The initial observations were made on 5 and 6-Oct.-2000 at the Nordic Optical Telescope (NOT) with the Andalucia Faint Object Spectrograph and Camera (ALFOSC), equipped with a Loral, Lesser thinned, 2048$\times$2048 CCD chip, and modified with our own control software to be able to observe in a high-speed multi-windowing mode. The sky area available for locating a reference star is limited to the area of the chip: $\sim$ $6.5 \times 6.5$ arcmin2. On 5-Oct.-2000, the observations started at UT 05:38 and covered a time period of 3590 s, and on 6-Oct.-2000 measurements started at UT 03:28 and extended over 10280 s.

We observed HS 0705+6700 using three reference stars to construct the relative light curve. The observations were made with a Bessel B-band filter in order to optimize detection of low level pulsations. A cycle time of 20 s was used, allowing an actual integration time of 16.5 s. A total of 634 exposures were collected on the nights of 5 and 6-Oct.-2000. The data were reduced online using the Real Time Photometry (RTP) program developed by one of us (RO) as part of his PhD project (Østensen  2000). More details about this software are given elsewhere (Østensen et al. 2001a).

The R-band photometry of HS 0705+6700 was obtained on 2-Nov.-2000 at the Calar Alto Observatory using the 2.2 m telescope with the CAFOS instrument. Observations started at UT 01:57, and the total length of the data set was 12841 s. A total of 598 measurements were made with a cycle time of 21 s (the integration time was 10 s). Each exposure, taken through a Johnson R filter, is a $2 \times 2$ binned subframe of the 2k $\times$ 2k blue-sensitive, back-illuminated SITe chip. The field around the target contains several other stars, five of which were used as reference stars. The basic data reduction as well as the relative aperture photometry was performed using the IDL software TRIPP (Schuh et al. 1999). The 1$\sigma $ error of the resulting normalized differential light curve, derived from the variations of all relative reference light curves, is 0.013.

Following the B and R light curves obtained on October and November 2000, additional photometric observations were collected with various smaller telescopes (on Tenerife, in Norway, Poland, and Greece) on five different nights scattered over the next five months (November 2000 to March 2001). Nine more primary minima were covered. The measurements were made with CCD cameras in different filters (R, I), and in one case with a classical photo-multiplier tube (PMT) photometer in unfiltered light. Dates and other details of this complementary photometry are contained in Table 2.

   
2.2 Spectroscopy

Optical spectra of HS 0705+6700 were obtained in March 2001 at the DSAZ observatory at the 3.5 m telescope with the Twin spectrograph in dichroic mode covering the wavelength ranges 3925 Å to 5015 Å in the blue channel and 5975 Å to 7070 Å in the red channel at a spectral resolution of 1 Å. Details of the observations are given in Table 1.

 

 
Table 1: Spectroscopic observations (heliocentric Julian Date for mid-exposure, length of exposure, and heliocentric radial velocity).

hel. JD (mid)		 exposure hel. RV
-2451900 time (s) (km s-1)

79.55107		 900 56.5
79.56562 900 -18.1
79.57960 900 -74.5
79.59264 900 -110.1
80.46672 600 -114.5
81.31732 600 -120.2
81.32809 600 -106.4
81.34120 900 -38.2
81.35216 600 4.6
81.36139 600 52.5
81.37098 600 32.9
81.38026 600 4.9
81.39023 600 -45.7
81.39943 600 -81.6
81.40900 600 -116.6


The data were reduced with the MIDAS package distributed by the European Southern Observatory ESO.

   
3 Photometric analysis

   
3.1 Ephemeris

Our B and R CCD photometry of October-November 2000 provided clear evidence that HS 0705+6700 is a short-period eclipsing binary. The complete phase coverage and high time resolution of the CCD light curves allowed for an accurate determination of minimum times and a period analysis.

The CCD B measurements carried out with the 2.5 m Nordic Optical Telescope covered a complete primary eclipse in each of the two nights of October 5 and 6, 2000. The CCD R photometry obtained with the CAFOS instrument attached to the Calar Alto 2.2 m telescope on November 2, 2000, continuously extended over more than one complete orbital cycle and covered two subsequent primary minima. Already from these four minimum times we derived an orbital period of 8263.88 s.

For a more refined period analysis nine more primary minima were used, which had been observed with several smaller telescopes between November 2000 and March 2001 (see Table 2).

 

 
Table 2: Times of primary minima derived from CCD and PMT photometric observations.

Date		 HJD Error Epoch O-Ca Method Filter Type Telescopeb Observersc

05-10-00		 2451822.75978 0.00005 0 -0.00004 Kwee B CCD NOT 2.5 m RØ, JES
06-10-00 2451823.71648 0.00010 10 +0.00019 Kwee B CCD NOT 2.5 m RØ, JES
02-11-00 2451850.59301 0.00011 291 +0.00001 parabola R CCD CA 2.2 m SS, JD
02-11-00 2451850.68866 0.00012 292 +0.00002 parabola R CCD CA 2.2 m SS, JD
30-11-00 2451878.71316 0.00003 585 +0.00005 Kwee - PMT IAC 0.8 m FJ
09-01-01 2451919.2670 0.0002 1009 -0.00029 Kwee I CCD Skb 0.6 m SZ
09-01-01 2451919.3627 0.0010 1010 -0.00024 parabola I CCD Skb 0.6 m SZ
09-01-01 2451919.4586 0.0001 1011 +0.00002 Kwee I CCD Skb 0.6 m SZ
15-02-01 2451956.4738 0.0013 1398 -0.00004 parabola R CCD Crc 0.5 m SZ
16-02-01 2451956.5697 0.0011 1399 +0.00022 parabola R CCD Crc 0.5 m SZ
17-02-01 2451957.5274 0.0002 1409 +0.00145 Kwee R CCD Crc 0.5 m SZ
27-03-01 2451996.3586 0.0001 1815 +0.00011 Kwee R CCD Kry 1.2 m SZ
28-03-01 2451997.3150 0.0001 1825 +0.00004 Kwee R CCD Kry 1.2 m SZ

a
Relative to the ephemeris given in Sect. 3.1.
b
NOT: Nordic 2.5 m, La Palma; CA: Calar Alto 2.2 m, Spain; IAC: IAC 0.8 m, Teide, Tenerife; Skb: Skibotn 0.6 m, Norway; Crc: Cracow Jagiellonian Obs. 0.5 m, Poland; Kry: Kryonerion 1.2 m, Greece.
c
RØ: Roy Østensen; JES: Jan-Erik Solheim; SS: Sonja Schuh; JD: Jochen Deetjen; FJ: Frank Johannessen; SZ: Stanislaw Zola.

Including these minima means a considerable broadening of the time base, allowing for more accurate period determination. The minimum times were determined either by the Kwee-van Woerden method (1956) or by fitting parabolas to the cores of the minima. Table 2 lists the minimum times together with other observational details.

The standard deviation from a linear O-C representation amounts to $1.5\times 10^{-4}$ days ($\approx$13 s), which is less than the mean time resolution between subsequent CCD exposures when monitoring the light curves (mostly about 20 s). Eight minima lie within a 1 $\sigma $ belt, and four others within a 2 $\sigma $ belt. There is only one primary minimum (the one of February 17, 2001, at epoch 1409) deviating by about 10 $\sigma $ from the linear regression. This timing was therefore not used for the period determination. From the remaining 12 primary minima distributed over a time span of nearly 6 months, the following linear elements for the heliocentric primary minimum were derived:

HJD = $2451822\fd75982$ + $0\fd09564665$ $\cdot E.$
$\pm 22$ $\pm 39$
This ephemeris was applied for the phasing of the light curves and of the spectroscopic observations analyzed in this paper.

   
3.2 Light curve solution

The B and R light curves obtained with the 2.5 m NOT and 2.2 m Calar Alto telescopes, respectively, were analyzed with the MORO code (Drechsel et al.  1995). This light curve solution program uses the Wilson-Devinney logistical approach (1971), but is based on a modified Roche model for the binary structure, taking into account the radiative interaction between the components of hot, close binaries. Also, the differential corrections procedure for parameter optimization is replaced by the more powerful simplex algorithm, which was first applied to eclipse light curve solutions by Kallrath & Linnell (1987). For more details and application examples see, e.g., Drechsel (2000) or Drechsel et al. (1995).

The B and R light curves were represented by normal points formed by binning the fluxes of individual measurements over narrow time intervals. One reason for this was to reduce the observational scattering to a smoother run, and on the other hand the computational performance was improved. The phase resolution of the normal points was generally chosen as 0.005 phase units (41 s), except for the core of the primary minimum, where a step width of 0.002 phase units (16 s) was used. The total binning window size was 0.02 phase units (165 s). Hence the 634 and 598 individual measurements of the B and R curves, respectively, were reduced to 212 normal points in each passband. Typically, 12 individual observations were averaged to form a single normal point. The input light curves (in intensity units) were normalized to unity at quadrature phase 0.25.

We used the principal Wilson-Devinney mode 2, which poses no restrictions on the presumed system configuration (detached or semi-detached), and links the luminosity of the secondary component to its effective temperature by means of the Planck law. The latter aspect is of nearly no importance here, because the luminosity ratio between primary and secondary flux contributions is so huge in this system (L1/L2 is of order 104 for B and 103 for R passbands), that the secondary is photometrically only evident through the reflection effect and shadowing of primary light. The B and R light curves were solved simultaneously to yield consistent solution parameters.

Since the total number of light curve parameters is considerably large (12 + 5 n), where n is the number of spectral passbands (filter light curves), i.e. equals 22 for our case of a simultaneous B and R fit, it is important to reduce the free parameter set by consideration of spectroscopic and theoretical boundary conditions and other consistency checks. Otherwise, too many free parameters would easily tend to produce underdetermined solutions with no guarantee of uniqueness.

As was obvious from the sinusoidal shape of the radial velocity curve (Sect. 4.1) and from the position of the secondary minimum at exactly phase 0.50, it was implicitly assumed that we are dealing with circular orbits (e = 0) of synchronously rotating components in this very close binary system, for which an extremely short synchronization time scale of a few decades is expected (Zahn 1977). According to the early spectral type of the primary we assumed a bolometric albedo A1 = 1; also its gravity darkening exponent was fixed at g1 = 1 as expected for radiative outer envelopes (von Zeipel 1924). For the cool convective secondary, g2 was set to 0.32 according to Lucy (1967). Already after the first trial runs with the secondary albedo A2 as a free parameter, it became obvious that the enormous reflection effect evident as a broad orbital hump centered on secondary eclipse, with an amplitude of about 12% of maximum light, requires a "mirror-like'' surface of the tidally locked secondary in the heated area facing the primary. Reasonable representations were only possible for complete reradiation (energy conservation), i.e. A2 was fixed at 1.0 in all further runs. Linear limb darkening coefficients x1(B,R) for the primary were interpolated from the tables of Wade & Rucinski (1985) and fixed at x1(B) = 0.26 and x1(R) = 0.19. Since it was known from an analysis of similar sdOB binaries with strong reflection effect (Hilditch et al. 1996) that the limb darkening coefficients of cool stars irradiated by a hot companion can strongly deviate from "normal'' values of very cool dwarf stars, it was decided to treat x2 as an adjustable parameter. From our spectroscopic analysis (Sect. 4) it was clear that the sdB primary must have an effective temperature close to 30000 K. Though T1 was always used as an adjustable quantity, it actually did not vary much during numerous optimization runs, and mostly remained within a narrow range between about 29000 and 30000 K, compatible with the spectroscopic error margin.

The remaining set of adjustable parameters comprises the orbital inclination i, the mass ratio q = M2/M1, the Roche potentials $\Omega_1$ and $\Omega_2$ of the two stellar surfaces, the color-dependent luminosity L1 of the primary and of a possible third light contribution l3, the effective temperatures T1 and T2, and the radiation pressure parameter $\delta_1$ (see Drechsel et al. 1995); $\delta_2$ was set equal to zero because the secondary temperature is low (about 3000 K), which means that radiation pressure forces exerted by this star are negligible. Finally, L2 was not adjusted as an independent parameter, but recomputed from the secondary radius r2 and its effective temperature.

A convergent simultaneous solution of the B and R light curves was achieved after several trial runs using different start parameter sets, most of which led to essentially identical final solutions. Table 3 gives a list of the fixed and adjusted parameters.

 

 
Table 3: Light curve solution of HS 0705+6700.

Fixed parameters:

A1 a		 1.0
A2 a 1.0
g1 b 1.0
g2 b 0.32
x1(B) c 0.26
x1(R) c 0.19
$\delta_2 ^{d}$ 0.0

Adjusted parameters:

i		 $84\hbox{$.\!\!^\circ$ }4 \pm 0\hbox{$.\!\!^\circ$ }3 $
$q\ ({=} M_2/M_1)$ $0.278 \pm 0.019 $
$\Omega_1$ $3.764 \pm 0.066 $
$\Omega_2$ $2.606 \pm 0.051 $
$T_{\rm eff}(1)$ 29600 K $\pm$ 800 K
$T_{\rm eff}(2)$ 2900 K $\pm$ 600 K
L1(B)e $0.99997 \pm 0.00003 $
l3(B)f $3.7\% \pm 0.6\% $
L1(R)e $0.99969 \pm 0.00031 $
l3(R)f $0.2\% \pm 0.2\% $
x2(B) $0.42 \pm 0.12 $
x2(R) $0.62 \pm 0.17 $
$\delta_1 ^{d}$ $0.025 \pm 0.011 $

Roche radiig:

$r_1({\rm pole})$		 $0.279 \pm 0.004 $
$r_1({\rm point})$ $0.287 \pm 0.002 $
$r_1({\rm side})$ $0.283 \pm 0.003 $
$r_1({\rm back})$ $0.285 \pm 0.003 $
$r_2({\rm pole})$ $0.219 \pm 0.001 $
$r_2({\rm point})$ $0.238 \pm 0.004 $
$r_2({\rm side})$ $0.225 \pm 0.002 $
$r_2({\rm back})$ $0.239 \pm 0.005 $

a
Bolometric albedo.
b
Gravitational darkening exponent.
c
Linear limb darkening coefficient; theoretical value taken from Wade & Rucinski (1985).
d
Radiation pressure parameter, see Drechsel et al. (1995).
e
Relative luminosity L1/(L1 + L2); L2 is not independently adjusted, but recomputed from r2 and $T_{\rm eff}(2)$.
f
Fraction of third light at maximum.
g
Fractional Roche radii in units of separation of mass centers.

The corresponding fitted light curves together with observations are shown in Fig. 1.
  \begin{figure} \par\includegraphics[width=15.6cm,clip]{ms1809f1r.eps}\end{figure} Figure 1: B and R light curves of HS 0705+6700 obtained on Oct. 5/6 (B) and Nov. 2, 2000 (R); the solid lines represent the best fit simultaneous solution according to the parameters listed in Table 3; the R light curve is offset by 0.1 intensity units relative to the B curve.
Open with DEXTER

It is obvious from the graph that the overall run of the B and R light curves is very well reproduced by the best fit theoretical curves (solid lines). Especially the shape of the primary eclipse minima and the pronounced reflection effect are fitted very well. A minor systematic deviation is apparent in the secondary minima: the fitted curves are somewhat too shallow in the center of the minimum, though the effect is hardly larger than the observational error margins. A physical explanation may be found in the treatment of the reflection effect. Our Wilson-Devinney-based solution code uses bolometric albedos and black body radiation to characterize the reflectivity of the irradiated surface layers. The upper limit of albedo is therefore restricted to 100% for complete reradiation of the incident flux, and in our case the adjusted albedo of the cool secondary was actually limited by this constraint. Albedos larger than 1 would be "unphysical'', if local non-Planckian deviations of the intensity distribution are not accounted for. Removing the constraint on A2 would result in an increased adjusted value of A2 of $\sim$1.1, and a deepening of the secondary minimum by a few millimag. Because of the tinyness of this effect and due to the highly complex physical problems connected with the external irradiation of stellar atmospheres we preferred not to use such purely phenomenological approximation and remained with the classical reflection effect approach. Also, a suspected shift of the secondary minimum in the B curve by a few 10-3 phase units relative to phase 0.50 cannot be modeled without introducing additional free parameters. If real, it would conceivably be caused by a non-axisymmetrical brightness distribution of the heated surface area of the secondary component.

The $1~\sigma$ standard deviation of the normal points from the computed light curve amounts to about 0.004 mag. It should be noted that the best fit in the B passband ( $\lambda_{{\rm eff}} = 435$ nm) requires a third light contribution of 3.7%, while the R curve ( $\lambda_{{\rm eff}} = 641$ nm) is fully consistent with l3 = 0. The same effect was observed in the closely related sdB binary HW Vir (Wood et al. 1993), in which the U and B filter measurements deviate from the computed curves resulting from a simultaneous UBVR fit by a similar amount, whereas the R curve shows no such systematic effect. A possible explanation might arise from the strong reflection effect in both systems: though energy is conserved in the bolometric reradiation of the heated surface layers, there could be some frequency redistribution of photons inherent in the complex scattering process in a way that higher-energy photons have larger scattering cross sections than those incident with longer wavelengths and/or are transformed into lower-energy photons by various absorption and reemission processes.

The photometric solution yields a close detached system configuration for HS 0705+6700. A meridional intersection of the surface equipotentials and the inner critical Roche lobe is shown in Fig. 2.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1809f2r.eps}\end{figure} Figure 2: Meridional intersection of the equipotential structure of HS 0705+6700 corresponding to the best fit photometric solution for a mass ratio q = 0.278; the inner critical Roche lobe is shown as dashed line.
Open with DEXTER

The cool secondary is found to be relatively closer to its Roche lobe than the primary, which appears only slightly distorted by tidal interaction ( $r_{{\rm point}}/r_{{\rm pole}} \approx$ 1.03 and 1.09, respectively, for the primary and secondary components). 3D-simulated aspects of the system at various orbital phases under a viewing angle corresponding to the derived orbital inclination of 84 $\hbox{$.\!\!^\circ$ }4$ are displayed in Fig. 3.
  \begin{figure} \par\includegraphics[width=14cm,clip]{ms1809f3r.eps}\end{figure} Figure 3: Aspects of HS 0705+6700 at orbital phases 0.25, 0.45, 0.50, 0.575 (left column, from top to bottom), 0.75, 0.95, 0.00, 0.075 (right column), viewed under the orbital inclination angle of 84 $\hbox{$.\!\!^\circ$ }4$.
Open with DEXTER

Though the simplex algorithm is a more powerful and numerically stable parameter optimization method than the differential corrections procedure, which is usually used in combination with the Wilson-Devinney approach, it also cannot completely rule out the possibility of convergence into a local minimum in the multi-dimensional parameter space. For this reason we experimented with a multitude of different start parameter sets to verify that our final solution corresponds to the deepest global minimum. We found good evidence that this solution indeed turned out to be preferred in most of our trial runs. We should, however, mention that there were a few other solutions which differ from our best fit mainly in their values of the mass ratio q. While the best fit gave q = 0.278, other solutions with larger alternative values of q = 0.346, 0.460, and 0.594 were also found. Yet the standard deviations of the fits for q = 0.46 and 0.59 are worse by about 5-10%, and they are also not consistent with our spectroscopic results (inconsistent value of the mass function, see Sect. 4). The photometric solution for q = 0.35 is of nearly identical numerical quality like our preferred one for q = 0.28, but in order to match the observed value of the mass function of f(m) = 0.0063 $M_{\odot}$, the primary mass had to be assumed as $\leq$0.3 $M_{\odot}$. Hence a value of $M_2 \leq 0.1$ $M_{\odot}$ would result. According to low-mass star models (e.g., Dorman et al. 1989), the mass-radius relation would then yield a secondary radius of the order of 0.10-0.12 $R_{\odot}$, which would be incompatible with the photometrically derived value.

It is a common problem inherent to light curve solution techniques that it is not easy to identify the deepest global minimum in the multi-dimensional parameter space. Since several parameters used to model the light curves are highly correlated, often a multitude of nearly equally good solutions can be found for different solution parameter sets. In our case, we also end up with various solutions with a comparable goodness of fit, which mainly differ in their q values (see above). The light curve of HS 0705+6700 is very similar to those of HW Vir and PG 1336-018. Wood et al. (1993) and Kilkenny et al. (1998) both encountered the same problem when solving the light curves of these systems and were able to obtain good solutions for a broad range of mass ratios. The simplex parameter optimization algorithm incorporated in our MORO solution code is already a powerful tool with respect to the ability to automatically scan the multi-dimensional space of adjustable parameters for the deepest minimum within broad parameter ranges. However, the dependency of the goodness of fit on the chosen parameter set can be highly complex, or the relation is locally "flat-bottomed'', so that a unique solution does not exist.

To demonstrate this behaviour a number of solutions with different mass ratios were enforced by fixing q at various values in the surroundings of our best solution. The goodness of fit is measured by the standard deviation $\sigma_{\rm fit}$, which is defined by

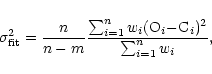\begin{displaymath}\sigma^2_{\rm fit} = \frac{n}{n-m} \frac{\sum_{i=1}^n w_i ({\rm O}_i{-}{\rm C}_i)^2}{\sum_{i=1}^n w_i} , \end{displaymath} (1)

where n is the number of observations (normal points) and m the number of adjustable quantities; Oi-Ci are the residuals between normal points and fitted curve, and wi are the individual weights of the normal points. The simplex routine uses these same $\sigma_{\rm fit}$ values also internally during each iteration step to control the optimization procedure. Table 4 summarizes the final $\sigma_{\rm fit}$ values of convergent solutions obtained for a grid of arbitrary q values,
 

 
Table 4: Goodness of light curve fit for various fixed q values compared with $\sigma $ of best fit solution with adjusted q.

q		 $\sigma_{B}$ $\sigma_{R}$ $\sigma_{\rm tot}$

0.20		 0.00433 0.00429 0.00428
0.25 0.00426 0.00426 0.00423
0.278a 0.00407 0.00403 0.00401
0.30 0.00411 0.00414 0.00409
0.35 0.00408 0.00402 0.00401
0.40 0.00421 0.00398 0.00406
a Adjusted q of final best solution.


which were kept fixed during these trial runs, while the rest of light curve parameters was adjusted to yield the best possible numerical representation of the observed B and R curves. We give $\sigma_{\rm fit}$ values for the composite set of simultaneously adjusted B and R light curves, $\sigma_{\rm tot}$, as well as the individual $\sigma_{\rm fit}$ values of the B and R curves, $\sigma_{B}$ and $\sigma_{R}$. The results for the trial solutions at q = 0.20, 0.25, 0.30, 0.35, and 0.40 are compared with our selected best solution for q = 0.278, which was obtained by adjusting q together with the whole parameter set. It is evident that there are two ranges of q around 0.28 and 0.35, where the standard deviations occupy local minima in the parameter space. The trial solution for q = 0.35 (fixed) nearly coincides with one of our previously discussed unrestricted solutions with q treated as a free parameter (resulting in q = 0.346). The distinction between the two alternative q values 0.28 and 0.35 apparently cannot be made solely based on numerical standards, since the difference of the respective $\sigma $ values is too small. Fortunately, in our case the available spectroscopic information (mass function,
  \begin{figure} \par\includegraphics[width=15.6cm,clip]{ms1809f4r.eps}\end{figure} Figure 4: Radial velocity curve of the sdB primary component in a circular orbit; velocities are heliocentrically corrected; the semi-amplitude K1 is 85.8 kms-1, the systemic velocity $\gamma _0 = -36.4$ kms-1; error bars correspond to $3~\sigma$ margins.
Open with DEXTER

mass-radius relation for the low-mass dwarf companion) could be used to sort out inconsistent photometric solutions. The small error given in Table 3 for $q = 0.278 \pm 0.019$ simply reflects the formal fit uncertainty within the local minimum in parameter space around q = 0.28, and does not account for systematic effects like ambiguity of solutions.

   
4 Spectroscopic analysis

The optical spectra allow to measure the radial velocity curve with good phase coverage as well as a quantitative spectral analysis to determine the atmospheric parameters and the projected rotational velocity.

   
4.1 Radial velocity curve

Radial velocities from all Twin spectra were derived by cross-correlating the observed helium and Balmer line spectra to a synthetic spectrum calculated from a model atmosphere (see below) and are listed in Table 1. The measurements are accurate to about $\pm 15$ kms-1 (3$\sigma $).

Since this system is single-lined the analysis is straightforward. A comparison of the best fit radial velocity curve and the measured values is shown in Fig. 4. The semi-amplitude is $K_1 = 85.8 \pm 3.7$ kms-1 and the systemic velocity $\gamma_0 = -36.4 \pm 2.9$ kms-1.

From the period and semi-amplitude the mass function is derived: $f(m) = 0.00626 \pm 0.00081$ $M_{\odot}$.

   
4.2 Spectrum fitting

In order to improve the S/N ratio the Twin spectra were radial velocity-corrected and then coadded. The coadded as well as the individual spectra were analyzed to derive atmospheric parameters using NLTE model atmospheres (Napiwotzki 1997) and a $\chi ^2$ procedure described by Napiwotzki et al. (1999).

Matching the synthetic Balmer (H$\beta$ to H$\epsilon$) and He I (4026 Å, 4471 Å and 4922 Å) line profiles to the observations resulted in a determination of effective temperature, gravity and He abundance. The resulting fit for the coadded spectrum is displayed in Fig. 5 and gives $T_{\rm eff} = 28\,800 \pm 300$ K,

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1809f5.eps}\end{figure} Figure 5: Fit of the Balmer and helium lines in the coadded spectrum of HS 0705+6700 by synthetic spectra calculated from NLTE model atmospheres.
Open with DEXTER

$\log g = 5.40 \pm 0.04$ and $\log (n_{\rm He}/n_{\rm H}) = -2.68\, \pm\, 0.05$. The quoted errors are derived from the $\chi ^2$ procedure applied to fit the line profiles.

We also analyzed the individual spectra in the same way as described above. Two spectra (at phases 0.701 and 0.855) were not useable for a quantitative spectral analysis because of insufficient S/N. These two phases, however, are covered by better spectra (at phases 0.711 and 0.849) anyway. The results for the remaining 13 phases are summarized in Table 5,

 

 
Table 5: Atmospheric parameters of HS 0705+6700.

phase		 $T_{\rm eff}$ (K) $\log g$ $-\log ({\rm He}/{\rm H})$

0.107		 $27\,300 \pm 836$ $5.41 \pm 0.10$ $2.50 \pm 0.11$
0.203 $27\,720 \pm 858$ $5.29 \pm 0.11$ $2.82 \pm 0.14$
0.276 $29\,748 \pm 901$ $5.48 \pm 0.14$ $2.60 \pm 0.22$
0.303 $29\,063 \pm 697$ $5.30 \pm 0.10$ $2.44 \pm 0.13$
0.400 $28\,072 \pm 854$ $5.28 \pm 0.11$ $2.55 \pm 0.12$
0.428 $28\,947 \pm 1600$ $5.12 \pm 0.23$ $2.99 \pm 0.49$
0.505 $28\,414 \pm 1002$ $5.30 \pm 0.13$ $2.63 \pm 0.12$
0.574 $29\,928 \pm 828$ $5.43 \pm 0.14$ $2.81 \pm 0.23$
0.601 $28\,649 \pm 751$ $5.59 \pm 0.11$ $2.54 \pm 0.11$
0.711 $30\,126 \pm 649$ $5.51 \pm 0.11$ $2.89 \pm 0.19$
0.742 $28\,813 \pm 849$ $5.50 \pm 0.12$ $2.78 \pm 0.15$
0.849 $28\,186 \pm 842$ $5.26 \pm 0.10$ $2.58 \pm 0.11$
0.992 $27\,102 \pm 1009$ $5.37 \pm 0.13$ $2.94 \pm 0.20$

Mean:		 $28\,621 \pm 919$ $5.37 \pm 0.12$ $2.70 \pm 0.17$

coadded		 $28\,755 \pm 280$ $5.40 \pm 0.04$ $2.68 \pm 0.05$


and are plotted in Fig. 6.
  \begin{figure} \par\includegraphics[width=8.3cm]{ms1809f6a.eps}\hspace*{5mm}\includegraphics[width=8.3cm]{ms1809f6b.eps}\end{figure} Figure 6: Variation of atmospheric parameters with phase; the error bars result from the $\chi ^2$ fit procedure described by Napiwotzki et al. (1999).
Open with DEXTER

Because of the reflection effect the Balmer lines might be distorted by reflected light from the secondary. Indeed, in the case of HW Vir Wood & Saffer (1999) found that $T_{\rm eff}$ varied by 1500 K and $\log g$ by 0.1 dex around the orbit. Two spectra of HS 0705+6700 were taken near primary and another near secondary minimum, for which we do not expect any contamination by reflected light.

The solution of the B light curve indicated the presence of third light. This could cause a systematic error for the spectroscopic analysis. The spectral characteristics of this light, however, are unknown. We made an experiment on an individual spectrum and subtracted 3% of the continuum from the blue spectra and repeated the fit. In this case the effective temperature is lowered by about the same amount as the 1$\sigma $ errors listed in Table 5. The change in gravity is only a few hundredth of a dex, less than the errors listed in this table. As possibly indicated by Fig. 6, there might be a slight variation of $T_{\rm eff}$ with orbital phase, but not so for $\log g$. Our spectra are probably of insufficient quality to reveal any phase-dependent variations of the atmospheric parameters at such a low level.

We finally adopted $T_{\rm eff} = 28\,800 \pm 900$ K, $\log g = 5.40 \pm 0.1$and $\log (n_{\rm He}/n_{\rm H}) = {-2.68} \pm 0.15$ for the atmospheric parameters of HS 0705+6700. The given errors were estimated from the scatter of the $T_{\rm eff}$ and $\log g$ values derived from the individual spectra and hence would cover the bandwidth of any possibly present systematic variation with phase.

We finally note that the spectroscopic $T_{\rm eff}$ is in excellent agreement with the one following from the photometric solution (Sect. 3.2).

4.3 Projected rotational velocity

The line profiles of H$\alpha $ and He I6678 Å could be used to determine the projected rotational velocity. We calculated the H$\alpha $ profiles from the final model and convoluted it with rotational profiles for various rotational broadening parameters. The best fit was again obtained by a $\chi ^2$ procedure as described by Heber et al.  (1997), which resulted in a projected rotational velocity of $v \sin i = 110^{+16}_{-13}$  kms-1 (3$\sigma $ errors). The corresponding fit is displayed in Fig. 7.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1809f7.eps}\end{figure} Figure 7: Determination of the projected rotational velocity; synthetic H$\alpha $ and He I line profiles calculated from the finally adopted model and the best fit $v\,\sin i = 110$ kms-1 are compared to the coadded spectrum; the same line profiles predicted for a non-rotating star are also shown as dashed lines.
Open with DEXTER

The rotation of HS 0705+6700 is expected to be tidally bound. In this case we can estimate the projected rotational velocity from the orbital period and the radius (see Sect. 5) to be 121+15-13  kms-1, in good agreement with the result from spectrum synthesis.

   
5 System parameters

   
5.1 HS 0705+6700

Even though the radial velocity amplitude of the companion is unknown we have sufficient information to calculate absolute system parameters due to the M-R relation provided by the $\log g$ determination (Sect. 4.2).

From the light curve we have derived a period of 8263.87 s, an inclination angle of $i = 84\hbox{$.\!\!^\circ$ }4$, and a mass ratio q = 0.278. Furthermore, we determined the radii for the binary components R1/a = 0.284 and R2/a = 0.230, where a is the separation of their mass centers. Using our measured K1 = 85.8 kms-1, $\log g_1 = 5.40$, and the inclination i, we derive M1 = 0.483 $M_{\odot}$, M2 = 0.134 $M_{\odot}$, R1 = 0.230 $R_{\odot}$, R2 = 0.186 $R_{\odot}$, and $a = 5.65 \times 10^{10}$ cm (=0.81 $R_{\odot}$). From these numbers we conclude that the companion is an M dwarf. According to the models for low-mass dwarf stars of Dorman et al. (1989), a star of 0.14 $M_{\odot}$ would have a radius of 0.17 $R_{\odot}$, fully consistent with the observations.

The above given parameters correspond to the photometric solution for q = 0.278. As can be seen from Fig. 8,

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1809f8.eps}\end{figure} Figure 8: Comparison of the position of HS 0705+6700 in the ( $T_{\rm eff}$, $\log g$) diagram to that of HW Vir, PG 1336-018 and PG 1017-086, EHB stars studied by Maxted et al. (2001a) and to evolutionary EHB tracks of Dorman et al. (1993); the tracks are labeled with the stellar mass.
Open with DEXTER

the position of HS 0705+6700 in the HRD is compatible with those of other EHB stars as well as with EHB evolutionary tracks of stars with corresponding masses. Considering the alternate photometric solution for q = 0.35, one would have to assume a lower primary mass of say M1 = 0.3 $M_{\odot}$. In principal, such mass could result as the end product of the common envelope evolution. The HRD position of the primary might then also match a track leading to a helium white dwarf. However, as already mentioned earlier, the reduced mass of the M dwarf would require a smaller radius for this star, hardly compatible with the light curve solution.

Given the most probable parameters and system configuration of HS 0705+6700 (Fig. 2), the further evolution might lead to the formation of a cataclysmic system with a period below the period gap. The process of angular momentum loss by gravitational radiation would require about 109 years for the binary components to merge. Should the radius of the sdB star along its track towards the white dwarf cooling sequence, however, increase sufficiently to reach its limiting lobe, another episode of rapid mass transfer and loss of mass and angular momentum, perhaps even another common envelope phase, could occur within a much shorter time scale. Yet, such prospects should be subject of detailed evolutionary calculations lying beyond the scope of this paper.

   
5.2 Similar systems

HS 0705+6700 is only the third eclipsing binary known to consist of an sdB star and an M dwarf companion. An orbital period of about 0.096 days places HS 0705+6700 in a period range, which coincides with the period gap of cataclysmic variables. There are two other surprisingly similar systems - HW Vir ( $P \approx 0.117$ d) and PG 1336-018 ( $P \approx 0.101$ d) - which have equally short periods within the CV period gap between about 2 and 3 hours (e.g., Shafter 1992). A non-eclipsing system (PG 1017-086) with an even shorter period (P = 0.073 d) than HS 0705+6700 was discovered recently by Maxted et al. (2001b). The shrinkage of the orbit from an originally much wider binary with a red giant component to a component separation of less than one solar radius can be explained by a common envelope stage, during which a large fraction of orbital angular momentum is lost. The system parameters of the three related sdB binaries are compared in Table 6.

 

 
Table 6: System parameters of three similar eclipsing sdB binaries.

HW Vir PG 1336-018 HS 0705+6700

Author		 Wood et al. (1993) Kilkenny et al. (1998) this paper
data UBVR UVR BR
P $2^{\rm h}48^{\rm m}$ $2^{\rm h}25^{\rm m}$ $2^{\rm h}18^{\rm m}$
q = M2/M1 $\sim$0.3 0.3 0.278
i $80\hbox{$.\!\!^\circ$ }6$ $81\hbox{$^\circ$ }$ $84\hbox{$.\!\!^\circ$ }4$
K1 87.9 kms-1 78 kms-1 85.8 kms-1
T1 $\sim$$ 33\,000$ K $ 33\,000$ K $29\,600$ K
T2 $\sim$3700 K $\sim$3000 K 2900 K
$\log g_1$ 5.64 5.7 5.40
M1 0.54 $M_{\odot}$ $\sim$0.50 $M_{\odot}$ 0.483 $M_{\odot}$
M2 0.18 $M_{\odot}$ 0.17 $M_{\odot}$ 0.134 $M_{\odot}$
R1 0.183 $R_{\odot}$ 0.165 $R_{\odot}$ 0.230 $R_{\odot}$
R2 0.188 $R_{\odot}$ 0.175 $R_{\odot}$ 0.186 $R_{\odot}$
a 0.89 $R_{\odot}$ 0.79 $R_{\odot}$ 0.81 $R_{\odot}$


In Fig. 8 we compare the position of the four systems with a sample of sdB stars recently analyzed by Maxted et al. (2001a) and with calculations for EHB evolution. As can be seen all four stars lie in the same region as the other sdB stars on the EHB band, and are therefore core helium burning stars with very small inert hydrogen-rich envelopes. In order to evolve to their present configuration the systems must have gone through a common envelope phase, when the primary was near the tip of the red giant branch. Both the very short periods as well as the extremely thin hydrogen layers on top of the helium cores are conceivably explained by such common envelope evolution connected with extensive mass loss.

In the case of HS 0705+6700 and the mentioned related systems the evolutionary scenario through which the sdB stars were formed is probably the same. This raises again the question whether all sdB stars are members of close binary systems and originate from the same common envelope evolution. To improve the statistical significance of such a hypothesis, it will therefore be of major importance to search for and analyze a larger number of sdB candidates with special emphasis on their possible binarity.

   
6 Conclusions

The sdB star HS 0705+6700 was discovered to be an eclipsing binary with an orbital period of 8263.87 s. The analysis of the light curve revealed that the mass ratio of the system is q = 0.28 and the inclination 84 $\hbox{$.\!\!^\circ$ }4$. The companion does not contribute to the optical light of the system, except for the light reflected from the hemisphere facing the sdB star. The semi-amplitude of the radial velocity curve K1 = 85.8 kms-1 and a mass function of f(m) = 0.00626 $M_{\odot}$ were derived. Accurate absolute masses and radii of the sdB primary and the M dwarf companion could be determined. The spectroscopic analysis of the sdB component resulted in $T_{\rm eff} = 28\,800 \pm 900$ K, $\log g = 5.40 \pm 0.1$, and $\log (n_{\rm He}/n_{\rm H}) = {-2.68} \pm 0.15$.

The position of the sdB star in the $\log g$- $T_{\rm eff}$ diagram coincides with the domain of many other EHB stars. The current location can be matched by the evolutionary track for such a star with corresponding mass. The photometric value of the mass ratio of q = 0.28 and the respective mass of the secondary are in good agreement with the observed mass function and with the predicted mass-radius relation for low-mass dwarf stars. Based on these arguments an alternate photometric q value of 0.35 appears less probable.

The further evolution of the system might lead to the formation of a cataclysmic system with a period below the CV period gap.

Acknowledgements

We thank E. M. Pauli and C. Karl for their assistance with the Twin observations and their reduction. Thanks are also due to L. Yungelson for helpful discussions on the evolutionary stage. We acknowledge valuable suggestions made by the referee, P. Maxted, to improve the manuscript.

The time-series data from the Nordic Optical Telescope have been taken using ALFOSC, which is owned by the Instituto de Astrofisica de Andalucia (IAA) and operated at the Nordic Optical Telescope under agreement between IAA and the NBIfAFG of the Astronomical Observatory of Copenhagen.

Part of this research has been made possible through DFG research grants We 1312/23-1 (JD) and Dr 281/13-1 (SS). The observations at Calar Alto were supported through DFG travel grant We 1312/28-1.

References

 
Copyright ESO 2001