A&A 379, 1045-1051 (2001)
DOI: 10.1051/0004-6361:20011375

Turbulent plasma model of the narrowband dm-spikes

M. Bárta - M. Karlický

Astronomical Institute of the Academy of Sciences of the Czech Republic, 25165 Ondrejov, Czech Republic

Received 17 April 2001 / Accepted 11 September 2001

Abstract
Starting from radio spectrum features of the narrowband dm-spikes, it is suggested that they are generated at positions in the solar flare atmosphere where the upper hybrid frequency is equal to the low harmonics of the electron cyclotron frequency. It is assumed that a radio source plasma is in a turbulent state. The upper hybrid waves are generated by an anisotropic electron beam which propagates along magnetic loop lines. Collisional damping and turbulent changes of plasma parameters in the radio source cause strong intensity-frequency variations of the upper hybrid waves. These waves are then transformed into observed narrowband dm-spikes. Using this model, the artificial radio spectra are computed. It is shown that a chain of narrowband spikes is generated at a one cyclotron harmonic, in one turbulent magnetic flux tube. On the other hand, a cloud of spikes (or their harmonic clouds) results from a superposition of many chains of spikes generated in many turbulent magnetic flux tubes (in several cyclotron harmonics). Finally, further features of the narrowband dm-spikes are discussed in the framework of the proposed model.

Key words: plasmas - Sun: flares - Sun: radio radiation


1 Introduction

The narrowband dm-spikes attract attention, mainly due to their exceptionally high brightness temperatures ( $T_{\rm b} \approx 10^{15}$ K) and their short durations ($\leq$0.1 s, see the review by Benz 1986). They have been studied in many papers (Slottje 1981; Karlický 1984; Fu et al. 1985; Stähli & Magun 1986; Güdel 1990; Krucker & Benz 1994; Aschwanden et al. 1998) and two classes of models have been suggested: a) based on the plasma emission mechanism (Kuijpers et al. 1981; Tajima et al. 1990; Wentzel 1991; Stepanov et al. 1999), and b) based on the electron-cyclotron maser mechanism (Wu & Lee 1979; Holman et al. 1980; Melrose & Dulk 1982; Vlahos & Sharma 1984; Winglee et al. 1988; Aschwanden 1990; Fleishman & Yastrebov 1994; Willes & Robinson 1996; Fleishman & Melnikov 1998). The statistical methods (Schwarz et al. 1993) applied to spike events show that the spectral structure of spikes is not stochastic and that neighboring spikes are correlated.

In our recent studies (Karlický et al. 1996, 2000) we have assumed a stratified atmosphere with certain scale heights. We then transformed the frequency scales into heights of the solar atmosphere and using a Fourier analysis we found the power-law spectra with power-law indices in the range of -0.80--2.85. Similar results were found also by Messmer & Benz (2000). In several events the power-law indices were close to -5/3, therefore it was suggested that the narrowband dm-spikes are generated by superthermal electrons in the MHD turbulence forming in the magnetic reconnection plasma outflows (Karlický et al. 1996; Zlobec & Karlický 1998).

In the present paper we keep this idea, but we combine this concept with the model suggested by several authors (Zheleznyakov & Zlotnik 1975; Kuijpers 1980; Mollwo 1983, 1988; Ledenev et al. 2001) for an explanation of the zebra pattern fine structure. The reason is that in some cases the narrowband dm-spikes change into zebras (e.g. Kuijpers et al. 1981). A similar model was used also for an interpretation of the bursts with rapid frequency variations (lace bursts) (Karlický et al. 2001).

In the following, first, the structural features of the narrowband dm-spikes are summarized. Then their model is presented. Finally, examples of artificial radio spectra with narrowband dm-spikes are shown.

2 An example of the narrowband dm-spikes

During the impulsive phase of the July 12, 2000 flare, superimposed on the broadband drifting pulsation structure, a cloud of narrowband dm-spikes was observed (Fig. 1). Here, several features typical of narrowband dm-spikes can be seen: a) the spikes are clustered in time in broadband pulses lasting several seconds, b) there are also clusters of spikes in the frequency bands (e.g. in the 1.3-1.6 GHz range), c) some spikes form drifting chains (see Fig. 1, the 1.0-1.3 GHz range, 10:34:20-10:34:50 UT), and d) after clouds of narrowband dm-spikes at 10:34:53-10:35:03 UT, a unique and very narrowband line was observed in the 1.20-1.34 GHz range. After this event, at 10:36:15-10:36:22 UT in the 1-2.6 GHz range the zebra pattern was observed. It is reminiscent of the well-known observations of 26 June 1978, presented in the paper by Kuijpers et al. (1981), where the spikes changed continuously into braided zebra patterns. For further observational facts concerning the narrowband dm-spikes, see papers by Benz (1986), Güdel & Benz (1990), Aschwanden et al. (1998), Fleishman & Melnikov (1998) and Mészárosová et al. (2000). For example, time profiles of individual spikes exhibit an exponential decay with rates in the range of the collisional plasma damping. Their polarization is found in a broad range from non-polarized up to fully polarized events, and so on.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{bk1684f1.eps} \end{figure} Figure 1: The 1.0-1.8 GHz radio spectrum observed at 10:34:20-10:35:04 UT, July 12, 2000 by the Ondrejov radiospectrograph (Jiricka et al. 1993).
Open with DEXTER

3 Model of the narrowband dm-spikes

3.1 Basic concept

Due to a global structure of clouds of the narrowband dm-spikes (drifting chains, their clustering in the frequency bands and very narrowband lines - see previous chapter) we suggest a model which is similar to those for zebra patterns and lace bursts (Zheleznyakov & Zlotnik 1975; Ledenev et al. 2001; Karlický et al. 2001), i.e. the spikes are generated at positions in the solar atmosphere where the following resonance condition is fulfilled:

 \begin{displaymath} \omega_{\rm UH}\equiv(\omega_{\rm pe}^2 + \omega_{\rm Be}^2)... ...\,\, \omega_{\rm Be},\,\,\, \omega_{\rm pe} > \omega_{\rm Be}, \end{displaymath} (1)

where $\omega_{\rm UH}$, $\omega_{\rm pe}$, and $\omega_{\rm Be}$ are the upper hybrid, electron plasma and cyclotron frequencies, and s is the integer harmonic number. But here, in accordance with our previous concept (Karlický et al. 1996; Zlobec & Karlický 1998), the MHD turbulence in spike radio sources is considered. It is known that in the reconnection process the electrons are accelerated: a) by the electric field $\vec E \sim \vec v \times \vec B$ (where $\vec v$ and $\vec B$ are the plasma velocity and the magnetic field) near the X-point of the magnetic reconnection (Sato et al. 1982) and b) in the MHD cascading turbulence in the reconnection outflows (LaRosa et al. 1994). Then these accelerated electrons propagate along magnetic field lines in the plasma reconnection outflows. As will be shown, during this propagation the beam of superthermal electrons with $T_{\perp}$ > $T_{\parallel}$ is formed ($T_{\perp}$ and $T_{\parallel}$ are the temperatures of energetic electrons across and along the magnetic field, respectively). Such an anisotropic beam is unstable (Mikhailovsky 1975). We consider the resonance at normal Doppler effect, i.e. $\omega - k_{\parallel} v_{\parallel} -s \omega_{\rm Be} = 0$. (Remark: for the bi-Maxwellian distribution function only the parallel driven instability needs to be considered. Therefore the non-relativistic approach is appropriate (Melrose 1986).) In such a case the growth rate of the unstable longitudinal waves can be expressed as:
 
$\displaystyle \gamma(\vec k) = -\frac{\sqrt{\pi}\alpha \omega^3} {v_{\rm Te\par... ...ega_{\rm Be} \left( 1 - \frac{T_{\parallel}}{T_{\perp}} \right)\right] \Biggr),$     (2)

where $\alpha$ is the ratio of the beam density $n_{\rm b}$ to the density of the background plasma n, $v_{\rm Te\parallel}$ is the thermal electron velocity along the magnetic field, $\vec k$ is the wave vector, $I_{s}(k_{\perp}v_{\perp}/\omega_{\rm Be})$ is the modified Bessel function, $z_{\perp} = k_{\perp}^2 k_{\rm B} T_{\perp}/ m_{\rm e} \omega_{\rm Be}^2$, $m_{\rm e}$ is the electron mass, $k_{\perp}$ is the transverse component of the wave vector, and

 \begin{displaymath} \omega(\vec k)=\sqrt{\frac{\omega_{\rm UH}^2+\sqrt{\omega_{\... ...frac{k_{\parallel}^2}{k_{\parallel}^2+ k_{\perp}^2}}}{2}}\cdot \end{displaymath} (3)

It can be seen that the growth rate is inversely proportional to $k_{\parallel}$. So in such a case the most effectively excited longitudinal waves are for $k_{\parallel} \ll k_{\perp}$. Thus, the frequency of these waves and the resonance condition can be expressed as $\omega \approx (\omega_{\rm pe}^2 + \omega_{\rm Be}^2)^{1/2}$ and $\omega \approx s \omega_{\rm Be}$, respectively. The generated upper hybrid waves are then transformed to the observable electromagnetic waves. Here, for simplification, we assume that the frequency of spikes is $\omega_{\rm el} \approx \omega_{\rm UH}$ (the coalescence of the upper hybrid wave with some low frequency waves).

As mentioned above, this type of model was used also for zebra pattern interpretation. In these models the radio sources of individual zebra lines are spatially separated. The distance between neighboring levels of the resonance can be written (see Zheleznaykov & Zlotnik 1975):

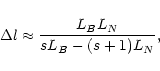\begin{displaymath}\Delta l \approx \frac{L_B L_N}{sL_B - (s+1) L_N}, \end{displaymath} (4)

where $L_B = B({\rm d}B/{\rm d}l)^{-1}$ and $L_N = 2 N ({\rm d}N/{\rm d}l)^{-1}$ are the characteristic scales of the magnetic field and electron density in radio sources. Similarly, the frequency separation of zebra lines is

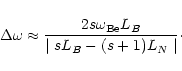\begin{displaymath}\Delta \omega \approx \frac{2 s \omega_{\rm Be} L_B}{\mid sL_B - (s+1) L_N \mid}\cdot \end{displaymath} (5)

Thus, when $L_B \gg L_N$ (a slow change in the magnetic field), $\Delta \omega \approx 2 \omega_{\rm Be}$. On the other hand, if $L_B \ll L_N$ (a fast change in the magnetic field) then $\Delta \omega \approx 2 \omega_{\rm Be} L_B/L_N \ll 2 \omega_{\rm Be}$. The last two formulas are used for the magnetic field determination. While Zheleznaykov & Zlotnik (1975) considered the case $L_B \gg L_N$, Ledenev et al. (2001) used the opposite case. Here, in accordance with Ledenev et al. (2001), we prefer the case with $L_B \ll L_N$because then (for small s) the estimated magnetic field is more realistic. Furthermore, as will be shown in the following, the separate s branches can explain the drifting chains of spikes and their clustering into some specific frequency bands.

3.2 Anisotropic beam formation

As mentioned above, the beam with the temperature anisotropy $T_{\parallel}\ll T_{\perp}$ can be formed by a propagation of electrons along magnetic field lines with the strength of B0. We studied an expansion of a hot electron gas from a localized region to relatively cold surrounding plasma, solving the linearized Vlasov equation for the electron distribution function in the form

 \begin{displaymath} \frac{\partial f}{\partial t}+{\bf v}\cdot\frac{\partial f}{... ...mes \vec B_0 \right)\cdot\frac{\partial f}{\partial \vec v}=0. \end{displaymath} (6)

In the present approximation the electric field caused by propagating electrons is neglected as well as a possible return current.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{bk1684f2.eps} \end{figure} Figure 2: The beam formed by a propagation of hot electrons along the magnetic field lines: a) the electron parallel velocity distribution for $v_{\perp }=0$ m s-1, and b) the electron perpendicular velocity distribution for $v_{\parallel }=10^7$ m s-1. All quantities are displayed in SI units.
Open with DEXTER

An initial electron distribution function was chosen as

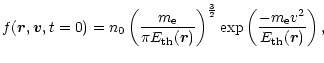$\displaystyle f(\vec r,\vec v,t=0)=n_0\left(\frac{m_{\rm e}}{\pi E_{\rm th}(\ve... ...right)^{\frac{3}{2}}\exp\left(\frac{-m_{\rm e} v^2}{E_{\rm th}(\vec r)}\right),$     (7)

where

\begin{displaymath}E_{\rm th}(\vec r)=2 k_B\left[T_{\rm c}+(T_{\rm h}-T_{\rm c})\cdot L(\vec r)\right] \end{displaymath}

and the localization function

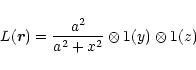
\begin{displaymath}L(\vec r)=\frac{a^2}{a^2+x^2}\otimes1(y)\otimes1(z) \end{displaymath}

describes the 1-D temperature distribution over the hot region, $T_{\rm h}$ and $T_{\rm c}$ are the electron temperatures of hot and cold plasmas, respectively. Such an initial distribution simply represents a slab of the hot plasma (with the characteristic thickness a) surrounded by a colder environment. The Eq. (6) can be easily solved using the transformation to the Lagrangian coordinates. The result is:
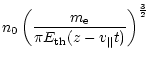$\displaystyle f(x,v_{\parallel},v_{\perp},t)$ = $\displaystyle n_0\left(\frac{m_{\rm e}}{\pi E_{\rm th}(z-v_{\parallel}t)}\right)^{\frac{3}{2}}$  
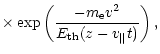    $\displaystyle \times\exp\left(\frac{-m_{\rm e} v^2}{E_{\rm th}(z-v_{\parallel}t)}\right),$ (8)

where $v_{\parallel}\equiv v_x$ is the velocity component parallel to the magnetic field B0. The results are shown in Fig. 2. The part a) represents the cut of the electron distribution function along the $v_{\parallel}$for $v_{\perp }=0$. An arrow points to the beam formed. The part b) shows the cut of the electron distribution function along the $v_{\perp}$ for $v_{\parallel }=10^7$ m s-1, which is near the center of the beam parallel velocity distribution. The temperature anisotropy of the beam can be seen. Both cuts were made for x=107 m and t=1.0 s. The temperatures of hot and cold plasmas are 106 K and 107 K, respectively, and the width of the hot region is a=106 m.

3.3 Simulation of radio spectra with narrowband dm-spikes

Suppose that the atmosphere in the source region (in the reconnection outflow - see Fig. 8) can be described as a bunch of solitary magnetic flux tubes, along which the magnetic field strength B and electron density n slowly decrease as:

n(x)=$\displaystyle n_0\left(1-\frac{x}{L}\right),\qquad x\in(0;L)$ (9)
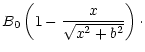B(x)=$\displaystyle B_0\left(1-\frac{x}{\sqrt{x^2+b^2}}\right)\cdot$ (10)

Here parameters L and b with dimensions of the length represent typical scales on which the magnetic field B and the electron density n vary and x is the length measured along the flux tube. The magnetic field strength and density at the base (x=0) of each flux tube B0 and n0, respectively, as well as
  \begin{figure} \par\includegraphics[width=8.6cm,clip]{bk1684f3.eps} \end{figure} Figure 3: A schematic picture of the double resonance in the turbulent radio source. The dashed lines show steady background values of the upper hybrid and one harmonic of the cyclotron frequencies along the source. The solid and dotted lines represent local values at a fixed time including the turbulent density and magnetic field perturbations. The small circles show the regions where the resonant condition (1) is fulfilled.
Open with DEXTER

scale parameters L and b are considered to be in some intervals for all the flux tubes. Then, on this stationary mean density profile the chaotically varying (in space and time) density and/or magnetic field perturbations are superimposed. Due to these changes the positions, where the resonance condition (1) is fulfilled, move inside each magnetic flux tube. A schematic view of such a situation is shown in Fig. 3.

Assuming that the radio source is optically thin, the total radio flux is simply the sum of contributions emitted by the length elements of each loop. First, for a fixed position on the loop x and specific time t the local frequencies $\omega_{\rm pe}$ and $\omega_{\rm Be}$ are computed. Then using the relations (3) and (2) the frequency and growth rate of unstable waves are evaluated in each grid point of the 2-D k-space. The amplitude of these waves is computed as follows:

 \begin{displaymath} E(\vec k,t+\Delta t)=E(\vec k,t)\cdot\exp[(\gamma(\vec k)-\nu)\cdot\Delta t]. \end{displaymath} (11)

Here $\nu$ designates the collisional damping of waves, independent of the wave vector. The thermal level is used for the initial electric field value of the unstable upper hybrid waves. Due to nonlinear effects the instability under study needs to be saturated at a certain level. To simulate this effect the algorithm used ensures that when waves reach some chosen saturation level the appropriate wave mode does not grow further. Similarly, the energy of any wave mode does not decrease below the thermal level. The nonlinear process that causes saturation of the instability is not studied here in detail. Nevertheless, from the spacecraft measurement of the energy density of the Langmuir waves, observed during interplanetary type III bursts (Thejappa & MacDowall 1998), the saturation level is estimated. Estimation gives for the amplitude of the electric field strength value 106 of the electric field strength corresponding to the thermal level wave energy.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{bk1684f4.eps} \end{figure} Figure 4: The algorithm scheme used for computation of the radio flux from a single flux tube source.
Open with DEXTER

There are two results of the presence of the MHD turbulence on the resulting radio emission: a) it chaotically changes the radio emission frequency, and b) the very fast plasma parameter changes in the radio source reduce or even stop the plasma instability under study. To simulate the latter effect, the time spent by each point of the source within the resonance is computed and when it becomes comparable or even less than the characteristic growth time, the instability is assumed to be not acting at all and, thus the growth rate is set to zero. This effect interrupts the radio emission.

In this phenomenological model the wave transformation processes are not analyzed. For details of considered transformation processes, see the paper by Zheleznyakov & Zlotnik (1975). Here, for model purposes we assume that the radio flux is proportional to the energy density of generated upper hybrid waves. Therefore the computed amplitudes of wave modes $E(\vec k,x,t)$ (for fixed times and positions) are squared and multiplied by a value of $k_{\perp}$ with respect to the cylindric symmetry of the problem. The obtained values for each mode are then sorted to frequency channels according to their frequencies (3). In the following step the time is increased ( $t\rightarrow t+{\rm d} t$) and new values of the radio emission in specific frequency channels are evaluated in the same way. Repeatedly using this procedure, the dynamic radio spectrum for one elementary source at one given harmonic s is obtained. A full spectrum of the whole source is computed as the sum of elementary spectra. First, the spectra are integrated over the loop length, then contributions of all loops at one harmonic s are summed and, finally radio emissions of all considered harmonics are superimposed. The algorithm for a single flux tube source is schematically shown in Fig. 4.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{bk1684f5.eps} \end{figure} Figure 5: a) The 1.0-2.0 GHz modelled radio spectrum of single spikes. The gray levels represent the radio flux in a logarithmic scale. b) The instantaneous spectrum of the spike at 0.4 s. The flux is in a linear relative scale. c) The time profile of the spike on the frequency 1412 MHz. The flux is in a linear relative scale.
Open with DEXTER

Examples of the modelled radio spectra are shown in Figs. 5, 6 and 7. As discussed in the following, we expect spikes radio sources in the magnetic reconnection outflows, where magnetic field gradients are probably higher then in the surrounding atmosphere. Therefore the following plasma parameters are used: $n_0=3\times 10^{16} ~\rm {m}^{-3}$, T=107 K, $L=4\times 10^7$ m, B0=0.02 T, and $b=5\times 10^5$ m. The superimposed disturbances have a spatial Fourier spectrum with a power-law form with the spectral index -2 in the range up to $10^4 ~{\rm m}^{-1}$, which is the minimum scale considered in the turbulence; phases are random and rms of the density perturbation reaches 10% of the static density profile. These values correspond to those observed in the solar wind space experiments (Schwenn & Marsch 1991) and they are also in agreement with the interpretation of the lace bursts (see Karlický et al. 2001). In the present case the magnetic field perturbations are not considered. The beam has the following parameters: $\alpha=10^{-9}$, $T_{\perp}=10^7$ K, $T_{\parallel}=10^3$ K, and the beam mean velocity along magnetic field lines $v_{\parallel}$ is taken to be zero. Only the harmonic with s=4 is considered.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{bk1684f6.eps} \end{figure} Figure 6: The 1.0-2.0 GHz modelled radio spectrum of the chain of spikes. The radio flux shown is in a logarithmic scale.
Open with DEXTER

Figure 5 shows the high-time resolution spectrum with single spikes and their instantaneous spectrum and time profile. In the model with one magnetic flux tube the spikes are organized in chains. An example of such a spectrum is presented in Fig. 6. Furthermore, a combination of the radio emission from many magnetic flux tubes lead to a superposition of many spike chains, thus forming a cloud of narrowband dm-spikes (Fig. 7). As can be seen the presented modelled spike spectra are similar to observed ones. Thus, we think that this model can be used for an interpretation of the narrowband dm-spikes.


  \begin{figure} \par\includegraphics[width=7cm,clip]{bk1684f7.eps} \end{figure} Figure 7: The 1.0-2.0 GHz modelled radio spectrum of the cloud of spikes. The radio flux shown is in a logarithmic scale.
Open with DEXTER

4 Discussion and conclusions

The model of the narrowband dm-spikes considering the MHD turbulence and plasma emission mechanism, based on the anisotropic beam instability and upper hybrid waves generation, is presented. Using this model, artificial radio spectra are computed. As shown, this model is able to explain the main characteristics of the narrowband dm-spikes, especially their spectral features:

1. The spike decay profile is determined by the collisional damping of the upper hybrid waves.

2. There is a minimum bandwidth of spikes given by a size of the k-space of unstable upper hybrid waves. The spikes with broader bandwith originate at spatially larger elementary sources or they are the result of a superposition of several individual spikes.

3. An interruption of spikes is given by very fast plasma parameter changes in a turbulent radio source. On the other hand, the slower plasma parameter changes change the spike emission frequency.

4. Drifting chains of spikes are generated through a spatial "motion" of the resonance condition in the turbulent plasma inside the individual magnetic flux tube.

5. A superposition of the spike chains produce a cloud of spikes in the radio spectrum. These clouds can be divided into several branches according to their s-harmonics.

6. The narrowband line observed after the spike cloud (Fig. 1) can be explained by the same model, but with reduced turbulence.

7. A propagation of an anisotropic inhomogeneous beam can explain broadband pulses with superimposed spikes.

8. The proposed model can also explain the observed time delays (2-5 s) between hard X-rays and spikes (Aschwanden & Güdel 1992). This is due to a propagation effect. While the X-ray emission is caused by electrons propagating parallel to the magnetic field lines, the spikes in our model require the perpendicular electrons. It needs some time for the formation of the distribution function generating spikes.

9. Further details of the model are under study.

The inclusion of turbulence is the most important aspect of the model. The considered microphysics of emission processes needs further verifications and modifications cannot be excluded.


  \begin{figure} \par\includegraphics[width=8cm,clip]{bk1684f8.eps} \end{figure} Figure 8: The scenario of the narrowband dm-spikes generated in the plasma reconnection outflows.
Open with DEXTER

In agreement with our previous papers (Karlický et al. 1996; Zlobec & Karlický 1998) we propose that the narrowband dm-spikes are generated in the turbulent plasma reconnection outflows (see Fig. 8). We think that superthermal particles, leading to kinetic instabilities, are accelerated near the X-point of the magnetic field reconnection or directly in the cascading MHD turbulence.

The present model of the narrowband dm-spikes shows that the braided zebra patterns, lace bursts and spikes belong to the same group of radio emissions and all these types of bursts are connected with the turbulence. We think that these bursts, especially the narrowband dm-spikes, provide a unique opportunity to study the flare turbulence.

Acknowledgements

This work was supported by the grants S1003006 and A3003003 of the Academy of Sciences of the Czech Republic.

References

 
Copyright ESO 2001