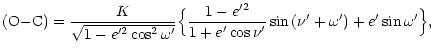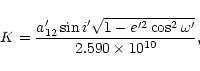A&A 379, 878-883 (2001)
DOI: 10.1051/0004-6361:20011357
The light and period changes of RT Andromedae
A. Erdem - O. Demircan - M. Güre
Çanakkale Onsekiz Mart University,
Faculty of Arts and Sciences, Department of Physics,
17100 Çanakkale, Turkey
Received 11 June 2001 / Accepted 5 September 2001
Abstract
The nature of the long-term orbital period variation and the light
level variation of RT And was studied based on all available
photometric observations. The (O-C) diagram formed by all
available times of eclipse minima could be either of a
quasi-sinusoidal form superimposed on a parabolic form, or a long
period sinusoidal form. The quasi-sinusoidal form with an
amplitude of  0.002 days and a period of
0.002 days and a period of 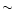 65 years could
be due to a cyclic magnetic activity modulation on the orbital
period of the system. Applegate's theory (Applegate 1992), in
this case, predicts an
65 years could
be due to a cyclic magnetic activity modulation on the orbital
period of the system. Applegate's theory (Applegate 1992), in
this case, predicts an 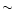 3 kG mean subsurface magnetic field
for the primary component of the system. The parabolic form
corresponds to a secular period decrease of about
3 kG mean subsurface magnetic field
for the primary component of the system. The parabolic form
corresponds to a secular period decrease of about
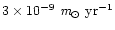 caused by mass loss from the system, and
the long-period sinusoidal form with an amplitude of
caused by mass loss from the system, and
the long-period sinusoidal form with an amplitude of 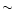 0.02 days
and a period of
0.02 days
and a period of 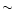 105 years corresponds to a secular period
change caused by the light-time effect due to an unseen third star
in the system. It was estimated that the unseen third star should
be a low mass (lower than
105 years corresponds to a secular period
change caused by the light-time effect due to an unseen third star
in the system. It was estimated that the unseen third star should
be a low mass (lower than
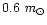 )
and faint
(
)
and faint
(
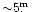 fainter than the system RT And) star, whose detection
is almost impossible. Future data will add information on the
nature of the secular (O-C) variation. Secular light level
variation of the system was found to be irregular and no
correlation was detected with the orbital period variation.
fainter than the system RT And) star, whose detection
is almost impossible. Future data will add information on the
nature of the secular (O-C) variation. Secular light level
variation of the system was found to be irregular and no
correlation was detected with the orbital period variation.
Key words: stars: binaries: eclipsing - stars: individual: RT And
RT And (BD +52 3383A, HIP 114484), as an interesting
eclipsing binary, has a long observational record. It belongs to
the short-period RS CVn type binaries (Hall 1976). Its first
photoelectric observations were made by Gordon (1948, 1955). She
reported a variable and asymmetric peculiar light curve.
3383A, HIP 114484), as an interesting
eclipsing binary, has a long observational record. It belongs to
the short-period RS CVn type binaries (Hall 1976). Its first
photoelectric observations were made by Gordon (1948, 1955). She
reported a variable and asymmetric peculiar light curve.
Later observations proved the substantial variability in all
phases of the light curve (Milano et al. 1981; Zeilik et al. 1989;
Pribulla et al. 2000; among others). The asymmetry in the light
curve has been interpreted as being produced by large cool star
spots on the primary star (Zeilik et al. 1989; Pribulla et al.
2000).
The period variation of the system was studied many times in the
past. First, Payne-Gaposchkin (1946) noted that previously
published periods were too long to satisfactorily reflect the 1579
Harvard patrol plates. A few years later, Gordon (1955) found that
the period found by Payne-Gaposchkin was too long to fit her
observations. Kristenson (1967), Williamon (1974) and Dean (1974)
discussed the abrupt period changes around 1914, 1940 and 1964.
The often-observed asymmetry of the minima and the different light
levels both during and outside of eclipse, expected by related
period jumps, were thought to be caused by discontinuities in the
mass exchange between the two components, as first suggested by
Wood (1950). Hall & Kreiner (1980) and Milano et al. (1981, 1986)
considered continuous period variation and derived quadratic
elements. Milano et al., however, noted that it is not possible to
ascertain, from their data, if the period variation is continuous
or formed by abrupt changes. They guessed the presence of a wave
with a period of about 44 years, superimposed on the parabolic
(O-C) diagram.
Later period studies of RT And by Borkovits & Hegedüs (1996),
Albayrak et al. (1999), and Pribulla et al. (2000) with more and
more extended data were all considered continuous period
variations. Borkovits & Hegedüs claimed that an unambiguous
identification of a third component is not possible for RT And,
although they represented the data very well with two light-time
orbits (P1=110 yr and P2=51 yr). Albayrak et al.
represented the data by a single light-time orbit (P=108 yr) as
the most possible cause of the cyclic period change. Finally,
Pribulla et al. represented the data equally well by two period
jumps in 1936 and 1966, a continuous period change combined with a
light-time orbit, and by two combined light-time orbits.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aefig1.eps} \end{figure}](/articles/aa/full/2001/45/aa1570/Timg6.gif) |
Figure 1:
The (O-C) diagram of RT And
formed by using Kholopov et al.'s (1985) linear light
elements (see Eq. (1)). |
| Open with DEXTER |
On the other hand, the possible relation between the long-term
asymmetry variation of the minima or different light levels of the
light curves and the period variation of RT And was suggested in
the past but never studied based on the observed data.
The aim of the present paper is to reconsider the long-term period
variation and the light curve asymmetry or the light level
variation of the system with the extended data and to search for a
possible correlation between them.
We have used all photographic and photoelectric minima from the
list compiled by Pribulla et al. (2000), except for the corrected
value of 51178.3440 instead of 51179.3440 (Agerer & Hübscher
2000). We had to add only some photoelectric minima observed
recently by Nelson (2000) and Bíró & Borkovits (2000).
The weights used for different data were the following:
photographic = 1 and photoelectric = 5.
As a first step, the (O-C) residuals were calculated by using the
light elements given by Kholopov et al. (1985); as
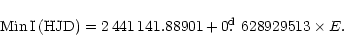 |
(1) |
From the (O-C) diagram in Fig. 1, the system's orbital period
change could be suggested to be parabolic or sinusoidal.
We have considered three possible mechanisms to explain the
orbital period change of the system: (i) mass loss from the
system, (ii) a light time effect due to a third body in the
system, and (iii) a period modulation due to the magnetic activity
cycle of a component star. We shall investigate the suggested
models in turn.
![\begin{figure}
\par\includegraphics[width=12.1cm,clip]{aefig2.eps} \end{figure}](/articles/aa/full/2001/45/aa1570/Timg8.gif) |
Figure 2:
a) The parabolic
representation of the (O-C) data, and b) the residuals from the
parabolic curve. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{aefig3.eps} \end{figure}](/articles/aa/full/2001/45/aa1570/Timg9.gif) |
Figure 3:
a) The tilted (eccentric) sinusoidal representation
of the (O-C) variation, and b) the residuals from the best fit
curve (solid line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=14.1cm,clip]{aefig4.eps} \end{figure}](/articles/aa/full/2001/45/aa1570/Timg10.gif) |
Figure 4:
The light level variation of RT And. The data were
obtained from the selected light curves, where the same comparison
star were used. The estimated error bars of the observational data
in the figure were, also, plotted. |
| Open with DEXTER |
The quadratic light elements of the system have been estimated by
the weighted least squares method as follows:
0pt
The quadratic fit and the O-C residuals from the parabola (as
given by Eq. (2)) are plotted in Fig. 2. The quadratic term in Eq. (2) shows that the orbital period of RT And is continuously
decreasing. The period decrease is found to be about
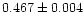 s per century.
s per century.
In binaries with solar type components, a continuous period
decrease may indicate that the binary is undergoing magnetic
breaking. In other words, if the outflowing mass is constrained by
magnetic fields to co-rotate with the mass-loosing star out to an
Alfvén radius which is sufficiently large, then the orbital
period will decrease because a large amount of angular momentum
per unit mass is removed from the system. This physical phenomenon
has been discussed in Hall & Kreiner's (1980) paper for RT And
together with 31 RS CVn type binaries and more recently in
Demircan's (1999) paper.
In Hall & Kreiner's (1980) model, the cooler component star is
assumed to be mass losing by a convectively driven stellar wind
mechanism. The estimated mass loss rate is about
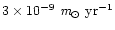 for the observed orbital period decrease
of RT And system. Demircan (1999) has obtained the semi-empirical
formula for the orbital period evolution of the RS CVn type
binaries by using the empirical relations between the orbital
angular momentum loss, mass loss and period variation. According
to his semi-empirical formula (e.g. his Eq. (7)), the mass loss
rate of the system can be estimated to be about
for the observed orbital period decrease
of RT And system. Demircan (1999) has obtained the semi-empirical
formula for the orbital period evolution of the RS CVn type
binaries by using the empirical relations between the orbital
angular momentum loss, mass loss and period variation. According
to his semi-empirical formula (e.g. his Eq. (7)), the mass loss
rate of the system can be estimated to be about
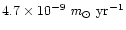 for the observed orbital period decrease
of RT And system. However, the mass loss consideration in Hall &
Kreiner (1980) and Demircan (1999) is not vectorial, thus whether
the magnetic wind can be polar or equatorial is not known.
for the observed orbital period decrease
of RT And system. However, the mass loss consideration in Hall &
Kreiner (1980) and Demircan (1999) is not vectorial, thus whether
the magnetic wind can be polar or equatorial is not known.
The parabolic variation of the (O-C) diagram in Figs. 1 and 2 can
well be a part of a sinusoidal form. So, a reasonable fit to (O-C)
variation can be achieved by using a sinusoidal ephemeris instead
of a parabolic form (cf., e.g. Irwin 1959):
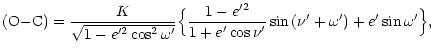 |
|
|
(3) |
where
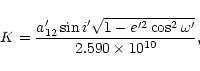 |
(4) |
is the semi-amplitude of the light-time effect (in days), a12is the semi-major axis of the absolute orbit of the center of mass
of the eclipsing pair around that of the whole system (in km),
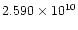 is the speed of light (in km/day), i' is
the inclination, e' is the eccentricity,
is the speed of light (in km/day), i' is
the inclination, e' is the eccentricity, 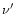 is the true
anomaly,
is the true
anomaly, 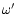 is the longitude of periastron passage of the
orbit of the three body system. T' and P12, which are the
secret parameters in Eq. (3), are the epoch of the periastron
passage and the period of this orbit, respectively.
is the longitude of periastron passage of the
orbit of the three body system. T' and P12, which are the
secret parameters in Eq. (3), are the epoch of the periastron
passage and the period of this orbit, respectively.
A weighted least squares solution of the T0, P,
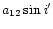 ,
e',
,
e', 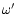 ,
T' and P12 parameters
found are given in Table 1. The sinusoidal best fit curve and the
residuals were plotted against epoch number in Fig. 3.
,
T' and P12 parameters
found are given in Table 1. The sinusoidal best fit curve and the
residuals were plotted against epoch number in Fig. 3.
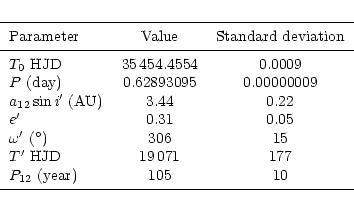
Table 1:
Parameters of the three-body orbit.
|
|
The most possible cause of the sinusoidal variation (if real) of
the (O-C) diagram is known to be the existence of an unseen third
star in the system. The parameters given in Table 1 show that the
eclipsing pair revolves around a center of mass of the three-body
system with a long period of 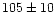 yr. The projected distance
of the center of mass of the eclipsing pair to the center of mass
of the triple system should be
yr. The projected distance
of the center of mass of the eclipsing pair to the center of mass
of the triple system should be
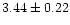 AU. These values lead
to a small mass function of
AU. These values lead
to a small mass function of
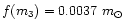 for the hypothetical third body. So, the
estimated mass of the third body ranges from
for the hypothetical third body. So, the
estimated mass of the third body ranges from
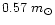 for
for
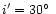 to
to
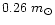 for
for
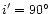 .
.
If the third body orbit is co-planar with the systemic orbit, the
semi-major axis a3 of the third body orbit around the center
of mass of the triple system would be about 25 AU. This value
shows that the third body, if it exists, lies far beyond the outer
Lagrangian points of RT And, and its orbit should be stable.
If the third body is a main-sequence star, the mass-luminosity
function (
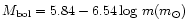 )
for the main-sequence stars with
)
for the main-sequence stars with
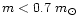 given by Demircan & Kahraman (1991) gives the
bolometric absolute magnitude of the third body as
given by Demircan & Kahraman (1991) gives the
bolometric absolute magnitude of the third body as
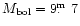 ,
whereas the bolometric absolute
magnitude of the system RT And is found to be about
,
whereas the bolometric absolute
magnitude of the system RT And is found to be about
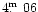 in
Pribulla et al.'s (2000) work. So, the third body would be about
in
Pribulla et al.'s (2000) work. So, the third body would be about
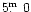 fainter than RT And, which is too faint for photometric or
spectroscopic detection. The semi-amplitude of the radial velocity
of the center of mass of the eclipsing pair, relative to the mass
center of triple system, turns out to be 1.03 kms-1, which is too
small for spectroscopic detection. The maximum angular separation
between the hypothetical third body and the eclipsing pair would
be about
fainter than RT And, which is too faint for photometric or
spectroscopic detection. The semi-amplitude of the radial velocity
of the center of mass of the eclipsing pair, relative to the mass
center of triple system, turns out to be 1.03 kms-1, which is too
small for spectroscopic detection. The maximum angular separation
between the hypothetical third body and the eclipsing pair would
be about
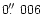 ,
which is also too small for observational
detection.
,
which is also too small for observational
detection.
The cyclic magnetic activity effect on the orbital periods of RS
CVn systems seems quite possible, since the components of these
systems are late type and they display spin-orbit coupling. So, as
an alternative explanation for cyclic changes of the orbital
periods of RS CVn systems, Applegate's (1992) gravitational
quadrupole coupling mechanism deserves attention. If the magnetic
activity can change the quadrupole moment of a star, the cyclic
exchange of angular momentum between the inner and outer parts of
the star can change the star's oblateness and radial differential
rotation. Any change in the rotational regime of a binary star
component due to magnetic activity would be reflected in the
orbit, as a consequence of the spin-orbit coupling. Finally, the
cyclic magnetic activity can modulate the orbital period of the
close binary system (Applegate 1992).
The residuals from the parabolic representation as plotted in
Fig. 2b indicate a low amplitude (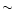 0.002 day) and a long
period (
0.002 day) and a long
period ( 65 years) oscillation. Using these parameters and
the absolute dimensions of RT And from Pribulla et al. (2000), in
Applegate's (1992) formulation we estimated the mean subsurface
magnetic field of the primary component to be about 3 kiloGauss,
which is provided by the periodic change of angular momentum
between the inner and outer part of the star.
65 years) oscillation. Using these parameters and
the absolute dimensions of RT And from Pribulla et al. (2000), in
Applegate's (1992) formulation we estimated the mean subsurface
magnetic field of the primary component to be about 3 kiloGauss,
which is provided by the periodic change of angular momentum
between the inner and outer part of the star.
As it was noted by Applegate (1992), such oscillations in the
orbital period should be connected to the long-term light level
variations.
In order to look for any long-term light variations of RT And, we
obtained 27 photoelectric light curves from Pribulla et al.
(2000). These data were obtained between 1948 and 1999. In the
observational data of the eight light curves between 1988 and
1997, the same comparison star was used. We considered, in every
light curve, the light levels at mid-primary and mid-secondary
eclipses (Min I and Min II) and Max I and Max II after primary and
secondary eclipses. Each of the light levels of four
characteristic phases were estimated on both B and V light curves.
The scatter diagrams of the light levels at maxima and minima
indicate no periodicity. However the data from selected light
curves indicate short-term (a few years) fluctuations (Fig. 4),
which are clearly not correlated with the period variation of the
system.
All possible characters of the (O-C) variation formed by all
available observed times of minima of RT And were interpreted in
terms of the orbital period variation and possible causes. Most
probably, the cyclic magnetic activity of the primary component,
mass loss from the system and an unseen third star in the system
play important roles in the orbital period (and thus (O-C))
variation. No sign of the expected correlation between orbital
period variation and the light variation was found from the
presently available data.
The last 85 years of data from RT And were found to be
insufficient to decide on the character of the secular (O-C)
variation; parabolic or sinusoidal. The present data in Fig. 1, in
fact, are slightly better represented (see Fig. 3) by a tilted
(eccentric) sinusoidal which strengthens the arguments for the
presence of a third body revolving around the binary in an
eccentric orbit. Future observations over next 20 years may help
us decide about the character of the variation. Such new data will
also be important in determining the sinusoidal long-term
modulation of the (O-C) variation.
Acknowledgements
The research was supported in part by the Çanakkale Onsekiz
Mart University Research Foundation under grant no 1999/FE/13.
- Agerer, F., & Hübscher, J. 2000,
IAU, IBVS, No. 4912
In the text
- Albayrak, B., Özeren, F. F., Ekmekçi,
F., & Demircan, O. 1999,
Rev. Mex. Astron. Astrofis., 35, 3
In the text
NASA ADS
- Applegate, J. H. 1992,
ApJ, 385, 621
In the text
NASA ADS
- Bíró, I. B., & Borkovits, T. 2000,
IAU, IBVS, No. 4967
In the text
- Borkovits, T., & Hegedüs, T. 1996,
A&AS, 120, 63
In the text
NASA ADS
- Dean, C. A. 1974,
PASP, 86, 912
In the text
NASA ADS
- Demircan, O. 1999,
in Magnetic Activity in Cool Stars,
ed. O. Demircan
(TUBITAK, Ankara), 425
In the text
- Demircan, O., & Kahraman, G. 1991,
Ap&SS, 181, 313
In the text
NASA ADS
- Gordon, K. 1948,
AJ, 53, 198
In the text
- Gordon, K. 1955,
AJ, 60, 422
In the text
NASA ADS
- Hall, D. S. 1976,
Proc. IAU Colloq., 29, 287
In the text
- Hall, D. S., & Kreiner, J. M. 1980,
AcA, 30, 387
In the text
NASA ADS
- Irwin, J. B. 1959,
AJ, 64, 149
In the text
NASA ADS
- Kholopov, P. N., et al. 1985,
General Catalogue of Variable Stars, 4th edition (Nauka Publishing House, Moskow)
In the text
- Kristenson, H. 1967,
BAICz, 18, 261
In the text
NASA ADS
- Milano, L., Russo, G., & Mancuso, S. 1981,
A&A, 103, 57
In the text
NASA ADS
- Milano, L., Mancuso, S., Vittone, A., et al. 1986,
Ap&SS, 124, 83
In the text
NASA ADS
- Nelson, R. H. 2000,
IAU, IBVS, No. 4840
In the text
- Payne-Gaposchkin, C. 1946,
ApJ, 103, 291
In the text
NASA ADS
- Pribulla, T., Chochol, D., Milano, L., et al. 2000,
A&A, 362, 169
In the text
NASA ADS
- Williamon, R. M. 1974,
PASP, 86, 924
In the text
NASA ADS
- Wood, F. B. 1950,
ApJ, 112, 196
In the text
NASA ADS
- Zeilik, M., Cox, D. A., De Blasi, C., et al. 1989,
ApJ, 345, 991
In the text
NASA ADS
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aefig1.eps} \end{figure}](/articles/aa/full/2001/45/aa1570/Timg6.gif)
![\begin{figure}
\par\includegraphics[width=12.1cm,clip]{aefig2.eps} \end{figure}](/articles/aa/full/2001/45/aa1570/Timg8.gif)
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{aefig3.eps} \end{figure}](/articles/aa/full/2001/45/aa1570/Timg9.gif)
![\begin{figure}
\par\includegraphics[width=14.1cm,clip]{aefig4.eps} \end{figure}](/articles/aa/full/2001/45/aa1570/Timg10.gif)