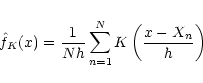 |
(19) |
To decrease the noise and allow a tractable use of the information present in small data samples, heavy smoothing techniques are often required. A common practice consists converting a set of discrete positions into binned "counts''. Binning is a crude sort of smoothing and many studies in statistical analysis have shown that, unless the smoothing is done in an optimum way, some, or even most, of the information content of the data could be lost. This is especially true when a large amount of smoothing is necessary, which then changes the "shape'' of the resulting function. In statistical terms, the smoothing process not only decreases the noise (i.e., the function's variance), but at the same time introduces a bias in the estimate of the function.
The variance-bias trade off is unavoidable but, for a given level of variance, the bias increase can be minimized. The correct manner of achieving that task is provided by the so-called non-parametric density estimate methods for the determination of the "frequency'' function of a given parameter or by the non-parametric regression methods for the determination of a smooth function ginferred from direct measurements of g itself. Moreover, adaptive non-parametric methods are designed to filter the data in some local, objective way minimizing the bias, in order to get the smooth desired function without constraining its form in any way. The theory and algorithms related to those methods, originally built to handle ill-conditioned problems (either under-determined or extremely sensitive to errors or incompleteness in the data), are widely discussed in the specialized literature and summarized in easy-to-read textbooks (e.g., Silverman 1986; Härdle 1990; Scott 1992).
The simplest of the available algorithms is provided by the kernel
estimator leading to the following form of the normalized
"frequency'' function
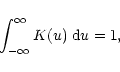 |
(20) |
In the adaptive kernel version, a local bandwidth
hn=h(Xn,f) is defined and used in Eq. (19). In order to
follow the "true'' underlying function in the best possible way, the
amount of smoothing should be small when f is large whereas more
smoothing is needed where f takes lower values. A convenient method
to do so consists in deriving first a pilot estimate ![]() of f, e.g. by
using an histogram or a kernel with fixed bandwidth
of f, e.g. by
using an histogram or a kernel with fixed bandwidth
![]() ,
and
then by defining the local bandwidths
,
and
then by defining the local bandwidths
![\begin{displaymath}h_n=h(X_n)=h_{\rm opt}[\tilde f(X_n)/s]^{-\alpha},
\end{displaymath}](/articles/aa/full/2001/45/aa1489/img78.gif) |
(21) |
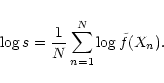 |
(22) |
The optimum kernel K may be taken as the one minimizing the integrated
mean square error beween f and ![]() (MISE), where
(MISE), where
![\begin{displaymath}{\rm MISE}(\hat{f}) = E\int\left[ \hat{f}(x) - f(x) \right]^2 {\rm d}x
\end{displaymath}](/articles/aa/full/2001/45/aa1489/img82.gif) |
(23) |
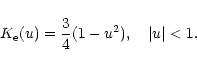 |
(24) |
The pilot smoothing length (
![]() )
is the only subjective
parameter required by the method. It relates to the quality of the
sampling of the variable under consideration. There are several ways for
automatically estimating an optimum value of
)
is the only subjective
parameter required by the method. It relates to the quality of the
sampling of the variable under consideration. There are several ways for
automatically estimating an optimum value of
![]() (see e.g. Silverman 1986 for an extensive review). A simple approach based
on the data variance gives in our case
(see e.g. Silverman 1986 for an extensive review). A simple approach based
on the data variance gives in our case
![]()
![]() .
As the derivative of the frequency function rather than the
function itself is actually used in
Eq. (6), a larger pilot smoothing length (
.
As the derivative of the frequency function rather than the
function itself is actually used in
Eq. (6), a larger pilot smoothing length (
![]() )
was
also considered in order to remove spurious small-statistics
fluctuations of the density estimate.
)
was
also considered in order to remove spurious small-statistics
fluctuations of the density estimate.
Copyright ESO 2001