

Up: The distribution of exoplanet
3 The Lucy-Richardson inversion algorithm applied to Abel's
integral equation
The Lucy-Richardson algorithm provides another robust way to invert
Eq. (4) (see also Cerf & Boffin 1994). The
method starts from the Bayes theorem on conditional probability in the
form
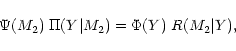 |
(9) |
where
R(M2 | Y) is the reciprocal kernel corresponding to the
integral equation inverse to the one that needs to be solved
(Eq. (1)):
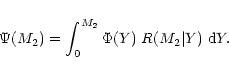 |
(10) |
The reciprocal kernel represents the conditional probability that the
binary system has a companion mass M2 when the observed
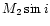 value amounts to Y. Thus, one has:
value amounts to Y. Thus, one has:
| R(M2|Y) |
= |
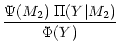 |
(11) |
| |
= |
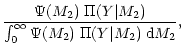 |
(12) |
which obviously satisfies the normalization condition
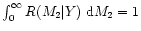 .
The problem in solving
Eq. (10) arises because R(M2|Y) also depends on
.
The problem in solving
Eq. (10) arises because R(M2|Y) also depends on
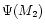 ,
so that an iterative procedure must be used. If
,
so that an iterative procedure must be used. If
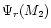 is the rth estimate of
is the rth estimate of 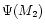 ,
it can be used to
obtain the (r+1)th estimate in the following way:
,
it can be used to
obtain the (r+1)th estimate in the following way:
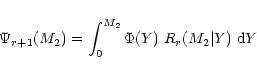 |
(13) |
with
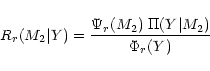 |
(14) |
and
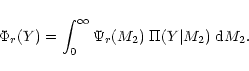 |
(15) |
Thus, 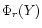 represents the corresponding rth estimate of the
observed distribution
represents the corresponding rth estimate of the
observed distribution 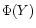 .
Equations (13) and (14)
together yield the recurrence relation for the
.
Equations (13) and (14)
together yield the recurrence relation for the 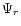 's,
's,
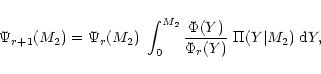 |
(16) |
with
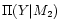 given by Eq. (3) for the problem under
consideration. The conditions for convergence of this recurrence
relation are discussed by Lucy (1974) and
Cerf & Boffin (1994). It needs only be remarked here that (i) the
iterative scheme converges if
given by Eq. (3) for the problem under
consideration. The conditions for convergence of this recurrence
relation are discussed by Lucy (1974) and
Cerf & Boffin (1994). It needs only be remarked here that (i) the
iterative scheme converges if 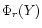 tends to
tends to 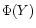 ,
given
the normalization of the probability
,
given
the normalization of the probability
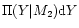 ,
and (ii)
the full convergence of the method is not necessarily desirable, as
the successive estimates
,
and (ii)
the full convergence of the method is not necessarily desirable, as
the successive estimates 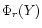 will tend to match
will tend to match 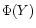 on
increasingly smaller scales, but the small-scale structure in
on
increasingly smaller scales, but the small-scale structure in
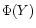 is likely to be dominated by the noise in the input
data. This is well illustrated in Fig. 2 below.
is likely to be dominated by the noise in the input
data. This is well illustrated in Fig. 2 below.
When the number of data points is small
(typically N <100; Cerf & Boffin 1994), it is advantageous to express 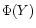 as
as
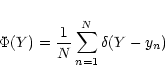 |
(17) |
where the
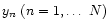 are the N individual measured
are the N individual measured
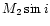 values and
values and 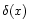 is the Dirac "function'' such that
is the Dirac "function'' such that
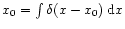 .
Substitution in Eq. (13)
then yields
.
Substitution in Eq. (13)
then yields
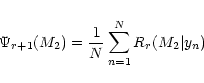 |
(18) |
where
Rr(M2|yn) is defined as in Eq. (14). The sample
size should nevertheless be large enough for the functions
Rr(M2|yn) to have sufficient overlap so as to produce a smooth
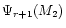 function.
function.
In the application of the method described in
Sect. 4, the initial mass distribution
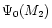 was taken as a uniform distribution, but it has been verified that this
choice has no influence on the final solution.
was taken as a uniform distribution, but it has been verified that this
choice has no influence on the final solution.


Up: The distribution of exoplanet
Copyright ESO 2001
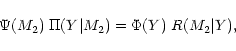
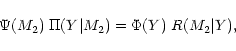
![]() value amounts to Y. Thus, one has:
value amounts to Y. Thus, one has:
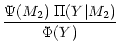
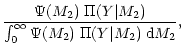
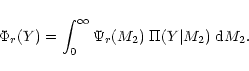
![]() as
as
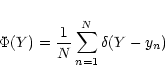
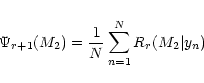
![]() was taken as a uniform distribution, but it has been verified that this
choice has no influence on the final solution.
was taken as a uniform distribution, but it has been verified that this
choice has no influence on the final solution.