A&A 379, 936-954 (2001)
DOI: 10.1051/0004-6361:20011384

Non-LTE line-formation for neutral and singly-ionized carbon

Model atom and first results on BA-type stars[*]

N. Przybilla1,2 - K. Butler1 - R. P. Kudritzki3


1 - Universitäts-Sternwarte München, Scheinerstraße 1, 81679 München, Germany
2 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85740 Garching bei München, Germany
3 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA

Received 23 April 2001 / Accepted 20 September 2001

Abstract
A comprehensive model atom for non-LTE line-formation calculations for neutral and singly-ionized carbon is presented. Highly accurate radiative and collisional atomic data are incorporated, recently determined for astrophysical and fusion research using the R-matrix method in the close-coupling approximation. As a test and first application of the model, carbon abundances are determined on the basis of line-blanketed LTE model atmospheres for five stars, the main sequence object Vega (A0V) and the supergiants $\eta $Leo (A0Ib), HD111613 (A2Iabe), HD92207 (A0Iae) and $\beta $Ori (B8Iae), using high S/N and high-resolution spectra at visual and near-IR wavelengths. The computed non-LTE line profiles fit the observations well for a single carbon abundance in each object. For two supergiants, $\eta $Leo and HD111613, lines of both species are simultaneously present in the spectra, giving consistent C I and C II abundances (within the error bars). However, the uncertainties of the abundances are large, on the order of $\sim$0.3dex ( ${\rm statistical}+{\rm systematical~error}$), thus the ionization equilibrium of C I/II is of restricted use for the determination of stellar parameters. All supergiants within our sample show a depletion of carbon on the order of 0.2-0.5 dex, indicating the mixing of CN-cycled material into the atmospheric layers, with the sum of the CNO abundances remaining close to solar. This finding is in accordance with recent stellar evolution models accounting for mass-loss and rotation. For Vega, an underabundance of carbon by 0.3 dex is found, in excellent agreement with the similar underabundance of other light elements. The dependence of the non-LTE effects on the atmospheric parameters is discussed and the influence of systematic errors is estimated. Special emphasis is given to the supergiants where a strong radiation field at low particle densities favours deviations from LTE. Non-LTE effects systematically strengthen the C I/II lines. For the C I lines in the infrared, a strong sensitivity to modifications in the photoionization and collisional excitation data is found. An increasing discrepancy between our model predictions and the observations for the C II doublet $\lambda \lambda $6578-82 is perceived with rising luminosity, while the other C II doublet and quartet lines remain consistent. Furthermore, the influence of microturbulence on the statistical-equilibrium calculations is investigated.

Key words: atomic data - line: formation - stars: abundances, early-type, supergiants


1 Introduction

Carbon - along with oxygen and nitrogen - belongs to the most abundant metals in (inter)stellar matter. An accurate knowledge of its abundance is of perennial interest in cosmochemical studies. Present-day abundances of carbon are preferentially derived from spectral analysis of either H II regions or young, early-type stars. But, analyses from both types of objects are not unproblematic, as the fraction of carbon bound in dust is a priori not known in H II regions (e.g. Mathis 1996; Esteban et al. 1998) and in early type stars CN-cycled matter might be mixed into the photospheric layers, even in main sequence objects (e.g. Lyubimkov 1991; Gies & Lambert 1992).

At extragalactic distances only the brightest objects are accessible to spectroscopy, i.e. H II regions and supergiants of the spectral types B and A (in the visual, due to their intrinsic luminosities and low bolometric corrections; e.g. Humphreys 1983; Kudritzki 1998). The latter are the evolved descendants of massive OB stars and they often show abundance patterns indicating mixing with nuclear burned material (Lennon et al. 1993; Venn 1995b, 1999; McErlean et al. 1999). These abundance patterns provide important constraints on the evolution of massive stars in our own and other galaxies, in particular, in connection with the use of new sophisticated models of stellar evolution including rotation and mass-loss (Meynet & Maeder 2000; Heger & Langer 2000). In addition, carbon abundances together with those of nitrogen and oxygen (note, that the sum of CNO remains unchanged during the mixing processes) define the content of light elements, which can be compared with the content of $\alpha$-process, iron-group and s-process elements in order to constrain the chemical evolution history of galaxies (Venn 1999; Venn et al. 2000, 2001).

A prerequisite for all further studies is an accurate determination of the stellar abundances. For luminous (supergiant) stars, this requires the consideration of deviations from LTE in the entire atmospheres exposed to a strong radiation field. Recent work on non-LTE model atoms for carbon in early-type stars mainly concentrated on the application to main sequence objects (Stürenburg & Holweger 1990; Takeda 1992; Rentzsch-Holm 1996 for C I - Eber & Butler 1988; Sigut 1996 for C II). Carbon abundances in late B and early A-type supergiants have only recently been studied in non-LTE (Venn 1995b; Takeda & Takada-Hidai 2000) on the basis of some of these models. The results obtained so far have not allowed us to draw clear conlusions about carbon abundances.

Considerable progress has been made in the determination of accurate atomic data during the last few years, mainly by the application of the R-matrix method. A large amount of radiative and collisional data has become available for C I/II due to the demands of astrophysical (nebular studies) and fusion (JET/ITER project) research. In view of this, a critical reinvestigation of the C I/II non-LTE problem seems appropriate.

This paper concentrates on the abundance determination of carbon from spectral lines of the neutral and singly-ionized species in early A-/late B-type stars, with special emphasis on supergiants. A comprehensive model atom for C I/II is presented in the next section together with a critical examination of the expected systematical uncertainties. We perform a consistent and simultaneous treatment of both ionization stages for the first time. The results from our non-LTE line-formation computations are discussed in Sect. 3, as is the influence of microturbulence. In the following section, carbon abundances for a test sample of five stars are determined from high S/N and high-resolution spectra. The findings are discussed in the context of previous abundance studies. Finally, a short summary is given in Sect. 5.

The application of the model to the determination of carbon abundances in supergiants throughout several Local Group galaxies - still accessible to high-resolution spectroscopy with large telescopes - will be the subject of further studies. Abundances for helium, nitrogen and oxygen determined with equally comprehensive non-LTE model atoms (Przybilla et al. 2000, hereinafter PaperI; Przybilla & Butler 2001, PaperIII) will help to constrain the evolutionary status of these objects in view of the new models for stellar evolution - see Przybilla et al. (2001b, PaperIV) for a discussion. A comparison of our model predictions with observed C I lines in later spectral types (in particular for the sun) and with C II lines in earlier B stars - at maximum strength - would also be of interest.

2 Model calculations

  
2.1 Model atmospheres and programs

The calculations are performed using the standard assumptions of plane-parallel, homogeneous and stationary stellar atmospheres in hydrostatic and radiative equilibrium. Carbon is assumed to be a trace element, despite its large abundance and its important contribution to the continuous opacity in the far-UV, between Ly$_{\alpha }$ and the Lyman edge. Thus, we obtain statistical equilibrium populations for C I/II while keeping the atmospheric parameters fixed. This restriction can only be overcome by future atmospheric models explicitly accounting for non-LTE.

The non-LTE C I/II line profiles are computed on the basis of ATLAS9 (Kurucz 1979, 1991) LTE line-blanketed model atmospheres using LTE Opacity Distribution Functions (ODFs, Kurucz 1992), also to account for line blocking in the spectrum synthesis. We use the Lemke version of this program, as obtained from the CCP7 software library (http://ccp7.dur.ac.uk/). For the calculation of model atmospheres of the most extreme supergiants close to the Eddington limit technical problems arise with this version. The pressure P in the outer layers of the atmosphere drops below the values for which the opacity data is tabulated (lower limit at $\log P$=-2, cgs units), implying extrapolation. Moreover, the local (gas) temperatures in the outermost model depth points for our A-type supergiants drop as low as $\sim$4000K. Thus the ODF data will overestimate the true opacity by large factors, as in LTE the contribution of neutral atom and molecular opacity dominate at these temperatures, while the real stellar plasma is exposed to a radiation field of $\sim$10000K, which ionizes the material and inhibits molecule formation. Effectively this results in an overestimation of the radiative acceleration $g_{\rm rad}$, which can exceed the surface gravity and therefore violate the hydrostatic equilibrium condition close to the Eddington limit. In order to overcome this problem, in the critical cases we replace the tabulated Rosseland opacities by Thomson scattering in the outermost depth points (at $\log P$<-2) and subsequently activate the tables over a transition region (-2$\le$$\log P$$\le$-1) to avoid discontinuities; ODF line opacities are also neglected for $\log P$<-2 and are activated in analogy to the Rosseland opacities. This procedure suffices to extend the range of model convergence closer to the Eddington limit while the original model structures are retained at higher surface gravities.

With the above assumptions, reliable analyses can be performed in the given temperature range from main sequence stars through to bright giants as indicated by Kudritzki (1988). A thorough discussion of the possible deviations from the standard assumptions on the model atmosphere structure of supergiants is given by Venn (1995a). Additionally, non-LTE effects are often less significant for the model structure than is line blanketing, as demonstrated by Przybilla (1997). Close to the Eddington limit (luminosity classes Iae and Ia+) further studies on this topic are desirable; appropriate stellar atmosphere models including non-LTE blanketing, spherical extension and the hydrodynamics of stellar winds are still in the phase of development and are not yet available for detailed abundance studies.


  \begin{figure} \par\hbox{ \includegraphics[width=8cm,clip]{ms1408f1a.eps}\hspace... ...} \includegraphics[width=8cm,clip]{ms1408f1d.eps}\hspace*{4mm}} \par\end{figure} Figure 1: Grotrian diagrams for C I, singlet (upper left) and triplet spin system (upper right) and for C II, doublets (lower left) and quartets (lower right). Note that both ionic species and all spin systems (with an additional quintet level at low excitation energy in C I) are treated simultaneously. Displayed are the radiative bound-bound transitions treated explicitly in non-LTE.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12cm,clip]{ms1408f2.eps}\hfill \parbox[b]{56mm}{ } \end{figure} Figure 2: Comparison of photoionization cross-sections from OP computations (full line) and from Henry (1970, dotted line). On the left hand side data for the ground states of C I and C II are displayed, on the right hand side data for the first and second excited levels of C I. The near-threshold regions of the latter two are dominated by broad resonances corresponding to autoionizing states.
Open with DEXTER

The line formation calculations are performed using the programs DETAIL and SURFACE (Giddings 1981; Butler & Giddings 1985), with the former solving the radiative transfer and the statistical equilibrium equations and the latter computing the emergent flux. Recent improvement by inclusion of an ALI scheme (using the treatment of Rybicki & Hummer 1991) allows the utilisation of quite elaborate model atoms while the necessary computational resources remain at a low level (typically $\sim$40min for a model convergence on a 500 MHz PIII CPU).

2.2 The model atom

2.2.1 Energy levels
The atomic model for carbon has to be fairly complete in order to predict the non-LTE effects quantitatively (cf. Stürenburg & Holweger 1990; Sigut 1996) and consequently to ensure the ionization balance between the atomic and singly-ionized species. Carbon is almost completely ionized throughout the atmosphere of BA-type stars, with a small fraction (several parts in a thousand) of C I at line-formation depths. Non-LTE effects are expected to be of importance for the interpretation of the C I/II lines at visual and near-IR wavelengths, which are all emerging from highly-excited levels.

Energy levels up to $\sim$0.37/0.67 eV below the ionization threshold as listed by Moore (1993) are therefore included explicitly in our C I/II model. Missing data for highly excited C II levels are adopted from Sigut (1996). This includes all energy levels with principal quantum number $n\leq6$and the $7{\rm s}$ states in C I and all levels with $n\leq9$ and $\ell\leq4$ in C II. Only the ground state of C III is considered, as the ionization energy of 47.89 eV is large. Fine structure splitting is not taken into account: sub-levels belonging to the same term are combined into a single level. The intermediate-coupling terms of C I are treated in LS-coupling for which Opacity Project (OP; see Seaton et al. 1994 for a general overview) radiative data is available. The resulting inconsistencies are expected to be negligible, as the deviations from pure LS-coupling are small.

Additionally, the remaining level populations of C I and C II up to n=10 and n=14, respectively, are computed in LTE relative to the ground state of the higher ionization stage, with energies derived from their quantum defects. They are considered only in the number conservation equation.

2.2.2 Radiative transitions
All optically allowed bound-bound transitions between energy levels with non-LTE populations are taken into consideration. The required oscillator strengths are adopted from OP data (Luo & Pradhan 1989) for C I and from Fernley et al. (available only from the TOPBASE database, Cunto & Mendoza 1992) for C II. In order to improve the computational efficiency, the individual lines of a multiplet are reduced to a single effective "multiplet line''.

Grotrian diagrams for C I and C II are displayed in Fig. 1. The non-LTE calculations are performed simultaneously for C I/II. Additional radiative coupling between the different spin systems of C I is provided by all intercombination transitions listed by Wiese et al. (1996). Intercombinations in C II on the other hand are neglected due to the very small transition probabilities. A detailed comparison of OP oscillator strengths for C I/II with experimental and theoretical work by other authors is performed by Luo & Pradhan (1989) and Yan et al. (1987); the majority of the data is expected to be accurate to within 10%, superseding most of the older data used in previous studies of non-LTE effects on C I or C II.

Photoionizations from all energy levels with non-LTE populations are treated, with cross-sections fitted to the OP data (Luo & Pradhan 1989 for C I and Fernley et al. for C II), as available through the TOPBASE database. A carefully chosen frequency grid ensures a thorough representation of the numerous resonances present in the results of the R-matrix calculations, typically being accurate to 10%. Cross-sections for energy levels missing in the OP data (for $\ell$=4 in C II) are calculated in the hydrogenic approximation (Mihalas 1978, p. 99). A comparison of OP cross-sections with those of Henry (1970) - usually used in previous non-LTE studies on C I/II - is given in Fig. 2. The OP cross-section for the C II ground state agrees well with that of the less elaborate approach, except for several sharp resonances. On the other hand the OP data for the three lowest C I states are systematically larger on the average, thus increasing the rate of photoionization. In addition, broad resonances corresponding to autoionizing states dominate the important near-threshold region, enlarging the cross sections considerably. For the higher excited levels of C I/II, the use of detailed OP data also significantly improves the description of the photoionization processes compared to most of the previous non-LTE studies of these ions.

In the first step of the computations, i.e. in DETAIL, the level populations are calculated using depth-dependent Doppler profiles, assuming LS coupling; microturbulence is explicitly accounted for by inclusion of an additional term in the Doppler width

 \begin{displaymath}% \Delta\lambda_{\rm D}=\frac{\lambda_{\rm0}}{c}\sqrt{v_{\rm th}^2 + \xi^2} \end{displaymath} (1)

where $\lambda_{\rm0}$ is the rest wavelength of the transition, c the speed of light, $v_{\rm th}$ the thermal velocity for the chemical species of interest and $\xi $ the microturbulent velocity; see Sect. 3.2 for a discussion. Both, continuous opacities and ATLAS9 line-distribution functions are accounted for in solving the radiation transfer.

These LS-coupling populations are then split according to the statistical weights of the individual sub-levels in order to calculate line profiles via SURFACE. In this step of calculation, Voigt profile functions are adopted and the same microturbulent velocity as in DETAIL is applied. Wavelengths are taken from Wiese et al. (1996) and Moore (1993) and transition probabilities from the sources indicated in Tables 5 and 6. The damping parameters are calculated from OP radiative lifetimes for the radiative widths and adopted from Griem (1964, 1974) for electron impact and ion broadening in C I/II. Missing collisional-damping data are computed from the approximation of Cowley (1971). Van der Waals damping is neglected in the parameter range considered here, as the atmospheric plasma is mostly ionized.

2.2.3 Collisional transitions
Substantial interest in accurate cross-sections for collisional excitation in C I/II for fusion-plasma modelling and astrophysical applications has recently led to computational efforts on a large scale. For a significant fraction (over 300 transitions) of the data needed in our work, detailed results are available from calculations carried out in the close-coupling approximation using the R-matrix method. We calculate effective collision-strengths for C I from the collisional cross-section computations of Dunseath et al. (1997), following Burgess & Tully (1992). Additional cross-sections for collisional excitation between the four lowest-lying energy levels are adopted from Thomas & Nesbet (1975). For C II, effective collision-strengths are taken from the work of Blum & Pradhan (1992). Error estimates for these data are difficult to obtain, as no comparison with other experimental or theoretical results is available for almost all transitions. For test purposes, we assume a factor of two in accuracy. Note that uncertainties in data obtained by the R-matrix method are typically of the order of a few 10%. For the remaining bulk of the transitions, approximate formulae must be used, giving threshold values accurate to a factor 2-3 at best. Van Regemorter's formula (Van Regemorter 1962) is applied for radiatively permitted transitions with OP oscillator strengths. For the optically forbidden transitions, the Allen formula (Allen 1973) is used with the collision strength set to1.0.

Experimental cross sections from Brook et al. (1978) and Yamada et al. (1989) are adopted for the collisional ionization of the ground states of C I and C II. The authors expect uncertainties of <30% and <20%, respectively, for the data at low energies, with significant improvements in the accuracy at higher energies. All the remaining collisional ionization data are computed using the Seaton formula (Seaton 1962) with threshold photoionization cross-sections from the OP data, where available, or from the hydrogenic approximation.

  
2.3 Background opacities


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1408f3.eps}\end{figure} Figure 3: Synthetic far-UV (astrophysical) fluxes from ATLAS9 supergiant models for $T_{\rm eff}$=9500K, $\log g$=2.0 and $\xi $=4kms-1at solar metallicity, accounting for continuous and (ODF) line opacity (full/dotted line) and continuous opacity only (dashed/dashed-dotted line) for solar/ 0.2$\times $solar carbon abundance and a correspondingly increased nitrogen abundance in the latter case. The locations of the relevant ionization edges and Ly$_{\alpha }$ are marked; continuous and dotted markers on the top give the positions of the resonance lines of C I and C II, respectively (Wiese et al. 1996).
Open with DEXTER

The stellar radiation field is strongly affected by continuous and line opacities which must be correctly accounted for, in particular, in statistical equilibrium calculations. Synthetic ( ATLAS9) far-UV fluxes for typical supergiant parameters are displayed in Fig. 3 for two sets of C and N abundances, together with the locations of the relevant opacity sources (ionization edges) and C I/II resonance lines in this wavelength region. The coarse wavelength resolution of the flux results from the 10Å-wide ODF bins. Ionization from the C I ground state is an important opacity source in the solar abundances model, next to the line opacity (with a significant contribution by Ly$_{\alpha }$). Its rôle diminishes for a carbon depleted (by a factor of five) model; here, the enhanced bound-free opacity from the first excited level of N I almost replaces it, except for the region between these two ionization edges. We assume that the depleted carbon is transformed into nitrogen, as might be expected if CN-cycled matter is mixed into the atmospheric layers. This LTE experiment should be viewed only as an instructive example for the effects anticipated, as a fully consistent treatment in non-LTE is beyond the scope of this paper, see also the remarks at the end of this section.

We therefore explicitly account for bound-free opacities of hydrogen, helium, nitrogen and oxygen in our statistical equilibrium calculations, with level populations calculated in non-LTE, using updated and extended versions of the H and He I model atoms of Husfeld et al. (1989) and the O I and N I/II model atoms (PapersI & III). All levels of H up to n=20 are treated explicitly in non-LTE, and for He I a number of spectral lines is added in the line formation; however, the changes do not affect the contribution of both elements to the background opacity. Line opacities are represented by LTE ODFs (Kurucz 1992) for the appropriate metallicity and microturbulence. The original sawtooth pattern is transformed into a step function by averaging over the 10Å-wide intervals. This procedure meets the requirements for calculating the radiation field as a whole. However, at certain important wavelengths a more detailed description is desirable. In particular, line opacities slightly longward of the Lyman and Balmer jump are only poorly reproduced in the ODF approach, especially for supergiants, as the merging hydrogen lines are inappropriately sampled. Moreover, most transition wavelengths for opacity calculations are only known from theoretical calculations which implies comparatively large errors (see e.g. Johansson & Leckrone 1996) and therefore inappropriate opacities. In particular, the vacuum ultraviolet region is affected, where the important ionization edges of C I are located. Thus, the ionizing radiation field might show some inaccuracies, impacting the ionization balance of carbon. C II, on the other hand, should be virtually unaffected by this, with its ionization edges located at wavelengths with negligible flux. A lot of important input has to be provided by atomic physicists to improve the situation.

Despite our success in reproducing the observations, our computations might also be affected by a systematic effect neglected in the atmospheric modelling. Non-LTE effects will cause an overionization of the relevant elements in the opacity determination. The backwarming introduced by line blanketing might therefore be overestimated in LTE, as well as the magnitude of line blocking. First calculations of non-LTE line-blanketed model atmospheres for main sequence A-types (Hubeny & Lanz 1993) indicate some changes in the expected direction and adequate models for the more interesting case of supergiants are just being investigated (J. Puls, private communication; Aufdenberg 2000) and are still not available for detailed abundance work.


  
Table 1: Uncertainties in the non-LTE analysis of carbon.


\begin{displaymath}\begin{tabular}{lllrrrrrr} \hline & & & \multicolumn{6}{c}{\... ....16 & $\pm$0.14 & $\pm$0.16 & $\pm$0.15\\ \hline \end{tabular}\end{displaymath}


  
2.4 Error estimates for the carbon non-LTE calculations

To assess the effects of atmospheric parameters and crucial atomic data on the accuracy of carbon abundances by our non-LTE approach, test calculations were performed for typical atmospheric parameters of BA-type stars: a main sequence model with 9500K/4.0 at $\xi=2$ $\mbox{km\,s}^{-1}$ and supergiant models with 9500K/2.0 at $\xi=4$ $\mbox{km\,s}^{-1}$ and with 9500K/1.2 and 12000K/1.8 at $\xi=8$ $\mbox{km\,s}^{-1}$, assuming solar metallicity. For each parameter or set of cross-sections varied, we calculated a small grid at different abundances to find out the systematic shift in abundance to fit the original line strengths. The results of the tests are summarised in Table 1. They correspond to the mean value obtained from a study of the lines $\lambda \lambda $4228, 4771, 5052, 5380, 6013, 6828, 7111, 7115, 9078, 9088, 9111 (C I) and $\lambda \lambda $3918, 4267, 6578, 6582 (C II).

The carbon non-LTE calculations turn out to react sensitively to inaccuracies in the stellar parameters and the atomic data. In general, the stronger lines are more susceptible, as they show stronger non-LTE effects. Changes in the effective temperature and surface gravity affect the delicate ionization balance of C I/II: within the assumed error bars for these parameters, the carbon abundance can be typically fixed only to approximately $\pm$0.1 dex. Inaccuracies in the microturbulent velocity primarily alter the strengths of lines on the flat part of the curve of growth. Effects of an increased microturbulence are therefore small, as most of the lines remain weak in the parameter range of our study. Only the near-IR lines of C I in the main sequence model and the C II lines in the hotter supergiant model are affected, resulting in abundance uncertainties of $\sim$0.15/0.06 dex. A modification of the stellar helium content affects the atmospheric structure (Kudritzki 1973) and considerable enrichment is expected for supergiants (e.g. Meynet & Maeder 2000). We therefore examine the effects of an increased helium abundance (by a typical amount) on the carbon lines: systematically lower abundances result for both ionization stages in all the supergiant models, while the lines in the main-sequence model are insensitive to such a change. In the following estimation of the systematic error we ignore this effect as we explicitly determine the helium abundance and account for it in the model atmosphere computations; unfortunately, this has not been done in most of similar studies found in the literature. Line-blocking effects introduced by metallicity variations on the order of 0.2 dex have a negligible impact on the C I/II line-formation calculations.

Inaccurate gf-values enter the abundance determination linearly, as long as the carbon lines remain weak as is mostly the cases in the present study. Modifications of the collisional-damping widths within a factor of 2 result in irrelevant changes of the line strengths, except for the infrared C I lines in the main sequence model, where small abundance corrections of $\sim$0.05 dex become necessary. No corrections have to be applied for variations in the photoionization cross-sections at the 10% level. On the other hand larger inaccuracies, a factor of 5 for example, strongly affect the lines of the minor ionic species of C I by way of a displaced ionization balance. The infrared C I lines react most sensitively, resulting in abundance corrections of $\sim$0.2 dex. In the hotter supergiant model a similar sensitivity is found for C II $\lambda$4267. Accurate photoionization data are therefore an important ingredient in the non-LTE calculations for carbon. Our model atom significantly improves the situation in comparison with former studies.

In the present work, detailed collisional excitation data are used for the first time for a considerable number of transitions in C I/II. Collisions play an important rôle in the abundance analyses, as is inferred from our test calculations (and as is also stated in previous studies). Even a systematic inaccuracy of a factor 2 in the collisional rates results in a $\sim$0.2 dex change in abundance derived from the C I $\lambda \lambda $ 9061-9111 lines in the main sequence model. This uncertainty increases to $\sim$0.5 dex in abundance, when the collisional rates are varied by a factor of 10. The weaker lines of C I and C II react less sensitively - abundance uncertainties typically amount to less than 0.1 dex. Due to the lower particle densities, accurate collisional data become less important in supergiants. Nevertheless, C II $\lambda$4267 is found to react sensitively to a reduction of the collisional rates in the supergiant models. Practically no influence on line strengths is found for a variation of the collisional ionization rates by an order of magnitude.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1408f4.eps}\end{figure} Figure 4: Non-LTE and LTE ionization balance of carbon for several sample stars of Sect. 4: Vega (solid lines and filled circles, respectively), $\eta $Leo (dotted lines/open circles) and HD92207 (dashed lines/open diamonds). Displayed are the ratios of the total level populations of the three ionization stages n(C I/II/III) to the total carbon population N(C) as a function of Rosseland optical depth $\tau _{\rm R}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1408f5.eps}\end{figure} Figure 5: Same as Fig. 4 for $\beta $Ori.
Open with DEXTER

A further source of systematic error is the continuum placement in the observed spectra. This strongly depends on the S/N ratio obtained. Our estimate in Table 1 should be applicable to high quality data with S/N$\gtrsim$100 only. In general, equivalent widths studies are more susceptible to this systematic error than the spectrum synthesis technique, which also accounts for the continuum regions explicitly.

The total uncertainties are computed from the sum of the squares of the appropriate uncertainties listed above, assuming them to be independent:

\begin{eqnarray*}% \sigma_{\rm sys}^2 & = & \sigma_{T_{\rm eff}}^2+\sigma_{\log ... ...i}^2+\sigma_{\rm [M/H]}^2+\sigma_{\log gf}^2+\sigma_{\rm damp}^2 \end{eqnarray*}



$\displaystyle \hspace{1.4cm} +~\sigma_{\rm rbf}^2+\sigma_{\rm cbb}^2+ \sigma_{\rm cbf}^2+\sigma_{\rm cont}^2.$     (2)

They should be viewed as the (conservative) systematic errors applicable to our non-LTE calculations on C I/II within our methodology (cf. Sect. 2.1). The total uncertainty ( ${\rm systematic}+{\rm statistic}$ on the 1$\sigma$-level) typically amounts to an unsatisfactory $\sim$0.3 dex.

  
3 Discussion

In this section we evaluate the advantages of time-consuming non-LTE calculations over a straightforward LTE analysis for the interpretation of the C I/II spectra of BA-type stars. The nature of the non-LTE effects is discussed for the stars of our test sample in Sect. 4. Next, the influence of the microturbulence parameter on the line formation calculations is studied. Finally, our results are compared with those of previous studies of non-LTE effects for neutral and singly-ionized carbon.

  
3.1 The non-LTE effects

The ionization balance of carbon in the photospheres of typical early A-type stars is displayed in Fig. 4. The dominant ionization stage in the line-formation region is C II, with small admixtures of C I (typically a few parts in a thousand) and C III, the latter showing a strong increase from $\sim$10-7 to 10-3 in fraction with increasing Rosseland optical depth $\tau _{\rm R}$. In the main sequence model, the ionization balance is shifted in favour of the lower ionization stage, due to the larger surface gravity and hence higher particle densities. The impact of an increase in $T_{\rm eff}$ on the ionization balance is shown in Fig. 5 for the late B-type supergiant $\beta $Ori. The changes are in the expected direction, i.e. shifting the balance to the higher ionization stage. In general, the total C II and C III populations are enhanced in non-LTE, while C I becomes overionized.


  
Table 2: Term identifiers.


\begin{displaymath}\begin{tabular}{l@{\hspace{1mm}}rl@{\hspace{.4cm}}l@{\hspace{... ...& $2\element[2]{s}\;\element[][1]{S}$\\ \hline \end{tabular} \end{displaymath}



  
Table 3: Line identification.


\begin{displaymath}\begin{tabular}{llr@{--}lr@{--}l} \hline\\ Ion & $\lambda$\,... ...{p}\;\element[\rm o][2]{P}$ & 86 & 87\\ \hline \end{tabular} \end{displaymath}



  \begin{figure} \par\includegraphics[width=18cm,clip]{ms1408f6.eps}\par\end{figure} Figure 6: Departure coefficients bi for C I/II as a function of Rosseland optical depth $\tau _{\rm R}$ for several of the sample stars of Sect. 4. In addition, data for a main sequence object at solar metallicity is displayed in the upper right panel. The formation depths of the line cores ( $\tau \approx 1$) for several transitions are indicated. Term identifiers and the levels involved in the transitions are found in Tables 2 and 3. For the Vega model, the departure coefficients for the lowest four levels are also shown after setting $J_{\nu }$=$B_{\nu }$ for the photoionization continua (dashed line). No further information on excited C II levels is given for the main-sequence models, as C II lines are absent in their spectra; the analogous argument holds for the excited C I levels in HD92207 and $\beta $Ori.
Open with DEXTER

Departure coefficients bi= $n_i^{\rm NLTE}/n_i^{\rm LTE}$(the ni denoting the level populations) for energy levels i are displayed in Fig. 6 as a function of $\tau _{\rm R}$ for our models of the objects discussed in Sect. 4. In addition, departure coefficients for a Vega-like model at solar elemental composition are also given to study the influence of metallicity on the carbon non-LTE calculations. All the observed C I/II lines in the visual/near-IR originate from fairly high-excited energy levels ($\gtrsim$7.5/14.5 eV). In Table 2, identifiers for the consecutively numbered energy terms of our C I/II model are given and the levels involved in the observed transitions are identified in Table 3.

Deep in the atmosphere, the departure coefficients approach unity as the density increases and collisional processes dominate, enforcing LTE (inner boundary condition). Farther out, non-LTE effects prevail and affect the level populations throughout the bulk of the photosphere. The most striking feature in the main sequence models is the marked underpopulation of the ground state and the energetically close singlet and quintet states, which are coupled collisionally; these four levels are largely decoupled from the remaining C I levels. Photoionizations depopulate these lowest levels efficiently and the departures increase as the line blocking is reduced (Vega model at Z=-0.5 dex vs. the $Z_{\odot}$ model). On the other hand, neglecting the non-LTE radiation field by replacing the mean intensity by the Planck function, $J_{\nu }$=$B_{\nu }$, in the photoionization continua results in a complete relaxation of the situation and the low-energy levels of C I stay close to their detailed-equilibrium value. Therefore, photoionization cross-sections of high accuracy - like those used in the present study - and a realistic radiation field are required to predict the non-LTE effects quantitatively.

The levels at higher excitation show departure coefficients slightly greater than unity in the line-formation region. But they contribute only little to the total C I population, resulting in the net overionization of this ionization stage. As the excitation energy of C I levels approaches the ionization threshold, the departures diminish due to the increasing collisional coupling with the ground state of C II, which is in LTE.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1408f7.eps}\end{figure} Figure 7: Ratio of line source function $S_{\rm L}$ to Planck function $B_{\nu }$ at line centre for diagnostic C I/II lines as a function of $\tau _{\rm R}$ for our models of $\eta $Leo (full lines) and $\beta $Ori (dotted lines). The formation depths of the line cores ($\tau $$\approx $1) are indicated.
Open with DEXTER

In the supergiant models non-LTE effects are increased, due to the lower particle densities and a more intense radiation field. The C I lines are progressively weakened at higher luminosities due to the increasing overionization and become unobservable in the objects at highest luminosity class (for the temperature range under consideration). Departure coefficients for a number of C I levels are therefore displayed for our $\eta $Leo model only, as the situation in HD111613 is found to be similar. The ground state is even more depopulated than in the main sequence case and the collisional coupling of the singlet and quintet terms at low excitation energy is weakened. Again, the more highly excited C I levels show only marginal deviations from LTE populations in the line-formation region.

C II lines become observable in early A-type supergiants and strengthen rapidly with increasing $T_{\rm eff}$. The doublet ground state and the collisionally coupled lowest quartet term remain in detailed balance throughout the depth range covered by our models, as expected for the main ionization stage. The populations of the excited energy levels important for the formation of the observed lines (see Table 3) deviate only marginally from LTE, as in the C I case. A marked overpopulation of the C III ground state is developing at small optical depth.

  \begin{figure} \par\includegraphics[width=7cm,clip]{ms1408f8a.eps}\hspace*{2mm} \includegraphics[width=7cm,clip]{ms1408f8b.eps} \end{figure} Figure 8: Theoretical lineprofiles for the$\eta $ Leo model (Sect. 4) with an increased microturbulence of $\xi $=10kms-1. Solid line: statistical-equilibrium calculation with microturbulence included (Eq. (1)); dotted line: without microturbulence.
Open with DEXTER

The non-LTE abundance corrections for our sample stars, as derived in Tables 5 and 6, are explained by the run of the departure coefficients and the corresponding line source function $S_{\rm L}$ for a given transition. Figure 7 shows the ratio of the line source function to the Planck function for diagnostic lines exemplarily for our models of $\eta $Leo and $\beta $Ori. A non-LTE strengthening of lines will occur for bi>bj, a condition which is met at the formation depths of the observed C I/II lines. Nevertheless, the ratio $S_{\rm L}$/$B_{\nu }$ at line-formation depths stays close to unity, as expected for small departures from detailed balance. The trend of $S_{\rm L}$/$B_{\nu }$ for the other supergiants is similar as in the given case. In our Vega model the departures from the LTE source function occur farther out in the atmosphere, thus affecting only the strongest lines (C I $\lambda \lambda $ 9061-9111).

An evaluation of the physical accuracy of our model atom for carbon turns out to be difficult due to the smallness of the non-LTE departures for levels involved in the observed transitions in the visual and the near-IR. No single process dominates, except for the strong sensitivity of the C I ground state to photoionization. Therefore, the scatter in the abundance found in our analysis, see Sect. 4.3, might be well explained by the remaining - nevertheless small - uncertainties of the atomic data used in our study, see also the scaling experiments on the atomic data in Sect. 2.4.

An additional source of uncertainty will influence our computations, but cannot be accounted for properly in our current approach: interaction of the Lyman series transitions with the C I ground state photoionization and some of the C I resonance lines are expected. This effect can only be handled in a simultaneous and consistent non-LTE treatment of radiative transfer and atmospheric structure calculations. It will primarily affect the four lowest-lying energy levels of C I, which are largely decoupled from the rest model atom, and will impact the emerging flux between Ly$_{\alpha }$ and the Lyman jump. Yet, the more excited energy levels should be only indirectly influenced.

  
3.2 Microturbulence

Microturbulence was originally introduced as a parameter to bring model calculations into better agreement with observation. The concept of some additional non-thermal line-broadening is not physically excluded, despite the lack of a comprehensive theoretical explanation for it at present.

Recently, McErlean et al. (1998) explicitly included microturbulence in the statistical-equilibrium calculations (with DETAIL, Eq. (1)) for helium in OB stars and find significantly different profiles as compared to the standard procedure of including microturbulence only in the final step of the spectrum synthesis (with SURFACE) for microturbulent velocities in excess of 10 km s-1.

This rather subtle effect depends on the details of the ionization balance and on the run of the departure coefficients for a given element (PaperI; Przybilla et al. 2001a, hereinafter PaperII). If the occupation numbers of the levels involved vary significantly over the line-formation depths, the radiative transitions occur under slightly different conditions as the formation depths of the line centres are pushed deeper into the atmosphere but simultaneously the frequency bandwidths for absorption are broadened by the increased microturbulent velocity. Changes in the non-LTE level populations and the line source functions might therefore result for different spectral lines. Hence, lines too weak to react sensitively to microturbulence in the classical sense might also be affected.

In Fig. 8, test calculations for our model of $\eta $Leo with an increased microturbulence are displayed. For the C I $\lambda \lambda $9061-9111 features the equivalent width increases by $\sim$8% as $\xi $is increased from 0 to 10 km s-1 in the statistical-equilibrium computations with DETAIL. The line-formation itself is performed with SURFACE on the basis of the resulting population numbers for $\xi $=10 km s-1 as in the classical approach. Equivalent widths for the other very weak C I lines are also increased, with variations of typically several percent. On the other hand, the (weak) C II lines remain virtually unaffected. For typical microturbulence values (<10 km s-1) found in our sample stars, the magnitude of this effect is reduced and should be negligible for observational data at a typical S/N of $\sim$100. Nevertheless, we prefer to perform our model calculations in a consistent way.

  
3.3 Comparison with other studies

Substantial efforts have been carried out in the past to determine the non-LTE effects on neutral and singly-ionized carbon quantitatively. For C I, Stürenburg & Holweger (1990, 1991) and Takeda (1992) provide extensive data on the early A-type main sequence star Vega and Venn (1995b) applies the Stürenburg & Holweger model to A-type supergiants. We will compare our results with these in the following. Non-LTE effects of C II are discussed exclusively for early-B/late-O stars (Eber & Butler 1988; Sigut 1996) at significantly higher temperatures than in the present work; a direct comparison is therefore not possible. Nevertheless, our model atom closely resembles the C II model of Sigut (1996), thus the present study can be viewed as an extension of that work to lower temperatures and surface gravities.

  
Table 4: Basic properties and atmospheric parameters for the test stars.


\begin{displaymath}\begin{tabular}{llllrrrrrrrrr} \hline HD & Name & Sp.\,Type &... ...$\pm$0.15 & $\pm$0.02 & $\pm$1 & $\pm$5\\ \hline \end{tabular}\end{displaymath}


First, we note that our abundance results for Vega (see Sect. 4.3) agree well with those of Stürenburg & Holweger (1990, 1991) and Takeda (1992), within the error margins. All three model atoms are fairly comprehensive in terms of the energy levels and the processes connecting them. Differences have therefore for the most part to be attributed to the atomic data, and to the physical assumptions used in the computations. In the direct comparison, our present model comprises of more accurate radiative data and detailed collisional data has been used for the first time. Also, the restrictions of fixed rates for the photoionizations have been eased. A number of C I resonance lines are situated at wavelengths where photoionizations from low-lying levels of this ion contribute to the background opacity (see Fig. 3). In principle, the assumption of fixed rates is no longer valid in this case, as the radiation field is now coupled to the statistical equilibrium. On the other hand, these resonance lines are strong - i.e. optically thick in their line-cores - and therefore basically in LTE, resulting in only small corrections to the derived abundances.

The departure coefficients for the three model atoms show qualitatively and quantitatively a similar behaviour in the line-formation region. Farther out, some discrepancies are apparent, in particular for the Stürenburg & Holweger model, but these cannot be verified for physical significance due to a lack of suitable observed lines. The depopulation of the lowest four levels in the Stürenburg & Holweger model is less prominent than in our case. We attribute this to the larger photoionization cross-sections (see Fig. 2) and to the larger number of UV resonance lines included in our model. Takeda's model predicts almost the same depopulations for these levels as does ours.

The supergiants offer a more critical test of non-LTE effects. We have the A0Ib supergiant $\eta $Leo in common with the sample of Venn (1995b) and Takeda & Takada-Hidai (2000). Unfortunately, both works do not provide the details (departure coefficients, line source-functions) that would allow an assessment of the accuracy of the model predictions. But, we confirm the non-LTE abundance corrections of Venn (1995b) for the C I multiplet $\lambda \lambda $ 9061-9111, allowing for small uncertainties due to residuals of Venn's telluric line removal. A similar carbon abundance is derived from an additional C I line accessible due to the higher S/N of our observations and several C II lines, thus indicating that the C I $\lambda \lambda $ 9061-9111 lines are indeed reliable abundance indicators. Venn's conclusion, that this is not the case - as Venn finds a significantly lower mean carbon abundance from these lines in the hotter stars of her sample (spectral classes A2-A0) than in the cooler F0-A3 types - has therefore to be reconsidered. An alternative explanation is indeed suggested by the new stellar evolution calculations including rotation (Meynet & Maeder 2000): a stronger depletion of carbon is expected for the more massive objects on the mean and in particular for objects performing a blue-loop at first dredge-up abundances. By coincidence, the hotter stars in Venn's sample are the more massive ones ($\gtrsim$10 $M_{\odot}$), cf. Table 6 in Venn (1995a), while the cooler are less massive ($\sim$5-8 $M_{\odot}$). A (re)analysis of a larger sample of carefully selected objects, for the more sensitive mixing indicator of nitrogen as well, might clarify this question. Moreover, in the particular case of $\eta $Leo, we find a high nitrogen abundance and also considerably enhanced helium (cf. Sect. 4.3), which both favour a low carbon abundance in terms of stellar evolution models. But no final conclusion can be drawn here as our calculations still show some discrepancies between the C I and C II abundances - nevertheless within the error margins - and there is also some indication of a strong sensitivity of the C I $\lambda \lambda $ 9061-9111 features to the atomic data used in the carbon model, which despite considerable improvements are not perfect. The comparison of our results for $\eta $Leo with those of Takeda & Takada-Hidai (2000) is even further inhibited due to the different temperature scales used in both studies, see Sect. 4.4.


  
Table 5: Abundance analysis for carbon in Vega.


\begin{displaymath}\begin{tabular}{lrrlr@{\hspace{0.1mm}}lrrr} \hline & & & & & ... ...\sigma$ & & & & & & & 0.11 & 0.10\\ [1.5mm] \hline\end{tabular}\end{displaymath}

Accuracy indicators: B: 10%, C: 25%, D: 50%. Sources of the gf values: OP: Opacity Project data, Luo & Pradhan (1989); WFD: Wiese et al. (1996). Entries in italics are not used in the determination of means and standard deviations. These are given for the non-LTE/LTE case.

  
4 Application to observations

4.1 The spectra

As a test and first application of the model atom, carbon abundances for five objects are determined: the main sequence star Vega (HD172167) and the supergiants $\eta $Leo (HD87737), HD111613, HD92207 and $\beta $Ori (HD34085). High-S/N and high-resolution spectra are used in this process, obtained with FEROS (Kaufer et al. 1999) at the ESO 1.52 m telescope in La Silla and FOCES (Pfeiffer et al. 1998) at the Calar Alto 2.2 m telescope. Detailed information on the spectra and data processing for three of the stars are given in PaperII.

Two additional FEROS spectra are analysed in the present work. A 10min exposure for HD111613 was obtained during the observing run in January, 1999. We also selected a publicly available spectrum of $\beta $Ori (#0783, 20s exposure), taken during Commissioning II time in November, 1998. Both spectra were processed like the other FEROS data. A S/N of several hundred is achieved, like in the case of the other three sample stars.

4.2 Determination of stellar parameters

The accuracy of an abundance analysis depends critically on the determination of precise stellar parameters (see Sect. 2.4). A purely spectroscopic approach is chosen for the present work, in order to avoid the restrictions encountered in any (spectro)photometric technique, namely inevitable extinction corrections and the lack of reliable photometric calibrations for the supergiants of interest.


  
Table 6: Abundance analysis for carbon in the supergiants.


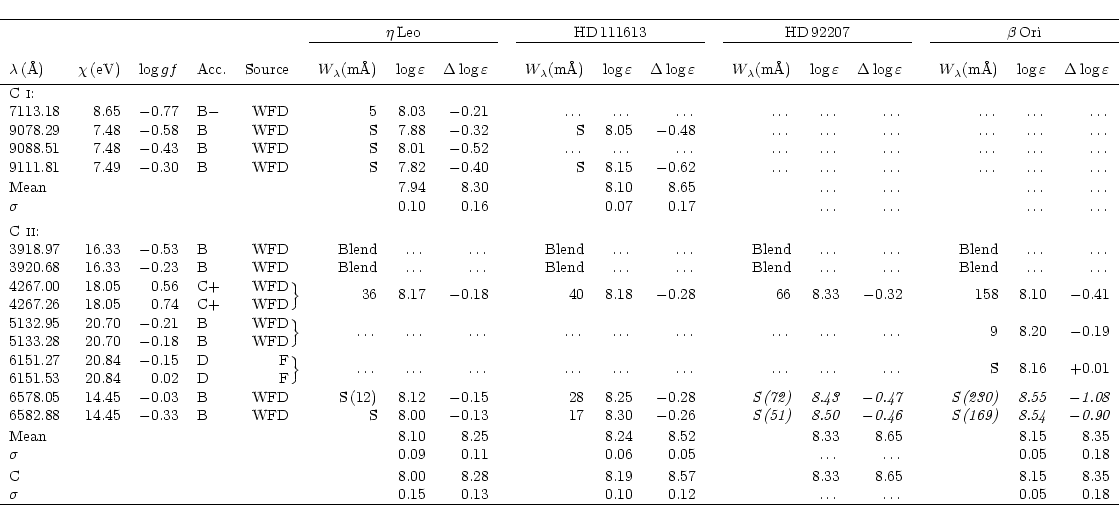
\begin{displaymath}\begin{tabular}{lrrlr@{\hspace{0.1mm}}lrrrrrrrrrrrrrrr} \hlin... ... & {\ldots} & {\ldots} & & & 0.05 & 0.18\\ \hline\end{tabular}\end{displaymath}

Sources of the gf values: F: Opacity Project data, Fernley et al. (available electronically from TOPBASE). See Table 5 for additional notes.

For the supergiants with well developed Mg I lines ($\eta $Leo and HD111613), stellar parameters are derived by the method described in PaperII. In brief, $T_{\rm eff}$ and $\log g$ are determined simultaneously by finding the ionization equilibrium of Mg I/II and by fitting the wings of the higher members from the Balmer series (typically from $\mbox{H}_{\gamma}$ upwards). After several steps to bring all parameters to convergence, values for effective temperature, surface gravity, helium content y (by number, from the application of the He I model atom of Husfeld et al. 1989), microturbulence $\xi $, metallicity and non-LTE abundances for the important background opacity species (see Sect. 2.3) are established. Rotational velocities $v\sin i$ and the radial-tangential macroturbulent velocity $\zeta_{\rm RT}$ are determined from the spectrum synthesis.

The same procedure is used for the parameter determination of $\beta $Ori and HD92207, except that the Mg I/II ionization equilibrium is replaced by that of N I/II (PaperIII). For HD92207, this implies some changes (see Paper III for details) in the stellar parameters as compared to those from PaperII, but the new values give an overall better concordance of theory and observation for this star. In addition, a consistent temperature for $\beta $Ori is found from the O I/II and S II/III equilibria and also from the N I/II balance in the case of in $\eta $Leo and HD111613. Finally, the atmospheric model of Castelli & Kurucz (1994) is adopted for Vega.

For the sample stars with C I and C II lines, it would also be desirable to include the carbon ionization equilibrium for the stellar parameter determination, but we refrain from this due to the comparatively large uncertainties involved (see Sect. 2.4). Nevertheless, the carbon abundances from both ionization stages agree for our models of $\eta $Leo and HD111613, within the 1$\sigma$-error bars ( ${\rm random}+{\rm systematic}$).

The basic properties and atmospheric parameters of the test stars are summarised in Table 4, together with the error estimates. Information on the basic properties are adopted from the Simbad database at CDS.


  \begin{figure} \par\resizebox{.33\hsize}{!}{\includegraphics{ms1408f9a.eps}}\hfi... ...ps}}\hfill \resizebox{.33\hsize}{!}{\includegraphics{ms1408f9o.eps}}\end{figure} Figure 9: Spectrum synthesis for selected C I/II lines in the test stars. Abscissa units are wavelengths in Å, ordinate is relative flux. Observed (thin solid) and computed (thick solid) non-LTE profiles for the mean carbon abundances in Tables 5 and 6 are displayed with line identifiers. Profiles for the appropriate LTE abundances are marked by a dotted line. Line formation for species other than H I, He I, C I/II, N I/II, O I/II, Mg I/II, S II/III, Ti II, Fe II is performed assuming LTE level populations (see PaperIV for details). The spectra in the red are contaminated by numerous sharp telluric lines. For the C II $\lambda \lambda $6578-82 features and C I $\lambda \lambda $9061-9111 in Vega, the local continuum is determined by the H$_{\alpha }$ wing and a far Paschen line wing, respectively.
Open with DEXTER

  
4.3 Abundance analysis

The results of the abundance analysis for carbon are summarised in Tables 5 and 6 which give the wavelength, excitation potential of the lower level and the adopted gf value for the observed lines, with accuracy indicators and sources for the gf values. Measured equivalent widths, derived non-LTE abundances

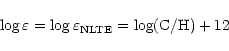\begin{displaymath}% \log \varepsilon = \log \varepsilon_{\rm NLTE} = \log ({\rm C}/{\rm H})+12 \end{displaymath} (3)

and non-LTE abundance corrections

\begin{displaymath}% \Delta\log \varepsilon = \log \varepsilon_{\rm NLTE} - \log \varepsilon_{\rm LTE} \end{displaymath} (4)

for the different stars are also displayed. Blended lines are marked by "S'' as long as an analysis via spectrum synthesis is still feasible. For lines originating in the hydrogen line wings the equivalent widths are measured against the local continuum ( $W_{\lambda}$ in parentheses). Non-LTE and LTE mean values and the line-to-line scatter ($\sigma$) are displayed separately for C I and C II, as is the combined carbon abundance. Note that the abundances are derived from the detailed spectrum synthesis results and not from an equivalent-width study. Non-LTE effects strengthen the C I/II lines systematically, thus the derived abundances decrease.

In Fig. 9 theoretical line profiles for the derived mean non-LTE carbon abundance are compared with the observations; good agreement is found. For comparison, profiles from the mean LTE abundance are also shown, which also give satisfactory fits, as the random errors are only slightly increased and the systematics due to rising departures from LTE with line strength are moderate. As some of the carbon lines are formed in the wings of H I lines, profiles for hydrogen are calculated on the basis of non-LTE level populations. Apart from these, the following elements are treated in non-LTE to account for line blends: He I (Husfeld et al. 1989), N I/II (PaperIII), O I/II (PaperI; Becker & Butler 1988), Mg I/II (PaperII), S II/III (Vrancken et al. 1996) and Ti II and Fe II (Becker 1998), with updated atomic data for some of the older models. The remaining elements are included in LTE for the spectrum synthesis. This allows almost the entire observed spectra to be reproduced and we can cross-check our carbon results with the blended C II features $\lambda \lambda $3918-20, which also match well for the derived mean carbon abundance. Fe I is expected to show a notable non-LTE overionization; indeed, the Fe I lines appear systematically too strong in our spectrum synthesis. A detailed study of the test stars is performed elsewhere (PaperIV).


  
Table 7: Light element abundances for the sample stars.


\begin{displaymath}\begin{tabular}{lr@{\hspace{1mm}$\pm$\hspace{1mm}}lr@ {\hspac... ...$-$0.03 & 0.05\,(11) & $\pm$0.00 & 0.04\\ \hline \end{tabular}\end{displaymath}

$^{\rm a}$PaperIV; $^{\rm b}$this work; $^{\rm c}$PaperIII; $^{\rm d}$PaperI.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig10.eps}\end{figure} Figure 10: Spectral region around H$_{\alpha }$ with prominent C II lines. The spectrum of HD92207 is shifted vertically by 0.4 units. Note that the C II lines are formed in the photospheric H$_{\alpha }$ wing, which is masked by subsequent (incoherent) electron scattering occuring in the extended stellar wind.
Open with DEXTER

For C II $\lambda \lambda $6578-82, we observe an increasing discrepancy between our model predictions and observations for increasing luminosity and line strength. The spectral region around H$_{\alpha }$ for luminous supergiants can only be properly modelled in a hydrodynamical approach, as it is dominated by stellar wind emission. In Fig. 10 observed spectra of H$_{\alpha }$ of the two most luminous supergiants in our sample are displayed, showing the typical P-Cygni profile and extended incoherent electron scattering wings (see McCarthy et al. 1997 for a discussion of this effect), with the C II lines embedded in these wings.

The increasing discrepancy might arise from weaknesses in our model atom, see Sect. 3.1. Alternatively, unaccounted effects might influence the line source-function of C II $\lambda \lambda $6578-82, namely the sphericity of the extended atmosphere and the velocity field due to the accelerating stellar wind. The former will dilute the radiation field, thus depressing the line source-function through photon escape, and the latter will desaturate the lines due to the Doppler shift experienced in the moving medium (Kudritzki 1992), resulting in a strengthening of the lines. Yet, a conclusive answer cannot be given within our present approach.

In Table 7 the results from the abundance analysis of the light elements (He, CNO) in the sample stars relative to the solar composition (Grevesse & Sauval 1998) are summarised, $[X/{\rm H}] = \log (X/{\rm H})_{\star} - \log (X/{\rm H})_{\odot}$, as needed in the subsequent discussion. We list the values obtained from the non-LTE analysis together with the 1$\sigma$-uncertainties from the line-to-line scatter and in the case of carbon from the systematic errors as well, cf. Sect. 2.4. The total number of analysed lines is given in parentheses. In the last column the sum of CNO in the sample stars relative to solar is diplayed.

Vega shows a carbon deficiency of 0.29 dex. This is comparable to the underabundance of other light elements but less then the typical $\sim$0.5 dex deficit of the heavier elements, which leads to the conclusion that Vega is a mild $\lambda$Bootis star (Venn & Lambert 1990).

The four supergiants in our sample show deficiencies in the carbon abundance, ranging from 0.2 to 0.5 dex below the solar value. This finding is in excellent accord with the predictions of the new stellar evolution models accounting for rotation (Meynet & Maeder 2000; Heger & Langer 2000), in particular, as a marked overabundance of nitrogen - and to smaller degree of helium - is also found in these objects, while the sum of the CNO abundances remains close to solar. CN-processed matter has apparently been mixed to the surface layers. The striking fact that the sample supergiant at lowest luminosity and therefore lowest mass, $\eta $Leo, shows the strongest carbon depletion (and a corresponding nitrogen enhancement) indicates a blue-loop scenario for this star, with a first dredge-up N/C ratio, cf. the 9$M_{\odot}$- approx. $\eta $Leo's mass - evolutionary track of Meynet & Maeder (2000). On the other hand, the remaining three supergiants seem to have evolved directly from the main sequence, see PaperIV for a further discussion.

  
4.4 Comparison with other analyses

In the following, our results for the sample stars are compared with those of other recent analyses. The abundance data are summarised in Table 8.


  
Table 8: Comparison of C I/II abundance determinations for the test stars.


\begin{displaymath}\begin{tabular}{lllll} \hline Source & $\log\varepsilon_{{\rm... ...8.02\pm0.05$\,(2) & {\ldots} & {\ldots}\\ \hline \end{tabular}\end{displaymath}


Listed are the abundances with 1$\sigma$ errors from the line-to-line scatter (number of lines analysed in parenthesis).


Vega
Vega is an important photometric standard and has therefore been the subject of several abundance studies. Practically all work concentrates on the weak lines in the visible and on the stronger features in the near-IR. The analyses of Venn & Lambert (1990) and Adelman & Gulliver (1990) are based on their own observations, whereas Takeda (1992) and Stürenburg & Holweger (1991) use the equivalent widths of Lambert et ²al. (1982). In general, the measured $W_{\lambda}$ agree well. Deviations from the stellar parameters used in the present work are small (they agree within the error bars), thus leading to comparable abundances. Differences in the gf values used for the analysis explain the discrepancies in the carbon abundances derived by Venn & Lambert (1990) and Lambert et al. (1982).

Our observations do not include the strong C I lines slightly longward of 1$\mu$. Adopting the equivalent width measurements of Lambert et al. (1982), we derive non-LTE abundances from these lines consistent with the results of Sect. 4.3. The strong lines show a marked non-LTE strengthening.

$\eta $ Leo
This A0Ib standard has also been a target for detailed abundance studies. In their recent non-LTE/LTE study, Takeda & Takada-Hidai (2000) find a C I abundance barely consistent with the results of the present study. The higher abundance is likely explained by their choice for the effective temperature ( $T_{\rm eff}$=10200K) with $\log g$ and $\xi $ values differing only slightly from our findings and the gf values being identical. Takeda's & Takada-Hidai's C II LTE abundance from the $\lambda$4267 feature can also be interpreted by the choice of an inappropriate $T_{\rm eff}$. Applying a non-LTE correction for this line would even worsen the situation, leading to the conclusion that the ionization balance for C I/II is violated in that work. On the other hand, Takeda & Takada-Hidai adopt gf values for this C II feature approx. 10% larger than ours, which leads to a slightly reduced abundance.

Venn (1995b) uses the Stürenburg & Holweger (1990) C I model to derive the carbon abundance for gf values and stellar parameters almost identical with those of the present work. Thus, the LTE and non-LTE abundances in both studies are in excellent agreement.

Only upper limits for the LTE abundance are given by Lambert et al.(1988). Lambert et al. do not provide enough details on their line-formation calculations but as their $T_{\rm eff}$ value exceeds ours by 900K some of the abundance discrepancy can be understood at least qualitatively. The same argument ( $T_{\rm eff}+800$K) applies to the result of Wolf (1971) who derives an LTE carbon abundance from the C II $\lambda$4267 feature. Moreover, Wolf's equivalent width measurement from the photographic data exceeds our value by 40%.

$\beta $ Ori
The B8Iae standard has not been studied for chemical abundances until recently. Takeda & Takada-Hidai (2000) derive a significantly lower C II LTE abundance from two lines in common with our analysis. The difference results most likely from Takeda's & Takada-Hidai's choice of stellar parameters. Their model is hotter by 1000K and the surface gravity is increased by 0.25dex, whereas the gf values agree well. In addition, McErlean et al. (1999) find a normal CN composition from a medium-resolution spectrum without giving further details.

  
5 Summary and conclusions

An extensive model atom for non-LTE line-formation calculations for neutral and singly-ionized carbon has been developed, based on the most accurate atomic data presently available. It allows the determination of carbon abundances with better accuracy than the models of previous studies; moreover, the influence of systematic error sources has also been estimated. Typical uncertainties (random+systematic) in the abundance determination from both ionic species are of the order 0.2-0.3 dex, for main sequence objects and supergiants of early-A and late-B spectral types alike. The ionization equilibrium of C I/II is therefore of restricted use for the determination of stellar parameters.

We have analysed high-quality observations for a sample of five objects. The following carbon abundances are derived:
Vega $\log ({\rm C/H})+12=8.23\pm0.11\pm0.15$ (22)
$\eta $Leo $\log ({\rm C/H})+12=8.00\pm0.15\pm0.15$ (7)
HD111613 $\log ({\rm C/H})+12=8.19\pm0.10\pm0.15$ (5)
HD92207 $\log ({\rm C/H})+12=8.33\pm0.15$ (1)
$\beta $Ori $\log ({\rm C/H})+12=8.15\pm0.05\pm0.15$ (3).
Our results support the claims for an underabundance of the light elements in Vega by $\sim$0.3 dex, in contrast to the $\sim$0.5 dex underabundance of the refractory ($\alpha$- and iron-peak) elements. For the supergiants, a carbon depletion of the order of 0.2-0.5 dex below solar is found, indicating the mixing of CN-cycled matter into atmospheric layers, as the sum of the CNO abundances remains close to solar. This observational finding is in excellent accordance with the predictions of the new stellar evolution calculations accounting for mass-loss and rotation. Our model calculations match the observed profiles well.

Marked non-LTE abundance corrections (up to 0.8 dex) are found for the strongest C I features at $\lambda \lambda $ 9061-9111 only. These lines and C II $\lambda$4267 also show a sensitivity to the atomic data used in the model atom. Our model computations for a mean C II abundance, as obtained from the other doublet and quartet lines, reveal an increasing discrepancy in the C II doublet $\lambda \lambda $6578-82 with rising luminosity, when compared with the observations. The reason for this and the exact driving mechanisms for the non-LTE effects in both, C I and C II, are difficult to identify, due to the smallness of the departures in the line-formation region. No single process dominates, instead the results depend on the details of the atomic data as a whole. An exception to this is the large depopulation of the four lowest energy levels of C I, which is triggered by photoionizations. The explicit consideration of the microturbulence parameter in the statistical-equilibrium calculations is of minor importance for carbon in the range of stellar parameters studied.

Acknowledgements
We are grateful to A. Kaufer for his help with obtaining some of the spectra at La Silla and to S. Tubbesing for his help with the data reduction. Our work has benefitted from the beautiful spectrum of Vega contributed by A. Korn. We would further like to thank J. Puls for helpful discussions and K. M. Dunseath, V. M. Burke, R. H. G. Reid and A. K. Pradhan for providing extended tabulations of collisional data in digital form. Funding through the MPIA, Garching, is gratefully acknowledged (NP). This research has made use of the Simbad database, operated at CDS, Strasbourg, France.

References

 
Copyright ESO 2001