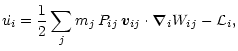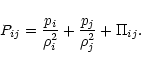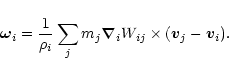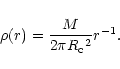A&A 379, 1123-1137 (2001)
DOI: 10.1051/0004-6361:20011352
SPH simulations of clumps formation by dissipative
collisions
of molecular clouds
II. Magnetic case
E. P. Marinho1 -
C. M. Andreazza1 - J. R. D. Lépine2
1 - Instituto de Geociências e Ciências Exatas, Departamento de
Estatística, Matemática Aplicada e Computação, UNESP, Rua 10, 2527, 13500-230 Rio Claro SP, Brazil
2 -
Instituto Astronômico e Geofísico,
Departamento de Astronomia, USP,
Av. Miguel Stefano, 4200,
04301-904 São Paulo SP, Brazil
Received 15 Mars 2001 / Accepted 24 September 2001
Abstract
We performed computer simulations of interstellar cloud-cloud collisions
using the three-dimensional smoothed particle magnetohydrodynamics
method.
In order to study the role of the magnetic field on the process of
collision-triggered fragmentation, we focused our attention on head-on
supersonic collisions between two identical spherical molecular-clouds.
Two extreme configurations of the magnetic field were adopted: parallel and
perpendicular to the initial clouds motion.
The initial magnetic field strength was approximately 12.0 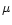 G.
In the parallel case, much more of the collision debris were retained in the
shocking region than in the non-magnetic case where gas escaped freely
throughout the symmetry plane.
Differently from the non-magnetic case, eddy-like vortices were formed.
The regions of highest vorticity and
the the regions of highest density are offset.
We found clumps formation only in the parallel case, however, they were
larger, hotter and less dense than in the analogous non-magnetic case.
In the perpendicular case, the compressed field works as a magnetic wall,
preventing a stronger compression of the colliding clouds.
This last effect inhibits direct contact of
the two clouds.
In both cases, we found that the field lines show a chaotic aspect in large
scales.
Also, the field magnitude is considerably amplified in the shock layer.
However, the field distribution is almost coherent in the higher density
regions.
G.
In the parallel case, much more of the collision debris were retained in the
shocking region than in the non-magnetic case where gas escaped freely
throughout the symmetry plane.
Differently from the non-magnetic case, eddy-like vortices were formed.
The regions of highest vorticity and
the the regions of highest density are offset.
We found clumps formation only in the parallel case, however, they were
larger, hotter and less dense than in the analogous non-magnetic case.
In the perpendicular case, the compressed field works as a magnetic wall,
preventing a stronger compression of the colliding clouds.
This last effect inhibits direct contact of
the two clouds.
In both cases, we found that the field lines show a chaotic aspect in large
scales.
Also, the field magnitude is considerably amplified in the shock layer.
However, the field distribution is almost coherent in the higher density
regions.
Key words: methods: numerical - MHD - ISM: clouds -
ISM: molecules - ISM: magnetic field
The star-formation activity in NGC 1333 (Loren 1976),
W49N
(Miyawaki et al. 1986;
Serabyn et al. 1993;
Buckley & Ward-Thompson 1996),
SgrB2 (Hasegawa et al. 1994),
and in the cometary cloud G110-3
(Odenwald et al. 1992),
among other
star-forming regions, has been interpreted in terms of star formation
triggered by collision between interstellar clouds.
On the other hand, there are observational
evidences that cloud-cloud collision may occur without star-formation,
as in
Heiles 2 (Little et al. 1978),
Draco nebula (Rohlfs et al. 1989),
LVC 127 (Meyerdierks 1992),
and
in IRAS 2306+1451 (Vallée 1995),
for instance.
These observational results show that the study of interstellar
cloud collisions is of
great importance not only to understand in what conditions
they can trigger star formation, but also
to understand how does cloud-cloud collision affect the structure and evolution
of the interstellar medium.
Several analytical and numerical hydrodynamics studies of collisions between
interstellar clouds have been made to investigate different aspects of this
process
(Stone 1970a, 1970b;
Hausman 1981;
Gilden 1984;
Lattanzio et al. 1985;
Keto & Lattanzio 1989;
Habe & Ohta 1992;
Pongracic et al. 1992;
Kimura & Tosa 1996;
Ricotti et al. 1997;
Miniati et al. 1997;
Klein & Woods 1998;
Marinho & Lépine 2000).
The final outcome of an individual collision event, like
disruption, coalescence, fragmentation, and star formation, depends on
many factors, like the density, shape and size of the clouds, their
relative velocity and impact parameter, and on the details of
the gas cooling mechanism, which in turn depends on metallicity etc.
Very few works have been addressed to magnetized cloud-cloud
collisions.
In their previous attempts to model the interactions between
diffuse magnetized clouds,
Clifford & Elmegreen (1983)
found that the magnetic
field enhances the exchange of momentum between clouds,
so that the effective cross
section is larger than the cloud's geometric cross section.
Elmegreen (1988)
studied collision fronts of magnetized clouds,
and showed an enhancement on both the density and the probability of
gravitational collapse in the parts
of molecular clouds that are
compressed parallel to the mean field.
In contrast, he found that the
collisional dissipation and the compression are small for the parts of
the clouds that are compressed perpendicular to the field.
More recently, using a two-dimensional magnetohydrodynamical model,
Miniati et al. (Miniati et al. 1999) simulated a head-on collision of two identical
diffuse clouds,
with a weak magnetic field (1.2 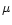 G).
They found that the cloud-cloud collision with the initial field lines oriented
parallel to the clouds velocity leads to almost complete coalescence of the
clouds, and that the clouds moving perpendicular to the initial magnetic
field forms a magnetic shield in front of both clouds.
This last effect inhibits direct contact of
the two clouds.
Finally,
Santillán et al. (1999)
simulated collisions of high velocity clouds
with a magnetized galactic disk, at different incidence angles and velocities,
and showed that the interactions
prevent the mass exchange between the halo
and the disk.
The collision can transform a high-velocity inflow into an
outflow with vertical gas structures.
These results indicate a strong
influence of the magnetic field when it is perpendicular to cloud
relative velocity.
G).
They found that the cloud-cloud collision with the initial field lines oriented
parallel to the clouds velocity leads to almost complete coalescence of the
clouds, and that the clouds moving perpendicular to the initial magnetic
field forms a magnetic shield in front of both clouds.
This last effect inhibits direct contact of
the two clouds.
Finally,
Santillán et al. (1999)
simulated collisions of high velocity clouds
with a magnetized galactic disk, at different incidence angles and velocities,
and showed that the interactions
prevent the mass exchange between the halo
and the disk.
The collision can transform a high-velocity inflow into an
outflow with vertical gas structures.
These results indicate a strong
influence of the magnetic field when it is perpendicular to cloud
relative velocity.
It is increasingly clear that the magnetic field is a crucial component of
the physics governing the evolution of interstellar clouds and star formation.
Magnetic fields have been detected throughout our Galaxy.
Observations suggest that the overall direction of polarization is roughly
parallel to the galactic disk (e.g. Zeldovich et al. 1983).
Moreover, the field is found to consist of an ordered component,
which is coherent over a few kiloparsecs, and a disordered or turbulent
component, which varies on scales as small as a few parsecs or less
(e.g. Zweibel 1999).
The field intensity of both components
is estimated to be about 2 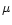 G
(Heiles 1996).
The Zeeman measurements of magnetic field are found in the range
of 7 to 16
G
(Heiles 1996).
The Zeeman measurements of magnetic field are found in the range
of 7 to 16 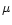 G
(Crutcher 1999)
in dark clouds,
3 to 12
G
(Crutcher 1999)
in dark clouds,
3 to 12 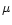 G in diffuse clouds (Myers et al. 1995; Heiles 1997), and
14 to 3100
G in diffuse clouds (Myers et al. 1995; Heiles 1997), and
14 to 3100 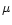 G in regions of massive star formation
(Crutcher 1999).
Also, strong magnetic fields are observed in shocks associated with
expanding interstellar shells, such as the Eridanus shell
(Heiles 1987).
The polarization data available for some dark clouds show
that the field is roughly oriented perpendicular to the projected cloud
elongation
(Heyer et al. 1987;
Strom et al. 1988).
However, in other dark clouds, the
field direction is roughly parallel to the dense filaments (Vrba et al. 1976;
Vrba et al. 1988).
Finally, for same regions such as R CrA cloud,
much more chaotic magnetic fields are observed (Vrba et al. 1981).
G in regions of massive star formation
(Crutcher 1999).
Also, strong magnetic fields are observed in shocks associated with
expanding interstellar shells, such as the Eridanus shell
(Heiles 1987).
The polarization data available for some dark clouds show
that the field is roughly oriented perpendicular to the projected cloud
elongation
(Heyer et al. 1987;
Strom et al. 1988).
However, in other dark clouds, the
field direction is roughly parallel to the dense filaments (Vrba et al. 1976;
Vrba et al. 1988).
Finally, for same regions such as R CrA cloud,
much more chaotic magnetic fields are observed (Vrba et al. 1981).
In this paper,
we investigate the collision between two identical
magnetized clouds,
using a three-dimensional smoothed particle magnetohydrodynamics (SPMHD)
code.
The clouds are initially an intermediate stage between homogeneous and
isothermal gas distribution.
We considered only supersonic collisions, which are the most common case in the
interstellar medium (Spitzer 1978).
We focused our attention on head-on collisions because they were the only case
where dense clumps were formed in previous hydrodynamics calculations
(Marinho & Lépine 2000, hereafter Paper I).
Two extreme field orientations were adopted:
parallel and perpendicular to the relative motion of the clouds.
The primary motivation of this paper is to investigate the
three-dimensional effects of the magnetic field on the dynamics of
cloud-cloud collision,
so that we can compare the present results with the analogous
non-magnetic case (Paper I).
2 Numerical methods
The present model for self-gravitating clouds motion is governed by the
compressible MHD equations, where the displacement current and
the effects of electrical resistivity,
as well as separation of ions and electrons, are neglected.
This can be reduced to the following Lagrangian equations:
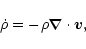 |
(1) |
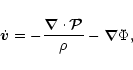 |
(2) |
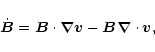 |
(3) |
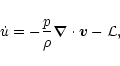 |
(4) |
where
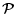 is the negative-definite stress tensor,
is the negative-definite stress tensor,
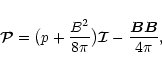 |
(5) |
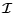 is the three dimensional unity tensor,
is the three dimensional unity tensor,
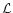 is the energy loss term, and
is the energy loss term, and 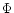 is the self-gravitational
potential that is calculated by the Barnes & Hut (1986) tree method.
is the self-gravitational
potential that is calculated by the Barnes & Hut (1986) tree method.
Equation (1) is not necessarily used along
with the integration
scheme since densities only depend on particles positions by means
of the nearest neighbor searching scheme (NNS), as described in Paper I.
Thus, updating positions is equivalent to update densities.
Regarding time saving, it may be useful to minimize the number
of NNS-calls on predicting the smoothing lengths by explicitly
integrating Eq. (1) (see Paper I and references
therein).
One important plasma kinematic information is the vorticity vector
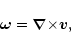 |
(6) |
which expresses the local fluid rotation rate,
and it is connected with the magnetic field by means
of the magnetic induction, Eq. (3),
which can be written as
(e.g., Polygiannakis & Moussas 1999)
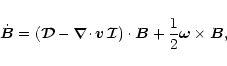 |
(7) |
with
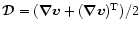 being the
strain-rate tensor.
being the
strain-rate tensor.
The term
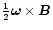 causes the magnetic field to wind about the vorticity vector,
but does not affect its magnitude.
On the other hand, the term
causes the magnetic field to wind about the vorticity vector,
but does not affect its magnitude.
On the other hand, the term
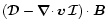 causes an exponential
magnetic-field increase under gas compression, or decrease
under gas expansion.
In fact,
for t much smaller than the typical time
scales,
the field magnitude grows
as
causes an exponential
magnetic-field increase under gas compression, or decrease
under gas expansion.
In fact,
for t much smaller than the typical time
scales,
the field magnitude grows
as
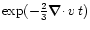 if only the term
if only the term
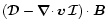 is taken into account.
is taken into account.
Analogously, the plasma forces
can affect the vorticity in a similar way as in
Eq. (7).
With some algebra, extracting the curl from both sides of Eq. (2),
we have the vorticity rate given by
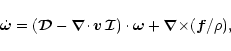 |
(8) |
where
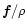 is the right-hand side of Eq. (2).
is the right-hand side of Eq. (2).
The term
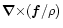 is much more complex than the term
is much more complex than the term
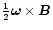 in Eq. (7).
However, we can affirm that the term
in Eq. (7).
However, we can affirm that the term
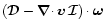 causes an exponential vorticity increase or decrease analogous to
the magnetic field case.
causes an exponential vorticity increase or decrease analogous to
the magnetic field case.
The smoothed particle magnetohydrodynamics (SPMHD) equations
are derived in the usual approach of writing symmetrically the
smoothed particle gradient (divergence and curl)
in order to allow momentum conservation (see, e.g.,
Monaghan 1992 for a review).
We adopted a symmetrized form
of the B-spline kernel as in Paper I. The smoothing lengths
are spherically defined by means of the octal-tree based
on NNS (see Paper I and references therein).
We define the following tensor:
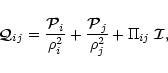 |
(9) |
where
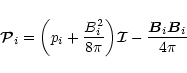 |
(10) |
and 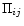 is the pairwise
artificial-viscosity coefficient (e.g., Monaghan 1992).
SPH densities,
is the pairwise
artificial-viscosity coefficient (e.g., Monaghan 1992).
SPH densities, 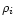 ,
are estimated by the traditional approach (see,
e.g., Monaghan 1992).
,
are estimated by the traditional approach (see,
e.g., Monaghan 1992).
Equation (9) is quite useful for notation saving and also
it allows the modularity used in our MHD subroutines.
The artificial-viscosity coefficient 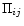 is
written to reproduce Alfvénic shocks in the stability
limit of the time integrator.
Analogously to the Monaghan & Gingold (1983) artificial viscosity,
we defined the SPMHD artificial viscosity as
is
written to reproduce Alfvénic shocks in the stability
limit of the time integrator.
Analogously to the Monaghan & Gingold (1983) artificial viscosity,
we defined the SPMHD artificial viscosity as
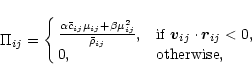 |
(11) |
where
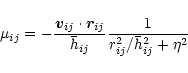 |
(12) |
and the coefficient
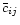 is defined as
is defined as
![\begin{displaymath}
\bar{c}_{ij}=
\biggl[
\bar s_{ij}^2+
\frac
{\vert\bar{\vec B...
...{ij}\vert
\right)^2}
{4\pi\bar{\rho }_{ij}}
\biggr]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2001/45/aa1280/img30.gif) |
(13) |
As in other works (e.g., Hernquist & Katz 1989), the following convention,
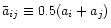 and
and
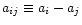 ,
is used in Eqs. (2)-(12).
,
is used in Eqs. (2)-(12).
The term
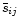 in the right-hand side of
Eq. (12) is the mean adiabatic sound
speed for particles i and j respectively,
and the magnetic term resembles the square of
the Alfvén speed
in the right-hand side of
Eq. (12) is the mean adiabatic sound
speed for particles i and j respectively,
and the magnetic term resembles the square of
the Alfvén speed
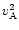 ,
but it equals zero for particles with relative velocity
,
but it equals zero for particles with relative velocity
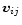 parallel to the mean magnetic field
parallel to the mean magnetic field
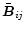 ,
and it is maximum for particles
with relative velocity
,
and it is maximum for particles
with relative velocity
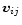 perpendicular to the mean
magnetic field
perpendicular to the mean
magnetic field
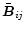 .
.
The SPMHD equations are given by
0pt
1.75pt
where
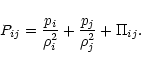 |
(17) |
The SPH-vorticity vector,
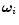 ,
is calculated from the
interpolated curl (see, e.g., Monaghan 1992):
,
is calculated from the
interpolated curl (see, e.g., Monaghan 1992):
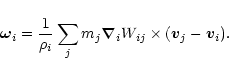 |
(18) |
Equations (13)-(15) can be easily adapted to the
integration scheme as described in Paper I.
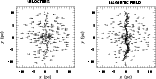 |
Figure 1:
Velocity (left panel) and magnetic
field (right panel)
configurations of a z=0 slice with 0.5 pc in thickness
at t=1.5 Myr in the parallel case.
The arrows indicate the field direction
and the length is
proportional to the field's magnitude. |
| Open with DEXTER |
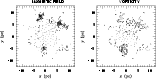 |
Figure 3:
The zy-projection of the magnetic field 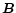 (left panel)
inside an x=3 pc slice with 0.5 pc in thickness,
and the SPH vorticity
(left panel)
inside an x=3 pc slice with 0.5 pc in thickness,
and the SPH vorticity
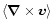 (right panel)
at t=2.5 Myr in the parallel case.
(right panel)
at t=2.5 Myr in the parallel case. |
| Open with DEXTER |
 |
Figure 4:
The SPH vorticity
projected onto the zy-plane at t=2.5 Myr (left panel) and
t=4.0 Myr (right panel), respectively,
in the parallel case. |
| Open with DEXTER |
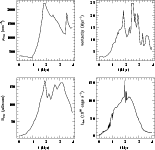 |
Figure 5:
The evolution (parallel case)
of the maximum values for
density (H cm-3),
vorticity (Myr-1),
magnetic field (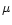 G),
respectively,
and the evolution of the energy-loss rate
(1033 ergs-1). G),
respectively,
and the evolution of the energy-loss rate
(1033 ergs-1). |
| Open with DEXTER |
 |
Figure 6:
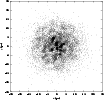
The collision debris of the parallel case at t=3.75 Myr.
This figure reveals more clearly the clumped structure of the remnants. |
| Open with DEXTER |
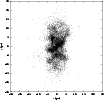 |
Figure 7:
A close view in the particle configuration projected onto the
xy-plane at 4 Myr in the parallel case.
The higher density regions ("clumps") are indicated by crosses.
|
| Open with DEXTER |
As in Paper I, the physical scales
[l]=1 pc,
[t]=1 Myr,
![$[m]=222.25~M_\odot$](/articles/aa/full/2001/45/aa1280/img53.gif) ,
were chosen to normalize the gravity constant:
,
were chosen to normalize the gravity constant:
![$G=1~[m]^{-1}\,[l]^{3}\,[t]^{-2}$](/articles/aa/full/2001/45/aa1280/img54.gif) .
The velocity unit is approximately 1 km s-1.
In these scales the magnetic field unit is approximately
.
The velocity unit is approximately 1 km s-1.
In these scales the magnetic field unit is approximately
![$[B]=12~\mu$](/articles/aa/full/2001/45/aa1280/img55.gif) G.
Other derived physical scales were energy
G.
Other derived physical scales were energy
![$[e]=4.230\times10^{45}$](/articles/aa/full/2001/45/aa1280/img56.gif) erg,
power
erg,
power
![$[\dot e]=1.340\times 10^{38}$](/articles/aa/full/2001/45/aa1280/img57.gif) ergs-1,
and density
ergs-1,
and density
![$[\rho]=1.505\times 10^{-20}$](/articles/aa/full/2001/45/aa1280/img58.gif) gcm-3.
gcm-3.
Similarly to Paper I, our interstellar cloud model consists of a mixture
of atomic and molecular
hydrogen, helium and traces of CO.
Initially, the clouds have a temperature of approximately 20 K.
The cooling and the heating mechanisms are the same as in Paper I,
as well as the
adopted chemical model for H and H2 balance, which reflects a strong
nonlinear dependency of the specific thermal energy on density and temperature.
We refer the reader to Paper I for further details concerning the thermal
and chemical models.
The simulation starts by impinging two identical
spherical clouds onto each other
at a supersonic relative speed of approximately 10 km s-1.
Both clouds have an initial mass of
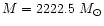 ,
a temperature
T = 20 K, and a cut-off radius
,
a temperature
T = 20 K, and a cut-off radius
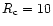 pc.
Each cloud contains 4096 particles
initially distributed by Monte Carlo, according to the density law
pc.
Each cloud contains 4096 particles
initially distributed by Monte Carlo, according to the density law
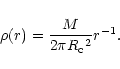 |
(19) |
The mean adiabatic sound-speed and the Alfvén speed are approximately
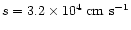 and
and
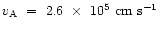 ,
respectively.
These values allow a supersonic shock with Mach numbers
,
respectively.
These values allow a supersonic shock with Mach numbers
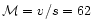 and
and
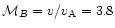 ,
respectively.
,
respectively.
In present work, we performed only simulations for the head-on case.
For the same initial conditions as in Paper I,
we set up two distinct experiments, labeled by the initial
magnetic field orientation:
parallel and
perpendicular to the initial clouds motion.
The magnetic field is initially homogeneous,
and we adopted an initial strength of 12 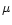 G
based on typical values observed in dark molecular clouds.
G
based on typical values observed in dark molecular clouds.
The code parameters were
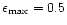 ,
,
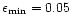 ,
,
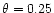 ,
,
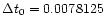 ,
,
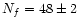 ,
,
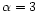 ,
,
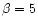 ,
,
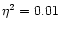 ,
and 8 time-bins were used in the integration scheme, allowing a minimum
time-step of
,
and 8 time-bins were used in the integration scheme, allowing a minimum
time-step of
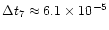 .
These values were based on accuracy/stability
considerations discussed in Paper I.
.
These values were based on accuracy/stability
considerations discussed in Paper I.
As in Paper I, the cloud models were not initially in hydrostatic equilibrium.
However,
the time scales involved in the internal cloud motions were one order of
magnitude larger than that
of the main term of the collision process,
so that we could assume that the relaxation effects were small compared to
the effects caused by the shock itself.
If we allowed the initial clouds to relax (under the imposed environment)
before the collision experiment
starts, our clouds would
never reach the hydrostatic balance since the involved processes are
dissipative and interact with the magnetic field under the MHD
approximation.
On the other hand, if we setup the initial conditions for adiabatic hydrostatic
equilibrium, as we switch on the cooling-heating mechanisms, and
also the magnetic field, the clouds assume a non-equilibrium
configuration with a similar behavior to the initial conditions
adopted in present
work.
Our definition
for clump is somewhat arbitrary
and has a geometrical basis.
Our algorithm uses a list of SPH
particles sorted according to their densities
to promote the densest particle
(with density
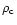 )
to the clump core,
and removes it from the list.
For this particle (clump core),
the algorithm searches for the
nearest neighbors satisfying the condition
)
to the clump core,
and removes it from the list.
For this particle (clump core),
the algorithm searches for the
nearest neighbors satisfying the condition
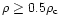 .
Each neighbor obeying the latter condition is promoted to
a clump member, and then
removed from the list to avoid overcounting and clump overlap.
We do not know where a clump ends but
where its
density drops to half the peak.
.
Each neighbor obeying the latter condition is promoted to
a clump member, and then
removed from the list to avoid overcounting and clump overlap.
We do not know where a clump ends but
where its
density drops to half the peak.
To avoid statistical fluctuations being
classified as clumps,
we have introduced in the clump analysis
a "floor condition" to reject
clump core candidates with densities lower than
the
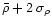 threshold, where
threshold, where
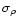 is the density dispersion.
Without this condition, a Monte Carlo generated
homogeneous sphere would be entirely recognized
as one single clump.
Thus, what we consider to be a real clump
is a density enhancement much above the
expectation value.
This procedure is repeated until the list of clump candidates
becomes empty.
is the density dispersion.
Without this condition, a Monte Carlo generated
homogeneous sphere would be entirely recognized
as one single clump.
Thus, what we consider to be a real clump
is a density enhancement much above the
expectation value.
This procedure is repeated until the list of clump candidates
becomes empty.
Figures 1 and 2
illustrate the configurations for
velocity and magnetic field
of a z=0 slice with 0.5 pc in thickness at 1.5
and 2.5 Myr, respectively.
It is evident from these figures that the magnetic field was amplified
in the shock layer, which was caused by the strong compression
that was mentioned previously (Sect. 2).
Differently from the non-magnetic case,
in which the maximum compression occurred at 1.5 Myr,
in present experiment the shocked clouds reached its maximum compression
at about 2.5 Myr,
but the maximum density peak,
observed for a particle centered in the densest clump,
occurred at 1.92 Myr.
One possible explanation is that the magnetic field retains most of the
colliding gas, unlike their hydrodynamics counterparts where the colliding gas
can freely escape throughout the symmetry plane.
Figure 3 shows the configurations for the magnetic field and
the vorticity
inside an x=3 slice with 0.5 pc in thickness at 2.5 Myr.
The slice is passing through four clumps, revealed by the arrows concentration
for both magnetic field and vorticity.
The vorticity distribution
reaches its maximum magnitude around the dense clumps.
In the high-vorticity region,
the magnetic field is amplified
in accordance with 2D simulations of shock cloud interaction (e.g.,
Mac Low et al. 1994; Jones et al. 1997).
The vorticity configuration can be seen in Fig. 4 for two epochs;
the plots reveal the eddies formed along with the collision,
and they survived until the end of the simulation.
The maximum vorticity magnitude (approximately 25 km s-1 pc-1)
at t=2.5 Myr (left panel) was the maximum reached during the experiment,
whereas the maximum vorticity magnitude at t=4.0 Myr (right panel) was
approximately 6.9 km s-1 pc-1.
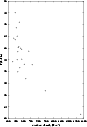 |
Figure 9:
Maximum density versus mean temperature in the identified
clumps in the parallel case
(the denser regions contoured by half the central density, as
in Paper I).
The plot reveals a slight correlation between central density and
temperature.
Denser regions are the colder ones. |
| Open with DEXTER |
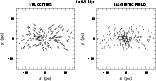 |
Figure 10:
From left to right, respectively, the velocity field and the magnetic
field of a slice with 0.5 pc in thickness passing through z=0 at
t=0.9 Myr in the perpendicular case. |
| Open with DEXTER |
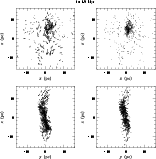 |
Figure 12:
Vorticity (left column) and magnetic field (right column) in two
orthogonal views (xz and yz) inside a thin slice of 0.5 pc
in the perpendicular case. |
| Open with DEXTER |
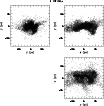 |
Figure 14:
The three orthogonal view of the collision debris of the
perpendicular field case. |
| Open with DEXTER |
We keep track of the evolution of the quantitative properties
associated to critical
regions by depicting their maximum values occurred in the collision at each
time-step.
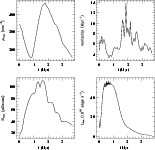
Figure 5 shows the evolution of the maximum values for
density
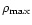 (in H mass per cubic centimeter),
vorticity magnitude
(in H mass per cubic centimeter),
vorticity magnitude
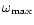 (in km s-1 pc-1) and
magnetic-field strength
(in km s-1 pc-1) and
magnetic-field strength
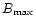 (in
(in 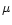 G), as well as the evolution
of
total luminosity
G), as well as the evolution
of
total luminosity
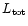 (in 1033 ergs s-1).
All the plots show simultaneous local peaks around 1.95 Myr, which can be a
consequence of the maximum compression reached by the clouds.
At this epoch, the maximum density, the maximum magnetic field and the total
luminosity reached their peak values of
(in 1033 ergs s-1).
All the plots show simultaneous local peaks around 1.95 Myr, which can be a
consequence of the maximum compression reached by the clouds.
At this epoch, the maximum density, the maximum magnetic field and the total
luminosity reached their peak values of
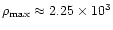 cm-3,
cm-3,
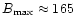
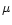 G, and
G, and
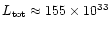 ergs s-1, respectively.
At
ergs s-1, respectively.
At
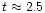 Myr there is a local peak in density synchronized with the
peak in vorticity, approximately 25 km s-1 pc-1(the maximum value of the
experiment).
They might be associated to a peak near 2.6 Myr in the evolution of the
maximum field strength.
However, the nearest peak in the luminosity evolution occurs just before, at
2.3 Myr.
There is a noticeable peak near 3.5 Myr in the evolution of the maximum
density, which is perhaps physically associated with the peak at the same
epoch in the evolution of the maximum vorticity.
However, this peak in the maximum density evolution is preceded by a peak in
the maximum magnetic field evolution near 3.2 Myr.
At 4 Myr, the maximum magnetic field strength is significantly greater
(
Myr there is a local peak in density synchronized with the
peak in vorticity, approximately 25 km s-1 pc-1(the maximum value of the
experiment).
They might be associated to a peak near 2.6 Myr in the evolution of the
maximum field strength.
However, the nearest peak in the luminosity evolution occurs just before, at
2.3 Myr.
There is a noticeable peak near 3.5 Myr in the evolution of the maximum
density, which is perhaps physically associated with the peak at the same
epoch in the evolution of the maximum vorticity.
However, this peak in the maximum density evolution is preceded by a peak in
the maximum magnetic field evolution near 3.2 Myr.
At 4 Myr, the maximum magnetic field strength is significantly greater
(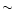
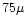 G) than the initial value.
The luminosity-evolution profile resembles the analogous non-magnetic case but
is reduced in amplitude by a factor of 1.63.
Also, the peaks in the luminosity occur in 1.92 Myr
in the MHD case and 1.48 Myr for the non-magnetic case.
G) than the initial value.
The luminosity-evolution profile resembles the analogous non-magnetic case but
is reduced in amplitude by a factor of 1.63.
Also, the peaks in the luminosity occur in 1.92 Myr
in the MHD case and 1.48 Myr for the non-magnetic case.
The collision debris are shown in Fig. 6 at 3.75 Myr.
This epoch is just 0.25 Myr after denser structures have formed (see
Fig. 5), but they eventually dissipate.
The collision remnants resemble qualitatively those shown in Paper I.
However, the clumped structure shown here is much coarser than that
shown in the analogous non-magnetic case (report to Fig. 5 in
Paper I).
The experiment stops at 4 Myr, and the collision remnants show
almost the same structures shown in Fig. 6,
but with a small variation in the density peak (see Fig. 5).
Using the same technique as in Paper I, we found 22 denser regions (clumps)
as shown in Figs. 7 and 8.
According to both figures, the clumps distribution forms elongated
structures in the xy-view.
The clumps have density-peaks in the 460-1359 Hcm-3 range.
However, the average density of each clump varies from 418 through
829 Hcm-3.
The temperature is approximately constant in the clumps and it lies
in the 11.75-55.15 K range. Each clump has effective size (rms)
between 0.15 pc and 0.50 pc.
The denser clumps are generally the smaller and colder ones (see
Fig. 9).
However, the densest (coldest) clump has effective radius of 0.44 pc.
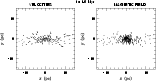
Figures 10 and 11 illustrate the configurations for velocity
and magnetic field of a z=0 slice with 0.5 pc in thickness at 0.9 and
1.6 Myr, respectively.
The clouds are magnetically supported, so that they collapse along the field
lines but not in perpendicular directions.
As a consequence, the clouds become flattened (Fig. 11).
The figures show that the magnetic-field strength is amplified in the
accretion layer, the region in which the velocity field converges.
Such a field compression forms a magnetic
shield in front of both cloud that inhibits a direct contact of the clouds.
Figure 12 shows the configuration
for vorticity and magnetic field of a slice with 0.5 pc in thickness at
time t=1.9 Myr.
The vorticity configuration of both slices is shown in the left column,
and the corresponding magnetic field configuration is shown in the right column.
In the xz-plane (top view) a high concentration of magnetic
field at position
(2,4) approximately, contoured by the vorticity vectors is evident.
In the yz-slice (the collision plane) there is an almost coherent vorticity
stream in the negative z-direction, whereas the magnetic-field is roughly in
the y-direction.
The evolutions of the maximum values for density, vorticity and magnetic
field, as well as the evolution of the total luminosity, are
shown in Fig. 13.
As in the parallel case (Fig. 5), some synchronized maxima occurred.
For instance, the evolution of the maximum-density and the maximum-vorticity
have their peaks of
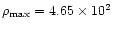 H cm-3 and
H cm-3 and
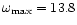 Myr-1, respectively, at about 1.8 Myr.
The maximum magnetic-field evolution has a peak of
Myr-1, respectively, at about 1.8 Myr.
The maximum magnetic-field evolution has a peak of
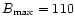
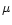 G at about 1.7 Myr.
The final maximum magnetic field is about three times its initial value.
The evolution of the total luminosity is quite different from the parallel
case: the maximum occurred about 0.65 Myr, whereas, in previous case it
occurred about 1.95 Myr.
Furthermore, the total amount of energy lost was smaller
than in the parallel case.
The evolution of the maximum magnetic-field
reveals an interesting behavior.
From 2.0 Myr and after, the maximum field-strength drops off
in a stepwise way, following the local peaks decay in the vorticity plot.
G at about 1.7 Myr.
The final maximum magnetic field is about three times its initial value.
The evolution of the total luminosity is quite different from the parallel
case: the maximum occurred about 0.65 Myr, whereas, in previous case it
occurred about 1.95 Myr.
Furthermore, the total amount of energy lost was smaller
than in the parallel case.
The evolution of the maximum magnetic-field
reveals an interesting behavior.
From 2.0 Myr and after, the maximum field-strength drops off
in a stepwise way, following the local peaks decay in the vorticity plot.
The collision remnants for the perpendicular case are shown in Fig. 14
at t=3.75 Myr.
No cloud fragmentation was observed.
However, it is evident from the figure the formation of
an elongated structures in the z-direction.
Similar results were found in 2D collision between supersonic diffuse
clouds by Miniati et al. (Miniati et al. 1999).
We studied two special cases of head-on supersonic collision between
two identical magnetized clouds using a three-dimensional SPMHD code.
In the first case, the magnetic field was initially parallel to the clouds
motion, and in the second case the field was initially perpendicular.
We focused on the effects of the magnetic field on the clumps formation by
cloud-cloud collision.
The initial conditions were the same as a previous work (Paper I) except
for the presence of a homogeneous magnetic field of approximately 12 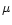 G.
G.
As an SPMHD innovation,
we modified the Monaghan & Gingold (1983) artificial
viscosity in order to reproduce
magnetohydrodynamics shock.
In fact, such an artificial viscosity model was crucial in the case of collision
perpendicular to the magnetic field.
A more detailed discussion of the present SPMHD code as well as a set of
MHD tests will be presented in a future work.
The magnetic field was amplified and deformed in the shocked layer in both
cases.
Its magnitude reached values as higher as 160 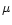 G and 110
G and 110 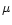 G in
the parallel and in the perpendicular cases, respectively, and decayed
subsequently.
The field distribution seems chaotic in larger scales, however,
it distributes more coherently in the clumps.
Moreover, in the first 1 Myr of the parallel case the magnetic field
evolved to a wiggled aspect in the shock layer but
remained almost homogeneous outside the shock.
The referee argued that
the Monte Carlo seed
density perturbations
were the responsible for the wiggles shown in the present results
and that they are germinated when
these inhomogeneities try to smooth out before hitting the shock.
This is a plausible explanation for this effect.
G in
the parallel and in the perpendicular cases, respectively, and decayed
subsequently.
The field distribution seems chaotic in larger scales, however,
it distributes more coherently in the clumps.
Moreover, in the first 1 Myr of the parallel case the magnetic field
evolved to a wiggled aspect in the shock layer but
remained almost homogeneous outside the shock.
The referee argued that
the Monte Carlo seed
density perturbations
were the responsible for the wiggles shown in the present results
and that they are germinated when
these inhomogeneities try to smooth out before hitting the shock.
This is a plausible explanation for this effect.
The presence of the magnetic field, with typical magnitudes of dark
molecular clouds, affects considerably the evolution of head-on cloud-cloud
collision.
Strong vortices were formed in contrast to the non-magnetic case.
They were distributed throughout the shocked layer, and they persist until
the end of the simulation.
In the parallel case the vorticity distribution presents an almost regular
pattern, whereas in the perpendicular case the vorticity distribution
looks chaotic.
Also, we noticed that the vorticity distribution contours the clumps and
that its magnitude grows proportionally to the distance to the clumps
mass-center, reaching its maximum at the clumps boundaries.
This interesting behavior could be interpreted as the gas (particles) having
a toroidal motion about the clump's mass-center.
However, one plausible explanation is that the clumps are traveling along
the field lines and against the low density regions.
This motion may be a result of the confinement caused by the field, since in
the non-magnetic case such a result did not occur.
The cloud compression was much more efficient in the parallel case than in the
perpendicular one.
In the former case, particles were confined by the field lines, and in the
later, the field lines were compressed in the shocked layer, forming a magnetic
shield that inhibits a direct contact of both clouds.
In the later case, the stored magnetic pressure slowly stops the clouds and
reverses their motions. Similar results were found in 2D collisions between
supersonic diffuse clouds by Miniati et al. (Miniati et al. 1999).
The large-scale density distribution in the parallel case resembles the
analogous non-magnetic case, but differs considerably on small scales.
However, the density distribution of the perpendicular case is quite
different from the non-magnetic case on all scales.
The clump formation was present in the parallel case, but it was absent
in the perpendicular case,
or at least not detectable by the adopted definition for clump.
Clumps had a population of 60-96 particles.
For the chosen number of neighbors (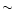 48), we conclude that the
formed clumps are in agreement with the resolution requirement.
The 22 formed clumps contain a total of 1728 particles.
However, as in Paper I, the gravity resolution
was limited by the lower and upper limits for
the adaptive softening length
48), we conclude that the
formed clumps are in agreement with the resolution requirement.
The 22 formed clumps contain a total of 1728 particles.
However, as in Paper I, the gravity resolution
was limited by the lower and upper limits for
the adaptive softening length
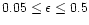 .
For regions where h<0.05 the smoothing length is
.
For regions where h<0.05 the smoothing length is
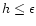 ,
and then the local Jeans mass becomes larger than
the minimum resolvable mass.
,
and then the local Jeans mass becomes larger than
the minimum resolvable mass.
For h>0.5 the smoothing length is
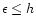 ,
and then we could have artificial fragmentation
but we did not have fragments greater than this upper limit.
Clumps have formed preferentially in the denser parts of the
collision remnants, where the local Jeans mass could be smaller than the
minimum resolvable mass.
,
and then we could have artificial fragmentation
but we did not have fragments greater than this upper limit.
Clumps have formed preferentially in the denser parts of the
collision remnants, where the local Jeans mass could be smaller than the
minimum resolvable mass.
Clumps were not detected in the parallel case,
nor in the off-center collision of Paper I,
even if we dropped the density floor down to
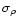 above the mean
density
above the mean
density 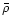 .
Also, we performed a collapse experiment with one
cloud, with the same initial cloud model, initially at rest,
and no fragments were detected.
These facts suggest that the
fragments formed in present work were not endemic (Whitworth 1998)
but in fact produced by the strong compression allowed by the
special field
orientation (parallel to the initial motion) combined with
the efficient cooling.
.
Also, we performed a collapse experiment with one
cloud, with the same initial cloud model, initially at rest,
and no fragments were detected.
These facts suggest that the
fragments formed in present work were not endemic (Whitworth 1998)
but in fact produced by the strong compression allowed by the
special field
orientation (parallel to the initial motion) combined with
the efficient cooling.
The presence of magnetic field just retarded the fragmentation process and
allowed the formation of larger and hotter clumps than in the non-magnetic case.
For instance, in the previous work we found clumps as dense as
104 Hcm-3, most of them
with sizes of the order of 10-1 pc and temperatures
in the 11-20 K range.
In present work, we found clumps with densities of the order of
103 Hcm-3, most of them with sizes ranging 0.3-0.5 pc and
temperatures in the 25-50 K range.
Acknowledgements
We are grateful to Anthony Whitworth, the referee, for
useful comments and suggestions.
E.P.M. and C.M.A. are thankful
to FAPESP for the financial support.
This research has made use of NASA's
Astrophysics Data System (ADS) Bibliographic Services.
- Barnes, J. E., & Hut, P. 1986, Nature, 324, 446
In the text
NASA ADS
- Buckley, H. D., & Ward-Thompson, D. 1996, MNRAS, 281, 294
In the text
NASA ADS
- Clifford, P., & Elmegreen, B. G. 1983, MNRAS, 202, 629
In the text
NASA ADS
- Crutcher, R. M. 1999, ApJ, 520, 706
In the text
NASA ADS
- Elmegreen, B. G. 1988, ApJ, 326, 616
In the text
NASA ADS
- Gilden, D. L. 1984, ApJ, 279, 335
In the text
NASA ADS
- Habe, A., & Ohta, K. 1992, PASJ, 44, 203
In the text
NASA ADS
- Hasegawa, T., Sato, F., Whiteoak, J. B., & Miyawaki, R. 1994, ApJ, 429, L77
In the text
NASA ADS
- Hausman, M. A. 1981, ApJ, 245, 72
In the text
NASA ADS
- Heiles, C. 1987, in Interstellar Processes, ed. D. J. Hollenbach, & H. A. Jr. Thronson (Dordrecht:Reidel), 171
In the text
- Heiles, C. 1996, in Polarimetry of the Interstellar Medium, ed. W. G. Roberge, & D. C. B. Whittet (San Francisco: ASP), PASP Conf. Ser. 97, 457
In the text
- Heiles, C. 1997, ApJS, 111, 245
In the text
NASA ADS
- Hernquist, L., & Katz, N. 1989, ApJS, 70, 419
In the text
NASA ADS
- Heyer, M., Vrba, F. J., Snell, R. L., et al. 1987, ApJ, 321, 855
In the text
NASA ADS
- Jones, T. W., Gaalaas, J. B., Ryu, D., & Frank, A. 1997, ApJ, 482, 230
In the text
NASA ADS
- Keto, E. R., & Lattanzio, J. C. 1989, ApJ, 346, 184
In the text
NASA ADS
- Kimura, K., & Tosa, M. 1996, å, 308, 979
In the text
NASA ADS
- Klein, R. I., & Woods, D. T. 1998, ApJ, 497, 777
In the text
NASA ADS
- Lattanzio, J. C., Monaghan, J. J., Pongracic, H., & Schwarz, M. P. 1985, MNRAS, 215, 125
In the text
NASA ADS
- Little, L. T., Riley, P. W., Macdonald, G. H., & Matheson, D. N. 1978, MNRAS, 183, 805
In the text
NASA ADS
- Loren, R. B. 1976, ApJ, 209, 466
In the text
NASA ADS
- Mac Low, M.-M., McKee, C. F., & Klein, R. I, 1994, ApJ, 433, 757
In the text
NASA ADS
- Marinho, E. P., & Lépine, J. R. D. 2000, A&AS, 142, 165 (Paper I)
In the text
- Meyerdierks, H. 1992, å, 253, 515
In the text
NASA ADS
- Miniati, F., Jones, T. W., Ferrara, A., & Ryu, D. 1997, ApJ, 491, 216
In the text
NASA ADS
- Miniati, F., Ryu, D., Ferrara, A., & Jones, T. W. 1999, ApJ, 510, 726
In the text
NASA ADS
- Miyawaki, R., Hayashi, M., & Hasegawa, T. 1986, ApJ, 305, 353
In the text
NASA ADS
- Monaghan, J. J. 1992, ARA&A, 30, 543
In the text
NASA ADS
- Monaghan, J. J., & Gingold, R. A. 1983. J. Comput. Phys., 52, 374
In the text
- Myers, P. C., Goodman, A. A., Güsten, R., & Heiles, C. 1995, ApJ, 442, 177
In the text
NASA ADS
- Odenwald, S., Fischer, J., Lockman, F. J., & Stemwedel, S. 1992, ApJ, 397, 174
In the text
NASA ADS
- Polygiannakis, J. M., & Moussas, X. 1999, Plasma Phys. Control. Fusion, 41, 967
In the text
- Pongracic, H., Chapman, S. J., Davies, J. R., et al. 1992, MNRAS, 256, 291
In the text
NASA ADS
- Ricotti, M., Ferrara, A., & Miniati, F. 1997, ApJ, 485, 254
In the text
NASA ADS
- Rohlfs, R., Herbstmeier, U., Mebold, U., & Winnberg, A. 1989, å, 211, 402
In the text
NASA ADS
- Serabyn, E., Güsten, R., & Schulz, A. 1993, ApJ, 413, 571
In the text
NASA ADS
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium (New York: Wiley)
In the text
- Stone, M. E. 1970a, ApJ, 159, 293
In the text
NASA ADS
- Stone, M. E. 1970b, ApJ, 159, 277
In the text
NASA ADS
- Strom, S. E., Strom, K. M., & Edwards, S. 1988, in Galactic and Extragalactic Star Formation, ed. R. E. Pudritz, & M. Fich (Dordrecht: Kluwer), 53
In the text
- Vallée, J. P. 1995, AJ, 110, 2256
In the text
NASA ADS
- Vrba, F. J., Coyne, G. V., & Tapia, S. 1981, ApJ, 243, 489
In the text
NASA ADS
- Vrba, F. J., Strom, S. E., & Strom, K. M. 1976, AJ, 81, 958
In the text
NASA ADS
- Vrba, F. J., Strom, S. E., & Strom, K. M. 1988, AJ, 96, 680
In the text
NASA ADS
- Whitworth, A. P. 1998, MNRAS, 296, 442
In the text
NASA ADS
- Zeldovich, Ya. B., Ruzmaikin, A. A., & Sokoloff, D. D. 1983, Magnetics Fields in Astrophysics (New York: Gordon & Breach)
In the text
- Zweibel, E. G. 1999, Physics of Plasma, 6, 1725
In the text
Copyright ESO 2001
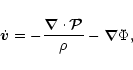
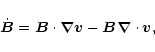
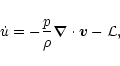
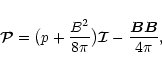
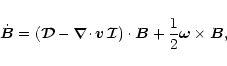
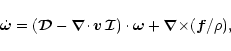
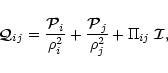
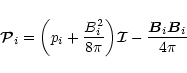
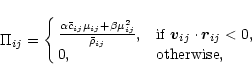
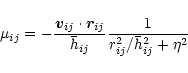
![\begin{displaymath}
\bar{c}_{ij}=
\biggl[
\bar s_{ij}^2+
\frac
{\vert\bar{\vec B...
...{ij}\vert
\right)^2}
{4\pi\bar{\rho }_{ij}}
\biggr]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2001/45/aa1280/img30.gif)
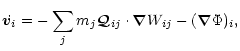
![$\displaystyle \dot{\vec B_i}
=
\frac 1{\rho_i}\sum\limits_jm_j[{\vec B}_i\cdot ({\vec v}_j-{\vec v}_i)]
{\vec{\nabla}}_iW_{ij}$](/articles/aa/full/2001/45/aa1280/img38.gif)
![$\displaystyle -\frac 1{\rho_i}{\vec B}_i\left[\sum\limits_jm_j({\vec v}_j-{\vec v}_i)
\cdot{{\vec{\nabla}}}_iW_{ij}\right],$](/articles/aa/full/2001/45/aa1280/img39.gif)