A&A 379, 917-923 (2001)
DOI: 10.1051/0004-6361:20011380

Statistics and supermetallicity: The metallicity of Mu Leonis

B. J.Taylor

Department of Physics and Astronomy, N283 ESC, Brigham Young University, Provo, UT 84602-4360, USA

Received 9 February 2001 / Accepted 2 October 2001

Abstract
For the often-studied "SMR'' giant $\mu $ Leo, Smith & Ruck (2000) have recently found that [Fe/H] $\sim +0.3$ dex. Their conclusion is tested here in a "statistical'' paradigm, in which statistical principles are used to select published high-dispersion $\mu $ Leo data and assign error bars to them. When data from Smith & Ruck and from Takeda et al. (1998) are added to a data base compiled in 1999, it is found that conclusions from an earlier analysis (Taylor 1999c) are essentially unchanged: the mean value of [Fe/H] $\sim +0.23 \pm 0.025$ dex, and values $\leq$+0.2 dex are not clearly ruled out at 95% confidence. In addition, the hypothesis that [Fe/H] $\geq +0.3$ dex which emerges from the Smith-Ruck analysis is formally rejected at 98% confidence. The "default paradigm'' which is commonly used to assess $\mu $ Leo data is also considered. The basic characteristics of that paradigm continue to be a) unexplained exclusion of statistical analysis, b) inadequately explained deletions from an [Fe/H] data base containing accordant data, and c) an undefended convention that $\mu $ Leo is to have a metallicity of about +0.3 dex or higher. As a result, it seems fair to describe the Smith-Ruck application and other applications of the default paradigm as invalid methods of inference from the data.

Key words: stars: abundances - stars: individual: $\mu $ Leo


1 Introduction

Not long ago, Taylor (1999c, hereafter T99) published a statistical analysis of published high-dispersion metallicities of $\mu $ Leo. This K giant plays a key role in the controversy about "super-metal-rich'' stars that was begun by Spinrad & Taylor (1969). T99 found that [Fe/H] $\sim$ $+0.24 \pm 0.03$ dex for $\mu $ Leo, and that this datum is not known to exceed +0.2 dex at 95% confidence.

Since the appearance of T99, Smith & Ruck (2000, hereafter SR) have published a high-dispersion analysis of $\mu $ Leo. Their value of [Fe/H] is $+0.29 \pm 0.03$ dex. At first glance, this result may appear to be similar to that of T99. However, it is in fact based on a fundamentally different approach to the $\mu $ Leo problem.

This paper has two aims: 1) to update the T99 analysis, and 2) to show that the T99 approach still yields superior results. The revised T99 analysis is described in Sect. 2 of this paper. The alternative non-statistical approach of SR and others and its results are reviewed in Sect. 3. A brief summary concludes the paper in Sect. 4.

2 The updated T99 analysis

2.1 The statistical paradigm

The T99 approach to data analysis will be described here as "the statistical paradigm''. This paradigm is based on the following six rules.

1.
Statistical analysis is applied to published values of [Fe/H].

2.
Adopted values of [Fe/H] are from high-dispersion analyses or from spectrum synthesis applied to photometry of weak-line clusters (see, for example, Gustafsson et al. 1974).

3.
The zero point for the adopted data is based solely on differential high-dispersion analyses. No f-value systems or values of the solar metallicity are required.

4.
Systematic corrections are included in the paradigm. They are applied if they can be based on published numerical evidence. "Extrinsic'' corrections are based on model-atmosphere results and line data from the literature. "Statistical'' corrections are derived by comparing data strings from different sources.

5.
Accidental errors are derived from scatter which persists after corrections for systematic effects have been applied. (See Sect. 6 of Taylor 2001).

6.
The burden of proof for deleting data is placed on the case for deletion. Deletions are made only if they can be justified by numerical evidence.

These rules have been used to analyze published data for $\mu $ Leo and about 1100 other giants. The result is a catalog of mean values of [Fe/H] which is described by Taylor (1999a). Further information about the analysis used to produce the catalog is given by Taylor (1998a, 1999b). This catalog participates in the analysis to be described below.

2.2 The $\mu $ Leo datum of Takeda et al. (1998)

The T99 analysis must be expanded to include two data, with one being that of SR and the other being from Takeda et al. (1998). The latter authors also give results for 30 other giants. As a first step in analyzing the Takeda et al. data, the following equations are applied to them:


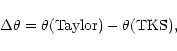\begin{displaymath}\Delta\theta = {\theta}{\rm (Taylor)} - {\theta}{\rm (TKS)}, \end{displaymath} (1)


\begin{displaymath}\Delta {\rm [Fe/H]} = [{\rm d}{\rm [Fe/H]}/{\rm d}\theta] \times \Delta\theta, \end{displaymath} (2)

and


\begin{displaymath}{\rm d}{\rm [Fe/H]}/{\rm d}\theta = -8.48 + 5.14\,\mkern2mu {\theta}{\rm (Taylor)}. \end{displaymath} (3)

"TKS'' refers to Takeda et al., $\theta \equiv 5040/T_{\rm e}$, and $T_{\rm e}$ is effective temperature. Equation (3) is a default relation which is discussed by Taylor (1998a, Sect. 5.4).

The equations are applied only if $\vert\Delta\theta\vert > 0.003$. For smaller values of $\vert\Delta\theta\vert$, [Fe/H] corrections are much smaller than the rms errors to be discussed below. Two required values of $\theta$(Taylor) are derived from published measurements of V-K (Johnson et al. 1966). The remaining values of $\theta$(Taylor) are from a temperature catalog which accompanies Taylor's [Fe/H] catalog (see Taylor 1999a).

Taylor (1998a, Table 3) lists a number of other extrinsic corrections that may be considered in the statistical paradigm. None of them appear to be required in this context. As a result, the next step in the analysis is taken by comparing the Takeda et al. values of [Fe/H] to counterparts from the Taylor [Fe/H] catalog. This comparison is performed by using a "comparison algorithm'' derived by Taylor (1991, Appendix B) and described conceptually by Taylor (1999b, Sect. 4.3).

The comparison algorithm yields a statistical correction of the sort referred to in rule (4) (see Sect. 2.1). The equations derived for that correction are as follows:


\begin{displaymath}{\rm [Fe/H](catalog)} = {\rm [Fe/H](TKS)} + Z + S{\theta}{\rm (Taylor)}, \end{displaymath} (4)

with


\begin{displaymath}Z = 0.70 \pm 0.24 \mkern6mu {\rm ~dex} \end{displaymath} (5)

and


\begin{displaymath}S = -0.68 \pm 0.23 \mkern6mu {\rm ~dex}. \end{displaymath} (6)

A t test shows that $S \neq 0$ at a confidence level C = 0.995. It is therefore concluded that a real systematic effect exists in the Takeda et al. data.

A second result yielded by the comparison algorithm is an rms error for the Takeda et al. data. The value obtained for $\sigma_{\rm TKS} = 0.061$ dex. Equations (4)-(6) may now be applied to the Takeda et al. datum for $\mu $ Leo, with $\sigma$(TKS) being attached to the corrected value. This process converts the original datum (+0.24 dex) to


\begin{displaymath}{\rm [Fe/H]} = +0.16 \pm 0.061 \mkern6mu {\rm ~dex}. \end{displaymath} (7)

This datum will be used in Sect. 2.4.

2.3 The $\mu $ Leo datum of SR

2.3.1 Comparing temperatures

When one turns to the SR analysis, two of its features draw immediate attention. For one thing, SR find that $T_{\rm c} = 4540 \pm 50$ K for $\mu $ Leo. The corresponding datum given in T99 is $4470 \pm 13$ K.

SR assume that the quoted results differ. This inference may be tested by considering data from a set of four papers which will be referred to here as the "SR set.'' In these papers, closely similar analyses of relatively weak lines are described (Drake & Smith 1991; Smith 1998, 1999; SR). Metallicities and temperatures for six giants are considered, with some temperatures being from spectroscopic analysis and others from the infrared flux method.

It will be assumed here that temperatures of these two kinds share a common zero point. That zero point can be checked because the Taylor temperature catalog contains entries for the same six giants. The comparison algorithm described above is applied to the two sets of temperatures. The results are as follows:

\begin{displaymath}\Delta T_{\rm c} = -6 \pm 20 \mkern6mu {\rm K} \end{displaymath} (8)

and


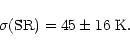\begin{displaymath}\sigma({\rm SR}) = 45 \pm 16 \mkern6mu {\rm K}. \end{displaymath} (9)

$\Delta T_{\rm c}$ is the formal correction to the SR temperatures, and it clearly is not significant at 95% confidence. The derived rms error $\sigma$(SR) applies for the data from the SR set. $\sigma$(SR) is found to be consistent with the rms errors of 35-50 K that are quoted in the SR set. There is therefore no evidence for an inconsistency between the Taylor-catalog data and those in the SR set.

2.3.2 Checking a zero point

The other issue that draws immediate attention is the zero point of the metallicities in the SR set. SR compare Hyades metallicities from the SR set and from strong-line profiles to a mean Hyades metallicity given by Perryman et al. (1998). The result of that comparison is cited as evidence that their zero point is correct.

A salient feature of this inference is the reliability of the Perryman et al. mean. There are noteworthy problems with that mean which are discussed by Taylor (2000, Appendix B; see especially Table B.1). Those problems may be resolved by using the results of two data reviews: Taylor (1994) has considered Hyades dwarfs, while Taylor (1998b) has considered Hyades giants. An average from those reviews will be adopted below.

Another issue of interest is statistical rigor. If the SR Hyades comparison is done statistically, it does not yield a zero correction with 100% confidence, as SR conclude. Instead, a range of possible corrections is obtained. The extent of that range must be assessed by using rms errors. By analyzing the errors available to SR, one finds that it is unlikely that SR made allowance for them (see Appendix A). This is another reason for a complete reappraisal of the SR zero point.

2.3.3 Adjustments and rms errors

To begin the reappraisal, three systematic corrections are considered. The first of them is based on model atmospheres. In the SR set, the Holweger-Müller (1974) model is adopted for the Sun. In three papers of the set, MARCS models (Bell et al. 1976) are adopted for program stars. The fourth paper (Drake & Smith 1991) includes a MARCS model, an empirical model, and two other models in an analysis of $\beta$ Gem. Drake & Smith regard the empirical model as the best stellar counterpart for the Holweger-Müller solar model. If the MARCS model is used instead, a correction of 0.02 dex should be added to the resulting value of [Fe/H] (see Sect. 5.1 of Drake & Smith). This correction is applied here to bring all the data in the SR set to their values for compatible model atmospheres.

To insure that all metallicities are based on completely uniform temperatures, temperature corrections are applied. To calculate these corrections, Eq. (3) is modified:

\begin{displaymath}{\rm d}{\rm [Fe/H]}/{\rm d}\theta = -7.71 + 5.14\theta. \end{displaymath} (10)

With its altered zero point, Eq. (10) adequately reproduces a temperature derivative implied by Table 2 of SR.

A zero-point [Fe/H] adjustment is the third kind of correction to be considered. Here, in contrast to the analysis of the Takeda et al. data, only Z is calculated (recall Eqs. (4)-(6)) because only a few contributing data are available. Moreover, a new problem arises: rms errors are available for Taylor-catalog data (as before), but strict equivalents are not available for data from the SR set. Moreover, the available data are too scant and too noisy to allow those equivalents to be obtained from the comparison algorithm.

In response to this problem, two solutions are performed. For solution 1, rule (5) is set aside and rms errors quoted in the SR set are adopted. For solution 2, rule (5) is satisfied by adopting an rms error of 0.106 dex. This is effectively the error that would have been applied if the SR set had been available when the Taylor catalogs were compiled[*].

The first steps of the correction process are summarized in Table 1. Note the differences between the Hyades data in the second and third lines of that table. For solution 1, the small rms errors of the Hyades data lead to a large weight for the Hyades contribution to the solution for Z. The resulting value of Z is statistically significant and will be applied. By contrast, the error adopted in solution 2 for the SR set dominates that solution. The resulting value of Z is not significant at 95% confidence and will not be applied. The two values of Z are given in Table 2, where the solution for the Takeda et al. results is included for the sake of completeness.

   
Table 1: Test solutions for data from SR set.

Entry		 $\phantom{\mathrm{^a}}$Solution 1 a $\phantom{\mathrm{^a}}$Solution 2 a

Assumed $\sigma$ per datum		 From Smith 0.106
  (1998, 1999)  
Hyades (Smith 1999) $\phantom{\mathrm{^b}}+\!0.196 \pm 0.021\mathrm{^b}$ $\phantom{\mathrm{^b}}+\!0.196 \pm 0.075\mathrm{^b}$
Hyades (Taylor 1998b) $\phantom{\mathrm{^c}}+\!0.104 \pm 0.009\mathrm{^c}$ $\phantom{\mathrm{^c}}+\!0.104 \pm 0.009\mathrm{^c}$
$\mu $ Leo (SR) $\phantom{\mathrm{^d}}+\!0.276 \pm 0.030\mathrm{^d}$ $\phantom{\mathrm{^d}}+\!0.276 \pm 0.106\mathrm{^d}$
a
The units of all numerical entries are dex.
b
The correction to compatible model atmospheres has been made, and Eq. (10) has been applied (see Sect. 2.3.3).
c
Dwarfs (Taylor 1994) and solution D for giants (Taylor 1998b) contribute to this mean value. The use of solution I for giants would not affect this result appreciably.
d
These are interim values. The corrections to be given in Table 2 have not (yet) been applied. The correction to compatible model atmospheres has been made, and Eq. (10) has been applied (see Sect. 2.3.3). The temperature correction is -0.034 dex.


   
Table 2: Statistical analyses for added $\mu $ Leo data.

Number Zero-point Scale   $\sigma$ per
Source of data $\phantom{\mathrm{^a}}$correction a $\phantom{\mathrm{^b}}$factor b $\phantom{\mathrm{^c}}C\mathrm{^c}$ $\phantom{\mathrm{^a}}$datum a

Takeda et al. (1998)		 30 $\phantom{-}0.70 \pm 0.24$ $-0.68 \pm 0.23$ 0.995 $\phantom{\mathrm{^d}}0.061\mathrm{^d}$
SR solution 1 e 4 $-0.073 \pm 0.021$ - 0.999 $\phantom{\mathrm{^e}}-\mathrm{^e}$
SR solution 2 e 4 $-0.041 \pm 0.056$ - - $\phantom{\mathrm{^e}}-\mathrm{^e}$
a
Units are dex.
b
Units are dex. The scale factor is multiplied by $\theta \equiv 5040/T_{\rm e}$.
c
This is the confidence level for a difference from zero. No entry is given if C < 0.95.
d
The derived number of degrees of freedom for this result is 6.1.
e
See Table 1. Results for $\beta$ Gem (Drake & Smith 1991) are not included because of uncertainty about the rms errors for data that contribute to the Taylor catalog (see Sect. 6 of Taylor 1998b). If those data are included with conservative weighting, the quoted result does not change appreciably.

2.4 Results from the complete updated $\mu $ Leo data base

The updated $\mu $ Leo data base will now be considered. For complete rules and procedures for assembling and analyzing the data, the reader is invited to consult Sects. 5 and 7 of T99. The discussion given here will include explanatory comments referring back to T99.

The first task at hand is to consider data that are set aside before averaging is performed. As is noted in Sect. 2.1, such editing must be derived from numerical evidence. The reasons for deleting data and the list of deleted data have not changed from T99, so the list is not repeated here. The list and its explanation may be found in Table 2 and Sect. 7.1 of T99.

The second task is to assemble accepted data with well-established zero points. Those data are listed in Table 3, with asterisks flagging results added in this paper. Note that all data added - including both the solution 1 and solution 2 SR data - fall well within the range of previous results.

 

 
Table 3: [Fe/H] for $\mu $ Leo a.

[Fe/H]
Source b (dex)

Gustafsson et al. (1974)		 $0.39 \pm 0.10$
Oinas (1974) $\,\geq$ $0.38 \pm 0.11\phantom{\geq}\mkern4mu$
(Bonnell & Branch 1979)  
McWilliam & Rich (1994) $0.35 \pm 0.11$
Gratton & Sneden (1990) $0.34 \pm 0.11$
Branch et al. (1978) $0.32 \pm 0.11$
Cayrel de Strobel (1991) $0.30 \pm 0.11$
SR (Solution 2) $**0.28 \pm 0.11**$
Williams (1971) $0.26 \pm 0.10$
McWilliam (1990) $0.25 \pm 0.12$
Peterson (1992) $0.20 \pm 0.11$
Blanc-Vaziaga et al. (1973) $0.20 \pm 0.11$
(Cayrel de Strobel 1991)  
SR (Solution 1) $**0.20 \pm 0.04**$
Brown et al. (1989) $0.18 \pm 0.09$
Takeda et al. (1998) $**0.16 \pm 0.06**$
Luck & Challener (1995) $0.14 \pm 0.11$
Ries (1981), Lambert & Ries (1981) $0.12 \pm 0.07$
Pagel (Bell 1976) $\,\leq$ $0.10 \pm 0.14\phantom{\leq}\mkern4mu$

a
The values of [Fe/H] quoted here and elsewhere in this paper are from the analyses described in T99 and this paper. Usually the analysis has changed the data somewhat from the way they appear in their source papers. Data added in this paper appear with asterisks.
b
If an earlier source of equivalent widths is analyzed in a later paper, the later paper is cited in parentheses.

The T99 procedure includes tests for excessive scatter and wild points. Details of those tests are not given here because they are unchanged from T99: neither excessive scatter nor wild points are found at 95% confidence. The data may therefore be averaged, using reciprocal squares of their rms errors as weights. Results of six trial averages are given in Table 4, which gives details about the way the averages are constructed.

One intended use of the Table 4 entries is to test the hypothesis that [Fe/H] < +0.2 dex. As in T99, there is at least one result on each side of this question, so its status remains unchanged. A second use which seems required by the SR analysis is to find out whether their conclusion that [Fe/H] $\geq +0.3$ dex is defensible in the statistical paradigm[*]. Using t tests of the Table 4 entries, this hypothesis is rejected at 98% confidence.

A third possible use of the Table 4 averages is to decide how well the metallicity of $\mu $ Leo is known. With the continuing problem with SMR status acknowledged, it seems fair to say that the metallicity is now known well enough for most other purposes. In particular, it would be feasible to use $\mu $ Leo as a comparison star when high-dispersion analyses of other K giants with strong absorption features are performed.

3 A contrasting perspective: SR and the "default paradigm''

There is a competitor to the analysis described above which may be described as a "default paradigm'' (Taylor 2001). Without using that name, T99 has described the properties of the default paradigm in some detail (see Sects. 2 and 8 of T99). In addition, it has been discussed in Sects. 6 and 7 of Taylor (2001). For that reason, only a brief review of the state of the paradigm before the appearance of SR will be given here.

The default paradigm is used to interpret values of [Fe/H] without statistical analysis. The paradigm is concerned only with the numbers which emerge from high-dispersion analyses, and is not concerned with the nature of the analyses themselves. The character of the default paradigm is effectively defined by its uses in the literature. The application of the paradigm to $\mu $ Leo data is of particular concern at present, but the paradigm is not inherently limited to data from any given star or group of stars.

The term "default paradigm'' has not been used in papers in which it has been applied. For this reason, concern has been expressed to the present author about the fairness of using such a term. Fortunately, the SR methodology reinforces the argument that the paradigm merits a label because of its methodological unity. The following points may be noted.

   
Table 4: [Fe/H] for $\mu $ Leo: averages a.

SR		 C96 Datum from Luck & Mean value  
solution $\phantom{^\mathrm{b}}$included? b Challener (1995) of [Fe/H] (dex) $\phantom{^\mathrm{c}}t^{\mathrm{c}}$

1		 No Spectroscopic $\log g$ $0.221 \pm 0.022$ 0.95
1 Yes Spectroscopic $\log g$ $0.230 \pm 0.022$ 1.38
1 Yes Physical $\log g$ $0.227 \pm 0.021$ 1.27
2 No Spectroscopic $\log g$ $\phantom{^\mathrm{d}}{\bf0.231} \pm {\bf0.025}^{\mathrm{d}}$ 1.24
2 Yes Spectroscopic $\log g$ $0.243 \pm 0.025$ 1.71
2 Yes Physical $\log g$ $0.239 \pm 0.023$ 1.60
a
Weighting is by inverse variances of rms errors from Table 3 and Sect. 2.4. The rms errors quoted in the table include a temperature contribution (see Eq. (4) of Taylor 1998a and Eq. (A2) of T99).
b
The Castro et al. (1996) datum is included in some trials and excluded from others because its zero point is fallacious and must be guessed (see Sect. 3 of T99). When it is included, [Fe/H] is taken to be $+0.460 \pm 0.106$ (see Eq. (5) of T99).
c
This is the value of $t \equiv \sigma^{-1} \{ {\rm [Fe/H]} - 0.2 \mkern6mu {\rm dex} \}$, with $\sigma$ and [Fe/H] being from the column just to the left. t is used to test the hypothesis that [Fe/H] $\leq 0.2$ dex. If this null hypothesis is rejected, $t \geq 1.66$ and is given in boldface. One-tailed t tests are applied here, as required.
d
This average is based on a conservative choice of input data and is recommended for general use.


   
Table 5: The default paradigm: post-1978 schools.

Principal   Principal
School defined in </I>a $\phantom{^\mathrm{b}}$datum$\mkern6mu$(dex) </I>b School defined in </I>a $\phantom{^\mathrm{b}}$datum$\mkern6mu$(dex) </I>b

Harris et al. (1987) </I>c		 +0.48 C96 </I>f +0.46
Eggen (1989) </I>d $+{\bf0.11}$ McWilliam (1997) </I>f,g +0.45
Gratton & Sneden (1990) </I>e +0.34 CdS et al. (1999) </I>h +0.33
McWilliam & Rich (1994) </I>f +0.42 SR +0.29
a
If the listed paper is not the source of the principal datum, that source is given in a footnote.
b
These data are quoted directly from the source papers, and so differ from their counterparts in Table 3.
c
The principal datum is from Branch et al. (1978).
d
The principal datum is from Lambert & Ries (1981).
e
The datum in this paper is later used to support the schools of Cayrel de Strobel et al. (1999) and SR.
f
This paper is part of a linked set of three papers. Original results in earlier papers contribute to schools in later papers.
g
The source of the principal datum is not stated. However, it can be recovered by averaging results from Branch et al. (1978), Gratton & Sneden (1990), McWilliam & Rich (1994), and C96. The Gratton-Sneden datum as rezeroed by C96 is required for this exercise. McWilliam indicates that results from the four cited papers should be the most trustworthy.
h
This paper is Cayrel de Strobel et al. (1999). The principal datum is an average from Gratton & Sneden (1990) and Cayrel de Strobel (1991).

1.
Error bars are stated in SR, but are not used in data comparisons (see especially Sect. 5 of SR, and again note Appendix A of this paper). For previous examples of this practice, compare the abstract and Table 6 of Gratton & Sneden (1990), Tables 12 and 13 of McWilliam & Rich (1994), and Tables 6 and 7 of Castro et al. (1996, hereafter C96). This practice underscores the non-statistical nature of the default paradigm.

2.
SR cite results from the statistical paradigm, but they tacitly reject that paradigm after introducing their value of [Fe/H], and they then apply the default paradigm instead. Their unsupported judgment that the default paradigm is superior appears also in Sect. 1 of C96.

3.
SR apply the term "recent'' to a Hyades data base which includes a result from Chaffee et al. (1971). This application extends the ill-defined use of "recent'' to justify data selections in the default paradigm (see Sect. 2.1 of T99).

4.
SR do not argue against all the $\mu $ Leo data which are listed by T99 and which appear to disagree with their result if their standards of judgment are applied. Omitted data may be either higher than theirs (Branch et al. 1978, +0.48 dex) or lower than theirs (Peterson 1992, +0.2 dex)[*]. The SR data editing is fully consistent with earlier applications of the default paradigm (see Sects. 2.1 and 2.3 of T99).

5.
SR adopt their datum as effectively definitive, and so establish the eighth in a series of "schools of thought'' that have been produced by the default paradigm since the effect of continuum placement on pre-1978 $\mu $ Leo metallicities was established (see Sects. IV and V of Taylor 1982). These schools are listed in Table 5 with their defining values of [Fe/H]. With the exception of Eggen's (1989) school (see the boldface entry in Table 5), all of the schools have defining data that lie above the mean. T99 noted that there was a tacit rule that only data that are higher than $1\sigma$ above the mean are described in decisive language (see Sect. 8 of T99). With the SR school included, an equivalent lower limit of about +0.3 dex appears.
It should be stressed that while SR have added to the applications of the default paradigm, they have not validated it. The paradigm's 0.3-dex lower limit, its rejection of data despite the fact that they cohere with data that are accepted, and its rejection of the statistical paradigm continue to be explained inadequately or not at all. As a result, it seems fair to describe all these aspects of the default paradigm as arbitrary, and to describe all of its applications - including the one by SR - as invalid methods of inference from the data.

4 Summary

When the SR and Takeda et al. data are added to the data base discussed by T99, the statistical paradigm yields a result that is essentially unchanged. One need only add that the hypothesis that [Fe/H] is actually $\geq $+0.3 dex for $\mu $ Leo is rejected at 98% confidence. That hypothesis, which emerges from applications of the default paradigm, rests on a tradition of invalid inferences from the $\mu $ Leo data base which is continued by SR.

Note added in proof: Very recently, it has been suggested in a public forum that result quality for $\mu $ Leo is related to spectral resolution. This hypothesis may be tested by considering 14 Table 3 data for which values of the resolution R are available. A regression of [Fe/H] against log10R yields a slope of $-0.045 \pm 0.040$ dex. This slope does not come close to significance at the $2\sigma$ level, so there is in fact no evidence that any particular value of R yields distinctive results.

Acknowledgements
I thank Mike and Lisa Joner for carefully proofreading this paper, and for suggesting a key improvement in the discussion. I also thank J. Ward Moody for suggesting the term "default paradigm''. Page charges for this paper have been generously underwritten by the College of Physical and Mathematical Sciences and the Physics and Astronomy Department of Brigham Young University.

Appendix A: SR: Their treatment of their zero point

For their mean Hyades result, Perryman et al. (1998) quote an error bar of 0.05 dex. If the contributing data used by Perryman et al. are examined, it is found that this error bar is not an rms error of the mean (Taylor 2000, Appendix B). For the sake of argument, however, suppose that SR did not examine those contributing data and that they treated the Perryman et al. error bar as an rms error of the mean. Given that error bar alone, the 95% confidence interval for the SR zero-point comparison is then approximately $\pm 0.10$ dex.

SR compare two Hyades data (from Smith 1999) with the Perryman et al. Hyades mean. Without error bars, the mean of the Smith data is +0.135 dex, while the Perryman et al. mean is +0.14 dex. The two values are "very close'', as SR state. Suppose, however, that the Perryman et al. error bar is now attached to the difference between those two data. In this case, one concludes at once that their apparent agreement is fortuitous.

If allowance is made for the rms errors of the Smith (1999) results, this conclusion is strengthened. Suppose now that it is exploited by allowing a correction to the SR $\mu $ Leo result of -0.1 dex. That result is then about +0.2 dex. SR describe it as a metallicity enhancement of about a factor of two, which would seem to require it to be close to +0.3 dex instead. All told, it appears that SR did not allow for the effect of the Perryman et al. error bar.

References

 

Copyright ESO 2001