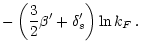A&A 379, 767-780 (2001)
DOI: 10.1051/0004-6361:20011370
Energy, entropy and mass scaling relations for elliptical galaxies.
Towards a physical understanding of their photometric properties
I. Márquez1 - G. B. Lima Neto2 - H. Capelato3 - F. Durret4,5 - B. Lanzoni4,6 - D. Gerbal4,5
1 - Instituto de Astrofísica de Andalucía (C.S.I.C.), Apartado 3004,
18080 Granada, Spain
2 -
Instituto Astronômico e Geofísico/USP, Av. Miguel Stefano 4200,
São Paulo/SP, Brazil
3 -
Instituto Nacional de Pesquisas Espaciais, São José dos Campos/SP,
Brazil
4 -
Institut d'Astrophysique de Paris, CNRS, 98bis Bld Arago, 75014 Paris,
France
5 -
DAEC, Observatoire de Paris, Université Paris VII, CNRS (UA 173),
92195 Meudon Cedex, France
6 -
Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
Received 22 December 2000 / Accepted 18 September 2001
Abstract
In the present paper, we show that elliptical galaxies (Es) obey a
scaling relation between potential energy and mass. Since they are relaxed
systems in a post violent-relaxation stage, they are quasi-equilibrium
gravitational systems and therefore they also have a quasi-constant specific
entropy. Assuming that light traces mass, these two laws imply that in the
space defined by the three Sérsic law parameters (intensity  ,
scale a and shape
,
scale a and shape  ), elliptical galaxies are distributed on two
intersecting 2-manifolds: the Entropic Surface and the
Energy-Mass Surface. Using a sample of 132 galaxies belonging to
three nearby clusters, we have verified that ellipticals indeed follow these
laws.
This also implies that they are distributed along the intersection line (the
Energy-Entropy line), thus they constitute a one-parameter family.
These two physical laws (separately or combined), allow to find the
theoretical origin of several observed photometrical relations, such as the
correlation between absolute magnitude and effective surface brightness, and
the fact that ellipticals are located on a surface in the
), elliptical galaxies are distributed on two
intersecting 2-manifolds: the Entropic Surface and the
Energy-Mass Surface. Using a sample of 132 galaxies belonging to
three nearby clusters, we have verified that ellipticals indeed follow these
laws.
This also implies that they are distributed along the intersection line (the
Energy-Entropy line), thus they constitute a one-parameter family.
These two physical laws (separately or combined), allow to find the
theoretical origin of several observed photometrical relations, such as the
correlation between absolute magnitude and effective surface brightness, and
the fact that ellipticals are located on a surface in the
![$[\log R_{\rm eff}, -2.5
\log \Sigma_0, \log \nu]$](/articles/aa/full/2001/45/aa10611/img17.gif) space.
The fact that elliptical galaxies are a one-parameter family has important
implications for cosmology and galaxy formation and evolution models.
Moreover, the Energy-Entropy line could be used as a
distance indicator.
space.
The fact that elliptical galaxies are a one-parameter family has important
implications for cosmology and galaxy formation and evolution models.
Moreover, the Energy-Entropy line could be used as a
distance indicator.
Key words: galaxies: clusters: individual (Coma, Abell 85,
Abell 496) - galaxies: elliptical and lenticular, cD - galaxies:
fundamental parameters - distance scale - gravitation
Elliptical galaxies (Es) present a striking regularity in their global
luminosity distributions in the sense that, within a wide range of sizes,
their light profiles can be described by simple functions, such as the
Sérsic law (Caon et al. 1993; Graham & Colless 1997; Prugniel & Simien 1997), which is a generalization of the
de Vaucouleurs R1/4 profile. This regularity implies that ellipticals
constitute a well defined family of galaxies. The regular properties of Es
have been the subject of different approaches, concerning both photometric and
spectroscopic parameters, resulting in well known relations such as the
Faber-Jackson and Kormendy relations (Faber & Jackson 1976; Kormendy 1977) or the Fundamental Plane (Djorgovski & Davies 1987; Dressler et al. 1987). Es are supposed to be formed under non collisional processes, where dissipation is expected to be negligible. Under these circumstances, both the initial conditions and the
gravitational forces are expected to have a crucial influence on their
properties.
In previous papers, we have addressed the question of how the properties of
Es may be a consequence of the physical laws they should obey. In
Gerbal et al. (1997) and Lima Neto et al. (1999, hereafter Paper I), we have calculated the specific entropy of Es and shown that the results of analysing the
cluster Es with Sérsic profiles are compatible with a unique
value for this specific entropy, assuming a constant mass/luminosity ratio.
In a subsequent paper, Márquez et al. (2000, hereafter Paper II), we have shown
that the specific entropy of Es was in fact correlated with the logarithm
of the total luminosity while the specific entropy of simulated halos of
collisionless particles was correlated with the logarithm of the total
mass. Moreover, we suggested that another physical law must be operating in
order to explain that Es reside in a thin line embedded in a surface
defined by a (almost) constant specific entropy.
In this paper, we show that this second physical law is in fact a
scaling relation between the potential energy and mass; photometrical
relations can be naturally derived from this scaling law under some
simplifying hypotheses. We also analyse what the consequences on the
origin and evolution of Es are. In Sect. 2 we present a short
theoretical introduction to the concepts we will deal with, from which
we derive a possible explanation for the existence of an energy-mass
relation, and we describe the passage from theoretical parameters to
observational ones using the Sérsic profile. We improve our analysis
taking into account a possible dependence of the mass to light ratio
on the total luminosity. In Sect. 3 we show that similar scaling
relations are also found in other types of self-gravitating systems.
In Sect. 4 we obtain the relations among the Sérsic parameters and
we compare the theoretical predictions with the results from
observational data in Sect. 5. The discussion and conclusions are
given in Sect. 6.
2 Theoretical background
In the standard model of structure formation, initially small
perturbations in the cosmic density field start growing in amplitude
at the same rate. At a given epoch, when their overdensity relative to
the average density is larger than a critical threshold that depends
on the assumed cosmology, they stop expanding with the Universe and
collapse. Bound objects then settle in an equilibrium configuration
through gravitational and radiative processes.
In the following (Sects. 2.1 and 2.2), we
propose two laws that elliptical galaxies should obey if they form and reach
(quasi) equilibrium under the action of gravitational processes only. As a
first approximation, we will assume that radiative processes play a minor role
compared to gravitation.
2.1 Specific entropy
Elliptical galaxies are thought to be in a quasi-equilibrium state, implying
that they should obey the virial theorem. The second law of thermodynamics
states that a system in equilibrium is in a maximum entropy configuration.
Since elliptical galaxies are gravitational systems, they never really reach
an equilibrium state during the time scale of the two-body relaxation.
However, even if the entropy S of an E galaxy is ever increasing on a
secular time scale, after violent relaxation one may consider that the system
is in a quasi-equilibrium stage, which is equivalent to saying that the
entropy is quasi-stationary.
Several works have been devoted to the problem of the entropy in gravitational
systems (see for instance Merritt 1999, and references therein). In a
previous paper (Paper I), we have shown that, assuming that an elliptical
galaxy is in a quasi-equilibrium stage, spherically symmetric with an
isotropic velocity distribution and constant mass-luminosity ratio, a
thermodynamic entropy function can be defined.
In Paper II, instead of using the thermodynamic definition of the entropy,
we adopted the microscopic Boltzmann-Gibbs entropy, defined from the
distribution function in the 6-dimensional phase space. In order to compare
objects of different masses in a consistent way, we have introduced the
specific entropy, i.e. the entropy normalized to the mass:
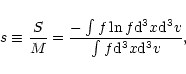 |
(1) |
where f is the distribution function. We have then shown that the specific
entropy s, computed under the previous hypotheses and using the Sérsic
profile is almost the same among Es (within 10%). In fact, based on N-body
simulations, we suggested that s is not strictly unique but, as a result of
merging processes, weakly depends on the logarithm of the galactic mass. We
then showed that the specific entropy and the luminosity are tightly
correlated. Adopting an appropriate M/L ratio (see Sect. 2.3.1
below) this translates to:
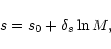 |
(2) |
where s0 and
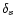 are to be determined by observations.
are to be determined by observations.
2.2 Scaling relation between potential energy and
mass
Let us consider a region with a characteristic length
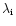 and a mean
density
and a mean
density
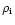 ,
in the initial density field (all quantities will be indexed
with i - for initial). This region is supposed to be the location of a
present E galaxy (its properties will be indexed with p - for present).
,
in the initial density field (all quantities will be indexed
with i - for initial). This region is supposed to be the location of a
present E galaxy (its properties will be indexed with p - for present).
One may suppose, at least to zeroth order, that the following quantities are
conserved during the formation and subsequent evolution of the structure:
- 1.
- the total mass:
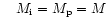 ;
;
- 2.
- the total energy:
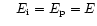 .
.
The total energy at the initial time is:
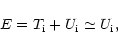 |
(3) |
(where T and U are the kinetic and potential energies), because
the kinetic energy is negligible compared to the potential energy.
At the present stage, when the galaxy is already relaxed, the two following
relations are verified:
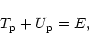 |
(4) |
and
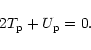 |
(5) |
Equation (5) is the virial relation, which of course does not hold
in the i-case.
Playing the game of addition, subtraction and comparison, we finally obtain the
usual relation for an initially cold gravitational system that collapses and
reaches equilibrium:
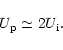 |
(6) |
Notice that, if the initial kinetic energy is taken into account, the above
relation should read
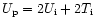 .
.
In the initial linear regime all quantities, such as the typical
perturbation length
 ,
its mass M, and its potential energy
U, are related to one another by scaling relations, e.g. (we will adopt
hereafter G=1):
,
its mass M, and its potential energy
U, are related to one another by scaling relations, e.g. (we will adopt
hereafter G=1):
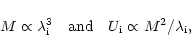 |
(7) |
implying that:
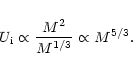 |
(8) |
Using relation (6), we then obtain:
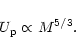 |
(9) |
If we consider the (small) contribution of the initial kinetic energy then the
above relation will be tilted,
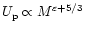 ,
where
,
where
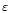 is a small number depending on the exact initial conditions,
e.g., the contribution of
is a small number depending on the exact initial conditions,
e.g., the contribution of 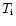 to the total energy and the initial density
fluctuation power spectrum.
to the total energy and the initial density
fluctuation power spectrum.
Equation (9) can be also written as:
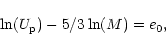 |
(10) |
where e0 is a constant to be determined by observations.
2.3 From theory to observations
2.3.1 Simplifying hypotheses
The relations given in Eqs. (2) and (10) are both
theoretically motivated laws that need to be translated into observable
quantities if one wants to test them observationally. In other words, we
need to go from the observed two dimensional light distribution to a three
dimensional mass distribution. Rather than doing a detailed dynamical and
morphological model, we will assume some simplifying hypotheses: spherical
symmetry, isotropic velocity dispersion tensor and a mass to light ratio
independent of galactic radius R.
The last of these hypotheses, i.e.,
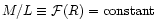 ,
implies that the mass distribution follows the
light profile, with the same scale length and shape. Notice that
the above "constant'' may in fact depend on the total galaxy mass or
luminosity (as we will see below). This hypothesis is clearly a rough
simplification: X-ray observation of giant ellipticals
(e.g. Loewenstein & White 1999), gravitational lensing analyses
(Griffiths et al. 1998), and dynamical studies
(e.g. Gerhard et al. 2001), suggest that
,
implies that the mass distribution follows the
light profile, with the same scale length and shape. Notice that
the above "constant'' may in fact depend on the total galaxy mass or
luminosity (as we will see below). This hypothesis is clearly a rough
simplification: X-ray observation of giant ellipticals
(e.g. Loewenstein & White 1999), gravitational lensing analyses
(Griffiths et al. 1998), and dynamical studies
(e.g. Gerhard et al. 2001), suggest that
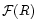 increases with
radius. This increase, however, seems to be important only beyond
increases with
radius. This increase, however, seems to be important only beyond
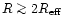 and current data is compatible with
and current data is compatible with
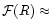 constant for
constant for
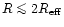 (Kronawitter et al. 2000).
(Kronawitter et al. 2000).
It has been argued (Bertin et al. 1992) that a significant amount of dark
matter can coexist with the stellar component without distorting the
luminosity profile either if both the stellar and dark matter profiles
have the same shape or if the dark matter is much more diffuse, i.e.,
with a larger scale length and lower central density. The former case
corresponds to our hypothesis of a constant
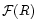 .
In the
latter case, the contribution of the dark matter component will be
important only in the external region of the galaxy.
.
In the
latter case, the contribution of the dark matter component will be
important only in the external region of the galaxy.
The spherical symmetry and isotropy hypotheses imply that the
distribution function is simply a function of one variable, the
binding energy. Although these hypotheses may hold in the internal
region, they must be poor approximations in the external regions of
the most flattened galaxies. However, there is no clear correlation
between ellipticity and luminosity and the effect of neglecting the
flattening should not produce any systematic error.
Finally, we will assume that mass and luminosity are related by a power-law:
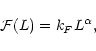 |
(11) |
where the index 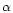 may be zero (equal mass to light ratio for all
ellipticals). The above functional form is suggested, e.g., by the analysis of
the tilt of the Fundamental Plane assuming homology
(e.g., Burstein et al. 1997; Jørgensen et al. 1999), where
may be zero (equal mass to light ratio for all
ellipticals). The above functional form is suggested, e.g., by the analysis of
the tilt of the Fundamental Plane assuming homology
(e.g., Burstein et al. 1997; Jørgensen et al. 1999), where
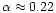 -0.32. Notice that the hierarchical merger simulations discussed by Capelato et al. (1995,1997) give a natural explanation for the origin of the Fundamental Plane
under the hypothesis of a constant value of
-0.32. Notice that the hierarchical merger simulations discussed by Capelato et al. (1995,1997) give a natural explanation for the origin of the Fundamental Plane
under the hypothesis of a constant value of
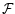 .
.
With the above hypotheses, the mass, potential energy and specific
entropy are easy to compute from the light distribution.
Our working model is the Sérsic (1968) luminosity profile:
![\begin{displaymath}\Sigma = \Sigma_0 \exp[-(R/a)^{\nu}],
\end{displaymath}](/articles/aa/full/2001/45/aa10611/img44.gif) |
(12) |
which describes well the observed surface profile distribution of ellipticals
(e.g., Caon et al. 1993; Graham & Colless 1997; Prugniel & Simien 1997, see also Sect. 6.1), and allows to compute analytically good approximations of all the needed quantities. We therefore adopt this profile to model the observed
surface brightness distribution of a sample of elliptical galaxies (see
Sect. 5.1), and to compute the physical quantities of
interest, like the total mass, the potential energy, the specific entropy,
etc. (see Tables A.1 and A.2 in the Appendix for
a summary of the formulae we use).
Note that the Sérsic law is a non-homologous generalization of the de Vaucouleurs profile, in the sense that a third parameter describing the shape of the
distribution (the structural parameter  )
is introduced and left free,
instead of being fixed to 0.25. This of course allows a better fit to the
observations (Graham & Colless 1997, and Papers I and II).
)
is introduced and left free,
instead of being fixed to 0.25. This of course allows a better fit to the
observations (Graham & Colless 1997, and Papers I and II).
We assume that only one dynamical component describes an elliptical galaxy and
ignore the possible presence of nuclear cusps or embedded discs. This
simplification is motivated by the fact that these components, if present,
usually represent at most a few percent of the total galactic mass
(cf., de Zeeuw & Franx 1991; Kormendy & Richstone 1995, and references therein; see also Saglia et al. 1997).
We stress here that we are doing a pure photometrical analysis and therefore
such a working model is required (with all its simplifying hypotheses) so that
we are able to derive dynamically related quantities like the specific entropy
or the potential energy.
3 Scaling relations: Elliptical galaxies only?
The derivation of the scaling relation between potential energy and
mass is based on fundamental principles (mass and energy
conservation). It can therefore be applied to any object formed by the
growth of density perturbations, driven by gravitational
interaction. Dark matter (DM) halos are therefore expected to follow
the same relation.
Assuming that collisionless N-body simulations provide a suitable
description of DM halo formation, relation (10) should then also
be found automatically in the results of such simulations. We have tested this
hypothesis by considering a cosmological N-body simulation with 5123particles in a 479 Mpc/h side box, characterized by the following
parameters: a 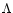 CMD cosmological model, with density parameters
CMD cosmological model, with density parameters
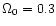 and
and
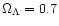 ,
Hubble constant
,
Hubble constant
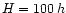 kms-1Mpc-1, h=0.7, and normalization
kms-1Mpc-1, h=0.7, and normalization
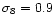 (Yoshida et al. 2001). The corresponding particle mass is
(Yoshida et al. 2001). The corresponding particle mass is
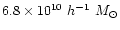 .
A sphere of radius
.
A sphere of radius
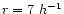 Mpc
around a very massive DM halo (
Mpc
around a very massive DM halo (
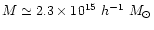 ,
virial radius
,
virial radius
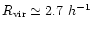 Mpc) has been
selected in the original simulation, and re-simulated at higher resolution (a
factor
Mpc) has been
selected in the original simulation, and re-simulated at higher resolution (a
factor 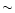 35 increase, to get a mass particle of about
35 increase, to get a mass particle of about
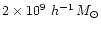 ). Assuming a minimum mass of 10 particles per halo,
this allows to resolve halos down to
). Assuming a minimum mass of 10 particles per halo,
this allows to resolve halos down to
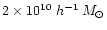 .
.
Figure 1 shows the distribution of potential energy
versus mass for the halos found within the selected sphere, their
masses ranging from 1012 to
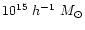 .
We have
selected the halos that had their kinetic to potential energy ratio closer to
the virial theorem value, i.e., the ones satisfying
.
We have
selected the halos that had their kinetic to potential energy ratio closer to
the virial theorem value, i.e., the ones satisfying
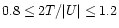 .
Due to the high resolution of the simulation, the computation of the potential
energy is very accurate, at least for all halos more massive than
.
Due to the high resolution of the simulation, the computation of the potential
energy is very accurate, at least for all halos more massive than 
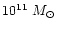 ,
i.e. composed by more than 100 particles.
,
i.e. composed by more than 100 particles.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10611f1.eps}
\end{figure}](/articles/aa/full/2001/45/aa10611/Timg60.gif) |
Figure 1:
Potential energy-mass relation for about 29000 dark matter halos
selected in a high-resolution N-body simulation (see text). The solid line
is the best fit to the data, with a slope of
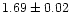 ,
in very good
agreement with the expected theoretical value of 5/3 (dashed line). ,
in very good
agreement with the expected theoretical value of 5/3 (dashed line). |
| Open with DEXTER |
A fit to the data indicates a power-law index of
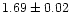 ,
very close to
the theoretical value of 5/3. The difference may be due to the fact that the
N-body simulation takes into account all dynamical processes (mass and
energy exchange and/or loss) self-consistently.
,
very close to
the theoretical value of 5/3. The difference may be due to the fact that the
N-body simulation takes into account all dynamical processes (mass and
energy exchange and/or loss) self-consistently.
We have also verified that this relation is independent on cosmology. In fact,
we found the same slope of the potential-energy mass relation for DM halos in
all the GIF Simulations (Kauffmann et al. 1999), run for four different cosmological
models: SCDM, OCDM, 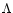 CDM,
CDM, 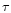 CDM.
CDM.
A comparable simulation of dark matter haloes was done by Jang-Condell & Hernquist (2001)
in a much lower mass range. In this simulation, each particle represents
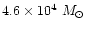 ,
and the range of halo masses is
,
and the range of halo masses is
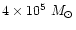 to
to
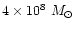 .
The potential energy calculated for 2501
bound halos also seems to follow a power law
.
The potential energy calculated for 2501
bound halos also seems to follow a power law
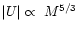 .
.
This is an example of the universality of the scaling relation
between potential energy and mass. Whereas out of the scope of this paper,
numerous questions obviously arise, such as the dependence (or independence)
of the index with redshift or with the cosmology assumed in the simulation.
Interestingly, the analysis of ROSAT-PSPC images of 24 clusters has
also revealed the existence of a scaling law between the cluster
potential energy and the mass of the X-ray gas, with a dependence
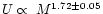 ,
again close to 5/3 (see Durret et al. 2001). Such a scaling law therefore appears to be general for
self-gravitating systems.
,
again close to 5/3 (see Durret et al. 2001). Such a scaling law therefore appears to be general for
self-gravitating systems.
4 Predicted relations among the Sérsic parameters
We now show that the two relations introduced in Sects. 2.1
and 2.2, constraining the distribution of gravitational
matter in galaxies, define two surfaces intersecting each other in the Sérsic parameter space [
 ].
].
The first relation comes from the relation between the specific entropy, s,
and the mass, M, that can be expressed as
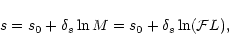 |
(13) |
cf. Eq. (2)![[*]](/icons/foot_motif.gif) . From the expression of the entropy in Table A.1, it
is straightforward to obtain the Entropic Surface in terms of the
Sérsic parameters, Eq. (A.1) shown in the Appendix.
. From the expression of the entropy in Table A.1, it
is straightforward to obtain the Entropic Surface in terms of the
Sérsic parameters, Eq. (A.1) shown in the Appendix.
The second relation is obtained using the definition of potential energy and
mass given in Tables A.1 and A.2, that
can be cast in a general form:
 |
(14) |
where
 and we have dropped the index "p''.
Using the luminosity and the potential energy derived for a mass
distribution following the Sérsic profile (cf.
Table A.1), it is easy to obtain the
Energy-Mass Surface in terms of the observed photometric
Sérsic parameters. The formula describing this surface is shown in
the Appendix, Eq. (A.2).
and we have dropped the index "p''.
Using the luminosity and the potential energy derived for a mass
distribution following the Sérsic profile (cf.
Table A.1), it is easy to obtain the
Energy-Mass Surface in terms of the observed photometric
Sérsic parameters. The formula describing this surface is shown in
the Appendix, Eq. (A.2).
A three dimensional representation of these two surfaces is given in
Fig. 2, in the [
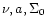 ]
space. The
intersection line (called the Entropy-Energy line in Paper II) is the locus
on which elliptical galaxies are
distributed in the space of the
Sérsic parameters.
]
space. The
intersection line (called the Entropy-Energy line in Paper II) is the locus
on which elliptical galaxies are
distributed in the space of the
Sérsic parameters.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10611f2.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg76.gif) |
Figure 2:
3-D representation of the specific entropy and
energy-mass 2-manifolds, using the coordinates: [
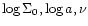 ]. In this example, we assume ]. In this example, we assume
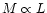 . . |
| Open with DEXTER |
Combining relations (A.1) and (A.2),
i.e. calculating the intersection of the Entropic and Energy-Mass surfaces,
two-by-two relations between the Sérsic parameters can be obtained. The general
[a,  ]
and [
]
and [
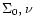 ]
relations are given in the Appendix. For
the particular case where
]
relations are given in the Appendix. For
the particular case where
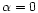 (constant M/L ratio),
(constant M/L ratio),
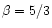 (cf. Sect. 2.2) and
(cf. Sect. 2.2) and
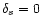 (unique specific
entropy), we have for the [a,
(unique specific
entropy), we have for the [a,  ]
relation:
]
relation:
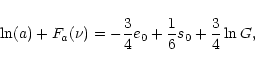 |
(15) |
and, for the [
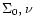 ]
relation:
]
relation:
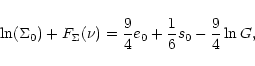 |
(16) |
The relation between a and 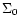 is obtained by combining
relations (15) and (16),
with
is obtained by combining
relations (15) and (16),
with  as a parameter.
as a parameter.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa10611f3.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg83.gif) |
Figure 3:
Histogram of the  distribution
superimposed on the wavelet reconstruction of the density distribution.
distribution
superimposed on the wavelet reconstruction of the density distribution. |
| Open with DEXTER |
5 Predictions faced to observations
5.1 Data set and distribution of the  parameter
parameter
The sample of elliptical galaxies we consider is described in detail in Paper II.
It is composed of 68 galaxies in the Coma Cluster, 30 in Abell 85 and 34
in Abell 496; their cluster membership is confirmed by their redshifts.
For all these galaxies, we have fitted the observed surface brightness
distribution (obtained by CCD imaging in the V band) by means of the Sérsic integrated profile, i.e., using the growth curve fitting method (see Papers I
and II, for a detailed description and discussion of the fitting procedure).
As explained in our previous papers, S0 galaxies were excluded from our sample
because they fall out of the correlations between the Sérsic parameters. To be
able to use all the data as a single set, the fitting parameters a and
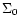 have been expressed in physical units, i.e., in kpc and
have been expressed in physical units, i.e., in kpc and
 /kpc2 respectively
/kpc2 respectively![[*]](/icons/foot_motif.gif) .
.
While in the de Vaucouleurs law a single value of  is used (
is used (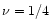 ), our data fitting reveals that this parameter can cover a
range of values, which are not centered on 0.25. We give in
Fig. 3 the density distribution of
), our data fitting reveals that this parameter can cover a
range of values, which are not centered on 0.25. We give in
Fig. 3 the density distribution of  obtained by wavelet reconstruction (see Fadda et al. 1998 for a
description of the method). The distribution is bi-modal, with a first
maximum around
obtained by wavelet reconstruction (see Fadda et al. 1998 for a
description of the method). The distribution is bi-modal, with a first
maximum around 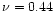 and a second, less pronounced, one around
and a second, less pronounced, one around
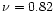 (close to 1, the typical value for dwarf spheroidal
galaxies); notice that in the previously published
(close to 1, the typical value for dwarf spheroidal
galaxies); notice that in the previously published  -histogram
(Paper I), this second maximum is already present, although not as
significantly. This is due to the fact that we are now working with a
larger sample, resulting from the combination of three separate data
sets. It is worth noting however that our sample is more than 97%
complete only up to magnitude
-histogram
(Paper I), this second maximum is already present, although not as
significantly. This is due to the fact that we are now working with a
larger sample, resulting from the combination of three separate data
sets. It is worth noting however that our sample is more than 97%
complete only up to magnitude 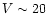 and the giant ellipticals of
Coma were not included because of saturation of the CCD; besides, the
CCD fields do not cover the entire clusters, but only the central
parts (in particular for Abell 85 and 496). Therefore both the
position of the two peaks and their relative intensities may be
somewhat different when considering complete samples.
and the giant ellipticals of
Coma were not included because of saturation of the CCD; besides, the
CCD fields do not cover the entire clusters, but only the central
parts (in particular for Abell 85 and 496). Therefore both the
position of the two peaks and their relative intensities may be
somewhat different when considering complete samples.
5.2 Entropy and energy-mass relations
As discussed in Sect. 2.3, the mass, entropy and
potential energy of all the galaxies in our sample were computed under the
hypothesis that light traces mass.
The uniqueness of the specific entropy of Es has been discussed and
established in Paper I, at least at zeroth order. In Paper II we have
shown that, as a result of energy and mass exchange in merging
processes, s0 weakly depends on the mass. A constant value
for the mass-to-light ratio was assumed in these two papers.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10611f4.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg89.gif) |
Figure 4:
Specific entropy versus mass for three values of
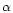 .
The bisector-OSL fits to our 132 galaxy sample are shown as
full lines. .
The bisector-OSL fits to our 132 galaxy sample are shown as
full lines. |
| Open with DEXTER |
We now calculate the specific entropy as a function of mass for three mass to
light relations:
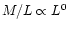 (constant mass to light ratio),
L0.25 (from Fundamental Plane studies, e.g., Burstein et al. 1997) and
L0.5 (extreme case). The results are shown in Fig. 4 and
the best power law fits corresponding to Eqs. (13) and (14) are given in Table 1.
(constant mass to light ratio),
L0.25 (from Fundamental Plane studies, e.g., Burstein et al. 1997) and
L0.5 (extreme case). The results are shown in Fig. 4 and
the best power law fits corresponding to Eqs. (13) and (14) are given in Table 1.
The potential energy is displayed in Fig. 5 as a
function of total mass (adopting G=1). A bisector-OLS (Ordinary Least
Square) power law fit (Feigelson & Babu 1992) gives a indexes
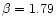 ,
1.83
and 1.85 for
,
1.83
and 1.85 for
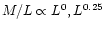 and L0.5 respectively (see
Table 1). However, if we impose
and L0.5 respectively (see
Table 1). However, if we impose
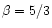 (as predicted in
Sect. 2.2, see Eq. (9)), the fit is still good
enough (within
(as predicted in
Sect. 2.2, see Eq. (9)), the fit is still good
enough (within 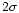 ,
cf. Table 1) to confirm that
Eq. (10) is a good approximation. Fish (1964) analysed a set of
24 Es, fitting their surface brightness profiles with the de Vaucouleurs law,
and found a power law index
,
cf. Table 1) to confirm that
Eq. (10) is a good approximation. Fish (1964) analysed a set of
24 Es, fitting their surface brightness profiles with the de Vaucouleurs law,
and found a power law index
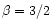 .
The improved accuracy of both our
data and our fitting procedure (using the Sérsic profile), as well as our larger
sample, allow us to definitely exclude
.
The improved accuracy of both our
data and our fitting procedure (using the Sérsic profile), as well as our larger
sample, allow us to definitely exclude
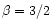 (see also
Sect. 3).
(see also
Sect. 3).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10611f5.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg95.gif) |
Figure 5:
Potential energy (with G=1) versus mass for three values of
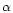 .
The power-law fits (full lines) give slopes of 1.79, 1.83 and 1.85
respectively from top to bottom (see Table 1). The theoretical
relation, with an index of 5/3, is also shown (dashed lines). .
The power-law fits (full lines) give slopes of 1.79, 1.83 and 1.85
respectively from top to bottom (see Table 1). The theoretical
relation, with an index of 5/3, is also shown (dashed lines). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{10611f6.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg108.gif) |
Figure 6:
Pairwise correlation between the Sérsic parameters [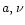 ],
[ ],
[
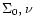 ]
and [ ]
and [
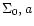 ]
(counter clockwise from top left).
The lines superimposed in each panel are the correlations predicted
from the theoretical slope ]
(counter clockwise from top left).
The lines superimposed in each panel are the correlations predicted
from the theoretical slope 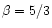 for
for
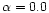 ,
0.25 and 0.50. ,
0.25 and 0.50. |
| Open with DEXTER |
From a mathematical point of view the primary parameters a,
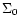 and
and  entering in the definition of the Sérsic profile
are independent from each other. But as discussed in
Sect. 4, the entropy and energy-mass relations,
Eqs. (A.1) and (A.2), imply the
existence of two-by-two relations between the three Sérsic
parameters. From the observational point of view, we know that a,
entering in the definition of the Sérsic profile
are independent from each other. But as discussed in
Sect. 4, the entropy and energy-mass relations,
Eqs. (A.1) and (A.2), imply the
existence of two-by-two relations between the three Sérsic
parameters. From the observational point of view, we know that a,
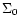 and
and  are in fact correlated (Young & Currie 1995;
Gerbal et al. 1997). We now explain these correlations as originating from the
physical laws discussed in Sect. 2.
are in fact correlated (Young & Currie 1995;
Gerbal et al. 1997). We now explain these correlations as originating from the
physical laws discussed in Sect. 2.
Figures 6 and 7
show the [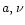 ], [
], [
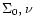 ], and [a,
], and [a,
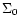 ]
relations for our sample of galaxies. The corresponding theoretical
relations, computed for
]
relations for our sample of galaxies. The corresponding theoretical
relations, computed for
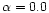 ,
0.25, 0.50 are superimposed on
the data for two cases: the fixed value of
,
0.25, 0.50 are superimposed on
the data for two cases: the fixed value of 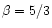 (the
theoretical prediction as in Eq. (8)) and the values
of
(the
theoretical prediction as in Eq. (8)) and the values
of 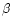 given in Table 1. The theoretical prediction
lies close to the data points, in particular for big galaxies (those
with the smallest
given in Table 1. The theoretical prediction
lies close to the data points, in particular for big galaxies (those
with the smallest  for
for 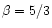 - see Sect. 6.1).
We note that in both cases the effect of changing the M/L ratios is small.
- see Sect. 6.1).
We note that in both cases the effect of changing the M/L ratios is small.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{10611f7.eps}\par\end{figure}](/articles/aa/full/2001/45/aa10611/Timg109.gif) |
Figure 7:
Pairwise correlation between the Sérsic parameters [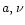 ], [ ], [
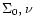 ]
and [ ]
and [
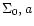 ]
(counter clockwise
from top left). The lines superimposed in each panel are the
correlations predicted from the Entropic Surface (with ]
(counter clockwise
from top left). The lines superimposed in each panel are the
correlations predicted from the Entropic Surface (with
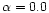 ,
0.25 and 0.50) and the fitted ,
0.25 and 0.50) and the fitted 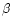 values for the energy-mass scaling
relations for these three values of
values for the energy-mass scaling
relations for these three values of 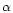 (see Table 1).
(see Table 1). |
| Open with DEXTER |
5.4 From theoretical to observed correlations
The well known photometric correlations which characterize elliptical
galaxies, are usually expressed by means of astrophysical quantities like
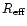 ,
,
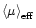 ,
and/or the absolute magnitude of the
galaxies. Since these quantities are combinations of the primary
parameters defining the Sérsic law, if these observed photometric correlations
do indeed contain information on the physics of the objects or on the
processes that drove their formation and evolution, one should, in principle,
be able to derive them from the "theoretical'' relations,
Eqs. (2) and (10). In doing so, we show that it is
indeed possible to give a physical interpretation to some of the observed
correlations and that they are not just artefacts of the definitions of the
parameters.
,
and/or the absolute magnitude of the
galaxies. Since these quantities are combinations of the primary
parameters defining the Sérsic law, if these observed photometric correlations
do indeed contain information on the physics of the objects or on the
processes that drove their formation and evolution, one should, in principle,
be able to derive them from the "theoretical'' relations,
Eqs. (2) and (10). In doing so, we show that it is
indeed possible to give a physical interpretation to some of the observed
correlations and that they are not just artefacts of the definitions of the
parameters.
Before going through the comparison between theory and observation however, it
is necessary to take into account the following points:
- 1.
- The correlations proposed in the literature (e.g., Young & Currie 1994;
Binggeli & Jerjen 1998) result from fitting procedures; the coefficients are just empirical. Moreover, for the sake of simplicity, attempts are usually done to linearize the
correlations. On the contrary, the coefficients that we derive are the
consequence of physical laws, and the relations we have found are non-linear.
- 2.
- The intersection of the specific entropy and of the energy-mass surfaces is a line
that we call the "Energy-Entropy line''. The region of this line populated by
ellipticals is not coplanar, but can be considered as located in a
plane in a restricted range of values.
5.4.1 Luminosity-effective radius relation
From the intersection of the specific entropy and of the energy-mass surfaces,
Eqs. (A.3) and (A.4) parametrized by  ,
we can
derive photometrical relations for Es galaxies using the formulae in
Table A.2.
,
we can
derive photometrical relations for Es galaxies using the formulae in
Table A.2.
In Fig. 8 we plot
the total luminosity as a function of
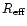 for our data.
for our data.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{10611f8.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg112.gif) |
Figure 8:
Luminosity versus effective radius for our 132 cluster ellipticals.
The theoretical relations obtained for a fixed 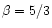 (left) and for the
fitted values of
(left) and for the
fitted values of 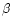 (right) are superimposed for the three different
values of
(right) are superimposed for the three different
values of 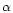 .
The theoretical relation given by Eq. (18) is
superimposed as a dot-dashed line. The continuous, dashed and dotted lines are
obtained using the intersection of the specific entropy-mass and energy-mass
relations, Eqs. (A.1) and (A.2). .
The theoretical relation given by Eq. (18) is
superimposed as a dot-dashed line. The continuous, dashed and dotted lines are
obtained using the intersection of the specific entropy-mass and energy-mass
relations, Eqs. (A.1) and (A.2). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{10611f9.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg113.gif) |
Figure 9:
Mean effective magnitude versus absolute magnitude. The results for
the different values of 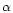 are plotted for the theoretical prediction
are plotted for the theoretical prediction
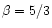 (left) and for the fitted values of
(left) and for the fitted values of 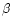 (right). The
theoretical relation given by Eq. (20) is superimposed as a
dot-dashed line. The continuous, dashed and dotted lines have the same meaning
as in Fig. 8.
(right). The
theoretical relation given by Eq. (20) is superimposed as a
dot-dashed line. The continuous, dashed and dotted lines have the same meaning
as in Fig. 8. |
| Open with DEXTER |
Using the definition of the potential energy, relation (10) can be
written as:
![\begin{displaymath}e_{0} = \frac{1}{3} [\ln M - 3\ln r_{\rm g}] ,
\end{displaymath}](/articles/aa/full/2001/45/aa10611/img114.gif) |
(17) |
where 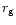 is the gravitational radius and M the mass. Assuming
that
is the gravitational radius and M the mass. Assuming
that
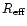 is proportional to
is proportional to 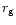 (which is a very good
approximation for galaxies described by the Sérsic profile, see
Table A.2), we then have:
(which is a very good
approximation for galaxies described by the Sérsic profile, see
Table A.2), we then have:
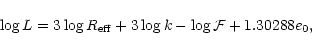 |
(18) |
where
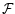 is the M/L ratio and k is the proportionality constant
between
is the M/L ratio and k is the proportionality constant
between
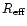 and
and 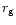 .
This relation is drawn with the dot-dashed
line in Fig. 8. Notice that the theoretical
slope of the L-
.
This relation is drawn with the dot-dashed
line in Fig. 8. Notice that the theoretical
slope of the L-
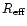 relation, in this case, depends only on the slope
of the scaling relation between mass and potential energy.
relation, in this case, depends only on the slope
of the scaling relation between mass and potential energy.
We can relax some simplifying hypotheses, proportionality between
 and
and 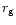 and constant M/L ratio and obtain a more general relation
between L and
and constant M/L ratio and obtain a more general relation
between L and
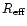 - the price to pay is a much more complicate
expression, instead of Eq. (18). The theoretical relations
obtained for a fixed
- the price to pay is a much more complicate
expression, instead of Eq. (18). The theoretical relations
obtained for a fixed 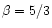 (left) and for the fitted values of
(left) and for the fitted values of 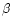 (right) are superimposed for the three different values of
(right) are superimposed for the three different values of 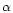 .
Within
the error bars, the relations are compatible with the data. The different
curves vary with M/L when
.
Within
the error bars, the relations are compatible with the data. The different
curves vary with M/L when 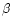 is fixed (
is fixed (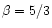 )
but lead to similar
curves when
)
but lead to similar
curves when 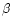 is free.
is free.
Our data and theoretical prediction are steeper than the results found
in the literature. Binggeli et al. (1984) derive
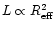 for galaxies with
for galaxies with
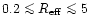 kpc. For smaller galaxies,
however, the slope steeps and reaches our theoretical value of 3. Schombert (1987) also finds that the L-
kpc. For smaller galaxies,
however, the slope steeps and reaches our theoretical value of 3. Schombert (1987) also finds that the L-
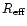 relation is
shallower for the brightest galaxies; for normal ellipticals he finds
relation is
shallower for the brightest galaxies; for normal ellipticals he finds
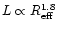 .
Even though these low values are not
incompatible with our data (within the error bars), it should be
stressed that previous L-
.
Even though these low values are not
incompatible with our data (within the error bars), it should be
stressed that previous L-
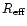 studies were based on the de
Vaucouleurs profile, while we fit our galaxies with the Sérsic law. As
we will see below, different modelling (i.e., de Vaucouleurs or Sérsic laws) of Es may change the observed correlations among their global
parameters.
studies were based on the de
Vaucouleurs profile, while we fit our galaxies with the Sérsic law. As
we will see below, different modelling (i.e., de Vaucouleurs or Sérsic laws) of Es may change the observed correlations among their global
parameters.
5.4.2 Magnitude-mean surface brightness correlation
Taking the definition of
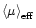 :
:
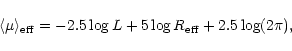 |
(19) |
we can combine it with the energy-mass scaling relation,
Eq. (17), eliminating the effective radius. The results for
the different values of 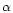 are plotted in
Fig. 9. The theoretical relations obtained for a
fixed
are plotted in
Fig. 9. The theoretical relations obtained for a
fixed 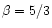 (left) and for the fitted values of
(left) and for the fitted values of 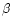 (right)
are superimposed for the three different values of
(right)
are superimposed for the three different values of 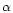 .
The
different curves vary with M/L when
.
The
different curves vary with M/L when 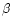 is fixed (
is fixed (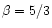 )
but
lead to similar curves when
)
but
lead to similar curves when 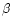 is free.
is free.
If we make the same assumptions as in
Sect. 5.4.1 above, we obtain a relation between
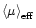 and L, or equivalently, in terms of the absolute
magnitude (
and L, or equivalently, in terms of the absolute
magnitude (
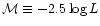 ):
):
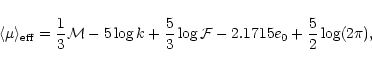 |
(20) |
traced as a dot-dashed line in Fig. 9, where the variables
have the same meaning as in Eq. (18). Note that this relation
does not predict two regimes but a single one. This is indeed in agreement
with the observations when the data are analysed with the Sérsic law, as done by
Jerjen & Binggeli (1997), and as shown in Fig. 9 for our galaxies.
Quantities like
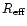 or
or
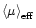 are different when
obtained through a de Vaucouleurs or a Sérsic fit (Graham & Colless 1997; Jerjen & Binggeli 1997): this probably
explains why Binggeli et al. (1984), who used the de Vaucouleurs profile, obtain a
broken power-law
are different when
obtained through a de Vaucouleurs or a Sérsic fit (Graham & Colless 1997; Jerjen & Binggeli 1997): this probably
explains why Binggeli et al. (1984), who used the de Vaucouleurs profile, obtain a
broken power-law
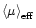 -
-
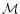 relation, while
Jerjen & Binggeli (1997) and us, using the Sérsic profile, find a single power-law.
relation, while
Jerjen & Binggeli (1997) and us, using the Sérsic profile, find a single power-law.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{10611f10.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg124.gif) |
Figure 10:
The theoretical relation given by the generalized form of the
right-hand side of Eq. (24) (solid, dashed and dotted lines)
is superimposed on the fit (long-short dashed line) obtained by
Khosroshahi (2000) (right-hand side of
Eq. (21)). The two vertical dotted lines correspond the range in
 used by Khosroshahi (2000). The dash-dotted lines correspond to
8% errors on the fit. The shape parameter,
used by Khosroshahi (2000). The dash-dotted lines correspond to
8% errors on the fit. The shape parameter,
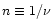 ,
is given at the
top of the figure to allow direct comparison with other authors. ,
is given at the
top of the figure to allow direct comparison with other authors. |
| Open with DEXTER |
5.4.3 Photometric plane
Khosroshahi et al. (2000) have fitted a set of infra-red profiles of E and spiral
bulges with the Sérsic law. They have shown that these galaxies lie on a
plane in the space defined by the set of coordinates
![$[\log R_{{\rm eff}}, \mu_{0},
\log \nu]$](/articles/aa/full/2001/45/aa10611/img125.gif) ,
with
,
with
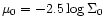 .
Notice that these authors
use
.
Notice that these authors
use 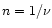 in the Sérsic law. The equation they find for this plane is:
in the Sérsic law. The equation they find for this plane is:
We will now derive a similar equation from a theoretical point of view. For
illustration purpose, we derive here the simplest case with constant mass to
light ratio (
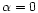 )
and
)
and
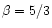 .
The general case is of course
similar but more cumbersome. Including the definition of
.
The general case is of course
similar but more cumbersome. Including the definition of 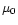 and the
relation between
and the
relation between
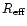 and a into Eqs. (A.1)
and (A.2), after some straightforward algebra, we obtain two
equations:
and a into Eqs. (A.1)
and (A.2), after some straightforward algebra, we obtain two
equations:
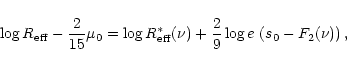 |
(22) |
and
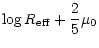 |
= |
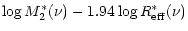 |
|
| |
|
- 1.303 e0 - 1.5113 . |
(23) |
A linear combination between Eqs. (22) and (23) gives:
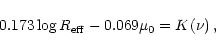 |
(24) |
with:
Relation (24) is obtained from theoretical relations;
on the other hand, relation (21) is a fit to the observed
data. The only differences between these two relations are the two
right-hand sides, i.e. (
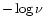 )
should be compared to
)
should be compared to 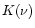 .
Only the forms of the two functions are to be compared since
the constant depends on the units chosen. In Fig. 10, we
call attention to the interval [0.25-0.7] in
.
Only the forms of the two functions are to be compared since
the constant depends on the units chosen. In Fig. 10, we
call attention to the interval [0.25-0.7] in  ,
which
2000 have used to define their photometrical plane. In
particular, their relation given by Eq. (21) and ours
[Eq. (24)] agree within 8% in this range. The good
agreement between the observed points of Khosroshahi et al. and our
theoretical relation shows that the photometric plane may be
understood as a consequence of the two laws discussed in the present
paper. Note however that it is possible to define a "plane'' only
because a limited range of values has been considered for
,
which
2000 have used to define their photometrical plane. In
particular, their relation given by Eq. (21) and ours
[Eq. (24)] agree within 8% in this range. The good
agreement between the observed points of Khosroshahi et al. and our
theoretical relation shows that the photometric plane may be
understood as a consequence of the two laws discussed in the present
paper. Note however that it is possible to define a "plane'' only
because a limited range of values has been considered for  (see
the beginning of Sect. 5.4).
(see
the beginning of Sect. 5.4).
6 Discussion and conclusions
6.1 Ellipticals as a single parameter family
The Sérsic profile is certainly not the ultimate profile to reproduce
the surface brightness of ellipticals, from brighter galaxies to dwarf
ellipticals (see Jerjen & Binggeli 1997).
The Sérsic profile cannot apply to fine features such as boxy isophotes,
central black hole, etc., but it allows a fit of sufficient quality
for our aims, since we use it only to describe large scale properties
(Caon et al. 1993; Graham & Colless 1997; Prugniel & Simien 1997; Márquez et al. 2000). A finer description, which is out of the scope of this paper, would certainly require another
parameter to reproduce the whole profile.
Although the use of the Sérsic profile may seem essential to our calculations,
it is nothing but an analytical expression which works well from the
theoretical point of view (essentially because it provides a shape factor) and
also observationally (it gives good fits). In fact any other function would be
equally appropriate - provided it allows to calculate the entropy, energy,
mass, etc. This is not the case for the de Vaucouleurs law
which is characterized by two parameters only, and for this reason does not
allow to define the specific entropy or energy-mass surfaces. Consequently, it is not possible to
define the Energy-Entropy line using the de Vaucouleurs law.
Notice that the de Vaucouleurs law is a homologous law, i.e., all models are deduced
from a unique template by two scaling transformations. The introduction of a
shape parameter in the Sérsic law destroys - mathematically speaking - this
homology. However, since all galaxies fitted by a Sérsic law roughly have
the same specific entropy, we can eliminate one parameter (
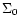 ,
say)
by replacing it with by its expression as function of the two remaining
parameters,
,
say)
by replacing it with by its expression as function of the two remaining
parameters,
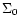 =
=
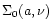 .
Therefore we have -
mathematically speaking - only two independent parameters, like the de Vaucouleurs law.
This procedure, however, does not lead to any kind of homology, for it is not
possible to define a "template'' from which any Sérsic distribution could be
derived only by scaling transformations.
.
Therefore we have -
mathematically speaking - only two independent parameters, like the de Vaucouleurs law.
This procedure, however, does not lead to any kind of homology, for it is not
possible to define a "template'' from which any Sérsic distribution could be
derived only by scaling transformations.
Since all elliptical galaxies also obey the energy-mass relation,
Eq. (10), we can further eliminate another parameter (a, say)
with the result that a single parameter is sufficient to characterize a
galaxy, for instance  .
In this case every galaxy is defined by its shape
parameter
.
In this case every galaxy is defined by its shape
parameter  :
generalizing the de Vaucouleurs law with the introduction of
:
generalizing the de Vaucouleurs law with the introduction of  allows to gather all ellipticals into a single large family, at least from the
photometric point of view.
allows to gather all ellipticals into a single large family, at least from the
photometric point of view.
The mass can then be rewritten formally as a function of  only as:
only as:
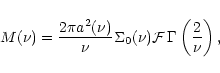 |
(25) |
where the equations for 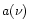 and
and
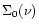 are given in
Eqs. (15) and (16). Moreover,
very large galaxies are endowed with small values of
are given in
Eqs. (15) and (16). Moreover,
very large galaxies are endowed with small values of  while dwarfs have
large values of
while dwarfs have
large values of  (e.g., Caon et al. 1993, see also Paper I; the equation
for
(e.g., Caon et al. 1993, see also Paper I; the equation
for 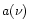 together with the definition of
together with the definition of
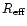 also implies this
result). Thus, the parameter
also implies this
result). Thus, the parameter  plays the role of a concentration
factor. This allows to understand why the de Vaucouleurs law cannot fit with good
confidence these two extreme cases.
plays the role of a concentration
factor. This allows to understand why the de Vaucouleurs law cannot fit with good
confidence these two extreme cases.
Equation (25) above is in fact a bijection
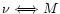 .
During the processes of formation and relaxation,
physics (described by the two laws discussed above) are necessarily acting so
that at the end the above bijection is actually verified.
.
During the processes of formation and relaxation,
physics (described by the two laws discussed above) are necessarily acting so
that at the end the above bijection is actually verified.
The interesting possibility of using the correlation between ![$[a,\nu]$](/articles/aa/full/2001/45/aa10611/img146.gif) as a
distance indicator has been proposed by Young & Currie (1995). This paper has been
followed by controversies (Binggeli & Jerjen 1998; Young & Currie 1998), essentially due, as we
understand it, to the following question: are distance indicators
sufficiently reliable to be usable for single galaxies, or can they only be
applied to clusters globally?
as a
distance indicator has been proposed by Young & Currie (1995). This paper has been
followed by controversies (Binggeli & Jerjen 1998; Young & Currie 1998), essentially due, as we
understand it, to the following question: are distance indicators
sufficiently reliable to be usable for single galaxies, or can they only be
applied to clusters globally?
Since the correlations on which are based the indicators proposed by Young & Currie
(1995) are consequences of the two laws discussed in this paper, it
appears possible to improve their quality. This is because the predicted
relations are essentially non-linear, while the observed correlations
have been tentatively fitted by phenomenological linear laws, as we
already pointed out.
This question has already been mentioned in Paper I and, in view of
the predicted theoretical relations presented here, we therefore hope
to improve the distance indicator based on the shape profile of Es (to
be analysed in depth in a forthcoming paper for a dozen clusters with
redshifts between 0.06 and 0.37).
6.3 Conclusions
We have shown both from theoretical reasons and from observations, that
elliptical galaxies obey a scaling relation between the potential energy and
mass (luminosity). In previous papers, we had already shown that Es share the
same specific entropy (Papers I) with a logarithm dependence on the galactic
mass (that may be due to an evolutionary process, e.g., hierarchical mergers
Paper II).
These two relations, 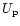 -M and s-
-M and s-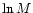 ,
give an explanation to
several observed correlations that have been proposed in the past by various
authors, such as the correlations between the shape factor and a length scale,
the correlation between the absolute magnitude and the central brightness, and
the photometric plane. Therefore they constitute a theoretical background for
a number of physical properties of elliptical galaxies.
,
give an explanation to
several observed correlations that have been proposed in the past by various
authors, such as the correlations between the shape factor and a length scale,
the correlation between the absolute magnitude and the central brightness, and
the photometric plane. Therefore they constitute a theoretical background for
a number of physical properties of elliptical galaxies.
The fact that elliptical galaxies lie on a line in the three dimensional space
of the Sérsic parameters implies that Es are indeed a one-parameter family.
This has important implications for cosmology and galaxy formation and
evolution models. Furthermore, the Energy-Entropy line could be used
as a distance indicator.
Acknowledgements
We acknowledge interesting discussions with Gary
Mamon. I.M. acknowledges financial support from the Spanish Ministerio
de Educación y Cultura and the Instituto de Astrofísica de
Andalucía (C.S.I.C.). This work is financed by DGICyT grants
PB93-0139, PB96-0921, the USP/COFECUB and the
CNPq/CNRS and C.S.I.C./CNRS
bilateral cooperation agreements. G.B.L.N.
acknowledges financial support from the FAPESP. B.L. is
supported by a Marie Curie Training Grant (category 20), under the TMR
Activity 3 of the European Community Program.
Appendix A: Formulae
General formulae useful for definitions or calculations of various
quantities linked with our definition of the Sérsic profile are given in
Tables A.1 and A.2.
Table A.2:
General formulae used in this paper. 2-D and 3-D quantities are marked
with subscript "2'' and "3'', respectively. Quantities marked with a "*''
are adimensional. Some of these expressions were first obtained in Paper I and
are presented here for completeness.
|
|
The relation between the specific entropy and the mass, Eq. (2)
can be expressed as a surface in the Sérsic parameters space with the help of
the mass to light ratio, Eq. (11):
where
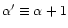 ,
,
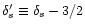 and
the function
and
the function
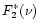 is defined in Table A.2.
is defined in Table A.2.
The scaling relation between the potential energy and the mass gives
another surface in the Sérsic parameters space:
where
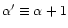 ,
,
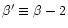 and
the function
and
the function
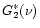 is defined in Table A.2.
is defined in Table A.2.
The intersection of the above two surfaces yields the locus where
elliptical galaxies are found in the Sérsic parameter space. Eliminating
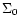 from Eq. (A.1) or Eq. (A.2)
we get:
from Eq. (A.1) or Eq. (A.2)
we get:
Note that 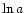 versus
versus  depends on the mass to light ratio
only indirectly via
depends on the mass to light ratio
only indirectly via
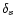 ,
s0,
,
s0, 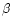 and e0. Likewise,
eliminating
and e0. Likewise,
eliminating 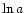 from the surface equations we obtain:
from the surface equations we obtain:
The relation between a and
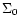 is obtained in parametric form
combining the above two equations and using
is obtained in parametric form
combining the above two equations and using  as a parameter.
as a parameter.
- Bertin, G., Saglia,
R. P., & Stiavelli, M. 1992, ApJ, 384, 423
In the text
NASA ADS
- Binggeli, B., Sandage, A.,
& Tarenghi, M. 1984, AJ, 89, 64
In the text
NASA ADS
- Binggeli, B., & Jerjen, H.
1998, A&A, 333, 17
In the text
NASA ADS
- Burstein, D., Bender, R., Faber, S. M.,
& Nolthenius, R. 1997, AJ, 114, 1365
In the text
NASA ADS
- Caon, N., Capaccioli, M.,
& D'Onofrio, M. 1993, MNRAS, 265, 1013
In the text
NASA ADS
- Capelato, H. V., de Carvalho, R. R.,
& Carlberg, R. G. 1995, ApJ, 451, 525
In the text
NASA ADS
- Capelato, H. V., de Carvalho, R. R.,
& Carlberg, R. G. 1997, in Galaxy Scaling Relations: Origins, Evolution and
Applications, ed. L. N. da Costa, & A. Renzini (Springer-Verlag), 331
In the text
-
Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59
In the text
NASA ADS
-
Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987, ApJ, 313, 42
In the text
NASA ADS
- Durret, F., Demarco, R.,
Magnard, F., & Gerbal, D. 2001, Rencontres de Moriond, March 10-17, 2001,
Les Arcs (Savoie), ed. D. Neumann et al. [astro-ph/0105496]
In the text
- Faber, S. M., & Jackson, R. E. 1976,
ApJ, 204, 668
In the text
NASA ADS
- Fadda, D., Slezak, E.,
& Bijaoui, A. 1998, A&AS, 127, 335
In the text
NASA ADS
- Feigelson, E. D., & Babu, G. J. 1992,
ApJ, 397, 55
In the text
NASA ADS
- Fish, R. A. 1964, ApJ, 139, 284
In the text
NASA ADS
- Gerbal, D., Lima Neto, G. B., Márquez, I.,
& Verhagen, H. 1997, MNRAS, 285, L41
In the text
NASA ADS
- Gerhard, O., Kronawitter, A., Saglia,
R. P., & Bender, R. 2001, AJ, 121, 1936
In the text
NASA ADS
- Graham, A. 1998, MNRAS, 295, 933
NASA ADS
- Graham, A., & Colless, M. 1997,
MNRAS, 287, 221
In the text
NASA ADS
- Griffiths, R. E., Casertano,
S., Im M., & Ratnatunga, K. U. 1998, MNRAS, 282, 1159
In the text
- Jang-Condell, H.,
& Hernquist, L. 2001, ApJ, 548, 68
In the text
NASA ADS
- Jerjen, H., & Binggeli, B. 1997, in
The Nature of Elliptical Galaxies, proceedings of the Second Stromlo
Symposium, ed. M. Arnaboldi et al., ASP Conf. Ser., 116, 239
In the text
- Jorgensen, I., Franx, M., Hjorth,
J., & van Dokkum, P. G. 1999, MNRAS, 308, 833
In the text
NASA ADS
- Kauffmann, G., Colberg, J. M.,
Diaferio, A., & White, S. D. M. 1999, MNRAS, 303, 188
In the text
NASA ADS
- Khosroshahi, H. G.,
Wadadekar, Y., Kembhavi, A., & Mobasher, B. 2000, ApJ, 531, L103
In the text
NASA ADS
- Kormendy, J. 1977, ApJ, 218, 333
In the text
NASA ADS
- Kormendy, J., & Richstone, D.
1995, ARAA, 33, 581
In the text
- Kronawitter, A., Saglia, R. P.,
Gerhard, O., & Bender, R. 2000, A&AS, 144, 53
In the text
NASA ADS
- Lima Neto, G. B., Gerbal, D.,
& Márquez, I. 1999, MNRAS, 309, 481 (Paper I)
In the text
NASA ADS
- Loewenstein, M.,
& White, R. E. 1999, ApJ, 518, 50
In the text
NASA ADS
- Márquez, I., Lima Neto,
G. B., Capelato, H., Durret, F., & Gerbal, D. 2000, A&A, 353, 873 (Paper II)
In the text
NASA ADS
- Merritt, D. 1999, PASP, 111, 129
In the text
NASA ADS
- Prugniel, Ph., & Simien, F.
1997, A&A, 321, 111
In the text
NASA ADS
- Saglia, R. P., Bertschinger, E.,
Baggley, G., et al. 1997, ApJS, 109, 79
In the text
NASA ADS
- Schombert, J. M. 1987, ApJS, 64, 643
In the text
NASA ADS
- Sérsic, J. L. 1968, Atlas de galaxias
australes, Observatorio Astronómico de Córdoba, Argentina
In the text
- Yoshida, N., & the Virgo Consortium
2001, in preparation
In the text
- Young, C. K., & Currie, M. J. 1994, MNRAS,
268, L11
In the text
NASA ADS
- Young, C. K., & Currie, M. J. 1995, MNRAS,
273, 1141
In the text
NASA ADS
- Young, C. K., & Currie, M. J. 1998, A&A,
333, 795
In the text
NASA ADS
- de Zeeuw, T., & Franx, M.
1991, ARAA, 29, 275
In the text
Copyright ESO 2001
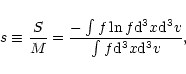
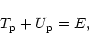
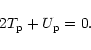
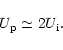
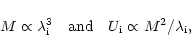
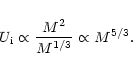
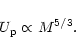
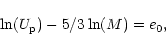
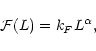
![\begin{displaymath}\Sigma = \Sigma_0 \exp[-(R/a)^{\nu}],
\end{displaymath}](/articles/aa/full/2001/45/aa10611/img44.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10611f1.eps}
\end{figure}](/articles/aa/full/2001/45/aa10611/Timg60.gif)
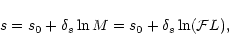

![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10611f2.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg76.gif)
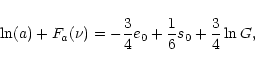

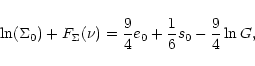
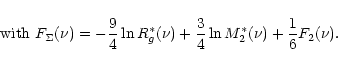
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa10611f3.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg83.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10611f4.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10611f5.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg95.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{10611f6.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg108.gif)
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{10611f7.eps}\par\end{figure}](/articles/aa/full/2001/45/aa10611/Timg109.gif)
![\begin{figure}
\par\includegraphics[width=18cm,clip]{10611f8.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg112.gif)
![\begin{figure}
\par\includegraphics[width=18cm,clip]{10611f9.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg113.gif)
![\begin{displaymath}e_{0} = \frac{1}{3} [\ln M - 3\ln r_{\rm g}] ,
\end{displaymath}](/articles/aa/full/2001/45/aa10611/img114.gif)
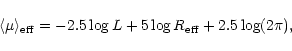
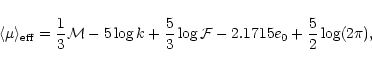
![\begin{figure}
\par\includegraphics[width=18cm,clip]{10611f10.eps}\end{figure}](/articles/aa/full/2001/45/aa10611/Timg124.gif)
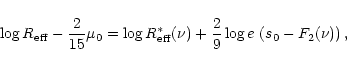
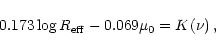
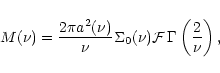
![$\displaystyle{G_{2}^{*}(\nu) \simeq \left( \frac{\Gamma[2/\nu]}{\nu
\Gamma\le...
...ht)^2 \, \exp \left( 1.7958
\nu^{-3/2} + 2.6374 \sqrt{\nu} -5.4843 \right) } $](/articles/aa/full/2001/45/aa10611/img155.gif)

![$\displaystyle + \displaystyle{\left(\alpha' \delta_{s}'+ \frac{3}{2}\right)
\ln \left[ \frac{2 \pi\Gamma(2/\nu)}{\nu}\right]} - F_{2}^{*}(\nu)$](/articles/aa/full/2001/45/aa10611/img194.gif)

![$\displaystyle + \displaystyle{ (\alpha' \beta' + 2) \ln \left[\frac{2 \pi
\Gamma(2/\nu)}{\nu}\right] - \ln[G_{2}^{*}(\nu)] }$](/articles/aa/full/2001/45/aa10611/img201.gif)
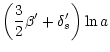
![$\displaystyle + \displaystyle{\left(\frac{3}{2} \beta'- 2
\delta_{s}'\right) \ln\left[\frac{2 \pi \Gamma(2/\nu)}{\nu}\right]}$](/articles/aa/full/2001/45/aa10611/img207.gif)
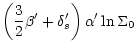
![$\displaystyle - 3 \left(\left[\frac{3}{2} \beta' - \delta_{s}'\right] \alpha' + \frac{3}{2}
\right)
\ln\left[\frac{2 \pi \Gamma(2/\nu)}{\nu}\right]$](/articles/aa/full/2001/45/aa10611/img212.gif)
![$\displaystyle + \left(\frac{3}{2} - 2 \alpha' \delta_{s}' \right) \ln[G 4 \pi^{2} \,
G_{2}^{*}(\nu)/k_{U}]$](/articles/aa/full/2001/45/aa10611/img213.gif)