3 Data analysis

As shown in Fig. 1, fields differ from each other in terms of the noticeable contrast in their stellar densities: Ruprecht 129 and Ruprecht 166 are the fields with the smallest and largest numbers of stars, respectively, the latter having more than 17 times the number of stars measured for the former. This result corroborates the fact that sky regions close to the direction towards the Galactic centre present strong variations in the stellar density at a fixed limiting magnitude, even though they are separated by few degrees. Taking into account these stellar density variations, an open cluster candidate might be identified by the concentration of a handful of bright stars which stand out from a slightly fainter surrounding field, or by a visible increase in the stellar population in a sky region, or by both criteria combined. Occasionally, apparent concentrations of bright stars located approximately along the same direction, or variations in the number of stars caused by the presence of interstellar clouds can lead to identification of unreal open clusters.

We analysed the possible existence of genuine open clusters within the object sample following two different approaches. On the one hand, we investigated the distribution of stars in the (V, B-V) and (V, V-I) CMDs and, on the other hand, we compared the number of stars counted within and outside the cluster candidate fields. From the complementary analysis of both approaches we will achieve a more robust confirmation of the physical reality of these objects.

3.1 Colour-magnitude diagrams

Since the size of our field of view ( $FOV \approx 4\hbox{$^\prime$ }\times 4\hbox{$^\prime$ }$) was considered rather small to outline the boundaries of all the cluster candidates, we used Digitized Sky Survey (DSS) images of 15 $\hbox{$^\prime$ }$ on a side to have a wider view of the selected fields. The fact that the selected objects cannot be embraced by our CCD images suggests that cluster candidates can be more extended than the area covered by the detector and/or that the observed fields do not differ clearly, in terms of stellar density, from their surrounding fields. A wider FOV thus provides a better framework for distinguishing the whole group of stars catalogued as a cluster candidate.

Bearing in mind that open clusters commonly have stars distributed following a non-spherical symmetry, for each object we traced a small circle around what appeared to be its central region, and an ellipse containing the circle to consider the whole extension of the cluster candidate. This ellipse resulted in a compromise between maximizing the object area and minimizing the field star contamination. We overplotted the chosen circles and ellipses on the schematic finding charts of Fig. 1. Cluster candidates are mostly centered on and entirely contained in the observed fields.

Figure 3: Colour-magnitude diagrams of stars in the field of Ruprecht 103. Stars within the circular (top) and elliptical (middle) extractions, as well as all measured stars (bottom) are shown.

Figure 4: Colour-magnitude diagrams of stars in the field of Ruprecht 124. Stars within the circular (top) and elliptical (middle) extractions, as well as all measured stars (bottom) are shown.

Figure 5: Colour-magnitude diagrams of stars in the field of Ruprecht 129. Stars within the circular (top) and elliptical (middle) extractions, as well as all measured stars (bottom) are shown.

Figure 6: Colour-magnitude diagrams of stars in the field of Ruprecht 146. Stars within the circular (top) and elliptical (middle) extractions, as well as all measured stars (bottom) are shown.

We then built (V, B-V) and (V, V-I) CMDs for the circular and elliptical extractions as well as for all the measured stars. These CMDs are shown in Figs. 3 to 7 for Ruprecht 103, 124, 129, 146 and 166, respectively. The upper panels in the figures correspond to the small circular extractions, whereas those in the middle and at the bottom of the figures are from the elliptical and total fields, respectively. If one of the observed candidates was an open cluster, we would expect to be able to define its fiducial Main Sequence (MS) from the circular extraction, and recognize all the cluster features and the unavoidable field star contamination from the elliptical one. Note that the Zero Age Main Sequence (ZAMS) does have a different curvature than the field MS, which follows a lower envelope and depends on the interstellar extinction parameters, namely $R = A_{\rm v}/E(B-V)$ (Burki & Maeder 1973). However, none of the extracted CMDs seems to reveal the presence of an open cluster MS, except possibly in the case of Ruprecht 166 (see discussion below). The star sequences seen in the distinct CMDs, specially for Ruprecht 124 and Ruprecht 129, appear to be formed from the superimposition of field stars of several spectral types affected by different amounts of interstellar absorption and/or located at different distances from the Sun.

The blue star sequence in the CMDs of Ruprecht 103 extends down to V $\sim$ 16 mag, where it undergoes a remarkable break and apparently becomes a vertical sequence at fainter magnitudes. This break is not typical of a cluster MS, thus favouring the conclusion that Ruprecht 103 is not an open cluster. Moreover, even considering the tilted sequence defined only by the bright stars, we were not able to find a young cluster with a main sequence as inclined as the one we observed. Notice that, under the same assumption, the object could not be of intermediate age or older because of the lack of fainter stars. On the other hand, the bigger the area of the extraction is, the more populated the same parts of the CMDs prove to be, which is an indicator that we are dealing with a uniform field star distribution. Similar characteristics can be recognized with fewer and more dispersed field MS stars in the CMDs of Ruprecht 146, which cannot be confirmed as an open cluster either. The CMDs of Ruprecht 124 and Ruprecht 129 show star sequences that cover a magnitude range of more than 5 mags and have inclinations similar to those of Ruprecht 103 and Ruprecht 146. These results, in addition to the increase in the number of stars outside of the tilted sequence with the extracted area in the field of Ruprecht 124, and the noticeable broadness of the star sequence in the CMDs of Ruprecht 129, are strong evidence against the physical reality of these objects as open clusters.

Finally, the case of Ruprecht 166 deserves particular attention. Its CMDs for the innermost regions appear to show an evolved upper MS, typical of intermediate age open clusters, which extends towards fainter magnitudes with a very important dispersion. The two brightest stars located to the upper-left part of the CMDs from the apparent MS should be considered field stars, if we wanted to keep the category of an intermediate age open cluster for the object. However, the (V, B-V) CMD for the elliptical extraction reveals that the apparent cluster MS is composed by a relatively tight star sequence, extended from $V \sim 13$ mag down to $V \sim 17$ mag, and by a populous clump of stars centered at (V, B-V) $\sim$ (18, 1.1). Both sequence and clump of stars have their counterparts in the (V, V-I) CMDs masked like a long MS. Unexpectedly, however, there is not only an abrupt change in the luminosity function along this apparent star sequence (lower panel of Fig. 7), but also an offset for faint stars towards redder colours, which suggest a different origin for these stars. Additionally, it is not possible to fit a ZAMS to the stars in the sequence and in the clump, simultaneously.

   

Table 7: Stellar densities derived for the selected fields

Name	$N_{\rm obj}$	$N_{\rm field}$
	(stars/arcmin2)	(stars/arcmin2)
Ruprecht 103	11	$9\pm1$
Ruprecht 124	13	$13\pm1$
Ruprecht 129	6	$7\pm1$
Ruprecht 146	6	$5\pm1$
Ruprecht 166	26	$22\pm2$

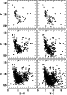Figure 7: Colour-magnitude diagrams of stars in the field of Ruprecht 166. Stars within the circular (top) and elliptical (middle) extractions, as well as all measured stars (bottom) are shown.

Figure 8: Relationship between the number of stars per square arcmin estimated for the object and its surrounding field. Open circles represent the values obtained by Bica et al. (2001) whereas filled circles correspond to results of Table 7. The solid line corresponds to the same number of stars for object and field, respectively.

3.2 Star counts

We performed star counts on the DSS images with the aim of looking for some excess of stars in the observed fields that could favour the status of the catalogued objects as open clusters. Firstly, we used the FIND task within the stand-alone version of the DAOPHOTII package (Stetson 1994) to identify as many stars as possible. We were particularly cautious in the assessment of the appropriate threshold to include in the coordinate list only those objects having stellar profiles. In addition, we checked the identified stars in the DSS images. Secondly, we counted the number of stars within circles of radius $\theta_{\rm obj}$, where $\theta_{\rm obj}$ represents the apparent major radius of each object. This conservative criterion of using circular regions for counting field stars that encompass the object ellipse is an attempt to compensate for the uncertainties in the defined object boundaries. We counted field stars within 100 circles selected randomly and spread throughout each DSS image, discarding those circular regions superimposed on a circle of radius $\theta_{\rm obj}$ centered on the object. The resulting mean values of the number of field stars ( $N_{\rm field}$), together with their corresponding standard deviations ( $\sigma_{N_{\rm field}}$) and the number of stars counted for the objects (same area as for the respective field) are listed in Table 7. As can be seen, object and field densities turned out to be indistinguishable within one or two $\sigma_{N_{\rm field}}$.