In this section, we show that the apodization functions obtained with the interferometric technique correspond to the cosine to the power of N apodizer and calculate the analytical expressions of the PSF for these apodization functions. For more generality and later use, we consider the case where the shift may be b times smaller than the optimal 1/L considered in the previous section.
The amplitude corresponding to the addition of two PSF images distant one another of
![]() can be
written as:
can be
written as:
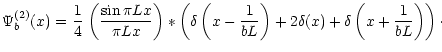 |
(4) |
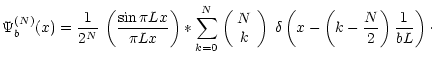 |
(6) |
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{MS1697f3.eps} %
\end{figure}](/articles/aa/full/2001/44/aa1697/Timg40.gif) |
Figure 3: From top to bottom: unapodized PSF, and successive order of N given in Table 1. Dashed plots corresponds to a cut of the PSF along the diagonal direction, as considered in the ASA Concept. |
| Apodization | Impulse responses (normalized) |
| unapodized: |
|
1st order, b=1 |
|
2nd order, b=1 |
|
3rd order, b=1 |
|
The corresponding amplitude in the pupil plane can be obtained directly as the Fourier transform of
Eq. (5). Using basic properties of the Fourier transform of a convolution product, we obtain the
simple expression:
The proposed interferometric technique may be a solution to produce these apodization functions for the ASA concept. To obtain the two dimensional apodizer, two successive devices must be successively used in orthogonal directions. Making b larger than one corresponds to the use of a partial cosine arch apodization: only the central part is used. This apodization will be of interest for coronagraphy (Sect. 4). The above expressions for the amplitude impulse response can be used for an analytical study of the ASA concept even if the interferometric technique is not used to produce the aperture transmission: the diffracted light intensity along the diagonal for a square aperture is simply written as the fourth power of the amplitudes given in Eqs. (7), (8) and Table 1. Illustrations of the diagonal diffracted light for the ASA are given in Fig. 3. These curves were already numerically given by Nisenson & Papaliolios (2001).
Copyright ESO 2001