A&A 379, 426-435 (2001)
DOI: 10.1051/0004-6361:20011316
Photometric validation of a model independent procedure
to extract galaxy clusters![[*]](/icons/foot_motif.gif)
E. Puddu1 - S. Andreon1 - G. Longo
1,2 - V. Strazzullo1 - M. Paolillo1,3 - R. R. Gal4
1 - Osservatorio Astronomico di Capodimonte, via Moiariello
16, 80131 Napoli, Italy
2 -
Dipartimento di Scienze Fisiche, Università Federico II,
Napoli, Italy
3 -
Dipartimento di Scienze Fisiche ed Astronomiche,
Università di Palermo, Napoli, Italy
4 -
Johns Hopkins University, Dept. of Physics and Astronomy,
3701 San Martin Dr., Baltimore, MD 21218, USA
Received 15 May 2001 / Accepted 20 September 2001
Abstract
By means of CCD photometry in three bands (Gunn g, r, i)
we investigate the existence of 12 candidate clusters extracted
via a model independent peak finding algorithm (Puddu et al. 2000)
from DPOSS data. The derived color-magnitude diagrams
allow us to confirm the physical nature of 9 of the cluster candidates,
and to estimate their photometric redshifts. Of the other
candidates, one is a fortuitous detection of a true cluster at
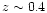 ,
one is a false detection and the last is undecidable on the basis
of the available data.
The accuracy of the photometric redshifts is tested on an additional
sample of 8 clusters with known spectroscopic redshifts. Photometric
redshifts turn out to be accurate within
,
one is a false detection and the last is undecidable on the basis
of the available data.
The accuracy of the photometric redshifts is tested on an additional
sample of 8 clusters with known spectroscopic redshifts. Photometric
redshifts turn out to be accurate within
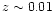 (interquartile range).
(interquartile range).
Key words: methods: data analysis - galaxies: clustering - galaxies: clusters:
photometric redshift
Clusters of galaxies are the largest virialized structures in the
Universe, and accurate knowledge of their global properties is
needed to constrain models of galaxy formation and evolution.
The first step in this direction requires the construction of a
statistically well-defined sample of clusters in the nearby universe
to be used as a "local template". Unfortunately, due to historical and
observational reasons, and in spite of much effort, existing samples cannot
be considered ideal. Existing cluster catalogs, in fact, fall into
three main categories: i) large catalogs derived from photographic
surveys (POSS-I, UKST) by visual inspection and covering wide
portions of the sky (Abell 1958; Abell et al. 1989; Zwicky et al. 1961-68)
but missing the needed depth, homogeneity and completeness
(Postman et al. 1986; Sutherland 1988); ii) catalogs machine extracted
with objective criteria from photographic plates (cf.
Dodd & MacGillivray 1986; Dalton et al. 1992; Lumsen et al. 1992),
reaching, in some cases, limiting magnitudes fainter than (i), but not covering
equally wide areas of the sky and so far available only for the Southern
hemisphere (only UKST plates);
iii) accurate and deeper catalogs usually derived from CCD data and
selected on the basis of objective criteria but covering
much smaller regions of the sky and containing only a small number of objects
(cf. Postman et al. 1996; Olsen et al. 1999).
Excluding the ones, which will be derived from the Sloan Digital Sky Survey (SDSS)
(Kim et al. 2000; Kepner et al. 1999),
for the Northern sky no automatically extracted catalogs of
galaxies (nor of clusters) could be produced until
the recent completion of the Digital Palomar Sky Survey (DPOSS).
DPOSS, which covers three bands (J,F,N), is characterized by
deeper limiting magnitudes than other catalogs extracted from
photographic surveys and therefore
offers an important opportunity to
investigate galaxy clusters in the nearby (i.e. z < 0.4) Universe.
Recently, DPOSS photometric calibration
(Weir et al. 1995) and extraction of the Palomar Norris Sky Catalog
(PNSC) were completed at Caltech in collaboration
with the observatories of Rome, Naples and Rio de Janeiro, partners in the
CRoNaRio project (Djorgovski et al. 1998a; Andreon et al. 1997). This catalog contains astrometric,
photometric
and morphological information for all objects detected
down to limiting magnitudes of
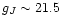 ,
,
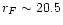 and
and
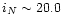 in the Gunn & Thuan photometric system.
With the availability of these new data, various methods to build galaxy
cluster catalogs based on color information have been
proposed (Gal et al. 1999; Gal et al. 2000a).
in the Gunn & Thuan photometric system.
With the availability of these new data, various methods to build galaxy
cluster catalogs based on color information have been
proposed (Gal et al. 1999; Gal et al. 2000a).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1478.fig1.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg10.gif) |
Figure 1:
Detected overdensities in the density map in a
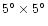 sky region centered at
RA = 1 h and Dec = +15
sky region centered at
RA = 1 h and Dec = +15 .
The smoothing on this map is performed by a .
The smoothing on this map is performed by a
 Gaussian filter.
Squares mark known Abell and Zwicky clusters. Circles mark putative -
previously unknown - clusters.
Gaussian filter.
Squares mark known Abell and Zwicky clusters. Circles mark putative -
previously unknown - clusters. |
| Open with DEXTER |
In order to exploit the scientific potential of the DPOSS, we developed a model
independent procedure to search for cluster candidates. The procedure is detailed
elsewhere and therefore we briefly summarize its main characteristics here
(Puddu et al. 2000; Puddu et al., in preparation).
First, for a given region of the sky, we extract the individual catalogs
obtained from the corresponding J, F and N DPOSS plates and calibrate them
to the g, r and i Gunn-Thuan System using the procedure described
in Weir et al. (1995). Then, after correcting
for misclassified objects in at least one of the three filters (see Puddu et al. 2000),
we produce a
matched (in the three bands) catalog complete to
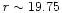 and
and
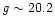 and, in order to ensure completeness, we disregard all objects
fainter then
and, in order to ensure completeness, we disregard all objects
fainter then
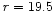 .
The spatial galaxy distribution in the matched catalog is then binned into
equal area square bins of 1.2 arcmin to produce a density map.
S-Extractor (Bertin & Arnouts 1996) is run on the resulting image in order to identify
and extract all the overdensities having number density 2
.
The spatial galaxy distribution in the matched catalog is then binned into
equal area square bins of 1.2 arcmin to produce a density map.
S-Extractor (Bertin & Arnouts 1996) is run on the resulting image in order to identify
and extract all the overdensities having number density 2 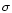 above
the
mean background and covering a minimum detection area of 4 pixels (equivalent
to 4.8 arcmin2) on the map convolved with a
above
the
mean background and covering a minimum detection area of 4 pixels (equivalent
to 4.8 arcmin2) on the map convolved with a
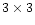 Gaussian filter. We wish to
stress that, as in the Schectman (1985)
approach, we are not assuming any a priori cluster model.
The procedure is run on a given plate catalog to
produce a preliminary candidate cluster catalog.
All previously known Abell and Zwicky clusters are
recovered together with many new cluster
candidates (Fig. 1 shows, as an example, DPOSS field 610)
which need to be confirmed.
The best way to validate cluster finding algorithms would be to apply them to a
field for which redshifts are available for a fairly deep magnitude limited
sample of galaxies. Since such a sample does not exist, we were obliged to follow an
alternative route.
It is well known that early-type galaxies are preferentially located in the
cores of rich clusters and that they present a small scatter in the
color-magnitude diagram (Dressler 1980; Dressler & Gunn 1992; Stanford et al. 1998).
These properties
turn the color-magnitude diagram into a powerful tool to disentangle true
clusters from overdensities of galaxies caused by random object alignment
along the line of sight.
In this paper we use the early type sequences detected in the
color-magnitude diagrams obtained from multiband
optical photometry to confirm a sample of 12 candidates.
These candidate clusters were selected from some fully reduced DPOSS
plates available at the time the test was performed. The selection was
performed randomly in order to include overdensities covering a wide
range of S/N ratios in the detection maps.
We also use a sample of 8 X-ray selected clusters
at nearby and intermediate redshift as templates
to calibrate the photometric redshift estimate.
The paper is structured as follows: in Sect. 2 we describe
the data and the data reduction strategy, in Sect. 3 we show the color-magnitude diagrams for the calibration
sample and illustrate the procedure implemented to derive
the photometric redshift
estimate, while in Sect. 4 we apply this method
to the candidates. In Sect. 5 conclusions and future
developments are discussed.
Gaussian filter. We wish to
stress that, as in the Schectman (1985)
approach, we are not assuming any a priori cluster model.
The procedure is run on a given plate catalog to
produce a preliminary candidate cluster catalog.
All previously known Abell and Zwicky clusters are
recovered together with many new cluster
candidates (Fig. 1 shows, as an example, DPOSS field 610)
which need to be confirmed.
The best way to validate cluster finding algorithms would be to apply them to a
field for which redshifts are available for a fairly deep magnitude limited
sample of galaxies. Since such a sample does not exist, we were obliged to follow an
alternative route.
It is well known that early-type galaxies are preferentially located in the
cores of rich clusters and that they present a small scatter in the
color-magnitude diagram (Dressler 1980; Dressler & Gunn 1992; Stanford et al. 1998).
These properties
turn the color-magnitude diagram into a powerful tool to disentangle true
clusters from overdensities of galaxies caused by random object alignment
along the line of sight.
In this paper we use the early type sequences detected in the
color-magnitude diagrams obtained from multiband
optical photometry to confirm a sample of 12 candidates.
These candidate clusters were selected from some fully reduced DPOSS
plates available at the time the test was performed. The selection was
performed randomly in order to include overdensities covering a wide
range of S/N ratios in the detection maps.
We also use a sample of 8 X-ray selected clusters
at nearby and intermediate redshift as templates
to calibrate the photometric redshift estimate.
The paper is structured as follows: in Sect. 2 we describe
the data and the data reduction strategy, in Sect. 3 we show the color-magnitude diagrams for the calibration
sample and illustrate the procedure implemented to derive
the photometric redshift
estimate, while in Sect. 4 we apply this method
to the candidates. In Sect. 5 conclusions and future
developments are discussed.
Table 1:
Selected overdensities.
Notes:(1) Zwicky cluster.
| OBJ |
RA (2000) |
Dec (2000) |
Richness within |
Detection |
| |
|
|
the isopleth |
S/N |
| 27_694(1) |
05 00 07.24 |
+10 15 52.00 |
76 |
8 |
| 44_778 |
08 59 52.68 |
+04 10 53.20 |
21 |
4 |
| 17_778 |
09 08 28.20 |
+06 03 39.55 |
63 |
8 |
| 5_778 |
09 12 11.09 |
+02 23 10.22 |
17 |
4 |
| 1_778 |
09 12 15.34 |
+02 32 18.11 |
48 |
7 |
| 64_781 |
09 57 25.10 |
+03 39 06.70 |
27 |
5 |
| 72_781 |
09 57 53.23 |
+03 27 10.09 |
59 |
7 |
| 6_725 |
15 24 52.60 |
+11 20 27.10 |
146 |
12 |
| 1_799(1) |
16 03 11.78 |
+03 14 17.63 |
132 |
11 |
| 24_694 |
05 03 38.92 |
+10 38 08.59 |
50 |
7 |
| 21_694 |
05 04 42.34 |
+10 48 49.00 |
70 |
8 |
| 26_727 |
15 57 48.70 |
+08 52 04.39 |
8 |
3 |
Table 2:
Sample of known clusters.
G&L: Gioia & Luppino (1994); S&R: Struble & Rood (1999).
| Id |
RA (J2000) |
Dec (J2000) |
z |
Ref. (z) |
| MS0821.5+0337 |
08 24 07.104 |
+03 27 45.22 |
0.347 |
G&L |
| Abell 1437 |
12 00 24.960 |
+03 20 56.40 |
0.1339 |
S&R |
| MS1253.9+0456 |
12 56 28.827 |
+04 40 01.87 |
0.23 |
G&L |
| Abell 1835 |
14 01 02.399 |
+02 52 55.20 |
0.2532 |
S&R |
| MS1401.9+0437 |
14 04 29.378 |
+04 23 00.33 |
0.23 |
G&L |
| MS1426.4+0158 |
14 28 58.768 |
+01 45 11.94 |
0.32 |
G&L |
| Abell 2033 |
15 11 23.518 |
+06 19 08.40 |
0.0818 |
S&R |
| MS1532.5+0130 |
15 35 02.739 |
+01 20 57.15 |
0.49 |
G&L |
All data used in this paper were obtained in imaging mode with
DFOSC at the ESO 1.54 m Danish telescope (La Silla - Chile) during two
observing runs (March 1999 and March 2000) blessed by dark time and
photometric conditions.
The CCD (LORAL/LESSER C1 W7) has
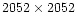 pixels, each pixel covering
pixels, each pixel covering
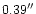 ,
corresponding to a field of
,
corresponding to a field of 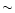
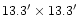 .
Data were taken in the g, r and i filters of
the Thuan & Gunn system (Thuan & Gunn 1976; Wade et al. 1979).
Seeing averaged
.
Data were taken in the g, r and i filters of
the Thuan & Gunn system (Thuan & Gunn 1976; Wade et al. 1979).
Seeing averaged 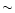
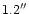 and was always better than
and was always better than
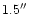 .
The slight difference between our setup and the original Thuan & Gunn
filters resulted in a significant color correction which had to be taken
into account in the calibration procedure.
Exposure times ranged from 40 to 50 min in the g band
and 20 to 30 min in the r and i bands, depending on the target.
In order to obtain higher S/N and more accurate photometric
measurements, exposures for those clusters at intermediate redshift
were usually repeated in two or three slightly offset frames.
The observed fields (all located in a region with
.
The slight difference between our setup and the original Thuan & Gunn
filters resulted in a significant color correction which had to be taken
into account in the calibration procedure.
Exposure times ranged from 40 to 50 min in the g band
and 20 to 30 min in the r and i bands, depending on the target.
In order to obtain higher S/N and more accurate photometric
measurements, exposures for those clusters at intermediate redshift
were usually repeated in two or three slightly offset frames.
The observed fields (all located in a region with
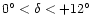 and therefore observable from both hemispheres) included
12 candidate clusters plus 8 clusters with known
redshifts to be used as comparison sample.
In order to use the same material to both calibrate the corresponding DPOSS
fields and to validate our algorithm, we selected galaxy overdensities in
such a way that we had at least two (up to four) candidates and/or
clusters in each DPOSS field. One candidate, observed on two different
nights, also provided an independent check of the photometric accuracy of the
second run.
For the comparison sample we selected 8 clusters from
the X-ray selected sample of Gioia & Luppino (1994) and Ebeling et al. (1996).
The equatorial coordinates of the observed fields are given
in Tables 1 and 2.
We wish to stress that one of the main problems encountered in our work was
the well known lack of a suitable set of photometric standards for the
Gunn-Thuan system which, along with the lack of faint stars suitable for CCD
observations, very often prevents good coverage of the airmass-color plane.
The problem is even worse for observers in the Southern hemisphere where
the number of available standards is uncomfortably small.
We succeeded, however, in observing an average of 4-5 standard stars per observing
night.
The raw images (both scientific and calibration) were prereduced using the
standard procedures available in the IRAF package.
First, the frames were corrected for instrumental effects (overscan
and bias) and flat fielded. Individual dome and sky flats in each filter
were median stacked to increase the S/N ratio.
For the first run, flatfielding was performed using sky flats only, but the
experience gained in this run suggested a slightly different
procedure for the second run, using dome flats to achieve better
correction of the small scale pixel-to-pixel variations.
Dome flats were first used to correct the sky flat frames for the higher
frequency fluctuations, and the resulting frames were then smoothed and stacked
to map the lower frequency fluctuations and combined with the average
dome flat to produce the final master flats.
In the first run, we divided the exposures into two or three frames for the same field; in
these
cases, the images were combined in each filter by medianing (three exposures)
or averaging (two exposures) the aligned frames.
Standard star photometry was performed using the apphot package in IRAF.
Due to the need to defocus most of the stars to avoid saturation, stars
were measured through 10 apertures with diameters up to 90 pixels
(
and therefore observable from both hemispheres) included
12 candidate clusters plus 8 clusters with known
redshifts to be used as comparison sample.
In order to use the same material to both calibrate the corresponding DPOSS
fields and to validate our algorithm, we selected galaxy overdensities in
such a way that we had at least two (up to four) candidates and/or
clusters in each DPOSS field. One candidate, observed on two different
nights, also provided an independent check of the photometric accuracy of the
second run.
For the comparison sample we selected 8 clusters from
the X-ray selected sample of Gioia & Luppino (1994) and Ebeling et al. (1996).
The equatorial coordinates of the observed fields are given
in Tables 1 and 2.
We wish to stress that one of the main problems encountered in our work was
the well known lack of a suitable set of photometric standards for the
Gunn-Thuan system which, along with the lack of faint stars suitable for CCD
observations, very often prevents good coverage of the airmass-color plane.
The problem is even worse for observers in the Southern hemisphere where
the number of available standards is uncomfortably small.
We succeeded, however, in observing an average of 4-5 standard stars per observing
night.
The raw images (both scientific and calibration) were prereduced using the
standard procedures available in the IRAF package.
First, the frames were corrected for instrumental effects (overscan
and bias) and flat fielded. Individual dome and sky flats in each filter
were median stacked to increase the S/N ratio.
For the first run, flatfielding was performed using sky flats only, but the
experience gained in this run suggested a slightly different
procedure for the second run, using dome flats to achieve better
correction of the small scale pixel-to-pixel variations.
Dome flats were first used to correct the sky flat frames for the higher
frequency fluctuations, and the resulting frames were then smoothed and stacked
to map the lower frequency fluctuations and combined with the average
dome flat to produce the final master flats.
In the first run, we divided the exposures into two or three frames for the same field; in
these
cases, the images were combined in each filter by medianing (three exposures)
or averaging (two exposures) the aligned frames.
Standard star photometry was performed using the apphot package in IRAF.
Due to the need to defocus most of the stars to avoid saturation, stars
were measured through 10 apertures with diameters up to 90 pixels
(
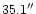 ), and the local sky was determined using a 10 pixel wide annulus outside of the largest aperture.
In order to determine the zero-point offset and the airmass and color terms
we used the 40 pixels (
), and the local sky was determined using a 10 pixel wide annulus outside of the largest aperture.
In order to determine the zero-point offset and the airmass and color terms
we used the 40 pixels (
 )
aperture, for the
focused and unsaturated stars, and the asymptotic magnitudes for the
defocused ones.
The IRAF fitparams task was used to fit the data with the relation
)
aperture, for the
focused and unsaturated stars, and the asymptotic magnitudes for the
defocused ones.
The IRAF fitparams task was used to fit the data with the relation
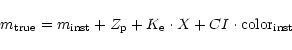 |
(1) |
where 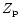 is the zero point of the magnitude scale;
is the zero point of the magnitude scale; 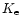 is the
extinction coefficient and X the airmass; CI is the instrumental color
term coefficient.
For the first run (March 1999), due to the paucity of standard stars,
we could determine single night coefficients only for the r and
i filters.
The coefficients were consistent from one night to the other
and we used a mean fit for the g-r color.
For the second run (March 2000) we instead derived the coefficients for
each night and in each band (using the g-r and r-i colors).
The resulting calibration coefficients of the various nights are
consistent within the errors and, therefore, in order to improve the quality
of the fit, we adopted a unique pair of extinction coefficient and color term
for the whole run. These constants were then used to derive the zero
points for each night.
In Fig. 2 we show for the g and r filters,
the fit residuals as a function of the estimated magnitude,
using different symbols for different nights.
is the
extinction coefficient and X the airmass; CI is the instrumental color
term coefficient.
For the first run (March 1999), due to the paucity of standard stars,
we could determine single night coefficients only for the r and
i filters.
The coefficients were consistent from one night to the other
and we used a mean fit for the g-r color.
For the second run (March 2000) we instead derived the coefficients for
each night and in each band (using the g-r and r-i colors).
The resulting calibration coefficients of the various nights are
consistent within the errors and, therefore, in order to improve the quality
of the fit, we adopted a unique pair of extinction coefficient and color term
for the whole run. These constants were then used to derive the zero
points for each night.
In Fig. 2 we show for the g and r filters,
the fit residuals as a function of the estimated magnitude,
using different symbols for different nights.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1478.fig2.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg28.gif) |
Figure 2:
Residuals for the g (upper panel)
and r (lower panel) fit. Different symbols refer to different nights.
The outlier point is Ross 683, which turns out to be
consistently brighter than expected in all four observed nights. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1478.fig3.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg29.gif) |
Figure 3:
Comparison between the photometry of the candidate
cluster 64_781 between nights 2 and 4: the plot shows the
g or r magnitude offset vs. the g or r magnitude. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1478.fig4.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg30.gif) |
Figure 4:
Color-color diagram for the Gunn & Thuan standards
(open circles) and for a sample of stars (filled symbols) extracted from the field
5_778. |
| Open with DEXTER |
The object catalogs were produced individually for each
band using S-Extractor: all objects larger than 4
pixels and 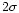 above the background counts were included
and their photometric and morphological features measured.
We used a photometric reference aperture with a diameter
above the background counts were included
and their photometric and morphological features measured.
We used a photometric reference aperture with a diameter 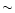 3 times larger than the average seeing.
For each CCD field, the three single band catalogs where
matched taking into account
the shifts between pointings (measured using
the geomap and geotrans IRAF tasks).
To obtain an estimate of the external photometric errors, the
candidate cluster 64_781 was observed on two
different nights. In this way we could evaluate possible
night-to-night magnitude offsets in both the g and r filters. The
typical weighted mean values for these offsets are 0.05 for the
g filter and 0.007 for the r filter, i.e. they are of
the same order as the rms errors from the three parameter calibration fit
(Fig. 3).
Since our goals require high accuracy for the
color determination, we further checked
the photometric calibration, using the following test: in the color-color diagram
(Fig. 4) we plotted the linear sequence of the
Gunn-Thuan standards (open circles) together with all
the unsaturated stars (S-Extractor stellarity index <0.8)
within the limiting magnitude, selected from
some CCD cluster candidate fields (in Fig. 4 we show
the 5_778 field). For all of these fields,
the sequence of the selected stars is linear (excluding the
very red sources, dominated by stars of spectral type M,
which have a constant g-r color while r-i depends
on the spectral subtype; see Fukugita et al. 1996;
Finlator et al. 2000) and overlap quite well with the standard sequence.
This means that the colors of the main
sequence stars are well determined, since the relation
between g-r and r-i is the same for the cluster field stars
and for the standards.
From the g and r matched catalogs
we excluded obvious stars (stellarity index
>0.95) and then selected a box of
3 times larger than the average seeing.
For each CCD field, the three single band catalogs where
matched taking into account
the shifts between pointings (measured using
the geomap and geotrans IRAF tasks).
To obtain an estimate of the external photometric errors, the
candidate cluster 64_781 was observed on two
different nights. In this way we could evaluate possible
night-to-night magnitude offsets in both the g and r filters. The
typical weighted mean values for these offsets are 0.05 for the
g filter and 0.007 for the r filter, i.e. they are of
the same order as the rms errors from the three parameter calibration fit
(Fig. 3).
Since our goals require high accuracy for the
color determination, we further checked
the photometric calibration, using the following test: in the color-color diagram
(Fig. 4) we plotted the linear sequence of the
Gunn-Thuan standards (open circles) together with all
the unsaturated stars (S-Extractor stellarity index <0.8)
within the limiting magnitude, selected from
some CCD cluster candidate fields (in Fig. 4 we show
the 5_778 field). For all of these fields,
the sequence of the selected stars is linear (excluding the
very red sources, dominated by stars of spectral type M,
which have a constant g-r color while r-i depends
on the spectral subtype; see Fukugita et al. 1996;
Finlator et al. 2000) and overlap quite well with the standard sequence.
This means that the colors of the main
sequence stars are well determined, since the relation
between g-r and r-i is the same for the cluster field stars
and for the standards.
From the g and r matched catalogs
we excluded obvious stars (stellarity index
>0.95) and then selected a box of 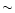 300 pixels in size
(corresponding to a typical
core cluster diameter of
300 pixels in size
(corresponding to a typical
core cluster diameter of 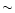 750 kpc at
750 kpc at
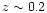 ),
centered on the approximate cluster center and a second
box of equal size located as far as possible from the cluster,
to be used for the evaluation of the background contribution.
),
centered on the approximate cluster center and a second
box of equal size located as far as possible from the cluster,
to be used for the evaluation of the background contribution.
Our procedure is summarized in Fig. 5,
![\begin{figure}
\par\includegraphics[width=17cm,clip]{1478f5.eps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg32.gif) |
Figure 5:
Complete set of plots for two confirmed (upper half) and
two uncertain (lower half) cluster candidates. Each set of plots consists
of color-magnitude diagrams for background + cluster box; color-magnitude diagrams
for background box; color-magnitude diagrams for statistically corrected cluster
objects; radial profiles and spatial distributions over the CCD field
of the objects within a color strip around the early-type sequence.
The four sets of plots refer respectively to: a) OV17_778, a typical rich
nearby cluster (
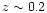 ); b) OV6_725, a poor cluster at redshift ); b) OV6_725, a poor cluster at redshift
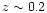 ;
c) OV21_694 and d) OV24_694, uncertain clusters,
with less evidence for the early-type sequence in the color-magnitude
diagrams, and for density peaks in the spatial distribution. ;
c) OV21_694 and d) OV24_694, uncertain clusters,
with less evidence for the early-type sequence in the color-magnitude
diagrams, and for density peaks in the spatial distribution. |
| Open with DEXTER |
which shows the results
for four sample candidates which are representative of the
various morphologies encountered.
For all candidates in our sample we first obtained the color-magnitude
diagrams for both the cluster and background objects. Then, in order to
enhance the early-type sequence, we performed the statistical subtraction of the
background contribution by eliminating
for each object in the background diagram the corresponding nearest
galaxy in the cluster+background diagram.
If we then isolate the objects contained within a narrow strip of
the color-magnitude diagram centered around the early-type sequence,
the galaxy overdensities become more evident in both the spatial
distribution and in the number counts radial profile
(Fig. 5; the radial profile was calculated by choosing as
cluster center the barycenter of the density distribution).
The plots in Fig. 5 can
be used as a criterion to distinguish true clusters (candidates
(a) and (b)), even if they are difficult to detect.
In some cases (usually candidates which are either
too distant or too poor), despite the presence of an apparent sequence
in the color-magnitude diagram,
the objects do not form a physical overdensity, but
turn out to be uniformly distributed on the sky. In these cases
it is more difficult to reach any definite conclusion about the physical
nature of the candidate.
We chose as templates a sample of X-ray clusters for which,
at least in principle, the early-type sequence in the
color-magnitude diagrams should be easily detectable.
This sample was also used
to investigate whether or not it was possible to derive an acceptable
estimate of the redshift from the g-r color of the early-type
sequences.
In Fig. 6 we plot the color-magnitude diagrams for the 8 clusters
in the X-ray sample including only the cluster contribution (i.e., after the
statistical subtraction of the background).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1478.fig9.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg33.gif) |
Figure 6:
Color-magnitude diagrams after statistical background
subtraction for the X-ray cluster sample. According to Gioia & Luppino (1994),
MS1401 is a loose cluster, without a dominant galaxy; MS1426 contains
spirals and possibly interacting systems, and moreover may be two clusters
in projection. A Seyfert galaxy at z=0.074 is present in the foreground
of the MS1532 field. Abell 2033 is of Bautz-Morgan type III and richness class 0. |
| Open with DEXTER |
It is quite evident that some of the early-type sequences are
only broadly outlined (MS1401, MS1426, MS1532), which may
be caused either by the intrinsic faintness of
the cluster members or by cluster structural features
(poorness, looseness and presence of interacting systems;
see the comments in Gioia & Luppino 1994 about these
three clusters). For each cluster we derived a median g-r color
using only the 5 brightest galaxies after the background
subtraction (continuous line),
from which we also estimated the redshift.
The crosses represent the g-r colors corresponding to the
literature redshifts.
Some techniques for deriving redshifts from broadband photometry
consist of matching observed elliptical galaxy
colors with those predicted from the Spectral Energy
Distributions (SEDs) (Visvanathan & Sandage 1977) of
a template elliptical galaxy at zero-redshift and corrected
according to the redshift: since ellipticals become redder as
their redshift increases and since the redshift dependent
correction (k-correction), is monotonically increasing in the near
and intermediate redshift Universe, colors can be used to infer
the cluster redshift.
There is no agreement in the literature for the g-r color
of ellipticals at zero-redshift:
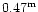 ,
according
to Schneider et al. (1983); 0.38 mag for Frei & Gunn (1994);
,
according
to Schneider et al. (1983); 0.38 mag for Frei & Gunn (1994);
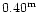 to
to
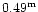 according to Fukugita et al. (1995). Differences in
these values likely depend on the galaxy spectrum template
adopted for the ellipticals and on the use
of a synthetic or an observed spectrum for the standard
stars defining the photometric system. To a lesser extent,
differences are due to the variations in the actual shape
of the Gunn g and r filters (convolved with the
atmosphere, mirror and glass transmissions, CCD quantum
efficiency, etc.) and possibly also to the
way in which the colors are computed.
In the absence of a definite value, we left the zero-redshift
color of ellipticals as the unique free parameter and constrained
it with our own observations by (robustly) fitting the
relation between color and redshift. Figure 7
shows (filled dots) the observed colors from the color-magnitude
relation
vs. known spectroscopic redshift for our X-ray cluster sample.
according to Fukugita et al. (1995). Differences in
these values likely depend on the galaxy spectrum template
adopted for the ellipticals and on the use
of a synthetic or an observed spectrum for the standard
stars defining the photometric system. To a lesser extent,
differences are due to the variations in the actual shape
of the Gunn g and r filters (convolved with the
atmosphere, mirror and glass transmissions, CCD quantum
efficiency, etc.) and possibly also to the
way in which the colors are computed.
In the absence of a definite value, we left the zero-redshift
color of ellipticals as the unique free parameter and constrained
it with our own observations by (robustly) fitting the
relation between color and redshift. Figure 7
shows (filled dots) the observed colors from the color-magnitude
relation
vs. known spectroscopic redshift for our X-ray cluster sample.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1478.fig10.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg37.gif) |
Figure 7:
The observed colors from the color-magnitude relation and
their errors for the X-ray cluster sample (filled circles)
are plotted, compared to the expected color of ellipticals (continuous line)
as a function of spectroscopic redshift. |
| Open with DEXTER |
The expected color
of ellipticals (continous line) were computed using
the Schneider et al. (1983) k-correction curve and our
own determination of the elliptical colors. The average g-rcolor of ellipticals of zero redshift turns out to be
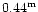 ,
i.e. the
average of the four previously quoted literature values. Errors on
the colors are given as one third of the interquartile range,
which roughly corresponds, for a Gaussian distribution of five points
to the error on the mean. We prefer these to the standard
error since they are more robustly determined. Figure 7
shows that all points are compatible with the curve within
,
i.e. the
average of the four previously quoted literature values. Errors on
the colors are given as one third of the interquartile range,
which roughly corresponds, for a Gaussian distribution of five points
to the error on the mean. We prefer these to the standard
error since they are more robustly determined. Figure 7
shows that all points are compatible with the curve within 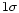 ,
excluding two points, which are
within
,
excluding two points, which are
within 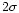 .
The agreement is good, provided that there is
only one free parameter (the rest-frame elliptical color).
Figure 8 compares the photometric redshift,
.
The agreement is good, provided that there is
only one free parameter (the rest-frame elliptical color).
Figure 8 compares the photometric redshift,
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1478.fig11.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg40.gif) |
Figure 8:
Photometric vs. spectroscopic redshift. The solid line
is the bisector and is not derived from data fitting. |
| Open with DEXTER |
estimated
from the color-magnitude diagrams and the spectroscopic
redshift. The agreement is good, and the error (interquartile range)
on the redshift is, on average,
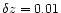 ,
i.e. 3000 kms-1.
Table 3 lists the estimated photometric redshifts, with the errors computed as
previously defined, for the putative clusters;
since these clusters are fairly rich systems, this error is likely to be a lower
limit.
In Fig. 9 we show the early-type sequences obtained (after
subtracting
the background) for the 12 candidate clusters in our sample.
We
confirm 9 of the 12 candidates as true clusters,
one is a fortuitous detection of a cluster at
,
i.e. 3000 kms-1.
Table 3 lists the estimated photometric redshifts, with the errors computed as
previously defined, for the putative clusters;
since these clusters are fairly rich systems, this error is likely to be a lower
limit.
In Fig. 9 we show the early-type sequences obtained (after
subtracting
the background) for the 12 candidate clusters in our sample.
We
confirm 9 of the 12 candidates as true clusters,
one is a fortuitous detection of a cluster at
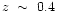 ,
one is a false detection and the last is undecidable on the basis
of the available data.
,
one is a false detection and the last is undecidable on the basis
of the available data.
The better definition of the early-type sequences observed in the DPOSS
confirmed clusters sample with respect to the X-ray sample is likely
due to the different specific properties of the two samples:
at a given z,
our optically selected clusters are on the average
richer and more centrally concentrated then the
X-ray selected ones.
For the cluster OV27_694, the early-type sequence is less defined due to
the overlap of two independent clusters/groups along the
line of sight.
The case of OV21_694 merits special attention.
As a visual inspection of the corresponding POSS-II F plate
shows, the marginal detection of an early type sequence (Figs. 5
and 9)
seems to be due to the chance alignment of a distant cluster (at
redshift
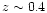 )
with a rich galaxy field.
The existence of such a
foreground rich field has therefore triggered the search algorithm.
As far as OV24_694 and OV26_727 are concerned, the marginal evidence for
an early-type sequence does not correspond to a defined
overdensity in the number count radial profiles (using galaxies in the
strip centered on the mean g-r color).
The case of OV26_727 is a false cluster detection, since it has a low S/N ratio
and low isophotal richness (see Table 1; it may be a group).
Visual inspection of the POSS-II plate shows that OV24_694 lies in
a crowded field rich with galaxies; from the sky diagram (Fig. 5d) it is also evident that a large fraction of these foreground galaxies
have the same color. Thus, this field could be part of a larger loose cluster
or a cluster in a region with variable background.
)
with a rich galaxy field.
The existence of such a
foreground rich field has therefore triggered the search algorithm.
As far as OV24_694 and OV26_727 are concerned, the marginal evidence for
an early-type sequence does not correspond to a defined
overdensity in the number count radial profiles (using galaxies in the
strip centered on the mean g-r color).
The case of OV26_727 is a false cluster detection, since it has a low S/N ratio
and low isophotal richness (see Table 1; it may be a group).
Visual inspection of the POSS-II plate shows that OV24_694 lies in
a crowded field rich with galaxies; from the sky diagram (Fig. 5d) it is also evident that a large fraction of these foreground galaxies
have the same color. Thus, this field could be part of a larger loose cluster
or a cluster in a region with variable background.
Table 3:
New redshift estimate.
(1): The faintness
of the galaxies, as observed both on CCD and on plate
suggests that the candidate cluster is far, as puts forward by
the redness of the color-magnitude relation;
(2): the color-magnitude shows a large scatter,
suggesting that this cluster is possibly contaminated by a
foreground group.
| OBJ |
z est. |
z est. min |
z est. max |
| 17_778 |
0.195 |
0.169 |
0.209 |
| 1_778 |
0.234 |
0.219 |
0.247 |
| 1_799 |
0.314 |
0.299 |
0.326 |
| 21_694(1) |
0.488 |
0.466 |
0.511 |
| 24_694 |
0.282 |
0.271 |
0.295 |
| 26_727 |
0.216 |
0.204 |
0.23 |
| 27_694(2) |
0.204 |
0.183 |
0.218 |
| 44_778 |
0.243 |
0.228 |
0.255 |
| 5_778 |
0.189 |
0.159 |
0.205 |
| 64_781 |
0.139 |
0.110 |
0.159 |
| 6_725 |
0.218 |
0.205 |
0.232 |
| 72_781 |
0.219 |
0.207 |
0.234 |
The aim of our work was to test the validity of a model independent cluster
finding algorithm, implemented to extract a statistically well defined sample
of cluster candidates from photometrically
calibrated DPOSS data (see Paper I for details).
The advantages of a model independent approach are that i) the program
does not assume any a priori knowledge about the clusters, and ii) it
objectively looks for statistically meaningful overdensities in the
galaxy density field.
The main problem in validating any cluster finding algorithm is the lack
of a suitable data set to use as a template, i.e., the lack of a
region of the sky containing a large sample of clusters with well
defined redshifts and properties.
In the absence of such a data set, we adopted a photometric approach based
on the use of the sequence defined in the
color-magnitude diagrams of clusters by bright early-type galaxies as a diagnostic tool.
We obtained deep multiband CCD photometry for a sample of 12 candidate
clusters extracted from the DPOSS data, plus an additional sample of 8
X-ray clusters with known redshifts to be used as a template to
calibrate the photometric redshift procedure.
Results may be summarizied as follows: among the 12 clusters candidates,
10 are confirmed clusters, 1 is false and 1 is uncertain. The X-ray
selected cluster sample was then used both to check the accuracy
(
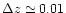 )
and to find the zero point (i.e., the average
zero-redshift g-r color for elliptical galaxies in our system:
(g-r)0
=0.44) for the photometric redshift procedure.
This procedure is being applied to a larger sample of clusters derived
from both DPOSS calibration data and from other archive datasets.
Future papers will deal with the analysis of a larger sample of clusters
(
)
and to find the zero point (i.e., the average
zero-redshift g-r color for elliptical galaxies in our system:
(g-r)0
=0.44) for the photometric redshift procedure.
This procedure is being applied to a larger sample of clusters derived
from both DPOSS calibration data and from other archive datasets.
Future papers will deal with the analysis of a larger sample of clusters
( 200) identified on both DPOSS and archive data and will focus
on the derivation and analysis of luminosity functions (both individual
and cumulative) and of radial number count profiles (Strazzullo 2001).
200) identified on both DPOSS and archive data and will focus
on the derivation and analysis of luminosity functions (both individual
and cumulative) and of radial number count profiles (Strazzullo 2001).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1478.fig12.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg44.gif) |
Figure 9:
Color-magnitude diagrams after statistical background
subtraction for the 12 candidate clusters with complete observations. The
three upper right diagrams refer to not confirmed candidates (OV21_694,
OV24_694, OV26_727). |
| Open with DEXTER |
- Abell, G. O. 1958, A&AS, 3, 211
In the text
- Abell, G. O., Corwin, H. G., & Olowin,
R. P. 1989, ApJS, 70, 1
In the text
- Andreon, S., Zaggia, S., de
Carvalho, R., et al. 1997, in Rencontres de
Moriond, ed. G. Mamon, T. X. Thuan, & Y. T. Van
(Éditions Frontières, Gif-sur-Yvette)
In the text
- Bertin, E., & Arnouts, S. 1996,
A&AS, 117, 393
In the text
NASA ADS
- Couch, W. H., Ellis, R. S., Malin,
D. F., et al. 1991, MNRAS, 249, 606
NASA ADS
- Dalton, G. B., Efststhiou, G., Maddox,
S. J., et al. 1992, ApJ, 390, L1
In the text
NASA ADS
- Djorgovski, S. G., de Carvalho,
R. R., Gal, R. R., et al. 1998, in IAU Symp. 179,
ed. B. J. McLean, D. A. Golombeck, J. J. E. Hayes,
& H. E. Payne (Kluwer Academic Publ), 424
- Djorgovski, S. G., Gal, R. R.,
Odewahn, S. C., et al. 1998, in Wide
Field Surveys in Cosmology, ed. S. Colombi, Y. Mellier, &
B. Raban (Éditions Frontières, Gif-sur-Yvette), 89
In the text
- Dodd, R. J., & MacGillivray,
H. T. 1986, AJ, 92, 706
In the text
NASA ADS
- Dressler, A. 1980, ApJ, 236, 351
In the text
NASA ADS
- Dressler, A., & Gunn, J. E. 1992,
ApJS, 78, 1
In the text
NASA ADS
- Ebeling, H., Voges, W., Bohringer,
H., et al. 1996, MNRAS, 283, 1103
In the text
NASA ADS
- Finlator, K., Ivezic, Z., Fan, X., et al. 2000, AJ, 120, 2615
In the text
NASA ADS
- Frei, Z., & Gunn, J. E. 1994, AJ, 108,
1476
In the text
NASA ADS
- Fukugita, M., Shimasaku,
K., & Ichikawa, T. 1995, PASP, 107, 945
In the text
NASA ADS
- Fukugita, M., Ichikawa, T., Gunn,
J. E., et al. 1996, AJ, 111, 1748
In the text
NASA ADS
- Gal, R. R., de Carvalho, R. R.,
Djorgovski, S. G., et al. 1998,
American Astronomical Society Meeting, 193, 202
- Gal, R. R., Odewahn, S. C., Djorgovski,
S. G., et al. 1999,
in Photometric Redshifts and Detection of High Redshift
Galaxies, ed. R.
Weymann et al., ASP Conf. Ser., 191, 185
In the text
- Gal, R. R., de Carvalho, R. R., Odewahn,
S. C., et al. 2000, AJ, 119, 12
In the text
NASA ADS
- Gal, R. R., de Carvalho, R. R., Brunner,
R., et al. 2000, AJ, 120, 540
NASA ADS
- Gioia, I. M., & Luppino, G. A. 1994,
AJS, 94, 5838
In the text
- Kepner, J., Fan, X., Bahcall, N., et al.
1999, ApJ, 517, 78
In the text
NASA ADS
- Kim, R., Strauss, M., Bahcall, N., et al.
2000, in Clustering at High Redshift,
ed. A. Mazure, O. Le Fevre, & V. Le Brun, ASP Conf. Ser.,
200, 422
In the text
- Lumsden, S. L., Nichol, R. C., Collins,
C. A., et al. 1992, MNRAS, 258, 1
In the text
NASA ADS
- Olsen, L. F., Scodeggio, M., da
Costa, L., et al. 1999, A&A, 345, 6810
In the text
- Postman, M., Geller, M. J., & Huchra,
J. P. 1986, AJ, 91, 1267
In the text
NASA ADS
- Postman, M., Lubin, L. M., Gunn,
J. E., et al. 1996, AJ, 111, 615
In the text
NASA ADS
- Puddu, E., Andreon, S., Longo, G.,
et al. 2000, MmSAI, vol. 71, No. 4, in press
In the text
- Schectman, S. A. 1985, AJS, 57, 77
- Schneider, D. P., Gunn,
J. E., & Hoessel, J. 1983, ApJ, 264, 337
In the text
NASA ADS
- Stanford, S. A., Eisenhardt, P. R.,
& Dickinson, M. 1998, 1998, ApJ, 492, 461
In the text
NASA ADS
- Strazzullo, V., Master Thesis, in preparation In the text
- Struble, M. F., & Rood, H. J. 1999,
ApJS, 125, 35
NASA ADS
- Sutherland, W. 1988, MNRAS, 234, 159
In the text
NASA ADS
- Thuan, T. X., & Gunn, J. E. 1976,
PASP, 88, 543
In the text
NASA ADS
- Visvanathan, N., & Sandage, A. 1977,
ApJ, 216, 214
In the text
NASA ADS
- Wade, R. A., Hoessel, J. G., Elias, J. H.,
et al. 1979, PASP, 91, 35
In the text
NASA ADS
- Weir, N., Djorgovski,
S. G., & Fayyad, U. M. 1995, AJ, 110, 1
In the text
NASA ADS
- Weir, N., Fayyad, U. M., Djorgovski,
S. G., & Roden, J. 1995, PASP, 107, 1243
In the text
NASA ADS
- Zwicky, F., Herzog, E., Wild, P., et al. 1961-68, Catalogue of Galaxies & Clusters of Galaxies
In the text
Copyright ESO 2001
![]() ,
one is a false detection and the last is undecidable on the basis
of the available data.
The accuracy of the photometric redshifts is tested on an additional
sample of 8 clusters with known spectroscopic redshifts. Photometric
redshifts turn out to be accurate within
,
one is a false detection and the last is undecidable on the basis
of the available data.
The accuracy of the photometric redshifts is tested on an additional
sample of 8 clusters with known spectroscopic redshifts. Photometric
redshifts turn out to be accurate within
![]() (interquartile range).
(interquartile range).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1478.fig1.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg10.gif)
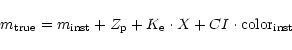
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1478.fig2.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1478.fig3.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1478.fig4.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{1478f5.eps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg32.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1478.fig9.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1478.fig10.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg37.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1478.fig11.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg40.gif)
![]() )
with a rich galaxy field.
The existence of such a
foreground rich field has therefore triggered the search algorithm.
As far as OV24_694 and OV26_727 are concerned, the marginal evidence for
an early-type sequence does not correspond to a defined
overdensity in the number count radial profiles (using galaxies in the
strip centered on the mean g-r color).
The case of OV26_727 is a false cluster detection, since it has a low S/N ratio
and low isophotal richness (see Table 1; it may be a group).
Visual inspection of the POSS-II plate shows that OV24_694 lies in
a crowded field rich with galaxies; from the sky diagram (Fig. 5d) it is also evident that a large fraction of these foreground galaxies
have the same color. Thus, this field could be part of a larger loose cluster
or a cluster in a region with variable background.
)
with a rich galaxy field.
The existence of such a
foreground rich field has therefore triggered the search algorithm.
As far as OV24_694 and OV26_727 are concerned, the marginal evidence for
an early-type sequence does not correspond to a defined
overdensity in the number count radial profiles (using galaxies in the
strip centered on the mean g-r color).
The case of OV26_727 is a false cluster detection, since it has a low S/N ratio
and low isophotal richness (see Table 1; it may be a group).
Visual inspection of the POSS-II plate shows that OV24_694 lies in
a crowded field rich with galaxies; from the sky diagram (Fig. 5d) it is also evident that a large fraction of these foreground galaxies
have the same color. Thus, this field could be part of a larger loose cluster
or a cluster in a region with variable background.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1478.fig12.ps} \end{figure}](/articles/aa/full/2001/44/aa1478/Timg44.gif)