A&A 379, 683-689 (2001)
DOI: 10.1051/0004-6361:20011307
S. Das
- I. Chattopadhyay
- A. Nandi
- S. K. Chakrabarti![]()
S. N. Bose National Centre for Basic Sciences, Salt Lake, Kolkata 700098, India
Received 15 May 2001 / Accepted 30 August 2001
Abstract
We self-consistently estimate the outflow rate from the
accretion rates of an accretion disk around a black hole
in which both the Keplerian and the sub-Keplerian matter
flows simultaneously. While Keplerian matter supplies
soft-photons, hot sub-Keplerian matter supplies thermal
electrons. The temperature of the hot electrons is decided by
the degree of inverse Comptonization of the soft photons.
If we consider only thermally-driven flows from
the centrifugal pressure-supported boundary layer around
a black hole, we find that when the thermal electrons are
cooled down, either because of the absence of the boundary
layer (low compression ratio), or when the surface of the
boundary layer is formed very far away, the outflow rate is
negligible. For an intermediate size of this boundary layer
the outflow rate is maximal. Since the temperature of the
thermal electrons also decides the spectral state of
a black hole, we predict that the outflow rate should be
directly related to the spectral state.
Key words: X-rays: stars - stars: winds, outflows - black hole physics
Most of the galactic black hole candidates are known to undergo
spectral state transitions (Tanaka & Lewin 1995; Chakrabarti &
Titarchuk 1995, hereafter CT95; Ebisawa et al. 1996). Two common states are
the so-called hard state and the soft state. In the former, soft-X-ray
luminosity is low and the energy spectral index
![]() (
(
![]() )
in the 2-10 keV range. In the latter state,
the soft-X-ray luminosity is very high, and hard-X-ray
intensity is negligible. There is also a weak power-law
hard-tail component with an energy spectral slope
)
in the 2-10 keV range. In the latter state,
the soft-X-ray luminosity is very high, and hard-X-ray
intensity is negligible. There is also a weak power-law
hard-tail component with an energy spectral slope
![]() .
In the two component advective flow (TCAF) model (CT95),
the viscous Keplerian disk resides
in the equatorial plane, while the weakly viscous sub-Keplerian flow
flanks the Keplerian component both above and below the
equatorial plane. The two components merge into a single component
when the Keplerian disk also become sub-Keplerian. It is suggested
(Chakrabarti 1990) that close to a black hole, at around 10-
.
In the two component advective flow (TCAF) model (CT95),
the viscous Keplerian disk resides
in the equatorial plane, while the weakly viscous sub-Keplerian flow
flanks the Keplerian component both above and below the
equatorial plane. The two components merge into a single component
when the Keplerian disk also become sub-Keplerian. It is suggested
(Chakrabarti 1990) that close to a black hole, at around 10-
![]() ,
(
,
(
![]() is the Schwarzschild radius,
is the Schwarzschild radius,
![]() and c are the mass of the black hole and the velocity of
light respectively) the sub-Keplerian flow slows down due
to the centrifugal barrier and becomes hotter. Chakrabarti
(1999, hereafter Paper I) shows that this centrifugal
pressure-supported boundary layer (CENBOL for short) region could be
responsible for the generation of thermally-driven outflowing
winds and jets and computed the ratio of the outflow to the inflow
rate assuming a simple conical accretion disk model.
and c are the mass of the black hole and the velocity of
light respectively) the sub-Keplerian flow slows down due
to the centrifugal barrier and becomes hotter. Chakrabarti
(1999, hereafter Paper I) shows that this centrifugal
pressure-supported boundary layer (CENBOL for short) region could be
responsible for the generation of thermally-driven outflowing
winds and jets and computed the ratio of the outflow to the inflow
rate assuming a simple conical accretion disk model.
In the present paper, we compute the absolute value
of the outflow rate as a function of the rates of the two inflow
components, Keplerian and sub-Keplerian. This we do
analytically following the recently developed
procedure of obtaining shock locations (Das et al. 2001). By dynamically mixing these
two components using solutions of the viscous transonic flows
we obtain the specific energy and angular momentum of the sub-Keplerian
region. We use these pair of parameters to locate shocks in the flow,
compute the compression ratio and from this, the outflow rate.
We note that as Keplerian matter is increased in the mixture, the shock
compression ratio goes down, and the outflow rate decreases. This is
also the case even from a radiative transfer point of view - when the
Keplerian rate is high, the CENBOL region is completely cooled
and the shock compression ratio ![]() .
Hence in the soft state,
which is due to increase of the Keplerian rate,
outflow should be negligible.
.
Hence in the soft state,
which is due to increase of the Keplerian rate,
outflow should be negligible.
In the next section, we present the governing equations to compute the outflow rates using a purely analytical method. We compute results for both the isothermal and adiabatic outflows. In Sect. 3, we present our results for a single component sub-Keplerian flow. We also produce examples of realistic disks with Keplerian and sub-Keplerian components and obtain outflow rates as functions of the inflow parameters. In Sect. 4, we discuss our results and draw conclusions.
We consider matter accreting on the equatorial plane of a
Schwarzschild black hole. Spacetime around the black hole is
described by the Paczynski-Wiita pseudo-Newtonian potential
![]() (Paczynski & Wiita
1980) where
(Paczynski & Wiita
1980) where
![]() is the mass of the black hole and G,
c are the gravitational constant and velocity of light respectively.
Here, r is the radial distance from the origin of
the co-ordinate in which the black hole is treated at the centre.
We use geometric units in which all the length, time and
velocity scales are measured in units of
is the mass of the black hole and G,
c are the gravitational constant and velocity of light respectively.
Here, r is the radial distance from the origin of
the co-ordinate in which the black hole is treated at the centre.
We use geometric units in which all the length, time and
velocity scales are measured in units of
![]() ,
,
![]() and c respectively. In future, we use
r to denote non-dimensional distance,
and c respectively. In future, we use
r to denote non-dimensional distance, ![]() and a
to denote the non-dimensional radial velocity and adiabatic
speed of sound respectively. In accretion or outflow,
we assume that the viscous stress is negligible so that
matter moves with a constant specific angular momentum.
Indeed, even if viscosity is not negligible, the
transport of angular momentum is slow compared to the
infall timescale. Hence, matter can have almost constant
specific angular momentum.
and a
to denote the non-dimensional radial velocity and adiabatic
speed of sound respectively. In accretion or outflow,
we assume that the viscous stress is negligible so that
matter moves with a constant specific angular momentum.
Indeed, even if viscosity is not negligible, the
transport of angular momentum is slow compared to the
infall timescale. Hence, matter can have almost constant
specific angular momentum.
In this case, the radial momentum equation for a non-dissipative
flow in vertical equilibrium is given by (Chakrabarti 1989),
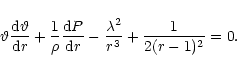 |
(1) |
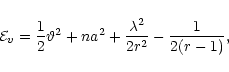 |
(2) |
The mass flux conservation equation in a flow which
is in vertical equilibrium is given by,
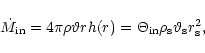 |
(3) |
A sub-Keplerian flow with a positive energy will pass through the outer sonic point and depending on whether the Rankine-Hugoniot condition is satisfied or not, a standing shock may form (Chakrabarti 1990; Chakrabarti 1996). If a standing shock forms, then the post-shock flow would become hotter and would emit hard X-ray radiation. This CENBOL region behaves similarly to the boundary of a normal star; it would be expected to drive outflows. Using Eqs. (2) and (3), it is easy to obtain shock locations (i.e., outer surface of the CENBOL) analytically. Briefly, the procedure to obtain shocks involves the following steps:
(a) For a given pair of specific energy
![]() and angular momentum
and angular momentum
![]() ,
one obtains a quartic equation for the sonic point
and solves it for the three sonic points located outside the horizon.
Two of them are saddle type or "X'' type sonic points and one is
a centre type or "O'' type sonic point.
,
one obtains a quartic equation for the sonic point
and solves it for the three sonic points located outside the horizon.
Two of them are saddle type or "X'' type sonic points and one is
a centre type or "O'' type sonic point.
(b) From the inner and the outer "X'' type points, Mach numbers are expressed as polynomials of radial distance r. These Mach number expressions satisfy constraints that they must have appropriate values at the sonic points.
(c) In addition, it is enforced that the Mach number invariants at the
shock location are also satisfied (![]() ).
).
(d) The resulting equation becomes quartic in ![]() and the shock locations
are obtained from its solution.
and the shock locations
are obtained from its solution.
Details are discussed in Das et al. (2001). We consider only
the region of the inflow parameter space (
![]() )
that is able to produce standing shocks.
)
that is able to produce standing shocks.
In the pre-shock region, matter is cooler and is sub-Keplerian.
Assuming
![]() (freely falling condition) and
(freely falling condition) and ![]() (cool gas)
in presence of angular momentum, matter will fall with a velocity,
(cool gas)
in presence of angular momentum, matter will fall with a velocity,
![\begin{displaymath}\vartheta(r)=\left[\frac {1}{r-1}-\frac {\lambda^2}{r^2} \right]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2001/44/aa1476/img29.gif) |
(4) |
At the shock
![]() ,
i.e., the boundary of the CENBOL,
the compression ratio is given by,
,
i.e., the boundary of the CENBOL,
the compression ratio is given by,
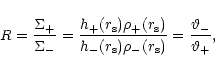 |
(5) |
At the shock, the total pressure (thermal and ram pressure) is balanced:
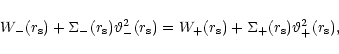 |
(6) |
We assume that in the pre-shock region, the thermal pressure
is small in comparison to the ram pressure,
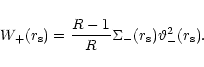 |
(7) |
![\begin{displaymath}C^2_{\rm s}=\frac {W_{+}}{\Sigma_{+}}=\frac {R-1}{R^2}\varthe...
...s}-\lambda^2(r_{\rm s}-1)}
{r^2_{\rm s}(r_{\rm s}-1)}\right],
\end{displaymath}](/articles/aa/full/2001/44/aa1476/img36.gif) |
(8) |
Up to the sonic point matter moves slowly and the density is higher.
Since the outflow would take place in a sea of radiation,
the momentum deposition is likely to be effective.
With the electron number density
![]() ,
yet photon number density
,
yet photon number density
![]() ,
it is
easier to deposit momentum only close to the black hole.
In radiation driven outflows from the stellar surface, it is
customary to assume flows to be isothermal until the sonic point.
We first compute outflow rates making this assumption.
Later we drop this assumption and show that the
general behaviour remains similar.
In addition, we assume that there is very little
rotation in the outflow. There is no a priori
reason to assume this, except that there is no observational support
of rotation in the jet and it is possible that due to radiative
viscosity most of the angular momentum is transported
very close to the black hole. Furthermore, it has been
observed that the effect of angular momentum in the outflow
is to bring the sonic points closer to the black hole,
especially away from the axis (Sakurai 1985; Chakrabarti 1986).
The general effect would produce a transverse structure in the
jet which we ignore in the present solution. It was shown
(Das & Chakrabarti 1999) that in presence of angular motion the
conical outflow is to be replaced by an annular flow confined by the
centrifugal barrier and the funnel wall. Generally speaking, the
outflow surface varies as r3/2. However, the inflow surface area
is still proportional to r2. Because of this asymmetry, the problem is
no longer tractable analytically and is beyond the scope of the present
paper.
,
it is
easier to deposit momentum only close to the black hole.
In radiation driven outflows from the stellar surface, it is
customary to assume flows to be isothermal until the sonic point.
We first compute outflow rates making this assumption.
Later we drop this assumption and show that the
general behaviour remains similar.
In addition, we assume that there is very little
rotation in the outflow. There is no a priori
reason to assume this, except that there is no observational support
of rotation in the jet and it is possible that due to radiative
viscosity most of the angular momentum is transported
very close to the black hole. Furthermore, it has been
observed that the effect of angular momentum in the outflow
is to bring the sonic points closer to the black hole,
especially away from the axis (Sakurai 1985; Chakrabarti 1986).
The general effect would produce a transverse structure in the
jet which we ignore in the present solution. It was shown
(Das & Chakrabarti 1999) that in presence of angular motion the
conical outflow is to be replaced by an annular flow confined by the
centrifugal barrier and the funnel wall. Generally speaking, the
outflow surface varies as r3/2. However, the inflow surface area
is still proportional to r2. Because of this asymmetry, the problem is
no longer tractable analytically and is beyond the scope of the present
paper.
The radial momentum balance equation in the outflow is given by
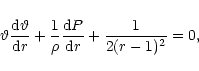 |
(9) |
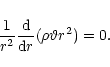 |
(10) |
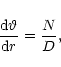 |
(11) |
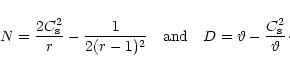 |
(12) |
Integrating the radial momentum equation, considering the sonic
point condition, we have,
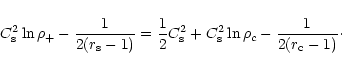 |
(13) |
![\begin{displaymath}\rho_{\rm c}=\rho_+\exp [-f],
\end{displaymath}](/articles/aa/full/2001/44/aa1476/img49.gif) |
(14) |
The outflow rate is given by
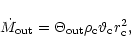 |
(15) |
From Eqs. (2) and (15) we get,
| = | ![$\displaystyle R_{\dot m}=\frac
{\Theta_{\rm out}}{\Theta_{\rm in}}\left[\frac {...
...]^{-{1/2}}\frac {RC_{\rm s} r^2_{\rm c}} {r_{\rm s}(r_{\rm s}-1)}\exp [-f]\cdot$](/articles/aa/full/2001/44/aa1476/img54.gif) |
(16) |
![\begin{displaymath}R = \frac{\Sigma_+}{\Sigma_-} = \frac{\vartheta_-}{\vartheta_...
...rac {1}{2} M_+^2 + n}{\frac {1}{2} M_-^2 +n}
\right ]^{1/2} ,
\end{displaymath}](/articles/aa/full/2001/44/aa1476/img56.gif) |
(17) |
At the other extreme, when the energy of the outflow does not change,
one can also obtain an analytical expression for the outflow rate
assuming the
![]() .
In this case, the entropy density of the
flow in the post-shock region is the same at the entropy density
of the entire outflow and the specific energy is also conserved
along the outflow. We assume that the turbulence generated at the
CENBOL has effectively transported angular momentum away. Thus, the
energy conservation equation gives
.
In this case, the entropy density of the
flow in the post-shock region is the same at the entropy density
of the entire outflow and the specific energy is also conserved
along the outflow. We assume that the turbulence generated at the
CENBOL has effectively transported angular momentum away. Thus, the
energy conservation equation gives
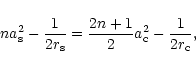 |
(18) |
| (19a) |
and
|
|
(19b) |
In an adiabatic flow with an equation of state
![]() (where K is a constant and a measure of entropy), one obtains,
assuming,
(where K is a constant and a measure of entropy), one obtains,
assuming,
![]() ,
,
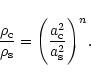 |
(20) |
![\begin{displaymath}R_{\dot m}= \frac{\Theta_{\rm o}}{\Theta_{\rm i}} \left(\frac...
...ac{4}{3}\left[\frac{8(R-1)}{R^2} -1\right]\right\}^{3/2} \cdot
\end{displaymath}](/articles/aa/full/2001/44/aa1476/img72.gif) |
(21) |
In Eq. (16), we presented the outflow/inflow rate ratio as a function of the compression ratio of the flow at the shock. The compression ratio is obtained from the specific energy and angular momentum using Eq. (17). First, we employ analytical means to obtain this for a single component sub-Keplerian disk. Second, we use a two component Keplerian/sub-Keplerian disk to actually compute these parameters from more fundamental parameters such as accretion rates and viscosity.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{1476f1.eps}
\end{figure}](/articles/aa/full/2001/44/aa1476/Timg73.gif) |
Figure 1:
Variation of the compression ratio of the
shocks as a function of specific energy |
| Open with DEXTER | |
In Fig. 1, we plot the analytical solution
of the compression ratio R as a function of the flow
parameters: specific energy ![]() and the specific
angular momentum
and the specific
angular momentum ![]() .
The shock strength generally
increases when energy decreases and the angular momentum
increases. This is because for low energy, the outer sonic
point and the shock form
very far away and the Mach number jumps from a very large number
to a very small number. If the angular momentum is decreased,
shock is produced only if the specific energy is high,
i.e., if the sonic points and the shocks are very close to the black hole.
Here, flow becomes subsonic before its Mach number could be very high.
.
The shock strength generally
increases when energy decreases and the angular momentum
increases. This is because for low energy, the outer sonic
point and the shock form
very far away and the Mach number jumps from a very large number
to a very small number. If the angular momentum is decreased,
shock is produced only if the specific energy is high,
i.e., if the sonic points and the shocks are very close to the black hole.
Here, flow becomes subsonic before its Mach number could be very high.
![\begin{figure}
\par\subfigure[]{
\includegraphics[width=6.6cm,clip]{1476f2a.eps} }
\subfigure[]{\includegraphics[width=6.7cm,clip]{1476f2b.eps} }\end{figure}](/articles/aa/full/2001/44/aa1476/Timg74.gif) |
Figure 2:
a) Variation of the ratio of outflow to inflow
rates
|
| Open with DEXTER | |
Figure 2a shows the principle result of our work when only one
sub-Keplerian accretion is chosen as the inflow. We plot the
ratio
![]() for a large number of specific angular momenta of the flow ranging from
1.57 (innermost) to 1.83 (outermost) at intervals of
d
for a large number of specific angular momenta of the flow ranging from
1.57 (innermost) to 1.83 (outermost) at intervals of
d
![]() .
The curves are drawn for all ranges of
specific energy
.
The curves are drawn for all ranges of
specific energy ![]() for which shocks are formed.
Along the X-axis the compression ratio R of these shocks is written.
Here to compute solid angles of the inflow and the outflow, we
assume the half opening angle of the outflow to be 10
for which shocks are formed.
Along the X-axis the compression ratio R of these shocks is written.
Here to compute solid angles of the inflow and the outflow, we
assume the half opening angle of the outflow to be 10![]() .
Therefore,
.
Therefore,
![]() .
.
![]() is given in the discussion following
Eq. (2). In Paper I, the compression ratio R was assumed to be a
parameter and
no angular momentum was assumed a priori. Presently,
we show the dependence on angular momentum.
The general character, namely,
that the outflow rate is negligible when the shock
is weak (
is given in the discussion following
Eq. (2). In Paper I, the compression ratio R was assumed to be a
parameter and
no angular momentum was assumed a priori. Presently,
we show the dependence on angular momentum.
The general character, namely,
that the outflow rate is negligible when the shock
is weak (![]() )
and falls off gradually
for strongest shock (
)
and falls off gradually
for strongest shock (
![]() ), remains the
same as in Paper I, however. There is a peak at about
), remains the
same as in Paper I, however. There is a peak at about
![]() .
Note that for a given R,
.
Note that for a given R,
![]() increases monotonically with specific angular
momentum
increases monotonically with specific angular
momentum ![]() .
This is because density of
CENBOL rises with
.
This is because density of
CENBOL rises with ![]() .
The curves
corresponding to
.
The curves
corresponding to
![]() and 1.73
are specially marked since there is a clear
difference in tendency of the variation of
and 1.73
are specially marked since there is a clear
difference in tendency of the variation of
![]() .
For instance, below
.
For instance, below
![]() ,
very strong
shocks are not possible at all and as a result the
outflow rate has a lower limit. For
,
very strong
shocks are not possible at all and as a result the
outflow rate has a lower limit. For
![]() such a limit does not exist.
such a limit does not exist.
The general behaviour of the outflow rate can be understood in the following way: when shocks are strong, they form very far out, and thus, even though the CENBOL area (which is basically the area of the base of the jet) increases, the net outflow rate is low. When the shock forms very close to the black hole, the temperature is high, and thus the outflow velocity is larger, but the CENBOL surface area goes down. Thus the product is low. For the intermediate cases the net effect is larger.
For comparison with the analytical work presented in Fig. 2a, in Fig. 2b we present a similar diagram drawn using a numerical computation of the shock locations (Chakrabarti 1989). Excellent agreement between these two figures implies that the approximations on which the analytical work was based are justified. All the features are reproduced well in Fig. 2a, except that for the weakest shocks outflow rate is not as low as in the numerical calculation of Fig. 2b.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{1476f3.eps}
\end{figure}](/articles/aa/full/2001/44/aa1476/Timg83.gif) |
Figure 3: Ratio of the outflow and the inflow rates as a function of the compression ratio of the inflow when the outflow is adiabatic. The general nature of the function remains the same as that of the isothermal outflow. |
| Open with DEXTER | |
We now present the nature of
![]() when the outflow is also chosen
to be adiabatic in Fig. 3. We used
when the outflow is also chosen
to be adiabatic in Fig. 3. We used
![]() for reference.
We observe that the peak is still located at around
for reference.
We observe that the peak is still located at around ![]() and the outflow
rate drops for very strong (
and the outflow
rate drops for very strong (![]() )
and very weak (
)
and very weak (![]() )
shocks.
We therefore believe that our conclusion about the behaviour of
)
shocks.
We therefore believe that our conclusion about the behaviour of
![]() is generic.
is generic.
Chakrabarti & Titarchuk (1995) proposed
that the spectral properties are better
understood if the disk solutions
of sub-Keplerian flows are included along with the
Keplerian flows. Recently, Smith et al. (2001a), Smith et al. (2001b),
Miller et al. (2001) found
conclusive evidence of these two components in many of
the black hole candidate accretion flows.
While the matter with higher viscosity flows
along the equatorial plane as a Keplerian disk (of
rate
![]() ), sub-Keplerian halo matter (of rate
), sub-Keplerian halo matter (of rate
![]() )
with lower viscosity flanks the Keplerian
disk above and below (Fig. 4a). Since the inner boundary condition
on the horizon forces the flow to be sub-Keplerian,
irrespective of their origin (Chakrabarti 1990, 1996)
matter mixes (at say,
)
with lower viscosity flanks the Keplerian
disk above and below (Fig. 4a). Since the inner boundary condition
on the horizon forces the flow to be sub-Keplerian,
irrespective of their origin (Chakrabarti 1990, 1996)
matter mixes (at say,
![]() )
from both the Keplerian
and sub-Keplerian flows before entering a black hole
to form a single component sub-Keplerian with an average
energy and angular momentum of
)
from both the Keplerian
and sub-Keplerian flows before entering a black hole
to form a single component sub-Keplerian with an average
energy and angular momentum of ![]() and
and ![]() respectively. The specific energy and angular
momentum of the mixed flow is computed from:
respectively. The specific energy and angular
momentum of the mixed flow is computed from:
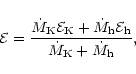 |
(22) |
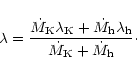 |
(23) |
![\begin{figure}
\par\subfigure[]{\includegraphics[width=7.3cm,clip]{1476f4a.eps} }
\subfigure[]{\includegraphics[width=7cm,clip]{1476f4b.eps} }\end{figure}](/articles/aa/full/2001/44/aa1476/Timg96.gif) |
Figure 4: a) Schematic diagram of the cross section of two-component accretion flow. See text for details; b) Solution of the two-component flow equations for two different viscosities. They are merged to form a single solution as depicted in Fig. 4a. |
| Open with DEXTER | |
Figure 4a shows a schematic diagram of the cross-section
of a two-component accretion flow. The transition radius
(
![]() )
where the Keplerian disk becomes sub-Keplerian,
and the shock location
)
where the Keplerian disk becomes sub-Keplerian,
and the shock location
![]() ,
are indicated. Figure 4b shows
two solutions (marked I and II) of the equations
governing a two-component flow
(Chakrabarti 1996) where
,
are indicated. Figure 4b shows
two solutions (marked I and II) of the equations
governing a two-component flow
(Chakrabarti 1996) where
![]() (Sub-Keplerian
matter from the Keplerian disk) and
(Sub-Keplerian
matter from the Keplerian disk) and
![]() (Sub-Keplerian halo) are plotted as a function of the logarithmic
radial distance. Viscosities chosen for these two components
are
(Sub-Keplerian halo) are plotted as a function of the logarithmic
radial distance. Viscosities chosen for these two components
are
![]() and
and
![]() respectively.
For
respectively.
For
![]() (lightly shaded region) the two sub-Keplerian
flows mix to create a single component. For simplicity,
we assume viscosity to be negligible in this region.
Thus, the specific angular momentum and specific energy
computed at
(lightly shaded region) the two sub-Keplerian
flows mix to create a single component. For simplicity,
we assume viscosity to be negligible in this region.
Thus, the specific angular momentum and specific energy
computed at
![]() from Eqs. (22) and (23) remain constant (
from Eqs. (22) and (23) remain constant (![]() )
for
)
for
![]() .
Dark solid curve (marked III) shows the angular momentum
distribution
.
Dark solid curve (marked III) shows the angular momentum
distribution
![]() of all possible mixtures
of the two components which allow shock formation. We chose a case
where
of all possible mixtures
of the two components which allow shock formation. We chose a case
where
![]() and
vary the Keplerian component
and
vary the Keplerian component
![]() where
where
![]() is the Eddington accretion rate.
is the Eddington accretion rate.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1476f5.eps}
\end{figure}](/articles/aa/full/2001/44/aa1476/Timg107.gif) |
Figure 5: Variation of outflow rates (left axis) with compression ratio at shocks (lower axis). The upper axis gives the variation of sub-Keplerian accretion rate and right axis gives the same for Keplerian accretion rate. |
| Open with DEXTER | |
In Fig. 5, the computed outflow rates are shown when
the half opening angle of the outflow is ![]() .
In this case,
.
In this case,
![]() The left axis shows the rate of
outflow
The left axis shows the rate of
outflow
![]() as a function
of the Keplerian disk rate (right panel) (
as a function
of the Keplerian disk rate (right panel) (
![]() )
and the halo rate (upper panel)
(
)
and the halo rate (upper panel)
(
![]() ). The lower
axis gives the compression ratio at the shock. The most important
conclusion that can be drawn here is that the outflow
rate steadily goes up as the Keplerian disk rate
). The lower
axis gives the compression ratio at the shock. The most important
conclusion that can be drawn here is that the outflow
rate steadily goes up as the Keplerian disk rate
![]() decreases and the spectrum goes to a harder state. When the
Keplerian rate is higher, the compression ratio is lower and
the outflow rate is also lower. This conclusion, drawn completely
from dynamical considerations, is also found to be true
from the spectral studies (CT95)
where it was shown that the post-shock region cools down and
the shock disappears (
decreases and the spectrum goes to a harder state. When the
Keplerian rate is higher, the compression ratio is lower and
the outflow rate is also lower. This conclusion, drawn completely
from dynamical considerations, is also found to be true
from the spectral studies (CT95)
where it was shown that the post-shock region cools down and
the shock disappears (
![]() ). Our work therefore
hints that the outflow would be negligible in softer states.
). Our work therefore
hints that the outflow would be negligible in softer states.
CT95 pointed out that the centrifugal pressure-supported boundary layer (CENBOL) of a black hole accretion flow is responsible for the spectral properties of a black hole candidate. In this Paper, we present analytical results to show that this CENBOL is also responsible for the production of the outflows, and the outflow rate is strongly dependent on the inflow parameters, such as specific energy and angular momentum. We showed that in general, the outflow rate is negligible when the shock is absent and very small when the shock is very strong. In intermediate strength, the outflow rate is the highest. As the specific angular momentum is increased, the outflow rate is also increased. This conclusion is valid when the flow is either isothermal or adiabatic.
We also demonstrated how a realistic two-component flow (TCAF) consisting of Keplerian and sub-Keplerian components produces a significant amount of outflow. Since matter close to a black hole is sub-Keplerian by nature, the two components must mix to form a single sub-Keplerian flow which has positive specific energy and almost constant specific angular momentum. We showed that as the Keplerian rate of the disk is increased, the outflow rate is decreased as the shock compression ratio approaches unity. This conclusion, drawn from a dynamical point of view, is also corroborated by the spectral behavior as well - as the Keplerian rate is raised, the post-shock region is cooled due to inverse Comptonization and the shock disappears. This reduces the thermal pressure drive and the resulting outflow rate is reduced.
Acknowledgements
This work is partly supported by a project (Grant No. SP/S2/K-14/98) funded by Department of Science and Technology (DST), Govt. of India.