A&A 379, 664-682 (2001)
DOI: 10.1051/0004-6361:20011198
D. I. Nagirner1 - J. Poutanen2,3
1 - Sobolev Astronomical Institute, St. Petersburg State University,
Staryj Peterhof, 198904 St. Petersburg, Russia
2 -
Stockholm Observatory, 106 91 Stockholm, Sweden
3 -
Astronomy Division, PO Box 3000, 90014 University of Oulu,
Finland
Received 9 February 2001 / Accepted 8 August 2001
Abstract
The relativistic kinetic equations describing time evolution
and space dependence of the density matrices of polarized photons and electrons
interacting via Compton scattering are deduced from the quantum Liouville
equation. The induced scattering and exclusion principle are taken into
account. The Bogoliubov method is used in the frame of quantum
electrodynamics. The equation for polarized radiation scattered by
unpolarized electrons is considered as a particular case and is
reformulated in terms of the Stokes parameters. The expressions for the
scattering amplitudes and cross-sections are derived simultaneously.
Key words: methods: analytical - radiation mechanisms: general - plasmas - polarization - scattering
Compton scattering is an important physical process in many astrophysical
systems, such as active galactic nuclei, X-ray binaries, and pulsar
magnetospheres (see e.g. reviews by Blandford & Scharlemann 1975;
Pozdnyakov et al. 1983; Poutanen 1998). Inverse Compton
scattering (i.e. scattering of soft photons by hot electron gas) is
believed to be the main mechanism of the X-ray/gamma-ray production in
accreting X-ray binaries (e.g. Sunyaev & Titarchuk 1980; Poutanen &
Svensson 1996), gamma-ray bright active galactic nuclei (e.g. Sikora et al. 1997), and possibly gamma-ray bursts (Stern 1999; Ghisellini &
Celotti 1999). The hard X-rays can interact with the cold material via
classical Compton scattering, losing their energy and producing a cutoff in
the "Compton reflected'' spectrum (e.g. George & Fabian 1991; Poutanen et al. 1996). Induced (stimulated) Compton scattering
becomes very important when the radiation brightness temperature is large
![]() ,
where
,
where
![]() is Thomson optical thickness.
Induced effects can distort the low frequency part of the radio-source
spectra even when
is Thomson optical thickness.
Induced effects can distort the low frequency part of the radio-source
spectra even when
![]() is small (Sunyaev 1971) and can influence the
heating of electrons near active galactic nuclei and pulsars (Levich &
Sunyaev 1971).
is small (Sunyaev 1971) and can influence the
heating of electrons near active galactic nuclei and pulsars (Levich &
Sunyaev 1971).
The process of multiple scattering of radiation is described by a kinetic equation. This equation can be easily written if we neglect the induced scattering and/or the polarization (see, e.g. Nagirner & Poutanen 1994 and references therein). Induced scattering leads to the appearance of nonlinear terms in the kinetic equation. Since the polarization of radiation is described by four parameters, one must write a vector kinetic equation, i.e. a system of four equations. The kinetic equation combining these two effects (polarization and induced scattering) was not derived self-consistently up to now. The aim of the present paper is to fill up this gap.
The first kinetic equation for Compton scattering with induced scattering
was written by Kompaneets (1956) and is known under his name. He
considered multiple scattering of homogeneous and isotropic radiation in
infinite space filled with homogeneous, nondegenerate thermal electron gas.
The gas was assumed to be non-relativistic (
![]() ), the
radiation to be rather soft (
), the
radiation to be rather soft (
![]() ), and the intensity of
radiation to be a sufficiently smooth function of frequency. Because of
small changes of photon frequency in a single scattering, the scattering
integral was transformed to a differential operator by the Fokker-Planck
method. The equation was rediscovered by Weymann (1966). More general
Fokker-Planck equations were deduced by Cooper (1971) and Barbosa (1982)
for more energetic electrons and photons, and by Molodtsov (1994) for the
anisotropic, degenerate and moving electrons. For very cold electron gas,
the Fokker-Planck equation was derived by Ross et al. (1978).
), and the intensity of
radiation to be a sufficiently smooth function of frequency. Because of
small changes of photon frequency in a single scattering, the scattering
integral was transformed to a differential operator by the Fokker-Planck
method. The equation was rediscovered by Weymann (1966). More general
Fokker-Planck equations were deduced by Cooper (1971) and Barbosa (1982)
for more energetic electrons and photons, and by Molodtsov (1994) for the
anisotropic, degenerate and moving electrons. For very cold electron gas,
the Fokker-Planck equation was derived by Ross et al. (1978).
The induced scattering effects strongly depend on the angular distribution of the radiation field. Babuel-Peyrissac & Rouvillois (1969) generalized the Kompaneets equation to nonhomogeneous and anisotropic radiation. Their equation contains an integral operator in angular variables, but a differential operator in frequency. A simplified form of that equation was used by a number of authors to study induced effects in pulsar magnetospheres and radio sources in active galactic nuclei (Wilson & Rees 1978; Coppi et al. 1993; Sincell & Krolik 1994; Lyubarskii & Petrova 1996; Sincell & Coppi 1996).
As it is mentioned above, the induced scattering makes equations nonlinear.
This effect can be simply taken into account in the equation if we limit
ourselves to one parameter, intensity I, ignoring polarization. The
scattering rate is increased by stimulated scattering by a factor
![]() (where
(where
![]() is the photon momentum after scattering)
comparing with the rate when only spontaneous scattering is considered. It
is this factor that the authors of the mentioned works (Kompaneets 1956;
Babuel-Peyrissac & Rouvillois 1969; Molodtsov 1994) have introduced into
the equations. Often kinetic equations (e.g. radiative transfer equation)
are deduced heuristically from intuitive considerations and previous
experience. However, in the case when polarization including induced
effects is considered, our intuition and experience are not enough and the
phenomenological approach fails. Therefore, one has to resort to deductive
methods. Note that in nearly all the works on Compton scattering the
electrons were assumed to be unpolarized and isotropic (or
monodirectional).
is the photon momentum after scattering)
comparing with the rate when only spontaneous scattering is considered. It
is this factor that the authors of the mentioned works (Kompaneets 1956;
Babuel-Peyrissac & Rouvillois 1969; Molodtsov 1994) have introduced into
the equations. Often kinetic equations (e.g. radiative transfer equation)
are deduced heuristically from intuitive considerations and previous
experience. However, in the case when polarization including induced
effects is considered, our intuition and experience are not enough and the
phenomenological approach fails. Therefore, one has to resort to deductive
methods. Note that in nearly all the works on Compton scattering the
electrons were assumed to be unpolarized and isotropic (or
monodirectional).
The first attempt to find out a rule for consideration of induced processes
simultaneously with polarization was undertaken by Pomraning (1974). In
terms of plane electromagnetic waves, he considered a source of polarized
emission interacting with already existing radiation field and deduced a
matrix describing the transformation of the Stokes parameters. The Stokes
vector corresponding to the induced process was presented as a product of a
![]() matrix N with the Stokes vector of the incoming radiation.
Calculating the elements of the matrix N, he averaged the product of
the quantities corresponding to the emitted (source photons) and passing by
(field photons) waves over the distributions of their phases assuming that
no correlation exists between the source and the field. This result is not
applicable to scattering because the scattered radiation does not have
random phases. In the resulting expression for N, only the elements in
the first row and the first column (i.e. related to the intensity) are
correct in the case of scattering (Stark 1981).
matrix N with the Stokes vector of the incoming radiation.
Calculating the elements of the matrix N, he averaged the product of
the quantities corresponding to the emitted (source photons) and passing by
(field photons) waves over the distributions of their phases assuming that
no correlation exists between the source and the field. This result is not
applicable to scattering because the scattered radiation does not have
random phases. In the resulting expression for N, only the elements in
the first row and the first column (i.e. related to the intensity) are
correct in the case of scattering (Stark 1981).
Derivation of the kinetic equation for the induced scattering of polarized radiation by non-relativistic electrons was given by Wilson (1978). He used the Maxwell equations, expansion electromagnetic field on set of harmonic oscillators, second quantization method and the non-relativistic perturbation theory. The scattering (a process of the fourth order in the approximation used) was represented as consequent absorption and emission. The products of the probabilities of these processes were replaced by the elements of the scattering matrix deduced according to the rules of quantum electrodynamics. While such a deduction is not self-consistent, the resulting equation is correct.
Wilson's results were used by Stark (1981) to deduce the generalization of
the Babuel-Peyrissac-Rouvillois (1969) equation for stimulated scattering
to linearly polarized radiation (two Stokes parameters). Hansen & Lilje
(1999) have corrected inaccuracies and misprints in Stark's work. Using a
version of Wilson's equation containing only non-linear terms, Wilson
(1982) and Coppi et al. (1993) showed that the induced scattering can
enhance the polarization (comparing to the spontaneous scattering)
producing also its strong frequency dependence. Induced Compton
backscattering, for example, can amplify an incident ![]() 1 per cent
polarization up to
1 per cent
polarization up to ![]() 50 per cent (Sincell & Coppi 1996). Accounting
for the polarization of radiation may lead to the results qualitatively
different from those obtained neglecting polarization. A small change in
the scattering rate (affected by polarization) can be strongly amplified
due to the non-linearity of the process.
50 per cent (Sincell & Coppi 1996). Accounting
for the polarization of radiation may lead to the results qualitatively
different from those obtained neglecting polarization. A small change in
the scattering rate (affected by polarization) can be strongly amplified
due to the non-linearity of the process.
The relativistic kinetic equation for the Stokes parameters taking into account the induced scattering was presented by Nagirner (1994) without deduction. The work of Wilson was not accessible for the author at that time. Shortly after that, the work of Ioffe made at the beginning of the 1950-ies was published (Ioffe 1994). In this work the equation was deduced (as Ioffe pointed out, with an approximate and a simplified method) for the so called polarization tensor which differs from the density matrix because the unphysical scalar and longitudinal photons are not excluded.
In this paper, we derive the relativistic kinetic equation for the photon gas interacting with the electron gas. The way of deduction is based on the methods of Bogoliubov (Bogoliubov & Gurov 1947) and Baranger (1958). The scheme closest to ours is used in Silin (1971), where the non-relativistic kinetic equation for interacting electrons was derived. In our paper, at every step of the derivation all the expressions and relations are demonstrated to be either explicitly relativistically covariant or they can be changed to relativistic forms. The final equations are explicitly relativistic. In order to elucidate these facts and to introduce suitable for our purposes notations, we are urged to present a number of known relations and schemes. We thus fully describe the method of the derivation of the equations in a self-contained way.
We make assumptions usual for the kinetic theory. Only binary collisions are accounted for. We assume the molecular chaos, i.e. the gas states are characterized by one-particle distribution functions. The characteristic temporal and space scales of a single interaction are assumed to be much smaller than the scales of significant changing of radiation and electron gas states. We use the principle of weakening of the correlations, which says that the correlations between particle states are expressed in terms of the same one-particle distribution functions. There are no other limitations on the states of interacting particles. Simultaneously with the kinetic equations, we obtain the expressions for the scattering amplitudes and (well known) cross-sections.
We first assume that both electrons and photons are polarized, then we average the equations over electron polarizations. An arbitrary anisotropy and nonhomogeneity of the radiation field and electron distribution are allowed. We also derive the kinetic equation describing the evolution of the electron gas.
According to the method of second quantization (see e.g. Bogoliubov &
Shirkov 1959; Schweber 1961), the two types of vector-operators
are introduced satisfying the following commutation relations
Generally speaking, one has to quantize the photon field in a finite volume
V (box), for example, of the parallelepiped shape with the sides equal to
![]() .
Then in every dimension of this volume
there can be a countable number of standing waves of the form
.
Then in every dimension of this volume
there can be a countable number of standing waves of the form
![]() ,
where
,
where
![]() and
nx,ny,nz are integers. Correspondently, the
number of creation and annihilation operators should be countable and the
commutation rules should contain discrete
and
nx,ny,nz are integers. Correspondently, the
number of creation and annihilation operators should be countable and the
commutation rules should contain discrete ![]() -functions, i.e. the
Kronecker symbols. However, in the limit
-functions, i.e. the
Kronecker symbols. However, in the limit
![]() the
countable set of standing waves transforms to the continuum and all
relations for the finite volume and its limiting case can be written in a
unified way (Bogoliubov & Shirkov 1959).
the
countable set of standing waves transforms to the continuum and all
relations for the finite volume and its limiting case can be written in a
unified way (Bogoliubov & Shirkov 1959).
For example, the orthogonality condition for the discrete case with the
integration over the box has the same form as in the continuum case, if the
![]() -function and the volume element of the three-dimensional momentum
space are taken in the discrete form:
-function and the volume element of the three-dimensional momentum
space are taken in the discrete form:
Let us expand vectors
![]() and
and
![]() along the unit vectors of the four-dimensional basis whose
vectors are orthonormal and their system is full:
along the unit vectors of the four-dimensional basis whose
vectors are orthonormal and their system is full:
In classical electrodynamics, the transversality relation was given by
equality to zero of the quantity (not an operator) formally coinciding with
(7). The equality of the amplitudes of scalar and longitudinal
potentials (or equality of both to zero) was the consequence of that
relation. In quantum electrodynamics, this relation is too stiff. One
cannot require equality of
![]() and
and
![]() ,
since they
satisfy different commutation relations which easily can be seen from
relation (4). The solution of that problem was given by
Gupta (1950) and Bleuler (1950) (see also Bogoliubov & Shirkov 1959;
Schweber 1961). We use their method.
,
since they
satisfy different commutation relations which easily can be seen from
relation (4). The solution of that problem was given by
Gupta (1950) and Bleuler (1950) (see also Bogoliubov & Shirkov 1959;
Schweber 1961). We use their method.
Only the operators with indices 1 and 2 are physical and only those should
enter the quantities having physical meaning. These operators satisfy the
commutation relations
The states of the electromagnetic field in the second-quantized
representation are described by the vectors with the arguments equal to
given momenta and polarization projections of the definite number of
photons. The initial vector that is used to obtain all other vectors is
the state vector of the photon vacuum ![]() .
It is normalized and
satisfies the condition of absence of photons:
.
It is normalized and
satisfies the condition of absence of photons:
![]() .
The second equality is valid for any momentum
.
The second equality is valid for any momentum
![]() and any polarization
and any polarization ![]() .
.
All other photon state vectors can be obtained from the vacuum state vector
by applying the creation operators but the vectors containing information
about the non-physical scalar and longitudinal photons should be excluded.
In the physical states, the operators of photon creation of these photons
should appear only in the combination
![]() ,
so that there always exist equal
amount of scalar and longitudinal photons. With the action of the operator
,
so that there always exist equal
amount of scalar and longitudinal photons. With the action of the operator
![]() on to such states, such photons mutually
cancel out. The product of the operators of creation and annihilation
in such a combination gives
on to such states, such photons mutually
cancel out. The product of the operators of creation and annihilation
in such a combination gives
![]() ,
which
acting on to the vector of the physical states gives zero. The full
product of the operators of creation and annihilation is reduced to
,
which
acting on to the vector of the physical states gives zero. The full
product of the operators of creation and annihilation is reduced to
![]() .
Here the summation is done over s=1, 2 (in the several following sections we
use only lower indices s). We omit unphysical photons hereafter from our
considerations.
.
Here the summation is done over s=1, 2 (in the several following sections we
use only lower indices s). We omit unphysical photons hereafter from our
considerations.
The physically allowed states of N photons with fixed momenta and
polarizations can be represented in the form
The orthogonality condition for the vectors of physical states follows from the
commutation relations (8) and takes the form
The results of the action of the creation and annihilation operators on to the
state vector are given by
In the second-quantization of the electron and positron fields (as in the
case of the electromagnetic field), the operators of annihilation and
creation satisfy the relations of the form
The electron-positron vacuum is defined with normalized vector ![]() as
a state where there are no particles, i.e.
as
a state where there are no particles, i.e.
The operators of creation and annihilation act on to the state vectors in
the following way
The density matrix of N-photon state (N is fixed) can be defined as an
averaged dyad product of the state vector with its conjugate
Let us introduce the notation for the kernel of the density matrix operator
0pt
It is obvious from definition (23), that the density matrix is a
self-conjugate operator, and it follows from (24) and
(25) that its kernel is a self-conjugate matrix, i.e. its
Hermitian conjugation (complex conjugation and the replacement of the lower
and the upper arguments with each other) is equal to the same kernel.
The trace of the density matrix
![]() by virtue of the normalization of the state vector.
by virtue of the normalization of the state vector.
The density matrix carries a lot of information, much more than the distribution function or even the polarization matrix which can be expressed through the density matrix. However, in order to derive the kinetic equation, the distribution functions are not enough and one has to introduce a set of functions containing the groups of variables with the dimension less than N, but larger than 1. We call them truncated density matrices.
Together with the N-particle density matrix we introduce matrices whose
kernels can be expressed through the integrals of the kernel of the original
matrix. A kernel of order l
The density matrices for particles (electrons) are introduced in a similar
manner, therefore we immediately write down the expression for the joint
density matrix for electrons and photons. It can be expressed through the
kernel in terms of the following integral
The kinetic equation for photons which we wish to deduce should be formulated for the one-particle polarization matrix depending on spatial coordinates, time, and photon momentum. Therefore, one has to make a transformation to such a matrix. We briefly describe the scheme for this transformation on the example of spinless particles.
Up to now we used the momentum representation where the density matrices
depend on a double set of momenta and polarization indices. The spinless
states could be described in the coordinate representation. Instead of the
matrix with two momenta arguments, we would have a matrix with two sets of
space coordinates. The transition from one representation to another can
be performed by Fourier transform. For the one-particle functions such a
transition is defined by the formula
In the case of photons, situation becomes even more complicated, since the
physical states with the transverse polarizations are connected to the
momentum and, for the photon matrices with the fixed spin projections,
transformations of the type (34) and (37) are not
possible. In that case, one has to return to the general polarization
states which include non-physical photons. The elimination of the later
should be done after the transition to equation similar to
(39). Here we also meet with the difficulties to satisfy the
relation
![]() .
.
Similar difficulty appears also in the case of electrons if one takes the
solutions with a given spirality (i.e., a projection of the spin on to the
momentum) as the basic solutions of the Dirac equations. In that case, the
transformations of the type (34) and (37) also are
not possible. However, one can get solutions with the projections of the
spin on to an arbitrary direction instead of the momentum. This can be
achieved by the method proposed by Foldy & Wouthuysen (1950) (see also
Schweber 1961). The mentioned transformations are then possible. The
transition to the equation of type (39) is done in the same
way as for the spinless particles and the spin indices are simply added.
Without making these derivation, we take that
In the normalization condition (30) the momenta
![]() and
and
![]() are equal to each other. Formally, for equal momenta the
are equal to each other. Formally, for equal momenta the
![]() -function in Eq. (41) becomes infinite. However,
since we operate with the quantities in the finite volume (basic box),
according to (2) one has to take
-function in Eq. (41) becomes infinite. However,
since we operate with the quantities in the finite volume (basic box),
according to (2) one has to take
The normalization condition for the electron polarization matrix can be
obtained from the equations analogous to (30) and
(2). The later takes the form
![]() ,
so that
,
so that
In spite of the fact that Eqs. (40) and (41)
are deduced in a non-relativistic way they are relativistically covariant.
Normalization conditions (43) and (45) are
written in the reference frames where the photon and electron gases are at
rest. The corresponding relativistically covariant equations in an
arbitrary frames are
Let us note that the interaction time T0 is also related to the
![]() -function. This relation is the relativistic counterpart of
(2), i.e. its time-like form
-function. This relation is the relativistic counterpart of
(2), i.e. its time-like form
Density matrix (33) satisfies the quantum Liouville
equation (Landau & Lifshitz 1977; Silin 1971; de Groot et al. 1980)
If
![]() ,
,
![]() ,
,
![]() ,
the electron Compton
operator
,
the electron Compton
operator
![]() contains two
integrals over four-dimensional space (
contains two
integrals over four-dimensional space (
![]() and
and
![]() ). Two
four-dimensional
). Two
four-dimensional ![]() -functions appear after calculating these
integrals. One of them disappears when we take the integral over
four-dimensional momentum of virtual electron
-functions appear after calculating these
integrals. One of them disappears when we take the integral over
four-dimensional momentum of virtual electron
![]() ,
whereas the
second one reflects the conservation laws. Thus integrals over the whole
time-space (x0=ct)
,
whereas the
second one reflects the conservation laws. Thus integrals over the whole
time-space (x0=ct)
If we omit all terms which are higher than the second order and those which
do not conserve the number and/or the quality of particles then the equation
for the photon-electron density matrix describing Compton scattering by
electrons takes the form
Let us write Eq. (60) not in the operator form, but via the kernel of the photon-electron matrix keeping temporarily the number of components fixed (specifically, N photons and N- electrons). Simultaneously we substitute the time argument t of the density matrix instead of t0, because this argument is macroscopic time.
According to Eq. (26) for photons and analogous for
electrons, we multiply Eq. (60) by the corresponding state
vectors and their conjugates on the left and right. We get
Let us write now the equation for the kernel of the truncated photon matrix
of the first order which follows from Eq. (62). We equate
all corresponding upper and lower polarization indices and momenta of
electrons and all (except the first) indices and momenta of photons, i.e.
we sum over indices and integrate over momenta. The result, according to the
definition (29), is then divided by
(N-1)!N-!
Let us now derive the equation for
![]() .
We
follow the same procedure as when deriving Eq. (64),
fixing the characteristics (momenta and indices) of one photon and one
electron in Eq. (62). One has to separate these variables
when we consider the action of annihilation and creation operators on them.
The resulting expression contains four couples of terms with pluses and
minuses. The first couple does not have summation at all (i.e.,
corresponds to r=1,j=1), the second and the third couples contain
summation over the photon and electron variables, respectively, and the
fourth couple contains summations over variables of both interacting
particles starting from r=2 and j=2. The terms in the last couple
(with double sums) give the same function
.
We
follow the same procedure as when deriving Eq. (64),
fixing the characteristics (momenta and indices) of one photon and one
electron in Eq. (62). One has to separate these variables
when we consider the action of annihilation and creation operators on them.
The resulting expression contains four couples of terms with pluses and
minuses. The first couple does not have summation at all (i.e.,
corresponds to r=1,j=1), the second and the third couples contain
summation over the photon and electron variables, respectively, and the
fourth couple contains summations over variables of both interacting
particles starting from r=2 and j=2. The terms in the last couple
(with double sums) give the same function
![]() and annihilate. We take
as the lhs of the equation the difference which stands on the second place
of Eq. (60). We omit here the argument t of the
density matrices in the rhs of the equation based on the assumption formulated
in the next section. We get
and annihilate. We take
as the lhs of the equation the difference which stands on the second place
of Eq. (60). We omit here the argument t of the
density matrices in the rhs of the equation based on the assumption formulated
in the next section. We get
The matrices depending on variables of a number of particles contain the
information about correlations between these particles. In kinetic theory,
usually one applies an approximation of molecular chaos (Silin 1971).
According to that approximation, there are no correlations before the
interaction, i.e.
The two-particle truncated matrices can be presented as products of the
one-particle density matrices accounting for the exchange effects
(symmetrical and anti-symmetrical forms for photons and electrons,
respectively)
Now we substitute Eqs. (66)-(68) into the
rhs of Eq. (65), and the resulting expression into
Eq. (64). At this step, after all substitutions, we
will use the fact that the matrices in the rhs of Eq. (65) do not depend on time during the interaction. Then we
can take the integrals over the space-time variables enter the matrices ![]() only. Simultaneously we let
only. Simultaneously we let
![]() ,
keeping
the upper limit t finite. As a result of this procedure four integrals
over space give four three-dimensional
,
keeping
the upper limit t finite. As a result of this procedure four integrals
over space give four three-dimensional ![]() -functions as in (55), namely two pairs of the type
-functions as in (55), namely two pairs of the type
Integrals over time with the upper limit t can be taken independently. They
have the form
The terms with absence of energy conservation in kinetic equations, as was noticed by Nagirner (1994), appear in Silin (1971) and Bomier (1991) who do not discuss this fact. In their papers, the interaction between electrons (Silin 1971) and between photons and atoms (Bomier 1991) does not depend on time. In our case, the Hamiltonian is more complicated and without the energy conservation law we cannot calculate the scattering amplitudes and the cross-sections of the process.
We suppose that such terms are not physical and must be excluded. The
interaction between photon and electron has finished before the density
matrix changes noticeably and the integration limit t must be taken
infinite. Then the resulting integral is given by Eq. (55). However, this procedure gives the cross-section twice
as large as the correct value. To overcome this difficulty we continue the
upper limit t to ![]() but take half of the result.
but take half of the result.
The next step is to use for the last time the assumption of the small scale
of the interaction. Instead of the one-particle kernels we use now their
diagonal in momentum forms (39) and (41).
Accounting for relation (49), the lhs of Eq. (64) then takes the form
The first two terms containing linearly the amplitude M given by
Eq. (56) cancel out. This follows from the equality
All the remaining twelve terms contain eight three-dimensional integrals
over photon and electron momenta. There are two four-dimensional and five
three-dimensional ![]() -functions in the integrand. All
three-dimensional
-functions in the integrand. All
three-dimensional ![]() -functions disappear when taking the integrals.
The resulting expression contains three three-dimensional integrals (one
over photon momenta and two over electron momenta), and two
four-dimensional
-functions disappear when taking the integrals.
The resulting expression contains three three-dimensional integrals (one
over photon momenta and two over electron momenta), and two
four-dimensional ![]() -functions,
-functions,
![]() and
and
![]() .
The first one reflects the energy and momentum
conservation laws. The second one cancels out since it also appears in the
lhs of Eq. (64) according to Eq. (72).
.
The first one reflects the energy and momentum
conservation laws. The second one cancels out since it also appears in the
lhs of Eq. (64) according to Eq. (72).
In the final expression, four out of twelve terms contain products of one photon and one electron matrices corresponding to the spontaneous scattering. Two of these terms entering with the plus sign are responsible for the emission and the two terms entering with the minus sign are responsible for the attenuation of the photon beam due to scattering. The remaining eight terms reflect the exchange effects. Four terms containing the product of one electron and two photon matrices correspond to the induced scattering, and four terms containing the product of one photon and two electron matrices reflect the exclusion principle. The induced scattering terms have the same signs as the spontaneous terms, while the exclusion principle terms have the opposite signs. After an elementary but very long deduction, we obtain the sought kinetic equation.
As we mentioned above, all the remaining terms in the rhs of
Eq. (64) after substitution of Eq. (66)
contain the factor
![]() which also exists in the lhs of
the equation. This factor therefore cancels out. We can now restore the
dependence of the photon matrix on time and spatial coordinates. Let us
also change the designations, writing the photon matrix in the lhs in the
form
which also exists in the lhs of
the equation. This factor therefore cancels out. We can now restore the
dependence of the photon matrix on time and spatial coordinates. Let us
also change the designations, writing the photon matrix in the lhs in the
form
![]() .
Rewriting the derivative over the line of
sight as the full derivative, the lhs of the equation takes the covariant
form
.
Rewriting the derivative over the line of
sight as the full derivative, the lhs of the equation takes the covariant
form
In the rhs of the equation we change the indices and add and subtract two
pairs of identical terms containing products of two photon and two electron
matrices for symmetry. The resulting kinetic equation takes the form
Note that the products of four matrices are added just for the symmetry of
the equation. If these four terms are dropped and we change some indices,
the equation takes the form
We note, that a possibility to calculate the scattering amplitudes appears after we choose the polarization basis for photons and the axis where one projects the electron spin. As the axis one can use the electron momenta. The situation is more complex for the polarization bases. We will give detailed description of that later and now turn to the equation for the electron distribution function.
Now we also can write down the kinetic equation for electrons. It can be
deduced following the same procedure as in the case of the photon equation.
However, due to the symmetry of Eq. (75), we can write
this equation by analogy. One just removes one integral over electron
momentum and adds one integral over photon momentum as well as sums over
photon polarization and removes summation over indices of electron
polarization (with the external momentum,
![]() ). The resulting
relativistic kinetic equation takes the form
). The resulting
relativistic kinetic equation takes the form
Matrix elements (56) for Compton scattering (amplitudes) can
be rather easily calculated for a special choice of polarization bases -
internal bases. We take the unit vectors of these bases in the following
form. For the photon of momentum
![]()
The values ![]() and
and ![]() are the photon energies before and after
scattering in the frame where the electron before interaction is at rest.
If we denote the cosine of scattering angle in this frame as
are the photon energies before and after
scattering in the frame where the electron before interaction is at rest.
If we denote the cosine of scattering angle in this frame as ![]() then
then
If indeed the summation is over only one pair of indices then the resulting
sum depends on the 6 remaining indices and contains 26=64 terms
altogether. If, on the other hand, the summation is fulfilled over two
pairs of indices, then the sum contains 24=16 terms. The term which
describes the attenuation of radiation belongs to the last category
We have deduced the formulae for the Compton scattering amplitudes (84) in a specially chosen internal polarization basis (80). However, the expressions (54) and (56) for these amplitudes contain unit vectors of some external bases which should reflect the geometry of the scattering medium. The photon density matrices entering the kinetic Eqs. (75)-(77) are connected to the same (external) vectors. Therefore, we must find transformations between the external and the internal bases.
Two sets of polarization vectors
![]() and
and
![]() together with the vector
together with the vector
![]() form two three-dimensional
bases with one common unit vector. Consequently, the external vectors and the
internal vectors are connected to one another via relation
form two three-dimensional
bases with one common unit vector. Consequently, the external vectors and the
internal vectors are connected to one another via relation
Multiplying both sides of Eqs. (88) by the Dirac matrices
we get
If electrons are unpolarized (i.e., Eq. (46) is valid),
then the matrix
![]() must be replaced by the product
must be replaced by the product
![]() .
The factor
.
The factor
![]() is replaced by
is replaced by
![]() ,
and one can sum over
the electron polarizations. For the external bases,
,
and one can sum over
the electron polarizations. For the external bases,
The expressions for the cross-sections (95) have the simplest
form in the internal polarization bases (80) and
(83). The matrix elements are then given by
(84) and therefore
Only 8 out of 16 elements of matrix (96) are not zeros, and only 5 elements are different
Combination (93) and (94) with (95)
gives the law of transformation of the cross-sections of polarized radiation
by unpolarized electrons. One can write a transformation, for example, in the
following way
Keeping in mind the formulae expressing transformation laws and omitting the
arguments of the T-matrices, we rewrite the kinetic equation for photons
with unpolarized electrons in the form
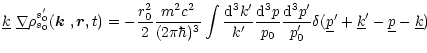 |
|||
| (99) |
The transformation from the polarization matrices to the Stokes parameters
is done with the aid of the formulae
As we have mentioned above, the equation of the form (101)
for non-degenerate electrons (not accounting for the exclusion principle)
was given in Nagirner (1994). The term with matrix A was omitted
there. It can be easily shown that this term disappears if the electrons
have an isotropic distribution (even if they are degenerate). In the major
part of Nagirner's paper, the isotropic electron distribution was assumed,
so that this omission did not introduced any errors![]() . The matrix A was omitted also in papers of the authors (Nagirner & Poutanen 1993,
1994) where the rhs of Eq. (101) was averaged over the
directions of electron momenta and the five functions describing the
redistribution of radiation in frequency, angles and polarization states
were obtained. However, these papers were devoted to the isotropic
electrons as well.
. The matrix A was omitted also in papers of the authors (Nagirner & Poutanen 1993,
1994) where the rhs of Eq. (101) was averaged over the
directions of electron momenta and the five functions describing the
redistribution of radiation in frequency, angles and polarization states
were obtained. However, these papers were devoted to the isotropic
electrons as well.
Electron isotropy means that the medium is locally isotropic, and therefore the attenuation (i.e. the terms corresponding to the last square brackets in Eq. (101)) is described not by the matrix, but only by the scalar determined by the Klein-Nishina cross-section, F. The cross-section averaged over momentum of scattered photons can be found in Nagirner & Poutanen (1994). Hence we can conclude here that polarized electrons can influence both the linear and circular polarization by means of attenuation through scattering. Unpolarized, even non-isotropic, electrons can introduce and change in this process only linear polarization.
In this paper, we have deduced the relativistic kinetic equations which describe the behavior of the rarefied photon and electron (or positron) gases interacting with each other via Compton scattering. We accounted here for stimulated effects for the photons and for the exclusion principle for the electrons. We considered arbitrary polarization states of photons and electrons. We presented also the kinetic equation for polarized photons scattered by unpolarized electrons in terms of the Stokes parameters. The expressions for the scattering amplitudes and cross-sections are derived simultaneously. There are no limitations on photon and electron energies.
Note that all the deductions were made by means of relativistic quantum electrodynamics methods and all the equations obtained are relativistically covariant. For particular scattering problems they, of course, must be adapted to the geometry and symmetries of a medium and initial and boundary conditions (see e.g. Nagirner & Poutanen 1993).
Finally, we would like to notice that the factors
![]() and
and
![]() accounting for the induced effects for photons
and the exclusion principle for electrons in the scalar kinetic equations,
should be replaced by the new factors
accounting for the induced effects for photons
and the exclusion principle for electrons in the scalar kinetic equations,
should be replaced by the new factors
![]() and
and
![]() in the kinetic equations
for polarized photons and electrons. This rule can help to formulate
kinetic equations for more complex processes for which a direct derivation
could be very complicated. The processes in strong magnetic fields can
serve as such examples.
in the kinetic equations
for polarized photons and electrons. This rule can help to formulate
kinetic equations for more complex processes for which a direct derivation
could be very complicated. The processes in strong magnetic fields can
serve as such examples.
Acknowledgements
This work was supported by the Swedish Natural Science Research Council, the Anna-Greta and Holger Crafoord Fund, the Royal Swedish Academy of Sciences, the Russian Federal Program "Astronomia'', and the Russian Leading Scientific Schools grant 00-15-96607. DIN is grateful to the Stockholm Observatory for the hospitality during his visit.