A&A 379, 245-256 (2001)
DOI: 10.1051/0004-6361:20011336

The $\zeta $Herculis binary system revisited

Calibration and seismology

P. Morel - G. Berthomieu - J. Provost - F. Thévenin

Département Cassini, UMR CNRS 6529, Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 4, France

Received 9 July 2001 / Accepted 14 September 2001

Abstract
We have revisited the calibration of the visual binary system $\zeta $Herculis with the goal to give the seismological properties of the G0IV sub-giant $\zeta $HerA. The sum of masses and the mass fraction are derived from the most recent astrometric data mostly based on the HIPPARCOS ones. We have derived the effective temperatures, the luminosities and the metallicities from available spectroscopic data and TYCHO photometric data and calibrations. For the calculations of evolutionary models we have used updated physics and the most recent physical data. A $\chi^2$ minimization is performed to approach the most reliable modeling parameters which reproduce the observations within their error bars. For the age of the $\zeta $Her binary system we have obtained $t_{\zeta\rm\,Her}=3387$ Myr, for the masses $m_{\zeta\rm\,Her\,A}=1.45\,M_\odot$ and $m_{\zeta\rm\,Her\,B}=0.98\,M_\odot$, for the initial helium mass fraction $Y_{\rm i}=0.243$, for the initial mass ratio of heavy elements to hydrogen $(\frac ZX)_{\rm i}=0.0269$ and for the mixing-length parameters $\Lambda_{\zeta\rm\,Her\,A}=0.92$ and $\Lambda_{\zeta\rm\,Her\,B}=0.90$ using the Canuto & Mazitelli (1991, 1992) convection theory. Our results do not exclude that $\zeta $HerA is itself a binary sub-system as has been suspected many times in the past century; the mass of the hypothetical unseen companion would be $m_{\zeta\rm\,Her\,A}\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hf... ...skip\halign{\hfil$\scriptscriptstyle ..., a value significantly smaller than previous determinations. A calibration made with an overshoot of the convective core of $\zeta $HerA leads to similar results but with a slight increase of $\approx$+250 Myr for the age. The adiabatic oscillation spectrum of $\zeta $HerA is found to be a complicated superposition of acoustic and gravity modes. Some of these waves have a dual character. This greatly complicates the classification of the non-radial modes. For $\ell =1$ the modes all have both energy in the core and in the envelope; they are mixed modes. For $\ell=2,3$ there is a succession of modes with energy either in the core or in the envelope with a few mixed modes. The echelle diagram used by the observers to extract the frequencies will work for $\ell=0,\,2,\,3$. The large difference is found to be of the order of $\overline{\Delta\nu_0}\approx 42\,\mu$Hz, in agreement with the Martic et al. (2001) seismic observations.

Key words: stars: binaries: visual - stars: evolution - stars: fundamental parameters - stars: individual: $\zeta $Her


  
1 Introduction

$\zeta $Herculis (40Her; BD+312884; STF2084; ADS10157; IDS16375+3147; WDS 16413+3136; HR6212; HD150680; HIP81693; $\alpha=16^{\rm h}41^{\rm m}17^{\rm s}$, $\delta=+31\hbox{$^\circ$ }36\hbox{$^\prime$ }10\hbox{$^{\prime\prime}$ }$ (2000)) is a well known bright visual and single lined spectroscopic binary system of naked-eye brightness. According to the CDS Simbad data base the system is composed of a 2.90 Vmagnitude G0IV sub-giant star and by a 5.53 Vmagnitude G7V dwarf star. The binarity was discovered by Herschell as early as 1782 (Aitken 1932) and the system has been carefully observed by visual binary observers for more than six revolutions back to the first reliable measurements by W. Struve in 1826. Several orbital solutions have been published from the early nineties to the present day. The latest are by Heintz (1994) and Söderhjelm (2000). The orbital elements are well determined. They have recently allowed improvements of Sproul Observatory and HIPPARCOS trigonometrical parallaxes. About a century ago, a duplicity of $\zeta $HerA was detected from micrometer and meridian observations (Lewis 1906). A period $P_{\rm Aa}=12$yr and a semi-major axis of $a_{\rm Aa}=0\hbox{$.\!\!^{\prime\prime}$ }25$was obtained for the sub-binary system $\zeta $HerAa. Ten years later, Comstock (1917) noted that the small irregularities of the areal velocity in the orbit have the effect of an invisible companion having a period of 18yr and an amplitude less than $0\hbox{$.\!\!^{\prime\prime}$ }1$. Later, a careful reanalysis of the available astrometric and spectroscopic observational material led Berman (1941) to conclude that"[$\ldots$] the presence of a third body revolving about the brighter component of $\zeta $Herculis is not definitely indicated''. The comparison between the observed position angles and distances and their values derived from its astrometric orbit allowed Baize (1976) to claim that $\zeta $HerA is split in two stars of respectively $1.05\,M_\odot$ and $0.19\,M_\odot$ with an orbital period $P_{\rm Aa}=10.5$yr and a semi-major axis $a_{\rm Aa}=0\hbox{$.\!\!^{\prime\prime}$ }06$. McCarthy (1983) reported that $\zeta $Her contains at least one unseen companion easily detected at $2.2\,\mu$m by infrared speckle interferometry. A note in the Fifth Catalog of Orbits of Visual Binary Stars (Hartkopf et al. 2000) stipulates: "No evidence in the speckle or Hipparcos data for the large-amplitude third-body orbit given by Baize''.

Lebreton et al. (1993) tried to determine both age and chemical composition of the system, modeling the two components simultaneously, but they did not succeeded in modeling the secondary consistently. Based on a precise spectroscopic analysis Chmielewski et al. (1995, hereafter C95) succeeded in modeling both components. They derived for the age $t_{\zeta\rm\,Her}=4.0\,\pm\,0.4$Gyr and for the masses of components respectively $1.3\,M_\odot$ and $0.9\,M_\odot$. Since 1995 the HIPPARCOS's parallax of $\zeta $Her has been available; it was recently improved by Söderhjelm (2000). The TYCHO & HIPPARCOS magnitudes are also available (Fabricius & Makarov 2000); they have been connected to the B, V and I magnitudes (Bessell 2000). New improved theoretical data are also available, viz. opacities, nuclear reaction rates and equation of state. The seismic observations of $\zeta $HerA recently carried out by Martic et al. (2001) indicate the presence of solar like oscillations.

The aim of the present paper is firstly to revisit the calibration of the $\zeta $Her binary system using updated physical data and theories and improved astrometrical and photometrical observational material, and secondly to give seismological properties of $\zeta $HerA which will be useful to exploit future asteroseismological observations.

Based on the reasonable hypothesis of a common origin for both components, i.e. same initial chemical composition and age, the calibration of a binary system consists of determining a consistent evolutionary history for the double star, given (1) the positions of the two components in the HR diagram, (2) the stellar masses and, if possible, (3) the present-day surface chemical compositions. The goal is to compute evolutionary models that reproduce the observations. The calibration yields estimates for the age, the initial helium mass fraction and the initial metallicity which are fundamental quantities for our understanding of the galactic chemical evolution. Within the error bars provided by astrometry, one also determines mass values consistent with the stellar structure modeling. According to the convection theory applied, one derives values for the "mixing-length parameter'' or "convection parameter'' $\Lambda$, ratio of the mixing-length to the pressure scale height. Once the physics is fixed, the modeling of the two components A and B of a binary system requires a set $\wp$ of seven so-called modeling parameters:

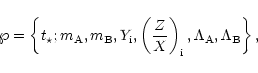
\begin{displaymath}\wp=\left\{t_\star ; m_{\rm A}, m_{\rm B}, Y_{\rm i}, \left(\frac ZX\right)_{\rm i}, \Lambda_{\rm A}, \Lambda_{\rm B}\right\},\end{displaymath}

where $t_\star$ is the age of the system, $m_{\rm A}$ and $m_{\rm B}$ are respectively the masses of components A & B, $Y_{\rm i}$ is the initial helium mass fraction, $\left(\frac ZX\right)_{\rm i}$ is the initial mass ratio of heavy elements to hydrogen, $\Lambda_{\rm A}$ and $\Lambda_{\rm B}$ are the mixing-length parameters. There are six observables, namely, the effective temperatures $T_{\rm eff\,A}$ & $T_{\rm eff\,B}$, the luminosities $L_{\rm A}$ & $L_{\rm B}$, the sum of masses $\cal S$ and the mass fraction $\cal B$ (cf. Eq. (2)). Once detailed spectroscopic analyses have been performed on the system, the present-day surface metallicities of stars come as additional observational constraints - in the case of $\zeta $Her the metallicity is available only for the brightest component. The paper is divided as follows. In Sects. 2.1, 2.2 and 2.3, respectively, we collect and discuss the astrometric, spectroscopic and photometric observations. In Sect. 3 we describe the computation of models and the search for the modeling parameters. In Sect. 4, we give the results with emphasis on the seismological analysis of $\zeta $HerA. Section 5 is devoted to a discussion and finally, we summarize our results and conclude in Sect. 6.

2 Observations of the visual binary $\zeta $Her

  
2.1 Astrometric data


   
Table 1: Relevant orbital elements of the $\zeta $Her binary system. P is the orbital period, a the semi-major axis, i the inclination and ethe eccentricity.

P		 a i e References

34.45yr		 $1\hbox{$.\!\!^{\prime\prime}$ }365$ $131\hbox{$.\!\!^\circ$ }6$ 0.464 Heintz (1994)
34.45yr $1\hbox{$.\!\!^{\prime\prime}$ }33$ $131\hbox{$.\!\!^\circ$ }$ 0.46 Söderhjelm (2000)

The knowledge of individual masses of each companion is one cornerstone of any calibration of a binary system. As illustrated by calibrations of $\alpha$Cen, (e.g. Morel et al. 2000), the resulting age is very sensitive to the values adopted for the masses of the components. We do not reproduce here the large bibliography on relevant astrometric data (e.g. C95); nevertheless we emphasize the discussion concerning the estimate of masses. For $\zeta $Her we are in the fortunate position of having two precise and independent determinations of the trigonometrical parallax and also improved orbital elements; from these data, two estimates of the sum of masses can be derived independently. A first determination is provided by a standard photographic parallax (Heintz 1994) using an improved relative orbit and 152 mid-nights of several decades of Sproul Observatory long focus photographic observations. The second one is the recently improved adjustment of parallax and orbital elements by Söderhjelm (2000) based on HIPPARCOS data collected during 3.25yr, old ground based observations and recent speckle-interferometry measurements. Table 1 lists the relevant orbital elements of these two recent astrometric orbits; they are so close that we can safely adopt the means listed in Table 3. The sum of masses is provided by Kepler's third law:

 \begin{displaymath} {\cal S}\equiv m_{\rm A}+m_{\rm B}=\frac{a^3}{\varpi^3P^2}, \end{displaymath} (1)

as usual P (yr) is the period, a (arcsec) is the semi-major axis of the relative orbit of the companion with respect to the primary, $m_{\rm A}$ and $m_{\rm B}$ are the masses (solar unit) of component A and B respectively and $\varpi$ (arcsec) is the parallax.

The outcome of standard long focus photographic parallax measurements is the so-called relative parallax  $\varpi_{\rm rel}$. It must be reduced to $\varpi_{\rm abs}$, the absolute parallax, by adding a correction representing the dependence weighted parallax of reference stars. The correction, of order 1 to 5 mas, is not accurately known (van deKamp 1967). For $\zeta $Her the correction is $0\hbox{$.\!\!^{\prime\prime}$ }0043$ (Lippincott 1981). With $\varpi_{\rm rel}=0\hbox{$.\!\!^{\prime\prime}$ }0974\pm0\hbox{$.\!\!^{\prime\prime}$ }0039$ (Heintz 1994) that leads to a photographic absolute parallax of $\varpi_{\rm abs}=0\hbox{$.\!\!^{\prime\prime}$ }102\pm0\hbox{$.\!\!^{\prime\prime}$ }0039$(standard deviation). The improved absolute parallax based on HIPPARCOS data and orbital ground-based measurements amounts to $\varpi_{\rm abs}=0\hbox{$.\!\!^{\prime\prime}$ }0937\pm0\hbox{$.\!\!^{\prime\prime}$ }0006$(Söderhjelm 2000). We adopt respectively for the parallax and the distance modulus of $\zeta $Her:

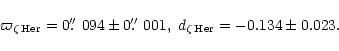
\begin{displaymath}\varpi_{\zeta\rm\,Her}=0\hbox{$.\!\!^{\prime\prime}$ }094\pm0... ....\!\!^{\prime\prime}$ }001,\ d_{\zeta\rm\,Her}= -0.134\pm0.023.\end{displaymath}

The sum of masses calculated with Eq. (1) is:

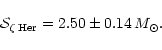
\begin{displaymath}{\cal S}_{\zeta\rm\,Her}=2.50\pm0.14\,M_\odot.\end{displaymath}

Note that the major source of error on the sum of masses remains the uncertainty on $\varpi$(Couteau 1978, 40, VI) even with modern estimates of the parallax. For the parallax, C95 have retained a value close to the former HIPPARCOS result $\varpi_{\zeta\rm\,Her}=0\hbox{$.\!\!^{\prime\prime}$ }0975$; with the same orbital elements, this larger value for the parallax leads to a smaller sum of masses ${\cal S}_{\zeta\rm\,Her}=2.4\,M_\odot.$

$\zeta $Her is one of the rare binary systems for which the mass fraction:

 \begin{displaymath} {\cal B}=\frac{m_{\rm B}}{m_{\rm A}+m_{\rm B}}, \end{displaymath} (2)

can be obtained both by astrometric and spectroscopic observational data. A first estimate of $\cal B$ is provided by photographic data. As the orbits of the primary and secondary are similar with respect to the center of masses, the semi-major axis @ of the orbit of the primary is related to a by $@={\cal B}a$. For the so-called resolved binaries the two companions are distinguishable by the detector and @ is directly derived from the observations. For unresolved binaries, the distance between the components is below the resolving power of the detector, in which case no separation is possible, and a composite image results. A close companion affects the center of light by pulling it toward the barycenter. With the photographic technique it is assumed that the measured position of the blended image represents the weighted center of light-intensity, or photocenter, of the components. In this case, the fractional distance $\beta$ of the primary to the photocenter, in terms of the distance between the two components, is given by (vandeKamp 1967):

 \begin{displaymath} \beta=\frac{L_{\rm B}}{L_{\rm A}+L_{\rm B}}=\frac1{1+10^{0.4\Delta m}}\cdot \end{displaymath} (3)

Here $L_{\rm A}$ and $L_{\rm B}$ are the luminosities of the components and $\Delta m$ the difference in magnitude. The fractional difference of photocenter to barycenter is therefore ${\cal B}-\beta$ and the semi-major axis of the photocenter orbit relative to the barycenter is $({\cal B}-\beta)a$. This $\beta$ correction also explicitly affects the derivation of the parallax. It has long been suspected that for a magnitude difference $\Delta m \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displa... ...finterlineskip\halign{\hfil$\scriptscriptstyle ... the position of blended images generally cannot be considered by the simple geometric Eq. (3) (Morel 1970; Feierman 1971). Likely, $\beta$ is also a function of the separation on the photographic plate, among other parameters. For the determination of the mass fraction of $\zeta $Her with $\Delta m=2.6$(Hoffleit & Jaschek 1982) Eq. (3) lead to $\beta=0.084$ while, from the work of Feierman (1971), $\beta=0.025$ (Lippincott 1981). These differences in $\beta$ lead to the discrepancies between the mass fraction derived by Heintz, ${\cal B}=0.412\pm 0.020$, and Lippincott, ${\cal B}=0.352\pm 0.020$, despite almost identical ${\cal B}-\beta$ values, namely 0.328 & 0.32. We shall refer to Heintz's (1994) value of ${\cal B}_{\rm p}=0.41\pm0.02$ as the "photographic'' mass ratio.

The second estimate of the mass fraction is provided by the spectroscopic orbit. For a single lined spectroscopic binary, with known orbital elements and parallax, the mass fraction is given by (e.g. Heintz 1971; Scarfe et al. 1983):

 \begin{displaymath} {\cal B}=\frac1{6.283}\frac{K_{\rm A}\varpi P\sqrt{1-e^2}}{a\sin i}\cdot \end{displaymath} (4)

As usual i is the inclination, e is the eccentricity and $K_{\rm A}$, in AUyr-1, is the velocity semi-amplitude of the primary star. Combined spectroscopic observations covering about four decades and astrometric measurements give $K_{\rm A}=4.01\pm0.04$kms-1 (Scarfe et al. 1983). From spectroscopy and orbital elements we obtain the "spectroscopic'' mass fraction:

\begin{displaymath}{\cal B}_{\rm s}=0.38\pm0.02.\end{displaymath}

We note the good agreement between spectroscopic and photographic determinations.

The mass fraction is not derived in the analysis of Söderhjelm (2000) despite an angular distance $\rho\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyl... ...criptscriptstyle ... larger than the grid step ( $1\hbox{$.\!\!^{\prime\prime}$ }208$) of HIPPARCOS (Martin et al. 1997), and changes of $\Delta\theta\sim10\hbox{$^\circ$ }$ and $\Delta\rho\sim0\hbox{$.\!\!^{\prime\prime}$ }10$ respectively in position angle and separation along the flight of the satellite.

For further investigations we shall adopt as the mass fraction of $\zeta $Her the weighted mean:

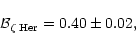
\begin{displaymath}{\cal B}_{\zeta\rm\,Her}=0.40\pm0.02,\end{displaymath}

between astrometric and spectroscopic values. C95 have adopted a slightly larger value ${\cal B}_{\zeta\rm\,Her}=0.42$.

With the values retained for ${\cal S}_{\zeta\rm\,Her}$ and ${\cal B}_{\zeta\rm\,Her}$ the individual masses are:

\begin{displaymath}m_{\zeta\rm\,Her\,A}=1.50\pm0.16, \quad m_{\zeta\rm\,Her\,B}=1.00\pm0.08.\end{displaymath}

Table 3 lists the astrometric data and the astrometric constraints we use for the calibration of the $\zeta $Her binary system.

  
2.2 Spectroscopic data

Effective temperatures and luminosities can be determined from both photometric and spectroscopic analyses. As a general rule, when available, it is the detailed spectroscopic analysis, using hydrogen line profiles, which provides the best estimates for effective temperatures, while bolometric magnitudes and luminosities are more accurately determined using photometric data and calibrations.

With classical 1.5m to 2.0m telescopes $\zeta $Her appears as a single star under average seeing conditions because of the large magnitude difference and of the small angular distance. Therefore isolated spectra of each component cannot be obtained. The available spectroscopic data in C95 allows the derivation of effective temperature only for $\zeta $HerA. We start with an estimate of $T_{\rm eff\,A}$ from Magain's (1987) calibration, assuming a metallicity of $[{\rm Fe/H}]=0.0$and color index (B-V)=0.65 (see Table 2). Then we perform a standard LTE detailed analysis using the curve of growth technique with models atmosphere from Gustafsson et al. (1975). Equivalent widths used are from C95 and the oscillator strengths are from Thévenin (1990). The microturbulence is fixed to 1.5kms-1. With the updated solar iron abundance $\log\epsilon_{\rm Fe}=7.46$(Holweger 1979; Asplund 2000) we derived the same metallicity $[{\rm Fe/H}]=0.04$ dex as C95. An ionization equilibrium is obtained from curves of growth of FeI and FeII which permits us to derive the surface gravity $\log g=3.85$. We correct the [Fe/H] value in Magain's (1987) formula and derived an improved temperature value of $T_{\rm eff\,A}=5\,820\pm 50$K and re-iterate the curve of growth analysis. Finally we deduce $\log g_{\rm A}=3.75\pm 0.15$ and $\rm [Fe/H]_A=+0.04\pm0.03$. With these improved input parameters the scattering of the curve of growth decreases and is satisfactory. C95 have derived a slightly smaller value for the gravity $\log g_{\rm A}=3.65\pm0.20$ invoking non- LTE effects. Such stars with solar abundances are not suspected to suffer from NLTE overionization (Thévenin & Idiart 1999), therefore the surface gravity of $\zeta $HerA can be considered as being well determined. It is remarkable that this new effective temperature value we derived, using both TYCHO's photometry (Fabricius & Makarov 2000) and spectroscopic analysis, is very close to $5\,825\pm40$K, the value obtained by C95 using both the photometry available in 1995 and the profile of H$\alpha$ corrected by the presence of the light of the secondary. The uncertainty on $\rm [Fe/H]_A$ has been estimated by varying  $T_{\rm eff}$ and $\log g$in their extremes and with the accuracy of the fit resulting from the quality of equivalent widths. The precision obtained for the metallicity is compatible with a value of 0.05dex, which is the more pessimistic estimate in C95. The precision obtained for the effective temperature results from the partial derivative of Magain's (1987) temperature formula combined with the abundance uncertainty and errors of the TYCHO magnitudes listed Table 2. For the effective temperature of $\zeta $HerA, C95 have obtained $\pm 40$K, a similar estimate.

The projected rotational velocity $v\sin i$ of $\zeta $HerA amounts to 3.9kms-1 (Fekel 1997). Assuming a parallel axis for rotation and orbital motion, $\sin i\approx0.655$, $\zeta $HerA is therefore a slow rotator. We can safely infer that it is the same for the less massive B component. So we can neglect the small rotational velocity in modeling the internal structure of both components.

  
2.3 Photometric data

We base the photometric analysis on magnitudes and color indexes taken from the TYCHO catalogue (Fabricius & Makarov 2000) as it provides consistent data for both components. For each component TYCHO's photometric system gives magnitudes $V_{\rm T}$ and $B_{\rm T}$ with an accuracy of the order of 0.01mag. HIPPARCOS's photometric system gives $H_{\rm P}$ magnitudes with an accuracy of the order of a few milli-magnitude. We use Bessell's (2000) relationships between color index $(B_{\rm T}-V_{\rm T})$ and $V-H_{\rm P}$, to derive the magnitudes in standard Johnson visual V and blue B filters. In view of Figs. 3 and 4 of Bessell's (2000) paper, the accuracy of calibrations are estimated to $\pm0.03$mag. The bolometric corrections, derived from Bessell et al. (1998) for each star are respectively:

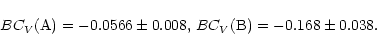
\begin{displaymath}{BC_V({\rm A})}=-0.0566\pm0.008, \, {BC_V({\rm B})}=-0.168\pm0.038.\end{displaymath}

To be consistent with the detailed spectroscopic analysis of $\zeta $HerA, the effective temperature of $\zeta $HerB is derived from Magain's (1987) formula using the color index (B-V)listed Table 2, the metallicity derived for $\zeta $HerA and the standard gravity of dwarf stars $\log g\sim 4.44$. The accuracy on $T_{\rm eff\,B}$ is derived as for $T_{\rm eff\,A}$. Resulting from the high accuracy of TYCHO magnitudes, we derive a better precision than C95. We obtain $T_{\rm eff\,B}=5300\pm150$K which is close to $5290\pm300$K, the value obtained by C95.

Table 2 lists the bolometric corrections, the bolometric magnitudes and luminosities computed with $M_{\rm bol,\,\odot}=4.74$ as the solar bolometric magnitude to be used with the Bessell et al. (1998) calibration. The Bessell (2000) photometric calibration allows us to derive the standard Johnson B and V magnitudes either from $(B_{\rm T} \& V_{\rm T})$ TYCHO magnitudes, or from $(B_{\rm T} \& V_{\rm T})$ and $H_{\rm P}$ HIPPARCOS magnitudes. The values obtained from each differ from each other by more than is expected from the accuracy of measurements. Moreover, fixing the color index (B-V), the effective temperatures calculated with different photometric calibrations (Magain 1987; Alonso et al. 1996; Flower 1996) differ by more than 150K. This indicates that the errors on data derived with the whole procedure may not have a standard Gaussian distribution. Therefore the uncertainties of quantities derived from photometric data are added in absolute value ( ${\cal L}^1$ norm) instead of standard quadrature ( ${\cal L}^2$ norm). Table 3 allows comparisons between the observational constraints retained in C95 and in this paper. The main differences are for the luminosity values owing to the smaller bolometric corrections and parallax we have used.


   
Table 2: Photometric data from TYCHO and HIPPARCOS and derived bolometric corrections, magnitudes and luminosities.

$\zeta $HerA $\zeta $HerB

$B_{\rm T}$		 $3.70\pm0.01$ $6.39\pm0.01$
$V_{\rm T}$ $2.98\pm0.01$ $5.47\pm0.01$
$H_{\rm p}$ $3.022\pm0.002$ $5.705\pm0.027$
B $3.539\pm0.055$ $6.369\pm0.081$
V $2.890\pm0.033$ $5.556\pm0.059$
(B-V) $0.649\pm0.088$ $0.81\pm0.140$
BCV $-0.0566\pm0.009$ $-0.168\pm0.026$
$M_{\rm bol}$ $2.699\pm0.065$ $5.254\pm0.108$
$L/L_\odot$ $6.55\pm0.39$ $0.62\pm0.06$


   
Table 3: Adopted observational data and derived constraints for the calibration of $\zeta $Her binary system.

this paper Chmielewski et al. (1995)

P		 $34.45\pm0.005$yr  
a $1\hbox{$.\!\!^{\prime\prime}$ }35\pm0\hbox{$.\!\!^{\prime\prime}$ }02$  
i $131\hbox{$.\!\!^\circ$ }3\pm0\hbox{$.\!\!^\circ$ }3$  
e $0.462\pm0.002$  
$K_{\rm A}$ $4.010\pm0.04$kms-1  
$\varpi$ $0\hbox{$.\!\!^{\prime\prime}$ }094\pm0\hbox{$.\!\!^{\prime\prime}$ }001$ $0\hbox{$.\!\!^{\prime\prime}$ }0975$
${\cal S}_{\zeta\rm\,Her}$ $2.50\pm0.14\,M_\odot$ $2.40\,M_\odot$
${\cal B}_{\zeta\rm\,Her}$ $0.40\pm 0.02$ 0.42
$T_{\rm eff\,A}$ $5820\pm50$K $5825\pm40$K
$L_{\rm A}/L_\odot$ $6.55\pm0.39$ $6.194\pm0.285$
$\rm [\frac{Fe}H]_{\rm A}$ $0.04\pm0.03$ $0.05\pm0.05$
$T_{\rm eff\,B}$ $5300\pm150$K $5290\pm300$K
$L_{\rm B}/L_\odot$ $0.62\pm0.06$ $0.575\pm0.069$

  
3 Evolutionary models

The mean angular separation between $\zeta $HerA & B being of the order of $\bar\rho=1\hbox{$.\!\!^{\prime\prime}$ }5$, the distance between the two companions amounts to $\simeq$150 AU. The tidal interactions between the two components are then negligible. We can safely assume that stars have evolved as single ones, ignoring each other.

Models have been computed using the CESAM code (Morel 1997). About 600 mass shells describe each model; this number increases up to 2100 for the model used in seismological analysis. Around 400 and 30 models are needed to describe the evolutions of $\zeta $Her A and B respectively.

Basically the physics employed is the same as in Morel et al. (2000). The ordinary assumptions of stellar modeling are made, i.e. spherical symmetry, no rotation, no magnetic field and no mass loss. The evolutions are initialized with homogeneous zero-age main-sequence models ( ZAMS). In the absence of satisfactory treatment of microscopic diffusion for stars with mass larger than $\approx$ $1.3\,M_\odot$, we do not take into account the diffusion of chemical species. This important assumption is discussed in Sect. 5.

3.1 Physical inputs

The relevant nuclear reaction rates are taken from the NACRE compilation (Angulo et al. 1999). We use the approximation:
 
           $\displaystyle \rm {\left[\frac{Fe}H\right]}$ $\textstyle \equiv$ $\displaystyle \log\left(\frac{Z_{\rm Fe}}Z\right)+\log\left(\frac ZX\right)- \log\left(\frac{Z_{\rm Fe}}X\right)_\odot$  
  $\textstyle \simeq$ $\displaystyle \log\left(\frac ZX\right) - \log\left(\frac ZX\right)_\odot$  

where $(\frac{Z_{\rm Fe}}Z)$ is the iron mass fraction within Z. We use the solar mixture of Grevesse & Noels (1993) i.e. $\left(\frac ZX\right)_\odot=0.0245$. We employed the OPAL equation of state (Rogers et al. 1996) and the opacities of Iglesias & Rogers (1992) complemented at low temperatures by Alexander & Ferguson (1994) opacities. In the convection zones the temperature gradient is computed according to the Canuto & Mazitelli (1991, 1992) convection theory. The mixing-length is defined as $l\equiv \Lambda H_{\rm p}$, where $H_{\rm p}$ is the pressure scale height and $\Lambda$ is the mixing-length parameter of order unity. $\zeta $HerA, more massive than $1.25\,M_\odot$, presents a convective core along the main-sequence. Following the prescriptions of Schaller et al. (1992) we have also calibrated the $\zeta $Her binary system with an overshooting of the convective core of $\zeta $HerA over the distance $O_{\rm v}=0.2\min\,(H_{\rm p}, R_{\rm co})$, where $R_{\rm co}$ is the core radius. The atmosphere is restored using Hopf's law (Mihalas 1978). We use the numerical trick of Henyey et al. (1965) to connect consistently the radiative and the convective parts of the atmosphere. Hence a smooth connection of the gradients is insured between the uppermost layers of the envelope and the optically thick convective bottom of the atmosphere. It is an important requirement for the calculation of eigenmode frequencies. The radius $R_\star$ of any model is taken at the optical depth  $\tau_\star$ where $T(\tau_\star)=T_{\rm eff}$, $\tau_\star=0.645$ with Hopf's law. The mass $M_\star$ of the star is defined as the mass enclosed in the sphere of radius $R_\star$. The external boundary is located at the optical depth $\tau_{\rm ext}=10^{-4}$, where the density is fixed at a standard value in Kurucz's (1991) atmosphere models: $\rho(\tau_{\rm ext})=3.55\times 10^{-9}$ gcm-3.

  
3.2 The search of calibration parameters

The calibration of a binary system is based on the adjustment of stellar modeling parameters to observational data at the age of the system. Fixing the physics, the effective temperature $T_{\rm eff}$, the luminosity L and the surface metallicity $\rm\left[\frac{Fe}H\right]_s$ of a stellar model have the formal dependences with respect to modeling parameters: 0pt
 
    $\displaystyle \log T_{\rm eff}(\star)_{\rm mod}=\log T_{\rm eff} \left(t_\star;m_\star,Y_{\rm i\star},{\rm\left[\frac{Fe}H\right]_i\star},\Lambda_\star\right),$  
    $\displaystyle \log \left(\frac{L(\star)}{L_\odot}\right)_{\rm mod}=\log\left(\f... ...\star,Y_{\rm i\star}, {\rm\left[\frac{Fe}H\right]_i\star},\Lambda_\star\right),$  
    $\displaystyle {\rm\left[\frac{Fe}H\right]_{\rm s}}(\star)_{\rm mod}= {\rm\left[... ...\star,Y_{\rm i\star}, {\rm\left[\frac{Fe}H\right]_i\star},\Lambda_\star\right),$ (5)

1.75pt where the subscript " $\rm _{mod}$'' refers to model values. Without microscopic diffusion almost no change in chemical composition due to nuclear reactions occurs in the envelope of a star as massive as $\zeta $HerA so $\rm [\frac{Fe}H]_{\rm s}\approx[\frac{Fe}H]_{\rm i}$ and Eq. (5) becomes trivial. The basic idea of the $\chi^2$ fitting has been developed by Lastennet et al. (1999). To find a set of modeling parameters:

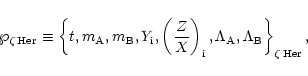
\begin{displaymath}\wp_{\zeta\rm\,Her} \equiv\left\{t,m_{\rm A},m_{\rm B}, Y_{\r... ...\rm i},\Lambda_{\rm A},\Lambda_{\rm B}\right\}_{\zeta\rm\,Her},\end{displaymath}

leading to observables as close as possible to the observational constraints $\log T_{\rm eff}(\zeta{\rm\,Her\,A})$, $\log \left(\frac{L(\zeta{\rm\,Her\,A})}{L_\odot}\right)$, $\log T_{\rm eff}(\zeta{\rm\,Her\,B})$, $\log \left(\frac{L(\zeta{\rm\,Her\,B})}{L_\odot}\right)$ and $\rm\left[\frac{Fe}H\right]_{\rm s}(\zeta{\rm\,Her\,A})$we minimize a $\chi^2(t_\star,m_{\rm A},m_{\rm B},Y_{\rm i},{\rm [\frac{Fe}H]_i}, \Lambda_{\rm A},\Lambda_{\rm B})$ functional defined as:
 
                            $\displaystyle \chi^2$   $\displaystyle = \left(\frac{{\rm\left[\frac{Fe}H\right]_s}({\rm A})_{\rm mod}-{... ...s}}({\rm A})} {\sigma\left({\rm [\frac{Fe}H]_{\rm s}}({\rm A})\right)}\right)^2$  
    $\displaystyle \quad+\sum_{\star={\rm A}, {\rm B}}\left[\left(\frac{\log T_{\rm ... ...ma\left(\log T_{\rm eff}(\star)\right)^{\raisebox{1.75ex}{~}}}\right)^2 \right.$  
    $\displaystyle \left.\quad+\left(\frac{\log\left(\frac{L(\star)}{L_\odot}\right)... ...\sigma\left(\log\left(\frac{L(\star)}{L_\odot}\right)\right)}\right)^{2}\right]$ (6)

where the $\sigma$'s are the uncertainties associated with the constraints. For sets of modeling parameters within the ranges detailed in Sect. 4.1, we have computed the evolution of models from homogeneous ZAMS (t=0) to $t\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...Gyr. Then the $\chi^2$ was computed using Eq. (6) in a refined grid obtained by interpolations. We kept for the solution the "best'' $\wp=\wp_{\zeta\rm\,Her}$ which corresponds to the  $\chi^2_{\rm min}$. After some hand adjustments these best modeling parameters served to compute the models of $\zeta $HerA and B. Table 4 lists the confidence limits of the modeling parameters of models computed in this paper. The confidence limits of each modeling parameter, the other being fixed, correspond to the maximum/minimum values it can reach, in order that the generated models fit the observable targets within their error bars. Owing to the uncertainties of the observation material, mainly on the effective temperature of $\zeta $HerB, we do not attempt to improve the solution, or to compute more precisely the error bars affecting the modeling parameters using the singular value decomposition of the design matrix as developed by Brown et al. (1994).
   
Table 4: Calibration parameters of $\zeta $Her binary system models lying within the uncertainty boxes. The observational constraints listed in Table 3 are recalled in parenthesis. The subscripts "$_{\rm i}$'' and "$_{\rm s}$'' respectively refer to initial and surface quantities.

$\zeta \,\rm Her\,A$ $\zeta\,\rm Her\,B$

$m/M_\odot$		 $1.45\pm 0.01$ $0.98\pm 0.02$
${\cal S}\,(M_\odot)$ $2.43\,(2.50\pm0.14)$
$\cal B$ $0.403\,(0.40\pm0.02)$
$Y_{\rm i}$ $0.243\pm 0.002$
$\rm [\frac{Fe}H]_{\rm s}$ $0.042 \,(0.04\pm0.003)$  
$\Lambda$ $0.92\pm0.05 $ $0.90\pm0.10 $
  Calibration without overshoot for $\zeta $HerA
age (Myr) $3\,387\pm15$
$T_{\rm eff}$(K) $5\,818\,(5\,820\,\pm50)$ $5\,413\,(5\,300\,\pm150)$
$L/L_\odot$ $6.72\,(6.55\pm0.39)$ $0.65\,(0.62\pm0.06)$
$\left(\frac ZX\right)_{\rm i}$ $0.0269\pm 0.0005$
$X_{\rm i}$ 0.737
$Z_{\rm i}$ 0.0198
$ R/R_\odot$ 2.56 0.915
$\overline{\Delta\nu_0}\,(\mu$Hz) 42.2 157.
  Calibration with overshoot for $\zeta $HerA
age (Myr) $3\,625\pm22$
$T_{\rm eff}$(K) $5\,798\,(5\,820\,\pm50)$ $5\,418\,(5\,300\,\pm150)$
$L/L_\odot$ $6.82\,(6.55\pm0.39)$ $0.65\,(0.62\pm0.06)$
$\left(\frac ZX\right)_{\rm i}$ $0.0272\pm 0.005$
$X_{\rm i}$ 0.737
$Z_{\rm i}$ 0.0200
$ R/R_\odot$ 2.61 0.920
$\overline{\Delta\nu_0}\,(\mu$Hz) 40.9 156.

  
4 Results

  
4.1 Calibration of $\zeta $Her

We have computed the evolution of models with initial helium mass fraction, initial ratio of heavy elements to hydrogen, masses and mixing length parameters respectively in the ranges $0.24\leq Y_{\rm i}\leq 0.27$, $0.026\leq [\frac ZX]_{\rm i}\leq 0.030$, $1.35\,M_\odot \leq m_{\zeta\rm\,Her\,A}\leq 1.65\,M_\odot$, $0.85\,M_\odot \leq m_{\zeta\rm\,Her\,B}\leq 1.15\,M_\odot$, $0.9 \leq \Lambda_{\rm\zeta\,Her\,A}\leq 1.1$ and $0.9 \leq \Lambda_{\rm\zeta\,Her\,B}\leq 1.1$. For the models of $\zeta $HerA, as soon as $\log T_{\rm eff\,A}\leq 3.765$ the evolution is halted. Table 4 lists the set of "best'' modeling parameters we adopt for the $\zeta $Her A & B models with and without overshooting of the convective core of the primary. Figure 1 shows the corresponding evolutionary tracks in the HR diagram. For the calibration with core overshooting of $\zeta $HerA, we have not recomputed specific sets of models to undertake another $\chi^2$ minimization. We fit the observable constraints within error boxes by adjustments of $t_\star$ and $(\frac ZX)_{\rm i}$, the other modeling parameters having the values obtained without overshooting. The larger value obtained for the age ($\sim$+250Myr) results from the larger amount of nuclear fuel available in the overshoot convection core.

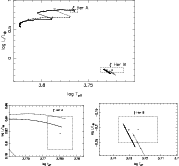  \begin{figure} { \psfig{figure=1660f1.eps,height=8.5cm,angle=270} } \vspace{0.5t... ...ace{0.5truecm} \psfig{figure=1660f3.eps,height=5.5cm,angle=270} }}\end{figure} Figure 1: Evolutionary tracks in the H-R diagram for models of $\zeta $HerA, & B without overshooting (full), with overshooting of  $0.2\,H_{\rm p}$ for the convective core of $\zeta $HerA (dot-dash-dot) and with a larger metallicity of 0.05 dex for $\zeta $HerB (dotted). The open squares correspond to the locus of $\zeta $HerB assuming this larger metallicity. Dashed rectangles delimit the uncertainty domains. Top panel: full tracks from ZAMS. The "+'' signs denote 1Gyr time intervals along the evolutionary tracks. Bottom left and right panels: enlargements around the observed $\zeta $HerA & B loci.
Open with DEXTER

  
4.2 Seismological analysis of $\zeta $HerA

The sub-giant star $\zeta $HerA has a convective envelope which may stochastically excite oscillations as is the case in the Sun. Some seismic observations of $\zeta $HerA have been done by Martic et al. (2001) and seem to indicate a narrow excess of power around a maximum at $675\,\mu$Hz in the power spectrum. It is thus interesting to consider the seismic properties of the model selected by the calibration.

For our $\zeta $HerA model without overshooting, we have computed a set of adiabatic frequencies of the normal modes for degrees $\ell =0,1,2,3$ in the frequency range 300 to $1000\,\mu$Hz. The model corresponds to an evolved star which has burnt all the hydrogen core and presents a radiative core and a convective envelope starting at $r_{\rm c} \sim 0.752\,R_\star$, ( $M_{\rm c} \sim 0.9929\,M_\star$). At age $t_{\zeta\rm\,Her}=3\,387$Myr the convective core which is present during the main sequence evolution has disappeared about 440Myr ago. A zone of varying chemical gradient was formed between the outer edge of the initial convective core and the center. This $\mu $-gradient gives a rapid variation of the sound speed and a large value of the maximum of Brunt-Väisälä frequency N (e.g. Unno et al. 1989):

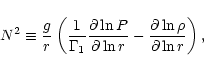
\begin{displaymath}N^2\equiv \frac gr\left(\frac1{\Gamma_1}\frac{\partial\ln P}{\partial\ln r} -\frac{\partial\ln\rho}{\partial\ln r}\right), \end{displaymath}

of the order of $3\,500\,\mu$Hz - as usual P is the pressure, $\rho $ the density, $\Gamma_1$the first adiabatic exponent and g the local gravity. It acts like a potential well that may trap gravity waves. Figure 2 shows the profiles of the Brunt-Väisälä frequency N and of Lamb frequencies $L_{\ell }$( $\ell=1,\,2,\,3$) with respect to the normalized radius $r/R_\star$, viz. the corresponding propagation diagram. Recall that the Lamb frequency writes:

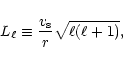
\begin{displaymath}L_\ell\equiv\frac{v_{\rm s}}r\sqrt{\ell(\ell+1)}, \end{displaymath}

e.g. Unno et al. (1989), $v_{\rm s}$ is the sound velocity.

Looking at the set of computed frequencies, we see that for each degree, the oscillation spectrum is no longer composed of two separated sets of modes with acoustic (p-modes) and gravity (g-modes) behavior as in solar-like stars but it is a complicated superposition of these two sets. Some of these waves have a dual character as they behave like pressure waves in the envelope of the star and gravity waves in the core. This greatly complicates the classification of the non-radial modes.

The distinction between the g- and p-modes can be made by considering their normalized integrated kinetic energy (or inertia) $E_{n,\ell }$ (e.g. Christensen-Dalsgaard & Berthomieu 1991). The energy of the p-modes does not depend on the degree. Figure 3 plots this quantity as a function of the frequency for $\ell =0,1,2,3$. The g-modes have a much larger energy than the p-modes. It appears that for $\ell =1$ the modes all have both energy in the core and in the envelop, so they are mixed modes. Figure 4, upper panel, shows the distribution of kinetic energy density of two of these modes along the radius of the star. For $\ell=2,3$ we have a succession of modes with energy either in the core or in the envelope with a few mixed modes as seen in Fig. 4, lower panel.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1660f4.eps} \end{figure} Figure 2: Propagation diagram: profiles as functions of the nondimensionned stellar radius, of Brunt-Väisälä frequency N and Lamb frequencies $L_{\ell }$ for degrees $\ell =1$ (dotted), $\ell =2$ (dot-dash) and $\ell =3$ (dot-dot-dot-dash). The horizontal lines correspond to the two modes $\ell =2,\ \nu =563.5\, \mu $Hz and $\nu =593.8\,\mu $Hz, the first one with gravity behavior and the second one with acoustic behavior. Figure 4 shows their eigenfunctions. The full line indicates the region of the star where the modes are propagative.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1660f5.eps} \end{figure} Figure 3: Logarithm of the normalized integrated kinetic energy $E_{n,\ell }$ of the modes as a function of frequency (in $\mu $Hz) for modes of degree $\ell =0$ (full), $\ell =1$ (dashed), $\ell =2$ (dot-dash), $\ell =3$ (dotted). Note that all the points corresponding to p-modes are on the full line.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=14.6cm,clip]{1660f6.eps} \end{figure} Figure 4: Density of kinetic energy $\rho r^2\delta r.\delta r^\ast $ of two modes with consecutive radial orders for $\ell =1$ (upper panels) and $\ell =2$ (lower panels) as a function of the normalized radius ($\rho $ is the density and $\delta r$ the displacement). Note that the modes $\ell =1$ are mixed modes while the modes $\ell =2$ are alternatively g- and p-modes.
Open with DEXTER

The set of frequencies with acoustic behavior can be analyzed by classical asymptotic tools. The acoustic characteristic mean large frequency spacing, also called "large difference'', corresponds to a mean of the quasi uniform spacing between mode frequencies with the same degree and consecutive orders, is given by:

 \begin{displaymath} \overline{\Delta\nu_0}=\left(2\int_0^{R_{\rm s}} \frac{{\rm d}r}{v_{\rm s}(r)}\right)^{-1}\sim 42\, \mu{\rm Hz}; \end{displaymath} (7)

where $R_{\rm s}$ corresponds to the radius of the outermost shell of the model. The scaling of Kjeldsen & Bedding (1995) gives a close value:

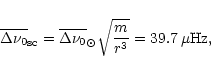
\begin{displaymath}\overline{\Delta\nu_0}_{\rm sc}=\overline{\Delta\nu_0}_\odot\sqrt{\frac m{r^3}} =39.7\,\mu{\rm Hz}, \end{displaymath}

where m and r are respectively the mass and the radius in solar units and $\overline{\Delta\nu_0}_\odot=134.9\,\mu$Hz. The computed frequencies are fitted to the following asymptotic relation (Berthomieu et al. 1993):

 \begin{displaymath} \nu_{{\it n},\ell} = \nu_0 +\Delta\nu_\ell (n-n_0) +a_\ell(n-n_0)^2. \end{displaymath} (8)

With radial order n between 10 and 20 and n0=15we obtain values for the mean large difference at a given degree listed Table 6. They are close to the large difference  $\overline{\Delta\nu_0}$, cf. Eq. (7), though smaller.

These values are to be compared to the observations of Martic et al. (2001) who derive a value around $42\,\mu$Hz from the construction of an echelle diagram. Figure 5 plots the large differences $\nu_{n,\ell}-\nu_{n-1,\ell}$ with respect to frequency. Except for modes $\ell =1$, the points corresponding to high frequency modes are close to the same flat curve around $41\,\mu$Hz, with oscillations due to the rapid variation of the adiabatic exponent $\Gamma_1$ in the helium ionization zone. As in the Sun, the g-modes have small amplitudes at the surface and thus they will be hardly observable. Therefore it is probable that the echelle diagram used by the observers to extract the frequencies, taking account of their asymptotic distribution, will work for $\ell=0,\,2,\,3$ but not for the mixed modes $\ell =1$. The fit of the small differences:

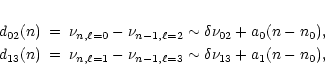
\begin{eqnarray*}d_{02}(n)&=&\nu_{n,\ell=0}-\nu_{n-1,\ell=2}\sim\delta\nu_{02}+a... ...&=&\nu_{n,\ell=1}-\nu_{n-1,\ell=3}\sim\delta\nu_{13}+a_1(n-n_0), \end{eqnarray*}


gives the following results ($\mu $Hz):

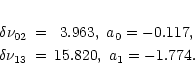
\begin{eqnarray*}\delta\nu_{02}&=&\ 3.963,\ a_0=-0.117,\\ \delta\nu_{13}&=&15.820,\ a_1=-1.774. \end{eqnarray*}


Figure 6 shows the asymptotic behavior of $\delta\nu_{02}$ with aligned points and the large dispersion of points for $\delta\nu_{13}$ due to the mixed character of the modes $\ell =1$.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1660f7.eps} \end{figure} Figure 5: Frequency differences between acoustic modes of same degree and consecutive radial order as function of the frequency (in $\mu $Hz).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1660f8.eps} \end{figure} Figure 6: Variation of the small differences d02 (full dots) and  $\frac35d_{13}$ (open dots), as a function of the frequency (in $\mu $Hz). The full and dotted lines represent their linear fit.
Open with DEXTER

The calibrated model of $\zeta $HerA calculated with overshoot of its convective core, has a larger radius inducing a smaller value of $\overline{\Delta\nu_0}$as seen in Table 4.

  
5 Discussion

The Achilles' heel of our calibration is the derivation of effective temperature and luminosity of $\zeta $HerB. It is based on the only reliable measurements of B and V magnitudes of each component by TYCHO and HIPPARCOS. The Bessell (2000) photometric calibration allows us to derive the standard Johnson B and V magnitudes either from $(B_{\rm T} \& V_{\rm T})$ TYCHO magnitudes, or from $(B_{\rm T} \& V_{\rm T})$ and $H_{\rm P}$ HIPPARCOS magnitudes. In the case of $\zeta $HerB, B and V magnitude values obtained in each way differ from each other by more than is expected from the accuracy of measurements. Moreover, fixing the color index (B-V), the effective temperatures calculated with different photometric calibrations (Magain 1987; Alonso et al. 1996; Flower 1996) differ by more than 150K. Fortunately, the scattering is not so large with the bolometric correction BCV. As a result, the effective temperature and the luminosity of $\zeta $HerB are hardly known with a relative accuracy better than 3% and 10% respectively. As a matter of comparison we have derived the effective temperature and the luminosity of $\zeta $HerA with better accuracy, respectively 0.8% and 6%.

We are aware that our models suffer from the absence of diffusion of chemicals species. We do not introduce it as we do not have a satisfactory description of the physical process which acts against the too large efficiency of the gravitational settling in the envelope of a main sequence stellar model with mass larger than $M\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ... i.e. without a significant outer convection zone (e.g. Schatzman 1969; Turcotte et al. 1998). The derived metallicity of $\zeta $HerA could not be representative of the initial mixture that formed $\zeta $HerA & B. Because of the large difference in mass between the components, the diffusion has been more efficient in $\zeta $HerA than in $\zeta $HerB and therefore the adopted metallicity for $\zeta $HerB needs to be increased. As the mass of $\zeta $HerB is close to the solar one, we can safely assume that the change in metallicity has occurred at the same rate in the Sun and in $\zeta $HerB. From ZAMS to the age $t\approx 3400$Myr, the metallicity of the Sun is increased by about 0.05dex. Using Magain's (1987) formula, an $\rm [Fe/H]_B$ increase corresponds to an increase of $\sim$+75K in effective temperature. Figure 1 shows that the locus (open square) of $\zeta $HerB in the HR diagram with $T_{\rm eff\,B}$ larger by 75K is closer than before to the evolutionary tracks. To go further one needs a measurement of the metallicity of $\zeta $HerB.

With $m_{\rm A}=1.50\,M_\odot$ and $m_{\rm B}=1.00\,M_\odot$it was not possible to obtain simultaneous satisfactory adjustments, within the error boxes, for both components. Realistic solutions are found with $m_{\rm A}=1.45\,M_\odot$. That may indicates that the suspected duplicity of $\zeta $HerA is perhaps real. In such a case the hypothetical unseen component $\zeta $Hera will be less massive than previously announced, $m_{\zeta\rm\,Her\,a}\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hf... ...skip\halign{\hfil$\scriptscriptstyle ... and will be a brown dwarf or a giant planet. Though Table 4 exhibits insignificant small differences between mixing length parameters of $\zeta $HerA & B, we obtained values of the order of unity, as expected with the Canuto & Mazitelli (1991, 1992) convection theory. The differences between the C95 and our calibrations mainly result from the difference in distance. In the HR diagram the locus of our $\zeta $HerA model is found in the Hertzsprung gap soon after the main sequence, as expected for a sub-giant star. In this part of the HR diagram, the effective temperature of a star model varies rapidly with respect to time. So the age is very sensitive to small changes of physics or of modeling parameter. The small uncertainty we give for the age corresponds to the crossing time of the error box in effective temperature. It is valid only with the physics we used and with the central values of other modeling parameters. In their study C95 obtained a value for the age: $t_{\zeta\,\rm Her}=4.0\pm0.4$Gyr close to ours. We emphasized the fact that the crossing time of the C95 error box in effective temperature ($\pm 40$K) is about twenty times smaller than their estimated accuracy in age.

   
Table 5: Mass ($M_\odot $), initial mass fraction of helium, initial ratio of heavy elements to hydrogen, age (Myr), radius ($R_\odot $), effective temperature (K) and large difference ($\mu $Hz) of $\zeta \,\rm Her\,A$ models - without overshooting - computed with modeling parameters within the error bar of Table 4.

M $Y_{\rm i}$ $(\frac ZX)_{\rm i}$ age R $T_{\rm eff}$ $\overline{\Delta\nu_0}$

Ag+		 1.45 0.243 0.0269 3400 2.58 5763 41.6
Ag- 1.45 0.243 0.0269 3372 2.53 5868 42.8
Am+ 1.46 0.243 0.0269 3315 2.59 5811 41.6
Am- 1.44 0.243 0.0269 3415 2.53 5808 42.7
Ay+ 1.45 0.245 0.0269 3298 2.57 5808 41.8
Ay- 1.45 0.242 0.0269 3332 2.55 5811 42.3
Az+ 1.45 0.243 0.0274 3376 2.55 5810 42.4
Az- 1.45 0.243 0.0264 3365 2.57 5808 41.8


   
Table 6: Theoretical global asymptotic quantities (in $\mu $Hz) describing the p-mode oscillations according to Eq. (8) for degrees $\ell =0,1,2,3$.

$\ell$		 $\nu_0$ $\Delta\nu_\ell$ $ a_\ell$

0		 654.0 40.7 0.130
1 659.5 38.8 0.336
2 650.4 40.8 0.094
3 645.0 40.7 0.111

Table 5 lists the ages, the radii, the effective temperatures and the large differences of $\zeta $HerA models computed with modeling parameters within their error bars, but for mixing-length parameters. The age of the model Ag- (respt. Ag+) corresponds to the time elapsed from ZAMS to the instant where the effective temperature crosses the left (respt. right) limit of the error box in the HR diagram, namely $\log T_{\rm eff}=3.768$ (respt. $\log T_{\rm eff}=3.761$). The ages of other models listed in Table 5 corresponds to the time elapsed from ZAMS to the instant where the effective temperature crosses the central value $\log T_{\rm eff}=3.765$. The variations of $\overline{\Delta\nu_0}$reflect the differences in radius and mass of star models. Table 5 shows that one derives unrealistic precision for the modeling parameters by defining their accuracy in such a way that any combination of them, within their error bars, will provide models of $\zeta $HerA & B within the observational constraints. Owing to the weakness of the observing material we do not attempt to derive the accuracy of the modelling parameters using the method developed by Brown et al. (1994). A more sensitive modeling parameter is the age due to the fast post main-sequence evolution of $\zeta $HerA. The accuracies of modeling parameters listed in Table 4 may be optimistic. They mean that, for a value of any modeling parameter within its interval of accuracy, one can find a set of other modeling parameters, each of them within its own accuracy limit, in such a way that they will provide models of $\zeta $HerA & B within the observational constraints.

  
6 Conclusion

Detailed evolutionary calculations of the visual binary system $\zeta $Herculis have been performed using OPAL opacities and equation of state, NACRE thermonuclear reaction rates, Canuto & Mazitelli (1991, 1992) convection theory. The effective temperature, surface gravity and metallicity of $\zeta $HerA have been reestimated using published spectroscopic data (Chmielewski et al. 1995; Thévenin 1990) and new photometric data of the TYCHO catalogue (Fabricius & Makarov 2000). The luminosity of $\zeta $HerA and the effective temperature and luminosity of $\zeta $HerB are calculated according to TYCHO and HIPPARCOS photometric data and Bessell (2000) calibrations. The sum of masses have been estimated using updated astrometric relative orbit and parallax determinations. The mass fraction is derived from spectroscopic and astrometric orbits. We have determined the most reliable solution within the confidence domains of the observable constraints via a $\chi^2$ minimization. Each solution is characterized by $\wp=\{t_{\rm\zeta\,Her},m_{\rm A},m_{\rm B},Y_{\rm i}, {[\rm\frac{Fe}H]_{\rm i}},\Lambda_{\rm A},\Lambda_{\rm B}\}$, where $t_{\rm\zeta\,Her}$ is the age of the system, $m_{\rm A}$ and $m_{\rm B}$ the masses of components A & B respectively, $Y_{\rm i}$ the initial helium content, ${\left[\rm\frac{Fe}H\right]_{\rm i}}$ the initial metallicity and $\Lambda_{\rm A}$ and $\Lambda_{\rm B}$ the convection parameter of each star model. We obtained $\wp_{\zeta\,\rm Her}= \{3387\,{\rm Myr},1.45\,M_\odot,0.98\,M_\odot, 0.243,0.0269,0.92,0.90\}$. As a sub-giant, in the HR diagram $\zeta $HerA is located beyond the main-sequence in the "Hertzsprung gap'', where the star loci move rapidly. So, all other modeling parameters being fixed, the locus of $\zeta $HerA takes only a couple of ten Myr to cross over the error box in effective temperature. Therefore, fixing the physics, the modeling parameters of the system appear artificially well defined. Fixing the masses obtained previously, we have calibrated the binary system assuming an overshoot of $0.20\,H_{\rm p}$, for the convective core of $\zeta $HerA. We did not obtain significantly different modeling parameters but a larger value for the age, namely $\sim$+250 Myr.

The adiabatic oscillation spectrum of $\zeta $HerA is found to be a complicated superposition of acoustic and gravity modes. Some of these waves have a dual character. This greatly complicates the classification of the non-radial modes. For $\ell =1$ the modes are mixed modes with both energy in the core and in the envelope, they are mixed modes. For $\ell=2,3$ there is a succession of modes with energy either in the core or in the envelope with a few mixed modes. This will have an implication for the properties of the echelle diagram used by observers which will have a smooth behavior only for the modes $\ell=0,\,2,\,3$. The large difference is found to be of the order of $\Delta\nu_0\approx 41\,\mu$Hz close to the preliminary value derived from observations by Martic et al. (2001).

Six years ago, in the conclusion of their study, Chmielewski et al. (1995) requested "[$\ldots$] to go further, (i) a better photometry of component B and (ii) the exact value of the parallax''. Our work shows that the calibration of $\zeta $Her remains a difficult task, even with the disposal of improved observational data. Among the binaries to be calibrated with some confidence, $\zeta $Herculis is one of the most interesting owing to the difference of evolutionary state of components resulting from their mass difference. Though difficult, $\zeta $Her is a reachable target for modern spectroscopic and photometric apparatus. $\zeta $Her deserves interest to improve the accuracy of the modeling constraints hence, of stellar models and seismological analysis. It is all the more desirable because seismic observations of $\zeta $HerA will hopefully give new constraints.

Acknowledgements
We thank M. Martic for having directed our attention to the opportunity to revisit the calibration of the $\zeta $Her binary system and to undertake the seismological analysis of the brightest component. We would like to express our thanks to the unknown referee, for helpful advises. This research has made use of the Simbad data base, operated at CDS, Strasbourg, France and of the WDS data base operating at USNO, Washington, DC, USA. This work has been performed using the computing facilities provided by the OCA program "Simulations Interactives et Visualisation en Astronomie et Mécanique (SIVAM)''.

References

 
Copyright ESO 2001