A&A 379, 8-20 (2001)
DOI: 10.1051/0004-6361:20011309
P. Valageas
Service de Physique Théorique, CEN Saclay, 91191 Gif-sur-Yvette, France
Received 28 May 2001 / Accepted 13 September 2001
Abstract
We develop a systematic method to obtain the solution of the collisionless Boltzmann equation which describes the growth of large-scale structures as a perturbative series over the initial density perturbations. We give an explicit calculation of the second-order terms which are shown to agree with the results obtained from the hydrodynamical description of the system. Then, we explain that this identity extends to all orders of perturbation theory and that the perturbative series actually diverge for hierarchical scenarios. However, since the collisionless Boltzmann equation provides the exact description of the dynamics (including the non-linear regime) these results may serve as a basis for a study of the non-linear regime. In particular, we derive a non-perturbative quadratic integral equation which explicitly relates the actual non-linear distribution function to the initial conditions (more precisely, to the linear growing mode). This allows us to write an explicit path-integral expression for the probability distribution of the exact non-linear density field.
Key words: cosmology: theory - large-scale structure of universe
In usual cosmological models large-scale structures in the universe have formed through the growth of small initial density perturbations by gravitational instability, see Peebles (1980). Moreover, in most cases of cosmological interest the power increases at small scales as in the CDM model (Peebles 1982). This leads to a hierarchical scenario of structure formation where smaller scales become non-linear first. Once they enter the non-linear regime high-density fluctuations form massive objects which will give birth to galaxies or clusters. Thus, it is important to understand the dynamics of these density perturbations in order to describe the large-scale structures we observe in the present universe.
The distribution of matter is usually described as a pressure-less fluid through the standard equations of hydrodynamics (continuity and Euler equation) coupled to the Poisson equation for the gravitational potential. Then, one often looks for a solution of the equations of motion under the form of a perturbative expansion (e.g., Fry 1984; Goroff et al. 1986; Bernardeau 1994). In fact, one cannot hope to describe the non-linear regime within such a framework since this hydrodynamical description becomes inexact as soon as shell-crossing appears. Then, there is no longer only one velocity at each point. Note that for hierarchical scenarios with no small-scale cutoff (i.e. the amplitude of density fluctuations diverges at small scales
![]() )
shell-crossing occurs as soon as t>0. Moreover, in the non-linear regime shell-crossing should play a key role (e.g., through virialization processes).
)
shell-crossing occurs as soon as t>0. Moreover, in the non-linear regime shell-crossing should play a key role (e.g., through virialization processes).
Therefore, in order to obtain a complete description of the dynamics one needs to go beyond the standard approximation of a pressure-less fluid. Then, one might add a pressure term to the hydrodynamical equations in order to describe the effects of multi-streaming, which provide some velocity dispersion (e.g., Buchert & Dominguez 1998; Buchert et al. 1999). However, this is not very satisfactory because collisionless and gaseous systems can exhibit very different behaviours starting from the same initial conditions. For instance, some physical processes are specific to collisionless systems (e.g., Landau damping, phase-mixing) and stability conditions for similar collisionless and gaseous systems are not always the same, see Binney & Tremaine (1987). Hence it is important to investigate the dynamics of density fluctuations within the framework of the collisionless Boltzmann equation, which provides an exact description of the system both in the linear and non-linear regimes.
Since this is a rather difficult task we may first try to devise a perturbative approach. This may then serve as a basis for further developments to tackle the non-linear regime. Thus, in this article we build a perturbative approach to the collisionless Boltzmann equation. One could also start from the BBGKY hierarchy, which can be derived from the Boltzmann equation. Such a study was performed in Bharadwaj (1996) where it was shown that the lowest non-linear order matches the results of the usual hydrodynamical approach. We recover this result here and we explain that indeed a perturbative method cannot handle shell-crossing. However, in the building of perturbative theory we also derive in this article some non-perturbative results which may prove to be useful for a study of the non-linear regime.
This paper is organized as follows. In Sect. 2 we write the equations of motion which describe the dynamics of the collisionless fluid. Then, in Sect. 3 we develop a systematic procedure to obtain the fluctuations of the distribution function as a perturbative series over the initial perturbations (or more precisely over the linear growing mode) in the case of a critical density universe. In doing so we also derive a non-perturbative quadratic integral equation which directly relates the actual non-linear distribution function to this linear mode. Next, we give in Sect. 4 the explicit calculations of the second-order terms. We explain in Sect. 5 why we recover the results of the hydrodynamical approach and why the perturbative series must diverge for hierarchical scenarios (with no small-scale cutoff). Then, we show in Sect. 6 how to extend this method to arbitrary cosmologies. Finally, we derive in Sect. 7 an explicit path-integral expression which describes the statistical properties of the exact non-linear density field.
The gravitational dynamics of a fluid of collisionless particles of mass m is given by the collisionless Boltzmann equation (Peebles 1980), coupled with the Poisson equation:
Note that in order to derive the collisionless Boltzmann equation one needs to neglect the two-particle correlations. Then, the gravitational interaction is described by a smooth gravitational potential which neglects the effects of the discrete character of the distribution of matter (e.g., Peebles 1980). This becomes exact in the continuous limit
![]() which we perform below in Eq. (2). However, one must also add some small-scale cutoff to the power-spectrum of the density fluctuations in order to guarantee small-scale smoothness.
which we perform below in Eq. (2). However, one must also add some small-scale cutoff to the power-spectrum of the density fluctuations in order to guarantee small-scale smoothness.
The definition itself of the problem we investigate here also involves an implicit "regularization'' of the gravitational interaction. Indeed, within an infinite uniform universe the gravitational force is not well defined since the pull due to the matter located within a small solid angle
![]() diverges as we integrate over all shells up to infinity. This problem is cured by first integrating the relevant integrals over angles, and next over radial distances (e.g., Peebles 1980). This can also be seen as the introduction of a large-scale cutoff L for the gravitational interaction which preserves rotational symmetry. More precisely, this means that in Fourier space we integrate on the wavenumber
diverges as we integrate over all shells up to infinity. This problem is cured by first integrating the relevant integrals over angles, and next over radial distances (e.g., Peebles 1980). This can also be seen as the introduction of a large-scale cutoff L for the gravitational interaction which preserves rotational symmetry. More precisely, this means that in Fourier space we integrate on the wavenumber ![]() over
over
![]() and in the final results we take the limit
and in the final results we take the limit
![]() .
In fact, except in Eq. (76) in Sect. 7 this feature will not show up in the equations we encounter in this article so that we can directly take
.
In fact, except in Eq. (76) in Sect. 7 this feature will not show up in the equations we encounter in this article so that we can directly take
![]() .
.
Next, we can absorb the mass m into the distribution function f and the momentum ![]() :
:
![]() ,
,
![]() ,
and we obtain:
,
and we obtain:
Here we consider the case of a critical density universe
![]() .
Then, the average comoving density is given by:
.
Then, the average comoving density is given by:
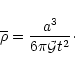 |
(10) |
The dynamics of the distribution function ![]() is fully determined by the non-linear Eq. (13) supplemented by initial conditions. At early times
is fully determined by the non-linear Eq. (13) supplemented by initial conditions. At early times
![]() the universe becomes homogeneous and the velocity is given by the Hubble flow (i.e.
the universe becomes homogeneous and the velocity is given by the Hubble flow (i.e.
![]() )
so that the perturbations vanish:
)
so that the perturbations vanish:
![]() .
Thus, at early times (or at large scales for CDM-like initial conditions) the equations of motion can be linearized and the distribution function is equal to the linear solution
.
Thus, at early times (or at large scales for CDM-like initial conditions) the equations of motion can be linearized and the distribution function is equal to the linear solution
![]() .
As time goes on, the perturbation grows and it eventually enters the non-linear regime. In the mildly non-linear regime, one can seek a solution of Eq. (13) in the form of a perturbative expansion over the linear mode
.
As time goes on, the perturbation grows and it eventually enters the non-linear regime. In the mildly non-linear regime, one can seek a solution of Eq. (13) in the form of a perturbative expansion over the linear mode
![]() .
Thus, we write the expansion:
.
Thus, we write the expansion:
However, in order to obtain an explicit expression for
![]() we must "invert'' the operator
we must "invert'' the operator ![]() in Eq. (19). More precisely, we need to build a kernel
in Eq. (19). More precisely, we need to build a kernel
![]() which satisfies:
which satisfies:
Thus, we now need to construct a solution
![]() to Eq. (20). To do so, we use the following trick. First, we define a new operator
to Eq. (20). To do so, we use the following trick. First, we define a new operator
![]() by:
by:
Here we note that instead of the operator
![]() defined by Eq. (22) we could have tried to use the operator
defined by Eq. (22) we could have tried to use the operator
![]() defined by:
defined by:
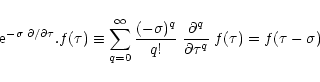 |
(27) |
From the recursion (21) we can also express
![]() explicitly in terms of the linear mode
explicitly in terms of the linear mode ![]() .
Indeed, we can easily check that we can write Eq. (21) as:
.
Indeed, we can easily check that we can write Eq. (21) as:
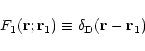 |
(29) |
Fortunately, for practical purposes the decaying modes should play no role:
![]() so that the decaying modes become negligible before one enters the non-linear regime. Hence it is convenient to restrict
so that the decaying modes become negligible before one enters the non-linear regime. Hence it is convenient to restrict
![]() to the linear growing mode and to take
to the linear growing mode and to take
![]() .
.
Here, we note that the expression (28) also shows that the expansion (16) can be formally reinterpreted as a perturbative expansion over powers of the "coupling constant'' g. Thus, the recursive solution defined by Eqs. (17) and (21) is also the perturbative solution of the integral equation:
The Eq. (31) is similar to the integral form of usual stochastic differential equations (e.g., Langevin equation) where ![]() would be called a noise term. Moreover, this formulation is very convenient since it reduces the three equations we started from (Boltzmann equation, Poisson equation, initial conditions) to the only one Eq. (31). Thus, the initial conditions
would be called a noise term. Moreover, this formulation is very convenient since it reduces the three equations we started from (Boltzmann equation, Poisson equation, initial conditions) to the only one Eq. (31). Thus, the initial conditions
![]() are encoded within the "evolution equation'' itself, which fully determines the properties of the distribution function
are encoded within the "evolution equation'' itself, which fully determines the properties of the distribution function ![]() once the characteristics of
once the characteristics of
![]() are specified. Here we note that a quadratic equation of the form (31) was derived in Scoccimarro (2000) from the usual hydrodynamical description. However, the latter formulation breaks down when shell-crossing occurs while Eq. (31) remains valid in the non-linear regime.
are specified. Here we note that a quadratic equation of the form (31) was derived in Scoccimarro (2000) from the usual hydrodynamical description. However, the latter formulation breaks down when shell-crossing occurs while Eq. (31) remains valid in the non-linear regime.
The perturbative expansion (21) can be conveniently written as a sum of tree-diagrams with a three-leg vertex. To do so, we first define the symmetrized kernel
![]() by:
by:
| |
Figure 1:
The two diagrams which give the fourth-order term
|
| Open with DEXTER | |
It is instructive to consider the simple case where ![]() and
and ![]() are mere numbers, rather than functions. Then we can absorb
are mere numbers, rather than functions. Then we can absorb
![]() into g and the integral Eq. (31) becomes:
into g and the integral Eq. (31) becomes:
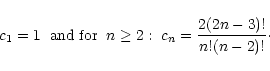 |
(36) |
We have described in the previous section the general structure of the evolution equation which governs the dynamics of the distribution function
![]() .
In particular, we have shown how we can obtain a perturbative expansion of
.
In particular, we have shown how we can obtain a perturbative expansion of
![]() over powers of the linear growing mode
over powers of the linear growing mode
![]() .
In this section, we apply these results to the specific case of gravitational clustering in an expanding universe (with
.
In this section, we apply these results to the specific case of gravitational clustering in an expanding universe (with
![]() ).
).
First, we have to obtain the linear growing mode
![]() (as explained in Sect. 3.2 we do not need the decaying modes). This function
(as explained in Sect. 3.2 we do not need the decaying modes). This function
![]() must belong to the kernel of the operator
must belong to the kernel of the operator ![]() ,
see Eq. (18), and grow with time. To get
,
see Eq. (18), and grow with time. To get
![]() one can simply consider the linear growing mode of the hydrodynamical approximation. Thus, in this approximation all particles at a given point
one can simply consider the linear growing mode of the hydrodynamical approximation. Thus, in this approximation all particles at a given point ![]() have the same peculiar velocity
have the same peculiar velocity ![]() defined by:
defined by:
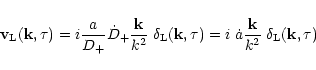 |
(38) |
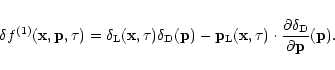 |
(42) |
Here, we can note that up to first-order our system can be described as a pressure-less fluid. Indeed, we have not included any velocity dispersion in the initial conditions. As is well-known, caustics will form as the density field evolves and multi-streaming regions appear. The perturbative approach should break down at this stage since it cannot go beyond these singularities. Thus, we shall check in the following sections that our perturbative treatment recovers the predictions of the standard perturbative approach applied to the equations of motion derived within the hydrodynamic approximation (see Peebles 1980 or Goroff et al. 1986 for a presentation of this method). This clearly implies that the perturbative method cannot handle the multi-streaming regime. However, we stress that the equations of motion (1), (12) and (31) remain valid in the non-linear regime after multi-streaming appears.
In order to handle the multi-streaming regime in a perturbative way, one may try to add a small velocity dispersion to the initial conditions. Indeed, this will smooth out the caustics encountered for a pressure-less fluid. Such an approach is investigated in Buchert & Dominguez (1998) and Buchert et al. (1999) for instance. However, it is clear that this is not sufficient to go beyond shell-crossing. Indeed, as non-linear structures form, shocks will appear around virialized objects. This can be seen from the analytic solution of gaseous spherical collapse in Bertschinger (1985). Then, a perturbative approach cannot give any information on the inner region beyond the shock. In particular, one cannot rely on a simple equation of state of the form ![]() for the pressure. Moreover, it is well-known that collisionless and gaseous systems can exhibit qualitatively different behaviours (e.g., existence of Landau damping and phase-mixing for the former, see Binney & Tremaine 1987). This is why it is important to devise methods which are based on the collisionless Boltzmann Eq. (1). This article is a first step in this direction.
for the pressure. Moreover, it is well-known that collisionless and gaseous systems can exhibit qualitatively different behaviours (e.g., existence of Landau damping and phase-mixing for the former, see Binney & Tremaine 1987). This is why it is important to devise methods which are based on the collisionless Boltzmann Eq. (1). This article is a first step in this direction.
Once the linear growing mode
![]() is specified we can derive the higher-order terms from the recursion (21). Thus, using the expression (43) and Eq. (B.1) obtained in Appendix B for the kernel
is specified we can derive the higher-order terms from the recursion (21). Thus, using the expression (43) and Eq. (B.1) obtained in Appendix B for the kernel
![]() we get after a simple calculation:
we get after a simple calculation:
It is interesting to compare this result for
![]() with the results obtained within the usual hydrodynamical approach. In this latter case, the system is fully defined by the density contrast and the mean fluid velocity at each point
with the results obtained within the usual hydrodynamical approach. In this latter case, the system is fully defined by the density contrast and the mean fluid velocity at each point ![]() (there is no velocity dispersion). Thus, we need to derive the density and the mean collective velocity from Eq. (44).
(there is no velocity dispersion). Thus, we need to derive the density and the mean collective velocity from Eq. (44).
From Eq. (5) and Eq. (44) we obtain the second-order term for the density contrast:
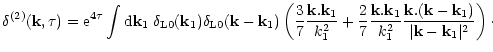 | (47) | ||
![$\displaystyle { \delta^{(2)}({\bf x},\tau) = {\rm e}^{4 \tau} \int {\rm d}{\bf ...
... \frac{2}{7} \left( \frac{{\bf k}_1.{\bf k}_2}{k_1 k_2} \right)^2 \right] \cdot$](/articles/aa/full/2001/43/aa1518/img161.gif) | (48) | ||
We can note that this result agrees with the calculations performed in Bharadwaj (1996) from the BBGKY hierarchy. Indeed, in that paper it was shown that the lowest order non-linear correction to the two-point correlation function derived from the BBGKY hierarchy (which remains valid in the non-linear regime after shell-crossing) matches the prediction of the standard hydrodynamical approach. Note that the BBGKY hierarchy can be derived from the collisionless Boltzmann Eq. (1), see Peebles (1980). Therefore, both works explicitly show that multi-streaming effects cannot be handled through a perturbative method.
From the distribution function ![]() we can also derive the mean velocity of the fluid. Indeed, the hydrodynamics equations are obtained from moments of the Boltzmann equation. In particular, the hydrodynamic peculiar velocity is defined by:
we can also derive the mean velocity of the fluid. Indeed, the hydrodynamics equations are obtained from moments of the Boltzmann equation. In particular, the hydrodynamic peculiar velocity is defined by:
In the previous section we noticed that the perturbative treatment of the collisionless Boltzmann equation yields the same results at second-order as the hydrodynamical approach when the linear mode is given by Eq. (43). In fact, it is easy to see that this equality extends to all orders of perturbation theory. Indeed, let us consider an initial condition of the form (43) which is very smooth. That is,
![]() shows no power at small scales (i.e. large wavenumbers k) and the flow is nonrotational, defined by the linear growing mode of hydrodynamics. Then, there is no shell-crossing until a finite time
shows no power at small scales (i.e. large wavenumbers k) and the flow is nonrotational, defined by the linear growing mode of hydrodynamics. Then, there is no shell-crossing until a finite time
![]() (i.e.
(i.e.
![]() ). This means that the hydrodynamical description is actually exact at early times
). This means that the hydrodynamical description is actually exact at early times
![]() :
at each point there is only one velocity. Then, until the non-zero time
:
at each point there is only one velocity. Then, until the non-zero time ![]() the solution of hydrodynamics (i.e. continuity and Euler equations) is also a solution of the collisionless Boltzmann equation from which they derive. This implies that the density contrast and velocity fields obtained by the perturbative theory in both frameworks are identical. Moreover, the form of the perturbative expansion does not depend on the properties of
the solution of hydrodynamics (i.e. continuity and Euler equations) is also a solution of the collisionless Boltzmann equation from which they derive. This implies that the density contrast and velocity fields obtained by the perturbative theory in both frameworks are identical. Moreover, the form of the perturbative expansion does not depend on the properties of
![]() ,
hence this identity holds for any initial conditions
,
hence this identity holds for any initial conditions
![]() .
As a consequence, if the linear mode is of the form of Eq. (43) the perturbative results obtained from the collisionless Boltzmann equation and from the hydrodynamical description are identical. Here, we note that this identity was explicitly derived at all orders within the framework of the Zel'dovich approximation in Bharadwaj (1996). Therefore, in order to study the non-linear regime one needs to devise non-perturbative methods applied to the collisionless Boltzmann Eq. (1).
.
As a consequence, if the linear mode is of the form of Eq. (43) the perturbative results obtained from the collisionless Boltzmann equation and from the hydrodynamical description are identical. Here, we note that this identity was explicitly derived at all orders within the framework of the Zel'dovich approximation in Bharadwaj (1996). Therefore, in order to study the non-linear regime one needs to devise non-perturbative methods applied to the collisionless Boltzmann Eq. (1).
On the other hand, in the case of CDM-like power-spectra (or power-law power-spectra) there is some power at all scales. In particular, the density fluctuations increase with no limit at small-scales (if we do not include a cutoff at small scales). Then, as soon as t>0 there is some shell-crossing. This implies that the hydrodynamical solution is no longer a solution of the collisionless Boltzmann equation (actually, the former is not well defined). Then, the perturbative expansion must diverge (otherwise the hydrodynamical solution and the Boltzmann solution would be identical since they would be equal to the same perturbative solution). Hence, we conclude that for hierarchical initial conditions the perturbative expansion is only asymptotic. If we include a cutoff at small scales for the initial power-spectrum the perturbative series may converge until the finite time ![]() when shell-crossing occurs for the first time (though this is not guaranteed a priori). However, it must diverge at later times which implies that the perturbative series diverges at all times of practical interest.
when shell-crossing occurs for the first time (though this is not guaranteed a priori). However, it must diverge at later times which implies that the perturbative series diverges at all times of practical interest.
In fact, the system we investigate here can actually be even more pathological than these results suggest. First, as we show in a companion paper (Paper II) where we develop a non-perturbative method to study the quasi-linear regime, the generating function of the cumulants of the density contrast obtained at leading order has a radius of convergence which is zero independently of shell-crossing for
![]() with n<0. This means that the high-density tail of the probability distribution function of the density contrast cannot be evaluated by perturbative means in this case. Secondly (and more importantly), the terms encountered in perturbative expansions actually diverge beyond some finite order for power-law power-spectra (e.g., Scoccimarro & Frieman 1996, Paper V). This implies that one can only use perturbation theory up to a finite order at best.
with n<0. This means that the high-density tail of the probability distribution function of the density contrast cannot be evaluated by perturbative means in this case. Secondly (and more importantly), the terms encountered in perturbative expansions actually diverge beyond some finite order for power-law power-spectra (e.g., Scoccimarro & Frieman 1996, Paper V). This implies that one can only use perturbation theory up to a finite order at best.
In this section, we show how we can extend the perturbative calculations developed in Sect. 3 for a critical density universe to arbitrary cosmological parameters. In the general case, the scale factor a(t) is no longer a power-law hence it is not useful to introduce the time coordinate ![]() as in Eq. (11). Thus, from Eq. (9) and keeping the coordinate t we define the operator
as in Eq. (11). Thus, from Eq. (9) and keeping the coordinate t we define the operator ![]() by:
by:
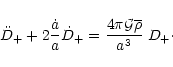 |
(57) |
| (59) | |||
| (60) | |||
| (61) |
Thus, in order to derive the perturbative expansion of the distribution function ![]() in the general case one first computes the terms
in the general case one first computes the terms
![]() up to the required order for a critical density universe, using the method developed in Sect. 3. This provides an explicit expression for
up to the required order for a critical density universe, using the method developed in Sect. 3. This provides an explicit expression for
![]() .
Then, one looks for a solution of Eq. (9) in the case of interest (which differs from the critical density universe) by keeping the same structure for
.
Then, one looks for a solution of Eq. (9) in the case of interest (which differs from the critical density universe) by keeping the same structure for
![]() but replacing all time-dependent factors by unknown functions of time. Then, these functions are determined by substitution into Eq. (9). The need for this two-step procedure comes from the fact that in the general case the calculation of the operator
but replacing all time-dependent factors by unknown functions of time. Then, these functions are determined by substitution into Eq. (9). The need for this two-step procedure comes from the fact that in the general case the calculation of the operator
![]() is not straightforward. More precisely, in order to derive
is not straightforward. More precisely, in order to derive
![]() one can still follow the procedure outlined in Appendix A up to Eq. (A.12). However, the recursion obeyed by the functions
one can still follow the procedure outlined in Appendix A up to Eq. (A.12). However, the recursion obeyed by the functions
![]() is no longer a simple Laplace convolution so that it is not obvious to find a simple analytic solution.
is no longer a simple Laplace convolution so that it is not obvious to find a simple analytic solution.
Finally, we briefly describe how one can use the integral Eq. (31) to obtain an explicit expression for the statistical properties of the distribution function. In this section, we shall work in real space ![]() ,
and we note
,
and we note
![]() the 7-dimensional coordinate
the 7-dimensional coordinate
![]() .
Thus, the fields
.
Thus, the fields
![]() and
and
![]() are real. Taking the Fourier transform of Eq. (31) we see that
are real. Taking the Fourier transform of Eq. (31) we see that
![]() and
and
![]() are related by the same quadratic equation where the kernel
are related by the same quadratic equation where the kernel
![]() is replaced by its real-space Fourier transform
is replaced by its real-space Fourier transform
![]() .
In practice we are not really interested in the exact solution
.
In practice we are not really interested in the exact solution ![]() associated with a given field
associated with a given field ![]() .
Indeed, since the initial condition
.
Indeed, since the initial condition ![]() is a random field we are only interested in the statistical properties of the distribution function
is a random field we are only interested in the statistical properties of the distribution function ![]() .
These can be derived from the functional Z[j] of the test field
.
These can be derived from the functional Z[j] of the test field
![]() defined by:
defined by:
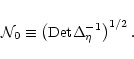 |
(65) |
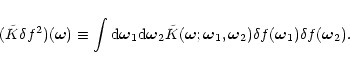 |
(68) |
| (70) |
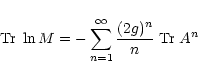 |
(71) |
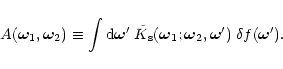 |
(72) |
| | |||
| |
(75) | ||
The correlation functions can be obtained from Eq. (77) as a perturbative series over the coupling constant g. Indeed, we noticed in Sect. 3.3 that this is equivalent to the usual expansion over the linear growing mode
![]() .
To do so we simply develop the exponential term in Eq. (77) over g K3 and g2 K4 as a series over g. This corresponds exactly to the Feynman diagrams in standard Quantum Field Theories for a "
.
To do so we simply develop the exponential term in Eq. (77) over g K3 and g2 K4 as a series over g. This corresponds exactly to the Feynman diagrams in standard Quantum Field Theories for a "
![]() '' theory (e.g., Zinn-Justin 1989) (note that we defined the kernels K3 and K4 in such a way that they are symmetric). One must merely pay attention to the fact that the kernels K3 and K4 are not pure numbers. Of course, this is due to the long-range character of gravity which leads to a non-local theory (while usual Quantum Field Theories are local). Note that we do not need the explicit expression of the inverse kernel
'' theory (e.g., Zinn-Justin 1989) (note that we defined the kernels K3 and K4 in such a way that they are symmetric). One must merely pay attention to the fact that the kernels K3 and K4 are not pure numbers. Of course, this is due to the long-range character of gravity which leads to a non-local theory (while usual Quantum Field Theories are local). Note that we do not need the explicit expression of the inverse kernel
![]() .
For instance, in order to compute the skewness some terms which depend on
.
For instance, in order to compute the skewness some terms which depend on
![]() appear but they actually cancel one another.
appear but they actually cancel one another.
In practice, the expression (77) is not very convenient for perturbative calculations and it is easier to use the direct method described in Sect. 3, or simply use the standard hydrodynamical approach. However, we stress that Eq. (77) presents the advantage to be an explicit non-perturbative expression for the functional Z[j]. Thus, one may hope to be able to extract some useful information from this relation for the non-linear regime. However, this is beyond the scope of this article.
Thus, in this article we have developed a systematic method to obtain the solution of the collisionless Boltzmann equation, which describes large-scale structure formation in the universe, as a perturbative series. Moreover, we have explained that these perturbative results are identical to those obtained from the hydrodynamical description of the fluid, if we start with the same initial conditions. Thus, multi-streaming cannot be handled through perturbative methods. Besides, for hierarchical scenarios the perturbative expansions diverge. The interest of this approach is that, contrary to the hydrodynamical model, the collisionless Boltzmann equation provides a rigorous description of the dynamics, even in the non-linear regime. Hence in order to tackle the non-linear regime where shell-crossing plays a key role one should use these equations of motions. Then, the results presented in this paper may serve as a basis for a study of the non-linear regime. In particular, we have obtained a non-perturbative integral Eq. (31) which explicitly relates the non-linear distribution function to the initial conditions. Besides, we have derived an explicit path-integral expression (77) which yields the correlation functions of the actual non-linear density field at all orders. Although this result provides a formal description of the statistics of the density field one still needs to check whether it is possible to extract some practical information from this expression. Thus, we shall describe in companion papers an alternative non-perturbative method, based on the path-integral (64), which allows one to derive rigorous results in the quasi-linear regime for the probability distribution of the density contrast for Gaussian initial conditions (Paper II) as well as for some non-Gaussian scenarios (Paper III). Such a formalism can also be used in the non-linear regime (Paper IV).
In order to obtain the kernel
![]() defined in Eq. (25) we first need to compute the exponential e
defined in Eq. (25) we first need to compute the exponential e
![]() .
Thus, for a given function
.
Thus, for a given function
![]() we look for the function
we look for the function
![]() defined by:
defined by:
![\begin{displaymath}U({\bf p},\sigma) \equiv B({\bf k},{\bf p},\tau,0) \; {\rm e}...
... ({\bf k}.{\bf p}) {\rm e}^{-\tau} [ {\rm e}^{-\sigma}-1 ] } ,
\end{displaymath}](/articles/aa/full/2001/43/aa1518/img254.gif) |
(A.6) |
![$\displaystyle {\cal K}({\bf p},\sigma\vert{\bf p}',\sigma') \equiv \theta(\sigm...
...{3i ({\bf k}.{\bf p}) {\rm e}^{-\tau} [ {\rm e}^{-\sigma}-{\rm e}^{-\sigma'} ]}$](/articles/aa/full/2001/43/aa1518/img255.gif) |
(A.7) |
| (A.9) |
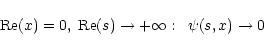 |
(A.18) |
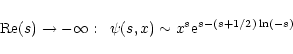 |
(A.20) |
From Eq. (A.22) and the expression (A.23) for the operator
![]() we can derive the explicit form of the kernel
we can derive the explicit form of the kernel
![]() defined in Eq. (25), using Eq. (15). First, we write the factor
defined in Eq. (25), using Eq. (15). First, we write the factor
![]() which appears in Eq. (15) as
which appears in Eq. (15) as
![]() .
Then, using Eq. (A.22) we see that
.
Then, using Eq. (A.22) we see that
![]() exhibits a factor
exhibits a factor
![]() .
Thus, the integration on
.
Thus, the integration on ![]() over the range
over the range
![]() is now straightforward and it yields a Heaviside factor
is now straightforward and it yields a Heaviside factor
![]() .
Next, a simple calculation yields for
.
Next, a simple calculation yields for
![]() :
:
Finally, as discussed in Sect. 3.2 we need to check that the kernel
![]() obtained in Eq. (B.1) satisfies Eq. (20). To do so, it is convenient to first integrate over s1 in Eq. (B.1). The integration of the first term is straightforward, using the inverse Laplace transform (A.21). In order to integrate the second term over s1 we use the identity (46). This allows us to express this factor in terms of
obtained in Eq. (B.1) satisfies Eq. (20). To do so, it is convenient to first integrate over s1 in Eq. (B.1). The integration of the first term is straightforward, using the inverse Laplace transform (A.21). In order to integrate the second term over s1 we use the identity (46). This allows us to express this factor in terms of
![]() and
and
![]() ,
so that the integration over s1 becomes quite simple. In particular, the contribution from the poles s1=-s2 and s1=1-s2 vanishes when we take the integration path over s2 to be
,
so that the integration over s1 becomes quite simple. In particular, the contribution from the poles s1=-s2 and s1=1-s2 vanishes when we take the integration path over s2 to be
![]() .
Then, we can write the kernel
.
Then, we can write the kernel
![]() as:
as: