In order to study the status and the possible evolution of clusters of galaxies at intermediate redshifts (
A&A 379, 21-34 (2001)
DOI: 10.1051/0004-6361:20011236
A. Zanichelli 1 - M. Vigotti 1 - R. Scaramella 2 - G. Grueff 3 - G. Vettolani 1
1 - Istituto di Radioastronomia - CNR, Via Gobetti 101, 40129
Bologna, Italy
2 - Osservatorio Astronomico di Roma, via Osservatorio 2, 00040
Monteporzio Catone (RM), Italy
3 - Dipartimento di Fisica, Università di Bologna, Via Irnerio
46, 40127 Bologna, Italy
Received 13 December 2000 / Accepted 6 August 2001
Abstract
In order to study the status and the possible evolution of clusters
of galaxies at intermediate redshifts (![]() 0.1-0.3), as well as their
spatial correlation and relationship with the local environment, we built a
sample of candidate groups and clusters of galaxies using radiogalaxies as
tracers of dense environments.
This technique - complementary to purely optical or X-ray cluster selection
methods - represents an interesting tool for the selection of clusters in a
wide range of richness, so to make it possible to study the global properties
of groups and clusters of galaxies, such as their morphological content,
dynamical status and number density, as well as the effect of the environment
on the radio emission phenomena.
In this paper we describe the compilation of a catalogue of
0.1-0.3), as well as their
spatial correlation and relationship with the local environment, we built a
sample of candidate groups and clusters of galaxies using radiogalaxies as
tracers of dense environments.
This technique - complementary to purely optical or X-ray cluster selection
methods - represents an interesting tool for the selection of clusters in a
wide range of richness, so to make it possible to study the global properties
of groups and clusters of galaxies, such as their morphological content,
dynamical status and number density, as well as the effect of the environment
on the radio emission phenomena.
In this paper we describe the compilation of a catalogue of ![]() 16000
radio sources in the region of the South Galactic Pole extracted from the
publicly available NRAO VLA Sky Survey maps, and the optical identification
procedure with galaxies brighter than
16000
radio sources in the region of the South Galactic Pole extracted from the
publicly available NRAO VLA Sky Survey maps, and the optical identification
procedure with galaxies brighter than
![]() in the EDSGC
Catalogue.
The radiogalaxy sample, valuable for the study of radio source populations down
to low flux levels, consists of 1288 identifications and has been used to
detect candidate groups and clusters associated to NVSS radio sources.
In a companion paper we will discuss the cluster detection method, the cluster
sample as well as first spectroscopic results.
in the EDSGC
Catalogue.
The radiogalaxy sample, valuable for the study of radio source populations down
to low flux levels, consists of 1288 identifications and has been used to
detect candidate groups and clusters associated to NVSS radio sources.
In a companion paper we will discuss the cluster detection method, the cluster
sample as well as first spectroscopic results.
Key words: catalogs - radio continuum: galaxies - galaxies: clusters: general - cosmology: observations
One of the major topics in modern cosmology concerns the dynamical status and evolution of groups and clusters of galaxies, as well as their abundance and spatial distribution, their morphological content and interactions with the environment. Groups and clusters of galaxies are indeed the largest, gravitationally bound, observable structures, and by studying their properties and the processes underlying their formation, much can be understood about the global cosmological properties of the universe.
In recent years, significant efforts have been made in searching for clusters at high redshifts; nevertheless the general properties and the physical processes at work in these large scale structures at moderate z are still unclear. To this aim, it is of fundamental importance to gather cluster samples representative of different dynamical structures - from groups to rich clusters - in a wide range of redshift and covering large areas of the sky.
First attempts to build wide-area cluster samples, like the ACO/Abell catalogue (Abell et al. 1989), were based on visual inspection of optical plates and only recently the first catalogues obtained through objective algorithms appeared (EDCC, Lumsden et al. 1992; APM, Dalton et al. 1994). The selection based on optical plates, however, limits the redshift range to about z < 0.2 and suffers from misclassifications due to projections effects along the line of sight, resulting on one side in spurious cluster detection and, on the other side, in wrong estimates of the cluster richness, that can affect the reliability of the derived cosmological parameters (van Haarlem et al. 1997). Alternatively, cluster samples at higher redshift have been built using a matched filter algorithm which makes use of both positional and deep multiband CCD photometric data over selected areas of few square degrees (Postman et al. 1996; Scodeggio et al. 1999).
Also, to find candidate clusters at intermediate redshift through color diagrams alone could bias the selection against clusters with a high fraction of blue galaxies, whose presence can be due to the occurrence of the Butcher-Oemler effect (Butcher & Oemler 1984) or to the fact that the cluster itself can be in the process of formation.
The X-ray emission properties of the hot intracluster medium have been widely used to build distant cluster samples, but this technique suffers from the limited sensitivity of wide-area X-ray surveys and from the possibility of evolutionary effects (Gioia et al. 1990; Henry et al. 1992; RDCS, Rosati et al. 1998).
Even more critical is the selection of groups of galaxies: these structures - which represent a sort of "bridge'' between rich clusters and the field - are of major interest for the understanding of galaxy interactions and evolutionary processes, but their detection is particularly difficult even at moderate redshifts due to their very low density contrast with respect to field galaxies distribution.
A different approach - complementary to purely optical or X-ray cluster
selection methods - is the use of radiogalaxies as suitable tracers of dense
environments. In recent studies (Prestage & Peacock 1988;
Hill & Lilly 1991; Allington-Smith et al. 1993;
Zirbel 1997; Miller et al. 1999) it has been shown that
Faranoff-Riley I and II radio sources are found in different environments, and
differ in the optical properties of their host galaxies as well.
FRI sources are found on average in rich groups or clusters at any redshift,
and are associated with elliptical galaxies, with the most powerful FRIs often
hosted by a cD or double nucleus galaxy (Zirbel 1996).
FRII radio sources are typically associated with disturbed ellipticals and
avoid cD galaxies, and at ![]() FRIIs are found in a wide range of
environments, including many rich clusters which rarely, if ever, host a FRII
radio source at low redshift (Zirbel 1996;
Hill & Lilly 1991).
FRIIs are found in a wide range of
environments, including many rich clusters which rarely, if ever, host a FRII
radio source at low redshift (Zirbel 1996;
Hill & Lilly 1991).
Radio selection should not impact on the X-ray or optical properties of the
cluster found in this way, since there is no significant correlation between
the radio properties of galaxies within a cluster with its ![]() (Feigelson et al. 1982; Burns et al. 1994), or with
richness of the cluster (Zhao et al. 1989;
Ledlow & Owen 1996).
Moreover, since no correlation exists between the properties of group members
and the radio characteristics of the radiogalaxies, radio-selected groups can
be used to study the general evolution of galaxies in groups
(Zirbel 1997).
(Feigelson et al. 1982; Burns et al. 1994), or with
richness of the cluster (Zhao et al. 1989;
Ledlow & Owen 1996).
Moreover, since no correlation exists between the properties of group members
and the radio characteristics of the radiogalaxies, radio-selected groups can
be used to study the general evolution of galaxies in groups
(Zirbel 1997).
Radiogalaxies can thus be used as tracers of dense environments at any epoch, and the evolution of galaxy groups and clusters can be studied lessening those biases that are the main drawbacks of pure optical or X-ray selected cluster samples.
A further point that makes this selection technique interesting is the possibility to investigate the effects of the environment on the radio-emission phenomena. Zirbel (1997) speculates the possibility of two distinct scenarios for the fueling of radio emission in FRI and FRII sources. The difference in the environments of FRII radio sources at low and high redshift suggests that the conditions to form such sources have changed with epoch, and the characteristics of their optical counterparts are consistent with the hypothesis of FRII radio emission being fueled by galaxy encounters. For FRI radio sources, it is suggested they may be drawn from different galaxy types, and be triggered by different mechanisms, depending on their power. The most powerful FRI sources are typically dominant galaxies and their environments seem to be consistent with the possibility of them being cooling flow galaxies: in this scenario, the cooling flow itself can provide the fuel for the radio source. The less powerful FRI sources do not always correspond to the first ranked galaxy, are not always found in the centre of the potential well, and some reveal signs of galaxy interactions (see e.g. Baum et al. 1988). It seems thus unlikely that the less powerful FRIs can be cooling flow galaxies, and the radio emission could be triggered by a different mechanism with respect to more powerful FRIs.
This scenario suggests that the radio source morphology is not only a function of the radio power, as suggested by theoretical models (Bridle & Perley 1984; Bicknell 1984, 1986), but depends also on the epoch of observation, that is the density and evolution of the intracluster medium. In this sense, the study of radio-selected groups and clusters over a wide range in radio power may help in understanding the physics of radio emission and the relationships between different classes of AGN.
To build such a sample of radio-traced clusters, the new radio surveys NRAO VLA Sky Survey (NVSS, Condon et al. 1998) and Faint Images of the Radio Sky at Twenty-centimeters (FIRST, Becker et al. 1995) offer an unprecedented possibility to study a wide-area, homogeneous sample of radio sources down to very low flux levels, together with a positional accuracy suitable for optical identifications.
Recently, Blanton et al. (2000) looked for moderate to high redshift clusters associated with a sample of radio sources from the FIRST survey, having a bent-double radio morphology. The presence of a distorted radio structure may be the consequence of the relative motion of the host galaxy in the intracluster medium, or of tidal interactions with other cluster galaxies, and thus can be used as an indicator of the presence of a cluster or group surrounding the radio source. From R-band imaging of the field surrounding bent-double radio sources, Blanton et al. (2000) selected ten candidates for multislit spectroscopy, and for eight of them they found evidence of a cluster associated to the radiogalaxy, with measured richnesses ranging from Abell class 0 to 2. As FRI sources more frequently show a distorted morphology, this sample contains mostly FRI radiogalaxies. Moreover, due to its high resolution, the FIRST survey may resolve out extended sources, making the FRI/FRII classification difficult.
The lower angular resolution of the NVSS survey makes this survey more suitable than the FIRST for the detection of extended regions of low surface brightness. We used the publicly available radio maps in the NVSS to build a sample of radio-optically selected clusters associated to FRI and FRII radio sources over a wide area in the sky. In this paper we describe the compilation of a radio source catalogue and the optical identification procedure with galaxies in the EDSGC Catalogue (Nichol et al. 2000) that led to the compilation of the radiogalaxy sample. In a companion paper (Zanichelli et al. 2001, Paper II) we will present the cluster selection method and the sample of candidate clusters we have obtained, as well as first spectroscopic results.
This paper is structured as follows: in Sect. 2 we give a description of the characteristics of NVSS radio data and discuss the need to compile a radio source catalogue in alternative to the NVSS publicly available one. The extraction of the radio source catalogue is presented in Sect. 3, together with a discussion on the classification of double radio sources. The radio source catalogue and its properties are discussed in Sects. 4 and 5. In Sect. 6 and following the optical identification procedure and the obtained radiogalaxy sample are described.
In this work we make use of data from the NRAO VLA Sky Survey (Condon et al.
1998). The NVSS started in 1993 with the VLA in D and DnC
configurations and has recently been completed. The NVSS covers the whole sky
north of
![]() at the frequency 1.4 GHz with resolution
at the frequency 1.4 GHz with resolution
![]() .
.
Data products consists of 2326
![]() maps in Stokes
I, Q, and U with pixel size
maps in Stokes
I, Q, and U with pixel size
![]() and rms brightness fluctuations
0.45 mJy beam-1. The positional rms in Right Ascension and Declination varies from
<
and rms brightness fluctuations
0.45 mJy beam-1. The positional rms in Right Ascension and Declination varies from
<
![]() for relatively strong (S > 15 mJy) point sources to
for relatively strong (S > 15 mJy) point sources to
![]() for the faintest (S = 2.3 mJy) detectable sources.
for the faintest (S = 2.3 mJy) detectable sources.
The positional accuracy, together with the low flux limit and moderate resolution of the survey makes the NVSS particularly suitable for the detection of low-surface brightness extended structures and for the search of optical counterparts of radio sources.
A list of about
![]() discrete sources is available as well, and has
been extracted from the survey images by fitting elliptical Gaussians to all
significant peaks (Condon et al. 1998). In the compilation of this
list, hereafter NVSS-NRAO catalogue, no attempt is made to classify sources
according to their morphology (double or pointlike sources).
discrete sources is available as well, and has
been extracted from the survey images by fitting elliptical Gaussians to all
significant peaks (Condon et al. 1998). In the compilation of this
list, hereafter NVSS-NRAO catalogue, no attempt is made to classify sources
according to their morphology (double or pointlike sources).
Nevertheless, when one wants to make optical identifications, a crucial point is the knowledge of the source structure. If a double source, for which we can expect to find the optical counterpart near the radio barycentre position, is erroneously treated as two single components, the identification procedure can lead to misleading results, thus seriously affecting the completeness and reliability of the identification program.
The blind use of a list of fitted components like the NVSS-NRAO catalogue is thus not optimal if one wants to get a radiogalaxy sample characterized by well defined statistical properties, suitable for further astrophysical applications. For this reason, we developed our own algorithm for the extraction of a radio source catalogue from the radio maps and for the morphological classification of the detected sources, as will be discussed in the next sections.
The operations performed by the extraction algorithm are divided in five modules: the source detection, the 1-Gaussian fit module, the evaluation of fit reliability, the 2-Gaussian fit module and the classification of double sources. More details on the operations performed by the algorithm are given in Appendix A.
The algorithm reads each NVSS FITS map, consisting in a
![]() pixel matrix (1
pixel matrix (1
![]() ), and then looks for emission
peaks: we adopted a threshold flux of
), and then looks for emission
peaks: we adopted a threshold flux of
![]() mJy beam-1, corresponding
to the
mJy beam-1, corresponding
to the ![]() level for the NVSS survey (rms noise on NVSS I images is
level for the NVSS survey (rms noise on NVSS I images is
![]() 0.45 mJy beam-1, Condon et al. 1998).
A different detection threshold has been applied to two sky regions where
strong residual diffraction lobes due to the presence of a very bright
(
0.45 mJy beam-1, Condon et al. 1998).
A different detection threshold has been applied to two sky regions where
strong residual diffraction lobes due to the presence of a very bright
(![]() 2.5 Jy) and extended source are found. To avoid detecting a large
number of spurious sources, for these regions we evaluated the local noise and
selected only those peaks with
2.5 Jy) and extended source are found. To avoid detecting a large
number of spurious sources, for these regions we evaluated the local noise and
selected only those peaks with
![]() .
.
A submatrix of
![]() pixels (
pixels (![]()
![]() )
around each peak is built, defining the region over which the operations
described in the next sections are executed.
)
around each peak is built, defining the region over which the operations
described in the next sections are executed.
A fit with a circular Gaussian function of fixed
![]() is
performed over each submatrix (see Appendix A); the FWHM of the
fitting function has been chosen to reproduce the nominal beam of the NVSS.
is
performed over each submatrix (see Appendix A); the FWHM of the
fitting function has been chosen to reproduce the nominal beam of the NVSS.
The use of a fixed FWHM has the consequence that it is not possible to
determine the angular dimension - and thus the integrated flux - of the
radio sources. Nevertheless, some tests showed that the use of a Gaussian of
variable size is not advantageous when fitting sources at low flux levels
(
![]()
![]() ), whose resulting positions and fluxes were found to be
inaccurate. We decided thus to fix the dimensions of the fit function and to
perform a fit with two Gaussian components in those cases when the
one-component fit was not satisfactory. In Sect. 3.3 the criteria
for performing a 2-component fit are described.
), whose resulting positions and fluxes were found to be
inaccurate. We decided thus to fix the dimensions of the fit function and to
perform a fit with two Gaussian components in those cases when the
one-component fit was not satisfactory. In Sect. 3.3 the criteria
for performing a 2-component fit are described.
Input parameters for the 1-component fit are x and y peak pixel coordinates
of the submatrix central point, and the measured flux at that pixel. For each
source, the algorithm computes the fit rms
![]() (see
Appendix A), which is used as a discriminant for the execution of
the 2-Gaussians fit.
(see
Appendix A), which is used as a discriminant for the execution of
the 2-Gaussians fit.
Inspecting the results obtained from the 1-component fit for some test sources,
we found that they are not satisfactory in terms of positional and photometric
accuracy when the fit rms
![]() mJy pixel
mJy pixel![]() .
The distribution of
.
The distribution of
![]() values in different flux bins showed
that the percentage of sources with
values in different flux bins showed
that the percentage of sources with
![]() mJy beam-1 for which
mJy beam-1 for which
![]() mJy pixel
mJy pixel![]() is reasonably low, of
the order of
is reasonably low, of
the order of ![]() .
We thus decided to apply a 2-component fit only to those
sources with both
.
We thus decided to apply a 2-component fit only to those
sources with both
![]() and
and
![]() .
If it happens that
.
If it happens that
![]() (
(![]()
![]() of these sources),
then the 1-component solution is restored.
of these sources),
then the 1-component solution is restored.
There are however two categories of sources for which the above criterion did not guarantee good results with the 1-component fit, and required a different approach: these cases are what we called "extended'' and "multiple'' sources.
When in presence of "extended'' sources, whose flux distribution presents a
"plateau'' instead of a well defined maximum, the algorithm can detect more
than one emission peak, and attempts to perform as many fits: this happens to
about the ![]() of the sources fitted with 1 Gaussian component, with no
dependence on their flux. It has been possible to identify two different
situations: if the distance between the fitted positions is less than
of the sources fitted with 1 Gaussian component, with no
dependence on their flux. It has been possible to identify two different
situations: if the distance between the fitted positions is less than
![]() then is always
then is always
![]() mJy pixel
mJy pixel![]() .
For distances between
.
For distances between
![]() and
and
![]() ,
on the contrary, at least one
fit has
,
on the contrary, at least one
fit has
![]() mJy pixel
mJy pixel![]() .
In the first case we verified that 1 Gaussian with fixed FWHM reproduces the
source correctly: the 1-component fit is considered valid, by assigning to the
radio source the position of the barycentre of the multiple fits.
In the second case, the effect of the source extension is not negligible and
the highest values of
.
In the first case we verified that 1 Gaussian with fixed FWHM reproduces the
source correctly: the 1-component fit is considered valid, by assigning to the
radio source the position of the barycentre of the multiple fits.
In the second case, the effect of the source extension is not negligible and
the highest values of
![]() and
and ![]() among those
fitted are attributed to the source, which is thus forced to the 2-component
fit.
among those
fitted are attributed to the source, which is thus forced to the 2-component
fit.
A further class of sources, the "multiple'' ones, has been identified during the implementation of the 2-component fit module: the dimension of the fit submatrix is such that the number of times it contains two sources is not negligible. We found that the presence of more than one source in the same fit submatrix seriously affects the minimization process and the accuracy of fitted parameters.
We took into consideration these situations by introducing the following
criterion: all those sources having a neighbour inside
![]() ,
with at
least one of them having
,
with at
least one of them having
![]() mJy pixel
mJy pixel![]() ,
are considered "double''. In such a case, a new fit submatrix is defined
around the central position between the two components and the source is
forced to the 2-component fit. A distance of
,
are considered "double''. In such a case, a new fit submatrix is defined
around the central position between the two components and the source is
forced to the 2-component fit. A distance of
![]() guarantees that the
structure of both components is well represented in the region defined by the
fit submatrix.
guarantees that the
structure of both components is well represented in the region defined by the
fit submatrix.
To keep track of the different operations and adopted criteria, multiple and extended sources have been marked with control flags. A further analysis of the classification of double sources has been made as the final step in the construction of the radio source catalogue (see Sect. 3.5).
The 2-component fit models sources with two Gaussian functions, each having
![]() .
Input parameters needed to describe the two functions
are: x and y peak pixel coordinates of the submatrix central point, peak
flux, distance in x and y between the two components (in pixels from the
barycentre), logarithmic ratio of fluxes of the two components.
Obviously, this amounts to assume that the brightness distribution of the source
is modelled as the sum of two pointlike sources.
.
Input parameters needed to describe the two functions
are: x and y peak pixel coordinates of the submatrix central point, peak
flux, distance in x and y between the two components (in pixels from the
barycentre), logarithmic ratio of fluxes of the two components.
Obviously, this amounts to assume that the brightness distribution of the source
is modelled as the sum of two pointlike sources.
Even if for true double radio sources it is seldom found a flux ratio
![]() ,
we allowed this parameter to be as high as
10, with a lower limit for the flux of a single component
,
we allowed this parameter to be as high as
10, with a lower limit for the flux of a single component
![]() mJy beam-1. This choice proved to be useful to correctly fit
the flux of those "extended'' sources discussed in Sect. 3.3.
In fact, due to our choice of fixed-size Gaussian functions, when dealing with
"extended'' sources for which a second peak is not detected, the extraction
algorithm may need a second component to correctly fit the source flux.
mJy beam-1. This choice proved to be useful to correctly fit
the flux of those "extended'' sources discussed in Sect. 3.3.
In fact, due to our choice of fixed-size Gaussian functions, when dealing with
"extended'' sources for which a second peak is not detected, the extraction
algorithm may need a second component to correctly fit the source flux.
For each double source the algorithm evaluates total flux and barycentre
position, as well as flux, coordinates and separation of the two components.
The fit rms
![]() is computed similarly to what is done
for the 1-component fit; if
is computed similarly to what is done
for the 1-component fit; if
![]() ,
and depending on the source control flags (if there are any), the 1-component
fit may have been considered valid.
,
and depending on the source control flags (if there are any), the 1-component
fit may have been considered valid.
The distinction made by the algorithm between single or double sources is strongly influenced by the sky distribution of radio sources and by the characteristics of the fit procedure, so that a certain number of spurious associations classified as double on the basis of a positional coincidence of single, non interacting components is expected. A further step in the compilation of the radio source catalogue is thus the estimate of the fraction of double radio sources that could have been so classified on the basis of the chance coincidence of two unrelated sources.
Given the observed surface density of NVSS radio sources, and under the
hypothesis that all of them are single sources, we looked at the probability
that a source has by chance a neighbour assuming a completely random sky
distribution. We considered regions of
![]() belonging to 6NVSS maps we analyzed. For each region we generated 5 random samples each
containing as many positions as the detected NVSS sources (i.e.
belonging to 6NVSS maps we analyzed. For each region we generated 5 random samples each
containing as many positions as the detected NVSS sources (i.e.
![]() ), associating to
them values of the flux randomly chosen among the measured ones.
We then looked for pairs in the random samples, i.e. sources having a neighbour
inside
), associating to
them values of the flux randomly chosen among the measured ones.
We then looked for pairs in the random samples, i.e. sources having a neighbour
inside
![]() ,
that is the maximum distance we allowed for the
classification of a double source.
,
that is the maximum distance we allowed for the
classification of a double source.
We detected an average of 409 spurious doubles over the 6 maps we took into
consideration for this analysis. Over the same sky region, there are 660
double radio sources in the catalog. In Fig. 1 the distributions
of the distance between components for
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10558f1.ps}\end{figure}](/articles/aa/full/2001/43/aa10558/Timg56.gif) |
Figure 1: Distribution of the separation between components, D, for 660 double catalogue radio sources (solid line) and 409 random doubles (dashed line), belonging to the 6 maps we examined (see text). |
| Open with DEXTER | |
We distinguish three different contamination situations depending on the
separation D between the radio components. When
![]() the mean
contamination is about
the mean
contamination is about ![]() and we decided to keep as valid the
algorithm classification: hereafter we will call these "close'' double radio
sources.
For separations larger than
and we decided to keep as valid the
algorithm classification: hereafter we will call these "close'' double radio
sources.
For separations larger than
![]() the probability of chance coincidence
is such that we can consider all of them as spurious doubles: the 709 radio
sources belonging to this interval have thus been included as two single
components among the list of single sources.
In the interval between
the probability of chance coincidence
is such that we can consider all of them as spurious doubles: the 709 radio
sources belonging to this interval have thus been included as two single
components among the list of single sources.
In the interval between
![]() and
and
![]() a decision can hardly be
made: the contamination rate for these radio sources is high (
a decision can hardly be
made: the contamination rate for these radio sources is high (![]()
![]() )
but
the number of expected true doubles is not negligible.
In order not to miss the corresponding optical identifications, we kept these
sources (hereafter "wide'' doubles) among the double ones, but for this group
we followed a more careful procedure during the search of optical counterparts
(see Sect. 7).
)
but
the number of expected true doubles is not negligible.
In order not to miss the corresponding optical identifications, we kept these
sources (hereafter "wide'' doubles) among the double ones, but for this group
we followed a more careful procedure during the search of optical counterparts
(see Sect. 7).
Our estimate of the number of random doubles, derived under the assumption of a uniform sky distribution of radio sources, does not take into account any effect due to clustering properties of radio sources. However, there is indication that the clustering of radio sources on angular scales greater than the NVSS resolution is weak (Magliocchetti et al. 1998), and thus it should not significantly alter our results.
Due to our choice of a maximum separation between radio source components of
![]() ,
our catalogue of double radio sources does not include the class
of "giant'' doubles. For a reliable detection of such sources, additional
radio data with a better angular resolution than that provided by the NVSS
survey alone would be needed, to allow the determination of the morphological
type and of the compact core component necessary for the identification of the
optical counterpart.
Samples of giant radio sources have been selected on the basis of many
different criteria on their angular size, radio power and optical magnitude
(see e.g. Cotter et al. 1996; Machalski et al. 2001)
so that it is not straightforward to give an estimate of the expected number of
missed giants in our catalogue.
,
our catalogue of double radio sources does not include the class
of "giant'' doubles. For a reliable detection of such sources, additional
radio data with a better angular resolution than that provided by the NVSS
survey alone would be needed, to allow the determination of the morphological
type and of the compact core component necessary for the identification of the
optical counterpart.
Samples of giant radio sources have been selected on the basis of many
different criteria on their angular size, radio power and optical magnitude
(see e.g. Cotter et al. 1996; Machalski et al. 2001)
so that it is not straightforward to give an estimate of the expected number of
missed giants in our catalogue.
The extraction algorithm has been applied to 31 NVSS maps in the region of
the South Galactic Pole. The algorithm classified as double 3371 radio
sources: among these, 709 have distance between components ![]()
![]() and
have been included in the list of pointlike radio sources.
and
have been included in the list of pointlike radio sources.
The resultant catalogue consists of ![]() single sources and 2662 double
radio sources over
single sources and 2662 double
radio sources over ![]() 550 sq degrees of sky. The distribution of peak
fluxes is shown in Fig. 2.
550 sq degrees of sky. The distribution of peak
fluxes is shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ms10558f2.ps}\end{figure}](/articles/aa/full/2001/43/aa10558/Timg64.gif) |
Figure 2:
Histogram of fluxes for pointlike a) and double b) radio sources
in the catalogue. There are 4 pointlike sources with Log
|
| Open with DEXTER | |
The catalogue is complete down to the NVSS flux limit 2.5 mJy beam-1 and, as can
be seen in Fig. 3,
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ms10558f3.ps}\end{figure}](/articles/aa/full/2001/43/aa10558/Timg65.gif) |
Figure 3: Positional uncertainties estimated by the radio source extraction algorithm for single a) and double b) radio sources as a function of peak flux. The dot-dashed line represent the errors derived from the formulae in Condon et al. (1998). In b) the dashed vertical line represents the flux limit for the 2 components fit (see Sect. 3.4). |
| Open with DEXTER | |
The electronic version of the radio source catalogue is available at the Centre de Données de Strasbourg (CDS).
As the accuracy in positions and fluxes can influence the photometric completeness of the radio source catalogue as well as reliability and completeness of the optical identifications, before looking for radio source counterparts some tests to verify the algorithm stability and reliability in computing positions and fluxes have been performed on the catalogue.
A first test to asses the accuracy of fluxes and positions computed by the radio source extraction algorithm described in the previous Sects. has been made with comparison to the NVSS-NRAO catalogue (Condon et al. 1998). The NVSS-NRAO catalogue does not provide any classification in single or double radio sources, and simply gives a list of components fitted with an elliptical Gaussian of variable size: for this reason, we restricted this quantitative analysis only to the single radio sources in our catalogue. A qualitative analysis of double radio sources has been made by visual inspection and described below.
We extracted from our catalogue a set of 323 pointlike radio sources
belonging to the central
![]() square degrees of the NVSS map I0016M24,
and compared their positions and fluxes with those found in the NVSS-NRAO
catalogue. To take into account the dependence of positional accuracy on the
source flux, this analysis has been made in the three flux intervals
square degrees of the NVSS map I0016M24,
and compared their positions and fluxes with those found in the NVSS-NRAO
catalogue. To take into account the dependence of positional accuracy on the
source flux, this analysis has been made in the three flux intervals
![]() mJy beam-1,
mJy beam-1,
![]() mJy beam-1 and
mJy beam-1 and
![]() mJy beam-1. The modules of the mean differences in Right
Ascension and Declination were found to vary from
mJy beam-1. The modules of the mean differences in Right
Ascension and Declination were found to vary from ![]() 0.5 to
0.5 to
![]()
![]() with a dependence on flux, with rms varying from
with a dependence on flux, with rms varying from
![]()
![]() for the lowest fluxes to
for the lowest fluxes to ![]()
![]() for sources brighter
than 8 mJy beam-1.
for sources brighter
than 8 mJy beam-1.
Photometric accuracy has been tested by comparing peak fluxes in the NVSS-NRAO
catalogue with those determined by our extraction algorithm: these last result
to be on average slightly underestimated, the median of the differences being
![]() mJy beam-1, of the order of the "CLEAN bias'' term
for which the published NVSS-NRAO flux values have been corrected.
mJy beam-1, of the order of the "CLEAN bias'' term
for which the published NVSS-NRAO flux values have been corrected.
In Fig. 4 the offset distribution in Right Ascension,
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ms10558f4.ps}\end{figure}](/articles/aa/full/2001/43/aa10558/Timg74.gif) |
Figure 4: a) Distribution of differences in Right Ascension for 323 pointlike radio sources in our catalogue with respect to NVSS-NRAO catalogue positions. b) NVSS-NRAO fluxes vs. radio source catalogue ones for the same set of sources. There are 4 off-plot sources brighter than 160 mJy beam-1. |
| Open with DEXTER | |
During this analysis we found that in some cases a bright pointlike radio source is split in more than one component by the NVSS-NRAO extraction algorithm. This fact can be ascribed to the use of a totally automatic extraction procedure, needed when managing such a huge amount of data. Nevertheless, it points out that the "blind'' use of a component catalogue like the NVSS-NRAO one for optical identifications of radio sources can introduce contamination and incompleteness effects in the sample of of optical counterparts.
As the NVSS-NRAO catalogue does not make any attempt in classifying double radio sources, a similar quantitative comparison has not been possible for double systems and we limited our analysis to the visual inspection of 68 cases of "close'' and "wide'' doubles in the catalogue. "Close'' pairs are generally fitted with 1 component in the NVSS-NRAO catalogue and we found a good agreement between the NVSS-NRAO component position and the barycentre in the radio source catalogue. A different situation exists for "wide'' pairs in the radio source catalogue: their radio structure, as seen on the radio maps, is typical of classical double radio sources. In such cases, for which the NVSS-NRAO catalogue lists only the positions of the two components, the optical counterpart is clearly to be searched near the radio barycentre position and thus would be missed if one makes a blind use of the NVSS-NRAO catalogue.
A further test has been made on the radio source catalogue by using sources in the overlapping regions between adjacent maps to check the stability of the extraction algorithm in reproducing fluxes and positions.
We compared catalogue data relative to 120 single sources (half of them with
fluxes larger than 10 mJy beam-1) and 53 double sources with those obtained by
fitting the same sources with the AIPS task JMFIT.
We again found consistency with what predicted for NVSS sources: errors on the
positions of single sources vary from ![]()
![]() at fluxes lower than
5 mJy beam-1, to
at fluxes lower than
5 mJy beam-1, to
![]() for
for
![]() mJy beam-1. For the double
sources we find slightly larger values,
mJy beam-1. For the double
sources we find slightly larger values, ![]()
![]() for
for
![]() mJy beam-1.
We can conclude that both for pointlike and double radio sources in our
catalogue, the positional accuracy is good enough to allow optical
identifications with galaxies brighter than
mJy beam-1.
We can conclude that both for pointlike and double radio sources in our
catalogue, the positional accuracy is good enough to allow optical
identifications with galaxies brighter than
![]() down to the
NVSS flux limit.
down to the
NVSS flux limit.
The variation of catalogue peak fluxes and peak fluxes obtained with JMFIT is
![]()
![]() for single sources, similar to the values found examining radio
sources in the overlapping regions; for double sources the fractional
variation reaches the
for single sources, similar to the values found examining radio
sources in the overlapping regions; for double sources the fractional
variation reaches the
![]()
![]() for fluxes larger than 15 mJy beam-1.
This higher value can be ascribed to a difficulty in representing the source
with two Gaussians of fixed FWHM as the source flux increases. However, these
results can be considered satisfactory as the uncertainties are not such to
compromise the reliability of the optical identifications.
for fluxes larger than 15 mJy beam-1.
This higher value can be ascribed to a difficulty in representing the source
with two Gaussians of fixed FWHM as the source flux increases. However, these
results can be considered satisfactory as the uncertainties are not such to
compromise the reliability of the optical identifications.
The optical identification procedure has been applied separately to the three classes of NVSS radio sources in our catalogue: pointlike, "close'' doubles and "wide'' doubles. "Wide'' doubles are in fact affected by a non-negligible probability of being erroneously classified as double systems by our extraction algorithm, that is, we do not know a priori when the optical counterpart is to be expected near the radio barycentre, which we assume as the most likely position if the classification is correct (Venturi et al. 1997; Prandoni et al. 2001) or near the components. We thus have followed a careful approach in the identification of these sources, as will be detailed in Sect. 7.
"Close'' doubles have a low probability of being spurious associations of single components, so that in principle they could be treated as the pointlike sources during the identification phase, by looking for counterparts near their barycentres. Nevertheless, pointlike and "close'' doubles have been kept distinct in the identification phase, since we verified (see Sect. 6.2) that for "close'' doubles it is not possible to fulfil the requirements of the Likelihood Ratio method (De Ruiter et al. 1977). This method - to be applied in order to keep the contamination from radio-optical chance coincidence sufficiently low in the radiogalaxy sample - has been used only for the list of optical counterparts of pointlike radio sources.
In the next subsections we discuss the properties of the optical data used for the compilation of the radiogalaxy sample and the determination of radio-optical positional uncertainties, necessary to define the optimal radius for the search of optical counterparts. More details on the Likelihood Ratio method and on results from simulated samples are given in Appendix B.
Optical identifications of radio sources in the NVSS catalog have been made
with galaxies in the Edinburgh-Durham Southern Galaxy Catalogue (EDSGC, Nichol
et al. 2000). The EDSGC lists photographic ![]() magnitudes
for
magnitudes
for ![]()
![]() galaxies over a contiguous area of
galaxies over a contiguous area of
![]() 1200 sq degrees at the South Galactic Pole.
For the construction of the catalogue glass copies of 60 plates IIIa-J of
the ESO/SERC Sky Survey at galactic latitude
1200 sq degrees at the South Galactic Pole.
For the construction of the catalogue glass copies of 60 plates IIIa-J of
the ESO/SERC Sky Survey at galactic latitude
![]() have
been digitalized with the microdensitometer COSMOS (MacGillivray & Stobie
1984).
The automatic algorithm for star/galaxy classification implemented in COSMOS
has been optimized so to achieve a completeness greater than
have
been digitalized with the microdensitometer COSMOS (MacGillivray & Stobie
1984).
The automatic algorithm for star/galaxy classification implemented in COSMOS
has been optimized so to achieve a completeness greater than ![]() and
stellar contamination less than
and
stellar contamination less than ![]() for magnitudes
for magnitudes
![]() .
Magnitudes have been calibrated via CCD sequences, providing a plate-to-plate
accuracy of
.
Magnitudes have been calibrated via CCD sequences, providing a plate-to-plate
accuracy of
![]() and an rms plate zero-point offset
of 0.05 magnitudes.
and an rms plate zero-point offset
of 0.05 magnitudes.
The EDSGC catalogue becomes rapidly incomplete above
![]() ,
thus we decided to consider only those galaxies with
,
thus we decided to consider only those galaxies with
![]() .
With this conservative choice, the properties of the final identification
sample (in terms of optical completeness and contamination) are well consistent
with the global ones of the EDSGC.
.
With this conservative choice, the properties of the final identification
sample (in terms of optical completeness and contamination) are well consistent
with the global ones of the EDSGC.
The search radius for optical identifications must be carefully chosen as it affects the completeness and reliability of the obtained radiogalaxy sample (see Appendix B). The optimal search radius is usually chosen on the basis of the total positional uncertainties, i.e. the combination of the radio error (comprehensive of the uncertainty introduced by the fit) which depends on source flux, and the accuracy on optical positions.
To avoid any kind of assumption on this term, we empirically determined the radio-optical positional accuracies from the distribution of the measured radio-optical offsets. Given the uncertainty in the classification of "wide'' double radio sources, we made this analysis only for pointlike and "close'' double sources.
We have first identified the ![]() pointlike radio sources in the catalogue
with EDSGC galaxies brighter than magnitude
pointlike radio sources in the catalogue
with EDSGC galaxies brighter than magnitude
![]() ,
looking for
the nearest object inside a large square region of size
,
looking for
the nearest object inside a large square region of size
![]() ,
centered
on each radio position.
The distributions of the observed radio-optical offsets in
,
centered
on each radio position.
The distributions of the observed radio-optical offsets in ![]() and
and
![]() have been analyzed in different bins of radio flux, selected in order
to contain approximately the same number of counterparts.
have been analyzed in different bins of radio flux, selected in order
to contain approximately the same number of counterparts.
Each offset distribution is the sum of two distinct distributions: a flat one
due to the uniform distribution of spurious counterparts, plus a Gaussian one
due to the true radio-optical associations.
To estimate the rms of this Gaussian, which is the desired positional
uncertainty, we first obtained an accurate measure of the mean level of
contaminants by making optical identifications of randomly generated samples.
We built 4 control samples, each containing ![]() random positions, and
looked for spurious optical counterparts in the same way as for catalogue
sources.
random positions, and
looked for spurious optical counterparts in the same way as for catalogue
sources.
By fitting the offset distributions with a Gaussian function plus a constant pedestal, given by the the contamination level in that flux range obtained from the control samples, we evaluated the total positional uncertainties shown in Table 1.
Similar values have
|
|
|
|
|
|
|
3 | 5.17 | 5.28 |
|
|
2 | 4.11 | 5.76 |
|
|
3 | 3.16 | 3.33 |
|
|
3 | 2.04 | 2.27 |
|
|
3 | 2.21 | 1.88 |
On the basis of the estimated positional uncertainties, for the optical
identification procedure of NVSS radio sources we thus adopted a search radius
of
![]() .
.
The Likelihood Ratio method has subsequently been applied to the list of
counterparts of pointlike sources, to discard those cases that are
statistically unlikely to be true radio-optical associations.
The same method proved to be inapplicable to the counterparts of "close''
doubles, as in this case the hypothesis of Gaussian-distributed positional
uncertainty, required by the Likelihood Ratio method, is not satisfied. As can
be seen from Fig. 5,
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ms10558f5.ps}\end{figure}](/articles/aa/full/2001/43/aa10558/Timg98.gif) |
Figure 5:
Radio-optical offsets in Right Ascension a) and Declination b)
for 218 barycentres of NVSS radio sources in the catalogue (empty areas) and
62 contaminants from random samples (shaded regions), optically identified
with galaxies inside a box of size
|
| Open with DEXTER | |
The list of NVSS pointlike radio sources identified with EDSGC galaxies
brighter than
![]() inside a circle of radius
inside a circle of radius
![]() consists of 1061 candidate counterparts, with an average of 254
contaminants from the control samples: the initial contamination is thus
consists of 1061 candidate counterparts, with an average of 254
contaminants from the control samples: the initial contamination is thus
![]() .
To this list of optical counterparts and to the counterparts
found in the control samples we applied the modified Likelihood Ratio method
described in Appendix B, evaluating LR for each source using the
positional uncertainty relative to its flux (see Table 1).
.
To this list of optical counterparts and to the counterparts
found in the control samples we applied the modified Likelihood Ratio method
described in Appendix B, evaluating LR for each source using the
positional uncertainty relative to its flux (see Table 1).
The Likelihood Ratio cutoff value for rejecting a counterpart as unlikely to be
true was found to be
![]() .
Out of the initial list of 1061
candidates, the final sample of optical identifications of pointlike NVSS radio
sources thus consists of 926 counterparts satisfying the condition
.
Out of the initial list of 1061
candidates, the final sample of optical identifications of pointlike NVSS radio
sources thus consists of 926 counterparts satisfying the condition
![]() ,
while the number of contaminants in this sample, given by
the mean number of spurious identifications in the control samples which have
,
while the number of contaminants in this sample, given by
the mean number of spurious identifications in the control samples which have
![]() ,
is
,
is
![]() .
.
The contamination percentage in the final sample of 926 optical counterparts
of NVSS pointlike radio sources is thus ![]()
![]() ,
while due to the
choice of the cutoff value for LR we expect to lose
,
while due to the
choice of the cutoff value for LR we expect to lose ![]() 24 true
identifications. This corresponds to a completeness of
24 true
identifications. This corresponds to a completeness of ![]()
![]() and
to a reliability of
and
to a reliability of ![]()
![]() :
we conclude that, with respect to
the initial list of 1061 candidate counterparts, the use of the modified
Likelihood Ratio has sensibly lowered the contamination level without
discarding a large number of real radio-optical associations. The
identification percentage, expressed as the ratio between the number of true
identifications and the total number of sources for which we looked for an
optical counterpart, is about
:
we conclude that, with respect to
the initial list of 1061 candidate counterparts, the use of the modified
Likelihood Ratio has sensibly lowered the contamination level without
discarding a large number of real radio-optical associations. The
identification percentage, expressed as the ratio between the number of true
identifications and the total number of sources for which we looked for an
optical counterpart, is about
![]() .
.
For the 1530 "close'' doubles we looked for an optical counterpart brighter
than
![]() at a distance
at a distance ![]()
![]() from the radio
barycentre, finding 169 identifications. The number of spurious
identifications obtained from the control samples is
from the radio
barycentre, finding 169 identifications. The number of spurious
identifications obtained from the control samples is ![]() :
the
contamination percentage in the sample of optically identified "close'' double
radio sources is then
:
the
contamination percentage in the sample of optically identified "close'' double
radio sources is then
![]() ,
while the identification percentage is
,
while the identification percentage is
![]() ,
consistent at the
,
consistent at the ![]() level with
the value found for pointlike sources.
level with
the value found for pointlike sources.
The identification procedure of the 1132 "wide'' double radio sources has
been made as follows: we first looked for an optical counterpart inside a
radius of
![]() both from the barycentre position and from the positions of
the two components, and then inspected those cases where more than one
identification is found for the same radio source.
both from the barycentre position and from the positions of
the two components, and then inspected those cases where more than one
identification is found for the same radio source.
We initially identified 232 positions; in 156 cases we identify either the
barycentre or one (or both) the components: in such cases, we consider valid
the identification even if this does not mean that we are keeping the true
optical counterpart.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ms10558f6.ps}\end{figure}](/articles/aa/full/2001/43/aa10558/Timg114.gif) |
Figure 6:
Optical identifications of double radio sources in the interval
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ms10558f7.ps}\end{figure}](/articles/aa/full/2001/43/aa10558/Timg115.gif) |
Figure 7: Peak flux a) and magnitude b) distributions for the 1288NVSS radio sources optically identified with EDSGC galaxies. There are 67 radiogalaxies brighter than 80 mJy beam-1 not shown in the flux histogram. |
| Open with DEXTER | |
In the remaining cases, a puzzling situation emerges as we find a counterpart
for both the barycentre and one component, or even for the barycentre and the
two components, so that a decision on the most reliable identification is
difficult to make.
To discard or retain an identification, we decided to proceed as follows:
when we identify the barycentre and 1 component with the same galaxy (25 cases), we assume that this happens because in the extraction algorithm we
allowed high flux ratios.
In fact, when a common identification is found for the barycentre and for one
of the components (normally the strongest) we consider valid the association
with the barycentre, even if this is somewhat arbitrary.
Large values of
![]() ,
up to 10, are a feature
introduced by our extraction algorithm and are not representative of the true
distribution of flux ratios for double radio sources (see discussion in
Sect. 3.4). To perform an analysis of flux ratios and arm-length
ratios, and to compare it with other samples, we would need radio maps with
much better resolution.
,
up to 10, are a feature
introduced by our extraction algorithm and are not representative of the true
distribution of flux ratios for double radio sources (see discussion in
Sect. 3.4). To perform an analysis of flux ratios and arm-length
ratios, and to compare it with other samples, we would need radio maps with
much better resolution.
| Radio | N | Contamination |
| Morphology | ||
| Pointlike | 926 | 16 |
| "Close'' double | 169 | 16% |
| "Wide'' double | 193 | 28 |
| Total | 1288 | 18 |
In the 12 cases when we identify the barycentre and one component with two different galaxies, or the barycentre and one component with the same galaxy but at the same time we find a different identification for the second component, or finally we identify separately both the barycentre and the two components, we decided which is the most likely identification by visually inspecting the field. These few cases are shown in Fig. 6.
When the radio source structure is similar to a "head-tail'' morphology, we considered the counterpart associated to the component corresponding to the radio source "head''. In the presence of extended but symmetric radio morphologies we retain the identification in the barycentre. An example of spurious double can be represented by B1471 in Fig. 6, the only case where we identify at the same time the barycentre and the two components with different galaxies. In this case we considered valid the two counterparts associated to the components of the double source.
By applying these criteria, we obtained a list of 193 optical counterparts of
"wide'' double radio sources. Because of the presence of an "intrinsic''
radio contamination, and given the subjective method adopted in the selection
of true counterparts, it is possible to give only a lower limit to the
contamination present in this list of identifications. The number of spurious
identifications is
![]() ,
that is a contamination percentage of
,
that is a contamination percentage of
![]()
![]() .
.
A summary of the different contamination levels as well as the number of optical counterparts found for each radio morphology we are considering is given in Table 2.
The final
radiogalaxy sample thus consists of 1288 sources optically
identified with galaxies brighter than
![]() in the EDSGC: in
Fig. 7 the magnitude and flux distributions for the radiogalaxy
sample are shown.
The overall contamination in the radiogalaxy sample is
in the EDSGC: in
Fig. 7 the magnitude and flux distributions for the radiogalaxy
sample are shown.
The overall contamination in the radiogalaxy sample is
![]()
![]() .
The identification percentage we find for NVSS sources is in agreement with
that found by Magliocchetti & Maddox (2001) for optical
identifications of higher-resolution FIRST radio sources with APM galaxies in
the equatorial region, once scaled to our radio flux and optical magnitude
limits.
In Paper II we will use a subset of our radiogalaxy sample, characterized by a
higher reliability, to look for intermediate redshifts cluster candidates
associated to NVSS radio sources.
.
The identification percentage we find for NVSS sources is in agreement with
that found by Magliocchetti & Maddox (2001) for optical
identifications of higher-resolution FIRST radio sources with APM galaxies in
the equatorial region, once scaled to our radio flux and optical magnitude
limits.
In Paper II we will use a subset of our radiogalaxy sample, characterized by a
higher reliability, to look for intermediate redshifts cluster candidates
associated to NVSS radio sources.
Aim of this work is to build a sample of radio-optically selected clusters of galaxies at intermediate redshift in order to study the evolution and general properties of groups and clusters as well as the effect of the environment on the radio emission phenomenon. In this paper we have discussed the compilation of a radio source catalogue from 31 NVSS radio maps covering the South Galactic Pole region, and the search of optical counterparts of these radio sources. The main reason to build a radio source catalogue alternative to the NVSS-NRAO publicly available one has been the need to classify radio sources according to their morphology - unresolved or double - so to properly search for their optical counterparts.
Our radio source catalogue has been built by detecting emission peaks above the
detection threshold
![]() mJy beam-1 and fitting Gaussian
components with FWHM equal to the NVSS beam size to the selected peaks. The
source detection algorithm first attempts a one-component fit to each peak and,
depending on the root mean square of the fit and on the distance between two
neighbour peaks, if necessary a two-components fit is performed.
mJy beam-1 and fitting Gaussian
components with FWHM equal to the NVSS beam size to the selected peaks. The
source detection algorithm first attempts a one-component fit to each peak and,
depending on the root mean square of the fit and on the distance between two
neighbour peaks, if necessary a two-components fit is performed.
Classification of double radio sources has been done by first allowing the
separation between components to be as large as
![]() and compiling a
first list of "tentative'' double sources. Then, given the NVSS low
resolution, a detailed analysis to discriminate between pointlike and double
sources has been done by studying the probability of classifying two single,
non interacting components as a double system on the basis of their separation.
From this analysis we found that the probability of two sources being a
physically bound system is negligible when their distance is greater than
and compiling a
first list of "tentative'' double sources. Then, given the NVSS low
resolution, a detailed analysis to discriminate between pointlike and double
sources has been done by studying the probability of classifying two single,
non interacting components as a double system on the basis of their separation.
From this analysis we found that the probability of two sources being a
physically bound system is negligible when their distance is greater than
![]() .
These doubles have been removed from the "tentative'' list and included as
single components among the unresolved sources while, on the opposite, the
classification of double sources is correct for those systems having
.
These doubles have been removed from the "tentative'' list and included as
single components among the unresolved sources while, on the opposite, the
classification of double sources is correct for those systems having
![]() ("close'' doubles).
In the intermediate range
("close'' doubles).
In the intermediate range
![]() the number of expected
spurious and true double sources are equivalent. These cases ("wide'' doubles)
have been included among double sources but for them a more careful optical
identification procedure has been performed.
the number of expected
spurious and true double sources are equivalent. These cases ("wide'' doubles)
have been included among double sources but for them a more careful optical
identification procedure has been performed.
The final radio source catalogue consists of ![]() single and 2662
double radio sources over
single and 2662
double radio sources over ![]() 550 sq degrees of sky, and is complete
down to
550 sq degrees of sky, and is complete
down to
![]() mJy beam-1.
mJy beam-1.
A quantitative test to assess the accuracy of the radio source extraction algorithm has been made comparing fluxes and positions of a set of radio sources in our catalogue with the correspondent values in the NVSS-NRAO catalogue. Since the NVSS-NRAO catalogue does not classify double radio sources this analysis has been possible for pointlike sources only. We found that our results are in agreement with the ones in the NVSS-NRAO catalogue, well inside the predicted errors for the NVSS (Condon et al. 1998). For what concerns double radio sources, we made a qualitative analysis by visually inspecting a set of "close'' and "wide'' doubles and looking at their characteristics in the NVSS-NRAO catalogue. We found a good agreement in flux and positions for "close'' doubles, while in most cases "wide'' ones clearly show a classical double radio morphology on the maps. In such cases, where the optical counterpart should be looked near the radio barycentre, the use of the NVSS-NRAO catalogue without a re-processing to detect double sources, would result in a loss of optical identifications and thus in a less complete radiogalaxy sample.
Optical identifications of radio sources in our catalogue have been made with
EDSGC galaxies (Nichol et al. 2000) down to a limiting magnitude of
![]() and adopting a search radius of
and adopting a search radius of
![]() .
.
Different strategies have been applied for the search of optical counterparts
of pointlike or double radio sources. For the latter, the probability of having
classified as a double system two physically disjointed sources on the basis of
their superposition in the sky is in fact dependent on the distance between the
two components.
The optical identification of the ![]() pointlike radio sources led to a
sample of 926 radiogalaxies. The statistical completeness and reliability of
this sample have been evaluated by means of the modified Likelihood Ratio
method proposed by De Ruiter et al. (1977) (see
Appendix B), to properly take into account the true optical
surface distribution of galaxies in the sky.
This sample is complete to
pointlike radio sources led to a
sample of 926 radiogalaxies. The statistical completeness and reliability of
this sample have been evaluated by means of the modified Likelihood Ratio
method proposed by De Ruiter et al. (1977) (see
Appendix B), to properly take into account the true optical
surface distribution of galaxies in the sky.
This sample is complete to
![]() and reliable to
and reliable to
![]() ,
with
an identification percentage of
,
with
an identification percentage of
![]() .
.
The optical identification of 1530 "close'' double radio sources (distance
between components
![]() )
has been made looking for a counterpart
near the barycentre position. For these sources, the probability of being a
spurious double is low,
)
has been made looking for a counterpart
near the barycentre position. For these sources, the probability of being a
spurious double is low,
![]()
![]() .
We optically identified 169
barycentres of "close'' doubles; in this case it was not possible to apply the
modified Likelihood Ratio method to evaluate the reliability and completeness
of the sample.
An estimate of the contamination level has been computed as the probability of
chance radio-optical superposition on the basis of the average observed optical
surface galaxy density. We found a contamination of
.
We optically identified 169
barycentres of "close'' doubles; in this case it was not possible to apply the
modified Likelihood Ratio method to evaluate the reliability and completeness
of the sample.
An estimate of the contamination level has been computed as the probability of
chance radio-optical superposition on the basis of the average observed optical
surface galaxy density. We found a contamination of
![]() for optical
identifications of "close'' double radio sources.
for optical
identifications of "close'' double radio sources.
Optical identifications of "wide'' doubles (distance between components
![]() )
are made difficult by the high percentage of
expected radio misclassification: the number of true radio associations is in
fact comparable with the number of radio contaminants. We thus looked for
optical counterparts both near the radio barycentre and near the radio
components positions, visually inspecting those cases where more than one
optical identification is found for the same radio source.
We found a list of 193 optical counterparts of "wide'' double radio sources,
with a contamination of the order of
)
are made difficult by the high percentage of
expected radio misclassification: the number of true radio associations is in
fact comparable with the number of radio contaminants. We thus looked for
optical counterparts both near the radio barycentre and near the radio
components positions, visually inspecting those cases where more than one
optical identification is found for the same radio source.
We found a list of 193 optical counterparts of "wide'' double radio sources,
with a contamination of the order of ![]()
![]() :
this contamination level must
be seen as a lower limit, as it does not take into account the joint
probability of having a optical spurious identification near the barycentre of
a spurious double radio source.
:
this contamination level must
be seen as a lower limit, as it does not take into account the joint
probability of having a optical spurious identification near the barycentre of
a spurious double radio source.
The final sample thus lists 1288 radiogalaxies and represents a valuable opportunity for the study of the multi-wavelength properties of the radiogalaxy populations down to a low flux level.
This sample has been used to look for galaxy clusters associated to NVSS radiogalaxies: in a following paper (Zanichelli et al. 2001) we discuss the cluster selection strategy and the first observational results, that prove this technique to be a powerful tool for the selection of galaxy groups and clusters at intermediate redshift.
To define flux and accurate positions of radio sources from NVSS maps, we
developed a code which performs a Gaussian bidimensional fit by means of a
minimization process. Starting from M functions in N variables,
![]() ,
the routine MINSQ
(Pomentale 1968) minimizes the sum:
,
the routine MINSQ
(Pomentale 1968) minimizes the sum:
![$\displaystyle f_k = {[a_k - G(x_k, y_k)]^2 \over \sigma^2}\cdot$](/articles/aa/full/2001/43/aa10558/img133.gif) |
(A.3) |
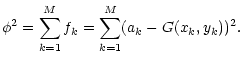 |
(A.4) |
The fit uncertainty associated to each source is thus writable as:
| (A.6) |
Starting from source pixel coordinates, Right Ascension and Declination have
been computed by means of the conversion formulae for the sine projection
used in the NVSS:
We have a "correct'' identification when the combined radio and optical positional uncertainties are such that the true counterpart of the radio source, if it exists, does not lie outside the area defined by the search radius and, at the same time, the first (nearest) contaminant is not closer to the radio source than the identification itself.
In the case when a correct identification does not exist (empty field), we will misidentify as true a contaminant each time a galaxy is found inside the search region. The percentage of identification is defined as the fraction of correct identifications with respect to the total number of radio sources for which an optical counterpart has been looked for.
The completeness of an optical identification program represents the fraction of correct identifications among the radio sources having an optical counterpart, while the reliability is defined as the fraction of counterparts that are true radio-optical associations, i.e. it is the complement to the contamination level in the sample.
Under the hypothesis that the positions of a radio source and its optical
counterpart are intrinsically coincident, it is possible to define the a
priori probability p(r|id) that the radio-optical offset is found in the
distance interval (
![]() )
due to the positional uncertainties.
Similarly, under the hypothesis that the counterpart is a contaminant, it is
possible to define the a priori probability p(r|c) that the
contaminant is found inside (
)
due to the positional uncertainties.
Similarly, under the hypothesis that the counterpart is a contaminant, it is
possible to define the a priori probability p(r|c) that the
contaminant is found inside (
![]() ).
).
For each radio source it is then possible to define the Likelihood Ratio LRas the ratio between these two probabilities: an optical counterpart is
considered as the true radio-optical association if p(r|id) is greater
than p(r|c) by a factor ![]() to be determined.
to be determined.
Nevertheless, what is actually computable from an identification program are the a posteriori probabilities p(id|r) and p(c|r) that, having found a counterpart at a given distance r from the radio source, we are dealing with the true identification or with a contaminant.
The Likelihood Ratio method (De Ruiter et al. 1977) makes use of
the Bayes theorem to express p(id|r) and p(c|r) in terms of LR,
that is by means of the correspondent a priori probabilities
p(r|id) and p(r|c):
By applying the Bayes theorem and under the assumption that the true
identification is always the nearest object to the radio source, p(id|r)and p(c|r) can be written as:
In general, the value of ![]() is close to
is close to ![]() 2.0, that means to
consider true all those identifications for which the a priori probability of
having correctly identified the radio source is twice the a priori probability
of having a contaminant.
2.0, that means to
consider true all those identifications for which the a priori probability of
having correctly identified the radio source is twice the a priori probability
of having a contaminant.
One critical factor in the Likelihood Ratio method proposed by De Ruiter et al. (1977) is the assumption of a constant optical surface density of galaxies. This does not allow to keep into account the real galaxy clustering and thus can heavily affect the estimates of C and R. To avoid this limitation, we applied a modified version of this method, which makes use of control samples to properly evaluate the contamination level in the optical identification samples.
Control samples of the same size as the radio source catalogue are built by
assigning to each entry a random position and, once defined the radius of the
search region, optically identified with galaxies as is done for the
radiogalaxy sample. We can write the expected number of contaminants in the
final identification sample as the average of the spurious identifications found in each
control sample:
![]() .
The expected number of true identifications will thus be given by the
difference between the total number of counterparts found, N, and the mean
number of contaminants:
.
The expected number of true identifications will thus be given by the
difference between the total number of counterparts found, N, and the mean
number of contaminants:
![]() .
We can obtain
also the identification percentage
.
We can obtain
also the identification percentage
![]() ,
where
,
where
![]() is the total number of radio sources for which we
have searched an optical counterpart.
is the total number of radio sources for which we
have searched an optical counterpart.
According to the Likelihood Ratio method, the completeness expresses the
fraction of real identifications for which ![]() ,
so we can write:
,
so we can write:
Similarly, we can write for the reliability:
That is, R is defined in terms of the fraction of contaminants that are
included in the sample due to the choice of the cutoff value ![]() .
.