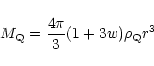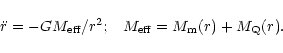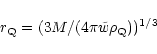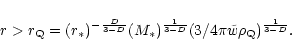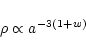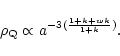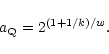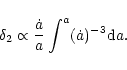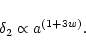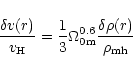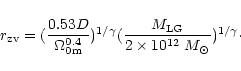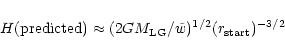A&A 378, 729-734 (2001)
DOI: 10.1051/0004-6361:20011257
The cold local Hubble flow as a signature of dark energy
Yu. V. Baryshev1,2 -
A. D. Chernin3,4,5 -
P. Teerikorpi3
1 - Institute of Astronomy, St. Petersburg State University,
Staryj Peterhoff, 198504 St. Petersburg, Russia
2 -
Isaac Newton Institute of Chile, Saint-Petersburg Branch, Russia
3 -
Tuorla Observatory,
University of Turku, 21500 Piikkiö, Finland
4 -
Division of Astronomy, University of Oulu, 90014 Finland
5 -
Sternberg Astronomical Institute, Moscow University, 119899 Moscow, Russia
Received 9 May 2001 / Accepted 6 September 2001
Abstract
The Local Group environment at 1-10 Mpc expands linearly and smoothly,
as if ruled by uniform matter, while
observations show on the same scales the very lumpy local galaxy universe.
This enigma in cosmology
has also been demonstrated by high-resolution N-body CDM simulations.
We suggest that the homogeneous dark energy component,
revealed by SNIa observations, may resolve the problem
of the local cold Hubble flow
within the highly non-uniform environment.
Linear density perturbations on a homogeneous background
with the equation of state
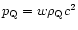 are decaying for w<-1/3.
Exact non-linear Einstein's equations for a spherically
symmetric matter concentration,
show that
there is a zero-mass surface where the positive mass of the local cloud
is compensated by the negative dark energy mass, and beyond
this surface
dark energy dominates dynamically.
In such regions the velocity dispersion is adiabatically cooling, and
this may explain why the Hubble law starts
on the outskirts of the Local Group, with the same H0 as
globally and with a remarkably small velocity dispersion.
are decaying for w<-1/3.
Exact non-linear Einstein's equations for a spherically
symmetric matter concentration,
show that
there is a zero-mass surface where the positive mass of the local cloud
is compensated by the negative dark energy mass, and beyond
this surface
dark energy dominates dynamically.
In such regions the velocity dispersion is adiabatically cooling, and
this may explain why the Hubble law starts
on the outskirts of the Local Group, with the same H0 as
globally and with a remarkably small velocity dispersion.
Key words: dark matter - cosmological parameters - Local Group
Recent studies of the local volume (<10 Mpc) show that
the velocity dispersion around
the local Hubble law is very low (
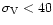 km s-1) (Ekholm et al. 2001; Karachentsev & Makarov 2000).
This highlights the riddle of the local Hubble law,
first recognized by Sandage et al. (1972): Why is the Hubble flow
so linear and cold in the very lumpy environment of the Local Group?
The N-body CDM simulations by Governato et al.
(1997)
have fully confirmed and even sharpened this problem.
km s-1) (Ekholm et al. 2001; Karachentsev & Makarov 2000).
This highlights the riddle of the local Hubble law,
first recognized by Sandage et al. (1972): Why is the Hubble flow
so linear and cold in the very lumpy environment of the Local Group?
The N-body CDM simulations by Governato et al.
(1997)
have fully confirmed and even sharpened this problem.
Here we argue that a possible solution for this problem may be found
in the remarkable
new coincidence that the antigravity of dark energy
starts to dominate over the gravity of lumpy matter at the
distance where the Hubble flow emerges.
In the standard cosmology
the Hubble law,
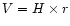 ,
is a strict consequence of
a uniform distribution of self-gravitating
matter (Robertson 1955; Peebles 1993).
Hence the predicted linear velocity field is only valid for scales
where the universe is uniform.
However, a very puzzling fact
long ago noted by Sandage et al. (1972),
is that
Hubble discovered his law in the distance interval 1-20 Mpc, where
the galaxies are very clumpily distributed.
Indeed, this was
deep inside a cell of uniformity having the size of at least
20 Mpc, which follows from the power-law correlation
function for field galaxies (Peebles 1993).
On all smaller scales the galaxies are fractally distributed,
forming strongly inhomogeneous structures
(Sylos Labini et al. 1998; Wu et al. 1999;
Tikhonov et al. 2000).
There is also observational evidence that fractality continues up to
100-200 Mpc (de Vaucouleurs 1971;
Sylos Labini et al. 1998;
Teerikorpi et al. 1998).
,
is a strict consequence of
a uniform distribution of self-gravitating
matter (Robertson 1955; Peebles 1993).
Hence the predicted linear velocity field is only valid for scales
where the universe is uniform.
However, a very puzzling fact
long ago noted by Sandage et al. (1972),
is that
Hubble discovered his law in the distance interval 1-20 Mpc, where
the galaxies are very clumpily distributed.
Indeed, this was
deep inside a cell of uniformity having the size of at least
20 Mpc, which follows from the power-law correlation
function for field galaxies (Peebles 1993).
On all smaller scales the galaxies are fractally distributed,
forming strongly inhomogeneous structures
(Sylos Labini et al. 1998; Wu et al. 1999;
Tikhonov et al. 2000).
There is also observational evidence that fractality continues up to
100-200 Mpc (de Vaucouleurs 1971;
Sylos Labini et al. 1998;
Teerikorpi et al. 1998).
On the other hand, in the same local volume
observations reveal
a linear distance-velocity relation which starts from the distance of
about 1 Mpc and
shows extremely low velocity scatter
with a dispersion <40 km s-1(Ekholm et al. 2001;
Karachentsev & Makarov 2000).
The linear Hubble law continues with the same Hubble constant
also outside the local volume up to larger distances
(Teerikorpi 1997;
Ekholm et al. 1999;
Giovanelli et al. 1999).
In the highly nonuniform local universe
such a cold linear Hubble flow seems to contradict
the standard picture where the Hubble law is the strict
consequence of homogeneity of matter distribution.
As illustrated by Weinberg's words:
"in fact, we would not expect
any neat relation of proportionality
between velocity and distance for these [closeby] ... galaxies''
(Weinberg 1977).
A quantitative formulation and study of this paradox
was given by Baryshev et al. (1998).
Sandage (1999, also 1986)
recently expressed this surprising situation, as
the "extremely local rate [of expansion] is the same as the global rate
to better than 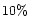 '', and an "explanation of why the local
expansion field is so noiseless remains a mystery''.
'', and an "explanation of why the local
expansion field is so noiseless remains a mystery''.
The expected coldness of the local Hubble flow was studied
quantitatively by Governato et al. (1997) using high resolution
CDM N-body simulations. They identified many "Local Groups''
to match the observed dynamics and environments of our Local Group.
Calculation of velocity dispersions in 5 Mpc volume around the "LG's''
led to an important result. For
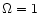 CDM model
the peculiar velocities have 300 km s-1
CDM model
the peculiar velocities have 300 km s-1
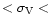 700 km s-1, and
for
700 km s-1, and
for
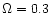 CDM model 150 km s-1
CDM model 150 km s-1
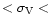 300 km s-1. They state
that "neither of these models are able to produce a single LG with a
local velocity dispersion comparable with the observed value''. Also,
no biasing scheme could reproduce the cold local flow.
300 km s-1. They state
that "neither of these models are able to produce a single LG with a
local velocity dispersion comparable with the observed value''. Also,
no biasing scheme could reproduce the cold local flow.
Karachentsev (1996) concluded
that the Local Group is typical among nearby groups.
Governato et al. (1997) also found that the LG candidates occupy
typical places in the hierarchic CDM structures. This justifies
the use of the environment of our Local Group as a representative test
object.
One may thus divide the enigma of the local Hubble flow into
the following problems:
(1) The linear velocity law appears at a distance 1.5 Mpc,
a small fraction of the scale where the galaxy
universe may finally appear uniform.
Why does our highly non-uniform environment expand as if it were
uniform?
(2) What makes the local Hubble flow so cold? Not only does the
Hubble law exist, but it has a remarkably small scatter (
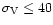 km s-1).
km s-1).
The Hubble diagram for high redshift type Ia
Supernovae (Riess et al. 1998; Perlmutter et al. 1999)
and the Boomerang and MAXIMA-1
measurements of the first acoustic peak location in
the angular power spectrum of the CMB
(de Bernardis et al. 2000; Jaffe et al. 2000)
restrict the standard
cosmological model close to the critical density
(
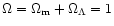 ), with a dominant
), with a dominant 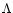 -like,
"dark energy''(DE) component at the
present epoch (
-like,
"dark energy''(DE) component at the
present epoch (
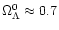 ).
).
The detection of the DE component provides a natural
candidate for a high-density uniform background.
In the cosmological
theory there are many kinds of dark energy candidates with
positive energy density (
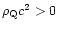 )
and negative pressure (
)
and negative pressure (
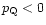 ).
The dark energy is a common name for:
Einstein's cosmological constant
).
The dark energy is a common name for:
Einstein's cosmological constant 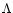 or cosmological vacuum,
time-variable
or cosmological vacuum,
time-variable 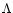 ,
scalar fields, and exotic substances
with negative pressure (Bahcall et al. 1999; Sahni &
Starobinsky 2000).
It is now much studied and also included in
cosmological tests (Wang et al. 2000; Podariu & Ratra
2000).
The main motivation for evolving DE is the "cosmic coincidence'': Why is
the rapidly decreasing energy density of
matter just now close to that of the unchanging vacuum?
,
scalar fields, and exotic substances
with negative pressure (Bahcall et al. 1999; Sahni &
Starobinsky 2000).
It is now much studied and also included in
cosmological tests (Wang et al. 2000; Podariu & Ratra
2000).
The main motivation for evolving DE is the "cosmic coincidence'': Why is
the rapidly decreasing energy density of
matter just now close to that of the unchanging vacuum?
A striking property of the DE having the
equation of state
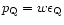 ,
,
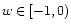 ,
is that its gravitating mass
,
is that its gravitating mass
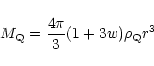 |
(1) |
is negative for w < -1/3.
This produces cosmological antigravity which
accelerates the expansion of the universe.
E.g. for Einstein's
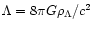 (cosmological vacuum
with w=-1)
(cosmological vacuum
with w=-1)
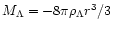 .
.
An important class of DE models is the so-called coupled quintessence
(see e.g. Wetterich 1995;
Amendola 1999), where the total (matter + DE)
energy momentum tensor is conserved, in contrast
to ordinary quintessence where the matter
and DE are separately conserved. For coupled quintessence, a
stationary DE model was recently found (Amendola & Tocchini-Valentini
2000) which predicts coherent
behaviour of matter and DE density at late cosmic epochs.
Below we show that especially such models are favorable
for explaining the cold local Hubble law.
We study a model where a separate spherical matter
"cloud'' lies on a homogeneous DE background.
The dark energy
exists alongside with luminous and dark matter in the immediate
environment of the matter cloud.
Cosmological vacuum (w=-1) is truly uniform.
Quintessence in general may vary in time and space,
but in some models DE may be regarded as homogeneous
on scales up to 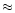 100 Mpc (Wang & Steinhardt 1998).
The dynamics of the cloud
is determined by the competition of the gravity of
matter and the antigravity of the DE.
100 Mpc (Wang & Steinhardt 1998).
The dynamics of the cloud
is determined by the competition of the gravity of
matter and the antigravity of the DE.
Now consider the radial law of the matter density.
The mass-to-luminosity ratio for different galaxy systems
seems to remain
constant for r > 0.5 Mpc (Bahcall et al. 1995), hence dark
matter is distributed like luminous matter on such scales.
The mean density of luminous (and hence, of dark) matter decreases
with increasing scale so that the mass grows as
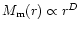 ,
where D, the fractal dimension,
is between 1 and 3 for scales at least up to 20 Mpc
(Sylos Labini et al. 1998; Wu et al. 1999;
Tikhonov et al. 2000).
Further evidence for the power-law density
comes from number
counts of galaxies. It was shown by
Baryshev (1981),
Klypin et al. (1989), and
Teerikorpi et al. (1998)
that the galaxy density around our Galaxy behaves as
a power-law with the exponent corresponding to
,
where D, the fractal dimension,
is between 1 and 3 for scales at least up to 20 Mpc
(Sylos Labini et al. 1998; Wu et al. 1999;
Tikhonov et al. 2000).
Further evidence for the power-law density
comes from number
counts of galaxies. It was shown by
Baryshev (1981),
Klypin et al. (1989), and
Teerikorpi et al. (1998)
that the galaxy density around our Galaxy behaves as
a power-law with the exponent corresponding to
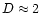 up to scales of about 200 Mpc.
up to scales of about 200 Mpc.
A recent analysis of the correlation function
for a sample of 330 galaxies within the local volume
(<10 Mpc) showed a fractal-like galaxy distribution with dimension
D=1.8 (Tikhonov et al. 2000).
This also justifies the power law as a
description of galaxy distribution around the LG.
The density of the homogeneous DE component is constant
(
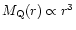 ), hence
it starts to dominate the matter component after
a distance
), hence
it starts to dominate the matter component after
a distance 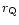 .
To estimate
.
To estimate 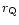 for the environment of
the Local Group, we use two models.
The first model generalizes Sandage's
(1986) point-mass model: a mass M is
placed on the dark energy background with density
for the environment of
the Local Group, we use two models.
The first model generalizes Sandage's
(1986) point-mass model: a mass M is
placed on the dark energy background with density
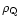 .
In the second model, a spherical mass distribution
.
In the second model, a spherical mass distribution
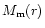 is on the DE background.
is on the DE background.
The dynamics of a spherically symmetric dust matter cloud
with density
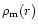 and energy-momentum tensor
and energy-momentum tensor
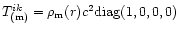 on the homogeneous quintessence background
having
on the homogeneous quintessence background
having
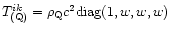 is
described by the exact Eintein's field equations.
The (1,1) component of the field equation,
in combination with the (0,0) component,
gives the following exact
equation of motion:
is
described by the exact Eintein's field equations.
The (1,1) component of the field equation,
in combination with the (0,0) component,
gives the following exact
equation of motion:
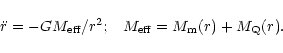 |
(2) |
Here
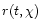 is the radial distance from the centre of the spherical cloud,
is the radial distance from the centre of the spherical cloud,
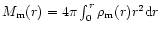 is the dust mass within the
sphere of radius r,
is the dust mass within the
sphere of radius r,
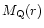 is the quintessence mass within the same radius and is
given by Eq. (1).
is the quintessence mass within the same radius and is
given by Eq. (1).
For the point-mass model
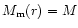 there is a distance
there is a distance 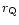 where
where
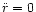 and the DE mass energy
equals that of the matter cloud, i.e.
and the DE mass energy
equals that of the matter cloud, i.e.
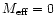 .
This zero-mass
radius is:
.
This zero-mass
radius is:
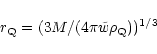 |
(3) |
where
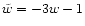 .
For w=-1/3 the gravitating mass of the DE is zero
and formally
.
For w=-1/3 the gravitating mass of the DE is zero
and formally
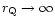 .
.
In the second model (
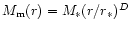 )
the dark energy term dominates dynamically at distances
)
the dark energy term dominates dynamically at distances
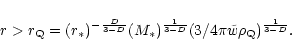 |
(4) |
Note that the distance 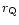 is defined by the ratio between
the local cloud mass and the global density of quintessence.
Beyond the zero-mass (screening) distance
is defined by the ratio between
the local cloud mass and the global density of quintessence.
Beyond the zero-mass (screening) distance 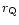 dark
energy density dominates
over the matter density.
The zero-mass distance for a given mass cloud
depends on cosmic time t (or scale factor a).
dark
energy density dominates
over the matter density.
The zero-mass distance for a given mass cloud
depends on cosmic time t (or scale factor a).
When the uniform DE background expands,
a galaxy which now is on the border of the DE dominated
region near the matter cloud, previously lied inside the gravity
dominated sphere. In terms of comoving coordinates, the border 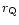 shifts
outwards for increasing redshift.
We calculate the temporal behaviour of the screening distance
for a few kinds of density evolution.
The relation between density and scale factor for a substance
with the equation of state
shifts
outwards for increasing redshift.
We calculate the temporal behaviour of the screening distance
for a few kinds of density evolution.
The relation between density and scale factor for a substance
with the equation of state
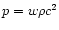 is
is
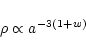 |
(5) |
where
a = S(t)/S(t0) is the normalized scale factor
and t0 is the present epoch.
We consider such epochs when the average (homogeneous)
density of matter
component
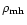 is less than the DE density
is less than the DE density
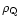 ,
as suggested by observations.
,
as suggested by observations.
To illustrate the model dependence of the zero-mass distance
we also take a model of "coherent'' behaviour for matter and quintessence:
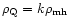 ,
where
,
where
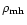 is the average matter density.
Such a relation was studied by Baryshev et al. (2000)
in order to solve the problem of the low velocity dispersion in the
local Hubble flow.
It naturally appears at the late cosmic epoch within
the model of stationary coupled dark energy, recently found by
Amendola & Tocchini-Valentini (2000).
For the coherent phase of the DE
there is a simple relation
between the density and the scale factor.
The condition that the covariant divergence
of the total energy-momentum tensor (DE + matter) is zero
implies that
is the average matter density.
Such a relation was studied by Baryshev et al. (2000)
in order to solve the problem of the low velocity dispersion in the
local Hubble flow.
It naturally appears at the late cosmic epoch within
the model of stationary coupled dark energy, recently found by
Amendola & Tocchini-Valentini (2000).
For the coherent phase of the DE
there is a simple relation
between the density and the scale factor.
The condition that the covariant divergence
of the total energy-momentum tensor (DE + matter) is zero
implies that
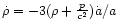 ,
where
,
where
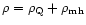 and
and
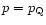 for dust-like matter (
for dust-like matter (
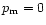 ).
Hence the coherent DE density behaves as
).
Hence the coherent DE density behaves as
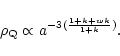 |
(6) |
For
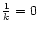 (no uniform matter) Eq. (6)
gives the usual quintessence behaviour
Eq. (5). General properties of 2-fluid
FLRW models (including coherent matter & DE)
are studied elsewhere (Baryshev et al. 2001).
(no uniform matter) Eq. (6)
gives the usual quintessence behaviour
Eq. (5). General properties of 2-fluid
FLRW models (including coherent matter & DE)
are studied elsewhere (Baryshev et al. 2001).
As an example we calculate the shift of 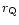 in time for three
DE models:
1) Cosmological constant
in time for three
DE models:
1) Cosmological constant 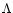 ,
2) quintessence
with w = -2/3, and 3) coherent quintessence with w = -2/3, k = 1.
First, we consider
the ratio between two metric distances
,
2) quintessence
with w = -2/3, and 3) coherent quintessence with w = -2/3, k = 1.
First, we consider
the ratio between two metric distances
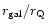 ,
where
,
where
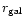 is the distance to a galaxy which now is in the DE
dominated region and takes part in the Hubble flow. The distance
is the distance to a galaxy which now is in the DE
dominated region and takes part in the Hubble flow. The distance
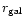 is
simply proportional to a. The behavior of the critical distance
is
simply proportional to a. The behavior of the critical distance
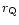 depends on the DE and matter models.
E.g. for the point-mass model the ratio is
depends on the DE and matter models.
E.g. for the point-mass model the ratio is
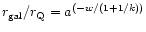 ,
which for 1/k=0 gives
a-w,
corresponding either to Einstein's
,
which for 1/k=0 gives
a-w,
corresponding either to Einstein's 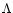 (w=-1) or
to the quintessence (
(w=-1) or
to the quintessence (
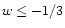 ).
).
We define a characteristic time when
the antigravity dominates in the vicinity of a matter cloud.
It is counted from
the local critical epoch 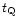 ,
corresponding to the scale factor
,
corresponding to the scale factor
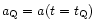 when DE antigravity starts to exceed
the gravity of the matter cloud
for a galaxy which
presently (t=t0) is at the distance
when DE antigravity starts to exceed
the gravity of the matter cloud
for a galaxy which
presently (t=t0) is at the distance
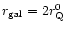 ,
well
within the DE dominated region. The
exact value of the
numerical factor is arbitrary,
but for the LG the number two corresponds to
,
well
within the DE dominated region. The
exact value of the
numerical factor is arbitrary,
but for the LG the number two corresponds to
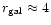 Mpc, i.e. intergroup distances.
E.g. for Sandage's point-mass model
thus defined critical scale factor is
Mpc, i.e. intergroup distances.
E.g. for Sandage's point-mass model
thus defined critical scale factor is
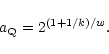 |
(7) |
With 1/k =0 this gives
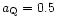 for w=-1 and
for w=-1 and
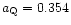 for w=-2/3,
while with k=1, w=-2/3 the critical epoch was earlier at
for w=-2/3,
while with k=1, w=-2/3 the critical epoch was earlier at
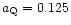 ,
and the galaxy spends a longer time in the DE dominated region.
Note that the local critical time
,
and the galaxy spends a longer time in the DE dominated region.
Note that the local critical time 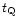 differs from the global
time when DE starts dominating over average matter.
differs from the global
time when DE starts dominating over average matter.
The effect of 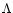 on the
evolution of primordial density fluctuations was studied by
Peebles (1980, 1984),
Lahav et al. (1991),
Carroll et al. (1992).
Matter perturbations in quintessence models are discussed by
Wang & Steinhardt (1998), Ma et al. (1999),
Sahni & Starobinsky (2000), and
Fabris & Goncalves (2000). It was shown that even
for
on the
evolution of primordial density fluctuations was studied by
Peebles (1980, 1984),
Lahav et al. (1991),
Carroll et al. (1992).
Matter perturbations in quintessence models are discussed by
Wang & Steinhardt (1998), Ma et al. (1999),
Sahni & Starobinsky (2000), and
Fabris & Goncalves (2000). It was shown that even
for
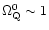 the DE has only a slight effect on the
total growth factor and the main effect
comes from
the DE has only a slight effect on the
total growth factor and the main effect
comes from
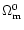 .
The small influence
derives from the short
time interval when DE dominates during
the late epoch of structure formation. These considerations
of the growth factor have led to the claim that the dark energy component
can not produce observable effects in the local dynamics.
.
The small influence
derives from the short
time interval when DE dominates during
the late epoch of structure formation. These considerations
of the growth factor have led to the claim that the dark energy component
can not produce observable effects in the local dynamics.
However, we emphasize that there are several reasons why the DE
component could have observable influence on the structure formation
dynamics. First, in different regions of the universe, DE
has dominated vastly different time intervals, depending on the
local matter density contrast.
Second, according to the exact dynamical equation (Eq. (2)),
on scales where
cosmological antigravity overcomes the gravity of local matter concentration,
the dynamics of a test galaxy does not depend on this local
mass concentration and hence undergoes adiabatic cooling.
Third, the existence of the growing mode itself essentially
depends on the equation of state of the background fluid.
Indeed, let us consider the linear growth of a density perturbation
on a homogeneous background
with the equation of state
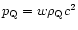 (constant w).
As is well-known
(Heath 1977; Peebles 1980;
Eisenstein 1997;
Peacock 1999) for the density
perturbation
(constant w).
As is well-known
(Heath 1977; Peebles 1980;
Eisenstein 1997;
Peacock 1999) for the density
perturbation
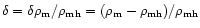 ,
where
,
where
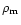 and
and
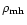 are the matter density and the
average (uniform) background matter density, there are two modes:
decaying, where
are the matter density and the
average (uniform) background matter density, there are two modes:
decaying, where
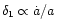 ,
and growing:
,
and growing:
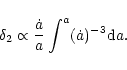 |
(8) |
For the flat FLRW model,
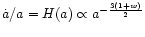 ,
and
,
and
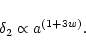 |
(9) |
Hence for DE (w < -1/3) the mode 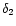 is decaying, too.
is decaying, too.
Therefore in the regions of the universe where dark energy dominates
new structures do not condense and linear perturbations of density and
peculiar velocities decay.
This effect was considered for
vacuum-dominated regions by Chernin et al. (2000)
using Zeldovich's (1965)
analysis of gravitational instability.
The zero-mass radius
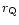 gives
the position of the border between the matter and
DE dominated regions. If a galaxy now beyond
gives
the position of the border between the matter and
DE dominated regions. If a galaxy now beyond
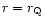 also
in the past was long enough
in the DE dominated region,
then the peculiar
velocities induced by local masses have
adiabatically cooled down (
also
in the past was long enough
in the DE dominated region,
then the peculiar
velocities induced by local masses have
adiabatically cooled down (
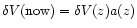 ).
Such DE dominated regions between mass
clouds are "pacific oceans'' where the linear
Hubble law appears and the global H0 may be
measured even locally.
).
Such DE dominated regions between mass
clouds are "pacific oceans'' where the linear
Hubble law appears and the global H0 may be
measured even locally.
Let us estimate the distance 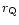 for the Local Group
in the case of the point-mass model and the cosmological vacuum
(w=-1 and
for the Local Group
in the case of the point-mass model and the cosmological vacuum
(w=-1 and
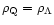 is
constant in time).
Van den Bergh (1999) gives
the mass of the LG as
is
constant in time).
Van den Bergh (1999) gives
the mass of the LG as
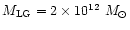 .
We adopt
this value but note that in recent data there is a tendency for
the LG mass to decrease (Evans et al. 2000;
Karachetsev & Makarov 2000).
.
We adopt
this value but note that in recent data there is a tendency for
the LG mass to decrease (Evans et al. 2000;
Karachetsev & Makarov 2000).
The vacuum density from SNIa observations is
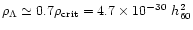 g/cm3.
Then the distance
g/cm3.
Then the distance
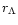 ,
where the vacuum starts to dominate,
is
,
where the vacuum starts to dominate,
is 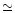 1.5 Mpc in the point-mass model.
If one changes
1.5 Mpc in the point-mass model.
If one changes
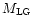 or
or
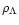 by a factor of two,
the zero-mass border shifts by 26 percent.
If one chooses the mass model with D=1and
by a factor of two,
the zero-mass border shifts by 26 percent.
If one chooses the mass model with D=1and
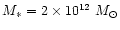 at r* =1 Mpc, Eq. (4)
yields
at r* =1 Mpc, Eq. (4)
yields
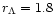 Mpc.
Mpc.
Thus
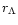 is robustly put into the range 1 to 2 Mpc.
This value is surprisingly close to the distance where the Hubble
law emerges, or 1.5 Mpc (Sandage 1986).
Is this just a coincidence? We think that this is
a key feature of the local matter flow. The dominance of
the dark energy at 1-2 Mpc and beyond means that it
provides the uniform background
for the Hubble flow of matter on such scales.
is robustly put into the range 1 to 2 Mpc.
This value is surprisingly close to the distance where the Hubble
law emerges, or 1.5 Mpc (Sandage 1986).
Is this just a coincidence? We think that this is
a key feature of the local matter flow. The dominance of
the dark energy at 1-2 Mpc and beyond means that it
provides the uniform background
for the Hubble flow of matter on such scales.
For predicting the distance where the growing
structure separates from the Hubble flow we use the
relation between peculiar velocity and density fluctuation
in the linear gravitational growth theory
with 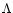 (Peebles 1984):
(Peebles 1984):
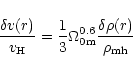 |
(10) |
where
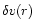 is the peculiar velocity,
is the peculiar velocity,
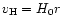 is the Hubble velocity,
is the Hubble velocity,
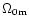 is the present matter density parameter.
An exact nonlinear spherical model of the velocity flow
within a power-law density field was recently studied by
Gromov et al. (2001) who confirmed the use of Eq. (10)
as a first approximation also for the
vacuum.
In the general case of DE the validity of this relation
should be studied separately, though the studies on the growth factor
(Wang & Steinhardt 1998; Ma et al. 1999) suggest that
it may be used for any w.
is the present matter density parameter.
An exact nonlinear spherical model of the velocity flow
within a power-law density field was recently studied by
Gromov et al. (2001) who confirmed the use of Eq. (10)
as a first approximation also for the
vacuum.
In the general case of DE the validity of this relation
should be studied separately, though the studies on the growth factor
(Wang & Steinhardt 1998; Ma et al. 1999) suggest that
it may be used for any w.
In our model of the LG the density fluctuation is
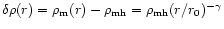 ,
with
,
with
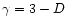 .
From the condition
.
From the condition
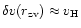 we get the zero-velocity distance
we get the zero-velocity distance
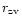 in terms of the LG mass
in terms of the LG mass
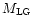 within 1 Mpc:
within 1 Mpc:
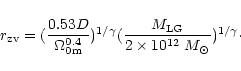 |
(11) |
For D=1 and
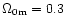 we get
we get
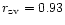 Mpc, and
for D=2,
Mpc, and
for D=2,
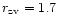 Mpc. Hence if the mass
of the LG is about
Mpc. Hence if the mass
of the LG is about
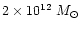 ,
in this case the
zero-mass distance
,
in this case the
zero-mass distance
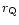 is close to the zero-velocity distance
is close to the zero-velocity distance
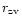 ,
and this allows us to see the Hubble flow within the local DE dominated
region.
,
and this allows us to see the Hubble flow within the local DE dominated
region.
As the short zero-velocity distance for the LG allows one to see
the DE dominated region, characterized by the cold linear Hubble
flow, one expects that the local value of the Hubble ratio is
not far from the global Hubble constant.
Indeed, observations confirm this on a few percent level
(Teerikorpi 1997; Ekholm et al. 1999;
Giovanelli et al. 1999; Freedman et al. 2001).
Even with the recently suspected significant
bias in extragalactic cepheid distances (Teerikorpi & Paturel 2001), this agreement
between the local and global rates of expansion remains.
Above we calculated the DE density from
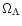 (from SNIa) and
assuming h=0.6. By the way,
if we had, independently of the Hubble constant,
some local measurement of the dominant uniform DE density, we could
test the consistency of the adopted cosmological model by predicting
the value of the Hubble constant via the relation
(from SNIa) and
assuming h=0.6. By the way,
if we had, independently of the Hubble constant,
some local measurement of the dominant uniform DE density, we could
test the consistency of the adopted cosmological model by predicting
the value of the Hubble constant via the relation
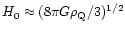 for the
for the
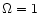 universe.
For example, if we roughly identify the distance
universe.
For example, if we roughly identify the distance
 where the Hubble law starts,
with the screening radius
where the Hubble law starts,
with the screening radius 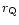 for our Local Group, then
we can calculate
for our Local Group, then
we can calculate
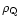 from Eq. (3) and
the expected value of H0 is
from Eq. (3) and
the expected value of H0 is
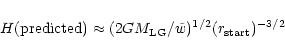 |
(12) |
where
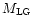 is the mass of the Local Group.
With the "standard'' values
is the mass of the Local Group.
With the "standard'' values
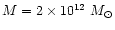 and
and
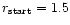 Mpc,
the Eq. (12) gives for H0 values from 53 km s-1/Mpc
(w=-1) to 74 km s-1/Mpc (w=-2/3), covering the values
obtained for H0 by different methods.
Mpc,
the Eq. (12) gives for H0 values from 53 km s-1/Mpc
(w=-1) to 74 km s-1/Mpc (w=-2/3), covering the values
obtained for H0 by different methods.
The peculiar velocities in the vicinity of
the Local Group are produced by all nearby mass inhomogeneities.
Because the distance 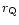 for the LG is less than the characteristic
distance between similar groups, one can consider the galaxies beyond
for the LG is less than the characteristic
distance between similar groups, one can consider the galaxies beyond
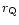 (but in the intergroup space) as adiabatically cooling free
particles.
(but in the intergroup space) as adiabatically cooling free
particles.
The possibility to solve the problem of low velocity dispersion
may be illustrated by the following simplified reasoning.
At any epoch a(t) and on the scale r one
may regard
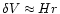 as an upper limit to the scatter around
the Hubble law.
In the non-linear clustering regime the velocity dispersion is about
Hr for a cluster with size r (Peebles 1980).
In the linear regime,
as an upper limit to the scatter around
the Hubble law.
In the non-linear clustering regime the velocity dispersion is about
Hr for a cluster with size r (Peebles 1980).
In the linear regime,
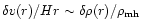 leads to
leads to
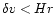 .
.
For models with zero curvature the Hubble constant
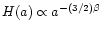 ,
where
,
where
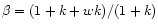 .
E.g. in the case of vacuum, i.e. w=-1 and 1/k=0 we have
.
E.g. in the case of vacuum, i.e. w=-1 and 1/k=0 we have
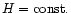 ,
and for dust matter k=0 hence
,
and for dust matter k=0 hence
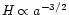 .
.
So the scatter
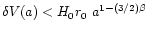 ,
where r0 is the considered scale at the
present epoch. E.g. for r0 = 5 Mpc and H0 = 60 km s-1/Mpc,
,
where r0 is the considered scale at the
present epoch. E.g. for r0 = 5 Mpc and H0 = 60 km s-1/Mpc,
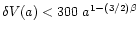 km s-1. This is also valid at the
critical epoch
km s-1. This is also valid at the
critical epoch 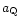 after which the peculiar velocities within
a DE dominated region start to cool down adiabatically,
so that
after which the peculiar velocities within
a DE dominated region start to cool down adiabatically,
so that
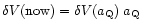 .
Hence one expects now
.
Hence one expects now
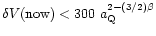 km s-1.
More conservatively, we also calculate a (larger) upper limit for
km s-1.
More conservatively, we also calculate a (larger) upper limit for
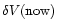 from the relation for dust (
from the relation for dust (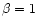 ), noting that
actually the dark energy does not fully dominate all the way from
), noting that
actually the dark energy does not fully dominate all the way from
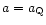 to a=1.
to a=1.
For examples we use
the epoch 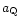 from Sect. 3.3.
In the case of the cosmological constant,
from Sect. 3.3.
In the case of the cosmological constant,
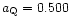 ,
hence
,
hence
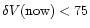 -212 km s-1.
For the DE with w = -2/3,
-212 km s-1.
For the DE with w = -2/3,
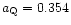 and
and
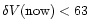 -178 km s-1, and
for the coherent evolution
w = -2/3, k=1,
the critical
-178 km s-1, and
for the coherent evolution
w = -2/3, k=1,
the critical
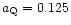 and one
expects
and one
expects
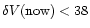 -106 km s-1.
-106 km s-1.
The numbers used above are not a unique choice,
but they well illustrate the expected cooling of the velocity dispersion
in different DE models. A complete
treatment of the dispersion problem needs high-resolution large-volume
simulations of structure formation on the evolving DE background, taking
into account the cooling processes in the
dark energy dominated regions.
Cosmological dark energy is now recognized as an important constituent
of the universe (see reviews by Bahcall et al. 1999;
Sahni & Starobinsky 2000; Chernin 2001).
It gives a new possibility to resolve
the old puzzle of the linear Hubble law existing within
the highly nonuniform local galaxy universe.
The antigravity and homogeneity of the cosmological DE
may explain the quiet Hubble flow close
to the Local Group.
In dark energy dominated regions of the universe ("pacific oceans'')
the Hubble law exists
due to the uniformity of the DE component, with the Hubble constant
determined by the dark energy density. The coldness of the local Hubble flow
follows from the fact that a galaxy, spending a sufficient time
in the DE dominated region where linear perturbations
decay as
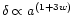 ,
looses its
peculiar velocity via adiabatic cooling.
Hence the mysterious quietness of the local Hubble flow does not
look dramatic in the context of the DE driven expansion.
The most effective decrease of velocity dispersion is found
for stationary coupled quintessence (Amendola & Tocchini-Valentini
2000; Baryshev et al. 2000) where the DE density
changes coherently with
the matter density in the late cosmic epoch.
,
looses its
peculiar velocity via adiabatic cooling.
Hence the mysterious quietness of the local Hubble flow does not
look dramatic in the context of the DE driven expansion.
The most effective decrease of velocity dispersion is found
for stationary coupled quintessence (Amendola & Tocchini-Valentini
2000; Baryshev et al. 2000) where the DE density
changes coherently with
the matter density in the late cosmic epoch.
High-resolution N-body simulations for QCDM models could
in principle restrict the evolution of dark energy in
late cosmological epochs, from an analysis of the velocity
scatter around "LG'' candidates. The existing N-body
results for 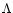 CDM models (Jenkins et al. 1998)
give similar velocity dispersions as OCDM models
(Governato et al. 1997), much higher than observed
around the Local Group.
In comparison, analytical results, based on the exact dynamical equation
(Eq. (2))
which is the (1, 1) component of Einstein's equations, show
that there is a zero-mass surface for any spherical matter concentration,
beyond which the dark energy dominates.
In such regions velocity dispersion is adiabatically cooling down.
This underlines the question how to take into account the analytical
results in N-body simulation
methods.
CDM models (Jenkins et al. 1998)
give similar velocity dispersions as OCDM models
(Governato et al. 1997), much higher than observed
around the Local Group.
In comparison, analytical results, based on the exact dynamical equation
(Eq. (2))
which is the (1, 1) component of Einstein's equations, show
that there is a zero-mass surface for any spherical matter concentration,
beyond which the dark energy dominates.
In such regions velocity dispersion is adiabatically cooling down.
This underlines the question how to take into account the analytical
results in N-body simulation
methods.
We conclude that even the closeby universe is now seen as a cosmic
laboratory where all physical ingredients:
luminous matter, dark matter, and dark energy, may be
detected.
Cosmology starts immediately
beyond the border of the Local Group.
In other environments the DE dominance starts at
smaller or larger distances. So, around the Coma
cluster the critical distance is 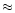 20 Mpc.
For a cosmologist in Coma, cosmology begins around such a distance.
20 Mpc.
For a cosmologist in Coma, cosmology begins around such a distance.
Acknowledgements
We are grateful to Chris Flynn for helpful comments and to
the referees L. Amendola and F. Governato for useful criticism and
suggestions.
Yu. B. and P. T. remember with pleasure the hospitality by Georges Paturel,
when they attended the informal Lyon meeting on cosmology in April 2000.
During this visit Yu. B. and P. T. performed the part of this work
concerning the coherently
behaving matter and dark energy.
This study has been supported by The Academy of Finland (projects
"Cosmology from the local to the deep galaxy universe'' and
"Galaxy streams and dark matter structures'').
-
Amendola, L. 1999 [astro-ph/9908023]
In the text
-
Amendola, L., & Tocchini-Valentini, D. 2000 [astro-ph/0011243]
In the text
-
Bahcall, N. A., Lubin, L. M., & Dorman, V. 1995, ApJ, 447, L81
In the text
NASA ADS
-
Bahcall, N., Ostriker, J., Perlmutter, S., & Steinhardt, P. 1999,
Science, 284, 1481
In the text
NASA ADS
-
Baryshev, Yu. 1981, Izvestiya SAO, 14, 24
In the text
-
Baryshev, Yu., Gromov, A., & Teerikorpi, P. 2001, in prep.
In the text
-
Baryshev, Yu., Sylos Labini, F., Montuori, M., Pietronero, L., & Teerikorpi, P. 1998,
Fractals, 6, 231
In the text
-
Baryshev, Yu., Chernin, A., & Teerikorpi, P. 2000 [astro-ph/0011528]
In the text
-
Carroll, S., Press, W., & Turner, E. 1992, ARA&A, 30, 499
In the text
NASA ADS
-
Chernin, A. 2001, Physics-Uspekhi, 44, in press
In the text
-
Chernin, A., Teerikorpi, P., & Baryshev, Yu. 2000, Adv. Space Res., in press
[astro-ph/0012021]
In the text
-
Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465
NASA ADS
-
de Bernardis, P., Ade, P. A. R., Bock, J. J., et al. 2000, Nature, 404, 955
In the text
NASA ADS
-
de Vaucouleurs, G. 1971, Science, 167, 1203
In the text
-
Eisenstein, D. 1997 [astro-ph/9709054]
In the text
-
Ekholm, T., Baryshev, Yu., Teerikorpi, P., Hanski, M., & Paturel, G. 2001,
A&A, 368, L17
In the text
NASA ADS
-
Ekholm, T., Lanoix, P., Teerikorpi, P., Paturel, G., & Fouqué, P. 1999,
A&A, 351, 827
In the text
NASA ADS
-
Evans, N., Wilkinson, M., Guhathakurta, P., Grebel, E., & Vogt, S.
2000, ApJ, 540, L9
In the text
NASA ADS
-
Fabris, J. C., & Goncalves, S. V. B. 2000 [gr-gc/0010046]
In the text
-
Freedman, W. L., Madore, B., Gibson, B. K., et al. 2001, ApJ, 553, 47
In the text
NASA ADS
-
Giovanelli, R., Dale, D., Haynes, M., Hardy, E., & Campusano, L. 1999,
ApJ, 525, 25
In the text
NASA ADS
-
Governato, F., Moore, B., Cen, R., et al. 1997, New Astr., 2, 91
In the text
NASA ADS
-
Gromov, A., Baryshev, Yu., Suson, D., & Teerikorpi, P. 2001,
Grav. & Cosm., 7, No. 2(26), 140
In the text
-
Heath, D. 1977, MNRAS, 179, 351
In the text
NASA ADS
-
Jaffe, A. H., Ade, P. A. R., Balbi, A., et al. 2000, Phys. Rev. Lett. 86, 3475
In the text
-
Jenkins, A., Frenk, C., Pearce, F., et al. 1998, ApJ, 499, 20
In the text
NASA ADS
-
Karachentsev, I. 1996, A&A, 305, 33
In the text
NASA ADS
-
Karachentsev, I., & Makarov, D. 2000, Preprint 151, Russian Academy of Science
In the text
-
Klypin, A., Einasto, L., Einasto, M., & Saar, E. 1989, MNRAS, 237, 929
In the text
NASA ADS
-
Lahav, O., Lilje, P., Primack, J., & Rees, M. 1991, MNRAS, 251, 126
In the text
-
Ma, C., Caldwell, R., Bode, P., & Wang, L. 1999, ApJ, 521, L1
In the text
NASA ADS
-
Peacock, J. A. 1999, Cosmological Physics (Cambridge: Cambridge
Univ. Press), 468
In the text
-
Peebles, P. J. E. 1980, The Large-Scale Structure of the Universe
(Princeton: Princeton Univ. Press)
In the text
-
Peebles, P. J. E. 1984, ApJ, 284, 439
In the text
NASA ADS
-
Peebles, P. J. E. 1993 Principles of Cosmology (Princeton: Princeton
Univ. Press)
In the text
-
Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565
In the text
NASA ADS
-
Podariu, S., & Ratra, B. 2000, ApJ, 532, L109
In the text
NASA ADS
-
Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009
In the text
NASA ADS
-
Robertson, H. P. 1955, PASP, 67, 82
In the text
NASA ADS
-
Sahni, V., & Starobinsky, A. 2000, Int. J. Mod. Phys. D9, 373
In the text
-
Sandage, A. 1986, ApJ, 307, 1
In the text
NASA ADS
-
Sandage, A. 1999, ApJ, 527, 479
In the text
NASA ADS
-
Sandage, A., Tammann, G., & Hardy, E. 1972, ApJ, 172, 253
In the text
NASA ADS
-
Sylos Labini, F., Montuori, M., & Pietronero, L. 1998,
Phys. Rep., 293, 61
In the text
NASA ADS
-
Teerikorpi, P. 1997, ARA&A, 35, 101
In the text
NASA ADS
-
Teerikorpi, P., Hanski, M., Theureau, G., et al.
1998, A&A, 334, 395
In the text
NASA ADS
-
Teerikorpi, P., & Paturel, G. 2001, A&A, submitted
In the text
-
Tikhonov, A., Makarov, D., & Kopylov, A. 2000,
Bull. Special Astrophys. Obs., 50, 39
In the text
-
van den Bergh, S. 1999, A&A Rev., 9, 273
In the text
-
Wang, L., Caldwell, R. R., Ostriker, J. P., & Steinhardt, P. J. 2000,
ApJ, 530, 17
In the text
NASA ADS
-
Wang, L., & Steinhardt, P. J. 1998, ApJ, 508, 483
In the text
NASA ADS
-
Weinberg, S. 1977, The First Three Minutes (Basic Books, New York), 26
In the text
-
Wetterich, C. 1995, A&A, 301, 321
In the text
NASA ADS
-
Wu, K. K. S., Lahav, O., & Rees, M. J. 1999, Nature, 397, 225
In the text
-
Zeldovich, Ya. B. 1965, Advan. Astron. Ap., 3, 241
In the text
Copyright ESO 2001