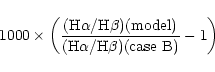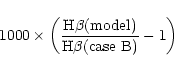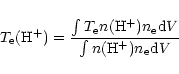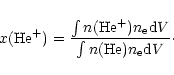A&A 378, 817-825 (2001)
DOI: 10.1051/0004-6361:20011303
Collisional excitation of hydrogen and the determination
of
the primordial helium abundance from H II regions
G. Stasinska 1 - Y. Izotov 2
1 - DAEC, Observatoire de Paris-Meudon, 92195 Meudon Cedex,
France
2 - Main Astronomical Observatory,
Ukrainian National Academy of Sciences, Kyiv 03680, Ukraine
Received 11 July 2001 / Accepted 10 September 2001
Abstract
This paper investigates the effect of
collisional enhancement of the hydrogen lines on the
derivation of the helium abundances in low metallicity H II regions.
For this, we have constructed a grid of photoionization models relevant
for the analysis of giant H II regions in blue compact galaxies.
We show that the effect of collisional excitation on the H /H
/H ratio
can be quite important (up to
8% or more). The impact of this effect on the determination of
the helium mass fraction has been tracked on four
low-metallicity blue compact galaxies for which Keck spectra
are available and which are among the best objects for the
quest for the pregalactic helium abundance.
We find that taking into account the effects of collisional excitation of hydrogen
results in an upward correction of the helium mass fraction Y by
up to 5%.
However, combined with other systematic effects usually not considered in the
determination of the helium abundance in low-metallicity
galaxies,
the resulting uncertainty should be much less.
ratio
can be quite important (up to
8% or more). The impact of this effect on the determination of
the helium mass fraction has been tracked on four
low-metallicity blue compact galaxies for which Keck spectra
are available and which are among the best objects for the
quest for the pregalactic helium abundance.
We find that taking into account the effects of collisional excitation of hydrogen
results in an upward correction of the helium mass fraction Y by
up to 5%.
However, combined with other systematic effects usually not considered in the
determination of the helium abundance in low-metallicity
galaxies,
the resulting uncertainty should be much less.
Key words:
galaxies: abundances -
galaxies: ISM -
galaxies: starburst - ISM: H II regions
Tests of the big bang models and the determination of cosmological
parameters require an accurate determination of the relative abundances
of the light isotopes produced during the big bang (Steigman et al. 1977;
Walker et al. 1991; Sarkar 1996).
The abundance of primordial 4He is mostly derived from the
helium abundances in metal-poor extragalactic
H II regions (Kunth & Sargent 1983; Pagel et al. 1992; Izotov & Thuan
1998) although other nebulae such as
H II regions in the Magellanic Clouds (Peimbert et al. 2000) or
planetary nebulae in the Galactic halo (Peimbert 1983, 1989, Clegg 1989)
have also occasionally been used. This is a challenging task, since
the required accuracy is on the one percent level.
In order to achieve such a goal, excellent quality observations are
obviously required together with an extremely reliable reduction
procedure. With the advent of very large telescopes and the progress
in detectors, recent years have produced a large amount of data
suitable for such an enterprise (Izotov et al. 1997; Izotov
& Thuan 1998; Izotov et al. 1999). As regards the
interpretation of the observed line intensities in terms of abundance
ratios, many problems occur and still remain to be overcome. For
example, the atomic data relevant for the helium line emissivities
have only recently reached a state compatible with the demand (Benjamin
et al. 1999). Among the problems to be solved for the determination of
the helium abundance in one nebula, and towards which various groups of
researchers have had different approaches, are: the stellar absorption
lines underlying the nebular emission lines, the reddening correction,
the distribution of the electron temperature inside the nebulae, the
density structure and its effect on the line emissivities, the optical
depth in the lines, the ionization correction to derive
the He/H ratio from the measured He+/H+ ratio. The next step is to
derive the pregalactic helium abundance from the measurement of the
helium abundance in a sample of galaxies, by extrapolating the
results towards zero metallicity. These problems have been
extensively discussed in a long list of papers including
Peimbert & Torres-Peimbert (1974, 1976), Stasinska (1980), Rayo et al. (1982),
Kunth & Sargent
(1983), Davidson & Kinman (1985), Dinerstein & Shields (1986), Pagel
et al.
(1986, 1992), Campbell (1992), Skillman & Kennicutt (1993), Balbes et al.
(1993), Mathews et al. (1993), Olive & Steigman (1995), Sasselov &
Goldwirth (1995), Olive et al. (1997), Steigman et al. (1997), Izotov &
Thuan (1998), Izotov et al. (1997, 1999), Armour et al. (1999),
Ballantyne et al. (2000), Viegas et al. (2000), Peimbert et al. (2000, 2001),
Olive & Skillman (2001), Sauer & Jedamzik (2001).
The present-day situation is that different groups reach different
estimates of the pregalactic helium abundance, mutually exclusive
within the quoted error bars. For example, Olive et al. (1997) give
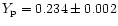 ,
while Izotov & Thuan (1998) give
,
while Izotov & Thuan (1998) give
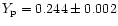 .
These two estimates lead to
very different cosmological implications, as discussed by Izotov et al.
(1999).
.
These two estimates lead to
very different cosmological implications, as discussed by Izotov et al.
(1999).
The effect on the pregalactic helium abundance determination arising
from deviation from case B theory for the hydrogen lines has been
relatively little discussed so far. The effect of finite optical depth
and dust on H emissivity have been discussed by Cota & Ferland
(1988) and Hummer & Storey (1992).
The effect of collisional excitation of the hydrogen lines by
thermal electrons has been pointed out by Davidson & Kinman (1985)
and discussed for the case of I Zw 18 by Sasselov & Goldwirth (1995)
and Stasinska & Schaerer (1999). Stasinska (2001)
has shown that this
effect can lead to an underestimation of the He I 5876/H
emissivity have been discussed by Cota & Ferland
(1988) and Hummer & Storey (1992).
The effect of collisional excitation of the hydrogen lines by
thermal electrons has been pointed out by Davidson & Kinman (1985)
and discussed for the case of I Zw 18 by Sasselov & Goldwirth (1995)
and Stasinska & Schaerer (1999). Stasinska (2001)
has shown that this
effect can lead to an underestimation of the He I 5876/H ratio
by as much as 10% in hot planetary nebulae, independent of the actual reddening of the
object.
ratio
by as much as 10% in hot planetary nebulae, independent of the actual reddening of the
object.
The purpose of the present paper is to systematically explore the
effects of collisional excitation of the hydrogen lines on the helium
abundance determinations in metal-poor giant H II regions. For this,
we use a grid of photoionization models of giant H II regions and
consider them in the light of
the spectral properties of a sample of blue compact H II galaxies.
This allows us to obtain a realistic estimate of
the effect of collisional excitation by thermal
electrons both on H and on H
and on H .
We then concentrate on a selection of
blue compact galaxies with particularly good quality spectroscopic
data, and track the effect of collisional excitation - at the level
predicted by the models - on the derived helium abundance for these
objects.
.
We then concentrate on a selection of
blue compact galaxies with particularly good quality spectroscopic
data, and track the effect of collisional excitation - at the level
predicted by the models - on the derived helium abundance for these
objects.
The photoionization models of giant H II regions are constructed
using the procedure described in Stasinska et al. (2001, hereinafter SSL2001)
to which we refer for details.
Briefly, we consider coeval stellar clusters of given initial
mass 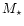 that ionize the surrounding gas, supposed to be of
same chemical composition as the stars. We assume
instantaneous bursts with a Salpeter
initial mass function and an upper stellar limit
that ionize the surrounding gas, supposed to be of
same chemical composition as the stars. We assume
instantaneous bursts with a Salpeter
initial mass function and an upper stellar limit
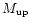 = 120
= 120 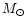 .
The radiation field is provided by the evolutionary synthesis
models of Schaerer & Vacca (1998)
based on the non-rotating Geneva stellar evolution models, with the
high mass-loss tracks of Meynet et al. (1994). The spectral energy
distributions for massive main-sequence stars are those given by the
CoStar models (Schaerer & de Koter 1997). The pure
He models of Schmutz et al. (1992) are used for Wolf-Rayet stars.
The ionization and temperature structure of the nebula is computed
with the photoionization code
PHOTO, as described in Stasinska & Leitherer (1996, hereinafter
SL96). We assume that the nebulae are spherical and radiation-bounded,
with uniform density n =10 cm-3 and filling factor
.
The radiation field is provided by the evolutionary synthesis
models of Schaerer & Vacca (1998)
based on the non-rotating Geneva stellar evolution models, with the
high mass-loss tracks of Meynet et al. (1994). The spectral energy
distributions for massive main-sequence stars are those given by the
CoStar models (Schaerer & de Koter 1997). The pure
He models of Schmutz et al. (1992) are used for Wolf-Rayet stars.
The ionization and temperature structure of the nebula is computed
with the photoionization code
PHOTO, as described in Stasinska & Leitherer (1996, hereinafter
SL96). We assume that the nebulae are spherical and radiation-bounded,
with uniform density n =10 cm-3 and filling factor
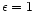 and that all the stars are located at the center.
As in our previous papers (SL96 and SSL2001) and in all the papers
based on static photoionization models, our models
do not consider the possible pollution of the nebulae
by stellar ejecta during the course of the evolution of the star clusters.
While this phenomenon may have important consequences,
it is not really relevant to the problem under study here.
and that all the stars are located at the center.
As in our previous papers (SL96 and SSL2001) and in all the papers
based on static photoionization models, our models
do not consider the possible pollution of the nebulae
by stellar ejecta during the course of the evolution of the star clusters.
While this phenomenon may have important consequences,
it is not really relevant to the problem under study here.
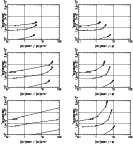 |
Figure 1:
Sequences of photoionization models for
instantaneous bursts of various metallicities.
The metallicity is indicated by the following symbols: circle for Z/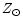 =
0.02, square for Z/
=
0.02, square for Z/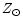 = 0.05, triangle for Z/
= 0.05, triangle for Z/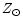 = 0.2.
The symbols mark time
steps of 1 Myr.
The models shown in the top panels have
= 0.2.
The symbols mark time
steps of 1 Myr.
The models shown in the top panels have 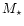 = 103 = 103 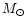 ,
those in the middle panels have ,
those in the middle panels have 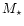 = 106 = 106 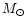 ,
those in the bottom panels have ,
those in the bottom panels have 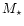 = 109 = 109 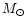 (see text).
The ordinate represents the temperature indicated by the [O III]
(see text).
The ordinate represents the temperature indicated by the [O III] 4363/[O III] 4363/[O III] 5007 line ratio.
In the left panels it is shown as a function of [O III] 5007 line ratio.
In the left panels it is shown as a function of [O III] 5007/[O II] 5007/[O II] 3727,
in the right panels as a function of [O III] 3727,
in the right panels as a function of [O III] 5007/H 5007/H . . |
| Open with DEXTER |
The grid used in the present study is composed of models with
metallicities Z of 0.2, 0.05 and 0.02 times the solar metallicity
(using the prescription of McGaugh (1991) for the relative abundances
of the elements).
As is known (e.g. Shields 1986) the emission line spectrum of photoionized nebulae
is essentially dependent on the spectral energy distribution
of the ionizing radiation field, on the metallicity and on the
ionization parameter U. For a constant density sphere Uis equal to
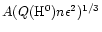 ,
where
,
where
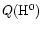 is the total number
of H Lyman continuum photons emitted by the ionizing source
(proportional to the mass of the star cluster) and
A is approximately given by
is the total number
of H Lyman continuum photons emitted by the ionizing source
(proportional to the mass of the star cluster) and
A is approximately given by
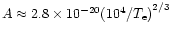 ,
where
,
where 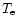 is the electron temperature.
At a given chemical composition, any combination of
is the electron temperature.
At a given chemical composition, any combination of
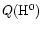 ,
n and
,
n and 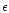 giving the same value of U will
result in the same emission line spectrum (at least when the
densities are sufficiently
low that cooling is not affected by collisional deexcitation of forbidden lines,
which is the case of the objects under study in this paper).
Three
different initial masses for the star
clusters are considered:
giving the same value of U will
result in the same emission line spectrum (at least when the
densities are sufficiently
low that cooling is not affected by collisional deexcitation of forbidden lines,
which is the case of the objects under study in this paper).
Three
different initial masses for the star
clusters are considered:
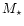 =103, 106,
and 109
=103, 106,
and 109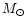 (assuming a lower IMF mass cut-off of
(assuming a lower IMF mass cut-off of
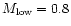
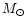 ). With such a grid, we reasonably cover the range
of metallicities and ionization parameters relevant to the objects we are interested in.
). With such a grid, we reasonably cover the range
of metallicities and ionization parameters relevant to the objects we are interested in.
For each model, we derive the electron temperature
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) from the computed [O III]
from the computed [O III] 4363/ [O III]
4363/ [O III] 5007 ratio
5007 ratio![[*]](/icons/foot_motif.gif) ,
using the same atomic data as in the photoionization code.
Figure 1 presents the sequences of models in the
,
using the same atomic data as in the photoionization code.
Figure 1 presents the sequences of models in the
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) versus
[O III]
versus
[O III] 5007/[O II]
5007/[O II] 3727 plane (left) and in the
3727 plane (left) and in the
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) versus
[O III]
versus
[O III] 5007/H
5007/H plane (right). The top panels correspond to a total initial
stellar mass of
plane (right). The top panels correspond to a total initial
stellar mass of 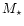 =103
=103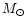 ,
the middle ones to
,
the middle ones to 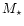 =106
=106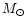 and the bottom ones to
and the bottom ones to 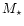 =109
=109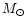 .
Symbols mark the epoch by time
steps of 106 yr,
starting from an age of 104 yr. Series with Z= 0.02
.
Symbols mark the epoch by time
steps of 106 yr,
starting from an age of 104 yr. Series with Z= 0.02 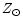 are represented by circles, series with Z= 0.05
are represented by circles, series with Z= 0.05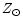 by squares, and series with Z= 0.2
by squares, and series with Z= 0.2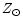 by triangles. The time evolution is from the right to the left in
these plots, since the ionization parameter decreases due
to gradual disappearance of the most massive stars. This provokes a
softening of the
ionizing radiation field, which induces a decrease in the electron temperature.
As expected,
the highest temperatures are found in the models with lowest metallicities
(cooling by collisional excitation of forbidden lines becomes less important)
and highest ionization parameters
(cooling by collisional excitation of H Lyman
by triangles. The time evolution is from the right to the left in
these plots, since the ionization parameter decreases due
to gradual disappearance of the most massive stars. This provokes a
softening of the
ionizing radiation field, which induces a decrease in the electron temperature.
As expected,
the highest temperatures are found in the models with lowest metallicities
(cooling by collisional excitation of forbidden lines becomes less important)
and highest ionization parameters
(cooling by collisional excitation of H Lyman  becomes less important).
becomes less important).
In the next section, we discuss the relevance of this grid of models
for the problem we are investigating in the present paper.
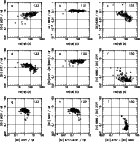 |
Figure 2:
Our
observational sample in various diagrams relating emission line
ratios and H equivalent width.
On the upper right of each panel is given the total number of the objects
appearing in the diagram.
The behaviour of the present sample in these diagrams
is very similar to the behaviour of the smaller sample shown by Stasinska et al. (2001)
in their Fig. 2.
equivalent width.
On the upper right of each panel is given the total number of the objects
appearing in the diagram.
The behaviour of the present sample in these diagrams
is very similar to the behaviour of the smaller sample shown by Stasinska et al. (2001)
in their Fig. 2. |
| Open with DEXTER |
Since ab initio models of nebulae photoionized by evolving starbursts
do not necessarily well
represent the observed properties of giant H II regions
(see discussion in SSL2001), we have to use them in
the light of observed properties of H II galaxies. For this, we consider
a sample
of blue compact galaxies observed since 1994 by Izotov and coworkers.
In addition to the 69 objects considered in the study
by SSL2001, it contains 64 new objects observed with
different telescopes, including Keck, VLT, MMT, 4 m and 2.1 m KPNO
(Izotov et al. 2001a,b; Guseva et al. 2001; Papaderos et al. 2001). The new
observations were reduced in the same way as those considered by SSL2001. In
all cases, the line intensities have been corrected for reddening by
using a procedure described in Izotov et al. (1994) in which the
reddening constant and stellar absorption in the Balmer lines are
determined simultaneously.
Figure 2 shows the same observational diagrams as Fig. 2 of
SSL2001 for the new sample of 133 objects.
Exactly the same trends are seen (with a slightly higher dispersion
due to the fact that some of the new data are of lower quality than
those of the sample considered by SSL2001). Therefore, we are dealing with
the same population of objects. Hence the conclusions of SSL2001
still apply: the sample is mostly composed of objects whose
ionization is produced by a starburst of age younger than about 5 Myr.
In the following, we will then restrict our considerations to models corresponding to
such ages.
Figure 3 shows the observed sample in the
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) versus
[O III]
versus
[O III] 5007/[O II]
5007/[O II] 3727 plane (left) and in the
3727 plane (left) and in the
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) versus
[O III]
versus
[O III] 5007/H
5007/H plane (right). By comparing with Fig. 1, we see that while the models with the highest
plane (right). By comparing with Fig. 1, we see that while the models with the highest
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) well reproduce
the [O III]
well reproduce
the [O III] 5007/H
5007/H ratios, they have
[O III]
ratios, they have
[O III] 5007/[O II]
5007/[O II] 3727 ratios much larger than observed in objects of similar values of
3727 ratios much larger than observed in objects of similar values of
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) .
For the range of observed values of [O III]
.
For the range of observed values of [O III] 5007/[O II]
5007/[O II] 3727, it is
impossible to obtain models with
3727, it is
impossible to obtain models with
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) around 20000 K.
One possible way to increase
the [O II] line intensity is to consider composite models, in which
part of the emission comes from higher density filaments. However,
it was impossible to find a prescription for the
composite models to
reproduce at the same time [O III]
around 20000 K.
One possible way to increase
the [O II] line intensity is to consider composite models, in which
part of the emission comes from higher density filaments. However,
it was impossible to find a prescription for the
composite models to
reproduce at the same time [O III] 4363/[O III]
4363/[O III] 5007, [O III]
5007, [O III] 5007/[O II]
5007/[O II] 3727 and the
electron density sensitive ratio [S II]
3727 and the
electron density sensitive ratio [S II] 6731/6717. The conclusion is that simple
photoionization models are unable to reproduce the high
[O III]
6731/6717. The conclusion is that simple
photoionization models are unable to reproduce the high
[O III] 4363/[O III]
4363/[O III] 5007 ratios that are observed in quite a number of giant H II
regions. A similar conclusion has been reached from
tailored model fitting of various giant H II regions (Campbell 1988;
Stasinska & Schaerer 1999; Luridiana
et al. 1999; Luridiana & Peimbert 2001). Reducing the abundances of
coolants such as carbon or silicon (on which there are virtually no
observational constrains) is insufficient to solve the problem. It
seems that an additional heating mechanism is at work, and a popular
candidate is shock heating. Whatever may be the origin of the
additional heating, this means that simple photoionization models
returning a [O III]
5007 ratios that are observed in quite a number of giant H II
regions. A similar conclusion has been reached from
tailored model fitting of various giant H II regions (Campbell 1988;
Stasinska & Schaerer 1999; Luridiana
et al. 1999; Luridiana & Peimbert 2001). Reducing the abundances of
coolants such as carbon or silicon (on which there are virtually no
observational constrains) is insufficient to solve the problem. It
seems that an additional heating mechanism is at work, and a popular
candidate is shock heating. Whatever may be the origin of the
additional heating, this means that simple photoionization models
returning a [O III] 5007/[O II]
5007/[O II] 3727 in the observed range are likely to have too low
an electron temperature, and that those returning a [O III]
3727 in the observed range are likely to have too low
an electron temperature, and that those returning a [O III] 4363/[O III]
4363/[O III] 5007 comparable with observations have too high a degree of ionization.
This means that the amount of collisional excitation they predict for
the hydrogen lines is likely a lower limit, since the contribution of
collisional
excitation increases with electron temperature and with the
proportion of residual neutral hydrogen.
5007 comparable with observations have too high a degree of ionization.
This means that the amount of collisional excitation they predict for
the hydrogen lines is likely a lower limit, since the contribution of
collisional
excitation increases with electron temperature and with the
proportion of residual neutral hydrogen.
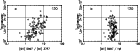 |
Figure 3:
Our
observational sample in the same planes as the models shown in Fig. 1. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{ms1650f4.eps}
\end{figure}](/articles/aa/full/2001/42/aa1650/Timg27.gif) |
Figure 4:
The same models as in Fig. 1 shown in the
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) versus [O III]
versus [O III] 5007/H 5007/H plane, but only for starburst ages up to 5 Myr.
As in Fig. 1, the models shown in the top panels have
plane, but only for starburst ages up to 5 Myr.
As in Fig. 1, the models shown in the top panels have
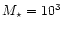 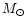 ,
those in the middle panels have ,
those in the middle panels have
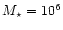 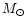 ,
those in the bottom panels have ,
those in the bottom panels have
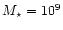 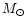 .
The numbers indicate, in units of 1 per 1000, the values of deviation from case B theory
for H .
The numbers indicate, in units of 1 per 1000, the values of deviation from case B theory
for H /H /H (left panels) and H
(left panels) and H (right panels).
See text for a more detailed explanation.
(right panels).
See text for a more detailed explanation. |
| Open with DEXTER |
In Fig. 4, we display the same sequences of models as in Fig. 1,
but up to ages of 5 Myr, in the
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) versus
[O III]
versus
[O III] 5007/H
5007/H plane. Again, the top panels correspond to a total initial
stellar mass of
plane. Again, the top panels correspond to a total initial
stellar mass of
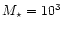
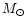 ,
the middle ones to
,
the middle ones to
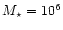
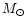 and the bottom ones to
and the bottom ones to
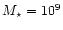
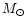 .
The collisional contribution
to the Balmer line emission is indicated in the following way. In the
left panels, next to the models are indicated the values of:
.
The collisional contribution
to the Balmer line emission is indicated in the following way. In the
left panels, next to the models are indicated the values of:
where the case B value of H /H
/H is computed for the temperature
is computed for the temperature
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) deduced from the [O III]
deduced from the [O III] 4363/[O III]
4363/[O III] 5007 ratio predicted by the model.
5007 ratio predicted by the model.
It is seen that in our models the H /H
/H ratios may be larger
than the case B value (at the temperature
ratios may be larger
than the case B value (at the temperature
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) )
by up to 8%. This
means that the reddening computed assuming the case B value of
the H
)
by up to 8%. This
means that the reddening computed assuming the case B value of
the H /H
/H ratios may be significantly overestimated.
ratios may be significantly overestimated.
In the right panels, next to the models, we indicate
(in units of 1 per 1000) the collisional
contribution to the emission in the H line:
line:
where H (case B) stands for the integrated emission of
the model in the H
(case B) stands for the integrated emission of
the model in the H line at the local electron temperature.
line at the local electron temperature.
Clearly, the collisional contribution to H in our models may reach 2%.
in our models may reach 2%.
The computations in PHOTO have been made with the collisional
excitation rate coefficients from Aggarwal (1983) for the n = 3level of hydrogen, and from Drake & Ulrich (1980) for higher levels.
Values given by other authors can be significantly different. For
example Aggarwal et al. (1991) give values that are larger than the ones from
Drake & Ulrich by up to a factor 2. Unfortunately, there is so far no
agreement on what are the most
reliable values of the collision strengths for hydrogen (Callaway 1994).
Note that there is no simple relation between the total H and H
and H emission
in our models, although at each point in the nebula the relation
between the H
emission
in our models, although at each point in the nebula the relation
between the H and H
and H emissivities is a function of the local
temperature only. The reason is that the electron temperature in our models
is not uniform, and the relation between local H
emissivities is a function of the local
temperature only. The reason is that the electron temperature in our models
is not uniform, and the relation between local H and H
and H emissivities do not propagate in a simple way into integrated line
ratios. It is for a similar reason that a temperature correction factor
tcf has been introduced by Sauer & Jedamzik (2001) to derive the helium
abundance from the ratios of helium to hydrogen line intensities.
emissivities do not propagate in a simple way into integrated line
ratios. It is for a similar reason that a temperature correction factor
tcf has been introduced by Sauer & Jedamzik (2001) to derive the helium
abundance from the ratios of helium to hydrogen line intensities.
In real nebulae, where the temperature structure is
much more erratic than in simple photoionization models,
the situation is probably even more complicated.
One might be tempted to use the ratio of H Lyman  to
H
to
H to better constrain the amount of collisional
excitation of hydrogen lines in real nebulae. However,
this proves difficult, because
the path of H Lyman
to better constrain the amount of collisional
excitation of hydrogen lines in real nebulae. However,
this proves difficult, because
the path of H Lyman  photons is strongly increased by scattering in
the ionized as well as in the neutral part of the nebula, during which absorption
by dust and molecular hydrogen occur. Therefore, the observed intensity of
H Lyman
photons is strongly increased by scattering in
the ionized as well as in the neutral part of the nebula, during which absorption
by dust and molecular hydrogen occur. Therefore, the observed intensity of
H Lyman  strongly depends on the gas and dust distribution and on the velocity field.
strongly depends on the gas and dust distribution and on the velocity field.
It is instructive to investigate what are the
effects of collisional excitation of the hydrogen lines on the derived
helium abundance. This is done in the present section on a few examples.
 |
Figure 5:
The same models as in Fig. 4. The symbols have the same meaning as in Fig. 1.
As in
Figs. 1 and 4, models shown in the top panels have
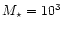 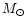 ,
those in the middle panels have ,
those in the middle panels have
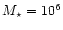 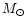 ,
those in the bottom panels have ,
those in the bottom panels have
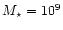 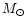 .
The left panels concern the
temperature structure of the models and show the ratio of .
The left panels concern the
temperature structure of the models and show the ratio of
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) /T(H+) versus [O III] /T(H+) versus [O III] 5007/H 5007/H .
The right panels concern the ionization structure
of hydrogen and helium and show (x(He+) + x(H+))/x(H+)
versus [O III] .
The right panels concern the ionization structure
of hydrogen and helium and show (x(He+) + x(H+))/x(H+)
versus [O III] 5007/H 5007/H . . |
| Open with DEXTER |
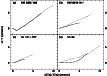 |
Figure 6:
The dependence of the relative correction of the He mass fraction
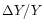 on the contribution of the collisional enhancement
on the contribution of the collisional enhancement
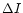 (H (H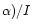 (H (H )
of the H )
of the H emission line in
four low-metallicity
blue compact galaxies. The solid line is the dependence when only the
intensity of H
emission line in
four low-metallicity
blue compact galaxies. The solid line is the dependence when only the
intensity of H emission line is decreased by the amount indicated by
the abscissa. The dotted line shows the dependence when the H
emission line is decreased by the amount indicated by
the abscissa. The dotted line shows the dependence when the H line intensity is decreased by this amount and the H
line intensity is decreased by this amount and the H line
intensity by one third of this amount.
line
intensity by one third of this amount. |
| Open with DEXTER |
We have selected 4 low-metallicity blue compact galaxies SBS 0335-052
(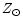 /40, Izotov et al. 2001b), SBS 0940+544 (
/40, Izotov et al. 2001b), SBS 0940+544 (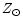 /27,
Guseva et al. 2001), Tol 1214-277 and Tol 65 (
/27,
Guseva et al. 2001), Tol 1214-277 and Tol 65 (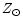 /23, Izotov et al.
2001a) from the sample presented in
Sect. 3, on the basis of their high-quality spectra obtained
with the Keck telescope and high electron temperatures in the range of 17000-20000 K derived from the [O III] line intensity ratios.
Because of the high electron temperature the effect of collisional
excitation on the helium abundance determination is expected to be relatively
large in these galaxies. To derive the 4He and heavy element abundances we
follow the prescriptions by Izotov et al. (1994),
but assuming that there is a certain percentage of collisional excitation in
the H
/23, Izotov et al.
2001a) from the sample presented in
Sect. 3, on the basis of their high-quality spectra obtained
with the Keck telescope and high electron temperatures in the range of 17000-20000 K derived from the [O III] line intensity ratios.
Because of the high electron temperature the effect of collisional
excitation on the helium abundance determination is expected to be relatively
large in these galaxies. To derive the 4He and heavy element abundances we
follow the prescriptions by Izotov et al. (1994),
but assuming that there is a certain percentage of collisional excitation in
the H and in the H
and in the H lines.
We assume that the temperature characteristic
of the emission of all He I lines is given by
lines.
We assume that the temperature characteristic
of the emission of all He I lines is given by
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) ,
and that the ionization correction factor for helium is
equal to 1. This is not exactly true for all our models, as seen
in Fig. 5, which shows (
,
and that the ionization correction factor for helium is
equal to 1. This is not exactly true for all our models, as seen
in Fig. 5, which shows (
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) /T(H+) (left panels) and (x(He+) +
x(He++))/x(H+) (right panels) for the same models as Fig. 4.
T(H+) is defined as
/T(H+) (left panels) and (x(He+) +
x(He++))/x(H+) (right panels) for the same models as Fig. 4.
T(H+) is defined as
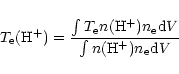 |
(1) |
and x(He+) is defined as
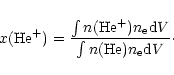 |
(2) |
However, since the four considered galaxies have
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) around 20000 K
and [O III]
around 20000 K
and [O III] 5007/H
5007/H larger than 3, our model grid indicates that our
approximations should be reasonable.
larger than 3, our model grid indicates that our
approximations should be reasonable.
In order to explore the effects of collisional excitation of the H lines, we
consider two different cases. In the first case the effect of collisional
excitation is accounted for by decreasing by some amount the intensity of the
H emission line and leaving unchanged the intensity of the H
emission line and leaving unchanged the intensity of the H emission line. In the second case we decrease the intensities of H
emission line. In the second case we decrease the intensities of H and H
and H emission lines assuming that the effect of the collisional
excitation on the H
emission lines assuming that the effect of the collisional
excitation on the H line intensity is three times smaller than that
on the H
line intensity is three times smaller than that
on the H line intensity.
For each assumed value of the contribution of the collisional enhancement to H
line intensity.
For each assumed value of the contribution of the collisional enhancement to H ,
,
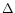 I(H
I(H )/I(H
)/I(H ),
we compute the extinction, correct the emission line ratios for reddening
and underlying stellar absorption, then recompute
),
we compute the extinction, correct the emission line ratios for reddening
and underlying stellar absorption, then recompute
![$T_{{\rm [O\ III]}4363/5007}$](/articles/aa/full/2001/42/aa1650/img6.gif) and derive the 4He and the
heavy element abundances. In the
analysis, we use the five strongest He I emission lines to derive
the helium mass fraction Y, after correction for collisional and
fluorescent excitation of the He I emission lines. In short, using
the intensities of the five He I emission lines, we evaluate the
electron number density
and derive the 4He and the
heavy element abundances. In the
analysis, we use the five strongest He I emission lines to derive
the helium mass fraction Y, after correction for collisional and
fluorescent excitation of the He I emission lines. In short, using
the intensities of the five He I emission lines, we evaluate the
electron number density 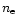 in the He+ zone and the optical depth
in the He+ zone and the optical depth
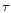 (
( 3889) in the He I
3889) in the He I  3889 line in a self-consistent
way, so that the He I
3889 line in a self-consistent
way, so that the He I  3889/
3889/ 5876,
5876,
 4471/
4471/ 5876,
5876,  6678/
6678/ 5876 and
5876 and
 7065/
7065/ 5876 line ratios have their recombination values, after
correction for collisional and fluorescent enhancement of the He I
emission lines. These effects are very strong in hot low-metallicity
H II regions. In particular, the correction of the He I
5876 line ratios have their recombination values, after
correction for collisional and fluorescent enhancement of the He I
emission lines. These effects are very strong in hot low-metallicity
H II regions. In particular, the correction of the He I
 5876 emission line for collisional and fluorescent enhancement
in SBS 0335-052 is
5876 emission line for collisional and fluorescent enhancement
in SBS 0335-052 is 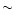 12%.
12%.
Of course, for each object, there is a maximum
contribution of collisional enhancement
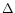 I(H
I(H )/I(H
)/I(H )
imposed by the observed
H
)
imposed by the observed
H /H
/H .
In reality, the range of possible values of
.
In reality, the range of possible values of
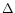 I(H
I(H )/I(H
)/I(H )
is
smaller because interstellar extinction must be present at some level.
We have checked that, after the completion of the whole procedure,
the higher order Balmer lines remain compatible with case B within observational errors
and uncertainties in the extinction law.
)
is
smaller because interstellar extinction must be present at some level.
We have checked that, after the completion of the whole procedure,
the higher order Balmer lines remain compatible with case B within observational errors
and uncertainties in the extinction law.
In Fig. 6 we show the variations of the correction
of the helium mass fraction 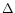 Y/Y derived
from the He I
Y/Y derived
from the He I  5876 emission line for the four galaxies we
investigated.
It is seen that the correction for the collisional enhancement of the
hydrogen lines results in an increase of the He abundance in all galaxies.
Qualitatively such a dependence can be explained by two effects: 1) the
correction of the H
5876 emission line for the four galaxies we
investigated.
It is seen that the correction for the collisional enhancement of the
hydrogen lines results in an increase of the He abundance in all galaxies.
Qualitatively such a dependence can be explained by two effects: 1) the
correction of the H line in the second case (dotted line) increases the
He I/H
line in the second case (dotted line) increases the
He I/H intensity ratios; 2) the correction of H
intensity ratios; 2) the correction of H and
H
and
H lines for collisional excitation decreases the extinction and hence
increases the intensity
of He I
lines for collisional excitation decreases the extinction and hence
increases the intensity
of He I  5876 emission line. Certainly, some part
of the deviation of the observed H
5876 emission line. Certainly, some part
of the deviation of the observed H /H
/H intensity ratio
from the case B value is due to interstellar extinction. Therefore, although
the effect of collisional excitation of the hydrogen lines on the
helium abundance is significant, it is unlikely that the correction
intensity ratio
from the case B value is due to interstellar extinction. Therefore, although
the effect of collisional excitation of the hydrogen lines on the
helium abundance is significant, it is unlikely that the correction
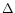 Y/Y exceeds 5%. At larger values of
Y/Y exceeds 5%. At larger values of
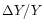 the
interstellar extinction derived from the H
the
interstellar extinction derived from the H /H
/H becomes
very small, less than the foreground extinction produced in our Galaxy.
Our estimate of
becomes
very small, less than the foreground extinction produced in our Galaxy.
Our estimate of
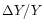 is not very certain and should be considered
as a qualitative indication of the relatively large positive correction
of the helium abundance if collisional excitation of the hydrogen
emission lines is taken into account.
An accurate determination of the helium abundance
requires detailed photoionization modeling of the
H II regions in individual galaxies, with all
relevant effects taken into account, and with all the
relevant line intensities satisfactorily reproduced.
Such an enterprise is still ahead of us.
is not very certain and should be considered
as a qualitative indication of the relatively large positive correction
of the helium abundance if collisional excitation of the hydrogen
emission lines is taken into account.
An accurate determination of the helium abundance
requires detailed photoionization modeling of the
H II regions in individual galaxies, with all
relevant effects taken into account, and with all the
relevant line intensities satisfactorily reproduced.
Such an enterprise is still ahead of us.
Our consideration of the collisional excitation of hydrogen emission lines
has shown that this effect can be particularly large,
as high as 8% for the H /H
/H ratio
in the low-metallicity extragalactic H II regions. If taken into
account it results in an upward correction of the helium abundance Y by
up to 5%, making the collisional excitation of hydrogen one of the most
important sources of systematics in the primordial helium abundance
determination. Some other sources of systematic uncertainties
should be considered as well. One of the most important sources may be the
"temperature fluctuations'' which, if present, result in the downward
correction of Y by
ratio
in the low-metallicity extragalactic H II regions. If taken into
account it results in an upward correction of the helium abundance Y by
up to 5%, making the collisional excitation of hydrogen one of the most
important sources of systematics in the primordial helium abundance
determination. Some other sources of systematic uncertainties
should be considered as well. One of the most important sources may be the
"temperature fluctuations'' which, if present, result in the downward
correction of Y by
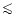 5% (e.g., Peimbert et al. 2000). Sauer &
Jedamzik (2001) considered the effect of the ionization structure and
large-scale temperature variations in the H II region on the 4He
abundance determination. Izotov et al. (2001a) compared the observed
properties of the high-excitation H II regions in the galaxies
Tol 1214-277 and Tol 65 with Sauer & Jedamzik models and found that a
small downward Y correction (by less than 1%) should be applied due to the two
mentioned effects. Finally, underlying stellar He I line absorption of
the ionizing clusters should be taken into account. However, this effect is
not large in the four considered blue compact galaxies because of the
large equivalent widths of emission lines and results in an upward Ycorrection by
5% (e.g., Peimbert et al. 2000). Sauer &
Jedamzik (2001) considered the effect of the ionization structure and
large-scale temperature variations in the H II region on the 4He
abundance determination. Izotov et al. (2001a) compared the observed
properties of the high-excitation H II regions in the galaxies
Tol 1214-277 and Tol 65 with Sauer & Jedamzik models and found that a
small downward Y correction (by less than 1%) should be applied due to the two
mentioned effects. Finally, underlying stellar He I line absorption of
the ionizing clusters should be taken into account. However, this effect is
not large in the four considered blue compact galaxies because of the
large equivalent widths of emission lines and results in an upward Ycorrection by
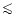 1%.
Combining all these systematic effects it appears that the helium
abundance derived by Izotov & Thuan (1998) and Izotov et al. (1999) in
low-metallicity blue compact galaxies could be underestimated by about 2-3%
only.
However, additional work has to be done to clarify the
importance of the systematic effects in the 4He abundance determination.
Especially, the mystery of the "temperature fluctuations'' has to be solved.
For this, a detailed modeling of the H II regions in each of the best
observed low-metallicity blue compact galaxies should be done.
1%.
Combining all these systematic effects it appears that the helium
abundance derived by Izotov & Thuan (1998) and Izotov et al. (1999) in
low-metallicity blue compact galaxies could be underestimated by about 2-3%
only.
However, additional work has to be done to clarify the
importance of the systematic effects in the 4He abundance determination.
Especially, the mystery of the "temperature fluctuations'' has to be solved.
For this, a detailed modeling of the H II regions in each of the best
observed low-metallicity blue compact galaxies should be done.
Acknowledgements
Y. I. I. has been partly supported by INTAS 97-0033 grant, and acknowledges
support from the "Kiev project'' of the Universite Paul Sabatier of Toulouse.
He is grateful for the hospitality of the Paris-Meudon Observatory and of the
Midi-Pyrenees Observatory where this work was conducted.
- Aggarwal, K. M. 1983, MNRAS, 202, 15
In the text
- Aggarwal, K. M., Berrington, K. A., Burke, P. G., Kingston,
A. E., & Pathak, A. 1991, J. Phys. B: At. Mol. Opt. Phys., 24, 1385
In the text
- Armour, M.-H., Ballantyne, D. R., Ferland, G. J., Karr, J.,
& Martin, P. G. 1999, PASP, 111, 1251
In the text
NASA ADS
- Balbes, M. J., Boyd, R. N., & Mathews, G. J. 1993, ApJ,
418, 229
In the text
NASA ADS
- Ballantyne, D. R., Ferland, G. J., & Martin, P. G. 2000,
ApJ, 536, 773
In the text
NASA ADS
- Benjamin, R. A., Skillman, E. D., & Smits, D. P. 1999, ApJ,
514, 307
In the text
NASA ADS
- Callaway, J. 1994, Atomic Data and Nuclear Data Tables, 57, 9
In the text
NASA ADS
- Campbell, A. 1988, ApJ, 335, 644
In the text
NASA ADS
- Campbell, A. 1992, ApJ, 401, 157
In the text
NASA ADS
- Clegg, R. E. S. 1989, in Planetary Nebulae,
ed. S. Torres-Peimbert (Dordrecht: Kluwer), IAU Symp., 131, 139
In the text
- Cota, S. A., & Ferland, G. J. 1988, ApJ, 326, 889
In the text
NASA ADS
- Davidson, K., & Kinman, T. D. 1985, ApJS, 58, 321
In the text
NASA ADS
- Dinerstein, H. L., & Shields, G. A. 1986, ApJ, 311, 45
In the text
NASA ADS
- Drake, S. A., & Ulrich, R. K. 1980, ApJS, 42, 351
In the text
NASA ADS
- Guseva, N. G., et al. 2001, A&A, in press, preprint
[astro-ph/0109256]
In the text
- Hummer, D. G., & Storey, P. J. 1992, MNRAS, 254, 277
In the text
NASA ADS
- Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al.
1999, ApJ, 527, 757
In the text
NASA ADS
- Izotov, Y. I., Chaffee, F. H., & Green, R. F. 2001a, ApJ,
in press, preprint [astro-ph/0109255]
In the text
- Izotov, Y. I., Chaffee, F. H., & Schaerer, D. 2001b, A&A,
in press, preprint [astro-ph/0109254]
- Izotov, Y. I., & Thuan, T. X. 1998, ApJ, 497, 227
In the text
NASA ADS
- Izotov,Y. I., Thuan T. X., & Lipovetsky, V. A. 1994,
ApJ, 435, 647
In the text
NASA ADS
- Izotov,Y. I., Thuan T. X., & Lipovetsky, V. A. 1997,
ApJS, 108, 1
In the text
NASA ADS
- Kunth, D., & Sargent, W. L. W. 1983, ApJ, 273, 81
In the text
NASA ADS
- Mathews, G. J., Boyd, R. N., & Fuller, G. M. 1993, ApJ, 403, 65
In the text
NASA ADS
- McGaugh, S. S. 1991, ApJ, 380, 140
In the text
NASA ADS
- Meynet, G., Maeder, A., Schaller, G., Schaerer, D., &
Charbonnel, C. 1994, A&AS, 103, 97
In the text
NASA ADS
- Luridiana, V., & Peimbert, M. 2001, ApJ, 553, 633
In the text
NASA ADS
- Luridiana, V., Peimbert, M., & Leitherer, C. 1999, ApJ, 527, 110
In the text
NASA ADS
- Olive, K. A., & Skillman, E. D. 2001, New Astron., 6, 119
In the text
NASA ADS
- Olive, K. A., & Steigman, G. 1995, ApJS, 97, 49
In the text
NASA ADS
- Olive, K. A., Steigman, G., & Skillman, E. D. 1997, ApJ, 483, 788
In the text
NASA ADS
- Pagel, B. E. J., Simonson, E. A., Terlevich, R. J., &
Edmunds, M. G. 1992, MNRAS, 255, 325
In the text
NASA ADS
- Pagel, B. E. J., Terlevich, R. J., & Melnick, J. 1986, PASP,
98, 1005
In the text
NASA ADS
- Papaderos, P., et al. 2001, in preparation
In the text
- Peimbert, M. 1983, in Primordial Helium, ed. P. A. Shaver,
D. Kunth, & Kjär (Garching: ESO), 267
In the text
- Peimbert, M. 1989, in Elements and the Cosmos, ed.
M. G. Edmunds, & R. J. Terlevich (Cambridge University Press), 196
In the text
- Peimbert, M., & Torres-Peimbert, S. 1974, ApJ, 193, 327
In the text
NASA ADS
- Peimbert, M., & Torres-Peimbert, S. 1976, ApJ, 203, 581
In the text
NASA ADS
- Peimbert, M. Peimbert, A., & Ruiz, M. T. 2000, ApJ, 541, 688
In the text
NASA ADS
- Peimbert, A. Peimbert, M., & Luridiana, V. 2001, preprint
[astro-ph/0107189]
In the text
- Rayo, J. F., Peimbert, M., & Torres-Peimbert, S. 1982, ApJ,
255, 1
In the text
NASA ADS
- Sarkar, S. 1996, Rep. Prog. Phys., 59, 1493
In the text
- Sasselov, D., & Goldwirth, D. 1995, ApJ, 444, 5
In the text
- Sauer, D., & Jedamzik, K. 2001, preprint [astro-ph/0104392]
In the text
- Schaerer, D., & de Koter, A. 1997, A&A, 322, 598
In the text
NASA ADS
- Schaerer, D., & Vacca, W. D. 1998, ApJ, 497, 618
In the text
NASA ADS
- Schmutz, W., Leitherer, C., & Gruenwald, R. 1992, PASP, 104, 1164
In the text
NASA ADS
- Shields, G. A. 1986, PASP, 98, 1072
In the text
NASA ADS
- Skillman, E. D., & Kennicutt, R. C., Jr. 1993, ApJ, 411, 655
In the text
NASA ADS
- Stasinska, G. 1980, A&A, 84, 320
In the text
NASA ADS
- Stasinska, G. 2001, preprint [astro-ph/0102403]
In the text
- Stasinska, G., & Leitherer, C. 1996, ApJS, 107, 661 (SL96)
In the text
NASA ADS
- Stasinska, G., & Schaerer, D. 1999, A&A, 351, 72
In the text
NASA ADS
- Stasinska, G., Schaerer, D., & Leitherer, C. 2001, A&A,
370, 1 (SSL2001)
In the text
NASA ADS
- Steigman, G., Schramm, D., & Gunn, J. 1977, Phys. Lett. B,
66, 202
In the text
- Steigman, G., Viegas, S. M., & Gruenwald, R. 1997, ApJ, 490, 187
In the text
NASA ADS
- Viegas, S. M., Gruenwald, R., & Steigman, G. 2000, ApJ, 531, 813
In the text
NASA ADS
- Walker, T. P., Steigman, G., Kang, H.-S., Schramm, D. M.,
& Olive, K. A. 1991, ApJ, 376, 91
In the text
Copyright ESO 2001



![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{ms1650f4.eps}
\end{figure}](/articles/aa/full/2001/42/aa1650/Timg27.gif)