Early type stars at high galactic latitudes

I. Ten young massive B-type stars[*],[*],[*]

M. Ramspeck - U. Heber - S. Moehler

Dr.-Remeis-Sternwarte, Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany

Received 4 July 2001 / Accepted 3 September 2001

Abstract
We present the results of quantitative spectral analyses of ten apparently normal B-type stars. These stars were found to be young massive B-type stars at distances of z=2.6 to 7.6kpc from the galactic plane based on their positions in the ( $ {T_{\rm eff}}$, $\log {g}$) diagram, normal abundance patterns and/or large projected rotational velocities. We discuss formation scenarios (runaway star scenarios versus a scenario for star formation in the halo) by comparing times-of-flight and evolutionary time scales. For all stars (except SB 357 and HS 1914+7139) both the scales are similar indicating that the stars could have formed in the galactic disk and been ejected from there soon after their birth. Derived ejection velocities range from 130km s-1 to 440km s-1 and may be used to constrain models for ejection mechanisms. Using new proper motion measurements we show that PHL 346, which was considered the most likely candidate for a young B-type star born in the halo, can be explained as a runaway star from the galactic plane.

Key words: Galaxy: halo - stars: early-type - stars: abundances - stars: kinematics - stars: evolution


  
1 Introduction

Main sequence B-type stars located far away from the galactic plane are a rare, albeit known phenomenon. In their pioneering paper, Greenstein & Sargent (1974) studied faint blue stars at high galactic latitudes and classified 25% of them as apparently normal OB-type stars at distances from the galactic plane of z= 1-3 kpc. More detailed studies have shown that many, but not all, of the apparently normal stars were in fact highly evolved low-mass stars. Surveys for UV excess objects (e.g., Palomar Green, Hamburg-Schmidt, Edinburgh Cape) have found many new candidates (e.g., Saffer et al. 1997; Rolleston et al. 1999; Magee et al. 1998) and some may be known even in other galaxies (M 31, Smoker et al. 2000). Their properties, possible evolutionary histories and formation mechanisms were reviewed by, e.g., Tobin (1987), Keenan (1992), and Heber et al. (1997).

Tobin (1987) also discusses the problem that some highly evolved stars spectroscopically mimic massive stars almost perfectly. The most striking example is PG 0832+676 which has been analysed several times. Its abundance pattern is close to normal. Only recently, Hambly et al. (1996) were able to firmly establish slight underabundances and a very low projected rotation velocity. Combining both results they concluded that PG 0832+676 in fact is a highly evolved star. Abundance analyses as well as determinations of rotational velocities are thus of essential importance for the verification of massive B-type star candidates. A high rotational velocity generally excludes a late evolutionary status of the star, as old, low-mass stars cannot rotate as fast as massive stars. This fact was used, e.g., by Heber et al. (1995, HS 1914+7139) and Schmidt et al. (1996, PG 0009+036) to identify massive B-type stars far from the Galactic plane from medium-resolution spectra.

The massive B-type stars in galactic halos can be separated kinematically into two different categories: those stars with a main sequence lifetime larger than the time they would need to travel from the plane to their present position and those with a main sequence lifetime too small to reach their current position assuming an acceptable velocity vertical to the galactic disk. The former ones are assumed to be born in the disk and thereafter ejected from it (runaway stars), while the latter are supposed to be born in the halo (see Conlon et al. 1988, 1990; Hambly et al. 1993, for more details). Since many years runaway stars are known to exist, whereas formation of massive stars in the halo has not yet been confirmed convincingly. The best studied candidate is PHL 346 (Ryans et al. 1996), a $\beta$ Cephei star in the halo (Dufton et al. 1998). A search for coeval stars around PHL 346 (Hambly et al. 1996) met with limited success, since only one out of 16 A- and B-type stars around PHL 346 was found to have the appropriate spectral type and radial velocity.

Calculations of galactic orbits are thus very important to determine the true nature of the stars, since they also allow to determine ejection velocities from the galactic disk. However, accurate proper motions are a prerequisite for such an analysis. A big step forward has been achieved by Thejll et al. (1997) and the Hipparcos/Tycho mission (Perryman et al. 1997; Høg et al. 2000).

In this paper we present the analysis of new high-resolution spectra for 10 apparently normal B-type stars. Half of the sample are new discoveries whereas the other half has already been studied previously (Conlon et al. 1992; Ryans et al. 1996; Rolleston et al. 1999; Heber et al. 1995). For the latter the times-of-flight quoted in the literature appear to be larger than the evolutionary times indicating they might have formed in the halo. However, proper motions were not available rendering these estimates of the times-of-flight uncertain. Since proper motion measurements became available recently for three of these stars, it was deemed necessary to reanalyse them from new high resolution spectra.

2 Observations and data reduction

We have obtained high resolution spectra for all programme stars using the HIRES spectrograph at the Keck I telescope, the FEROS spectrograph at the ESO 1.5 m telescope, the FOCES spectrograph at the DSAZ 2.2 m telescope and the CASPEC spectrograph at the ESO 3.6 m telescope (see Table 1). Since the normalization procedure for the Echelle spectra is cumbersome for the rather broad Balmer lines (see below) it was deemed necessary to secure low resolution spectra at least for some of the programme stars to obtain independent estimates of the atmospheric parameters, in particular of the gravities. Appropriate spectra were obtained at Calar Alto and at ESO. Details are given in Table 1. For PG 1511+367, PG 1533+467 and PG 1610+239 we have new low resolution spectra presented in this paper. These spectra were taken with the TWIN spectrograph at the DSAZ 3.5 m telescope and reduced as described in Edelmann et al. (2001). The low resolution spectrum of PG 0122+214 were reduced as described in Moehler et al. (1997).

For the Keck-HIRES spectra observed in 1998 the blue cross disperser was used and the spectra cover the blue spectral range (3600 to 5130 Å). The standard data reduction as described by Zuckerman & Reid (1998) resulted in spectral orders that have a somewhat wavy continuum. Due to the merging of the higher Balmer lines the removal of the remaining waviness is difficult. We used the spectrum of H1504+65 (a very hot pre-white dwarf devoid of hydrogen and helium, Werner 1991), which was observed in the same night, for rectification of our spectra. Its spectrum has only few weak lines of highly ionized metals in the blue (3600-4480 Å) where the strong Balmer lines are found in the B-type stars. Therefore we normalized individual spectral orders 1 to 20 (3600-4480 Å) of the B-type stars by dividing through the smoothed spectrum of H1504+65. The remaining orders were normalized by fitting the continuum with spline functions (interpolated for orders 26 and 27 which contain H$\beta$). Judging from the match of line profiles in the overlapping parts of neighboring orders this procedure worked extremely well. In 1996 the red cross disperser of the Keck-HIRES spectrograph was used and therefore the blue part of the spectrum shortwards of 4200 Å was not recorded. Since no merging Balmer lines are present in this spectral range the waviness of the spectrum could be removed by fitting the continuum with spline functions. For orders containing broad Balmer lines the fit functions were interpolated between neighbouring orders.

The FOCES spectra were reduced as described in Pfeiffer et al. (1998) with a software package developed by the Munich Group. For the FEROS data the MIDAS reduction pipeline (François 1999) was used. For CASPEC data the procedure described by Heber et al. (1986) was applied. The CASPEC and FEROS spectra were normalized in a similar way as described for the Keck HIRES spectra of 1996.

Due to an error in the wavelength calibration no reliable radial velocity could be measured for HS 1914+7139.

 

 
Table 1: Observational parameters.
Name Observation Date & Telescope & Resolution Wavelength Range
  Time (UT) Instrument (FWHM Å) (Å)
  Echelle spectra:
PG 0122+214 July 20, 1998 14:48 Keck HIRES 0.09 3600-5130
PG 1511+367 July 20, 1999 20:30 Calar Alto 2.2 m FOCES 0.15 3890-6995
PG 1533+467 July 19, 1999 21:00 Calar Alto 2.2 m FOCES 0.15 3890-6995
PG 1610+239 July 24, 1996 - Keck HIRES 0.09 4265-6720
PG 2219+094 July 20, 1999 03:00 Calar Alto 2.2 m FOCES 0.15 3890-6995
PHL 159 Sep. 12, 1998 22:00 Calar Alto 2.2 m FOCES 0.15 3870-6830
PHL 346 Oct. 19, 1986 22:50 ESO 3.6 m CASPEC 0.20 4070-5130
SB 357 Oct. 1984 ESO 3.6 m CASPEC 0.20 4060-5090
HS 1914+7139 June 05, 1996 13:08 Keck HIRES 0.09 4280-6720
BD-15$^\circ $115 Sep. 08, 2000 07:49 ESO 1.5 m FEROS 0.09 3630-8860
  low resolution spectra:
PG 0122+214 Aug. 07, 1990 02:32 Calar Alto TWIN 3.5 m 3.5 3875-5010
PG 1511+367 July 18, 1999 20:49 Calar Alto TWIN 3.5 m 2.9 3350-7700
PG 1533+467 July 18, 1999 21:00 Calar Alto TWIN 3.5 m 2.9 3350-7700
PG 1610+239 Apr. 11, 2001 Calar Alto TWIN 3.5 m 1.0 4100-4950
PG 2219+094$^\star$ June 10, 1987 08:35 ESO MPIA 2.2 m B&C 2.5 4035-4900

$\textstyle \parbox{15cm}{$^\star$\space Moehler et~al. (1990).}$


3 Atmospheric parameters and projected rotational velocities

To derive atmospheric parameters (effective temperature, surface gravity, and photospheric helium abundance) and projected rotational velocities all Balmer lines and the He  I lines $\lambda\lambda$ 4026 Å, 4388 Å, 4438 Å, 4472 Å, 4713 Å, 4922 Å, 5016Å, 5048 Å, 5678 Å, in the observed spectra were fitted with synthetic line profiles calculated from model atmospheres.

We computed LTE model atmospheres using the program of Heber et al. (2000), which calculates plane parallel, chemically homogeneous and fully line blanketed models, using the opacity distribution functions for metal line blanketing by Kurucz (1979, ATLAS6). From these model atmospheres synthetic spectra were calculated with Lemke's version[*] of the LINFOR program (developed originally by Holweger, Steffen, and Steenbock at Kiel University). The spectra include the Balmer lines H$_\alpha$ to H22 and the He I lines listed above and the grid covers the range 11000 K$\leq$  $ {T_{\rm eff}}$ $\leq$ 40000 K, 3.5 $\leq$ $\log {g}$ $\leq$ 6.5 and $-4.0 \leq$  ${{\rm\log}{\frac{n_{\rm He}}{n_{\rm H}}}}$ $\leq -0.5$ at solar metallicity.

The fit procedure is based on a $\chi^{2}$ test using the routines developed by Bergeron et al. (1992) and Saffer et al. (1994) and modified by Heber et al. (1997) to derive also the rotational velocity. The theoretical spectra are convolved with the instrument profiles (Gaussian with the appropriate instrumental FWHM) and a rotational profile. The fit program then normalizes theoretical and observed spectra using the same continuum points. Example fits for a rapidly rotating and a slowly rotating programme star are shown in Fig. 1 for hydrogen and helium lines, whilst Fig. 2 compares the metal line spectra of slowly rotating (PHL 159, BD-15$^\circ $115) stars and a rapidly rotating star (PG 1533+467).

  \begin{figure} \par\includegraphics[angle=270,width=17.3cm,clip]{ms1632f1.eps} \end{figure} Figure 1: Fit examples for a slowly rotating star (BD-15$^\circ $115, left hand side) and a rapidly rotating star (PG 1533+467, right hand side).
Open with DEXTER


  \begin{figure} \includegraphics[angle=270,width=16.6cm,clip]{ms1632f2.eps} \end{figure} Figure 2: Wavelength range with strong N  II and O  II lines to show examples for spectra of slowly rotating (bottom, middle) and rapidly rotating (top) stars.
Open with DEXTER


  

 
Table 2: Atmospheric parameters and rotational velocities for the progamme stars as derived from high and low resolution spectroscopic data and comparison of these data with the effective temperatures calculated from Strømgren photometry. The rotational velocities derived from the high resolution data were used to fit the low resolution spectra.
  High Resolution Low Resolution Photometry
Name $ {T_{\rm eff}}$ ${\log(\frac{g}{\rm cm~s^{-2}})}$ ${\log\frac{N({\rm He})}{N(\rm H)}}$ $v \sin i$ $ {T_{\rm eff}}$ ${\log(\frac{\it g}{\rm {cm~s}^{-2}})}$ $ {T_{\rm eff}}$ E(b-y)
  (K)     (km s-1) (K)   (K)  
PG 0122+214 18300 3.86 -0.98 117 18700 3.90 18500 (1) 0.0
PG 1511+367 16100 4.15 -1.16 77 15600 4.20 15900 (1) 0.0
PG 1533+467 18500 4.09 -0.94$^\star$ 215 17700 3.93 17700 (1) 0.020
PG 1610+239 15500 3.72 -0.84$^\star$ 75 15400 3.69 18600 (1) 0.082
PG 2219+094 19500 3.58 -1.00$^\star$ 225 18200 3.52 16700 (2) 0.037
              19500 (3) 0.081
PHL 159 18500 3.59 -0.84 21 - - 20900 (4) 0.025
PHL 346 20700 3.58 -1.00 45 - - 22300 (7) 0.037
SB 357 19700 3.90 -1.00$^\star$$^\star$ 180 - - 19700 (5) 0.052
              19700 (8) 0.061
              19800 (9) 0.037
BD-15$^\circ $115 20100 3.81 -0.97 35 - - 19800 (5) 0.0
              20200 (6) 0.0
HS 1914+7139 17600 3.90 -0.99 250 18100 3.60 - -

$\textstyle \parbox{15.8cm}{ $^\star$\space $ {T_{\rm eff}}$ , $\log {g}$ { }fix... ...e{kihi77}); (8) Kilkenny D. (\cite{kil95}); (9) Graham et al. (\cite{grsl73}).}$


The fit procedure was executed for all high and low resolution spectra and the results are listed in Table 2[*]. Formal fitting errors are very small for the high resolution spectra, on average $\Delta {T_{\rm eff}=100~\rm K}$, $\Delta {\log g=0.02}$. Systematic errors (e.g. continuum placement, uncertainties in line broadening theory) are certainly larger and therefore dominate the error budget. We estimate errors in effective temperatures conservatively as 5% and adopted an error of $\pm$0.1dex for the gravities. The fitting errors for the Helium abundance are on average $\Delta {\log (n({\rm He})/n(\rm H))=0.05}$. Since sharp Helium lines as well as broad Helium lines are well reproduced (see Fig. 1) systematic errors due to He  I line broadening theory appear to be small and we adopted an error of $\pm$0.1dex in all cases.

For rapidly rotating stars the $\chi^{2}$ minimum is too poorly defined to allow a reliable determination of the He abundance simultaneously. Therefore, in a first step the helium abundance was kept fixed at -1.00 (i.e. solar) for the fit procedure. In a second iteration step the helium abundance was determind by fitting the helium lines while keeping the $ {T_{\rm eff}}$ and $\log {g}$ fixed at those values determined in the first iteration step. For all stars (except HS 1914+7139) Strømgren photometry is available, which allowed an independent determination of the effective temperature. We used the program of Moon (1985) as modified by Napiwotzki et al. (1993) to derive the effective temperature and the reddening and compare the photometric temperatures to the spectroscopic ones in Table 2. There is a good agreement between results from low and high resolution spectra and photometry, except for PG 1610+239, PHL 159 and PHL 346. The spectrum of SB 357 shows the presence of emission in $\rm {H_{\beta}}$ and $\rm {H_{\gamma}}$ but not in $\rm {H_{\delta}}$. Therefore the effective temperature were obtained from Strømgren photometry and the surface gravity from fitting the far wings of the hydrogen lines. The helium lines of this object were difficult to fit, but the observation is compatible with normal abundance and there is no indication of emission in any of the helium lines observed. The parameters used for further analyses were taken from the high resolution spectra, because of the larger wavelength coverage and the excellent quality of the fits. In the case of PG 1533+467, however, the wavelength coverage of the low resolution spectrum is larger than that of the high resolution one and therefore we used the average. The finally adopted parameters are listed in Table 6. Results are shown in a ( $ {T_{\rm eff}}$, $\log {g}$) diagram (Fig. 3).

4 Chemical abundances

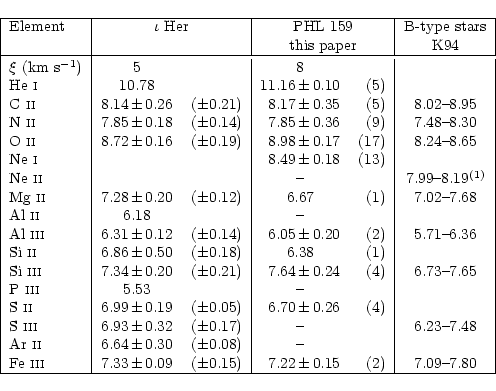
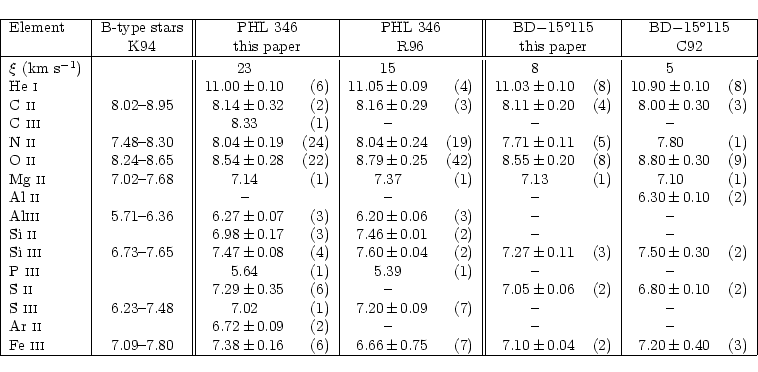
Seven programme stars (PG 0122+214, PG 1511+367, PG 1533+467, PG 1610+239, PG 2219+094, HS 1914+7139 and SB 357) display highly broadened lines (due to rotation, see Table 2). Only the strongest metal lines (e.g. C  II 4267 Å, Mg  II 4481 Å) could be identified. Therefore it was impossible to perform a detailed abundance analysis.

The equivalent widths were measured employing the nonlinear least-squares Gaussian fitting routines in MIDAS with central wavelength, central intensity and full width at half maximum as adjustable parameters. For metal lines located in the wings of Balmer or helium lines an additional Lorentzian function is used to describe the line wings of the latter.

Metal lines of the species C  II, C  III, N  II, O  II, Ne  I, Mg  II, Al  II, Al  III, Si  II, Si  III, P  III, S  II, S  III, Ar  II and Fe  III were identified in the sharp-lined spectra of BD-15$^\circ $115, PHL 159 and PHL 346. The atomic data for the analysis were taken from several tables:

1.
CNO from Wiese et al. (1996);
2.
Fe from Kurucz (1992) and Ekberg (1993);
3.
Ne, Mg, Al, Si, S, P, Ar from Hirata et al. (1995).

  \begin{figure} \par\includegraphics[angle=360,width=8.8cm,clip]{ms1632f3.eps} \end{figure} Figure 3: Positions of the programme stars (filled circles) in a ( $ {T_{\rm eff}}$, $\log {g}$) diagram with evolutionary tracks calculated by Schaller et al. (1992) for determining the masses and evolution times.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=360,width=17.3cm,clip]{ms1632f4.eps} \end{figure} Figure 4: LTE abundances (relative to $\iota $ Her) and errors of the programme stars. Abundances derived from singly ionized elements are shown as filled circles and from doubly ionized ones as filled triangles.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=360,width=8.8cm,clip]{ms1632f5.eps} \end{figure} Figure 5: Like Fig. 4: LTE abundances (relative to $\iota $ Her) for PHL 159. Abundances derived from neutral elements are shown as open circles, from singly ionized ones as filled circles and from doubly ionized ones as filled triangles.
Open with DEXTER

The LTE abundances were derived by using the classical curve-of-growth method and the LINFOR program (version of Lemke, see above). In this case the model atmospheres were generated for the appropriate values of effective temperature, gravity and solar helium and metal abundance with the ATLAS9 program of Kurucz (1992).

Then we calculated curves of growth for the observed metal lines, from which abundances were derived. Blends from different ions were omitted from the analysis. In the final step the abundances were determined from a detailed spectrum synthesis (using the LINFOR code described above) of all lines measured before. The results of the LTE abundance analysis and the rms errors for PHL 346 and BD-15$^\circ $115 are shown in Table 4 and compared with other analyses and for PHL 159 in Table 3. Besides the statistical rms errors (given in Tables 3 and 4) the uncertainties in $ {T_{\rm eff}}$, $\log {g}$ and microturbulent velocity (see below) contribute to the error budget. In order to minimize the systematic errors we use the B-type star $\iota $ Her as a comparison star. This star has been analysed by Hambly et al. (1997). We redetermined the LTE abundances of $\iota $ Her using the same atomic data, model atmosphere and spectrum synthesis code as for our programme stars and took the equivalent widths measured by Hambly et al. (1997).

Our results for $\iota $ Her agree to within 0.1dex with those of Hambly et al. (1997) except for C  II (0.12dex), Si  III (0.17dex), S  III (0.21dex) and Fe  III (0.36dex). In particular our statistical error for Fe  III is much lower than that of Hambly et al. (1997). These differences can be attributed to different oscillator strengths used.

Results are given in Tables 3 and 4 and systematic errors are adopted for our programme stars as well. These errors are incorporated in the error bars plotted in Figs. 4 and 5.

  
Table 3: LTE abundances of PHL 159 compared with $\iota $ Her as a comparison star and the range of LTE abundances from 21 B-type stars analysed by Kilian (1994). For $\iota $ Her the abundances are determined with the equivalent widths from Hambly et al. (1997). For $\iota $ Her systematic errors due to uncertainties of atmospheric parameters have been determined in this work and are listed in parentheses.


\begin{displaymath}\begin{tabular}{\vert l\vert r@{$\,\pm\,$}rr\vert r@{$\,\pm\,... ...) & \multicolumn{3}{c\vert}{7.09--7.80} \\ \hline \end{tabular}\end{displaymath}

References: $\rm K94=Kilian$ (1994),
(1) See text for a discussion of the Ne abundances.


  
Table 4: Comparison of LTE abundances for PHL 346 and BD-15$^\circ $115 with results from literature. The number of spectral lines used is given in brackets. Errors for the programme stars are statistical errors only.


\begin{displaymath}\begin{tabular}{\vert l\vert r@{$\,\pm\,$}rr\vert\vert r@{$\,... ...& 7.10 & 0.04 & (2) & 7.20 & 0.40 & (3) \\ \hline \end{tabular}\end{displaymath}


References: $\rm K94=Kilian$ (1994); $\rm R96=Ryans$ et al. (1996); $\rm C92=Conlon$ et al. (1992).

The determination of elemental abundances is interlocked with the microtubulent velocity $\xi$. This can be derived if a sufficient number of lines of one ion can be measured over a wide range of line strengths. In our programme stars N  II and O  II lines are most suitable for this purpose since many lines of these ions can be identified. Microturbulent velocities of $\xi$ = 8 km $\rm {s^{-1}}$ were found for PHL 159 and BD-15$^\circ $115, while a rather high value of $\xi$ = 23 km $\rm {s^{-1}}$ was deduced for PHL 346. Our results for PHL 346 and BD-15$^\circ $115 are somewhat larger than those derived by Ryans et al. (1996) and Conlon et al. (1992), see Table 4.

Remarkable is the large difference ($\approx$1.0dex) between the Si  II and Si  III abundances. This has been found in several analyses of the comparison star $\iota $ Her as well (Hambly et al. 1997, 0.67dex). In a differential analysis these systematic errors cancel to a large extent. NLTE effects are small for all elements ($\le$0.1dex, Kilian 1994) except for Ne  I. As demonstrated by Auer & Mihalas (1973) LTE calculations overestimate the neon abundance. They carried out NLTE calculations for Ne  I in $\iota $ Her and derived a neon abundance (close to solar) which is lower by 0.60 dex than our LTE result. Therefore our absolute Ne abundances are overestimated. The abundances of the programme stars with respect to $\iota $ Her are plotted in Fig. 4.

1.
BD-15$^\circ $115 All abundances are in good agreement with $\iota $ Her (to within error limits) except for Mg and Fe which are underabundant by about 0.2dex. Our results are in accordance with those of a previous analysis of the star by Conlon et al. (1992, see Table 4), except for Si for which the authors derive a considerably larger abundance.
2.
PHL 346 Abundances of C, N, O, Al, Si, S, Ar and Fe are in good agreement with those in $\iota $ Her. P is enriched by about 0.15dex, Mg is depleted by about 0.15dex. Our results agree well with those derived by Ryans et al. (1996) except for Si  II and Fe  III. For the latter our result has a much smaller error.
3.
PHL 159 Mg, Al and S are significantly depleted and O enriched by 0.3dex, whereas the other elements are in good agreement with those of the comparison star.

Spectral analyses of massive B-type stars in open clusters as well as in the field (e.g. Gies & Lambert 1992; Kilian 1994; Cunha & Lambert 1994) have revealed considerable variations of metal abundances from star to star (even within an open cluster). Kilian (1994) carried out spectral analyses of 21 B-type stars in two open clusters and in the field and determined abundances of C, N, O, Ne, Mg, Al, Si, S, and Fe. We compare our results for PHL 346, BD-15$^\circ $115, PHL 159 and $\iota $ Her to her LTE results in Tables 3 and 4. Since her programme stars are somewhat hotter than ours, the Ne abundance is based on Ne  II lines, whereas we had to use Ne  I lines. Correcting for the significant NLTE effect on Ne  I (0.56 dex, see above) the neon abundance of PHL 159, the only programme star for which it has been measured, is found to be consistent with Kilian's distribution. The abundances we derived for all metals of PHL 346, BD-15$^\circ $115 and $\iota $ Her lie well within Kilian's distribution indicating that they are bona fide main sequence B-type stars. For PHL 159, however the O  II abundance is higher and the Mg  II abundance lower than in Kilian's distribution, whereas the other metals are consistent with that distribution. Therefore PHL 159 might either be a massive B-type star with rather peculiar abundances of the elements O and Mg or an evolved, low mass B-type star that mimics a massive B-type star quite closely.

5 Masses, distances and evolutionary times

The derived atmospheric parameters were compared to two sets of evolutionary tracks (from the Geneva group, Schaller et al. 1992; and the Padua group, Salasnich et al. 2000) to estimate stellar masses and evolutionary times ${T_{\rm evol}}$ (see Fig. 3) by interpolation. The results do not depend on the model grid used. Derived masses differ by less than 0.1$M_{\odot}$ and evolutionary lifetimes by less than 4 Myr (except PG 1610+239: 17 Myr). Errors for the evolutionary lifetimes in Table 6 include errors propagated from uncertainties in atmospheric parameters as well as from the use of the two model sets.

The distance has been calculated from mass, effective temperature, gravity and the dereddened apparent magnitude of the stars:

\begin{displaymath}d = 1.11 \sqrt{\frac{M_{\star}F_V}{g}\times 10^{0.4V_0}} {\rm [kpc]} \end{displaymath}

where ${M_{\star}}$ is the stellar mass in $M_{\odot}$, g is the gravity in cm  $\rm {s^{-2}}$, FV is the model atmosphere flux at the stellar surface in units of $10^8{\,}{\rm {erg \ cm^{-2}{ }\,s^{-1}{ }\,\AA^{-1}}}$ and V0 is the dereddend apparent visual magnitude.

6 Kinematics

6.1 Radial velocities and proper motions

Radial velocities of the slowly rotating programme stars were derived from the lineshift of metal lines. For the rapidly rotating stars only the Balmer and He I lines could be used. Radial velocities obtained this way were then corrected to heliocentric values and the results are listed in Table 6. The error of the velocities estimated from the scatter of the velocities derived from individual lines is about 3-11 km $\rm {s^{-1}}$. Our measurements agree to within error limits with previous estimates (see Table 6).

Proper motions were taken from literature and are listed in Table 5.

 

 
Table 5: Data of proper motion. The position angle is counted positive east of north.
Name $\mu$ (mas/y) Position angle $^\circ $ Reference
PG 0122+214 3.4 $\pm$ 2.3 234 $\pm$ 71 1
PG 1533+467 16.8 $\pm$ 3.6 326 $\pm$ 0 1
PG 1610+239 8.1 $\pm$ 4.0 150 $\pm$ 16 1
PG 2219+094 6.2 $\pm$ 3.6 194 $\pm$ 47 1
BD-15$^\circ $115 9.0 $\pm$ 2.7 92 $\pm$ 10 2
PHL 346 8.9 $\pm$ 3.1 144 $\pm$ 20 3

References: (1) Thejll et al. (1997); (2) Perryman et al. (1997); (3) Tycho-2 catalog, Høg et al. (2000).


 

 
Table 6: Physical and kinematic parameters of the programme stars. Five stars have been analysed previously. The results of these analyses from literature are given for comparison. The errors of the evolutionary times are formal errors introduced by the errors in $ {T_{\rm eff}}$ and $\log {g}$.
Name $ {T_{\rm eff}}$ ${\log(\frac{g}{\rm cm~s^{-2}})}$ $v_{\rm rad}$ $v_{\rm e}$ M d z $T_{\rm flight}$ ${T_{\rm evol}}$
  K   km s-1 km s-1 $M_{\odot}$ kpc kpc Myr Myr
PG 0122+214 18300 3.86 $26\pm 5$ 290 6.7 9.6 6.2 $51 \pm 24$ $35 \pm 6$
                   
PG 1511+367 16100 4.15 $102\pm 11$ 300: 4.8 3.8 3.2 24: $34 \pm 7$
                   
PG 1533+467 18100 4.00 $33\pm 6$ 440 6.0 3.0 2.4 $20 \pm 4$ $33 \pm 5$
                   
PG 1610+239 15500 3.72 $91\pm10$ 130 5.8 8.4 5.9 >62 $54 \pm 10$
                   
PHL 159 18500 3.59 $88\pm 3$ 320: 8.0 5.3 3.2 31: $28 \pm 2$
                   
PG 2219+094 19500 3.58 $-24\pm9$ 220 8.7 9.8 6.1 $43 \pm 22$ $27 \pm 2$
(1) 17900 3.60 -7 - 7.5 - - 67 41
                   
BD-15$^\circ $115 20100 3.81 $93\pm 4$ 410 8.0 4.9 4.8 $30 \pm 5$ $26 \pm 4$
(2) 19500 3.50 94 - 10.0 - - 47 20
                   
HS 1914+7139 17600 3.90 - 330: 6.2 14.9 6.0 91:$^\star$ 39 $\pm$ 6
(3) 18000 3.75 -39 - 6.5-10.0 16-18.4 - - -
                   
PHL 346 20700 3.58 $63\pm4$ 350 9.9 8.7 7.4 $27 \pm 7$ $19 \pm 2$
(4) 22600 3.60 $ 66\pm10$ - 13.0 - 8.7 - 11
                   
SB 357 19700 3.90 $58\pm 10$ 230: 7.4 7.9 7.8 61: $26 \pm 4$
(2) 19000 3.70 54 - 8 - 9.0 64 25

$\textstyle \parbox{160mm}{{References}: (1) Rolleston et~al. (\cite{roha99}); ... ... et~al. (\cite{hemo95}).\\ : Uncertain due to the lack of proper motion data.}$  


6.2 Times-of-flight and ejection velocities

The times-of-flight, which the stars need to reach their current halo positions from the galactic disk, were calculated with the program ORBIT6 developed by Odenkirchen & Brosche (1992). This numerical code calculates the orbit of a test body in the Galactic potential of Allen & Santillan (1991). The complete set of cylindrical coordinates is integrated and positions and velocities are calculated in equidistant time steps. The input for this program version are equatorial coordinates, distance d from the sun, heliocentric radial velocities and observed absolute proper motions. Values for proper motions are given in Table 5. The proper motions for PHL 159, PG 1511+467, SB 357 and HS 1914+7139 were set to zero, because no measurements are available. We followed the orbits backwards in time (time steps of 0.01-0.1 Myr). The time of passage through the galactic disk (= change of sign in z-position relative to the disk) defines the time-of-flight $T_{\rm flight}$. The velocity at the time of first crossing of the galactic plane is regarded as the ejection velocity $v_{\rm e}$and is also calculated by the program ORBIT6.

Results for all parameters of the programme stars (effective temperature, gravity, radial velocity, ejection velocity, mass, distance, age and time-of-flight) are summarised in Table 6. For the origin of the stars (see next section) the ages ( ${T_{\rm evol}}$) and the times-of-flight ( $T_{\rm flight}$) are important. We improved $T_{\rm flight}$ for BD-15$^\circ $115 and PHL 346 for which proper motion measurements have become available recently. For BD-15$^\circ $115 we derive a somewhat lower $T_{\rm flight}$ than Conlon et al. (1992) and find $T_{\rm flight}$ to be consistent with ${T_{\rm evol}}$ to within our error limits. For PHL 346 we confirm that $T_{\rm flight}$ is slightly larger than ${T_{\rm evol}}$, but given the error limits this is insignificant.

For PG 2219+094 we find $T_{\rm flight}$ and ${T_{\rm evol}}$ to be lower than derived by Rolleston et al. (1999) and $T_{\rm flight}$ to be consistent with ${T_{\rm evol}}$. For PG 1610+239 the time-of-flight is poorly constrained and only a lower limit could be determined which is consistent with the estimate of the evolutionary time.

7 Discussion

We have carried out quantitative spectral analyses of ten apparently normal B-type stars. Their positions in the ( $ {T_{\rm eff}}$, $\log {g}$) diagram are consistent with models for main sequence stars. SB 357 shows emission in $\rm {H_{\beta}}$ and $\rm {H_{\gamma}}$, which confirms its classification as a Be star (Heber & Langhans 1986; Kilkenny 1989). Seven of the stars have rotational velocities >70 km $\rm {s^{-1}}$making detailed abundance analyses impossible. Mostly normal abundances with respect to $\iota $ Her were determined for BD-15$^\circ $115, PHL 159 and PHL 346. The Mg and O abundances of PHL 159 are significantly different from the comparison star and other normal B-type stars (Kilian 1994).

Calculated orbits based on measurements of radial velocity and proper motion allowed to determine times-of-flight from the galactic plane to their present position.

7.1 Runaway stars

Times-of-flight for PG 1511+367 and PG 1533+467 are smaller than the evolutionary times, indicating that these stars have been formed in the galactic plane and were then ejected (runaway stars). The times-of-flight are similar to the evolutionary times for PG 0122+214, PG 2219+094, PHL 159, BD-15$^\circ $115, and PG 1610+239, which implies that the stars could also have formed in the galactic disk and were then ejected very soon after their birth. Ejection velocities for all programme stars range from 130km s-1 to 440km s-1.

Three mechanisms for the production of runaway stars have been proposed in the literature:

i)
In the binary supernova scenario (Zwicky 1957; Blaauw 1961) the runaway star receives its velocity after a supernova explosion in a massive close binary. After the explosion the binary occasionally dissociates and the secondary is traveling with a velocity comparable to its pre-explosion orbital velocity. Calculations by Iben & Tutukov (1996) indicate that the runaway star can gain a velocity of 100 to 200km s-1;

ii)
In the dynamical ejection scenario (Poveda et al. 1967; Gies & Bolton 1986) the runaway star gains its velocity through a dynamical interaction with one or more stars. The most efficient encounter is that between two close binaries in a stellar association or open cluster, which in most cases results in the ejection of two runaway stars and one eccentric binary (Hoffer 1983; Mikkola 1983). Calculations by Leonard (1991) show that even velocities in excess of 1000km $\rm {s^{-1}}$ can be gained in rare cases;

iii)
It has been conjectured that star formation can be triggered by the interaction of the gas of the galactic disk with an infalling satellite dwarf galaxy. The momentum transferred to the gas results in a significant velocity component of the newly born stars perpendicular to the galactic plane. This scenario has been supported by the discovery of the encounter with the Sagittarius dwarf galaxy (Ibata et al. 1994).
The availability of precise milliarcsecond astrometry for nearby stars through the Hipparcos satellite and pulsar astrometry and timing measurements have recently demonstrated that both the binary supernova scenario and the dynamical ejection scenario are viable. By calculating orbits for runaway stars, pulsars and open clusters it recently became possible to associate runaway stars and pulsars with their nascent clusters (Hoogerwerf et al. 2000, 2001).

Our programme stars are too far away and their space motions are therefore not known accurately enough to allow to identify their relation to a young cluster or association in the galactic plane. However, the ejection velocities determined for our programme stars may be important to identify the mechanism which led to their ejection from the galactic plane, once reliable theoretical predictions become available for the different scenarios discussed above. Six stars have escape velocities exceeding 300km s-1 which seems too large to be achievable by the binary supernova scenario.

7.2 Stars born in the galactic halo?

Four stars in our sample have been proposed in the literature as candidates for B-type stars formed in the galactic halo because their times-of-flight were found to be considerably larer than the evolutionary time scales (Conlon et al. 1992; Keenan et al. 1986; Heber et al. 1995). As discussed above our new analysis of BD-15$^\circ $115 demonstrates that its time-of flight is consistent with the evolutionary time. Hence it could be runaway star, too.

For SB 357 and HS 1914+7139 the times of flight are more than twice as large as the evolutionary times, which would make formation in the disk unlikely. However, their times-of-flight are uncertain due to the lack of proper motion measurements. Such data are urgently needed before any firm conclusions can be drawn. Therefore we are reluctant to regard these stars as born in the halo.

PHL 346 has been proposed as a candidate massive B-type star born in the halo (Ryans et al. 1996; Hambly et al. 1996). Based on the new Tycho proper motion measurement, our analysis indicates that $T_{\rm flight}$ is marginally larger than ${T_{\rm evol}}$ and PHL 346 can be a runaway star, too.

Hence no conclusive candidate for a young massive B-type star formed in the halo remains in our sample. Proper motions for the four stars lacking any measurement should urgently be determined.

Acknowledgements
M.R. gratefully acknowledge financial support by the DFG (grant He1356/27-1). We thank Michael Odenkirchen who kindly provided us with his code ORBIT6 for the calculation of the kinematic orbits, Heinz Edelmann who carried out the DSAZ FOCES and ESO FEROS observations and Neil Reid, Ralf Napiwotzki and Klaus Werner who obtained the Keck HIRES spectra for us. S.M. was supported by a grant (50 OR 96029-ZA) from the Bundesministerium für Bildung und Forschung through the DLR.

References

 
Copyright ESO 2001