One of the key problems debated in recent years is the evolutionary status of very metal-deficient BCDs: are these galaxies young or old? To resolve this problem an analysis of the stellar populations is required. The metallicity of the galaxy is one of the key parameters that determines the photometric properties of stellar populations. Izotov & Thuan (1999), considering the abundance ratios of the heavy elements in BCDs, have suggested that the BCDs with 12 + log (O/H)
![]() 7.6 might be young unevolved galaxies. SBS 0940+544 fulfills this abundance condition.
Furthermore, the nitrogen-to-oxygen abundance ratios log(N/O) = -1.65
7.6 might be young unevolved galaxies. SBS 0940+544 fulfills this abundance condition.
Furthermore, the nitrogen-to-oxygen abundance ratios log(N/O) = -1.65 ![]() 0.02 and -1.60
0.02 and -1.60 ![]() 0.05 derived respectively from the Keck II and MMT spectra (Table 3) are confined to the narrow range obtained earlier by Thuan et al. (1995) and Izotov & Thuan (1999) for extremely metal-poor BCDs. The constancy of the N/O abundance ratio in these BCDs
with a very small spread of values around the mean suggests that the production of primary nitrogen occurs in massive stars only and hence these systems are likely to be young, since intermediate-mass stars have not had time to release their nucleosynthetic products. On the other hand, some recent chemical evolution models have been succesful in reproducing the observed constancy of the N/O ratio, with nitrogen produced by the longer-lived intermediate-mass stars (Pilyugin 1999; Henry et al. 2000).
0.05 derived respectively from the Keck II and MMT spectra (Table 3) are confined to the narrow range obtained earlier by Thuan et al. (1995) and Izotov & Thuan (1999) for extremely metal-poor BCDs. The constancy of the N/O abundance ratio in these BCDs
with a very small spread of values around the mean suggests that the production of primary nitrogen occurs in massive stars only and hence these systems are likely to be young, since intermediate-mass stars have not had time to release their nucleosynthetic products. On the other hand, some recent chemical evolution models have been succesful in reproducing the observed constancy of the N/O ratio, with nitrogen produced by the longer-lived intermediate-mass stars (Pilyugin 1999; Henry et al. 2000).
Deep V, R, I, and H![]() imaging, high signal-to-noise ratio spectra showing strong emission lines and the detection of hydrogen Balmer absorption lines in the main body of SBS 0940+544 enable the study of stellar populations and constraint of their ages through various techniques.
imaging, high signal-to-noise ratio spectra showing strong emission lines and the detection of hydrogen Balmer absorption lines in the main body of SBS 0940+544 enable the study of stellar populations and constraint of their ages through various techniques.
The light of the brightest H II region of the galaxy is dominated by a very young stellar population. The very blue continuum and large EW(H![]() )
= 241-250 Å (Fig. 5, Table 2) are consistent with an age of an instantaneous burst not exceeding 4 Myr, for a metallicity Z = 1/20-1/50
)
= 241-250 Å (Fig. 5, Table 2) are consistent with an age of an instantaneous burst not exceeding 4 Myr, for a metallicity Z = 1/20-1/50 ![]() (Fig. 6). However, despite that young age, no Wolf-Rayet stars are detected in our high signal-to-noise ratio spectra. We also note that the nebular He II
(Fig. 6). However, despite that young age, no Wolf-Rayet stars are detected in our high signal-to-noise ratio spectra. We also note that the nebular He II ![]() 4686 emission line is not detected in the MMT spectrum and its intensity in the Keck II spectrum is only 0.6% of H
4686 emission line is not detected in the MMT spectrum and its intensity in the Keck II spectrum is only 0.6% of H![]() ,
or several times weaker than in the very metal-deficient BCDs I Zw 18, SBS 0335-052 and Tol 1214-277 with detected Wolf-Rayet stellar populations (Izotov et al. 1997a; Izotov et al. 1999; Fricke et al. 2001).
,
or several times weaker than in the very metal-deficient BCDs I Zw 18, SBS 0335-052 and Tol 1214-277 with detected Wolf-Rayet stellar populations (Izotov et al. 1997a; Izotov et al. 1999; Fricke et al. 2001).
The interpretation of the photometric data for the brightest H II region is not straightforward because of the strong contamination of stellar radiation by the emission of the ionized gas. The colour V-I ![]() -0.5 mag is too blue to be explained even by the
youngest stellar population, because
-0.5 mag is too blue to be explained even by the
youngest stellar population, because ![]() 40% of the V light is contributed by the very strong oxygen emission lines [O III]
40% of the V light is contributed by the very strong oxygen emission lines [O III] ![]() 4959,
4959, ![]() 5007. Therefore broad-band photometry
alone is not sufficient to constrain the age of young star-forming regions. However, spectroscopic data in conjunction with photometric data allows us to disentangle stellar from gaseous emission.
5007. Therefore broad-band photometry
alone is not sufficient to constrain the age of young star-forming regions. However, spectroscopic data in conjunction with photometric data allows us to disentangle stellar from gaseous emission.
Data for bright H II regions do not permit the detection of the small fraction of light contributed by an old stellar population (e.g., Papaderos et al. 1998; Fricke et al. 2001; Noeske et al. 2000). The old population in such regions, if present, is hidden by the strong emission from the young stars and the gas ionized by the numerous massive stars in the star-forming region. More promising for the detection of an old stellar population is the study of the underlying extended emission from the host galaxy as gaseous contamination is minimized there. Nearly all BCDs show an underlying stellar component with red colours, consistent with ages greater than a few Gyr (Loose & Thuan 1986; Papaderos et al. 1996a,1996b; Telles & Terlevich 1997). However, the colours of the extended emission in the few very low metallicity BCDs are consistent with younger ages.
Another method for deriving ages is by fitting the observed galaxy spectral energy distribution (SED) with theoretical SEDs for various stellar population ages and star formation histories. This method has been applied to several extremely metal-deficient BCDs with Z = (1/20-1/40)![]() (e.g., SBS 0335-052, Papaderos et al. 1998; SBS 1415+437, Thuan et al. 1999a; and Tol 1214-277, Fricke et al. 2001). The SED of the underlying stellar component in these galaxies, obtained after subtraction of the ionized gas emission from the observed spectrum,
could be fitted by a stellar population not older than a few hundred Myr.
(e.g., SBS 0335-052, Papaderos et al. 1998; SBS 1415+437, Thuan et al. 1999a; and Tol 1214-277, Fricke et al. 2001). The SED of the underlying stellar component in these galaxies, obtained after subtraction of the ionized gas emission from the observed spectrum,
could be fitted by a stellar population not older than a few hundred Myr.
However, both methods are subject to uncertainties introduced by extinction. Therefore, other less extinction-dependent methods are desirable to better constrain the age of stellar populations. We use in this section two such methods. One relies on the Balmer nebular emission line equivalent widths and the other on the Balmer stellar absorption line equivalent widths. Such an analysis is feasible because of the exceptionally high quality of the Keck II and MMT spectra. Because age estimates from all the above mentioned methods depend on the adopted star formation history in the galaxy, we next consider different scenarios of star formation (instantaneous burst, continuous star formation) with varying extinction and star formation rate (SFR). We then put together the constraints imposed on the stellar age and extinction by all four methods to draw a consistent picture for the populations in SBS 0940+544.
| Telescope | # of region | Distancea | Apertureb | F(H |
F(H |
EW(H |
EW(H |
C(H |
|
| Keck IIe | 1 | 6.3 |
|
|
|
|
|
|
|
| 2 | 9.1 |
|
|
|
|
|
|
||
| 3 | 12.2 |
|
|
|
|
|
|
||
| 4 | 16.4 |
|
|
|
|
|
|
||
| MMTe | 1a | 6.3 |
|
|
|
|
|
|
|
| 2a | 9.0 |
|
|
|
|
|
|
||
| 3a | 12.6 |
|
|
|
|
|
|
||
| 4a | 16.8 |
|
|
|
|
|
|
||
| MMTf | 5 | 8.0 |
|
|
|
|
|
|
|
| 6 | 7.0 |
|
|
|
|
|
|
a Distance in arcsec from the brightest H II region.
b Aperture x![]() y where x is the slit width and y the size
along the slit in arcsec.
y where x is the slit width and y the size
along the slit in arcsec.
c In units 10-16 erg s-1 cm-2.
d In Å.
e Slit orientation with position angle PA = -41![]() .
.
f Slit orientation with position angle PA = 0![]() .
.
Under the assumption of an ionization-bounded H II region, the strongest hydrogen recombination emission lines H![]() and H
and H![]() provide an estimate of the age of the young stellar population when late O and early B stars are still present. The ionizing flux from such a young stellar population and hence the equivalent widths of the Balmer emission lines have a very
strong temporal evolution.
provide an estimate of the age of the young stellar population when late O and early B stars are still present. The ionizing flux from such a young stellar population and hence the equivalent widths of the Balmer emission lines have a very
strong temporal evolution.
Fluxes and equivalent widths of the H![]() and H
and H![]() emission lines are obtained for all four regions in the main body. Because the H
emission lines are obtained for all four regions in the main body. Because the H![]() emission line is narrower than the absorption line in
these regions and does not fill the absorption component, its flux was measured using the continuum level at the bottom of the absorption line. This level has been chosen by visually interpolating from the absorption line wings to the center of the line. The extinction coefficient C(H
emission line is narrower than the absorption line in
these regions and does not fill the absorption component, its flux was measured using the continuum level at the bottom of the absorption line. This level has been chosen by visually interpolating from the absorption line wings to the center of the line. The extinction coefficient C(H![]() )
in those regions is derived from the H
)
in those regions is derived from the H![]() /H
/H![]() flux ratio. For this, the theoretical recombination H
flux ratio. For this, the theoretical recombination H![]() /H
/H![]() flux ratio of 2.8 is adopted, which is typical for hot low-metallicity H II regions. No correction for the absorption line equivalent width has been made in this case. Results of the measurements together with errors are shown in Table
4. In Fig. 6 we compare the measured H
flux ratio of 2.8 is adopted, which is typical for hot low-metallicity H II regions. No correction for the absorption line equivalent width has been made in this case. Results of the measurements together with errors are shown in Table
4. In Fig. 6 we compare the measured H![]() and H
and H![]() emission line equivalent widths with those predicted at a given age of an instantaneous burst. The time
evolution of the H
emission line equivalent widths with those predicted at a given age of an instantaneous burst. The time
evolution of the H![]() and H
and H![]() emission line equivalent widths for the heavy element mass fractions
emission line equivalent widths for the heavy element mass fractions ![]() /50 (thick solid lines) and
/50 (thick solid lines) and ![]() /20 (thick dashed lines) is calculated using the galactic evolution code PEGASE.2 (Fioc & Rocca-Volmerange 1997). This code is based on the Padua isochrones (Bertelli et al. 1994) and stellar atmosphere models from Lejeune et al. (1998). Thin solid and dotted horizontal lines indicate respectively the highest and lowest observed equivalent widths of H
/20 (thick dashed lines) is calculated using the galactic evolution code PEGASE.2 (Fioc & Rocca-Volmerange 1997). This code is based on the Padua isochrones (Bertelli et al. 1994) and stellar atmosphere models from Lejeune et al. (1998). Thin solid and dotted horizontal lines indicate respectively the highest and lowest observed equivalent widths of H![]() and H
and H![]() for the 4 regions
of the underlying galaxy. The shaded region shows that the ages range between 10 and 20 Myr, meaning that the gas in the main body is likely ionized by early B stars rather than by O stars.
for the 4 regions
of the underlying galaxy. The shaded region shows that the ages range between 10 and 20 Myr, meaning that the gas in the main body is likely ionized by early B stars rather than by O stars.
This age estimate is valid if the population of ionizing stars is large enough and can be described by an initial mass function (IMF) with an analytical form, for example a Salpeter IMF. However, in the case of the main body of SBS 0940+544, the number of ionizing stars is small and stochastic
effects in the distribution of stars of different masses might be important. In particular, because of stochastic star formation, the ionization may be caused by a few O stars instead of a population of B stars. Taking the number of ionizing Lyc photons to be respectively 1049 s-1
and 1048 s-1 for a O7 V and a B0 V star (Vacca et al. 1996), we find from the observed fluxes of the H![]() emission line that the number of O7 V and B0 V stars is in the range 2-7 and 23-70, respectively, depending on the location in the main body (see Table 4). Assuming a Salpeter IMF with a slope 2.35, and upper and lower star mass limits of 120
emission line that the number of O7 V and B0 V stars is in the range 2-7 and 23-70, respectively, depending on the location in the main body (see Table 4). Assuming a Salpeter IMF with a slope 2.35, and upper and lower star mass limits of 120 ![]() and 2
and 2 ![]() ,
we derive a total mass 104-105
,
we derive a total mass 104-105 ![]() for the young stellar population. Cerviño et al. (2000) have analyzed the stochastic nature of the IMF in young stellar clusters with solar metallicity. In particular, they find that
in the range of equivalent widths EW(H
for the young stellar population. Cerviño et al. (2000) have analyzed the stochastic nature of the IMF in young stellar clusters with solar metallicity. In particular, they find that
in the range of equivalent widths EW(H![]() )
= 1-10 Å, the dispersion of age at fixed EW(H
)
= 1-10 Å, the dispersion of age at fixed EW(H![]() )
is not greater than 5%-10% if the total mass of the cluster lies in the range 104-105
)
is not greater than 5%-10% if the total mass of the cluster lies in the range 104-105 ![]() .
Hence, we argue that stochastic effects in SBS 0940+544 do not significantly change our age estimate from the hydrogen emission line equivalent widths.
.
Hence, we argue that stochastic effects in SBS 0940+544 do not significantly change our age estimate from the hydrogen emission line equivalent widths.
Another extinction-insensitive method for determining the age of stellar populations is based on equivalent widths of absorption features. It can be used for larger ages than the nebular emission line method because the longer-lived B and A stars show more prominent hydrogen absorption lines.
Gonzalez Delgádo & Leitherer (1999) and Gonzalez Delgádo et al. (1999) calculated a grid of synthetic profiles of stellar hydrogen Balmer absorption lines for effective temperatures and gravities characteristic of starburst galaxies. They developed evolutionary stellar population synthesis models, synthesizing the profiles of the hydrogen Balmer absorption lines from H![]() to H13 for instantaneous bursts with ages ranging from 106 to 109 yr, in the case of a stellar initial mass function with a Salpeter slope and mass cutoffs
to H13 for instantaneous bursts with ages ranging from 106 to 109 yr, in the case of a stellar initial mass function with a Salpeter slope and mass cutoffs
![]() = 1
= 1 ![]() and
and
![]() = 80
= 80 ![]() .
Their models predict a steady increase in the equivalent widths with age. However, at larger ages
.
Their models predict a steady increase in the equivalent widths with age. However, at larger ages
![]() 1 Gyr the situation is the opposite and the equivalent widths of the absorption lines decrease with age (Bica & Alloin 1986).
1 Gyr the situation is the opposite and the equivalent widths of the absorption lines decrease with age (Bica & Alloin 1986).
| Telescope | # of region | Distancea | Apertureb | EW(H |
EW(H |
EW(H |
EW(H |
|
| Keck IId | 1 | 6.3 |
|
|
|
|
|
|
| 2 | 9.1 |
|
|
|
|
|
||
| 3 | 12.2 |
|
|
|
|
|
||
| 4 | 16.4 |
|
|
|
|
|
||
| MMTd | 1a | 6.3 |
|
|
|
|
|
|
| 2a | 9.0 |
|
|
|
|
|
||
| 3a | 12.6 |
|
|
|
|
|
||
| 4a | 16.8 |
|
|
|
|
|
||
| MMTe | 5 | 8.0 |
|
|
|
|
|
|
| 6 | 7.0 |
|
|
|
|
|
a Distance in arcsec from the brightest H II region.
b Aperture x![]() y where x is the slit width and y the size
along the slit in arcsec.
y where x is the slit width and y the size
along the slit in arcsec.
c In Å.
d Slit orientation with position angle PA = -41![]() .
.
e Slit orientation with position angle PA = 0![]() .
.
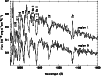 |
Figure 7:
Keck II spectra of regions 1 and 3 (respectively at 6
|
The hydrogen absorption lines due to the underlying stellar populations are seen clearly along the whole elongated main body of SBS 0940+544. We show in Fig. 7 the H![]() ,
H
,
H![]() and other hydrogen absorption lines in two regions along the slit oriented with position angle
PA = -41
and other hydrogen absorption lines in two regions along the slit oriented with position angle
PA = -41![]() .
A weak K Ca II absorption line is also present. While the H
.
A weak K Ca II absorption line is also present. While the H![]() nebular emission line is superimposed on the absorption line in region 1, it is not seen in region 3.
nebular emission line is superimposed on the absorption line in region 1, it is not seen in region 3.
We measured the parameters of the H![]() and H
and H![]() absorption lines in 4 regions along the main body. A careful placement of the continuum is very important for deriving accurate EWs. To define the continuum level, we select several points in the spectral regions free of nebular and stellar lines. The continuum is then fitted by cubic splines and the quality of the continuum fit
is visually checked. Although the contamination of the absorption lines by nebular emission in regions 2, 3 and 4 is very small, not more than a few percent, we have corrected the absorption equivalent widths for it. For this purpose the expected fluxes of the H
absorption lines in 4 regions along the main body. A careful placement of the continuum is very important for deriving accurate EWs. To define the continuum level, we select several points in the spectral regions free of nebular and stellar lines. The continuum is then fitted by cubic splines and the quality of the continuum fit
is visually checked. Although the contamination of the absorption lines by nebular emission in regions 2, 3 and 4 is very small, not more than a few percent, we have corrected the absorption equivalent widths for it. For this purpose the expected fluxes of the H![]() and H
and H![]() emission lines have been calculated from the flux of the H
emission lines have been calculated from the flux of the H![]() emission line. Then these fluxes have been subtracted from the negative fluxes of the absorption lines. Here we adopt theoretical recombination H
emission line. Then these fluxes have been subtracted from the negative fluxes of the absorption lines. Here we adopt theoretical recombination H![]() /H
/H![]() and H
and H![]() /H
/H![]() flux ratios at an electron temperature
flux ratios at an electron temperature ![]() = 104 K and an electron number density
= 104 K and an electron number density ![]() = 102 cm-3. We do not correct for extinction. Extinction correction would result in lower
= 102 cm-3. We do not correct for extinction. Extinction correction would result in lower
![]() and smaller ages. Hence the ages derived in this section are upper limits.
and smaller ages. Hence the ages derived in this section are upper limits.
We measured equivalent widths for only the H![]() and H
and H![]() absorption lines. Although higher-order hydrogen Balmer absorption lines are seen in the spectrum of the main body, they are not suitable for age determination because of (a) the relatively low signal-to-noise ratio of the spectra at short wavelengths and uncertainties in the placement of the continuum in the blue region due to many blended absorption features, and (b) the weak dependence of their equivalent widths on age (Gonzalez Delgádo et al. 1999). Additionally, the H
absorption lines. Although higher-order hydrogen Balmer absorption lines are seen in the spectrum of the main body, they are not suitable for age determination because of (a) the relatively low signal-to-noise ratio of the spectra at short wavelengths and uncertainties in the placement of the continuum in the blue region due to many blended absorption features, and (b) the weak dependence of their equivalent widths on age (Gonzalez Delgádo et al. 1999). Additionally, the H![]() absorption line is blended with the H Ca II absorption line.
absorption line is blended with the H Ca II absorption line.
The measured and corrected equivalent widths of H![]() and H
and H![]() absorption lines in the Keck II and MMT spectra are listed in Table 5. The errors include uncertainties in the placement of the continuum. In Fig. 8 the measured (dashed lines) and corrected (solid lines) equivalent widths of the H
absorption lines in the Keck II and MMT spectra are listed in Table 5. The errors include uncertainties in the placement of the continuum. In Fig. 8 the measured (dashed lines) and corrected (solid lines) equivalent widths of the H![]() and H
and H![]() absorption lines are shown for the 4 regions along the main body of SBS 0940+544. Note that the corrected equivalent widths of H
absorption lines are shown for the 4 regions along the main body of SBS 0940+544. Note that the corrected equivalent widths of H![]() and H
and H![]() do not show statistically significant spatial variations.
do not show statistically significant spatial variations.
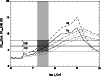 |
Figure 9:
Equivalent widths of H |
Figure 9 shows the predicted behaviour of the equivalent widths of H![]() (thick solid line) and H
(thick solid line) and H![]() (thick dashed line) absorption lines with age for an instantaneous burst at a metallicity Z = 1/20
(thick dashed line) absorption lines with age for an instantaneous burst at a metallicity Z = 1/20 ![]() from Gonzalez Delgádo et al. (1999) for ages
from Gonzalez Delgádo et al. (1999) for ages ![]() 1 Gyr and Bica & Alloin (1986) for ages >1 Gyr. The upper and lower limits of the corrected EW(H
1 Gyr and Bica & Alloin (1986) for ages >1 Gyr. The upper and lower limits of the corrected EW(H![]() )
and EW(H
)
and EW(H![]() )
in the 4 regions along the main body of the galaxy are shown respectively by thin solid and dotted horizontal lines. The shaded rectangular region gives age limits, ranging between 15 and 50 Myr. Though slightly larger, this age estimate is
consistent with that obtained from the nebular emission line analysis, particularly since it constitutes an upper limit. Instantaneous burst models also predict low EW(H
)
in the 4 regions along the main body of the galaxy are shown respectively by thin solid and dotted horizontal lines. The shaded rectangular region gives age limits, ranging between 15 and 50 Myr. Though slightly larger, this age estimate is
consistent with that obtained from the nebular emission line analysis, particularly since it constitutes an upper limit. Instantaneous burst models also predict low EW(H![]() )
and
EW(H
)
and
EW(H![]() )
at age
)
at age ![]() 10 Gyr. However, this age is inconsistent with the one derived from the emission line equivalent widths.
10 Gyr. However, this age is inconsistent with the one derived from the emission line equivalent widths.
Useful constraints on the ages of stellar populations can also be obtained from the spectral energy distribution (SED). As already pointed out, this method is subject to the effects of interstellar extinction. However, the combination of the spectral energy distribution method with the methods discussed in Sects. 5.1.1 and 5.1.2 can be used for a simultaneous derivation of the age and extinction.
To fit the observed SEDs, we use the galactic evolution code PEGASE.2 (Fioc & Rocca-Volmerange 1997) to produce a grid of theoretical SEDs for an instantaneous burst of star formation and ages ranging between 0 and 10 Gyr, and a heavy element mass fraction of Z = 1/20 ![]() .
An initial mass function with a Salpeter slope (
.
An initial mass function with a Salpeter slope (![]() = -2.35), and upper and lower mass limits of 120
= -2.35), and upper and lower mass limits of 120 ![]() and 0.1
and 0.1 ![]() are adopted. Because the equivalent widths of hydrogen emission lines in all 4 regions along the main body are small, the contribution of the ionized gas
emission is not significant. For this reason we do not include gaseous emission in the SED calculations. Hence, photometric and spectroscopic data give us direct information
on stellar populations if the interstellar extinction is known.
are adopted. Because the equivalent widths of hydrogen emission lines in all 4 regions along the main body are small, the contribution of the ionized gas
emission is not significant. For this reason we do not include gaseous emission in the SED calculations. Hence, photometric and spectroscopic data give us direct information
on stellar populations if the interstellar extinction is known.
The extinction in each region can be estimated from the observed decrement of the Balmer emission lines. Many strong hydrogen emission lines are present in the brightest H II region a
(Fig. 5) which allow a precise determination of the extinction. From the Keck II and MMT spectra of this region we derive very low values of C(H![]() ), 0.08
), 0.08 ![]() 0.02 and 0.00
0.02 and 0.00 ![]() 0.01 respectively. The H
0.01 respectively. The H![]() and H
and H![]() emission lines are also present in the main body, though weaker. We use the fluxes of these lines to derive C(H
emission lines are also present in the main body, though weaker. We use the fluxes of these lines to derive C(H![]() )
in different regions along the slit. The results are shown in Table 4 and in Fig. 10. We
note that, in general, the extinction in the main body, derived from the observed Balmer decrement, is significantly larger than that in the brightest H II region, with a maximum C(H
)
in different regions along the slit. The results are shown in Table 4 and in Fig. 10. We
note that, in general, the extinction in the main body, derived from the observed Balmer decrement, is significantly larger than that in the brightest H II region, with a maximum C(H![]() )
)
![]() 0.3 in region 3 at a distance of
0.3 in region 3 at a distance of ![]() 12
12
![]() (or
(or ![]() 1.5 kpc) from the brightest H II region.
1.5 kpc) from the brightest H II region.
In principle, the extinction can also be derived from the SEDs of regions 1-4, adopting the age of the stellar population derived from the equivalent widths of the hydrogen emission and absorption lines. First we assume C(H![]() )
= 0. Then the observed SEDs are redder than the theoretical SED of a stellar population with age t = 20 Myr (lower spectra in Figs. 11a-d). One of the reasons for the difference between the observed and theoretical SEDs is that interstellar extinction in the main body is not negligible and it
modifies the observed spectral energy distribution. To derive C(H
)
= 0. Then the observed SEDs are redder than the theoretical SED of a stellar population with age t = 20 Myr (lower spectra in Figs. 11a-d). One of the reasons for the difference between the observed and theoretical SEDs is that interstellar extinction in the main body is not negligible and it
modifies the observed spectral energy distribution. To derive C(H![]() )
we adopt an age
of the stellar population in each of the regions 1-4 equal to 20 Myr, as a representative value derived from the hydrogen emission and absorption line equivalent widths. We then compute the extinction coefficient C(H
)
we adopt an age
of the stellar population in each of the regions 1-4 equal to 20 Myr, as a representative value derived from the hydrogen emission and absorption line equivalent widths. We then compute the extinction coefficient C(H![]() )
to achieve the best agreement between the observed SED after correction for interstellar extinction and the theoretical SED. The observed extinction-corrected
SEDs are superimposed on the synthetic 20 Myr stellar population SED for regions 1 to 4 in Figs. 11a-d (upper spectra). They are labeled by the derived values of C(H
)
to achieve the best agreement between the observed SED after correction for interstellar extinction and the theoretical SED. The observed extinction-corrected
SEDs are superimposed on the synthetic 20 Myr stellar population SED for regions 1 to 4 in Figs. 11a-d (upper spectra). They are labeled by the derived values of C(H![]() ). These values are consistent with those derived from the H
). These values are consistent with those derived from the H![]() /H
/H![]() flux ratios (Table 4, Fig. 10). However, despite this consistency, it is seen from Fig. 11, that the observed SEDs (upper spectra) at
flux ratios (Table 4, Fig. 10). However, despite this consistency, it is seen from Fig. 11, that the observed SEDs (upper spectra) at ![]()
![]() 3900 Å are not well fitted by the theoretical SEDs. Hence, we conclude that the instantaneous burst models do not adequately reproduce the observed properties of the SBS 0940+544 main body.
3900 Å are not well fitted by the theoretical SEDs. Hence, we conclude that the instantaneous burst models do not adequately reproduce the observed properties of the SBS 0940+544 main body.
Our estimates for the stellar population age in SBS 0940+544 made in Sect. 5.1 are based on the assumption of an instantaneous burst of star formation. Now we consider how the age of the
stellar population is changed if star formation is continuous. For this we adopt a constant star formation rate in the interval between the time ![]() when star formation starts and
when star formation starts and ![]() when it stops. Time is zero now and increases to the past. It is customary to consider models with a constant star formation rate, with star formation continuing until now, i.e. with
when it stops. Time is zero now and increases to the past. It is customary to consider models with a constant star formation rate, with star formation continuing until now, i.e. with ![]() = 0. However, we will also consider models with
= 0. However, we will also consider models with ![]() > 0 because of the following reason. The number of the ionizing photons in regions 1-4 derived from the H
> 0 because of the following reason. The number of the ionizing photons in regions 1-4 derived from the H![]() luminosity is in the range N(Lyc) = (2-7)
luminosity is in the range N(Lyc) = (2-7) ![]() 1049 s-1, several times lower than N(Lyc) emitted by a single star with mass
1049 s-1, several times lower than N(Lyc) emitted by a single star with mass ![]() 100
100 ![]() (Vacca et al. 1996). Hence, an IMF with a high
(Vacca et al. 1996). Hence, an IMF with a high
![]() does not strictly apply. There are however several circumstances which may explain the lack of ionizing photons: (a) stochastic effects on the IMF; (b) the major part (more than 50%) of the ionizing photons escapes the H II region or is absorbed by dust; (c) the IMF upper mass limit is truncated at
does not strictly apply. There are however several circumstances which may explain the lack of ionizing photons: (a) stochastic effects on the IMF; (b) the major part (more than 50%) of the ionizing photons escapes the H II region or is absorbed by dust; (c) the IMF upper mass limit is truncated at ![]() 30
30 ![]() ;
(d) star formation in regions 1-4 stopped several Myr ago, i.e.
;
(d) star formation in regions 1-4 stopped several Myr ago, i.e. ![]() > 0. We have considered all of these possibilities (except for (a)) in fitting the data and found that the result is not changed significantly. Therefore, in the subsequent discussion we use models with
> 0. We have considered all of these possibilities (except for (a)) in fitting the data and found that the result is not changed significantly. Therefore, in the subsequent discussion we use models with
![]() = 120
= 120 ![]() and
and ![]()
![]() 0.
0.
We use the model equivalent widths of hydrogen emission and absorption lines and SEDs for instantaneous bursts (Fioc & Rocca-Volmerange 1997; Gonzalez Delgádo et al. 1999; Bica & Alloin 1986) to calculate the temporal evolution of the equivalent widths of hydrogen emission and absorption lines in the case of continuous constant star
formation. The results are given in Figs. 6 and 9. The temporal dependences of the equivalent widths of the H![]() and H
and H![]() emission lines (Fig. 6), and the H
emission lines (Fig. 6), and the H![]() and H
and H![]() absorption lines (Fig. 9)
are shown for continuous star formation starting at time
absorption lines (Fig. 9)
are shown for continuous star formation starting at time ![]() ,
as defined by the abscissa value, and stopping at
,
as defined by the abscissa value, and stopping at ![]() = 0 Myr (dotted line) and
= 0 Myr (dotted line) and ![]() = 8 Myr (dash-dotted line). The equivalent widths of the H
= 8 Myr (dash-dotted line). The equivalent widths of the H![]() and H
and H![]() emission lines and of the H
emission lines and of the H![]() and H
and H![]() absorption lines in the spectrum of the stellar population formed between
absorption lines in the spectrum of the stellar population formed between ![]() and
and
![]() are represented in Figs. 6 and 9 by the values of EW at time
are represented in Figs. 6 and 9 by the values of EW at time ![]() .
At a fixed EW, it is seen that the younger the youngest stars, the larger the time interval
.
At a fixed EW, it is seen that the younger the youngest stars, the larger the time interval
![]() ,
i.e. the older the oldest stars.
,
i.e. the older the oldest stars.
Can the observed SEDs of regions 1-4 be fitted with only a young stellar population continuously formed over the last 100 Myr? To fit the observed SEDs and derive the extinction in regions 1-4
of the main body in the case of continuous star formation, we consider star formation occurring between ![]() = 8 Myr and
= 8 Myr and ![]() = 100 Myr. This model predicts EW(H
= 100 Myr. This model predicts EW(H![]() )
= 7.2 Å, EW(H
)
= 7.2 Å, EW(H![]() )
= 6.0 Å, and EW(H
)
= 6.0 Å, and EW(H![]() )
= 3.5 Å, EW(H
)
= 3.5 Å, EW(H![]() )
= 21.2 Å,
close to the values observed in regions 2 and 3 (Tables 4 and 5). However, the observed emission line equivalent widths in regions 1 and 4 are larger than the predicted values. For these two regions, a more appropriate model is that with
)
= 21.2 Å,
close to the values observed in regions 2 and 3 (Tables 4 and 5). However, the observed emission line equivalent widths in regions 1 and 4 are larger than the predicted values. For these two regions, a more appropriate model is that with ![]() < 100 Myr and/or
< 100 Myr and/or ![]() < 8 Myr. We show in Fig. 12 the results of our fitting. As in the case of an instantaneous burst, we adjust the extinction coefficient C(H
< 8 Myr. We show in Fig. 12 the results of our fitting. As in the case of an instantaneous burst, we adjust the extinction coefficient C(H![]() )
to achieve the best agreement between the observed SED after correction for interstellar extinction and the theoretical SED. The observed extinction-corrected SEDs are superimposed on the synthetic stellar population SED for regions 1 to 4 in Figs. 12a-d. They are labeled by the derived values of C(H
)
to achieve the best agreement between the observed SED after correction for interstellar extinction and the theoretical SED. The observed extinction-corrected SEDs are superimposed on the synthetic stellar population SED for regions 1 to 4 in Figs. 12a-d. They are labeled by the derived values of C(H![]() ). These values
are in agreement with those derived from the H
). These values
are in agreement with those derived from the H![]() /H
/H![]() flux ratio. Note that the synthetic SEDs with continuous star formation reproduce better the observed spectra in the spectral
range
flux ratio. Note that the synthetic SEDs with continuous star formation reproduce better the observed spectra in the spectral
range ![]() < 3900 Å than those calculated on the assumption of an instantaneous burst.
This makes continuous star formation in the main body of SBS 0940+544, occuring during the last 100 Myr, a possible interpretation.
< 3900 Å than those calculated on the assumption of an instantaneous burst.
This makes continuous star formation in the main body of SBS 0940+544, occuring during the last 100 Myr, a possible interpretation.
We next consider different continuous star formation scenarios in which an old stellar population is present in the main body of SBS 0940+544. For this, we again adopt C(H![]() )
= 0 and consider models with constant and varying SFRs with ages ranging between 0 and 10 Gyr. Specifically, for a varying SFR, we consider two periods of continuous star formation with constant but different SFRs, occurring in the age interval
)
= 0 and consider models with constant and varying SFRs with ages ranging between 0 and 10 Gyr. Specifically, for a varying SFR, we consider two periods of continuous star formation with constant but different SFRs, occurring in the age interval ![]() 100 Myr and >100 Myr. To quantify the recent-to-past star formation rate ratio, we introduce the parameter b = SFR(t
100 Myr and >100 Myr. To quantify the recent-to-past star formation rate ratio, we introduce the parameter b = SFR(t ![]() 100 Myr)/SFR(t > 100 Myr). First we consider models with constant star formation during the whole 0-10 Gyr range, i.e. models with b = 1. In Figs. 13a-d we show such SEDs superimposed on the observed spectra of regions 1-4. It is evident that these models do not reproduce the observed SEDs. However, by increasing the parameter b we can fit the observed SEDs. These theoretical SEDs are labeled by b > 1 in Figs. 13a-d. The predicted equivalent widths of the emission and absorption hydrogen lines are also in agreement with the observed ones. If non-negligible extinction is present in regions 1-4 then to fit the observed SEDs, the parameter b should be further increased. In particular, if the extinction C(H
100 Myr)/SFR(t > 100 Myr). First we consider models with constant star formation during the whole 0-10 Gyr range, i.e. models with b = 1. In Figs. 13a-d we show such SEDs superimposed on the observed spectra of regions 1-4. It is evident that these models do not reproduce the observed SEDs. However, by increasing the parameter b we can fit the observed SEDs. These theoretical SEDs are labeled by b > 1 in Figs. 13a-d. The predicted equivalent widths of the emission and absorption hydrogen lines are also in agreement with the observed ones. If non-negligible extinction is present in regions 1-4 then to fit the observed SEDs, the parameter b should be further increased. In particular, if the extinction C(H![]() )
= 0.28 derived for region 2 from the H
)
= 0.28 derived for region 2 from the H![]() /H
/H![]() flux ratio is adopted then the parameter b should be as high as
flux ratio is adopted then the parameter b should be as high as ![]() 100 to fit observations.
100 to fit observations.
In summary, analysis of the spectroscopic data for the main body of SBS 0940+544 shows that
the stellar population can be equally well reproduced by a model of continuous star formation during the last 100 Myr, or by a model in which stars are continuously formed in the period 0-10 Gyr.
In the former case, the extinction, as derived from the H![]() /H
/H![]() flux ratio, should be taken into account. In the latter case, a fit to the observed SED is only possible when b> 5, i.e. the star formation rate in the main body of SBS 0940+544 has significantly increased over the last 100 Myr.
flux ratio, should be taken into account. In the latter case, a fit to the observed SED is only possible when b> 5, i.e. the star formation rate in the main body of SBS 0940+544 has significantly increased over the last 100 Myr.
An upper limit to the age of the stellar population in SBS 0940+544 can in principle be derived from photometric and spectroscopic measurements of the faint (
![]() 24-24.5 mag arcsec-2) region d (cf. Fig. 1a).
24-24.5 mag arcsec-2) region d (cf. Fig. 1a).
As discussed in Sect. 3.1 the V-I and V-R colours in this region are only slightly redder than the average respective values of 0.58 mag and 0.33 mag derived for the outskirts of SBS 0940+544 from Fig. 4, thus it may be considered representative for the stellar LSB component.
The spectrum of region d extracted from the MMT #2 spectrum (position angle PA = 0![]() )
(cf. Fig. 1b) within a 4
)
(cf. Fig. 1b) within a 4
![]() 8
8 ![]() 1
1
![]() 5 aperture is shown in Fig. 14 and labeled "1''. Because of its very low intensity, the spectrum is smoothed by a 5-point box-car. No appreciable emission or absorption lines are seen in the spectrum, probably because of the low signal-to-noise ratio. Therefore, we cannot estimate an age of the stellar populations in region d by extinction-independent methods, or decide on whether the red colours of this region are caused by enhanced extinction or by an intrinsically red stellar population. Spectrum "1'', when not corrected for extinction, is fitted by a theoretical SED of a stellar population continuously formed with constant star formation rate between 100 Myr and 10 Gyr ago.
5 aperture is shown in Fig. 14 and labeled "1''. Because of its very low intensity, the spectrum is smoothed by a 5-point box-car. No appreciable emission or absorption lines are seen in the spectrum, probably because of the low signal-to-noise ratio. Therefore, we cannot estimate an age of the stellar populations in region d by extinction-independent methods, or decide on whether the red colours of this region are caused by enhanced extinction or by an intrinsically red stellar population. Spectrum "1'', when not corrected for extinction, is fitted by a theoretical SED of a stellar population continuously formed with constant star formation rate between 100 Myr and 10 Gyr ago.
However, in the presence of extinction the range of ages can be increased or the upper age limit can be significantly reduced. If a value of C(H![]() )
= 0.1 is assumed for region d then the corrected spectrum (labeled "2'' in Fig. 14) is fitted by a theoretical SED of a
stellar population continuously formed with constant star formation rate between 20 Myr and 10 Gyr ago. However, it is unlikely to reduce the lower age limit to values less than 10-15 Myr, otherwise emission lines must be present in the spectrum of region d. If a value of C(H
)
= 0.1 is assumed for region d then the corrected spectrum (labeled "2'' in Fig. 14) is fitted by a theoretical SED of a
stellar population continuously formed with constant star formation rate between 20 Myr and 10 Gyr ago. However, it is unlikely to reduce the lower age limit to values less than 10-15 Myr, otherwise emission lines must be present in the spectrum of region d. If a value of C(H![]() )
= 0.15 is assumed then the corrected spectrum (labeled "3'' in Fig. 14) is fitted by the theoretical SED of a stellar population continuously formed with a constant star formation rate
between 100 Myr and 1 Gyr ago. The poor signal-to-noise ratio of the spectrum of region d precludes reliable estimates of the age for this region.
)
= 0.15 is assumed then the corrected spectrum (labeled "3'' in Fig. 14) is fitted by the theoretical SED of a stellar population continuously formed with a constant star formation rate
between 100 Myr and 1 Gyr ago. The poor signal-to-noise ratio of the spectrum of region d precludes reliable estimates of the age for this region.
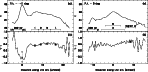 |
Figure 15:
a) The V surface brightness distribution along the slit oriented at position angle PA = -41 |
As emphasized in the previous discussion, photometric data alone do not allow to draw definite conclusions on the age of the stellar populations. However, they can provide a consistency check of the stellar population ages derived from the spectra. Are the ages of the stellar populations derived above compatible with the broad-band colours?
We derived V and I surface brightness and colour distributions for the regions covered by the spectroscopic observations at both slit orientations and compared them with predictions from our population synthesis modeling. The results of this comparison are shown in Fig. 15. The predicted colours obtained from convolving the theoretical SEDs with the appropriate filter bandpasses are shown by different symbols. The transmission curves for the Johnson V and Cousins I bands are taken from Bessel (1990). The zero points are from Bessel et al. (1998).
Since the contribution of the ionized gas emission to the total brightness of the brightest H II region (a) of SBS 0940+544 is high, the theoretical SED for this region has been constructed in the following way. We have used the 4 Myr stellar population SED for a heavy element mass fraction Z = ![]() /20. The observed gaseous SED is then added to the calculated stellar SED, its contribution being determined by the ratio of the observed equivalent width
of the H
/20. The observed gaseous SED is then added to the calculated stellar SED, its contribution being determined by the ratio of the observed equivalent width
of the H![]() emission line to the one expected for pure gaseous emission. To calculate the gaseous continuum SED, the observed H
emission line to the one expected for pure gaseous emission. To calculate the gaseous continuum SED, the observed H![]() flux and the electron temperature have been derived from the optical spectrum (Tables 2 and 3). The contribution of the
free-bound, free-free and two-photon continuum emission has been taken into account for the spectral range from 0 to 5
flux and the electron temperature have been derived from the optical spectrum (Tables 2 and 3). The contribution of the
free-bound, free-free and two-photon continuum emission has been taken into account for the spectral range from 0 to 5 ![]() m (Aller 1984; Ferland 1980). Emission lines are superposed on the gaseous continuum SED with intensities derived from spectra in the spectral range
m (Aller 1984; Ferland 1980). Emission lines are superposed on the gaseous continuum SED with intensities derived from spectra in the spectral range
![]() 3700-7500 Å. Outside this range, the intensities of emission lines (mainly hydrogen lines) have been calculated from the extinction-corrected flux of H
3700-7500 Å. Outside this range, the intensities of emission lines (mainly hydrogen lines) have been calculated from the extinction-corrected flux of H![]() .
.
As evident from Fig. 15b the observed colour of the brightest H II region
is very blue V-I ![]() -0.6 mag and cannot be reproduced by a stellar population of any age.
In particular, the V-I colour equal to -0.1 mag of a 4 Myr old stellar population (upper open square) is significantly redder than that observed. However, the synthetic colour of a 4 Myr stellar population together with the ionized gas (filled square) is very similar to the observed colour. We also show by the lower open square the colour of pure ionized gas emission. It is very blue (V-I
-0.6 mag and cannot be reproduced by a stellar population of any age.
In particular, the V-I colour equal to -0.1 mag of a 4 Myr old stellar population (upper open square) is significantly redder than that observed. However, the synthetic colour of a 4 Myr stellar population together with the ionized gas (filled square) is very similar to the observed colour. We also show by the lower open square the colour of pure ionized gas emission. It is very blue (V-I ![]() -0.9 mag) if the observed intensities of the emission lines (Table 2) and the redshift of SBS 0940+544 are taken into account.
-0.9 mag) if the observed intensities of the emission lines (Table 2) and the redshift of SBS 0940+544 are taken into account.
We already pointed out that the contribution of the gaseous emission is small in the main body. Therefore, we do not take it into account and consider the colours of a stellar population continuously formed with a constant star formation rate between 8 Myr and 100 Myr ago and reddened by interstellar extinction. In Fig. 15b we show by filled circles the colours of four regions with extinction coefficients derived from the best of the theoretical fits to the observed extinction-corrected spectra (spectra in Figs. 12a-d). Open circles show the predicted colours of a stellar population continuously formed between 0 and 10 Gyr ago, assuming enhanced star formation during last 100 Myr, as defined by parameter b in Figs. 13a-d (upper spectra). The agreement between the V-I colours obtained from the photometric data and those derived from the spectral energy distributions in both scenarios is very good.
We also compare the colour of the southern region d (Fig. 15d) with predictions. Because of the noisy spectrum and large photometric errors for this region a broad range of ages can
be consistent with the observed colour. In particular, the colour of the stellar population continuously formed with a constant star formation rate between 100 Myr and 1 Gyr ago and reddened with extinction C(H![]() )
= 0.15 is shown in Fig. 15d by the filled circle, while the colour of the stellar population continuously formed with a constant star formation
rate between 20 Myr and 10 Gyr ago and reddened with extinction C(H
)
= 0.15 is shown in Fig. 15d by the filled circle, while the colour of the stellar population continuously formed with a constant star formation
rate between 20 Myr and 10 Gyr ago and reddened with extinction C(H![]() )
= 0.1 is shown by the open circle. They are in good agreement with the observed colour for this region.
)
= 0.1 is shown by the open circle. They are in good agreement with the observed colour for this region.
Finally, an upper age limit for stellar populations in SBS 0940+544 can be estimated from the V-R and V-I colours of the outermost regions without spectroscopic observations. The mean colours in the outskirts of the LSB component of V-R = 0.33 ![]() 0.04 and V-I = 0.58
0.04 and V-I = 0.58 ![]() 0.03 (Fig. 4) are compatible with those of a stellar population forming continuously for the last several Gyr and assuming that star formation continues until now. However, the spatial distributions of the old and young stellar populations inferred from HST colour-magnitude diagrams of some galaxies, are different (e.g. Schulte-Ladbeck et al. 1998). The oldest stars are seen at largest distances, where younger stars are not detected. It is likely that stars in these extended haloes were formed during the galaxy formation era and no new stars have formed since then, or stars have diffused to haloes from the inner regions where they were born. If this is the case for the outermost regions of SBS 0940+544, then to explain their observed V-R and V-I colours, the upper age limit should be significantly reduced, because no young stellar population is present there.
In that case, the observed colours would be compatible with an upper age limit of
0.03 (Fig. 4) are compatible with those of a stellar population forming continuously for the last several Gyr and assuming that star formation continues until now. However, the spatial distributions of the old and young stellar populations inferred from HST colour-magnitude diagrams of some galaxies, are different (e.g. Schulte-Ladbeck et al. 1998). The oldest stars are seen at largest distances, where younger stars are not detected. It is likely that stars in these extended haloes were formed during the galaxy formation era and no new stars have formed since then, or stars have diffused to haloes from the inner regions where they were born. If this is the case for the outermost regions of SBS 0940+544, then to explain their observed V-R and V-I colours, the upper age limit should be significantly reduced, because no young stellar population is present there.
In that case, the observed colours would be compatible with an upper age limit of ![]() 1 Gyr for the stellar LSB component.
1 Gyr for the stellar LSB component.
Copyright ESO 2001