A&A 378, 883-897 (2001)
DOI: 10.1051/0004-6361:20011297

On the origin of orthogonal polarization modes
in pulsar radio emission

S. A. Petrova

Institute of Radio Astronomy, Chervonopraporna St. 4, Kharkov 61002, Ukraine

Received 25 January 2001 / Accepted 26 August 2001

Abstract
This paper is devoted to studying the conversion of ordinary superluminous waves into extraordinary waves in an ultrarelativistic highly magnetized plasma of pulsars. The conversion appears to take place in the region of quasi-longitudinal propagation with respect to the magnetic field. Although the propagation of waves in pulsar magnetospheres is generally quasi-transverse, due to refraction the wave vector can for a short while become nearly aligned with the ambient magnetic field. As a result of the conversion, the originally ordinary wave turns into two waves, the ordinary and extraordinary. It is found that at pulsar conditions the conversion of the ordinary waves can be significant, i.e. a considerable part of the energy can be transmitted to the extraordinary waves. The process is suggested to underlie the observed transitions between the orthogonal polarization states in pulsar radiation. The connection of conversion with magnetospheric refraction implies a number of observational consequences which agree well with the observed features of the orthogonally polarized modes. In particular, it becomes possible to explain both the longitudinal location of the prominent orthogonal transitions and the high-frequency depolarization of pulsar radiation. Further polarization evolution of the natural waves resulting from the conversion is investigated as well. It is found that the polarization-limiting effect can account for both the change in the sense of circular polarization during the orthogonal transitions and the non-orthogonality of the observed modes. It is shown that any technique of mode separation should allow for the consequences of the polarization-limiting effect.

Key words: plasmas - polarization - waves - pulsars: general


1 Introduction

1.1 Observational evidence for orthogonally polarized modes

Pulsar radio emission usually shows a high percentage of linear polarization, with the position angle changing across the pulse. A smooth monotonic variation of the position angle with pulse longitude can be explained within the framework of a well-known rotating-vector model (Radhakrishnan & Cooke 1969): the vector of the local magnetic field at the emission region, which is thought to determine the orientation of the polarization plane of pulsar radiation, changes its projection onto the plane of the sky as the pulsar rotates. The resultant S-shaped swing of the position angle is indeed consistent with that observed for many pulsars. However, in a number of cases this smooth swing is broken by abrupt, approximately $90^\circ$ transitions in position angle (e.g., Manchester et al. 1975). The single-pulse observations have demonstrated that for each of the orthogonal modes the position angle variations roughly follow the predictions of the rotating-vector model (Backer et al. 1976), while the switching between the modes is a stochastic process (Cordes et al. 1978).

The comprehensive observational data (Manchester et al. 1975; Cordes et al. 1978; Backer & Rankin 1980; Stinebring et al. 1984a,b) have proved that the phenomenon of orthogonal polarization modes (OPMs) is a fundamental property of pulsar radiation. It is observed for almost all pulsars (of those subjected to detailed polarization studies) and takes place over the whole range of pulse longitudes, with the frequency of mode occurence varying considerably over a pulse. The OPM-phenomenon can be observed over a broad frequency range (from 100 MHz Suleymanova & Pugachev 2000 to 10 GHz Xilouris et al. 1995) and it appears to be strongly coupled to the intensity variations at all time scales, from micropulses and subpulses (Cordes & Hankins 1977) to single pulses (Cordes et al. 1978) and mode-changing average intensity profiles (Rankin 1988). The observed $90^\circ$-jumps of the position angle of linear polarization are found to be accompanied by a sense reversal in circular polarization (Cordes et al. 1978), so that the transitions between the polarization states are purely orthogonal. At higher frequencies both modes seem to become comparable in intensity and frequency of mode occurence for most of the pulse, causing a marked depolarization in average profiles (Manchester et al. 1975).

Despite the apparent progress in studying the main features of OPMs, to date there is no commonly accepted interpretation of this phenomenon. Moreover, the very question whether the OPMs are disjoint or superimposed still remains open. Indeed, the observational data yield no direct evidence whether at any instant only one OPM is active or whether both modes occur simultaneously, with the resultant position angle being that of the dominant mode. The first attempts to construct mode-separated profiles of the observed pulsars were based on the assumption of disjoint OPMs (Cordes et al. 1978; Rankin 1988; Gil et al. 1991; Gil et al. 1992). Recently the technique for calculating the mode profiles was developed for the model of superposed OPMs (McKinnon & Stinebring 1998, 2000). Both these methods provide convenient representation of the observational data. However, the assumptions of disjoint and superimposed modes lead to essentially distinct mode-separated profiles, so that the question arises regarding what the true polarization properties of OPMs are. Apparently, to choose between the disjoint and superimposed models one should have a notion of the underlying mechanism of generation of OPMs.

1.2 Earlier theoretical approaches

Since the discovery of OPMs in pulsar radiation (Manchester et al. 1975) numerous ideas were put forward to explain this phenomenon. In some theories the mode switching is supposed to be intrinsic to the radio emission mechanism (e.g., Gangadhara 1997). In this way, however, one faces another global problem: the emission mechanism itself is still obscure. The only undoubted factor is that pulsar radio emission is a result of some processes in the magnetospheric plasma streaming along the open magnetic field lines. Narrowness and stability of the observed pulses imply that the radio emission originates well within the magnetosphere. It is important that the process of radio emission adjusts to the presence of the magnetospheric plasma: whatever the emission mechanism it can produce only the natural waves of the ambient plasma. It should be mentioned that the disjoint OPMs constructed on the basis of the observational data cannot be intrinsic to the emission mechanism, since the natural waves are, by definition, completely polarized, whereas the disjoint modes usually show partial polarization. Within the framework of superimposed OPMs, two natural waves should be produced independently (to provide an incoherent mixture of radiation with two polarization states), but at the same time the efficiencies of the two mechanisms should vary in a way so as to account for the complex picture of the observed OPM-transitions as well as the high-frequency depolarization of pulsar radiation.

In a number of theories the orthogonal transitions in pulsar polarization are regarded as a consequence of the propagation effects. The first theories have related the OPM-phenomenon to the cyclotron absorption (Manchester et al. 1975) or induced scattering (Blandford & Scharlemann 1976) occasionally preferential for one of the modes. The early studies of the natural waves in pulsar plasma have led to a new view of the nature of OPM-transitions (Melrose 1979; Allen & Melrose 1982). The natural waves appear to be linearly polarized in orthogonal planes. Having different refractive indices, they become separated in space and in angle during their propagation through the plasma, with the value of the separation being strongly dependent on the conditions in the ambient plasma. This separation was suggested to underlie the observed transitions between OPMs.

Further investigation of the dispersive properties of pulsar plasma (e.g., Arons & Barnard 1986) gave rise to a more rigorous numerical treatment of refraction (Barnard & Arons 1986). The resultant knowledge of the features of wave behaviour in the magnetospheric plasma became a corner-stone of the comprehensive qualitative picture of the OPM-phenomenon developed by McKinnon (1997) (see also von Hoensbroech et al. 1998; von Hoensbroech 1999).

An ultrarelativistic highly magnetized plasma allows three natural waves. One of them, the extraordinary one, has a vacuum dispersion law and therefore propagates without refraction. Given the oblique propagation with respect to the magnetic field, one branch of the dispersion curve corresponding to ordinary waves is completely subluminous, while the other is completely superluminous. The subluminous waves are found to be "ducted'' along the magnetic field lines (Barnard & Arons 1986). Given that the waves in a broad frequency range originate at approximately the same altitude in the open field line tube, the lower the frequency - the stronger refraction. So at low enough frequencies the ordinary subluminous mode is well separated from the extraordinary mode due to efficient refraction, whereas at higher frequencies they overlap.

Supposing that these modes are generated by independent mechanisms and compete in intensity one can explain the occasional transitions between the orthogonal polarization states as well as the high-frequency depolarization of pulsar radio emission. However, one cannot but mention that the extraordinary mode (being characterized by the vacuum dispersion law) is not generated by any common processes in the plasma; at the same time, the ordinary subluminous wave (being easily generated, e.g., by the plasma instabilities) experiences severe Landau damping and therefore does not escape directly from the magnetosphere. Note that linear coupling of the subluminous mode to the superluminous one is inefficient at pulsar conditions (Bliokh & Lyubarskii 1996).

1.3 Working model

As shown by Lyubarskii (1996), the subluminous waves suffer intense induced scattering off the plasma particles. As a result, the waves become superluminous, with the frequencies being of the order of the local Lorentz-shifted proper plasma frequency:

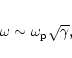
\begin{eqnarray*}\omega\sim\omega_{\rm p}\sqrt{\gamma}, \end{eqnarray*}


where $\omega_{\rm p}$ is the customary plasma frequency, $\gamma$ the plasma Lorentz-factor.

The investigation of refraction was extended to the ordinary superluminous waves originating at the characteristic plasma frequencies (Lyubarskii & Petrova 1998; Petrova & Lyubarskii 2000; Petrova 2000). It was found that in this case refraction is determined mainly by the gradient of the plasma number density across the open field line tube. According to standard models (e.g., Arons & Scharlemann 1979), the plasma number density decreases toward both the magnetic axis and tube edges. It is obvious that in the course of refraction a ray diverges from its initial orientation in the direction of the plasma density decrease. So the rays originating in the inner part of the tube bend toward the magnetic axis, whereas those emitted in the outer part of the tube deviate outwards. If refraction is strong enough, the rays emitted in the inner part of the tube can intersect the magnetic axis and come into the opposite half of the tube, where they start to deviate in the opposite direction because of oppositely directed transverse density gradient. Since in our consideration the waves are supposed to originate at the local characteristic plasma frequency (i.e. a sort of radius-to-frequency mapping), refraction appears to become more intense at higher frequencies (e.g., Lyubarskii & Petrova 1998), contrary to the conclusion of Barnard & Arons (1986). These basic features of ray behaviour in pulsar plasma proved to have a number of observational consequences. It was shown that refraction not only influences the pulse width and its frequency dependence (Lyubarskii & Petrova 1998), but also modifies the profile shape, giving rise to ray grouping into separate components (Petrova & Lyubarskii 2000; Petrova 2000).

Note that refraction is significant only at distances of the order of the emission altitude, $r\sim r_{\rm e}$, since the plasma number density rapidly decreases with the distance. Further on the waves propagate along straight lines. It should be pointed out that at $r\sim r_{\rm e}$ the scale length for beatings between the non-damping natural modes, $L_{\rm b}$, is much less than the characteristic scale length for change in the plasma parameters, L. Therefore the modes do not interact with each other and their polarization evolution can be described in terms of geometrical optics. The primordial ordinary waves considered in our model remain polarized in the same plane as the wave vector and external magnetic field, the polarization plane being slowly rotating along the trajectory due to change in the orientation of the ambient magnetic field. As soon as the plasma number density decreases considerably, $L_{\rm b}$ matches L; then geometrical optics fail, the polarization plane no longer follows the local orientation of the magnetic field and wave mode coupling holds. As a result, the wave polarization becomes elliptical, with the polarization ellipse rotating along the trajectory. After the plasma density becomes negligible, the waves preserve their polarization state. This is a so-called polarization-limiting effect (Cheng & Ruderman 1979; Stinebring 1982; Barnard 1986; Petrova & Lyubarskii 2000). It is found to be responsible for the partial circular polarization often observed in pulsar radiation.

1.4 Statement of the problem

The present paper is devoted to further investigation of pulsar polarization. Namely, it suggests the explanation of the OPM phenomenon which arises naturally within the framework of the above model of wave propagation in the magnetospheric plasma: the presence of the two OPMs is attributed to the linear conversion of waves in the region of quasi-longitudinal propagation with respect to the magnetic field. Note that the possibility of the non-linear conversion of the waves in pulsar plasma has already been considered by Lyutikov (1999). Here we concentrate purely on the linear effects.

It is known that at the conditions relevant to pulsar plasma the wave propagation is generally quasi-transverse. However, according to numerical ray tracings (e.g., Lyubarskii & Petrova 1998; Petrova 2000), it is a common situation that the rays which have suffered refraction (in either an outward or inward direction) further on pass through the region, where the wave vector is nearly aligned with the ambient magnetic field. Indeed, the outward ray deviation is later on compensated for by the magnetic line divergence. The same happens for the inner rays which have intersected the magnetic axis in the course of refraction.

In the region of quasi-longitudinal propagation the refractive indices of the non-damping natural waves become essentially close to each other, so that geometrical optics breaks and linear coupling holds. As a result, the energy can be partially transmitted into the other (extraordinary) mode. It is shown that at the reasonable conditions in pulsar plasma the ordinary wave can be almost completely transformed into the extraordinary one. Out of the region of conversion the resultant waves propagate independently (geometrical optics is again valid until they reach the polarization-limiting region). It will be shown that as a result of the polarization-limiting effect the polarization of both types of waves becomes elliptical, with the sense being opposite and the position angle being shifted in such a way that the modes remain orthogonal.

Whether one mode or another is dominant depends on the conditions in the region of conversion, which are expected to suffer temporal variations. Furthermore, changes in the plasma density distribution can affect refraction, so that for a fixed ray the regime of quasi-longitudinal propagation arises or does not arise. (An idea of temporal variations in the plasma distribution is supported by the fact that pulsar profiles are only stable on average.)

Since at higher frequencies refraction becomes more prominent, the possibility of longitudinal propagation is met for most of the rays, so that the resultant OPM-transitions can lead to significant depolarization of the observed emission. Thus, the linear conversion of the primordial ordinary superluminous waves can really account for the main features of the observed OPM-phenomenon.

The present paper is arranged as follows. In Sect. 2 we derive the equations describing polarization evolution in an ultrarelativistic magnetized plasma taking into account finiteness of the magnetic field strength. Linear conversion of the natural modes of pulsar plasma is considered in Sect. 3. Wave propagation in the polarization-limiting region is also examined there. In Sect. 4 we compare the consequences of our theory with the observed features of the OPM-phenomenon. The results are summarized in Sect. 5.

2 General equations

Let us consider the polarization evolution along the wave trajectory in the magnetospheric plasma. Such a problem has already been studied in application to polarization-limiting effect (Lyubarskii & Petrova 1999; Petrova & Lyubarskii 2000). In that case the plasma was supposed to be embedded in an infinitely strong magnetic field. Indeed, well within the magnetosphere the magnetic field strength is so high that the critical angle for the circularly polarized natural modes is too small. So in general the wave propagation is quasi-transverse with respect to the magnetic field, i.e. the non-coupled natural waves are linearly polarized. Then for the polarization evolution there is no essential distinction between whether the magnetic field strength is regarded as finite or infinite.

In the region of quasi-longitudinal propagation, polarization of the natural modes can differ essentially becoming almost circular. Although this region is rather narrow, it is of a particular interest for the present consideration, since it is the region where the conversion of waves is expected to occur. So it is reasonable to take into account both the finiteness of the magnetic field strength and the difference in the distribution functions of the plasma constituents.

Note that the region of conversion lies at distances ${\sim} r_{\rm e}$ (see below), in which case we can ignore the magnetosphere rotation. As was found earlier (Petrova & Lyubarskii 2000), the corrections allowing for the rotational aberration are not significant even in the polarization-limiting region, though it is situated much higher.

The wave fields ${\vec E}$ and ${\vec B}$ are described by the Maxwell's equations:

    $\displaystyle \nabla\times {\vec B}=-\frac{i\omega}{c}{\vec E}+\frac{4\pi}{c}\sum_\alpha {\vec j}_{\alpha},$ (1)
    $\displaystyle \nabla\times {\vec E}=\frac{i\omega}{c}{\vec B},$ (2)
    $\displaystyle -i\omega q_{\alpha}n_{\alpha}+{\rm div}{\vec j}_{\alpha}=0.$ (3)

Here ${\vec j}_{\alpha}$ is the linearized current density for each of the particle species $\alpha$ ( $\alpha =1,2$):

\begin{eqnarray*}{\vec j}_{\alpha}\equiv q_{\alpha}[n_{\alpha}{\vec v}_{0\alpha}+n_{0\alpha} {\vec v}_{\alpha}], \end{eqnarray*}


$q_{\alpha}=\pm e$ the particle charge, ${\vec v}_{0\alpha}$ and $n_{0\alpha}$the particle velocities and number densities unperturbed by the wave, ${\vec v} _\alpha$ and $n_{\alpha}$ the small perturbations of these quantities. In our consideration the plasma is assumed to be cold. Although for the real pulsars it is not so, the results are believed to be qualitatively the same. Indeed, despite the particles of each species streaming along the magnetic lines with a large spread in Lorentz-factors, $\gamma\sim 10{-}10^3$ (e.g., Arons 1981), only those with the momenta close to some characteristic value contribute essentially to ${\vec j}_{\alpha}$ (for more details see, e.g., review by Lyubarskii 1995). Since electrons and positrons move along the curved magnetic lines in the rotating magnetosphere, their velocities should be somewhat different (e.g., Cheng & Ruderman 1977). This follows directly from combining the continuity equation with the requirement to supply the Goldreich-Julian current density in each point of the magnetosphere.

The equation of the particle motion in the external magnetic field of the strength ${\vec B}_0$ is written as follows:

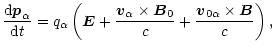$\displaystyle \frac{{\rm d}{\vec p}_{\alpha}}{{\rm d}t}=q_\alpha\left({\vec E}+... ...alpha \times {\vec B}_0}{c}+\frac{{\vec v}_{0\alpha}\times {\vec B}}{c}\right),$     (4)

where ${\vec p}_\alpha$ is the linearized particle momentum caused by the wave, $\frac{\rm d}{{\rm d}t}\equiv -i\omega +{\vec v}_0\cdot\nabla$ is the total derivative. Note that for the ultrarelativistic particles streaming along the magnetic lines

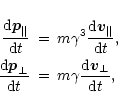
\begin{eqnarray*}\frac{{\rm d}{\vec p}_\Vert}{{\rm d}t}&=&m\gamma^3\frac{{\rm d}... ...perp}{{\rm d}t}&=&m\gamma\frac{{\rm d}{\vec v}_\perp}{{\rm d}t}, \end{eqnarray*}


where ${\vec p}_\Vert$ and ${\vec p}_\perp$ are the momentum components parallel and perpendicular to the external magnetic field, ${\vec v}_\Vert$ and ${\vec v}_\perp$ the corresponding components of the particle velocity. The set of Eqs. (1)-(4) yields a complete description of the wave fields and the plasma particle motion in these fields.

The tracing of the polarization evolution of the waves starts from the region where refraction is already inefficient (i.e., $1-n\ll 1$, where n is the refractive index of the ordinary superluminous waves; the extraordinary waves are not subject to refraction at all). At the same time, in this region the difference between the refractive indices of the waves still should be high enough to prevent the mode coupling: $\frac{\omega}{c}r\Delta n\gg 1$. Then the geometrical optics approximation is valid and the wave behaviour is well known: the polarization plane follows the orientation of the ambient magnetic field.

Seeing that the waves propagate along straight lines, one can choose a three-dimensional Cartesian coordinate system with the z-axis along the wave trajectory. So all the quantities in Eqs. (1)-(4) depend only on the z-coordinate. Moreover, further simplification is possible. The wave modes propagating in opposite directions do not interact with each other given that the refractive indices are far from zero (i.e. in the absence of reflections). Hence, we shall treat only the waves propagating in the positive direction of the z-axis. Since the refractive indices of the waves considered are very close to unity, the spatial dependence of the wave electric field can be presented as follows:

$\displaystyle E_{x,y,z}=\widetilde{E}_{x,y,z}(z)\exp\Big(i\frac{\omega}{c}z\Big),$     (5)

where $\widetilde{E}_{x,y,z}$ are the slowly varying wave amplitudes:
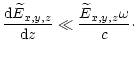$\displaystyle \frac{{\rm d}\widetilde{E}_{x,y,z}}{{\rm d}z}\ll \frac{\widetilde{E}_{x,y,z}\omega}{c}\cdot$     (6)

All the remaining perturbed quantities can certainly be presented in the same form. Hereafter the tildes will be omitted for the sake of convenience. The scale length for change in the unperturbed medium parameters is also assumed to be much larger than the wavelength.

Keeping in mind the above considerations and using Eq. (2) one can write the component equations for the equation of motion (4) as follows:

    $\displaystyle -i\omega m\gamma_\alpha^3(1-\beta_{0\alpha} b_z)\left [v_{x\alpha}b_x+v_{y\alpha}b_y+ v_{z\alpha}b_z\right ]=q_\alpha(E_xb_x+E_yb_y+E_zb_z),$  
    $\displaystyle -i\omega m\gamma_\alpha (1-\beta_{0\alpha} b_z)\left [v_{y\alpha}b_x- v_{x\alpha}b_y\right ]=q_\alpha (E_yb_x-E_xb_y)(1-\beta_{0\alpha} b_z)$  
    $\displaystyle +q_\alpha\frac{B_0}{c} \left [v_{z\alpha}(b_x^2+b_y^2)-v_{x\alpha... ...z)\left [v_{z\alpha}(b_x^2+b_y^2)- v_{x\alpha}b_xb_z-v_{y\alpha}b_yb_z\right ]=$  
    $\displaystyle q_\alpha (E_xb_x+E_yb_y) (b_z-\beta_{0\alpha})-q_\alpha E_z(b_x^2+b_y^2)+q_\alpha\frac{B_0}{c} \left [v_{y\alpha}b_x-v_{x\alpha}b_y\right ],$ (7)

where bx,y,z are the Cartesian components of the unit vector of the external magnetic field, ${\vec B}_0=B_0{\vec b}$, $\beta_{0\alpha}$ is the unperturbed particle velocity in units of c, and ${\vec v}_{0\alpha}\Vert {\vec b}$. From Eq. (7) one can find the perturbations of the particle velocity:
$\displaystyle v_{x\alpha}$ = $\displaystyle \frac{q_\alpha^2B_0\left [E_yb_z{-}\beta_{0\alpha}E_xb_xb_y{-} \b... ...y(b_y^2{+}b_z^2){-}E_zb_y\right ]}{m^2c(\omega_{\rm H}^2{-}\omega^ {\prime 2})}$  
  + $\displaystyle \frac{iq_\alpha\omega^\prime}{m(\omega_{\rm H}^2-\omega^{\prime^2... ...pha b_x[E_xb_x+E_yb_y+E_zb_z]}{m\gamma_\alpha^3\omega (1- \beta_{0\alpha}b_z)},$  
$\displaystyle v_{y\alpha}$ = $\displaystyle \frac{q_\alpha^2B_0\left [E_x(\beta_{0\alpha} (b_x^2{+}b_z^2){-}b... ...\alpha}E_yb_xb_y{+}b_xE_z\right ]}{m^2c(\omega_{\rm H}^2{-}\omega^ {\prime 2})}$  
  + $\displaystyle \frac{iq_\alpha\omega^\prime}{m(\omega_{\rm H}^2-\omega^{\prime^2... ...pha b_x[E_xb_x+E_yb_y+E_zb_z]}{m\gamma_\alpha^3\omega (1- \beta_{0\alpha}b_z)},$  
$\displaystyle v_{z\alpha}$ = $\displaystyle \frac{iq_\alpha b_z[E_xb_x+E_yb_y+E_zb_z]}{m\gamma_\alpha^3\omega... ...yb_x-E_xb_y)(1-\beta_{0\alpha}b_z)} {m^2c(\omega_{\rm H}^2-\omega^{\prime 2})},$ (8)

where $\omega_{\rm H}\equiv\frac{eB_0}{mc}$ is the gyrofrequency, $\omega^\prime \equiv\gamma_\alpha\omega (1-\beta_{0\alpha}b_z)$ the frequency in the particle rest frame. From the continuity Eq. (3) one easily obtains:
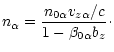$\displaystyle n_\alpha =\frac{n_{0\alpha} v_{z\alpha}/c}{1-\beta_{0\alpha}b_z}\cdot$     (9)

Combining Eqs. (1), (2) and (9) yields:
$\displaystyle \frac{{\rm d}E_x}{{\rm d}z}{+}\frac{2\pi}{c}\sum_\alpha \frac{q_\... ...a}b_z}[v_{x\alpha}(1{-}\beta_{0\alpha}b_z){-}v_{z\alpha} \beta_{0\alpha}b_x]=0,$ (10)
$\displaystyle \frac{{\rm d}E_y}{{\rm d}z}{+}\frac{2\pi}{c}\sum_\alpha \frac{q_\... ...a}b_z}[v_{y\alpha}(1{-}\beta_{0\alpha}b_z){+}v_{z\alpha}\beta_{0\alpha} b_y]=0,$
Ez+$\displaystyle \frac{4\pi i}{\omega}\sum_\alpha \frac{q_\alpha n_{0\alpha}v_{z\alpha}}{1- \beta_{0\alpha}b_z}=0.$

From Eqs. (8) and (10) one finds:
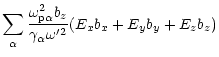Ez=$\displaystyle \sum_\alpha \frac{\omega_{\rm p\alpha}^2b_z}{\gamma_\alpha\omega^{\prime 2}} (E_xb_x+E_yb_y+E_zb_z)$
$\displaystyle {+}\sum_\alpha \frac{\omega_{\rm p\alpha}^2\gamma_\alpha}{\omega_... ...mega^{\prime 2}}[(E_xb_x{+}E_yb_y)(b_z{-}\beta_{0\alpha}){-}E_z(b_x^2{+}b_y^2)]$
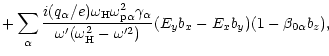$\displaystyle +\sum_\alpha \frac{i(q_\alpha /e)\omega_{\rm H}\omega_{\rm p\alph... ...ime (\omega_{\rm H}^2-\omega^{\prime 2})}(E_yb_x-E_xb_y)(1-\beta_{0\alpha}b_z),$ (11)

where $\omega_{\rm p\alpha}\equiv\sqrt{\frac{4\pi e^2n_{0\alpha}}{m}}$ is the plasma frequency for each of the particle species. Taking into account that in the emission region $\frac{\omega_{\rm p}^2\gamma}{\omega^{\prime 2}}\sim 1$ and $\frac{\omega^\prime}{\omega_{\rm H}}\ll 1$, whereas further on $\omega_{\rm p}$and $\omega_{\rm H}$ decrease with the altitude, one can see that far enough from the cyclotron resonance region (where $\omega^\prime\sim\omega_{\rm H}$) $E_z\ll E_x,E_y$. The cyclotron resonance radius is believed to lie even higher than the polarization-limiting region, so that in our consideration the waves are almost transverse. Then using Eqs. (8) and (10) we obtain finally:
$\displaystyle \frac{{\rm d}E_x}{{\rm d}z}$+$\displaystyle \frac{i\omega}{2c}[Ab_x(E_xb_x+E_yb_y)-BE_x+iGE_y]=0,$
$\displaystyle \frac{{\rm d}E_y}{{\rm d}z}$+$\displaystyle \frac{i\omega}{2c}[Ab_y(E_xb_x+E_yb_y)-BE_y-iGE_x]=0,$ (12)

where

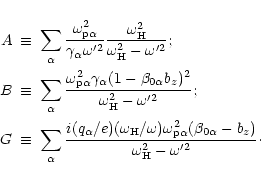
\begin{eqnarray*}A&\equiv&\sum_\alpha \frac{\omega_{\rm p\alpha}^2}{\gamma_\alph... ...\beta_{0\alpha}-b_z)} {\omega_{\rm H}^2-\omega^{\prime 2}}\cdot \end{eqnarray*}


The set of Eqs. (12) describes the polarization evolution of the waves in an ultrarelativistic highly magnetized plasma. Setting $\omega_{\rm H}\to\infty$ immediately turns the above equations into Eq. (13) in Petrova & Lyubarskii (2000), which corresponds to the case of an infinitely strong magnetic field. Neglecting the z-dependence of the unperturbed plasma parameters in Eq. (12), one comes to the homogeneous problem. Then the solution can be found in the form:

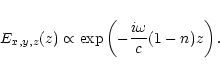
\begin{eqnarray*}E_{x,y,z}(z)\propto\exp \left(-\frac{i\omega}{c}(1-n)z\right). \end{eqnarray*}


Setting the determinant of the system equal to zero, one can obtain the customary expressions for the refractive indices of the ordinary and extraordinary waves in the homogeneous highly magnetized ultrarelativistic plasma (cf., e.g., Melrose 1979, given that $b_x=\theta$, by=0).

3 Linear coupling of waves in pulsar plasma

3.1 The region of quasi-longitudinal propagation

To study the problem of linear conversion of waves it is necessary to specify the location of the region of quasi-longitudinal propagation. Ray propagation in the magnetosphere is generally quasi-transverse. Given that a ray is emitted tangentially to the field line of a dipolar magnetic field and propagates along a straight line, the tilt of the wave vector to the ambient magnetic field increases monotonically along the trajectory due to magnetic line curvature. However, refraction of waves in pulsar plasma can be significant (Barnard & Arons 1986; Lyubarskii & Petrova 1998), so that both the wave vector direction and the ray trajectory can be considerably modified. Since the plasma number density decreases rapidly along the ray trajectory, refraction appears to cease at distances ${\sim} r_{\rm e}$; further on the rays follow a straight line and can pass through the region where they are almost aligned with the ambient magnetic field.

Given that the rays propagate in the plane of magnetic lines (the xz-plane), it is not difficult to find that after refraction the polar angle of the ray trajectory, $\chi$, is given by the expression:

$\displaystyle \chi =\theta_{\rm f}-\frac{z_{\rm f}}{z}(\theta_{\rm f}-\chi_{\rm f}).$     (13)

Here $\chi_{\rm f}$ is the polar angle at the distance $z_{\rm f}$, where refraction becomes inefficient and the propagation becomes straight-line, $\theta_{\rm f}$ the tilt of the wave vector to the magnetic axis at $z_{\rm f}$. Then
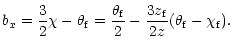$\displaystyle b_x=\frac{3}{2}\chi-\theta_{\rm f}=\frac{\theta_{\rm f}}{2}-\frac{3z_{\rm f}}{2z}(\theta_{\rm f}- \chi_{\rm f}).$     (14)

One can see that at $z>z_{\rm f}$ the component bx changes the sign on condition that
$\displaystyle \theta_{\rm f}>\frac{3}{2}\chi_{\rm f}.$     (15)

Refraction in the outer part of the open field line tube makes the wave vector deviate away from the magnetic axis, with the trajectory bending in the same direction. Numerical ray tracings show that the wave vector deviation is more prominent than the trajectory bending (cf., e.g., Fig. 1 in Lyubarskii & Petrova 1998). Provided that refraction in the outer part of the tube is efficient, the condition (18) is typically satisfied. The rays emitted in the inner part of the tube deviate toward the magnetic axis and can intersect it. As the ray comes into the opposite half of the tube, the wave vector almost immediately starts to deviate in the opposite direction, due to the oppositely directed plasma density gradient; the trajectory bends similarly, but much slower (see, e.g., Fig. 1c in Petrova 2000). So for the inner rays the inequality (18) can be satisfied as well.

Figure 1 shows the location of the region of quasi-longitudinal propagation, $z_{\rm c}$, for the rays with different final tilts to the magnetic axis (in the case of the central cut of the emission cone by the sight line, $\theta_{\rm f}$corresponds to pulse longitude) at two different frequencies. The data presented in this figure are obtained through numerical solution of ray equations in pulsar plasma (Eq. (9) in Petrova 2000). The distribution of the plasma number density across the open field line tube is taken in the form of two Gaussians centred on the characteristic field lines symmetrically with respect to the magnetic axis. Because of the symmetry of the problem only one half of the pulse profile is plotted.

  \begin{figure}\includegraphics[width=9cm,clip]{M1063F1.EPS} \end{figure} Figure 1: Location of the region of quasi-longitudinal propagation, $z_{\rm c}$, for the rays with different final tilts to the magnetic axis; asterisks and points correspond to the lower and higher frequency, respectively; the frequency ratio is 1:11; $z_{\rm f}$ is fixed at $2r_{\rm e}$.
Open with DEXTER

As is evident from Fig. 1, the regime of quasi-longitudinal propagation is characteristic of a number of rays (both inner and outer). Note that for both frequencies the same number of initially equidistant rays was considered. One can see that in Fig. 1 the rays at the higher frequency (points) are more numerous than those at the lower frequencies (asterisks). So at higher frequencies, where refraction is more efficient, the quasi-longitudinal regime holds for the larger part of the pulse. For most of the rays $z_{\rm c}\sim z_{\rm f}$, i.e. the region of interest lies not too high in the magnetosphere.

One more marked feature can be observed in Fig. 1: for the high-frequency inner rays the curve is double-valued. The point is that due to refraction two rays emitted at different angles to the magnetic axis can have the same final tilts, whereas their trajectories are different (for more details see, e.g., Petrova 2000), so that at a given pulse longitude one can observe the rays coming from different locations in the magnetosphere. Each of these rays passes only once through the region of quasi-longitudinal propagation (for the two rays at a fixed pulse longitude $z_{\rm c}$ has distinct values).

It should be mentioned that in the present consideration we concentrate on the qualitative features of ray behaviour on account of refraction which make possible the regime of quasi-longitudinal propagation. The quantitative results depend on the concrete form of the assumed plasma density distribution. For that reason we do not give the numerical values of ray frequencies in Fig. 1 (the frequency ratio is derived from the ratio of the emission altitudes on the basis of radius-to-frequency mapping, $\nu\propto r^{-3/2}$). Note that at a fixed frequency the observed profile widths and shapes are known to be quite distinct for different pulsars; this hints at an actual variety in the parameters of pulsar plasma.

Recall that above we have considered ray propagation in the plane of magnetic lines. In reality the waves can slightly bend from this plane either because of refraction in the plasma with a non-axisymmetric density distribution or because of the magnetosphere rotation. So in general by is not equal to zero, though far enough from $z_{\rm c}$, it is much less than bx (for numerical estimates see Sect. 3.6).

3.2 Linear conversion in the limit $\mathsfsl{B_0\to \infty}$

Now let us turn to linear conversion of waves. For the sake of clarity we start from the case of an infinitely strong magnetic field. Then the set of Eqs. (12) is reduced to the form:

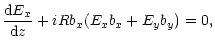$\displaystyle \frac{{\rm d}E_x}{{\rm d}z}+iRb_x(E_xb_x+E_yb_y)=0,$      
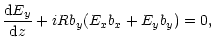$\displaystyle \frac{{\rm d}E_y}{{\rm d}z}+iRb_y(E_xb_x+E_yb_y)=0,$     (16)

where

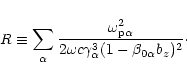
\begin{eqnarray*}R\equiv\sum_\alpha \frac{\omega_{{\rm p}\alpha}^2}{2\omega c\gamma_\alpha^3(1- \beta_{0\alpha}b_z)^2}\cdot \end{eqnarray*}


Given that $Rz\gg 1$ and at least one of the magnetic field direction cosines bx, by is not too small, geometrical optics are valid and the solution of Eq. (13) can be searched for in the form:
$\displaystyle E_{x,y}= (a_{0x,y}+\frac{1}{N}a_{1x,y}+\dots)\exp (iNF(z)),$     (17)

with N being a large parameter of the order of Rz. Then it is easy to find that
$\displaystyle E_x^{({\rm o})}$=$\displaystyle \frac{b_x}{\sqrt{b_x^2+b_y^2}}\exp \left[-i\int R(b_x^2+b_y^2){\rm d}z\right],$  
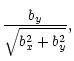$\displaystyle E_y^{({\rm o})}$=$\displaystyle \frac{b_y}{\sqrt{b_x^2+b_y^2}}\exp \left[-i\int R(b_x^2+b_y^2){\rm d}z\right],$  
$\displaystyle E_x^{({\rm e})}$=$\displaystyle \frac{b_y}{\sqrt{b_x^2+b_y^2}},$  
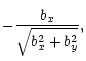$\displaystyle E_y^{({\rm e})}$=$\displaystyle -\frac{b_x}{\sqrt{b_x^2+b_y^2}},$ (18)

where the indices o and e correspond to the customarily-defined ordinary and extraordinary waves in the magnetized plasma.

In a narrow region close to $z_{\rm c}$ both bx and by are so small that the approximation of geometrical optics is broken. On both sides out of this region the solution of Eq. (13) is the linear combination of the natural waves (Eq. (15)), with the coefficients at $z<z_{\rm c}$ and $z>z_{\rm c}$ being distinct. For example, if at $z<z_{\rm c}$ we have only the ordinary wave, at $z>z_{\rm c}$ both natural waves arise.

To find the intensity ratio of the outgoing waves it is necessary to obtain the exact solution of Eq. (13) in the region of conversion. Note that in this case we can use the quasi-homogeneous approximation: within the narrow region of interest, $\frac{\vert z-z_{\rm c}\vert}{z_{\rm c}}\ll 1$, one can present bxin the form: $b_x=\theta (z-z_{\rm c})/z_{\rm c}$, where $\theta =\frac{{\rm d}b}{{\rm d}z/z_{\rm c}} \vert_{z=z_{\rm c}}\sim\theta_{\rm f},\chi_{\rm f}$, while all the other quantities have approximately the same values as at $z=z_{\rm c}$. Hence, for the region of conversion the set of Eq. (13) is written as

$\displaystyle \frac{{\rm d}E_x}{{\rm d}u}$+$\displaystyle iu^2E_x=-i\xi uE_y,$  
$\displaystyle \frac{{\rm d}E_y}{{\rm d}u}$+$\displaystyle i\xi^2E_y=-i\xi uE_x,$ (19)

where $u\equiv (Rz_{\rm c}\theta^2)^{1/3}(z-z_{\rm c})/z_{\rm c}$, $\xi\equiv (Rz_{\rm c}\theta^2)^ {1/3}b_y/\theta$ and $R\equiv R(z_{\rm c})$. From Eq. (19) one can see that at $\xi\sim 1$ the wave amplitudes Exand Ey evolve considerably as u changes from ${\sim} {-1}$ to ${\sim} 1$. Hence, the characteristic length of the region of conversion is $\Delta u\sim 1$, i.e. $\Delta z/z_{\rm c}\sim (Rz_{\rm c}\theta^2)^{-1/3}$. Recall that $Rz_{\rm c}\theta^2$ is the large parameter of the geometrical optics appriximation: $Rz_{\rm c}\theta^2\sim N\sim z_{\rm c}\omega/c$ (cf. Eq. (14)). On the one hand, $\Delta z$ is essentially small compared to $z_{\rm c}$. On the other hand, the region of conversion contains $N^{2/3}\gg 1$ wavelengths, so that it is large enough to allow significant conversion of the natural waves. In spite of considerable variation over $\Delta z$, the wave amplitudes change slowly on the scale of a wavelength, i.e. Eq. (6) is still valid.

Despite the considerable simplification provided by the quasi-homogeneous approximation, the set of Eq. (19) remains too complicated: its exact solution cannot be expressed via the known functions. Note that in contrast to the above situation, the problem of linear conversion in a non-relativistic, weakly magnetized plasma allows an exact analytical solution (it is expressed via the functions of a parabolic cylinder) and it is well studied in application to solar plasma (see, e.g., Zhelezniakov 1996 and references therein).

Let us assume that $\xi \ll1$. Then the solution of Eq. (19) can be found by means of successive approximations. Presenting the wave amplitudes in the form

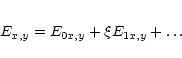
\begin{eqnarray*}E_{x,y}=E_{0x,y}+\xi E_{1x,y}+\dots \end{eqnarray*}


and taking into account that the incident wave is ordinary (i.e., at $u\to -\infty$ Ey=0) one can obtain to the first order in $\xi $:
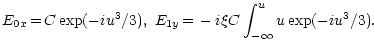$\displaystyle E_{0x}\,{=}\,C\exp (-iu^3/3),\ E_{1y}\,{=}\,-i\xi C\int_{-\infty}^u u\exp (-iu^3/3).$     (20)

Setting $u\to\infty$ yields:
$\displaystyle E_x=C,\quad E_y=-3^{1/6}\Gamma (2/3)C\xi,$     (21)

where $\Gamma (2/3)$ is the gamma-function. To fit the solutions (15) and (21) together it is necessary to substitute $z=z_{\rm c}(1+(Rz_{\rm c}\theta^2)^{-1/3}u)$ in Eq. (15) and set $Rz_{\rm c}\theta^2 \to\infty $ at a fixed u. Keeping in mind that $\xi \ll1$, one can find that the ordinary wave is polarized along the x-axis, while the extraordinary one is polarized along the y-axis. So, as is obvious from Eq. (21), both natural waves are present in the outgoing radiation:

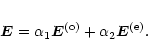
\begin{eqnarray*}{\vec E}=\alpha_1{\vec E}^{({\rm o})}+\alpha_2{\vec E}^{({\rm e})}. \end{eqnarray*}


It is of a particular interest to find the conversion coefficient, Q, i.e. the part of the energy of the primordial ordinary waves which is transmitted to the extraordinary mode:

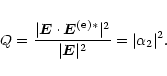
\begin{eqnarray*}Q=\frac{\vert{\vec E}\cdot{\vec E}^{({\rm e})*}\vert^2}{\vert {\vec E}\vert^2}= \vert \alpha_2\vert^2. \end{eqnarray*}


(Note that the energy conservation, $\frac{{\rm d}}{{\rm d}z}(E_xE_x^*+E_yE_y^*)=0$, follows straightly from Eq. (19)). Apparently, in the case considered

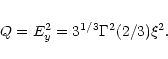
\begin{eqnarray*}Q=E_y^2=3^{1/3}\Gamma^2(2/3)\xi^2. \end{eqnarray*}


Hence, as long as $\xi \ll1$, Q increases with $\xi $. Indeed, according to Eq. (19), as $\xi $ increases, the modes are more strongly coupled, in which case the conversion is more prominent. In the opposite limiting case, $\xi \gg 1$, the conversion is expected to be negligible, since the geometrical optics approximation is not violated at all.

The coefficient of conversion calculated numerically as a function of $\xi $is plotted in Fig. 2. One can see that the conversion is significant for $\xi\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle .... It should be pointed out that the physical meaning of the parameter $\xi $ is the phase difference of the natural modes acquired during their passing through the region of conversion. Indeed, the characteristic length of the region of conversion is $\Delta u\sim\xi^{-1}\sim (Rz_{\rm c}\theta^2) ^{-1/3}\theta/b_y$, i.e. $\Delta z/z_{\rm c}\sim (Rz_{\rm c}\theta^2)^{-1/3}\Delta u \sim (Rz_{\rm c}\theta^2)^{-2/3}\theta/b_y$. Taking into account that the difference of the refractive indices is $\Delta n=R\frac{c}{\omega}b_y^2$, we find: $\frac{\omega}{c}\Delta n\Delta z=(Rz_{\rm c}\theta^2)^{1/3}b_y/\theta \equiv\xi$.

  \begin{figure}\includegraphics[width=8.8cm,clip]{M1063F2.EPS}\end{figure} Figure 2: The degree of mode conversion, Q, as a function of mode phase difference, $\xi $, in the limit of an infinitely strong magnetic field.
Open with DEXTER

As is clear from Fig. 2, Q does not exceed 0.5. Hence, if the approximation of an infinitely strong magnetic field is the case, the extraordinary mode never dominates over the ordinary one, though the intensities can be comparable and, correspondingly, the outgoing radiation can be strongly depolarized.

3.3 Linear conversion in the limit $\mathsfsl{b_y=0}$

Let us turn to the opposite limiting case: by=0, whereas B0 is finite and $G\neq 0$. Then the set of Eq. (12) is written as

$\displaystyle \frac{{\rm d}a_x}{{\rm d}z}$+iRbx2ax-Rgay=0,  
$\displaystyle \frac{{\rm d}a_y}{{\rm d}z}$+Rgax=0, (22)

where $E_{x,y}\equiv a_{x,y}\exp (i\frac{\omega}{c}\int B{\rm d}z)$ and $g\equiv G/A$. Given that $Rz\gg 1$ and bx2 is far enough from zero, geometrical optics holds and the solution of Eq. (22) takes the form:
$\displaystyle a_x^{({\rm o})}$=$\displaystyle \frac{i(b_x^2/2+\sqrt{b_x^4/4+g^2})}{\sqrt{g^2+[b_x^2/2+ \sqrt{b_x^4/4+g^2}]^2}}$
$\displaystyle \times\exp \left[-i\int R(b_x^2/2+\sqrt{b_x^4/4+g^2}){\rm d}z\right],$
$\displaystyle a_y^{({\rm o})}$=$\displaystyle \frac{g}{\sqrt{g^2+[b_x^2/2+ \sqrt{b_x^4/4+g^2}]^2}}$
$\displaystyle \times\exp \left[-i\int R(b_x^2/2+\sqrt{b_x^4/4+g^2}){\rm d}z\right],$
$\displaystyle a_x^{({\rm e})}$=$\displaystyle \frac{i(b_x^2/2-\sqrt{b_x^4/4+g^2})}{\sqrt{g^2+[b_x^2/2- \sqrt{b_x^4/4+g^2}]^2}}$
$\displaystyle \times\exp \left[-i\int R(b_x^2/2-\sqrt{b_x^4/4+g^2}){\rm d}z\right],$
$\displaystyle a_y^{({\rm e})}$=$\displaystyle \frac{g}{\sqrt{g^2+[b_x^2/2- \sqrt{b_x^4/4+g^2}]^2}}$
$\displaystyle \times\exp \left[-i\int R(b_x^2/2-\sqrt{b_x^4/4+g^2}){\rm d}z\right].$ (23)

At $g\to 0$ the electric field components of the natural waves in the above equation certainly coincide with those given by Eq. (15) at $b_y\to 0$.

In the region $\frac{\vert z-z_{\rm c}\vert}{z_{\rm c}}\ll 1$ Eq. (22) can be treated in the quasi-homogeneous approximation. So we obtain:

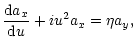    $\displaystyle \frac{{\rm d}a_x}{{\rm d}u}+iu^2a_x=\eta a_y,$  
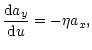    $\displaystyle \frac{{\rm d}a_y}{{\rm d}u}=-\eta a_x,$ (24)

where $\eta\equiv (Rz_{\rm c}/\theta)^{2/3}g$. The wave coupling described by Eq. (24) is qualitatively similar to that studied in the previous subsection. The parameter $\eta $ again can be interpreted as a phase difference between the modes which is gained while they are passing through the region of conversion. At $\eta =0$ the natural waves are independent. As $\eta $ increases, the wave conversion becomes more and more efficient. At $\eta \gg 1$ the waves are again independent. The numerically calculated dependence of the conversion coefficient on $\eta $ is presented in Fig. 3. One can see that the conversion is significant at $\eta\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyl... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ...and the peak value of Q slightly exceeds 0.5. So the outgoing radiation can be considerably depolarized, but the extraordinary mode cannot be noticeably stronger than the ordinary one.
  \begin{figure}\par\includegraphics[width=8.8cm,clip]{M1063F3.EPS}\end{figure} Figure 3: The degree of mode conversion, Q, as a function of mode phase difference, $\xi $, in the limit by=0.
Open with DEXTER

3.4 General case

The above results pose the question of whether the conversion is efficient at $\xi\sim\eta$, i.e. given that both by and g cannot be neglected. In the geometrical optics approximation the solutions of Eq. (12) are as follows:

ax=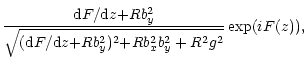$\display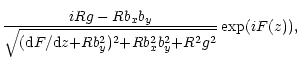style \frac{{\rm d}F/{\rm d}z{+}Rb_y^2}{\sqrt{({\rm d}F/{\rm d}z{+}Rb_y^2)^2{+}Rb_x^2b_y^2+R^2g^2}}\exp (iF(z)),$  
ay=$\displaystyle \frac{iRg-Rb_xb_y}{\sqrt{({\rm d}F/{\rm d}z{+}Rb_y^2)^2{+}Rb_x^2b_y^2{+}R^2g^2}}\exp (iF(z)),$ (25)

where $F(z)\equiv \int^zR[-(b_x^2+b_y^2)/2\pm\sqrt{(b_x^2+b_y^2)^2/4+g^2}]{\rm d}z$, the signs "+" and "-" refer to the extraordinary and ordinary waves, respectively.

The quasi-homogeneous problem is reduced to the form:

$\displaystyle \frac{{\rm d}a_x}{{\rm d}u}$+$\displaystyle iu^2a_x+i\xi ua_y-\eta a_y=0,$  
$\displaystyle \frac{{\rm d}a_y}{{\rm d}u}$+$\displaystyle i\xi ua_x+i\xi^2a_y+\eta a_x=0.$ (26)

Figures 4a,b show the conversion coefficient obtained numerically on the basis of Eqs. (26) and (25) for various values of $\xi $ and $\eta $. As is evident from Fig. 4, the ordinary waves can almost completely be transformed into the extraordinary ones. Provided that $0.1\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... and $0.1\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... the extraordinary waves dominate in the outgoing radiation.
  \begin{figure} \par\subfigure[]{\includegraphics[width=8.8cm,clip]{M1063F4A.EPS} } \par\subfigure[]{\includegraphics[width=8.8cm,clip]{M1063F4B.EPS} } \end{figure} Figure 4: The degree of mode conversion for various $\xi $and $\eta $; a) Q versus $\xi $; $\eta =0.1,\, 0.3,\, 0.5$; b) Q versus $\eta $; $\xi =0.4,\, 0.6,\, 0.8$.
Open with DEXTER

3.5 Polarization-limiting effect

After leaving the region of conversion the waves propagate independently until the geometrical optics approximation is violated. The plasma number density decreases along the trajectory and the waves tend to become the vacuum electromagnetic ones. As soon as the difference in the refractive indices becomes so small that the scale length for beatings between the natural waves becomes comparable to the scale length for change in the plasma parameters,

$\displaystyle \frac{\omega}{c}r\Delta n\sim 1,$     (27)

the natural modes are again coupled. At least, after the plasma density decreases considerably, the wave propagation is no longer affected by the medium and the polarization remains fixed. The mode coupling in the so-called polarization-limiting region leads to changes in the polarization state of the escaping waves. Namely, the waves acquire some circular polarization, with the position angle of the linear polarization being somewhat shifted.

It should be noted that the consequences of the mode coupling are essentially distinct from the linear conversion studied above. The problem is that in the region of conversion Eq. (27) is satisfied twice: at first $\Delta n$ decreases strongly because $b_x\to 0$ and then it increases up to its initial value. As $\Delta n\to 0$ the incident ordinary wave suffers the polarization changes similar to those resulting from the polarization-limiting effect. Later on, as $\Delta n$ starts increasing, this modified wave is split into two natural waves.

The polarization-limiting effect has been already studied in detail in application to the ordinary waves (Petrova & Lyubarskii 2000). It was found that a number of features of the observed polarization profiles can be attributed to this effect. Now we turn to it once more in order to compare the evolution of both orthogonal modes. Let us assume that the plasma number density decreases as z-3 and $b_x={\rm const.}$, $b_y\propto z$. Although this model is somewhat abstract, it appears to be sufficient to clarify the qualitative picture of the polarization-limiting effect for both natural modes.

As was already discussed at the beginning of Sect. 2, far from the region of conversion the approximation of an infinitely strong magnetic field is appropriate. Then the set of Eqs. (12) can be presented in the form:

$\displaystyle \frac{{\rm d}E_x}{{\rm d}w}$-$\displaystyle is(w)wE_x-is(w)\mu E_y=0,$  
$\displaystyle \frac{{\rm d}E_y}{{\rm d}w}$-$\displaystyle is(w)\mu E_x-is(w)\mu^2/wE_y=0.$ (28)

Here $w\equiv z_{\rm p}/z$, $z_{\rm p}$ is the polarization-limiting radius determined by the following relation:

\begin{eqnarray*}&&R(z_{\rm p})[b_x^2+b_y^2(z_{\rm p})]z_{\rm p}=1, \\ &&\mu\eq... ...)_{z=z_{\rm p}},\ s(w)\equiv\frac{1+\mu^2}{(1+\mu^2/w^2)^2}\cdot \end{eqnarray*}


From Eq. (28) one can see that the evolution of the wave polarization is completely determined by the parameter $\mu $. Recall that the waves are emitted in the plane of magnetic lines, i.e. initially by=0, and further along the trajectory the polarization is adjusted to the ${\vec k}\times {\vec b}$-plane. So $\mu \ll 1$ implies that in the regime of geometrical optics (i.e., before $z_{\rm p}$) the polarization plane rotates weakly. In the opposite case, $\mu \gg 1$, the electric field of a natural wave changes drastically. For example, the ordinary wave, which is initially polarized along the x-axis, enters the polarization-limiting region with the electric vector almost aligned with the y-axis. Hence, in the problem considered, the parameter $\mu $is a measure of rotation of the polarization plane of natural waves in the approximation of geometrical optics; at the same time, it completely determines wave mode coupling in the polarization-limiting region (cf. Eq. (28)) and can be interpreted as a phase difference between the modes which is acquired in the course of coupling.

Now let us turn to the numerical results on the final polarization state of the waves escaping from the plasma. The degree of circular polarization is characterized by the normalized Stokes parameter V:

V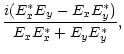$\textstyle \equiv$$\displaystyle \frac{i(E_x^*E_y-E_xE_y^*)}{E_xE_x^*+E_yE_y^*},$ (29)

and the position angle, $\psi$, of the linear polarization is defined as follows:
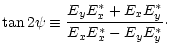$\displaystyle \tan 2\psi\equiv\frac{E_yE_x^*+E_xE_y^*}{E_xE_x^*-E_yE_y^*}\cdot$     (30)

The final values of V and $\psi$ calculated numerically from Eq. (28) as functions of $\mu $ are plotted in Fig. 5. In Fig. 5a the most important issue is that for two natural waves the resultant circular polarization has the opposite sense at any $\mu $. Furthermore, as is apparent from Fig. 5b, the position angle of both natural waves is shifted in exactly the same manner, so that the waves remain orthogonally polarized. Thus, given that the linear conversion is the case, the outgoing radiation is a mixture of the two types of natural waves and the waves with the dominant intensity determine both the position angle and the sense of circular polarization of pulsar radiation.
  \begin{figure} \par\subfigure[]{\includegraphics[width=8.8cm,clip]{M1063F5A.EPS} } \par\subfigure[]{\includegraphics[width=8.8cm,clip]{M1063F5B.EPS} } \end{figure} Figure 5: Consequences of the polarization-limiting effect; a) degree of the circular polarization versus mode phase difference, $\mu $; the upper curve corresponds to the extraordinary waves, the lower one refers to the ordinary waves; b) shift in the position angle of linear polarization versus $\mu $; the lower curve corresponds to the extraordinary waves, the upper one refers to the ordinary waves.
Open with DEXTER

3.6 Numerical estimates

As is found in the previous subsections, the linear conversion is governed by the parameters $\xi $ and $\eta $, while the polarization-limiting effect is determined by $\mu $. Now we proceed to the numerical estimates of these parameters in application to typical pulsar conditions.

Although R is the sum over the particle species, it is clear that either one of the addends contributes chiefly or both contributions are nearly equal. So for our estimates one can write: $Rz_{\rm c}\sim\frac{\omega z_{\rm c}}{c}\frac{\omega_{\rm p}^2\gamma}{\omega^2}$; here it is taken into account that in the region of conversion $b_x,b_y\ll 1/\gamma$and $\omega_{\rm H}\gg \omega^\prime$. The waves are supposed to originate at the characteristic plasma frequency, i.e. at the emission origin $\omega\gamma \theta_{\rm e}^2\sim\omega_{\rm pe}\sqrt{\gamma}$, and further along the trajectory the plasma number density, N, decreases as z-3, so that $\omega_{\rm p} \propto\sqrt{N}\propto z^{-3/2}$. Assuming that $\omega =f\omega_{\rm pe}\sqrt {\gamma}$ with $f\equiv (\theta_{\rm e}^2\gamma)^{-1}\sim 1$ one can obtain:

$\displaystyle Rz_{\rm c}\theta^2=2.7\times 10^{4}f_{-0.5}^{-2}\theta_{-1}^2\nu_9z_8(5z_{\rm e}/z_{\rm c})^3,$     (31)

where $f_{-0.5}\equiv\frac{f}{0.3}$, $\theta_{-1}\equiv\frac{\theta}{0.1}$, $\nu_9\equiv\frac{\nu}{10^9\,{\rm Hz}}$, $z_8\equiv\frac{z_{\rm c}}{10^8\, {\rm cm}}\cdot$ The minimum value of byis determined by the rotational effect and can be written as

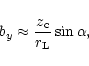
\begin{eqnarray*}b_y\approx\frac{z_{\rm c}}{r_{\rm L}}\sin\alpha , \end{eqnarray*}


where $r_{\rm L}\equiv 5\times 10^9 P$ cm is the light cylinder radius, P the pulsar period, $\alpha$ the angle between the magnetic and rotational axes of the pulsar. Then
$\displaystyle \xi\equiv (Rz_{\rm c}\theta^2)^{1/3}b_y/\theta =f_{-0.5}^{-2/3}\theta_{-1}^{-1/3} \nu_9^{1/3}z_8^{1/3}(5z_{\rm e}/z_{\rm c})\zeta_{-1.5},$     (32)

where $\zeta_{-1.5}\equiv\frac{b_y/\theta}{3\times 10^{-2}}\cdot$

Note that in contrast to R the expression for G contains the difference of the contributions of electrons and positrons. Therefore one can write:

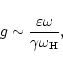
\begin{eqnarray*}g\sim\frac{\varepsilon\omega}{\gamma\omega_{\rm H}}, \end{eqnarray*}


where $\varepsilon\equiv\Delta v/c$ is the normalized difference in the velocities of the two particle species. The value of $\varepsilon$ is determined by the multiplicity factor of the secondary plasma, $\kappa$: $\varepsilon\sim\kappa^{-1}$ (Cheng & Ruderman 1977) or it may be somewhat less (Buschauer & Benford 1977). Unfortunately, $\kappa$ will be known exactly only after the self-consistent theory of the electron-positron cascade is developed. Here we take $\kappa =10^2$. In our model the conversion occurs far from the radius of cyclotron resonance, $r_{\rm H}$, for which the condition $\omega\gamma\theta^2/2=\omega_{\rm H}$ is satisfied. Let us take that $z_{\rm c}/r_{\rm H}\sim 0.1$ and correspondingly, $\omega\gamma\theta^2/\omega_{\rm H}\sim 10^{-3}$, since $\omega_{\rm H}\propto B_0\propto z^{-3}$. Hence, using Eq. (31) we find:
$\displaystyle \eta \,{\equiv}\, (Rz_{\rm c}\theta^2)^{2/3}g/\theta^2{=}0.1\vare... ...2}f_{-0.5}^{-4/3} \theta_{-1}^{-8/3}z_8^{2/3}\nu_9^{2/3}(5z_{\rm e}/z_{\rm c}).$     (33)

In the right-hand sides of Eqs. (32) and (33) all the quantities are normalized by their characteristic values. Although in reality they can be somewhat different, the conditions for efficient conversion, $0.1\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... and $0.1\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ..., are expected to be easily satisfied. The explicit frequency dependence of $\xi $ and $\eta $ is not too strong; in addition, it is necessary to keep in mind that all the other quantities (except $\varepsilon$) can also depend on $\nu$ implicitly. One can expect that significant conversion can occur over a broad enough frequency range.

The result of the polarization-limiting effect is determined by the parameter

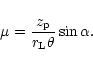
\begin{eqnarray*}\mu =\frac{z_{\rm p}}{r_{\rm L}\theta}\sin\alpha . \end{eqnarray*}


Unfortunately, to date there is no reliable estimate of the polarization-limiting radius. If $z_{\rm p}/r_{\rm L}\sim 0.1$ and $\theta \sim 0.1$, then $\mu\sim 1$. As can be seen from Fig. 5, in the region $\mu\sim 1$ even relatively small variations of $\mu $ can lead to a significant change in the polarization of the outgoing waves. In particular, this may account for the observed randomization of the position angle.

4 Discussion

We have found that in the open field line tube of a pulsar the ordinary waves can be partially converted into extraordinary ones. For the reasonable parameters of the magnetospheric plasma, the conversion can be significant. As a result of this effect two natural modes of the plasma arise. In the light of our model of the OPM-phenomenon the standard definitions of both disjoint and superimposed modes should be somewhat reconsidered. Originally a single mode is emitted. It is the conversion that causes OPMs, and none of the modes observed is the mode produced directly by the emission mechanism. In the region of conversion the primordial mode turns into two modes, the ordinary and extraordinary ones, which can be easily recognized as the superimposed OPMs. On the other hand, the OPM-transitions are due to the switching between significant and insignificant conversion, and only one of these states is the case at a fixed instant and at a fixed longitude; therefore the radiation resulting from significant and insignificant conversion can be presented as disjoint modes. Then at any instant the disjoint mode is the sum of two superimposed modes, so that its partial polarization is explained naturally.

The conversion takes place in the region where the wave vector is almost aligned with the ambient magnetic field. The latter can be the case for the rays which have been refracted outwards from the magnetic axis and further propagate along straight lines in the magnetic field with the diverging field lines. As was shown in Petrova & Lyubarskii (2000), these rays form the conal components of the total intensity profile. The regime of quasi-longitudinal propagation is most easily realizable for the outermost rays. Note that for many pulsars the orthogonal transitions are indeed particularly apparent at the outer edges of the conal components (e.g., Rankin 1983). In this respect it is interesting to mention the mode-separated double profiles of PSR 0525+21 calculated in the assumption of superposed OPMs (McKinnon & Stinebring 2000). In this case the profile of the secondary mode has very steep inner edges and nearly zero intensity in the central part. So one can conclude that the secondary mode exists only at the outer edges of the profile, at longitudes beyond some threshold value, where the conversion becomes significant.

The quasi-longitudinal propagation and the consequent conversion are peculiar not only for the periphery of the profile. This also happens for the inner rays which deviate toward the magnetic axis and intersect it with the subsequent turn in the opposite direction (cf. Fig. 1). The prominent orthogonal transitions can really be seen in the central parts of the profiles (e.g., Gil et al. 1992). For example, in the inner conal component of PSR 0329+54, only the secondary (disjoint) mode is present (Gil et al. 1992), indicating that the conversion is particularly significant.

Thus the relationship between the observed loci of the most prominent OPM-transitions and the components of the total-intensity profiles can be explained in our theory. Moreover, the geometry of magnetospheric refraction suggests that the regime of quasi-longitudinal propagation can be in principle met for the rays at any pulse longitude. So the conversion can occur throughout the pulse, with the efficiency at various longitudes being substantially different. This is compatible with the general picture of the observed OPM-phenomenon (e.g., Stinebring et al. 1984).

As a result of the conversion, the OPMs emerge with a certain intensity ratio (which is governed by the parameters $\xi $ and $\eta $) and the position angle of the outgoing radiation is that of the dominant mode. So the question arises: what is the nature of the switching between the OPMs. First of all, the switching mechanism can be based on the alternation between the significant conversion and the absence of conversion, in which case refraction is too weak to provide the quasi-longitudinal propagation of rays. In addition, even if the ray trajectory contains the segment of quasi-longitudinal propagation, the efficiency of the conversion (i.e. the intensity ratio of the outgoing waves) can vary considerably on account of change in the conditions inside the region of conversion (i.e., because of changes in the values of $\xi $ and $\eta $).

Note that the difference in the energy and shape of the single pulses of a pulsar hints at significant temporal variations of the plasma density distribution within the open field line tube. Firstly, the intensity variations can arise because the emission mechanism is associated with the plasma; secondly, changes in the profile shape can be attributed to refraction (which depends on the plasma density distribution). Being related to the variations of the plasma density distribution as well, the OPM-switching should be correlated with the variations in the intensity and shape of the single pulses. The results on the correlation of the observed OPMs with the intensity of the pulse imply that the conversion occurs only if the intensity is above some threshold value (Cordes et al. 1978; Suleymanova & Pugachev 2000). However, it is difficult to comment on this conclusion in the absence of a notion about the emission mechanism.

The connection between the OPMs and the variations in the profile shape has an observational support. The conal components of one of the two mode-separated profiles (obtained with the assumption of disjoint OPMs) in some pulsars are shifted out of the profile centre (e.g., Gupta et al. 2000). So the enhancement of refraction is simultaneously responsible for both the component shifting and significant conversion. In a number of cases the asymmetry in the distribution of OPMs across the profile can be related to the asymmetry in the profile shape (Gil 1987; Gil et al. 1991, 1992), both being the consequences of refraction in the asymmetric plasma density distribution. The most apparent results can be obtained for the pulsars with the mode-changing profiles, in which case one can expect significant variations of the plasma density. For example, the normal and abnormal modes of the intensity profile of PSR 1604-00 appear to correspond to the primary and secondary polarization modes, respectively (Rankin 1988).

The observations of the OPMs at different frequencies show slight shifts in the dominance of OPMs at a given longitude and changes in the longitude range over which they are visible (Stinebring et al. 1984). The first feature can be attributed to variation of the parameters $\xi $ and $\eta $ with the frequency and consequent variation of the efficiency of conversion, whereas the second one can be explained by changes in the orientation of the rays (including those which pass through the region of quasi-longitudinal propagation) on account of the frequency dependence of refraction.

At high enough frequencies refraction is so strong that the regime of quasi-longitudinal propagation holds for most of the rays and, correspondingly, the conversion becomes efficient for most of the pulse. This is believed to result in considerable depolarization of pulsar radiation. Most of the pulsars really show significant depolarization toward high frequencies (e.g., Morris et al. 1981). As a general rule, at low frequencies the degree of linear polarization varies slightly, but beyond some critical frequency, $\nu_{\rm c}$, it begins to rapidly decrease with the frequency. Within the scope of the above considerations, $\nu_{\rm c}$ can be interpreted as the frequency at which refraction is significant for most of the open field line tube. Note that $\nu_{\rm c}$is usually close to the critical frequency in the frequency dependence of pulse width (e.g., McKinnon 1997; Suleymanova & Pugachev 1998). The latter frequency has the same interpretation: it is the frequency at which refraction becomes efficient for most of the rays (for more details see Lyubarskii & Petrova 1998). Moreover, the index of depolarization appears to be correlated with the width of the core component: less core widths signify stronger depolarization (Xilouris et al. 1995). This correlation is also explained naturally if one takes into account that refraction acts to decrease the width of the core component (the rays deviate toward the magnetic axis).

Toward very low frequencies (${\sim}100$ MHz) the degree of linear polarization increases strongly (Suleymanova & Pugachev 2000) indicating that most of the rays do not suffer conversion. Indeed, at low frequencies refraction is too weak to provide the regime of quasi-longitudinal propagation over a wide range of pulse longitudes. At the same time, in those parts of the profile where both OPMs still exist the secondary polarization mode can become more prominent compared to the primary one (Suleymanova & Pugachev 2000). One can suppose that in this situation the values of $\xi $ and $\eta $ are particularly favorable for the efficient conversion in those scarce regions where the quasi-longitudinal propagation still occurs (though refraction is weak).

Although at low frequencies refraction generally tends to weaken, the quantity of this weakening is determined by the concrete conditions in the plasma of a given pulsar. Therefore at a fixed frequency the efficiency of refraction (and the consequent effects) can differ essentially for different pulsars. A diversity of physical conditions in pulsar plasma reveals itself, e.g., in the fact that the critical frequency for depolarization along with the depolarization index vary from pulsar to pulsar. While studying the consequences of the propagation effects it should be kept in mind that low frequencies are not those beyond some numerical value, but those at which refraction is sufficiently weak.

As was found in Sect. 3.5, in the polarization-limiting region the ordinary and extraordinary waves acquire the circular polarization of opposite signs. Therefore the sign of the resultant circular polarization of the outgoing radiation is determined by the dominant mode. Hence, the OPM-transitions should be accompanied by change in the sense of circular polarization. This is in complete agreement with the observations (e.g., Cordes et al. 1978). In addition, the polarization-limiting effect leads to the shift in position angle of linear polarization. The value of the shift is determined by the parameter $\mu $ (Eq. (34)) and it is equal for both modes. Given that $\mu $ is subjected to temporal variations (e.g., $\theta$ is changed due to variations in the strength of refraction or $z_{\rm p}$ is altered because of change in the plasma parameters), the distribution of OPMs in position angle should be broadened. This is just what is observed (e.g., Backer & Rankin 1980; Stinebring et al. 1984; McKinnon & Stinebring 1998). In some cases the modes are clearly non-orthogonal (Stinebring et al. 1984; Gil et al. 1991, 1992). The non-orthogonality of the modes follows naturally if one supposes that the variations of the conditions in the region of conversion are correlated with those in the polarization-limiting region. Then substantial change in the efficiency of conversion and the consequent switching between the modes are accompanied by considerable variation of the shift in position angle on account of the polarization-limiting effect. Note that the shift in position angle of each mode is connected with the amount of circular polarization, both being the consequences of the polarization-limiting effect. Unfortunately, for the observational data this relationship has not been investigated yet.

Note that any technique of separating the OPMs in the observed radiation can give reasonable results only if the polarization-limiting effect is allowed for (or if it is negligible). Examples of such reasonable results for the model of superposed modes can be found in McKinnon & Stinebring (2000), where the pulsars with small amounts of circular polarization (i.e. weak polarization-limiting effect) are considered.

5 Conclusions

The present paper continues to study the propagation of the natural waves in an ultrarelativistic highly magnetized pulsar plasma. We have considered the conversion of the ordinary superluminous waves into the extraordinary waves which takes place in the region of quasi-longitudinal propagation with respect to the magnetic field. Although the wave propagation in pulsar magnetospheres is generally quasi-transverse, for a small segment of the wave trajectory the regime of quasi-longitudinal propagation can be met if one takes into account the effect of refraction in the plasma. As a result of the conversion of the ordinary wave, both the ordinary and extraordinary waves arise. It has been found that at typical pulsar conditions the conversion can be significant, so that a considerable part of the energy of the ordinary waves can be transmitted to the extraordinary ones.

Since the natural waves considered are orthogonally polarized, the position angle of the outgoing radiation is that of the dominant mode. The waves resulting from the conversion can compete in intensity, giving rise to orthogonal transitions in the polarization state of pulsar radiation. The mode switching is expected to occur either if refraction becomes too weak to provide quasi-longitudinal propagation of the waves or if the conditions in the region of conversion are changed significantly. Both these possibilities follow directly from the temporal variations in the plasma density distribution which have the observational support. Thus the conversion can account for the OPM-phenomenon characteristic of pulsar radiation.

Since at higher frequencies refraction is stronger, the regime of quasi-longitudinal propagation becomes realizable for most of the rays. Then the longitude ranges corresponding to the prominent OPM-transitions are enlarged and cover most of the pulse. As a result, the outgoing radiation can be substantially depolarized. The high-frequency depolarization of pulsar radiation is a well-known observational fact. As a rule, it reveals itself beyond some critical frequency. Within the framework of our considerations, the latter is thought to be the frequency at which refraction becomes efficient for most of the rays.

The waves escaping from the region of conversion are subsequently subjected to the polarization-limiting effect as they leave the magnetospheric plasma. Owing to this effect the waves acquire some circular polarization, with the sense being opposite for the initially ordinary and extraordinary waves. Therefore the resultant sense of circular polarization is determined by the dominant mode. Hence, the OPM-transitions should be accompanied by change in the sense of the circular polarization. This, too, is commonly observed.

In addition, the polarization-limiting effect leads to the shift in the position angle of linear polarization. For fixed conditions it is equal for both natural waves. However, due to temporal variations in the plasma density distribution the shift in position angle is altered, so that the distribution of the observed OPMs in position angle should be somewhat broadened. This indeed agrees with observations. In some cases the observed OPMs are clearly non-orthogonal, indicating that the variations of the conditions in the region of conversion are strongly correlated with those in the polarization-limiting region; then the OPM-switching is accompanied by significant change in the shift of position angle. Since the polarization-limiting effect can be strong enough to reveal itself in the observational data, any technique of mode separation should allow for the consequences of this effect.

Thus, the conversion of the natural waves in the magnetospheric plasma can explain the main features of the OPM-phenomenon observed in pulsar radiation.

References

 
Copyright ESO 2001