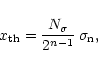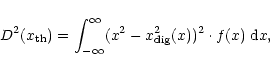A&A 378, 700-709 (2001)
DOI: 10.1051/0004-6361:20011226
The effect of digitisation on the signal-to-noise ratio of a pulsed radio signal
M. L. A. Kouwenhoven1 -
J. L. L. Voûte2
1 -
Astronomical Institute, Utrecht University, PO Box 80000, 3508 TA Utrecht, The Netherlands
2 -
Astronomical Institute "Anton Pannekoek", Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
Received 16 July 2001 / Accepted 29 August 2001
Abstract
We discuss the effect of digitisation on the signal-to-noise ratio of pulsed radio signals. We describe a general n-bit digitiser and show that a symmetric and equidistant digitiser has two free parameters: the threshold and the output value. We derive the best choice of these values for a 1, 1.5, 2, 4 and 8-bit digitiser and calculate the signal-to-noise ratio after digitisation of an undetected signal and of a detected signal with a Gaussian or a 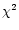 -distribution. Measurements made using PuMa, the new digital pulsar machine at the Westerbork Synthesis Radio Telescope, are presented and are shown to agree with the theoretical response of the digitiser.
-distribution. Measurements made using PuMa, the new digital pulsar machine at the Westerbork Synthesis Radio Telescope, are presented and are shown to agree with the theoretical response of the digitiser.
Key words: instrumentation: miscellaneous - methods: data analysis -
pulsars: general
A pulsar signal that is received by a radio telescope, can be described as amplitude modulated Gaussian noise (Rickett 1975). The periodic noise from the pulsar is weak and is added to
steady noise from the sky background and the receiver. The signal-to-noise ratio (SNR) of the individual pulses of many pulsars is much less than one. In that case, the pulsation can be found
by squaring (i.e. detecting) the signal and adding the pulses together (i.e. folding).
The group velocity of electromagnetic waves propagating in the interstellar medium is modified in a frequency-dependent way by the interaction between the waves and free electrons. This effect is called dispersion and causes the pulses from a pulsar to be smeared over significant
bandwidths. There are two ways to remove this dispersion from a radio signal: coherently and
incoherently.
In the coherent case the amplified voltages from the antenna are digitised and sampled. These recorded data are Fourier transformed off-line. Each Fourier component is rotated by a frequency dependent phase angle. After the inverse transformation a dispersion-free voltage time series is obtained (Hankins 1971).
For incoherent dedispersion the incoming bandwidth is split into a number of sub-bands (channels) by analogue filters or by a digital Fourier transform. The signal in each channel is then squared.
The resulting power time series are delayed by the proper amount of time before the channels are added together. This delay can be applied on-line in hardware (Taylor & Huguenin 1971) or in off-line data processing after digitisation, sampling and recording. The resulting time series has a lower sampling rate than the original one: time resolution has been converted into frequency resolution.
Most radio pulsar observations include at least one digitisation and sampling step. The signal that comes from a radio telescope is always analogue, which means that it is continuous both in time and in its value. Sampling is the process which makes a signal discrete in time. No information is lost in this process, provided that the samples are taken at a rate of at least twice the highest frequency present in the input signal (Nyquist theorem). Digitising is the process which makes a signal discrete in its values. In this process information is lost. The amount of loss depends on the number of possible output values.
During digitisation both amplitude and phase information are lost. The loss of phase information is described for a general signal by Cooper (1970) and for the specific case of a pulsar observation by Jenet & Anderson (1998) and Stairs et al. (2000). Our paper concentrates on the loss of the amplitude information by studying the signal-to-noise ratio of the digitised signal in comparison with the SNR of the incoming signal.
This study was performed as part of the calibration process of PuMa. PuMa is the new digital pulsar machine, constructed for the Westerbork Synthesis Radio Telescope (WSRT, Voûte et al. 2001). The changes of the SNR along the signal path of WSRT are described in Kouwenhoven & Voûte (2001). To test whether PuMa is performing up to its specifications, it is necessary to understand all changes of the SNR and especially the digitisation losses. Therefore, we provide a theoretical description of a digitiser and compare the test results of PuMa with this theory.
Section 2 describes the input signal we have used for our derivations and calculations. Section 3 describes a general digitiser and the settings of its free parameters, in particular for a 1, 1.5, 2, 4 and 8-bit digitiser. In Sect. 4 the effect of the digitisation is studied as a function of the incoming SNR, starting with the case of a 2-bit digitiser. We compare the results with measurements made with PuMa in Sect. 5. Finally, we discuss the difference between our theory and work presented in earlier papers (Sect. 6).
2 Description of the input signal
Two types of signal can be distinguished: raw voltage data ("undetected signal") and squared voltage data (power data or a "detected signal"). In the latter case the distribution of the signal can be 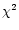 or Gaussian. The effects of digitisation differ for all these cases and each will be described separately. In this section we first describe the signal itself.
or Gaussian. The effects of digitisation differ for all these cases and each will be described separately. In this section we first describe the signal itself.
 |
Figure 1:
Time series of a pulsar signal with a rectangular envelope a) and noise from the receiver and the background sky b). The addition of these signals is modulated Gaussian noise c). The dotted lines mark the boundaries between the on- and off-pulse. The mean (dashed line) of the input signal is constant over the whole interval. After squaring the mean increases during the on-pulse d). The distribution of the signal is changed by smoothing, but this does not affect the (relative) means e). All vertical scales are arbitrary. The strength of the pulsar signal is highly exaggerated compared to most real pulsar observations. |
| Open with DEXTER |
We start with a generalised pulsed signal. The incoming signal x(t) has two components: a constant noise component
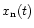 ,
which is the sum of the sky background, the receiver noise etc. and secondly, the signal
,
which is the sum of the sky background, the receiver noise etc. and secondly, the signal
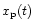 from the pulsar, which is a periodic increase of the noise level. It is assumed that this signal has a rectangular envelope: zero during the intervals in which the pulsar signal is beamed away from us ("off-pulse") and with a constant power during the intervals W in which the pulse can be seen ("on-pulse"). An example is shown in Figs. 1a-c.
from the pulsar, which is a periodic increase of the noise level. It is assumed that this signal has a rectangular envelope: zero during the intervals in which the pulsar signal is beamed away from us ("off-pulse") and with a constant power during the intervals W in which the pulse can be seen ("on-pulse"). An example is shown in Figs. 1a-c.
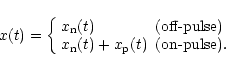 |
(1) |
The off- and on-pulse intervals repeat with the pulsar rotation period. For real pulsars the power will change within the on-pulse in a way that is characteristic for each pulsar (the pulse "profile"). This is not considered in this paper.
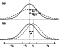 |
Figure 2:
Gaussian distribution function of the signal during the off-pulse (solid line) and the on-pulse (dashed line). In case of an undetected signal a) the distribution becomes wider during the on-pulse: the standard deviation increases from
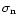 to
to
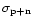 .
In case of a detected and smoothed signal b) the distribution shifts towards higher values by an amount .
In case of a detected and smoothed signal b) the distribution shifts towards higher values by an amount 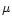 .
Below the plots the digitiser thresholds (vertical dashes) and output values X are indicated for the case of 2-bit digitiser. .
Below the plots the digitiser thresholds (vertical dashes) and output values X are indicated for the case of 2-bit digitiser. |
| Open with DEXTER |
Both components are Gaussian, i.e. have a Gaussian distribution function f(x):
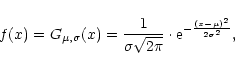 |
(2) |
where 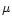 is the mean and
is the mean and 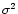 the variance of the signal x(t) (
the variance of the signal x(t) (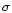 is called the standard deviation). The signals
is called the standard deviation). The signals
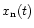 and
and
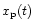 are both voltage time series and have
a zero mean:
are both voltage time series and have
a zero mean:
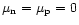 .
The variance of both components are
.
The variance of both components are
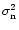 and
and
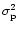 ,
respectively. Since the sum of two Gaussian signals has again a Gaussian distribution,
,
respectively. Since the sum of two Gaussian signals has again a Gaussian distribution,
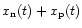 is also Gaussian. It has a mean
is also Gaussian. It has a mean
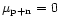 and a variance
and a variance
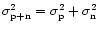 (see Fig. 2a).
(see Fig. 2a).
The signal-to-noise ratio SNR is defined as the relative increase of the power during the on-pulse:
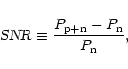 |
(3) |
where 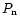 and
and
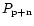 are the power of the noise and of the combined pulsar signal and noise, respectively. Since the mean level
are the power of the noise and of the combined pulsar signal and noise, respectively. Since the mean level 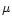 is zero, the power P of a Gaussian signal is equal to its variance
is zero, the power P of a Gaussian signal is equal to its variance 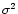 .
So, in this case:
.
So, in this case:
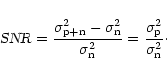 |
(4) |
As will be shown, the variance of the signal changes due to digitisation and this depends on the standard deviation 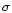 of the signal to be digitised. The signal-to-noise ratio after digitisation SNR
of the signal to be digitised. The signal-to-noise ratio after digitisation SNR
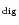 is:
is:
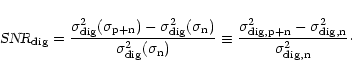 |
(5) |
We define the digitiser efficiency factor:
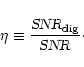 |
(6) |
This efficiency factor is dependent on the number of bits of the digitiser, the digitiser settings and the incoming signal-to-noise ratio. It differs for an undetected and a detected signal.
In the detection stage the signal is squared (Fig. 1d). After squaring, the signal has a non-zero mean. The power of the signal is no longer equal to the variance of the signal and the SNR definition given in Eq. (4) is no longer valid. Eq. (3) requires the absolute value of the off-pulse power 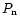 ,
but this information is lost in the digitisation process, if the values of the thresholds are not recorded. Thus, we define the signal-to-noise ratio of a detected signal (SNR
,
but this information is lost in the digitisation process, if the values of the thresholds are not recorded. Thus, we define the signal-to-noise ratio of a detected signal (SNR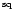 )
to be the difference between the mean level during the off- and on-pulse relative to the off-pulse noise:
)
to be the difference between the mean level during the off- and on-pulse relative to the off-pulse noise:
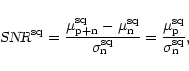 |
(7) |
where
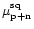 and
and
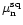 are the mean of the squared signal during the on- and off-pulse, respectively, and
are the mean of the squared signal during the on- and off-pulse, respectively, and
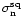 is the standard deviation of the signal during the off-pulse (e.g. Bhattacharya 1998). Both SNR-definitions (Eqs. (5) and (7)) use parameters which can be determined directly from a time series and do not depend on the absolute value of the voltage or power, respectively, only on their relative scaling. The digitiser efficiency factor for a squared signal
is the standard deviation of the signal during the off-pulse (e.g. Bhattacharya 1998). Both SNR-definitions (Eqs. (5) and (7)) use parameters which can be determined directly from a time series and do not depend on the absolute value of the voltage or power, respectively, only on their relative scaling. The digitiser efficiency factor for a squared signal
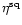 is defined as:
is defined as:
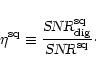 |
(8) |
Note that for a squared but unsmoothed signal, SNR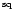 is a factor
is a factor 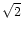 smaller than the SNR before squaring. This is not important for calculating SNR efficiency factors, since the factors
smaller than the SNR before squaring. This is not important for calculating SNR efficiency factors, since the factors 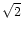 cancel in Eq. (8).
cancel in Eq. (8).
After squaring the signal has a 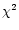 -distribution with one degree of freedom:
-distribution with one degree of freedom:
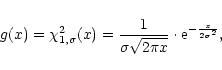 |
(9) |
where 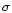 is the standard deviation of the undetected signal, g(x) has a mean of
is the standard deviation of the undetected signal, g(x) has a mean of 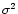 and a variance of
and a variance of 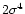 .
.
The signal is usually smoothed after squaring (Fig. 1e). There are several ways to smooth a signal. For an analogue signal the simplest way of smoothing is using a low-pass filter. This will remove all frequencies higher than a certain cut-off frequency from the signal. For a signal that is discrete in time (a sampled signal) the simplest way is to add two consecutive samples, thereby reducing the time resolution by a factor two. The distribution function of this smoothed signal is the auto-convolution of Eq. (9), which is a 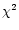 -distribution with two degrees of freedom. Analogously, adding k samples results in a
-distribution with two degrees of freedom. Analogously, adding k samples results in a 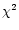 -distribution with k degrees of freedom:
-distribution with k degrees of freedom:
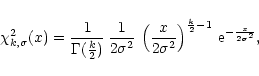 |
(10) |
which has a mean
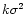 and a variance
and a variance
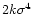 .
.
If many samples are added (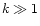 )
the distribution approaches a Gaussian (central limit theorem) with the same mean and standard deviation. We assume that the off-pulse mean has been subtracted,
so
)
the distribution approaches a Gaussian (central limit theorem) with the same mean and standard deviation. We assume that the off-pulse mean has been subtracted,
so
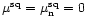 .
During the on-pulse, the mean increases to
.
During the on-pulse, the mean increases to
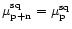 and the standard deviation from
and the standard deviation from
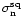 to
to
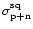 :
the Gaussian distribution is shifted and has become wider. However, the widening can be neglected if enough smoothing has been applied: if the smoothing is made by adding k consecutive samples, the ratio of the standard deviation during the on- and off-pulse in case of a weak pulsar (
:
the Gaussian distribution is shifted and has become wider. However, the widening can be neglected if enough smoothing has been applied: if the smoothing is made by adding k consecutive samples, the ratio of the standard deviation during the on- and off-pulse in case of a weak pulsar (
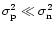 )
is given by
)
is given by
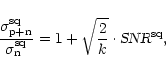 |
(11) |
where
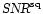 is given by Eq. (7). Therefore, for large values of k with respect to
is given by Eq. (7). Therefore, for large values of k with respect to
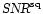 the Gaussian distribution only shifts to higher values during the on-pulse (see Fig. 2b).
the Gaussian distribution only shifts to higher values during the on-pulse (see Fig. 2b).
3 Description of the digitiser
An n-bit digitiser has N = 2n discrete output levels, except in the case of a so-called 1.5-bit digitiser, which has 3 output levels. The digitiser determines the output value by comparing the input signal level with N-1 threshold values
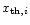 :
one boundary between each two
output levels. The output signal
:
one boundary between each two
output levels. The output signal
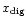 can be described as:
can be described as:
 |
(12) |
The settings of an n-bit digitiser have 2N-1 degrees of freedom: N-1 threshold levels and N output values. Often, the output of the digitiser is just the numeric value of the bits as such and
the conversion from n-bit integer i to float value Xi is made at a later stage.
3.1 Setting considerations
General-use digitisers make as few assumptions about the distribution of the signal that needs to be digitised as possible. If it is assumed that the signal has a symmetrical distribution around its mean 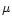 it is common to set the middle threshold at
it is common to set the middle threshold at 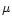 and set the other thresholds symmetrically around it.
and set the other thresholds symmetrically around it.
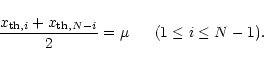 |
(13) |
In that case the output values are also chosen symmetrically around some constant C, which is the mean of all output values and can be chosen equal to 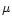 .
.
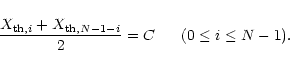 |
(14) |
Since the exact shape of the distribution is not known, the thresholds and the output values are set equidistant. This also has the advantage that the conversion process from the n-bit integer i to the float Xi is a simple linear calculation.
So, in case of 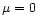 ,
the thresholds and output values are
,
the thresholds and output values are
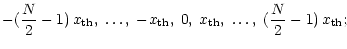 |
|
|
(15) |
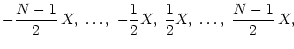 |
|
|
(16) |
where X is the step between the output values. The number of free parameters has now gone down to 2, of which X is merely a scaling factor. A change of its value will have no influence on the SNR of an undetected or a detected signal. Therefore, we choose its value such that the power of the incoming signal is conserved:
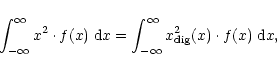 |
(17) |
where f(x) is the distribution function of x. The only remaining parameter to be set is the threshold value
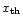 .
This parameter is chosen such that the quantisation noise is as small as possible, so any information loss is as small as possible. This leads to the requirement of minimal distortion. The square of the distortion of a signal is defined as:
.
This parameter is chosen such that the quantisation noise is as small as possible, so any information loss is as small as possible. This leads to the requirement of minimal distortion. The square of the distortion of a signal is defined as:
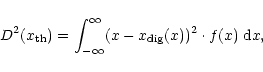 |
(18) |
where
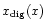 is dependent on
is dependent on
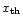 .
The value of D2 should be minimised with respect to
.
The value of D2 should be minimised with respect to
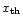 :
:
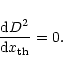 |
(19) |
In the next subsections we discuss the optimal settings for an n-bit digitiser (n = 1, 1.5, 2, 4, 8) in the case of a Gaussian signal. Since most pulsars are weak and have a small duty cycle, the settings of the digitiser are completely determined by the off-pulse. Since the off-pulse of an undetected and of a detected and smoothed signal have the same type of distribution, the settings of the digitiser do not depend on the signal type. Therefore, the following settings can be used generally.
A 1-bit digitiser has two output levels 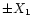 (X1 = X/2) and one threshold. This threshold is set at the mean of the signal for symmetry reasons, i.e. at zero level for a voltage signal. The requirement of power conservation (17)
results in
(X1 = X/2) and one threshold. This threshold is set at the mean of the signal for symmetry reasons, i.e. at zero level for a voltage signal. The requirement of power conservation (17)
results in
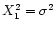 ,
so
,
so
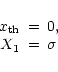 |
(20) |
and the square of the distortion equals
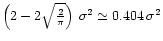 .
The mean and the variance of the digitised signal are equal to the mean and variance of the incoming signal:
.
The mean and the variance of the digitised signal are equal to the mean and variance of the incoming signal:
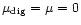 and
and
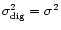 .
.
We will discuss one example of a digitiser with non-equidistant output values and that is
the case of a non-equidistant 2-bit digitiser. This digitiser has three thresholds
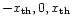 and four output values
and four output values
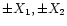 with
0 < X1 < X2. Since there are now three free parameters, power conservation can be required over the intervals
with
0 < X1 < X2. Since there are now three free parameters, power conservation can be required over the intervals
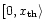 (
(
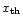 not included) and
not included) and
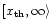 (the negative intervals give identical equations):
(the negative intervals give identical equations):
| X12 |
= |
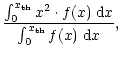 |
(21) |
| X22 |
= |
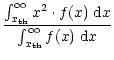 |
(22) |
and the demand of minimal distortion leads to minimalisation of
D2 =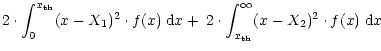 |
(23) |
=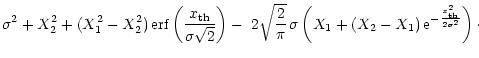 |
(24) |
Note that Eqs. (21) and (22) follow from differentiating Eq. (23) with respect to X1 and X2. We now have a set of three coupled equations. A numerical hill-climbing routine gave the following solution for a Gaussian signal:
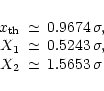 |
(25) |
and the square of the distortion is equal to
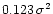 .
.
The settings of an equidistant 2-bit digitiser can be calculated in a similar way as for a non-equidistant digitiser with
X1 = X /2 and
X2 = 3 X/2 (Eq. (16)). Power conservation is now only demanded over the total interval
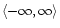 (Eq. (17)). The
numerical solution is:
(Eq. (17)). The
numerical solution is:
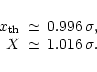 |
(26) |
The square of the distortion is around
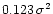 .
This is about equal to the distortion by a non-equidistant digitiser, since
.
This is about equal to the distortion by a non-equidistant digitiser, since
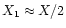 and
and
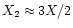 .
.
Commonly, the values for the threshold and the output level are rounded-off:
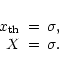 |
(27) |
We call this the "uniform" 2-bit setting. However, the power of the signal is not preserved:
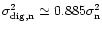 .
.
The settings of a 1.5-bit digitiser can be calculated from the non-equidistant 2-bit digitiser by setting X1 = 0 and X2 = X. The requirement of power conservation leads to:
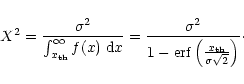 |
(28) |
Solving this equation and minimising Eq. (24) results in:
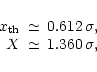 |
(29) |
with a squared distortion of the signal of
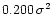 .
.
In similar ways the threshold level and output values of a 4-bit and an 8-bit digitiser can be calculated. All results are summarised in Table 1.
4 SNR loss
In this section the behaviour of a digitiser as a function of the incoming SNR is studied and the degradation of the SNR for a weak signal is determined. First, we will discuss a general non-equidistant 2-bit digitiser. From this the result for a 1, a 1.5 and an equidistant 2-bit digitiser can easily be derived. After that, the other digitisers will
be treated.
 |
Figure 3:
Digitised signal-to-noise ratio as a function of the incoming signal-to-noise ratio for several n-bit digitisers in the case of a) an undetected signal, b) a detected signal with a  distribution with k degrees of freedom and c) a detected signal with a Gaussian distribution. The dashed line is the response of an ideal digitiser.
distribution with k degrees of freedom and c) a detected signal with a Gaussian distribution. The dashed line is the response of an ideal digitiser. |
| Open with DEXTER |
To determine the digitiser efficiency factor 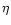 for an undetected signal, the power (i.e. the variance) during the on- and off-pulse after the digitisation should be calculated and compared with the power during the on- and off-pulse before digitisation. If the input signal is Gaussian and the thresholds and output values are set symmetrically, the mean of the digitised signal will be zero. The variance is calculated by integrating the square of the digitised values normalised with the Gaussian distribution function:
for an undetected signal, the power (i.e. the variance) during the on- and off-pulse after the digitisation should be calculated and compared with the power during the on- and off-pulse before digitisation. If the input signal is Gaussian and the thresholds and output values are set symmetrically, the mean of the digitised signal will be zero. The variance is calculated by integrating the square of the digitised values normalised with the Gaussian distribution function:
During the on-pulse the variance changes slightly to
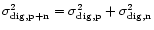 .
The Gaussian distribution function becomes wider, but the thresholds remain at their original positions, determined by the off-pulse variance, see Fig. 2.
.
The Gaussian distribution function becomes wider, but the thresholds remain at their original positions, determined by the off-pulse variance, see Fig. 2.
If a Gaussian distributed signal with mean 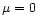 and variance
and variance 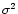 is digitised by a non-equidistant 2-bit digitiser as described in the previous section, the mean remains
zero and
is digitised by a non-equidistant 2-bit digitiser as described in the previous section, the mean remains
zero and
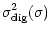 = =![$\displaystyle X_1^2 \;
\mbox{\rm erf}\left( \frac{x_{\rm th}}{\sigma \sqrt{2}} ...
... -
\mbox{\rm erf}\left( \frac{x_{\rm th}}{\sigma \sqrt{2}} \right) \right]\cdot$](/articles/aa/full/2001/41/aah3011/img98.gif) |
(32) |
The relative change in the power of the digitised signal is derived from Eqs. (5) and (32):
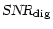 = =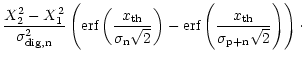 |
|
| |
|
|
(33) |
This curve is displayed in Fig. 3a for the uniform choices of X1, X2 and
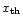 .
For small values of the SNR the
digitised SNR is linear with the incoming one. Above
.
For small values of the SNR the
digitised SNR is linear with the incoming one. Above
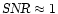 the curve levels off. The signal during the on-pulse
has become so strong that mostly the outer values (
the curve levels off. The signal during the on-pulse
has become so strong that mostly the outer values (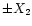 )
appear.
)
appear.
From Eq. (33) the digitiser efficiency factor for a weak pulsar can be approximated by:
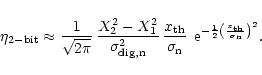 |
(34) |
The digitiser is usually set according to the off-pulse variance. If the requirement of power conservation is met, the variance of the
digitised signal is equal to the variance of the off-pulse noise:
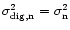 .
.
These equations apply for all n-bit digitisers with 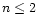 :
the equations for an equidistant 2-bit
digitiser are obtained by substituting X1 = X/2 and
X2 = 3X/2. A 1.5-bit
digitiser is obtained after setting X1 = 0 and a 1-bit digitiser after X1 =
X2. All results are listed in Table 1.
:
the equations for an equidistant 2-bit
digitiser are obtained by substituting X1 = X/2 and
X2 = 3X/2. A 1.5-bit
digitiser is obtained after setting X1 = 0 and a 1-bit digitiser after X1 =
X2. All results are listed in Table 1.
From Eq. (34) it follows that the digitiser efficiency factor of a 1-bit
digitiser in the case of an undetected signal is zero. The variance of the signal after 1-bit
digitisation is equal to
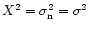 .
If the variance of the incoming signal increases during the on-pulse, the variance of the
digitised signal remains the same. The powers of the digitised signal during the on- and off-pulse are equal. A 1-bit digitiser with its threshold set at the mean of the input signal cannot discover whether the signal strength changes. Note that this digitiser can detect such a change when its threshold is set at another value, e.g.
.
If the variance of the incoming signal increases during the on-pulse, the variance of the
digitised signal remains the same. The powers of the digitised signal during the on- and off-pulse are equal. A 1-bit digitiser with its threshold set at the mean of the input signal cannot discover whether the signal strength changes. Note that this digitiser can detect such a change when its threshold is set at another value, e.g.
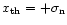 .
.
Nevertheless, with a digitiser with its threshold set at the mean of the input signal, it is possible to detect a dispersed signal. The process of coherent dedispersion uses the phase information that is stored in the crossings of the mean level to partly restore the original pulsed signal.
We calculate the digitised variance of an undetected signal to
determine the dynamic behaviour and the digitiser efficiency factor of a n-bit
digitiser with n>2:
![$\displaystyle %
\sigma_{\rm dig}^2 (\sigma) =
\left( \frac{1}{2} N - \frac{1}{2...
...ht)
- \mbox{\rm erf}\left( \frac{k x_{\rm th}}{\sigma\sqrt{2}} \right)
\right].$](/articles/aa/full/2001/41/aah3011/img109.gif) |
|
|
(35) |
From this the function
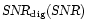 can be calculated. The values for a 4 and 8-bit digitiser are plotted in Fig. 3a. The SNR is better preserved than in the 2-bit case and the flattening starts at higher values of the incoming SNR. The digitiser efficiency factors in Table 1 are calculated by using a small value of SNR (viz. 10-4).
can be calculated. The values for a 4 and 8-bit digitiser are plotted in Fig. 3a. The SNR is better preserved than in the 2-bit case and the flattening starts at higher values of the incoming SNR. The digitiser efficiency factors in Table 1 are calculated by using a small value of SNR (viz. 10-4).
The digitiser efficiency factor
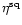 for a detected signal is calculated by determining the mean and the standard deviation of the signal after digitisation.
for a detected signal is calculated by determining the mean and the standard deviation of the signal after digitisation.
and the incoming
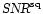 is
is
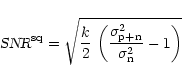 |
(38) |
(see also Eq. (11)). The SNR efficiency factor depends on the actual settings. The settings as discussed in Sect. 3.1 apply to symmetrical distribution functions of the incoming signals and 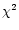 -distributions are not
symmetrical. Nevertheless, we have derived the efficiency factors using the same settings. The results for a uniform 2-bit digitiser are shown in Fig. 3b. For small values of
-distributions are not
symmetrical. Nevertheless, we have derived the efficiency factors using the same settings. The results for a uniform 2-bit digitiser are shown in Fig. 3b. For small values of
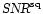 the efficiency is much better than in the undetected case and this efficiency improves for larger values of k. The
the efficiency is much better than in the undetected case and this efficiency improves for larger values of k. The  line is identical to the efficiency function for a Gaussian distributed signal.
line is identical to the efficiency function for a Gaussian distributed signal.
With these settings the lower levels are hardly if ever used for small values of k. Assuming a Gaussian signal when determining the digitiser settings of 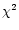 -distributed signal with a small number of degrees of freedom does not produce an efficient digitiser.
PuMa (see Sect. 5) checks if the lowest possible value of the signal (i.e. zero) is below the lowest threshold. If not, it will increase all thresholds such that the lowest threshold is at
-distributed signal with a small number of degrees of freedom does not produce an efficient digitiser.
PuMa (see Sect. 5) checks if the lowest possible value of the signal (i.e. zero) is below the lowest threshold. If not, it will increase all thresholds such that the lowest threshold is at
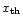 above the zero level (Voûte & van Haren 1999).
PuMa calculates the total intensity data (Stokes I parameter) by performing a
Fourier transform and adding the squares of the real and imaginary parts. The number of degrees of freedom is therefore at least 2. This special case is plotted in Fig. 3b with a dotted line. From this figure it is clear that in this case PuMa uses more efficient digitiser settings than the standard case (i.e. settings for a Gaussian signal).
above the zero level (Voûte & van Haren 1999).
PuMa calculates the total intensity data (Stokes I parameter) by performing a
Fourier transform and adding the squares of the real and imaginary parts. The number of degrees of freedom is therefore at least 2. This special case is plotted in Fig. 3b with a dotted line. From this figure it is clear that in this case PuMa uses more efficient digitiser settings than the standard case (i.e. settings for a Gaussian signal).
During the on-pulse the Gaussian distribution function shifts from
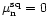 to
to
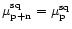 .
Here, it is neglected that the distribution function also becomes broader. We first discuss the non-equidistant 2-bit digitiser.
.
Here, it is neglected that the distribution function also becomes broader. We first discuss the non-equidistant 2-bit digitiser.
The on-pulse mean of the signal after digitisation is given by:
where
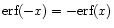 .
.
The signal-to-noise ratio
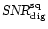 can now be derived. This curve is plotted in Fig. 3c. Again, the efficiency for small values of the
can now be derived. This curve is plotted in Fig. 3c. Again, the efficiency for small values of the
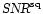 is better than in the previous case. However, for large values the
is better than in the previous case. However, for large values the
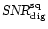 is constant. Only the highest output value will occur and the digitiser is completely saturated.
is constant. Only the highest output value will occur and the digitiser is completely saturated.
For a small shift with respect to the threshold level (
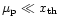 ), the digitiser efficiency factor is approximated by:
), the digitiser efficiency factor is approximated by:
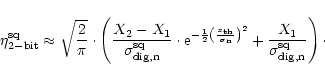 |
(40) |
If the power is conserved, the standard deviation of the noise before and after digitisation is equal:
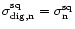 .
.
From these equations the efficiency functions for a 1, a 1.5 and all 2-bit digitisers can be derived. A 1-bit digitiser has no difficulty to detect a change in mean of the incoming signal. In general, a digitiser has less effect on the SNR of a detected signal than on the SNR of a non-detected signal: for symmetry reasons it is easier to find a mean
in a detected digitised signal than to find a change of the variance in a non-detected digitised signal.
To determine the dynamic behaviour and the digitiser efficiency factor of a n-bit digitiser with n>2, the digitised mean of the detected signal should be calculated:
![$\displaystyle %
\mu_{\rm dig}^{\rm sq}(\mu,\sigma) = \frac{1}{2} \; X \; \mbox{...
...box{\rm erf}\left( \frac{kx_{\rm th}- \mu}{\sigma\sqrt{2}} \right)
\right]\cdot$](/articles/aa/full/2001/41/aah3011/img128.gif) |
|
|
(41) |
The efficiency functions are plotted in Fig. 3c for a 4 and an 8-bit digitiser. Note that the degradation is very small. The turning points of all curves are all between an incoming SNR of 1 to 4. The dynamic range of an 8-bit digitiser can be
enormously increased (i.e. this turning point can be shifted to higher values) when the threshold level
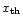 and output value X are chosen as if it were a 4-bit digitiser. In that case the distance between the thresholds is larger than it is in the normal 8-bit case and the highest threshold is now at
and output value X are chosen as if it were a 4-bit digitiser. In that case the distance between the thresholds is larger than it is in the normal 8-bit case and the highest threshold is now at
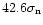 (
(
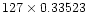 ,
see Table 1) instead of at
,
see Table 1) instead of at
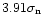 .
The SNR will be slightly more degraded, but the response of the digitiser will be linear up to an incoming signal-to-noise ratio of about 40.
.
The SNR will be slightly more degraded, but the response of the digitiser will be linear up to an incoming signal-to-noise ratio of about 40.
5 PuMa measurements
 |
Figure 4:
Ratio of the observed and expected digitised signal-to-noise ratio as a function of the
incoming signal-to-noise ratio for several n-bit digitisers. The upper panel shows the case of an undetected signal, the lower panel shows the case of a detected signal. The dashed line indicates
a ratio of unity. |
| Open with DEXTER |
We have used these equations to verify the operation of PuMa, an almost completely digital pulsar machine, which is operational at the Westerbork Synthesis Radio Telescope (see Voûte et al. 2001 and for a more technical description: van Haren et al. 2000).
In the first (analogue) stage of PuMa an incoming band of 10 MHz is 12-bit digitised and sampled at 20 MHz (Nyquist rate). These samples are transferred to a cluster of digital signal processor
(DSP) boards. These processors have two modes of operation.
Mode 0 is a baseband sampling mode. The data are 2, 4 or 8-bit sampled after a possible bandwidth reduction by a digital Finite Impulse Response (FIR) filter. PuMa uses FIR filters with symmetrical
coefficients to preserve the phase of the signal. The resulting undetected data are suited for later
off-line coherent dedispersion.
The second mode (Mode 1) is a digital filterbank mode, in which temporal resolution is converted to spectral resolution. Each 2n consecutive samples of both polarisations are complex Fourier
Transformed to get n spectral channels (
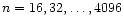 within 10 MHz). The resulting complex data of both polarisations are (cross-)mul-tiplied to get the four Stokes parameters (I, Q, U and V). Consecutive data points can be added per channel to smooth the data and to reduce the effective sampling time. For each channel the resulting time series are 1, 2, 4 or 8-bit digitised and stored. The data from all channels can be added after incoherent dedispersion during the off-line data reduction.
within 10 MHz). The resulting complex data of both polarisations are (cross-)mul-tiplied to get the four Stokes parameters (I, Q, U and V). Consecutive data points can be added per channel to smooth the data and to reduce the effective sampling time. For each channel the resulting time series are 1, 2, 4 or 8-bit digitised and stored. The data from all channels can be added after incoherent dedispersion during the off-line data reduction.
We observed rectangular pulses with a known SNR, generated by an artificial pulsar: a noise generator, which can be modulated with a square wave. We performed test runs with PuMa in
Mode 0 with 2, 4 and 8-bit digitisation. Prior to each run the digitiser levels were set in a so-called pre-run. In this pre-run PuMa determined the variance of the signal without any modulation and set its thresholds equidistantly with
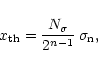 |
(42) |
where n is the number of bits and 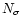 is the number of sigma's to map, which can be specified by the user. We used
is the number of sigma's to map, which can be specified by the user. We used
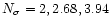 for the (uniform) 2, 4, 8-bit run, respectively. We used one polarisation and a FIR factor 2, i.e. a bandwidth of 5 MHz, because of data-rate constraints for the 8-bit run.
for the (uniform) 2, 4, 8-bit run, respectively. We used one polarisation and a FIR factor 2, i.e. a bandwidth of 5 MHz, because of data-rate constraints for the 8-bit run.
In each run we observed pulses from the artificial pulsar with 11 different signal-to-noise ratios, ranging from 0.06 to 100. We calculated the observed
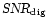 by determining the on- and
off-pulse variances (Eq. (5)). We compared these ratios with the expected values from the previous section. The off-pulse variance in the 4 and 8-bit case was not equal to the
expected value of 1. This was probably due to a slight error in the setting of the thresholds during the pre-run. Therefore, we used the actual values of
by determining the on- and
off-pulse variances (Eq. (5)). We compared these ratios with the expected values from the previous section. The off-pulse variance in the 4 and 8-bit case was not equal to the
expected value of 1. This was probably due to a slight error in the setting of the thresholds during the pre-run. Therefore, we used the actual values of
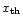 to determine the
to determine the
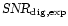 from Eq. (35).
from Eq. (35).
The ratios of the observed and expected values are plotted in the upper panels of Fig. 4. The observed values are in excellent agreement with the expected values.
Only the highest SNR-ratio of the 4-bit run differs by three times the error from unity. The error bars are mainly due to the uncertainties in the fit of the SNR of the artificial pulsar. Note
that the errors within one run are not independent, since they all include the same error in the fit of the SNR of the artificial pulsar and the error in the off-pulse variance determination, which was done only once per run.
Since these observed values are equal to the expected ones, we conclude that there was no significant loss of SNR due to the 12-bit digitising in the first (analogue) stage of PuMa.
We performed similar Mode 1 runs for 1, 2, 4 and 8-bit digitisation. The incoming band of 10 MHz was split into 32 channels. The squared data were smoothed by adding 768 samples to get a Gaussian distribution. The thresholds were set by changing the scale and offset manually (see the PuManual,
Voûte & van Haren 1999) until the thresholds were correct for at least one channel. The thresholds could not be set correctly for all channels at the same time, since they are set
identically for all channels and the bandpass of the artificial pulsar was much less flat than the bandpass during a normal observation, e.g. due to aliasing effects in the analogue stage.
In each run we observed a signal from the artificial pulsar with 14 different
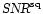 levels, ranging from 0.16 to 14 after squaring and smoothing. Observing higher values was not useful, since the digitised signal was already saturated, i.e. in the flat part of the curves in Fig. 3c.
levels, ranging from 0.16 to 14 after squaring and smoothing. Observing higher values was not useful, since the digitised signal was already saturated, i.e. in the flat part of the curves in Fig. 3c.
For each run we selected the channel for which the thresholds were set optimally and which where non-aliased. The expected values of the signal-to-noise ratio
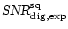 were calculated from Eqs. (39) and (41), where we used the actual setting of
were calculated from Eqs. (39) and (41), where we used the actual setting of
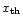 ,
which was slightly different from the value in Table 1 for the 4 and 8-bit runs.
,
which was slightly different from the value in Table 1 for the 4 and 8-bit runs.
Again, the observed values match the expected ones within the uncertainties of the test (lower panels of Fig. 4). The errors are mainly determined by the inaccuracy in the
determination of
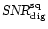 from our observations.
from our observations.
6 Discussion
Table 2:
Settings of a 2-bit digitiser (equidistant and non-equidistant) calculated with the method of Max (1976), Jenet & Anderson (1998) and this paper.
| |
|
Max |
|
J & A |
|
This paper |
| |
|
equi |
non |
|
non |
|
equi |
non |
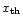 |
|
0.9957 |
0.9816 |
|
0.9674 |
|
0.9957 |
0.9674 |
| |
|
|
|
|
|
|
|
|
| X1 |
|
0.4979 |
0.4528 |
|
0.5419 |
|
0.5304 |
0.5243 |
| X2 |
|
1.494 |
1.510 |
|
1.618 |
|
1.591 |
1.5653 |
The settings of a digitiser have been discussed before by other authors (Max 1976; Jenet & Anderson 1998; Stairs et al. 2000) as have been the effects of digitisation on the SNR (Cooper 1970; Jenet & Anderson 1998). Our work differs from these earlier works in a few respects.
Cooper (1970) describes the effect of the digitisation of two partly coherent signals. These signals z1 and z2 are Gaussian with zero mean and variance 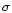 .
They can be written as
z1 = x + y1 and
z2 = x + y2, where x is the coherent part, with mean zero and variance
.
They can be written as
z1 = x + y1 and
z2 = x + y2, where x is the coherent part, with mean zero and variance
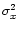 and y1 and y2 are the incoherent parts. The correlation coefficient of the two signals is
and y1 and y2 are the incoherent parts. The correlation coefficient of the two signals is
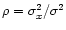 .
Cooper derives that for a weakly correlated signal (
.
Cooper derives that for a weakly correlated signal (
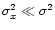 )
the correlation coefficient after digitising is:
)
the correlation coefficient after digitising is:
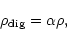 |
(43) |
with
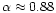 for a 2-bit digitiser with uniform settings. This factor
for a 2-bit digitiser with uniform settings. This factor 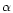 is also the ratio of the SNR of the digitised and of the undigitised correlated signal. Cooper's theory applies to radio synthesis observations and to pulsar observations that digitise undetected data before they are coherently dedispersed.
is also the ratio of the SNR of the digitised and of the undigitised correlated signal. Cooper's theory applies to radio synthesis observations and to pulsar observations that digitise undetected data before they are coherently dedispersed.
These pulsar observations are described by Jenet & Anderson (1998). They derive the effect on the SNR due to the loss of coherency, i.e. the loss of phase information in the signal. This is different from our theory, which describes the effect on the SNR due to the loss of amplitude information. Jenet & Anderson can neglect this effect since they use thresholds that are adapted whenever the variance changes (e.g. during the on-pulse): their digitiser settings are always (also during the on-pulse) set optimally. However, these changing thresholds produce extra dips on either side of a dedispersed pulse (see their paper for explanation).
If one uses fixed thresholds and the undetected signal shows modulation at the point of digitisation
(e.g. during a high frequency observation with a small bandwidth) our theory should be applied in
addition to the Jenet & Anderson theory. However, their theory does not deal with the SNR loss of a detected signal (in case of incoherent dedisperion).
Our method of setting the digitiser thresholds and output values differs from that of Jenet & Anderson as well. They set their thresholds by demanding that the partial derivatives of D2 with
respect to the threshold and output values are zero, while we demand that the total derivative with respect to
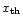 is zero and that power is conserved. Besides, Jenet & Anderson use so-called power optimised levels: they define D2 as
is zero and that power is conserved. Besides, Jenet & Anderson use so-called power optimised levels: they define D2 as
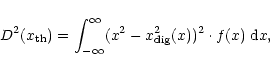 |
(44) |
Stairs et al. (2000) set their thresholds and output values by minimising the error in the time-of-arrival of the digitised pulses.
Our method for setting the digitiser thresholds also differs from the method described by Max (1976). He sets the thresholds and output values by minimising the square of the
distortion (Eq. (18)) with respect to both
 and
and
 .
His output values Xi are the centroids of the distribution function f(x) between
.
His output values Xi are the centroids of the distribution function f(x) between
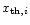 and
and
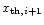 and his threshold values
and his threshold values
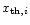 lie in the middle between Xi-1 and Xi. As a result his output values are not equidistant. Because the value of X is just a scale factor that is not important for the SNR, we minimise the distortion only to
lie in the middle between Xi-1 and Xi. As a result his output values are not equidistant. Because the value of X is just a scale factor that is not important for the SNR, we minimise the distortion only to
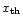 and we set X by requiring power conservation.
and we set X by requiring power conservation.
Table 2 shows the best settings of an equidistant and a non-equidistant 2-bit digitiser calculated with three different methods (Max, Jenet & Anderson and our method). We conclude that the differences between the methods are small.
Acknowledgements
Some of the principles of this paper were developed after a course by Shri Kulkarni at the California Institute of Technology. We thank the staff of the Westerbork Synthesis Radio Telescope and especially R. Ramachandran and R. Strom for their support during our test observations. We thank B. Stappers of the University of Amsterdam for his contribution to the development of the PuMa reduction software and for his comments on the manuscript. The artificial pulsar was built by the astronomical department of the California Institute of Technology.
-
Bhattacharya, D. 1998, in The Many Faces of Neutron Stars., ed. R., Buccheri,
J., van Paradijs, & M. A., Alpar (Dordrecht: Kluwer Academic Publishers), 103
In the text
-
Cooper, B. F. C. 1970, Aust. J. Phys., 23, 521
In the text
-
Hankins, T. H. 1971, ApJ, 169, 487
In the text
NASA ADS
-
Jenet, F. A., & Anderson, S. B. 1998, PASP, 110, 1467
In the text
NASA ADS
-
Kouwenhoven, M. L. A., & Voûte, J. L. L. 2001, A&A, submitted
In the text
-
Max, J. 1976, in Waveform Quantization and Coding, ed. N. S., Jayant, IEEE PRESS
Selected Reprint Series (New York: IEEE Press), 16
In the text
-
Rickett, B. J. 1975, ApJ, 197, 185
In the text
NASA ADS
-
Stairs, I. H., Splaver, E. M., Thorsett, S. E., et al. 2000, MNRAS, 314, 459
In the text
NASA ADS
-
Taylor, J. H., & Huguenin, G. R. 1971, ApJ, 167, 273
In the text
NASA ADS
-
van Haren, P. C., Voûte, J. L. L., Beijaard, T. D., et al. 2000, IEEE Trans. Nucl. Sci.,
accepted
In the text
-
Voûte, J. L. L., Kouwenhoven, M. L. A., van Haren, P. C., et al. 2001,
A&A, submitted
In the text
-
Voûte, J. L. L., & van Haren, P. C. 1999, PuManual, Manual for PuMa, the
Pulsar Machine for the Westerbork Synthesis Radio Telescope
In the text
Copyright ESO 2001

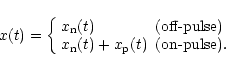
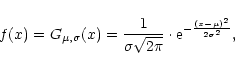
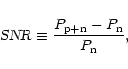
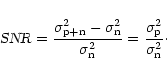
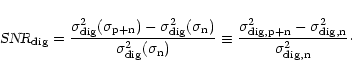
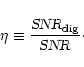
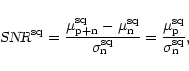
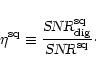
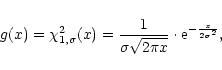
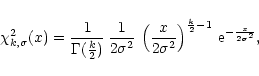
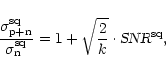

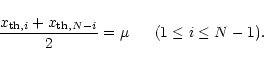
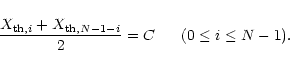
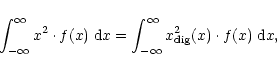
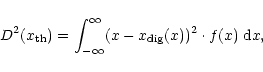
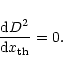
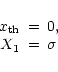
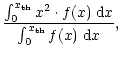
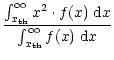
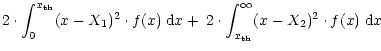
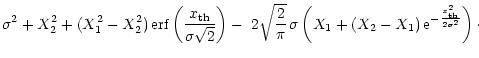
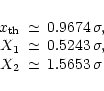
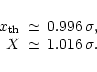
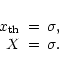
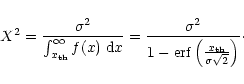
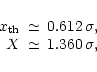

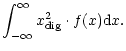
![$\displaystyle X_1^2 \;
\mbox{\rm erf}\left( \frac{x_{\rm th}}{\sigma \sqrt{2}} ...
... -
\mbox{\rm erf}\left( \frac{x_{\rm th}}{\sigma \sqrt{2}} \right) \right]\cdot$](/articles/aa/full/2001/41/aah3011/img98.gif)
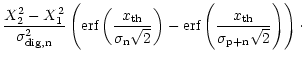
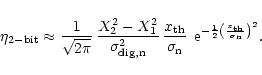
![$\displaystyle %
\sigma_{\rm dig}^2 (\sigma) =
\left( \frac{1}{2} N - \frac{1}{2...
...ht)
- \mbox{\rm erf}\left( \frac{k x_{\rm th}}{\sigma\sqrt{2}} \right)
\right].$](/articles/aa/full/2001/41/aah3011/img109.gif)
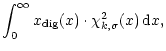
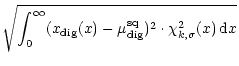
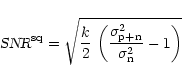
![$\displaystyle \phantom{+} \;
\frac{X_2}{2}
\left[ 1 - \mbox{\rm erf}\left(
\fra...
...\rm th}- \mu_{\rm p}^{\rm sq}}{\sigma_{\rm n}^{\rm sq}\sqrt{2}}
\right) \right]$](/articles/aa/full/2001/41/aah3011/img119.gif)
![$\displaystyle + \; \frac{X_1}{2} \left[ \mbox{\rm erf}\left(
\frac{\mu_{\rm p}^...
...\rm th}- \mu_{\rm p}^{\rm sq}}{\sigma_{\rm n}^{\rm sq}\sqrt{2}}
\right) \right]$](/articles/aa/full/2001/41/aah3011/img120.gif)
![$\displaystyle - \; \frac{X_1}{2} \left[ \mbox{\rm erf}\left(
\frac{x_{\rm th}+ ...
...t(
\frac{\mu_{\rm p}^{\rm sq}}{\sigma_{\rm n}^{\rm sq}\sqrt{2}}
\right) \right]$](/articles/aa/full/2001/41/aah3011/img121.gif)
![$\displaystyle - \; \frac{X_2}{2} \left[ 1 -\mbox{\rm erf}\left(
\frac{x_{\rm th}+ \mu_{\rm p}^{\rm sq}}{\sigma_{\rm n}^{\rm sq}\sqrt{2}}
\right) \right],$](/articles/aa/full/2001/41/aah3011/img122.gif)
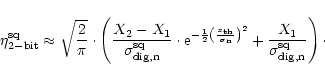
![$\displaystyle %
\mu_{\rm dig}^{\rm sq}(\mu,\sigma) = \frac{1}{2} \; X \; \mbox{...
...box{\rm erf}\left( \frac{kx_{\rm th}- \mu}{\sigma\sqrt{2}} \right)
\right]\cdot$](/articles/aa/full/2001/41/aah3011/img128.gif)