A&A 378, 608-626 (2001)
DOI: 10.1051/0004-6361:20010893
V. Ossenkopf - C. Trojan - J. Stutzki
Physikalisches Institut, Universität zu Köln, Zülpicher Straße 77, 50937 Köln, Germany
Received 15 November 2000 / Accepted 18 June 2001
Abstract
We present observations of 15 massive cores in three different CS
transitions from the FCRAO 14 m and the KOSMA 3 m telescope.
We derive physical parameters of these cores using different
approaches to the line radiative transfer problem. The local
radiative transfer approximations fail to provide reliable values
except for the column densities. A self-consistent explanation of
the observed line profiles is only possible when taking density
gradients and an internal turbulent structure of the cores into
account. The observational data can be fitted
by a spherically symmetric radiative transfer model including
such gradients and a turbulent clumping.
We find that the observed massive cores are approximately virialised
with a clumpy density profile that decays with a radial exponent of
about -1.6 down to a relatively sharp outer boundary.
We show that a careful analysis of spatially unresolved multi-line
observations using a physical radiative transfer model can provide
values for physical parameters that could be obtained otherwise only
by direct observations with much higher spatial resolution. This applies
to all quantities directly affecting the line excitation, like the
mass and size of dense cores. Information on the exact location or
number of clumps, of course, always
has to rely on high-resolution observations e.g. from interferometers.
Key words: line: profiles - radiative transfer - ISM: clouds - ISM: structure - radio lines: ISM
Whereas the average density in molecular clouds falls between about 50 and 1000 cm-3, observations of high-dipole-moment molecules like CS or NH3 reveal cores with densities up to 106 cm-3. Massive cores are typically somewhat warmer than their embedding molecular cloud and show sizes of about 1-3 pc and masses between some ten and some thousand solar masses. They appear as relatively bright objects in molecular line maps so that they are favoured objects from the viewpoint of the observations. The observed line widths of 2-15 kms-1 are considerably larger than thermal, indicating turbulent motions, possibly induced by outflows from star-forming activity. Many of them are associated with young OB or T Tauri stars suggesting that massive cores are sites of massive and multiple star formation (cf. Myers 1999). For a better understanding of star formation we have to know the physical parameters within these cores, i.e. the geometrical structure, the density, velocity, and temperature distribution.
Dense cores are best traced by molecules like CS, HC3N, NH3, and H2CO characterised by high critical densities even for low transitions. Throughout this paper we will use the term "core'' for the dense inner part of a cloud which is directly visible in CS, whereas the rest of the cloud may contribute to the radiative excitation but is mostly visible in CO rather than in CS. We call smaller substructures within the cores "clumps''. Meta-stable transitions of NH3 provide reasonable estimates for the kinetic core temperature and the simultaneous observation of several lines from the same isotope provide combined information both on the density and the temperature structure. Here, we use observations of the 2-1, 5-4, and 7-6 transitions of CS and C34S obtained with the FCRAO 14 m and the KOSMA 3 m telescopes to study 15 massive cores and complement our observations with CS data from the literature to derive the physical core parameters.
Plume et al. (1997) observed about 150 massive cores in CS and C34S using the IRAM 30 m telescope. With an escape probability approximation they derive relatively similar physical parameters for most cores. We compare their results to the parameters obtained for the cores from our sample and test to which extent these results reflect the constraints provided by the set of lines observed, the limitations of the data analysis or the real physical properties of the cores. To study the influence of the data analysis we compare the escape probability approximation with a self-consistent radiative transfer code computing the excitation conditions in an inhomogenous core with internal turbulence.
In Sect. 2 we provide a short overview on the sample and the observations. Section 3 discusses the traditional way to derive the cloud parameters from the observations. Using the mathematical description of the radiative transfer problem in Appendix A we compute cloud parameters in an escape probability approximation. In Sect. 4 the fully self-consistent radiative transfer code from Appendix B is used to derive the cloud parameters. Section 5 compares the resulting data with parameters obtained from independent observations and discusses implications for the physics of massive cores.
The selection of the sample of massive cores was determined by the need of bright "standard'' sources for the SWAS satellite which has a spatial resolution of about 4 arcmin in the frequency range between 490 and 560 GHz. For a comparison to data obtained at similar angular resolution we used observations taken with the array receiver of the FCRAO 14 m telescope at 98 GHz (about 1 arcmin resolution) and performed complementary observations with the 3 m KOSMA telescope at 245 and 343 GHz where its beam size is approximately 2 arcmin.
The sources were selected from the SWAS source list (Goldsmith et al., priv. comm.) to be observable from the FCRAO and KOSMA and bright enough to be detectable in a reasonable integration time. Table 1 lists the 15 sources selected with their central position.
| Source |
|
|
| W49A |
|
|
| W33 |
|
|
| W51A |
|
|
| W3(OH) |
|
|
| W3 |
|
|
| S255 |
|
|
| S235B |
|
|
| S106 |
|
|
| Serpens |
|
|
| DR21 |
|
|
| Mon R2 |
|
|
| NGC 2264 |
|
|
| OMC-2 |
|
|
|
|
|
|
| NGC 2024 |
|
|
NGC 2024 is not part of the SWAS sample but we have observed this region
as a standard for comparison: it is relatively close (![]() 450 pc) and
has been studied already by numerous authors using various techniques. An
extended map of the cloud and its environment in CS 2-1 was
provided by Lada et al. (1991), and line profiles in four transitions
of the main CS isotope are given by Lada et al. (1997). Mezger et al. (1992)
have identified seven clumps in NGC 2024 from dust observations using the
IRAM 30 m telescope
whereas the FCRAO and KOSMA beams can only distinguish between the two bright
clumps FIR3 and FIR5. The data analysis is performed for the position of
the brightest clump FIR5. Here, the KOSMA beam also
contains weak contributions from FIR4, FIR6, and FIR7.
450 pc) and
has been studied already by numerous authors using various techniques. An
extended map of the cloud and its environment in CS 2-1 was
provided by Lada et al. (1991), and line profiles in four transitions
of the main CS isotope are given by Lada et al. (1997). Mezger et al. (1992)
have identified seven clumps in NGC 2024 from dust observations using the
IRAM 30 m telescope
whereas the FCRAO and KOSMA beams can only distinguish between the two bright
clumps FIR3 and FIR5. The data analysis is performed for the position of
the brightest clump FIR5. Here, the KOSMA beam also
contains weak contributions from FIR4, FIR6, and FIR7.
| CS 2-1 | CS 5-4 | CS 7-6 | |||||||
| Source |
|
|
|
|
|
|
|||
| [K] | [K kms-1] | [kms-1] | [K] | [K kms-1] | [kms-1] | [K] | [K kms-1] | [kms-1] | |
| W49A(a) | 3.77 | 35.17 | 8.75 | 1.54 | 12.61 | 7.69 | 1.23 | 12.15 | 9.28 |
| W49A(b) | 4.34 | 32.76 | 7.10 | 2.04 | 18.70 | 8.62 | 1.06 | 9.52 | 8.43 |
| W33 | 9.74 | 67.24 | 6.49 | 3.76 | 27.40 | 6.84 | 2.94 | 17.44 | 5.57 |
| W51A | 10.86 | 110.51 | 9.56 | 4.99 | 67.89 | 12.78 | 3.38 | 40.63 | 11.28 |
| W3(OH) | 5.50 | 26.48 | 4.53 | 2.13 | 10.13 | 4.46 | 1.25 | 5.81 | 4.40 |
| W3 | 7.67 | 38.97 | 4.77 | 1.35 | 7.72 | 5.36 | 1.56 | 8.44 | 5.08 |
| S255 | 8.02 | 21.55 | 2.53 | 2.91 | 10.13 | 3.28 | 1.67 | 5.29 | 2.99 |
| S235B | 6.38 | 16.21 | 2.39 | 0.85 | 2.67 | 2.97 | 0.42 | 1.10 | 2.53 |
| S106 | 3.29 | 8.19 | 2.34 | 0.83 | 2.11 | 2.40 | 0.65 | 2.23 | 3.23 |
| Serpens | 3.74 | 9.36 | 2.35 | 0.67 | 2.52 | 3.59 | 0.39 | 1.68 | 4.11 |
| DR21 | 6.48 | 25.00 | 3.62 | 2.41 | 9.74 | 3.80 | 2.92 | 10.92 | 3.51 |
| Mon R2 | 5.53 | 12.26 | 1.90 | 2.15 | 6.52 | 2.38 | 1.70 | 3.83 | 1.95 |
| NGC 2264 | 5.64 | 21.90 | 3.66 | 2.30 | 9.48 | 3.89 | 1.25 | 5.42 | 3.91 |
| OMC-2 | 5.62 | 9.26 | 1.55 | 1.96 | 5.93 | 2.85 | 0.92 | 1.54 | 1.58 |
| 4.22 | 11.10 | 2.47 | 2.07 | 2.30 | 1.04 | <0.2 | - | - | |
All sources except NGC 2024 were observed in CS 2-1 by Howe (priv.
comm.) using the FCRAO 14 m telescope providing a resolution of 53''.
and a main beam efficiency
![]() .
The cores were
covered by 30-point maps with a sampling of 50''.
The CS 2-1 spectra for the southern core in NGC 2024 were taken
from Lada et al. (1997).
.
The cores were
covered by 30-point maps with a sampling of 50''.
The CS 2-1 spectra for the southern core in NGC 2024 were taken
from Lada et al. (1997).
The CS 5-4 and 7-6 observations used the dual channel KOSMA SIS receiver
with noise temperatures of about 95 K in the 230 GHz branch and 120 K
in the 345 GHz branch. The 3 m telescope provides a spatial resolution
of 110'' in CS 5-4 and 80'' in CS 7-6. The default observing mode
for all cores were cross scans with a separation of 50'' between
subsequent points. Only for NGC 2024 complete 5![]() 5' maps were
obtained. At the time of the observations the telescope surface
provided main beam efficiencies
5' maps were
obtained. At the time of the observations the telescope surface
provided main beam efficiencies
![]() and
and
![]() respectively for the two transitions.
For all measurements we use the conservative estimate of about 10%
uncertainty for the main beam efficiency, another 10% atmospheric
calibration uncertainty and add another 5% for possible drifts etc.
As systematic errors they might sum up linearly to a total
calibration error of at most 25%.
respectively for the two transitions.
For all measurements we use the conservative estimate of about 10%
uncertainty for the main beam efficiency, another 10% atmospheric
calibration uncertainty and add another 5% for possible drifts etc.
As systematic errors they might sum up linearly to a total
calibration error of at most 25%.
The FCRAO spectrometer had a channel width of 19.5 kHz corresponding to a velocity spacing of 0.060 kms-1. For the broad lines from the sample four velocity channels were binned. The resulting rms falls between 0.2 and 0.45 K. The KOSMA spectra were taken with the medium resolution spectrometer (MRS) and the low resolution spectrometer (LRS) providing channel widths of 167 kHz and 688 kHz, respectively. Depending on the different combinations of these backends with the receivers at 245 and 343 GHz we obtain velocity spacings between 0.15 and 0.84 kms-1. The particular spacing is not important for the analysis performed here because none of the lines shows strong spectral substructure. All points were integrated up to a noise limit of 0.1 K per channel.
For most sources the CS 2-1 maps show an approximately elliptical
intensity peak with a weak elongation at scales of a few times the
resolution. In W49A, Serpens, DR21, Mon R2, OMC-2, ![]() Oph A,
and NGC 2024 we can distinguish a second intensity
maximum apart from the central position. Table 2
summarises the parameters of the line profiles at the central
position for all cores. The majority of line profiles are approximately
Gaussian as indicated by integrated line intensities close
to the Gaussian value of
Oph A,
and NGC 2024 we can distinguish a second intensity
maximum apart from the central position. Table 2
summarises the parameters of the line profiles at the central
position for all cores. The majority of line profiles are approximately
Gaussian as indicated by integrated line intensities close
to the Gaussian value of
![]() in Table 2.
Broad wings are only visible in S255, W33, and DR21.
in Table 2.
Broad wings are only visible in S255, W33, and DR21.
W49 shows a double-peak structure which has been
interpreted e.g. by Dickel & Auer (1994) as the footprint of large scale
collapse. They fitted HCO+ line profiles by a spherical
collapse model but concluded that additional components are
needed to explain the observations. Using the radiative transfer code
from Appendix B we have tested their infall model and found
that, while reproducing the HCO+ profiles,
it completely fails to explain the CS observations.
The enhanced blue emission characteristic for collapse is
visible only in CS 7-6. In CS 2-1 and 5-4 we rather find an enhanced
red emission. No spherically symmetric collapse model
can explain these observations. Instead of constructing
a more complex model we have simply decomposed the
emission into two separate components with a relative
velocity of 8.5 kms-1 in the line of sight denoted as W49A
![]() and W49A
and W49A
![]() .
From the modelling in Sect. 4 it turns
out that we cannot even distinguish whether the two components are
moving towards each other or apart as long as they do not line up
exactly along the line of sight. Hence, we will treat them
separately in the following, ignoring any possible interaction.
Further observations including other tracers should be included
to better resolve the situation.
.
From the modelling in Sect. 4 it turns
out that we cannot even distinguish whether the two components are
moving towards each other or apart as long as they do not line up
exactly along the line of sight. Hence, we will treat them
separately in the following, ignoring any possible interaction.
Further observations including other tracers should be included
to better resolve the situation.
| Transition |
|
|
|
| [K] | [K kms-1] | [kms-1] | |
| C32S 5-4 | 5.19 | 11.65 | 2.10 |
| C32S 7-6 | 3.63 | 9.13 | 2.38 |
| C34S 5-4 | 1.19 | 2.22 | 1.75 |
| C34S 7-6 | 0.65 | 0.98 | 1.45 |
In NGC 2024 we also mapped the less abundant isotope
C34S with KOSMA in addition to the main CS isotope
observed in all cores. The observed line
parameters are given in Table 3.
Lada et al. (1997) provided detailed CS spectra for the
southern core at the position of the FIR5.
They obtained in the CS 2-1 transition
![]() K,
K,
![]() kms-1 at 24'' resolution,
in CS 5-4
kms-1 at 24'' resolution,
in CS 5-4
![]() K,
K,
![]() kms-1 at 30''resolution, in CS 7-6
kms-1 at 30''resolution, in CS 7-6
![]() K,
K,
![]() kms-1at 20'' resolution, and in CS 10-9
kms-1at 20'' resolution, and in CS 10-9
![]() K,
K,
![]() kms-1 at 14'' resolution.
kms-1 at 14'' resolution.
To interpret the small amount of information contained in observations of at most five transitions showing mainly Gaussian profiles and essentially unresolved, approximately circular symmetric intensity distributions, we need a simple cloud model that is both physically reasonable and characterised by few parameters. An obvious choice is a spherically symmetric model. This geometry reflects early phases and the large scale behaviour of several collapse simulations (e.g. Galli et al. 1999), whereas the inner parts of collapsing clouds are probably flattened structures (e.g. Li & Shu 1997).
Even in spherical geometry there is no simple way to solve the radiative transfer problem relating the cloud parameters to the emitted line intensities (see Appendix A.1). Thus we cannot compute the cloud properties directly from the observations.
A common approach is the escape probability
approximation discussed in detail in Appendix A.2. Assuming that all
cloud parameters, including the excitation temperatures, are constant
within a spherical cloud volume one can derive a simple
formalism relating the three parameters kinetic temperature
![]() ,
gas density
,
gas density
![]() ,
and column density
of radiating molecules on the scale of the global velocity
variation
,
and column density
of radiating molecules on the scale of the global velocity
variation
![]() to
the line intensity at the cloud model surface.
No assumption on molecular abundances is required.
to
the line intensity at the cloud model surface.
No assumption on molecular abundances is required.
Since a telescope does not provide a simple pencil beam
we have to correct the model surface brightness
temperature by the beam filling factor
![]() ,
given as
the convolution integral of the normalised intensity distribution with
the telescope beam pattern, to compute the observable beam temperature.
Unfortunately, the brightness profile of the source is a non-analytic function
where we can only give simple expressions for the central value
observed in a beam much smaller than the source or
for the integral value observed in a beam much larger than the source
(Eqs. (A.9) and (A.11)).
For intermediate situations we approximate the beam temperature
by starting from both limits and using a beam filling factor given by
the convolution integral of two Gaussians.
The difference between the two values provides an estimate of
the error made in the beam convolution.
,
given as
the convolution integral of the normalised intensity distribution with
the telescope beam pattern, to compute the observable beam temperature.
Unfortunately, the brightness profile of the source is a non-analytic function
where we can only give simple expressions for the central value
observed in a beam much smaller than the source or
for the integral value observed in a beam much larger than the source
(Eqs. (A.9) and (A.11)).
For intermediate situations we approximate the beam temperature
by starting from both limits and using a beam filling factor given by
the convolution integral of two Gaussians.
The difference between the two values provides an estimate of
the error made in the beam convolution.
To compute the integral we fitted the observed brightness distributions
by Gaussians. Most cores are well approximated
by slightly elongated Gaussians. W49A, S235B, Serpens, and ![]() Oph A
show asymmetric scans so that the size determination is somewhat
uncertain. The fit error is about 0.3' for these three sources.
For the rest of the cores we obtain typical values of less than 0.2'.
The true object size finally follows from the deconvolution
of the measured intensity distribution with the telescope beam.
The resulting source sizes in
Oph A
show asymmetric scans so that the size determination is somewhat
uncertain. The fit error is about 0.3' for these three sources.
For the rest of the cores we obtain typical values of less than 0.2'.
The true object size finally follows from the deconvolution
of the measured intensity distribution with the telescope beam.
The resulting source sizes in ![]() and
and ![]() are given in
Table 4. As the geometric mean is sufficient to
compute the beam filling factor we do not expect any serious error
from the fact that the cross-scans in
are given in
Table 4. As the geometric mean is sufficient to
compute the beam filling factor we do not expect any serious error
from the fact that the cross-scans in ![]() and
and ![]() do
not necessarily trace the major axes of the brightness distribution.
For sources which are considerably smaller than the
beam widths of 53'', 107'', and 80'', respectively,
only a rough size estimate is possible
according to the nonlinearity of the deconvolution. This holds
for W49A, W3, S235B, and partially S255. Most clouds, however, show
an extent of the emission which is close to the beam size.
do
not necessarily trace the major axes of the brightness distribution.
For sources which are considerably smaller than the
beam widths of 53'', 107'', and 80'', respectively,
only a rough size estimate is possible
according to the nonlinearity of the deconvolution. This holds
for W49A, W3, S235B, and partially S255. Most clouds, however, show
an extent of the emission which is close to the beam size.
In general different values are obtained for the spatial FWHMs
in the different lines. In Table 4 we find two
classes of sources
with respect to the variation of the source size depending on the
transition observed. Most cores show a monotonic decrease of the
visible size when going to higher transitions. This is expected
from the picture that higher transitions are only excited in
denser and smaller regions. Serpens, ![]() Oph A, and NGC 2024, however
show the smallest width of the fit in the CS 2-1 transition. This
is explained by eye inspecting the 2-1 maps and corresponding
high-resolution observations from the literature where we see that the three
sources break up into several clumps which are only separated in the
53'' beam but unresolved in the KOSMA beams.
In these cases, we have restricted the analysis to the major core
seen in the CS 2-1 maps using its size to compute the beam filling,
although this approach introduces a small error in the data analysis
by assigning the whole flux measured in the higher transitions
to this central core.
Oph A, and NGC 2024, however
show the smallest width of the fit in the CS 2-1 transition. This
is explained by eye inspecting the 2-1 maps and corresponding
high-resolution observations from the literature where we see that the three
sources break up into several clumps which are only separated in the
53'' beam but unresolved in the KOSMA beams.
In these cases, we have restricted the analysis to the major core
seen in the CS 2-1 maps using its size to compute the beam filling,
although this approach introduces a small error in the data analysis
by assigning the whole flux measured in the higher transitions
to this central core.
| Source | FWHM in |
FWHM in |
||||
| 2-1 | 5-4 | 7-6 | 2-1 | 5-4 | 7-6 | |
| W49A | 1.0 | 1.1 | 0.3 | 1.5 | 1.7 | 1.3 |
| W33 | 1.7 | 1.7 | 1.4 | 1.7 | 1.3 | 1.0 |
| W51A | 1.9 | 1.7 | 1.7 | 2.1 | 2.2 | 1.1 |
| W3(OH) | 2.1 | 1.1 | 1.3 | 1.7 | 1.4 | 1.4 |
| W3 | 1.0 | 0.6 | 0.8 | 1.0 | 0.6 | 0.3 |
| S255 | 1.9 | 1.6 | 1.1 | 1.2 | 0.6 | 1.1 |
| S235B | 1.0 | 2.2 | 1.1 | 0.9 | 0.2 | 0.3 |
| S106 | 3.0 | 1.6 | 2.5 | 2.2 | ||
| Serpens | 2.0 | 2.2 | 2.1 | 2.3 | ||
| DR21 | 3.0 | 2.6 | 1.8 | 1.5 | 1.7 | 1.8 |
| Mon R2 | 3.2 | 3.0 | 1.1 | 3.6 | 3.2 | 1.6 |
| NGC 2264 | 3.2 | 1.7 | 0.6 | 2.9 | 2.1 | |
| OMC-2 | 2.4 | 1.4 | 0.6 | 2.5 | 1.4 | 0.6 |
| 1.3 | 3.0 | 2.6 | 1.9 | 2.9 | 2.5 | |
| NGC 2024 | 1.1 | 1.1 | 1.3 | 1.3 | 2.5 | 2.3 |
The size of the resulting parameter range in
![]() ,
,
![]() ,
and
,
and
![]() is determined by the accuracy of the
observations. For two cores it was only possible to set a lower limit
to the gas density.
Moreover, we were not able to provide any good constraint to the cloud
temperature for all sources. Values between about 30 K and 150 K are
possible.
Hence, an independent determination of the cloud temperatures is required.
Several different methods based on optically thick CO, NH3 or
dust observations are discussed in the literature and we used the
values from the references given in Table 5. In addition
to these values we also used 50 K as assumed by Plume et al. (1997) as
"standard'' temperature in the parameter determination for
massive cores.
is determined by the accuracy of the
observations. For two cores it was only possible to set a lower limit
to the gas density.
Moreover, we were not able to provide any good constraint to the cloud
temperature for all sources. Values between about 30 K and 150 K are
possible.
Hence, an independent determination of the cloud temperatures is required.
Several different methods based on optically thick CO, NH3 or
dust observations are discussed in the literature and we used the
values from the references given in Table 5. In addition
to these values we also used 50 K as assumed by Plume et al. (1997) as
"standard'' temperature in the parameter determination for
massive cores.
| Source |
|
|
|
|
|
| [K] | [cm-3] | [cm-2/kms-1] | |||
| W49A(a) | 20
|
>
|
|
1.3 | |
| 50
|
|
1.5 |
|
1.2 | |
| W49A(b) | 20
|
|
1.6 |
|
1.3 |
| 50
|
|
1.5 |
|
1.2 | |
| W33 | 40
|
|
1.7 |
|
1.2 |
| 50
|
|
1.6 |
|
1.2 | |
| W51A | 20
|
|
1.6 |
|
1.7 |
| 50 |
|
1.5 |
|
1.4 | |
| 57
|
|
1.4 |
|
1.4 | |
| W3(OH) | 30
|
|
1.5 |
|
1.2 |
| 50 |
|
1.4 |
|
1.2 | |
| W3 | 30
|
|
2.9 |
|
1.5 |
| 50 |
|
1.8 |
|
1.4 | |
| 55
|
|
1.6 |
|
1.3 | |
| S255 | 40
|
|
1.6 |
|
1.3 |
| 50 |
|
1.5 |
|
1.3 | |
| S235B | 40
|
|
1.5 |
|
1.3 |
| 50 |
|
1.5 |
|
1.3 | |
| S106 | 10
|
|
|
1.4 | |
| 25
|
|
1.5 |
|
1.4 | |
| 50 |
|
1.6 |
|
1.4 | |
| Serpens | 25
|
|
1.2 |
|
1.5 |
| 50 |
|
1.6 |
|
1.5 | |
| DR21 | 35
|
|
1.7 |
|
1.9 |
| 50 |
|
1.6 |
|
1.4 | |
| Mon R2 | 25
|
|
1.8 |
|
1.5 |
| 50
|
|
1.7 |
|
1.7 | |
| NGC 2264 | 25
|
|
2.4 |
|
2.6 |
| 50 |
|
2.3 |
|
2.5 | |
| OMC-2 | 19
|
|
1.6 |
|
1.4 |
| 24
|
|
1.5 |
|
1.4 | |
| 50 |
|
1.7 |
|
1.4 | |
| 25
|
|
1.6 |
|
1.4 | |
| 50 |
|
1.8 |
|
1.5 | |
| NGC 2024 | 25
|
|
2.9 | >
|
|
| 40
|
|
2.0 | >
|
||
| 50 |
|
1.7 | >
|
Table 5 lists the parameters from the escape
probability model for all
cores. Whereas the column density is well constrained for
most clouds, there is a considerable uncertainty in the gas
density resulting from the unknown cloud temperature.
At the temperature of 50 K we obtain average values and logarithmic
standard deviation factors of
| (1) | |||
| (2) | |||
For NGC 2024 we are able to test the consistency of the results
from the CS and the C34S observations. The resulting hydrogen
densities agree for both isotopes within 20% at all temperatures
assumed. We obtain
![]() cm-3 at 25 K (Mezger et al. 1992) and
cm-3 at 25 K (Mezger et al. 1992) and
![]() cm-3 at 40 K (Ho et al. 1993). Unfortunately, this
is a core where we can only give a lower limit to the column densities.
The limits deviate by a factor 13, which is significantly
different from the terrestrial isotopic ratio of 23 but close
to the value 10 derived by Mundy et al. (1986) for the isotopic ratio in NGC 2024.
cm-3 at 40 K (Ho et al. 1993). Unfortunately, this
is a core where we can only give a lower limit to the column densities.
The limits deviate by a factor 13, which is significantly
different from the terrestrial isotopic ratio of 23 but close
to the value 10 derived by Mundy et al. (1986) for the isotopic ratio in NGC 2024.
The escape probability model provides a first estimate
to the physical parameters but its limitations are obvious.
It is definitely not justified to assume constant parameters
within the whole cloud. Moreover, several observations are in contradiction to
the parameters from the escape probability models.
Lada et al. (1997) detected the CS 10-9 transition in NGC 2024 and
Plume et al. (1997) observed the 10-9 and 14-13 transitions in
S255 and W3(OH). The critical densities for these transitions are
about
![]() cm-3 and
cm-3 and
![]() cm-3 respectively.
From the densities in Table 5
one would conclude that these transitions
are not excited. Hence, a more sophisticated model has to be applied
to obtain a physically reasonable explanation of the measurements.
Plume et al. (1997) suggested a two-component model or continuous
density gradients to resolve this contradiction. We will discuss a
self-consistent radiative transfer model including a radial
density profile in the following.
cm-3 respectively.
From the densities in Table 5
one would conclude that these transitions
are not excited. Hence, a more sophisticated model has to be applied
to obtain a physically reasonable explanation of the measurements.
Plume et al. (1997) suggested a two-component model or continuous
density gradients to resolve this contradiction. We will discuss a
self-consistent radiative transfer model including a radial
density profile in the following.
We performed non-local radiative transfer simulations using the line radiative transfer code SimLine introduced in detail in Appendix B. SimLine is a FORTRAN code to compute the profiles of molecular rotational lines in spherically symmetric clouds with arbitrary density, temperature and velocity distribution. It consists of two parts: the self-consistent solution of the balance equations for all level populations and energy densities at all radial points and the computation of the emergent line profiles observed by a telescope with finite beam width and arbitrary offset. The optical depths in the lines may vary from minus a few, corresponding to weak masking, to several thousand.
Already in the spherically symmetric description of a core we face a large number of parameters. For all quantities (hydrogen density, kinetic temperature, velocity dispersion, molecular abundances) a radial function has to be found. Regarding the limited amount of information available from the three transitions, this leaves many options open. We decided to assume simple power-law radial functions and a central region with constant parameters for all quantities in the core simulations. This reduces the number of parameters to two (central value and radial exponent) for each gas property, plus the outer and inner radius.
The parameter fit procedure used the multidimensional downhill simplex
algorithm from Press et al. (1992). Although it is not
the most efficient way in terms of convergence speed it turned
out to be very robust in all situations considered. Because a downhill
simplex code does not necessarily find the global minimum of
the ![]() function we performed for each core several runs
with randomly chosen initial simplex covering a large part of the
physically reasonable parameter space. For all clouds we made at
least 30 runs to get a rough idea of the topology of the
function we performed for each core several runs
with randomly chosen initial simplex covering a large part of the
physically reasonable parameter space. For all clouds we made at
least 30 runs to get a rough idea of the topology of the ![]() function. For cores like W33 this turned out to be sufficient
since only one large minimum showed up which was found in almost
half of the runs. The other extreme is S106 where we needed
almost 1000 runs to be sure that we found the global minimum.
Here, the
function. For cores like W33 this turned out to be sufficient
since only one large minimum showed up which was found in almost
half of the runs. The other extreme is S106 where we needed
almost 1000 runs to be sure that we found the global minimum.
Here, the ![]() function was quite complex with numerous
local minima. Future improvements of the fit procedure should include
more sophisticated algorithms like simulated-annealing approaches.
function was quite complex with numerous
local minima. Future improvements of the fit procedure should include
more sophisticated algorithms like simulated-annealing approaches.
The noise in the line profiles produces some graininess of the ![]() function when directly fitting the measured profiles. This
results in a very slow convergence of the algorithm close to the
minimum. A considerable acceleration can be
obtained by not fitting the measured noisy data but a smooth approximation
to them. The line profiles were represented by a superposition of
a Gaussian and a Lorentzian profile. This allows a good characterisation
of all measured profiles including the reproduction of asymmetric
profiles, self-absorption dips and line wings.
function when directly fitting the measured profiles. This
results in a very slow convergence of the algorithm close to the
minimum. A considerable acceleration can be
obtained by not fitting the measured noisy data but a smooth approximation
to them. The line profiles were represented by a superposition of
a Gaussian and a Lorentzian profile. This allows a good characterisation
of all measured profiles including the reproduction of asymmetric
profiles, self-absorption dips and line wings.
Taking the three measured transitions and their
spatial extent as the quantities to be reproduced by a ![]() fit
we find that we are able to derive at most six parameters to
a reasonable accuracy. Fits with seven or eight free parameters,
although still slightly improving the numerical
fit
we find that we are able to derive at most six parameters to
a reasonable accuracy. Fits with seven or eight free parameters,
although still slightly improving the numerical ![]() value, do
not produce any significant changes above the noise limit.
This is comparable to the results by Young et al. (1998) fitting the full
position velocity map of a particular core in a single transition.
There is however a number of additional parameters
where the model can derive certain limits.
Hence, we have to decide first which parameters should be fitted
directly, which parameters may be constrained by preventing
reasonable fits when outside a certain range, and which parameters
can be guessed independently from a physical line of reasoning. This is
discussed in detail for all quantities in the following subsections.
value, do
not produce any significant changes above the noise limit.
This is comparable to the results by Young et al. (1998) fitting the full
position velocity map of a particular core in a single transition.
There is however a number of additional parameters
where the model can derive certain limits.
Hence, we have to decide first which parameters should be fitted
directly, which parameters may be constrained by preventing
reasonable fits when outside a certain range, and which parameters
can be guessed independently from a physical line of reasoning. This is
discussed in detail for all quantities in the following subsections.
Unfortunately,
it is impossible to give an comprehensive error estimate for
the parameters derived from the simulations. This would need
a description of the six-dimensional surface in the parameter space
within which none of the observational error bars is exceeded.
According to the complex topology of the ![]() function
it is not possible to give an easy description for the six-dimensional
valley around the global minimum or its boundaries.
function
it is not possible to give an easy description for the six-dimensional
valley around the global minimum or its boundaries.
As a simple alternative we performed only one-dimensional
variations to get a rough estimate
of the maximum error in the parameters that we must expect. After
the convergence of the ![]() fit, each of the fit parameters
was varied up and down until one of the computed lines
deviated by the assumed maximum observational error of 25%
from the measured lines. The central values of the different
functions were varied independently. When changing the
inner radius, the central values of the gas parameters were adjusted
to keep the functions in the power-law region unchanged.
When varying exponents the corresponding central values were
corrected in such a way that the parameters at the density of
fit, each of the fit parameters
was varied up and down until one of the computed lines
deviated by the assumed maximum observational error of 25%
from the measured lines. The central values of the different
functions were varied independently. When changing the
inner radius, the central values of the gas parameters were adjusted
to keep the functions in the power-law region unchanged.
When varying exponents the corresponding central values were
corrected in such a way that the parameters at the density of
![]() cm-3 remained constant. By the selection of this
density as the fix point when changing the slope, we scan about the
maximum possible range of the exponents. This provides a
conservative estimate of the maximum error.
cm-3 remained constant. By the selection of this
density as the fix point when changing the slope, we scan about the
maximum possible range of the exponents. This provides a
conservative estimate of the maximum error.
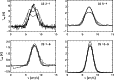 |
Figure 1: Line profiles observed at the central position of S255 in four CS transitions together with best-fit models. The dashed line represents the microturbulent approximation, the dotted line stands for clumping in velocity space with cell sizes of 0.01 pc and the solid line includes the additional effect of density clumping where the combined abundance is reduced by a factor 100. |
| Open with DEXTER | |
In spite of the large number of free parameters in the cloud models it is impossible to fit the line profiles with a smooth density and velocity distribution. The typical self-absorbed profiles known for all microturbulent codes (White 1977) appear in this case. Thus we have to take into account the effects of internal clumping and turbulence leading to a more realistic picture and preventing strong self-absorption.
SimLine treats turbulence and clumping in a local statistical approximation following Martin et al. (1984) (see Appendix B.2). The cloud material is subdivided into small coherent units (clumps) with only thermal internal velocity dispersion. The relative motion of many units then provides the full velocity profile. Martin et al. (1984) showed that the effective optical depth of such an ensemble can be considerably reduced compared to the microturbulent approximation. The relative reduction of the total optical depth depends on the optical depth, i.e. of size the coherent units.
This description does not need any assumptions on the nature of the turbulence creating the internal cloud structure. The reduction occurs in the same way whether clumps are units of the same velocity in a medium of constant density, representing the behaviour of incompressible turbulence, or whether they are density enhancements in a thin inter-clump medium. The different nature of these two scenarios has to be taken into account, however, when computing the excitation. Both the average gas density, providing a measure for the column density and thus the line intensity, and the local density, providing the collisional coupling to the gas, enter the balance equations. In case of coherent units in velocity space both densities agree.
For density clumps we use the additional simplification to treat the cloud locally as a two-component medium neglecting the contribution of the inter-clump medium to the radiative transfer. Then the collisional excitation is provided by the density in the clumps and the column density is provided by the average density. The ratio between the two quantities reflects the filling factor of the volume occupied by dense clumps. From the mathematical point of view this is equivalent to the treatment of the cloud as a homogenous medium where the clumping occurs only in velocity space and the abundance of the radiating molecules is reduced. Hence, it is impossible to separate the influence of the filling factor from that of the molecular abundance so that the line fit provides only a combined quantity which we will denote combined abundance in the following. Beside the modification of the molecular abundance the statistical turbulence description introduces the size of the coherent units as an additional parameter.
Figure 1 demonstrates the influence
of the turbulence. It shows the central line profiles of the
best fits to the S255 observations using different
assumptions on the turbulent nature.
We selected S255 here because we can exploit the
advantage of additional data for the CS 10-9 transition measured by
Plume et al. (1997) providing more constraints on the cloud
model![]() .
In all models the core is optically thin in CS 7-6 and 10-9,
so that the reduction of the optical depth by the turbulent
clumping produces only minor changes in these lines. In CS 2-1
the differences are, however, most obvious. In the microturbulent
description and for the incompressible turbulence we find
self-absorbed line profiles. A reasonable fit to the
observations is only possible using the turbulence model including
clumps with enhanced density. The reduction of the effective optical
depth of the cloud by increasing the optical depth of the coherent
units produces narrower lines providing a better
fit to the observed line profiles.
.
In all models the core is optically thin in CS 7-6 and 10-9,
so that the reduction of the optical depth by the turbulent
clumping produces only minor changes in these lines. In CS 2-1
the differences are, however, most obvious. In the microturbulent
description and for the incompressible turbulence we find
self-absorbed line profiles. A reasonable fit to the
observations is only possible using the turbulence model including
clumps with enhanced density. The reduction of the effective optical
depth of the cloud by increasing the optical depth of the coherent
units produces narrower lines providing a better
fit to the observed line profiles.
We find that the parameter fits do not provide accurate values for the clump size and the combined abundances reflecting the volume filling factor. They only constrain an interval of possible values. We obtained good fits to the observations for the full range of clump sizes between about 0.005 and 0.05 pc. This size scale is confirmed by independent determinations of clump sizes by high-resolution observations in some of our cores. For NGC 2024 Mezger et al. (1992) determined a radius of dense condensations around 0.015 pc and the interferometric studies by Wiesemeyer et al. (1997) showed values between 0.005 and 0.01 pc. In W3 Tieftrunk et al. (1998) observed compact clumps with a size of 0.02 pc and in OMC-2 Chini et al. (1997) found dust condensations with radii between 0.01 and 0.05 pc.
For a better comparison to turbulence theory we prefer
to specify the cell size in terms of the turbulent correlation
length
![]() which should be on the order of 0.1 pc
(Miesch et al. 1994; Goodman et al. 1998). The size of the units
which are coherent with respect to the line radiative
transfer is smaller by the ratio of the thermal line width to the total
velocity dispersion. Thus the size range
found corresponds to correlation lengths between 0.04 and 0.4 pc.
In the following computations we use the intermediate value of 0.1 pc as
correlation length for all clouds.
which should be on the order of 0.1 pc
(Miesch et al. 1994; Goodman et al. 1998). The size of the units
which are coherent with respect to the line radiative
transfer is smaller by the ratio of the thermal line width to the total
velocity dispersion. Thus the size range
found corresponds to correlation lengths between 0.04 and 0.4 pc.
In the following computations we use the intermediate value of 0.1 pc as
correlation length for all clouds.
Regarding the combined abundances we find two classes of objects.
The majority of cores, including the example of S255, is well fitted
by values between 10-11 and 10-10, whereas a second class,
consisting of W3, Serpens, and S106 needs values between
10-10 and 10-9 for a good fit. Because we do not know
the molecular abundances there is no way to translate these values
directly into clump filling factors. Assuming the CS abundances
of
![]() to
to
![]() obtained by Hatchell et al. (1998)
for several star-forming cores, the first class corresponds to
filling factors around 0.01, whereas the CS abundance of
obtained by Hatchell et al. (1998)
for several star-forming cores, the first class corresponds to
filling factors around 0.01, whereas the CS abundance of
![]() from Plume et al. (1997) corresponds to a filling factor of 0.1. The filling
factors in the second group are ten times higher accordingly. In all following
computations we have used a combined abundance factor of
from Plume et al. (1997) corresponds to a filling factor of 0.1. The filling
factors in the second group are ten times higher accordingly. In all following
computations we have used a combined abundance factor of
![]() for the first and
for the first and
![]() for the second group. In the translation
to cloud masses we will use the intermediate CS abundance of
for the second group. In the translation
to cloud masses we will use the intermediate CS abundance of
![]() .
.
As an additional parameter quantifying turbulence in a one-dimensional cloud model we have to take a radial variation of the turbulent velocity distribution into account to explain the observed size-line width and size-density relations (Larson 1969). Exponents of this radial dependence between about 0.1 and 0.7 are typically discussed (see e.g. Goodman et al. 1998). We left the width and the exponent of the turbulent velocity distribution as free parameters and obtained exponents between 0.15 and 0.65.
Any physically reasonable cloud model should include a spatial dependence
of the gas parameters. Collapse simulations might provide
reasonable model assumptions for the density structure.
Bodenheimer & Sweigart (1968) and Shu (1977) have shown that an isothermal sphere
evolves into a power law density profile
![]() with
with
![]() .
Homologous collapse
simulations provide an exponent
.
Homologous collapse
simulations provide an exponent
![]() (Dickel & Auer 1994)
and the free-fall collapse discussed by Welch et al. (1987) results in a density
exponent
(Dickel & Auer 1994)
and the free-fall collapse discussed by Welch et al. (1987) results in a density
exponent
![]() .
The inside-out collapse model (Shu 1997)
combined two regions of different exponents and recent more
sophisticated collapse simulations (see e.g. Basu & Mouschovias 1995)
show more complex density structures with an average
exponent
.
The inside-out collapse model (Shu 1997)
combined two regions of different exponents and recent more
sophisticated collapse simulations (see e.g. Basu & Mouschovias 1995)
show more complex density structures with an average
exponent
![]() between 1.5 and 1.7. Dust observations of
the density profile of protostellar cores show evidence both for
cores with a typical r-2 profile and for cores with flat
density structure and a sharp outer edge (André et al. 1999).
Thus we expect exponents between about 1.5 and 2.0 in our power-law
density model which is bound by an outer cut-off and a central constant
region. Although this simple model may not reflect
the whole complexity of the density profile we can hardly
derive any more information from the limited observations
available. We left the central density and the density exponent
as free parameters to be fitted. The resulting exponents span the
relatively wide range between 1.1 and 2.2.
between 1.5 and 1.7. Dust observations of
the density profile of protostellar cores show evidence both for
cores with a typical r-2 profile and for cores with flat
density structure and a sharp outer edge (André et al. 1999).
Thus we expect exponents between about 1.5 and 2.0 in our power-law
density model which is bound by an outer cut-off and a central constant
region. Although this simple model may not reflect
the whole complexity of the density profile we can hardly
derive any more information from the limited observations
available. We left the central density and the density exponent
as free parameters to be fitted. The resulting exponents span the
relatively wide range between 1.1 and 2.2.
In the fit of the radii confining the power-law density profile
we face two problems. We cannot distinguish changes of the model
parameters on the smallest size scales where even the highest
observed transition is thermalised because of the high density.
Thus we can only set an upper limit
![]() to the radius of the central region where a transition from the power
law behaviour in the envelope to constant parameters might occur.
Only in four clouds - Serpens, Mon R2,
to the radius of the central region where a transition from the power
law behaviour in the envelope to constant parameters might occur.
Only in four clouds - Serpens, Mon R2, ![]() Oph A, and the
b-component of W49A - the strength of the CS 7-6 line
sets an upper limit to the density so that we can derive the inner
radius directly from the observations. In all parameter fits, we left
the central radius as a free parameter. After the fit we
increased the radius until the maximum deviation in one
of the lines reached 5%. This provides a reasonable upper
limit to the inner radius in all cases where the line profiles are
independent of the density structure below this limit and gives
only small modifications in the four cases where the inner
radius was already well constrained by the fit.
Oph A, and the
b-component of W49A - the strength of the CS 7-6 line
sets an upper limit to the density so that we can derive the inner
radius directly from the observations. In all parameter fits, we left
the central radius as a free parameter. After the fit we
increased the radius until the maximum deviation in one
of the lines reached 5%. This provides a reasonable upper
limit to the inner radius in all cases where the line profiles are
independent of the density structure below this limit and gives
only small modifications in the four cases where the inner
radius was already well constrained by the fit.
The outer radius of the cloud is also quite uncertain. We can
easily provide a value for the extent of gas at densities above about
![]() cm-3 based on the spatial extent of the CS 2-1 emission
and the line profiles. But it is not possible to derive a reliable value
for the extent of low density gas. We can only give a lower limit to the
outer radius and thus the mass of the massive cores considered.
As the density exponents are typically shallower than -2, a majority of
mass could be present beyond this radial limit at low
densities invisible in CS. We excluded the outer radius from the
parameter fit using a sufficiently large value for all clouds and
performed later a separate run reducing the radius to find the minimum
outer radius
cm-3 based on the spatial extent of the CS 2-1 emission
and the line profiles. But it is not possible to derive a reliable value
for the extent of low density gas. We can only give a lower limit to the
outer radius and thus the mass of the massive cores considered.
As the density exponents are typically shallower than -2, a majority of
mass could be present beyond this radial limit at low
densities invisible in CS. We excluded the outer radius from the
parameter fit using a sufficiently large value for all clouds and
performed later a separate run reducing the radius to find the minimum
outer radius
![]() in a way equivalent to the
maximisation of the inner radius described above.
in a way equivalent to the
maximisation of the inner radius described above.
The temperature distribution of massive cores
is still a matter of debate (cf. Garay & Lizano 1999).
During early phases of cloud collapse the temperature should remain
constant as long as the core remains optically
thin. Deviations are to be expected, however, as protostellar
sources are formed in most of our cores, leading to an internal
heating of the cloud. Moreover in thin outer regions external
heating can be important. Based on several observational results
Scoville & Kwan (1976) set up a spherical cloud model with a warm
inner region resulting in an temperature profile
![]() with
with
![]() .
.
Hence, we should also derive the core temperature and the temperature exponent from the radiative transfer model. In a first run we have investigated the influence of a temperature gradient in S255 when fitting only the central line profiles. We compared the best fit models to the S255 observations using either a constant cloud temperature, a temperature decaying with the exponent -0.4, or the temperature exponent as a free parameter. The latter case provided a best fitting exponent of -0.12. All three fits showed an excellent agreement in terms of the central line profiles falling almost exactly on the solid curves in Fig. 1. Thus, it is impossible to favour a certain exponent from the least squares fit of the line profiles only.
In Table 6 we see the resulting values for the other
core parameters. The average temperature given here is computed
as the mass-weighted average up to
![]() .
As main difference we find a kind of compensation between temperature
and density exponent. The sum of both exponents is kept approximately
constant to fulfil the constraints given by the line ratios.
Temperature and density gradient act in a similar manner, leading to
higher excitation in regions which are either denser or warmer.
The variation of
the density gradient, however, changes the extent of the emission
in the CS 2-1 transition (the change is much smaller in the higher
transitions). Consequently, we can constrain the temperature exponent
when taking the observed size of the source into account. The beam convolved
FWHM of the CS 2-1 emission in S255 falls between 1.5' and 2.1'
clearly excluding models with steep temperature gradients.
.
As main difference we find a kind of compensation between temperature
and density exponent. The sum of both exponents is kept approximately
constant to fulfil the constraints given by the line ratios.
Temperature and density gradient act in a similar manner, leading to
higher excitation in regions which are either denser or warmer.
The variation of
the density gradient, however, changes the extent of the emission
in the CS 2-1 transition (the change is much smaller in the higher
transitions). Consequently, we can constrain the temperature exponent
when taking the observed size of the source into account. The beam convolved
FWHM of the CS 2-1 emission in S255 falls between 1.5' and 2.1'
clearly excluding models with steep temperature gradients.
|
|
|
|
|
|
|
|
|
| [K] | [K] | [cm-3] | [pc] | [ |
['] | ||
| 0.0 | 47 | 47 | -1.5 | 3300 | 1.1 | 1200 | 1.8 |
| -0.12 | 73 | 52 | -1.3 | 2500 | 1.3 | 1500 | 2.2 |
| -0.4 | 220 | 52 | -1.0 | 1000 | 2.5 | 7000 | 3.6 |
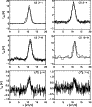 |
Figure 2: Observed line profiles and best fit model to the observations of NGC 2024 using a CS to C34S abundance ratio of 13. |
| Open with DEXTER | |
Beside the temperature gradient we can expect the formation
of compact H II regions in the centre of a star forming core.
Using the parameters of the central H II region derived
by Dickel & Auer (1994) for W49 (R=0.2 pc,
![]() cm-3,
cm-3,
![]() K) we have compared the resulting CS
lines when either including or neglecting the H II region
in the radiative transfer computations
(see Appendix B.3). We find that the influence
of the H II region is negligible in this example for the four
CS transitions considered here.
K) we have compared the resulting CS
lines when either including or neglecting the H II region
in the radiative transfer computations
(see Appendix B.3). We find that the influence
of the H II region is negligible in this example for the four
CS transitions considered here.
In general H II regions have two dominant effects on the line profiles. The integrated brightness changes the molecular excitation throughout the cloud and is visible as continuum emission. Moreover, the molecular material in front of an H II region, appears partially in absorption. A large H II region with electron densities being a factor 10 or more higher than in the example above, would thus result in distinct changes in the lines. Depending on the configuration and velocity structure, the CS lines may appear in absorption or with P Cygni profiles. Moreover, a strong continuum emission would be observed at all frequencies considered. However, bright H II regions with high electron densities are unlikely to be that extended (Wood & Churchwell 1989). For ultracompact H II regions the change of the line profiles by absorption is negligible due to the small angular size of the H II region so that the molecular excitation is the remaining effect. From the lack of a bright continuum underlying the lines we can, however, exclude configurations with a bright H II region here. Weaker compact or ultracompact H II regions - although possible - were not included in the fit computations as they would only influence material in their close environment which cannot be resolved in this study.
Regarding the chemical evolution of massive cores one should also
expect a variation of the molecular abundances of CS and C34S.
However, our present knowledge is still insufficient to guess reliable
values here (cf. Bergin & Langer 1997).
As discussed in Sect. 4.2,
it is also not possible to fit the abundance independently from the
clump filling factor, so that we adopted here a constant CS abundance
of
![]() relative to H2 ignoring any radial variation of the
abundances.
relative to H2 ignoring any radial variation of the
abundances.
An additional test is only possible for NGC 2024 where C34S is
sufficiently bright so that we could include it
in the fits. Figure 2 shows the best fit
model to all six available line profiles.
Equivalent to the results from the escape probability
model we get the best match for a relative molecular
abundance X(CS)/X(C34S
![]() .
All six
lines are simultaneously fitted.
.
All six
lines are simultaneously fitted.
None of the cores except W49A show clearly asymmetric profiles as a signature of systematic internal velocities. The weak wings seen in a few of the other lines at low resolution are insufficient to derive any collapse or outflow model. Thus we have fitted all cores with a static model.
Table 7 lists the resulting best fit
parameters for all cores with their error intervals. As discussed in
Sect. 4.3 the
intervals for the radii are in most cases only limited
at one end. The central density refers to the value
at the radius
![]() .
.
Comparing the different cores we find that the inner and outer radii are mainly determined by the selectional bias from the observability as one massive core. The most distant cores are only detectable with the KOSMA telescope if they are relatively large whereas at small distances only small cores are unresolved.
The minimum central density fitting
the CS lines varies between 106 cm-3 for W49A(b)
and
![]() cm-3 for NGC 2024.
The high value derived for NGC 2024 is due to the availability of
the CS 10-9 observations tracing higher densities.
With the three CS lines measured for most cores, only the
density range below about 107 can be reliably traced, so that we
have to take the central density for all clouds
except W49A(b), Serpens, Mon R2, and
cm-3 for NGC 2024.
The high value derived for NGC 2024 is due to the availability of
the CS 10-9 observations tracing higher densities.
With the three CS lines measured for most cores, only the
density range below about 107 can be reliably traced, so that we
have to take the central density for all clouds
except W49A(b), Serpens, Mon R2, and ![]() Oph A as lower limits.
The density exponent covers the range between -1.1 and -2.2
where the majority of clouds shows values around -1.6 corresponding
to large-scale collapse models (Sect. 4.3).
Oph A as lower limits.
The density exponent covers the range between -1.1 and -2.2
where the majority of clouds shows values around -1.6 corresponding
to large-scale collapse models (Sect. 4.3).
Although we don't have a sample where we can expect to set up statistically significant correlations we can interpret some general relations. It turns out that the parameters are not completely independent of each other. Whereas the majority of clouds shows an average temperature between 20 and 50K, the three clouds which needed a larger combined abundance factor corresponding to a higher clump filling factor in the turbulence description (W3, S106, Serpens) also tend to require relatively high temperatures. There is a clear correlation between the cloud temperature and the turbulent line width indicating that heating and turbulent driving might have a related cause. The cores with a significant temperature exponent also show a relatively steep density exponent whereas a steep density exponent itself does not necessarily require a temperature exponent. These internal relations should be explained from the physical nature of the clouds.
|
|
|
|
|
|
|
|
|
| [pc] | [pc] | [cm-3] | [K] | [cm-3] | [ |
||
| 4 | 0.06 | 1.1 |
|
-1.5 | 47 | 3600 | 1000 |
| 3 | 0.11 | 1.1 |
|
-1.4 | 49 | 3700 | 1000 |
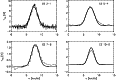 |
Figure 3: Best fit models to the S255 observations fitting only the three lower transitions (solid lines) or all four transitions (dotted line). |
| Open with DEXTER | |
|
|
|
|
|
|
|
|
|
| [pc] | [pc] | [cm-3] | [K] | [kms-1] | |||
| 4 | [:0.08] | [0.66:] | [1.6:2.2]
|
-[1.3:1.7] | [41:52] | [1.6:2.9] | [-0.01:0.42] |
| 3 | [:0.21] | [0.68:] | [4.4:6.1]
|
-[1.2:1.8] | [40:59] | [1.7:3.2] | [-0.07:0.70] |
| Source |
|
|
|
|
|
|
D |
| [cm-3] | [1023 cm-2] | [K] | [ |
[ |
[pc] | ||
| W49A(a) |
|
2.6 | 4.6 | 92 | 15000 | 22000 | 11000 |
| W49A(b) |
|
0.80 | 4.8 | 109 | 19000 | 14000 | 11000 |
| W33 |
|
2.3 | 3.8 | 28 | 7400 | 6300 | 4000 |
| W51A |
|
3.0 | 9.8 | 43 | 54000 | 30000 | 7500 |
| W3(OH) |
|
1.0 | 1.5 | 39 | 1900 | 1900 | 2200 |
| W3 |
|
3.6 | 9.7 | 41 | 1700 | 1100 | 2200 |
| S255 |
|
1.1 | 0.78 | 47 | 870 | 530 | 2500 |
| S235B |
|
0.66 | 0.22 | 20 | 180 | 210 | 1800 |
| S106 |
|
0.32 | 0.23 | 137 | 280 | 200 | 600 |
| Serpens |
|
0.22 | 0.17 | 93 | 53 | 80 | 310 |
| DR21 |
|
0.82 | 0.79 | 83 | 1800 | 1800 | 3000 |
| Mon R2 |
|
0.22 | 0.18 | 54 | 310 | 260 | 950 |
| NGC 2264 |
|
0.46 | 0.71 | 37 | 450 | 720 | 800 |
| OMC-2 |
|
0.34 | 0.24 | 27 | 95 | 52 | 400 |
|
|
0.12 | 0.12 | 20 | 96 | 34 | 160 | |
| NGC 2024 |
|
1.3 | 1.6 | 36 | 17 | 35 | 420 |
The main constraint to the core parameters that we can derive is set by the molecule and the transitions observed. They are only sensitive to a relatively narrow density range. We can test the limitation of the fits provided by the restriction to three line profiles by comparing the results obtained for cores where we have additional CS 10-9 profiles. With the data from Plume et al. (1997) for S255 we investigate how much information is lost due to the lack of CS 10-9 data in most cores. Figure 3 shows the resulting best fits to the central line profiles in S255 when either all four lines are fitted or only the information from the lower three transitions is used. Table 8 lists the corresponding model parameters from the fits. Isothermal models provided good fits to the data and the derived physical parameters are almost identical except for the inner radius. The additional information from the CS 10-9 transition can set a smaller limit here corresponding to the higher central densities. When predicting the 10-9 line data from the best fit of the three other lines the intensity is too low by only about 20% (Fig. 3). Hence, we expect reliable results also for those cores where only three lines are observed but it would be favourable to add information from higher transitions for a better resolution of the densest inner region.
Moreover, a fourth line will reduce the error bars of the parameters. In Table 9 we compare the error obtained for the S255 observations using either the three- or the four-lines fit. As discussed above the possible range of the inner and outer radii is limited only in one direction. Thus, the fourth line mainly reduces the uncertainty of the inner radius. It hardly influences the error of the outer radius and the density at the inner radius but it also reduces the error of the density exponent, the temperature and the velocity structure. Thus the inclusion of additional lines in the model fits would also give a better constraint of the parameters derived.
Table 10 shows quantities characterising the global properties of the clouds computed from the fit parameters in Table 7. The average density in the second column is given by the cloud mass within the outer radius. We see the strong discrepancy between the average density (Table 10) and the central clump density (Table 7) reflecting a very inhomogenous structure with low volume filling factor of dense clumps.
In the Cols. 3 and 4 of Table 10 one can compare the
average column density towards the centre in the nonlocal model with
the column density computed from the escape probability model.
Here, we have used the molecular column densities from Table 5
assuming a CS abundance of
![]() .
We find an agreement within a factor
of about 1.5, despite the completely different
analysis applied, except for W49A, W51, and W3 where the column density
from the escape probability model is more than a factor of two higher
and S235B where it is lower. S235B, W49A, and W3 are
the smallest sources in our sample unresolved even in the
CS 2-1 beam. Here, the beam filling factors used in the escape probability
model are uncertain so that they may be responsible for the difference.
For W51A, no simple explanation
for the difference is obvious. It is however, by far the most
massive core in our sample so that it might be somewhat peculiar
from that point of view. In general, we find that the escape probability
analysis provides a reasonable determination for the column density
when we have a good estimate of the beam filling factor. It fails to
derive correct densities or sizes.
.
We find an agreement within a factor
of about 1.5, despite the completely different
analysis applied, except for W49A, W51, and W3 where the column density
from the escape probability model is more than a factor of two higher
and S235B where it is lower. S235B, W49A, and W3 are
the smallest sources in our sample unresolved even in the
CS 2-1 beam. Here, the beam filling factors used in the escape probability
model are uncertain so that they may be responsible for the difference.
For W51A, no simple explanation
for the difference is obvious. It is however, by far the most
massive core in our sample so that it might be somewhat peculiar
from that point of view. In general, we find that the escape probability
analysis provides a reasonable determination for the column density
when we have a good estimate of the beam filling factor. It fails to
derive correct densities or sizes.
Columns 6 and 7 in Table 10 shows the core masses
computed in two different ways.
Column 6 gives the integrated mass of the model cloud assuming the
smallest fitting outer radius and the maximum possible central radius.
The influence of the inner radius on the total mass is negligible, but the uncertainty
from the lack of information on the outer radius has to be kept in mind.
Increasing the amount of virtually invisible material around the core
by increasing the outer cloud radius can easily increase the total mass
by more than a factor 10. As the mass computation relies on the knowledge of the
CS molecular abundance (Sect. 4.2), the resulting
values are to be changed if the true abundances deviate from the
assumed value of
![]() .
.
Column 7 contains the core virial mass assuming equipartition
of kinetic and gravitational energy in a homogenous spherical cloud. We used
the central CS 2-1 line profile and the size of the cloud visible in this
transition to estimate the velocity dispersion in the line of sight
and the radius. Following Lang (1980)
we obtain the virial mass by
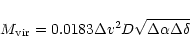 |
(3) |
For all clouds except ![]() Oph A the agreement between the two masses
falls within a factor of two. The behaviour of
Oph A the agreement between the two masses
falls within a factor of two. The behaviour of ![]() Oph A is due to the
radius of the excitation model which is larger than the smallest
resolved core, as discussed above. Hence, it provides a larger mass than
the virial estimate which uses this visible core size. The general
good agreement is quite amazing regarding the uncertainty of the outer boundary
of the models. The clouds seem to be virialised and the CS abundance
estimate holds approximately for all clouds.
Oph A is due to the
radius of the excitation model which is larger than the smallest
resolved core, as discussed above. Hence, it provides a larger mass than
the virial estimate which uses this visible core size. The general
good agreement is quite amazing regarding the uncertainty of the outer boundary
of the models. The clouds seem to be virialised and the CS abundance
estimate holds approximately for all clouds.
The agreement of the mass from the SimLine fits with the virial mass and independent estimates from the literature indicates that the cores are well confined and our minimum outer radius corresponds to a real, relatively sharp boundary for most cores in agreement with the results from continuum observations of several cores by André et al. (1999). Future investigations are, however, necessary to confirm this result because the nature of virialisation is still not understood and it is therefore not clear how much of the "invisible'' low density mass would contribute to the virial mass.
To judge the reliability of the parameters derived here, we can compare them with core parameters obtained independently from observations in other tracers and with other telescopes. In general they provide only values for few of the cloud parameters but they may serve as an independent test of our results. We cannot include a complete discussion of the literature concerning the 15 massive cores considered here. Rather we restrict ourselves to a few selected observations showing the general power and limitations of the method.
For NGC 2024 we have compared our data with results from complementary
high-resolution observations in Table 11. Mezger et al. (1992)
combined the results of SEST observations at 1.3 mm with IRAM 30 m
continuum maps at 870 ![]() m to identify several clumps in NGC 2024
and to deduce their physical properties from the continuum fluxes.
The given values correspond to FIR5 falling at our central position.
Wiesemeyer et al. (1997)
used a spherically symmetric continuum transfer model to derive the
physical parameters of FIR5 from 3 mm continuum observations
taken with the IRAM Plateau de Bure interferometer combined with the
data from Mezger et al. (1992) and VLA 1.3 cm observations of Gaume et al. (1992).
Depending on the assumed luminosity and dust properties
they found a range of parameters fitting the observed continuum.
The last line in Table 11 represents the results from
the SimLine fit to our data.
In contrast to Table 10, the central column density
given here is not averaged but computed towards a central clump to
allow a better comparison with the dust observations which are
able to resolve this clump.
m to identify several clumps in NGC 2024
and to deduce their physical properties from the continuum fluxes.
The given values correspond to FIR5 falling at our central position.
Wiesemeyer et al. (1997)
used a spherically symmetric continuum transfer model to derive the
physical parameters of FIR5 from 3 mm continuum observations
taken with the IRAM Plateau de Bure interferometer combined with the
data from Mezger et al. (1992) and VLA 1.3 cm observations of Gaume et al. (1992).
Depending on the assumed luminosity and dust properties
they found a range of parameters fitting the observed continuum.
The last line in Table 11 represents the results from
the SimLine fit to our data.
In contrast to Table 10, the central column density
given here is not averaged but computed towards a central clump to
allow a better comparison with the dust observations which are
able to resolve this clump.
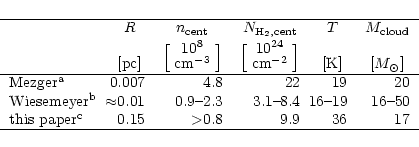
|
We see that one cannot reveal the true radius of the core from our low resolution observations. Moreover, the CS observations cannot trace the same high densities as the dust observations so that they provide only a lower limit. It is, however, already close to the central density given by Wiesemeyer et al. (1997). The mass and column density derived from our radiative transfer computations agree quite well with the values provided by the high-resolution observations. A possible explanation for the difference between the gas kinetic temperature and the dust temperatures was provided already by Schulz et al. (1991). They performed NH3 and CS observations of NGC 2024 and obtained temperatures between 35 and 40 K at the position considered. Using a two-component dust model they demonstrated that these temperatures are also consistent with the observations by Mezger et al. (1992). Altogether we are able to derive realistic values for the core parameters with a clumpy radiative transfer model even if we are not able to deduce the exact object size as we cannot resolve it.
W51 consists of three compact molecular cores located within about
one arcmin. Interferometric observations by Young et al. (1998)
and the combination of line and
continuum measurements by Rudolph et al. (1990) seem to indicate
collapse of the component W51e2 with a mass of about 40000 ![]() .
The mass determined by the SimLine fit is 54000
.
The mass determined by the SimLine fit is 54000 ![]() .
The FCRAO and KOSMA observations show no signatures of collapse as
they are probably blurred by our low spatial resolution.
Sievers et al. (1991) obtained temperatures between
20K and 57K and Zang & Ho (1997) derived 40-50 K for an inner
region of about 0.2 pc and 25-30K for the outer cloud based on
NH3 observations. We were able to fit the observations with an
isothermal cloud at 44 K, however cannot exclude such a temperature
structure. Young et al. (1998) used an LTE code assuming spherical
or spheroidal symmetry to simulate the inner 0.2 pc region of W51e2
fitting the observed ammonia data. They obtained density gradients
of -1.8 to -2.2 somewhat steeper than in our fit, indicating that
a dense central region might be surrounded by an envelope
with a flatter density gradient. Their central densities between
1.5 and
.
The FCRAO and KOSMA observations show no signatures of collapse as
they are probably blurred by our low spatial resolution.
Sievers et al. (1991) obtained temperatures between
20K and 57K and Zang & Ho (1997) derived 40-50 K for an inner
region of about 0.2 pc and 25-30K for the outer cloud based on
NH3 observations. We were able to fit the observations with an
isothermal cloud at 44 K, however cannot exclude such a temperature
structure. Young et al. (1998) used an LTE code assuming spherical
or spheroidal symmetry to simulate the inner 0.2 pc region of W51e2
fitting the observed ammonia data. They obtained density gradients
of -1.8 to -2.2 somewhat steeper than in our fit, indicating that
a dense central region might be surrounded by an envelope
with a flatter density gradient. Their central densities between
1.5 and
![]() cm-3 bracket our value of
cm-3 bracket our value of
![]() .
The assumption of a smooth medium by Young et al. (1998) results
in a central temperature estimate below 25K and a steep
temperature gradient. I.e. significantly lower temperatures than
in our clumpy turbulent model. We have tested this behaviour by trying to
fit the data without clumping in our model and also got low
temperatures below 20 K but quite bad
.
The assumption of a smooth medium by Young et al. (1998) results
in a central temperature estimate below 25K and a steep
temperature gradient. I.e. significantly lower temperatures than
in our clumpy turbulent model. We have tested this behaviour by trying to
fit the data without clumping in our model and also got low
temperatures below 20 K but quite bad ![]() values. Thus the
correct treatment of the internal clumping is essential for a
reliable temperature derivation.
values. Thus the
correct treatment of the internal clumping is essential for a
reliable temperature derivation.
W3(OH) was studied e.g. by Wilson et al. (1991) using VLA observations
of methanol and OH and by Tieftrunk et al. (1998) and Helmich et al. (1996)
with single dish observations of ammonia and HDO, respectively.
The KOSMA beam covers several maser spots
and a luminous mm continuum source - probably a class 0 object. Wilson
et al. (1991) obtained a kinetic temperature of the molecular cores of
20K, whereas Tieftrunk et al. (1998) derived 27K. Both agreed with our
total mass estimate of about 2000 ![]() .
The radius of 1.3 pc
determined by Tieftrunk is somewhat smaller than the value computed from
our model, but clearly within the error bar. From the HDO excitation
Helmich et al. (1996) conclude dust temperatures above 100K at densities
between 105 and 106 cm-3, with few embedded clumps at
107 cm-3. This clump density and the column density
of about
.
The radius of 1.3 pc
determined by Tieftrunk is somewhat smaller than the value computed from
our model, but clearly within the error bar. From the HDO excitation
Helmich et al. (1996) conclude dust temperatures above 100K at densities
between 105 and 106 cm-3, with few embedded clumps at
107 cm-3. This clump density and the column density
of about
![]() cm-2 agree approximately with the values from
our spherical model. The temperature of
39 K determined from the CS observations falls into the range discussed
but the difference to the methanol and ammonia values asks for an
explanation. Around the massive
core there is probably still an extended envelope of gas at low densities
insufficient to excite the observed CS transitions (Tieftrunk et al. 1998).
cm-2 agree approximately with the values from
our spherical model. The temperature of
39 K determined from the CS observations falls into the range discussed
but the difference to the methanol and ammonia values asks for an
explanation. Around the massive
core there is probably still an extended envelope of gas at low densities
insufficient to excite the observed CS transitions (Tieftrunk et al. 1998).
W3 was studied in detail by Tieftrunk et al. (1995, 1997, 1998) using C34S,
C18O, NH3, and continuum observations. Our beam covers the
two bright components W3 Main and W3 West. Moreover, the region
contains some ultracompact H II regions related to infrared sources.
The molecular line emission peaks at a position close to W3 West. The line
velocity of our CS observations at -42 kms-1 agrees with the
velocity of W3 West indicating this component as the main originator
of the observed CS emission.
The combination of single dish and VLA observations by Tieftrunk et al.
(1997, 1998) showed extended gas at a temperature of 25-45K, a
density of 104 cm-3, an size of about 1 pc, and a total
mass of 1100-1400 ![]() .
This corresponds well to the parameters
derived from the KOSMA observations. We have
traced the emission to the somewhat larger radius of 1.4 pc, but within
a radius of 1 pc we get about the same average density of
.
This corresponds well to the parameters
derived from the KOSMA observations. We have
traced the emission to the somewhat larger radius of 1.4 pc, but within
a radius of 1 pc we get about the same average density of
![]() cm-3. Our mass estimate of 1100
cm-3. Our mass estimate of 1100 ![]() and the average
temperature of 41 K also agree. The VLA observations
showed several very compact clumps with a size of 0.02 pc, densities
of 107 cm-3, and
and the average
temperature of 41 K also agree. The VLA observations
showed several very compact clumps with a size of 0.02 pc, densities
of 107 cm-3, and
![]() K. They are not resolvable
from our data, but correspond to the clumps in the turbulence description
and the core parameters derived from
the radiative transfer model show a similar size and density. In the
smooth temperature distribution assumed in the radiative transfer model
we are not able to resolve hot spots with 250 K but found the
need for an increased temperature towards the centre.
K. They are not resolvable
from our data, but correspond to the clumps in the turbulence description
and the core parameters derived from
the radiative transfer model show a similar size and density. In the
smooth temperature distribution assumed in the radiative transfer model
we are not able to resolve hot spots with 250 K but found the
need for an increased temperature towards the centre.
From the group of low mass cores, Castets & Langer (1995) analysed CS
observations of OMC-2 by means of an LVG analysis providing
![]() K,
a density of
K,
a density of
![]() cm-3 and a CS column density of
cm-3 and a CS column density of
![]() cm-2 in agreement with our results.
They found already indications for substructure with clump radii
of about 0.022 pc and higher densities in observations with higher resolution.
Our analysis shows densities of at least
cm-2 in agreement with our results.
They found already indications for substructure with clump radii
of about 0.022 pc and higher densities in observations with higher resolution.
Our analysis shows densities of at least
![]() cm-3at a scale of 0.019 pc. The virial mass of 71
cm-3at a scale of 0.019 pc. The virial mass of 71 ![]() computed
by Castets & Langer is only somewhat smaller than our mass estimate
of 95
computed
by Castets & Langer is only somewhat smaller than our mass estimate
of 95 ![]() .
Recent 1.3 mm observations by Chini et al. (1997) show at
least 11 embedded condensations in OMC-2 with masses between 5 and
8
.
Recent 1.3 mm observations by Chini et al. (1997) show at
least 11 embedded condensations in OMC-2 with masses between 5 and
8 ![]() and temperatures between 20 and 33 K whereas 350
and temperatures between 20 and 33 K whereas 350 ![]() m continuum
data by Lis et al. (1998) reveal even 30 clumps but lower temperatures of
17 K supporting our approach of the clumpy cloud model.
m continuum
data by Lis et al. (1998) reveal even 30 clumps but lower temperatures of
17 K supporting our approach of the clumpy cloud model.
The comparison shows that different tracers see different parts
of a cloud corresponding to different physical conditions. Results
from other authors based on CS observations agree in most cases
quite well, whereas the results from other tracers may considerably
differ. The relatively large uncertainty
in the temperature structure that we cannot resolve within our
analysis asks for additional observations in higher transitions
or at better spatial resolution. For nearby clouds like NGC 2024,
OMC-2 or ![]() Oph A we get a good agreement with results from
high-resolution or even interferometric observations, whereas
for distant massive cores like W49A and W51A there are several
open question, especially regarding the temperature structure.
Oph A we get a good agreement with results from
high-resolution or even interferometric observations, whereas
for distant massive cores like W49A and W51A there are several
open question, especially regarding the temperature structure.
All massive cores seem to be approximately virialised independent of their internal structure with respect to the number, distribution and luminosity of young stars. Although one could expect that violent bipolar outflows observed in some cores will drastically change the energy balance in the core, the physics of the turbulence in the cores seems to be extremely stable guaranteeing a continuous state of virialisation.
The relatively sharp outer boundary suggested by the mass estimates can be interpreted in terms of collapse models. The collapse of an isothermal sphere would result in a self-similar density distribution without clear boundary whereas our results rather tend towards the scenario of a finite-size Bonnor-Ebert condensation (Bonnor 1956). The outer boundary is, however, not well determined but only set by the mass constraints because the radiative transfer model itself cannot exclude a continuation of the density structure to larger radii.
The density exponent of about -1.6 derived for most cores is consistent with several collapse models (see Sect. 4.3) but deviations from the exponent for particular clouds up to values around -2 have to be explained.
On the other hand we have seen that simple collapse models are not relevant for the massive cores considered here. Clumpiness is a main feature of all clouds and smooth microturbulent models are not able to explain the observed lines. In agreement with other high-resolution observations we find typical clump sizes of 0.01-0.02 pc at least for the nearby cores. In massive distant cores the situation might be more complex including a hierarchy of clump sizes resulting in a larger uncertainty of the temperature profile derived from our model.
We have shown that the careful analysis of multi-line single dish observations with a relatively large beam can provide a set of information comparable to single-line interferometric observations. From a careful excitation analysis using a self-consistent radiative transfer computation it is possible to deduce some sub-resolution information. We can infer clump sizes, masses and densities at scales below a tenth of the beam size. However, interferometric observations are necessary to determine the exact core geometry including the location and number of clumps within a dense core.
The spherically symmetric radiative transfer code used here is able to take into account radial gradients in all quantities and internal clumpiness of the cloud. It enables a reliable deduction of the physical parameters from line profiles observed in sources with a size close to the spatial resolution limit. The method allows to analyse similar observations of objects like star-forming cores in distant galaxies unresolvable by all today's means. For a better resolution of the internal temperature structure the approach should be combined with sophisticated models on the energy balance including the continuum radiative transfer in the future. Although the simple escape probability analysis gives a reasonable estimate for the column density, it fails regarding the density and temperature structure.
The line analysis shows two essential points:
i)
The main constraints on the structural quantities which can be deduced
from the observations are set by the tracer.
The range of densities and temperatures that one can determine
from the radiative transfer calculations is restricted by
the transitions observed. In case of the CS 2-1, 5-4, and 7-6 lines,
the covered densities range from about
![]() to
107 cm-3. With additional information from the
CS 10-9 the upper limit can be extended by another factor 5.
The information from the rarer C34S isotope cannot extend
the density interval but reduces the error bars and provides
better estimates for the clumpiness of the medium.
The high resolution observations discussed in Sects.
3.2 and 5.4
show that different tracers provide access to different types
of information whereas the parameters from our CS observations
agree well with the CS results there.
to
107 cm-3. With additional information from the
CS 10-9 the upper limit can be extended by another factor 5.
The information from the rarer C34S isotope cannot extend
the density interval but reduces the error bars and provides
better estimates for the clumpiness of the medium.
The high resolution observations discussed in Sects.
3.2 and 5.4
show that different tracers provide access to different types
of information whereas the parameters from our CS observations
agree well with the CS results there.
ii) Temperature and clumpiness are related quantities. When
turbulent clumping in the cloud is neglected, the temperature
determination will necessarily fail. On the other hand does
accurate information on the clumpy structure of a massive core help to
constrain the temperature structure. Additional observations in
higher transitions or complementary estimates of the clumpiness
will help to reduce the uncertainty of the temperatures. Thus
spatial resolution is still essential. For nearby clouds
we get a good agreement with results from other high-resolution
observations, but for distant massive cores the temperature structure
is still an open question.
All massive cores that we have analysed are characterised by turbulent clumpiness with typical clump sizes of 0.01-0.02 pc. The clouds are approximately virialised and show density gradients around -1.6 but with a scatter between -1.1 and -2.2. Large parts of the cores follow a constant temperature, but we must admit a considerable uncertainty in the most inner and outer parts. The correlation between the cloud temperature and the turbulent line width indicates that related processes should be responsible for heating and turbulent driving.
Future observations of dense cores should focus on different tracers to gain access to additional information which cannot be deduced from a single tracer such as CS. As a drawback, the full uncertainty of today's chemical models will enter and partially limit the interpretation of the observations.
Acknowledgements
We thank J. Howe for providing us with the CS 2-1 observational data. We are grateful to the anonymous referee for many detailed comments helping to improve the paper considerably. This project was supported by the Deutsche Forschungsgemeinschaft through the grant SFB 301C. The KOSMA 3m radio telescope at Gornergrat-Süd Observatory is operated by the University of Cologne and supported by the Land Nordrhein-Westfalen. The receiver development was partly funded by the Bundesminister für Forschung and Technologie. The Observatory is administered by the Internationale Stiftung Hochalpine Forschungsstationen Jungfraujoch und Gornergrat, Bern. The research has made use of NASA's Astrophysics Data System Abstract Service.
SimLine solves the line radiative transfer problem discussed
in Appendix A.1 in a spherically symmetric configuration by means
of a ![]() -iteration. The code is similar to the concept described by
Dickel & Auer (1994) but it contains several extensions and achieves
a higher accuracy from an adaptive discretisation of all independent
quantities.
-iteration. The code is similar to the concept described by
Dickel & Auer (1994) but it contains several extensions and achieves
a higher accuracy from an adaptive discretisation of all independent
quantities.
SimLine integrates the radiative transfer Eq. (A.2)
for a number of rays numerically.
In spherical symmetry it is sufficient to consider the propagation
of radiation in one arbitrary direction which is taken as z here.
The integral is computed stepwise from zi-1 to zi
In spherical symmetry the spatial integration of the radiative energy
density (Eq. (B.12)) can be reduced to
With the values of the radiative energy density at each radial point and for
each transition, the system of balance equations can be solved
providing new level populations. Here, a LU decomposition algorithm
with iterative improvement (Press et al. 1992) is used. The new level populations
are used in the next iteration as input for the radiative transfer equation.
The whole ![]() -iteration scheme is
solved using the convergence accelerator introduced by Auer (1987).
-iteration scheme is
solved using the convergence accelerator introduced by Auer (1987).
Depending on the physical situation the initial guess is either the optically thin limit, thermalisation or the solution of the radiative transfer equation using the LVG approximation (Eq. (B.15)). The stability of the local radiation field is used as convergence criterion. The number of iterations required for convergence depends strongly on the optical depth of the model cloud. For the examples discussed in this paper only about a dozen iterations were necessary but other test cases with complex molecules like water, non-monotonic velocity gradients, and high optical depths require several hundred iterations.
The turbulence description uses two additional parameters for
each spatial point: the width of the velocity distribution
![]() providing the
local emission profile for optically thin lines and the correlation length
of the macroturbulent density or velocity distribution
providing the
local emission profile for optically thin lines and the correlation length
of the macroturbulent density or velocity distribution
![]() .
.
The width of the velocity distribution ![]() is composed of a
turbulent and a thermal contribution
is composed of a
turbulent and a thermal contribution
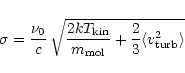 |
(B.3) |
For the local treatment of coherent units in a turbulent medium the
considered volume element is subdivided into numerous
clumps with a thermal internal velocity dispersion.
When each clump is characterized by a Gaussian density distribution
of molecules with about the same velocity
![]() the effective absorption coefficient at the considered
velocity for the whole medium is
the effective absorption coefficient at the considered
velocity for the whole medium is
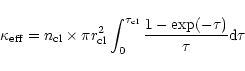 |
(B.4) |
When the turbulent velocity dispersion ![]() is at least three times
as large as the thermal velocity dispersion
is at least three times
as large as the thermal velocity dispersion
![]() ,
we obtain
an effective absorption coefficient
,
we obtain
an effective absorption coefficient
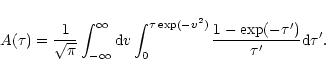 |
(B.6) |
To simulate the effect of a central continuum
source in the cloud, it is possible to assume an H II region in the cloud
centre.
The H II region is characterised by two parameters, the electron density
![]() and the kinetic electron temperature
and the kinetic electron temperature ![]() .
.
The absorption coefficient for electron-ion bremsstrahlung in the
Rayleigh-Jeans approximation is given by:
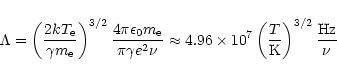 |
(B.8) |
For a thermal plasma, the emission coefficient follows
from the Planck function
When the level populations are known, the beam temperature relative
to the background is computed by the convolution of the emergent intensity
with the telescope beam.
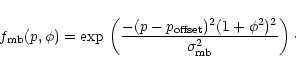 |
(B.11) |
The design of the code is directed towards a high accuracy of the computed line profiles. All errors in the different steps of the program are explicitly user controlled by setting thresholds. All discretisations necessary to treat the problem numerically are performed in an adaptive way, i.e. there is no predefined grid and all grid parameters will change during the iteration procedure. The system of balance equations is truncated whenever the excitation of all higher levels falls below a chosen accuracy limit.
Furthermore, the code was pushed towards a high flexibility, i.e. the ability to treat a very broad range of physical parameters with the same accuracy and without numerical limitations. The systematic velocities e.g. may range from 0 to several times the turbulent velocity and the optical depths may vary from negative values for weak masing to values of several thousands.
The program is not optimised towards a high speed. Other codes with lower inherent accuracy may easily run a factor 10 faster, and further improvements are possible. Nevertheless, the code is suitable for an interactive work even on a small PC with execution times of a few seconds for the models considered in this paper.
The physical parameters of a cloud model and the
emerging line profiles and intensities are linked by the
radiative transfer problem. It relates the molecular emission
and absorption coefficient at one point to the
radiation field determined by the emission and transfer of
radiation at other locations in the cloud.
The quantity entering the balance equations for the level populations at
a point ![]() is the local radiative energy density u within
the frequency range for each transition:
is the local radiative energy density u within
the frequency range for each transition:
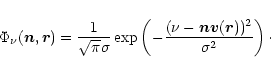 |
(A.3) |
For a molecular cloud this results in a huge system of integral equations interconnecting the level populations and intensities at all points within a cloud.
A simple way to avoid the nonlinear equation system is the escape
probability approximation that is widely applied to interpret
molecular line data.
It is based on the assumption that the excitation, and thus the
absorption and emission coefficients, are constant within
those parts of a cloud which are radiatively coupled.
Then the radiative transfer equation (Eq. (B.13)) can be
integrated analytically. We obtain for the integrated radiative
energy density:
| = | 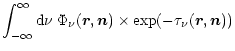 |
(A.5) | |
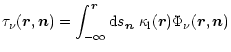 |
(A.6) |
There are two main concepts to define the interaction region and thus to
compute the escape probability. The first one is the large velocity
gradient approximation introduced by Sobolev (1957). Here,
the interaction region is determined by a velocity gradient in the cloud
that displaces the line profiles along the line of sight so that
distant regions are radiatively decoupled. When the resulting interaction
region is sufficiently small it is justified to assume constant parameters.
The escape probability then follows
We used another method, the static escape probability
model. It does not depend on the velocity structure but
assumes a special geometry of
the interaction region. Stutzki & Winnewisser (1985) solved the problem for
a homogenous spherical cloud with constant excitation parameters.
The resulting escape probability is taken to be constant
The surface brightness temperature towards the centre of the cloud is
given by the same expression as Eq. (A.9) when we use
the line integrated optical depth at the cloud centre
![]() instead of
instead of
![]() .
It decays with growing distance from the cloud
centre. Averaged over the whole cloud, the brightness temperature
at the line centre is given by
.
It decays with growing distance from the cloud
centre. Averaged over the whole cloud, the brightness temperature
at the line centre is given by
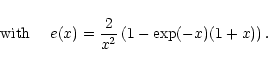
When the velocity gradient in the LVG approximation is computed from
the total line width and the cloud size, it turns out that both methods
agree when applied to observations with a small beam towards the cloud
centre. Only for large-beam observations, they differ in the functions
in Eqs. (A.9) and (B.22), which are either
![]() or
or ![]() ,
but result in similar values.
,
but result in similar values.
By setting up a table of beam temperatures from Eqs. (A.9)
and (B.22) and comparing the observed line intensities
with the tabulated values we can derive three parameters from the
observations: the kinetic
temperature
![]() and the gas density
and the gas density
![]() providing
mainly the source function, and the column density of the considered
molecules relative to the line width
providing
mainly the source function, and the column density of the considered
molecules relative to the line width
![]() providing the photon
escape probability.
providing the photon
escape probability.