A&A 378, 309-315 (2001)
DOI: 10.1051/0004-6361:20011191
R. Vainio1,2,![]() -
R. Schlickeiser2
-
R. Schlickeiser2
1 - Space Research Laboratory, Department of Physics, 20014 Turku
University, Finland
2 - Insitut für Theoretische Physik, Lehrstuhl IV:
Weltraum- und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
Received 16 February 2001 / Accepted 27 August 2001
Abstract
Alfvén-wave transmission through a parallel shock in case of an
anisotropic gas pressure (
![]() )
is considered from
the point of view of test particle acceleration in such shock waves. Treating
the shock's gas compression ratio and the firehose factor,
)
is considered from
the point of view of test particle acceleration in such shock waves. Treating
the shock's gas compression ratio and the firehose factor,
![]() ,
on both sides of the shock as given
parameters, we calculate the wave-transmission coefficients for
circularly-polarized Alfvén waves of finite amplitude. We also give an equation
for the shock's gas compression ratio including the effects of pressure
anisotropy and waves. We study wave transmission and test-particle acceleration
in a model, where the downstream plasma is isotropic and the upstream plasma
remains stable against the firehose instability (
,
on both sides of the shock as given
parameters, we calculate the wave-transmission coefficients for
circularly-polarized Alfvén waves of finite amplitude. We also give an equation
for the shock's gas compression ratio including the effects of pressure
anisotropy and waves. We study wave transmission and test-particle acceleration
in a model, where the downstream plasma is isotropic and the upstream plasma
remains stable against the firehose instability (![]() ). The results can
be arranged in a following manner with respect to the upstream parallel plasma
beta,
). The results can
be arranged in a following manner with respect to the upstream parallel plasma
beta,
![]() (with B0being the ordered magnetic field): (i) for shocks with
(with B0being the ordered magnetic field): (i) for shocks with
![]() the results for particle acceleration are only quantitatively different for
anisotropic upstream plasma; (ii) for
the results for particle acceleration are only quantitatively different for
anisotropic upstream plasma; (ii) for
![]() ,
large
anisotropies alter the wave-transmission and particle acceleration picture
completely relative to the isotropic case yielding much harder energy spectra
with spectral indices
,
large
anisotropies alter the wave-transmission and particle acceleration picture
completely relative to the isotropic case yielding much harder energy spectra
with spectral indices
![]() for all shocks with 1<r<4; (iii) for
very hot and firehose-stable plasmas, the qualitative changes in particle
acceleration due to pressure anisotropies are limited to the weakest shocks and,
thus, should be analyzed in a non-linear manner to confirm the results.
for all shocks with 1<r<4; (iii) for
very hot and firehose-stable plasmas, the qualitative changes in particle
acceleration due to pressure anisotropies are limited to the weakest shocks and,
thus, should be analyzed in a non-linear manner to confirm the results.
Key words: acceleration of particles - shock waves - turbulence
Diffusive shock acceleration (Axford et al. 1977; Krymsky 1977; Bell 1978; Blandford & Ostriker 1978) is a universal mechanism for the acceleration of non-thermal particle populations (Drury 1983; Blandford & Eichler 1987). Since energetic particles can be confined near the shock by plasma turbulence, they are accelerated due to two effects: (i) first-order Fermi acceleration due to multiple crossings of the shock compression front and (ii) stochastic second-order Fermi acceleration in the turbulent fields near the shock. Assuming that the turbulence consists of low-frequency waves on both sides of the shock enables one to investigate the relative importance of these two mechanisms. In this picture, the presence of the second-order Fermi effect requires waves propagating in both directions relative to the mean magnetic field. This condition is always satisfied in the shock's downstream region since an upstream Alfvén wave, when transmitted through a fast-mode shock, converts to two downstream waves propagating in both directions relative to the field (McKenzie & Westphal 1969). However, a consideration of the acceleration time scales of the two mechanisms shows that (i) is much faster than (ii), and should dominate acceleration under the assumption that the upstream waves are self-generated by the cosmic rays streaming against the plasma flow and, therefore, propagating in the backward direction relative to the flow (Vainio & Schlickeiser 1998, 1999).
When the second-order Fermi acceleration is neglected one obtains the canonical
power-law (over momentum) test-particle energy spectrum,
Vainio & Schlickeiser (1998) studied the transmission of Alfvén waves
through a parallel shock wave and calculated the resulting scattering-center
compression ratio for a model neglecting the effect of waves on the shock's gas
compression ratio. They showed that the scattering-center compression ratio
tends to infinity at shocks with
![]() ,
where
,
where
![]() is the upstream
plasma beta
is the upstream
plasma beta![]() , and P1 and B0 are the (isotropic) upstream gas
pressure and the ordered magnetic field, respectively. At this limit, the
Alfvénic Mach number of the shock,
, and P1 and B0 are the (isotropic) upstream gas
pressure and the ordered magnetic field, respectively. At this limit, the
Alfvénic Mach number of the shock,
![]() ,
and the
downstream backward Alfvén waves become standing waves in the shock frame
yielding formally infinite intensities for these waves. This singularity is not
a physical one, and is removed by the inclusion of wave pressure and energy flux
to the shock's Rankine-Hugoniot equations (Vainio & Schlickeiser
1999). The scattering-center compression ratios remain high also in the
self-consistent wave-transmission model which, therefore, is able to produce
test-particle spectra that are harder than the limiting value of
,
and the
downstream backward Alfvén waves become standing waves in the shock frame
yielding formally infinite intensities for these waves. This singularity is not
a physical one, and is removed by the inclusion of wave pressure and energy flux
to the shock's Rankine-Hugoniot equations (Vainio & Schlickeiser
1999). The scattering-center compression ratios remain high also in the
self-consistent wave-transmission model which, therefore, is able to produce
test-particle spectra that are harder than the limiting value of ![]() occurring for rk=r=4 in the original magnetostatic formulation of
diffusive test-particle acceleration at non-relativistic shocks.
occurring for rk=r=4 in the original magnetostatic formulation of
diffusive test-particle acceleration at non-relativistic shocks.
Anisotropic gas pressure modifies the dispersion relation of the low-frequency (Alfvén) waves. As noted by Schlickeiser & Vainio (1998), the important effects on particle acceleration in the model of Vainio & Schlickeiser (1998, 1999) were the result of the inclusion of finite phase speeds of the waves into the theory. Furthermore, pressure anisotropies also modify the jump relations at the shock in a non-trivial way. We know from observations that the pressure in the solar wind is anisotropic (see, e.g., Marsch 1991 for a review). Particle reflection from the shock also adds its contribution to the pressure anisotropy, so the gas pressure just upstream a shock is probably anisotropic even if the far upstream conditions were isotropic.
The purpose of this paper is to investigate the influence of pressure anisotropies on the wave transmission problem, shock compression ratios, and the resulting test-particle acceleration at parallel shocks. Although we will discuss briefly the pressure anisotropies associated with nonthermal particles, it is beyond the scope of the present study to develop a theory with self-consistent determination of pressure anisotropies around the shock. Thus, the effects of anisotropy are studied in a simplified way treating the anisotropy of the gas on both sides of the shock as a known parameter, and constraining its values so that the plasma stays stable against the upstream firehose stability criterion. Similar ideas have been employed previously by, e.g., Lyu & Kan (1986) in a study of plasma parameters at shocks measured in near-Earth space.
In a plasma with a non-zero magnetic field, the motion of the particles along
the magnetic field lines differs fundamentally from their motion perpendicular
to the field lines. This points at the necessity of allowing different amounts
of random energy for particle motions parallel and perpendicular to the field,
respectively. One expects the distribution function to have an axial symmetry
around the local magnetic field ![]() ,
if the Larmor radii of the
particles are very small compared to the density scale in the perpendicular
direction. Then the gas pressure is a tensor
,
if the Larmor radii of the
particles are very small compared to the density scale in the perpendicular
direction. Then the gas pressure is a tensor
We consider the conservation laws across a planar shock discontinuity. In
addition to the macroscopic conservation laws, we use Maxwell's equations
![]() and
and
![]() ,
and Ohm's law in form
,
and Ohm's law in form
![]() to
arrive at jump conditions (see also Lyu & Kan 1986)
to
arrive at jump conditions (see also Lyu & Kan 1986)
Pressure anisotropies also modify the dispersion relation of Alfvén waves, which
at long-wave-length limit becomes (e.g., Stix 1962)
Combining Ohm's and Faraday's laws gives the relation
If
![]() and
and
![]() ,
the flow around the
shock is entirely super-Alfvénic. Then all upstream Alfvén waves are convected
through the shock to become downstream Alfvén waves. Some waves are transmitted
retaining their propagation direction relative to the flow, but others get
reflected, i.e., assume the other propagation direction. Alfvén-wave
transmission through a parallel shock wave can be calculated by taking the
tangential magnetic-field and velocity components to be due to waves,
,
the flow around the
shock is entirely super-Alfvénic. Then all upstream Alfvén waves are convected
through the shock to become downstream Alfvén waves. Some waves are transmitted
retaining their propagation direction relative to the flow, but others get
reflected, i.e., assume the other propagation direction. Alfvén-wave
transmission through a parallel shock wave can be calculated by taking the
tangential magnetic-field and velocity components to be due to waves,
![]() and
and
![]() .
We shall first
investigate the transmission coefficients in a shock with a pre-described gas
compression ratio. Thus, by using the first four jump conditions,
Eqs. (8-9), together with
Eqs. (15-16) and assuming a
degenerate upstream cross helicity,
.
We shall first
investigate the transmission coefficients in a shock with a pre-described gas
compression ratio. Thus, by using the first four jump conditions,
Eqs. (8-9), together with
Eqs. (15-16) and assuming a
degenerate upstream cross helicity,
![]() ,
we find after an amount of straight-forward algebra
,
we find after an amount of straight-forward algebra
Let us, next, calculate the gas compression ratio for a shock propagating with
Mach number M into a gas with parallel plasma beta,
![]() and firehose factor
and firehose factor
One should also check for the physicality of the obtained shock solutions. We
will not analyze this in detail, but note only that if the analysis of the
entropy change across the shock is based on ideal gas law, we can write (Lyu &
Kan 1986)
The easiest way to analyze the compression ratio as a function of Mach number is
to solve for b or
![]() in
Eqs. (22-23), regard it
as a function of two variables (r and M), and to contour plot it fixing
the values of other parameters. Thus, e.g.,
in
Eqs. (22-23), regard it
as a function of two variables (r and M), and to contour plot it fixing
the values of other parameters. Thus, e.g.,
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2708f1.ps}
\end{figure}](/articles/aa/full/2001/40/aah2708/Timg93.gif) |
Figure 1:
Gas compression ratio of a parallel shock with
|
| Open with DEXTER | |
The Alfvén-wave transmission coefficients for the shocks in
Fig. 1 are given in
Fig. 2. We choose outwards-propagating (h=-1) upstream waves consistent with their generation by counter-streaming
particles. For the colder upstream gas, the transmission coefficients are
affected only a little by the pressure anisotropy, but for the hotter case we
see substantial effects; especially the reflection coefficient is substantially
increased in presence of anisotropies. Generally, T>R, for h=-1, but for
a marginally firehose-stable upstream plasma (
![]() ), the downstream
state tends to an equipartition between forward and backward propagating Alfvén
waves (
), the downstream
state tends to an equipartition between forward and backward propagating Alfvén
waves (![]() )
as
)
as ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2708f2.ps}
\end{figure}](/articles/aa/full/2001/40/aah2708/Timg99.gif) |
Figure 2:
The transmission coefficients T and R for parallel shocks with
|
| Open with DEXTER | |
The most important parameter controlling the energy spectrum of cosmic rays
accelerated by a shock wave is the compression ratio of the scattering centers
that are responsible for the isotropization of the energetic particles. In case
of Alfvén waves generated in the upstream region, we may write
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2708f3.ps}
\end{figure}](/articles/aa/full/2001/40/aah2708/Timg107.gif) |
Figure 3:
Scattering-center compression ratio of a parallel shock with
|
| Open with DEXTER | |
The results for the scattering-center compression ratio were also calculated for
the interesting case of
![]() at several values of the
firehose factor (Fig. 4) to see, how large
anisotropies are needed for qualitative effects on particle acceleration from
pressure anisotropies. It is evident that relatively small values, below
at several values of the
firehose factor (Fig. 4) to see, how large
anisotropies are needed for qualitative effects on particle acceleration from
pressure anisotropies. It is evident that relatively small values, below
![]() ,
are needed to produce large effects on particle
acceleration. But, for
,
are needed to produce large effects on particle
acceleration. But, for
![]() the scattering-center compression
ratio is above 4 for all 1<r<4.
the scattering-center compression
ratio is above 4 for all 1<r<4.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2708f4.ps}
\end{figure}](/articles/aa/full/2001/40/aah2708/Timg112.gif) |
Figure 4:
Scattering-center compression ratio of a parallel shock with
|
| Open with DEXTER | |
Perhaps the most unexpected result of our calculation is the ability of weakly
compressive (
![]() )
shocks to accelerate particles efficiently in warm
plasmas. This result, however, depends crucially on the assumption of the shocks
ability to isotropize the fluid. If r differs considerably from unity, one can
probably safely assume that the small-wavelength magnetic turbulence generated
in the shock transition can be responsible for the isotropization. On the other
hand, the transverse magnetic field attains large values across the
)
shocks to accelerate particles efficiently in warm
plasmas. This result, however, depends crucially on the assumption of the shocks
ability to isotropize the fluid. If r differs considerably from unity, one can
probably safely assume that the small-wavelength magnetic turbulence generated
in the shock transition can be responsible for the isotropization. On the other
hand, the transverse magnetic field attains large values across the
![]() shocks with
shocks with
![]() regardless of the compression
ratio. This can also add to the isotropization of the particles since the field
changes direction across the shock at scales comparable to the ion Larmor
radius. However, the shocks with small r do not contain large amounts of
energy to be given for accelerated particles. When at the same time the
test-particle spectral index is below 2, the pressure in accelerated particles
diverges without a cutoff in the spectrum. The less there is energy available,
the smaller value for the cutoff-momentum must be, and it may well turn out that
the weak shocks can not be described by the test-particle picture at all. The
confirmation of this requires non-linear analysis, which we shall undertake in
the future.
regardless of the compression
ratio. This can also add to the isotropization of the particles since the field
changes direction across the shock at scales comparable to the ion Larmor
radius. However, the shocks with small r do not contain large amounts of
energy to be given for accelerated particles. When at the same time the
test-particle spectral index is below 2, the pressure in accelerated particles
diverges without a cutoff in the spectrum. The less there is energy available,
the smaller value for the cutoff-momentum must be, and it may well turn out that
the weak shocks can not be described by the test-particle picture at all. The
confirmation of this requires non-linear analysis, which we shall undertake in
the future.
We will briefly discuss the pressure anisotropies created by the shock-related
non-thermal particles assuming non-relativistic particle speeds for
simplicity. For particles accelerated at the shock to speeds clearly exceeding
the shock-frame scattering-center speed, V1, particle scattering results in a
distribution function,
![]() ,
that is only weakly dependent on the pitch-angle,
,
that is only weakly dependent on the pitch-angle,
![]() .
In the upstream wave frame, the small anisotropic portion of the
distribution,
.
In the upstream wave frame, the small anisotropic portion of the
distribution,
![]() where
where
![]() denotes angle averaging, is antisymmetric relative
to
denotes angle averaging, is antisymmetric relative
to ![]() if the net magnetic helicity of the waves is zero (e.g., Schlickeiser
1989), which we assume. Thus, the pressures due to these particles are
if the net magnetic helicity of the waves is zero (e.g., Schlickeiser
1989), which we assume. Thus, the pressures due to these particles are
| (29) | |||
| (30) |
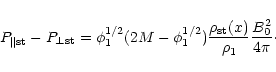 |
(31) |
Another contribution to the pressure anisotropy comes from the particles that
have just been reflected by the shock and subsequently been picked up by the
upstream waves. Let us, for simplicity, consider a cold background plasma, and
assume that the shock reflects a small fraction of the incoming
background-plasma ions back to the upstream region. We model those particles as
a beam with a density of
![]() propagating along the
magnetic field away from the shock and include also the particles that return to
the shock after their isotropization by the upstream waves. Specifically, in the
upstream wave frame we take the distribution function for the reflected and
returning particles to be
propagating along the
magnetic field away from the shock and include also the particles that return to
the shock after their isotropization by the upstream waves. Specifically, in the
upstream wave frame we take the distribution function for the reflected and
returning particles to be
![\begin{displaymath}f_{\rm rr}(x,v,\mu)=n_{\rm b}(x)[\delta(\mu+1)+\mbox{$\frac 12$ }
M/(M-\phi_1^{1/2})] F(v),
\end{displaymath}](/articles/aa/full/2001/40/aah2708/img130.gif) |
(32) |
![\begin{displaymath}P_{\parallel{\rm rr}}-P_{\perp{\rm rr}}=
M[4M+\mbox{$\frac 12...
...^{1/2})]
\frac{\rho_{\rm b}(x)}{\rho_1}\frac{B_0^2}{4\pi}\cdot
\end{displaymath}](/articles/aa/full/2001/40/aah2708/img132.gif) |
(33) |
We have considered the Alfvén-wave transmission and test-particle acceleration
problem (Vainio & Schlickeiser 1998, 1999) for shocks with
anisotropic pressure. In our model, the firehose factors on both sides of the
shock are predetermined parameters. For a detailed analysis, we chose a model
with isotropic downstream pressure, and upstream pressure anisotropy that is
bounded by the requirement of firehose stability. We showed that the pressure
anisotropies have only a minor effect on wave transmission and particle
acceleration for plasmas with low ![]() .
However, plasmas with upstream
.
However, plasmas with upstream
![]() and
and
![]() seem
to develop qualitative effects on both the wave transmission and particle
acceleration relative to the isotropic-pressure case. Our study revealed the
capability of weak shocks propagating into such plasmas to accelerate particles
effectively by creating a large change in the average scattering-center speed
across the shock though the increase of the phase speed of low-frequency waves
across the shock. Plasmas with large values of beta,
seem
to develop qualitative effects on both the wave transmission and particle
acceleration relative to the isotropic-pressure case. Our study revealed the
capability of weak shocks propagating into such plasmas to accelerate particles
effectively by creating a large change in the average scattering-center speed
across the shock though the increase of the phase speed of low-frequency waves
across the shock. Plasmas with large values of beta,
![]() ,
can not develop very large anisotropies (
,
can not develop very large anisotropies (
![]() )
without becoming firehose unstable, which again prevents large
deviations in our model between the anisotropic and isotropic cases except for
the weakest shocks with
M<Misotr(r=1). The low-Mach-number
shocks are weakly entropy increasing in the ideal gas model and should,
therefore, be studied more carefully using kinetic analysis. In conclusion, the
results of our study point out the importance of kinetic analysis of up- and
downstream plasma to fully understand the physics of shock acceleration.
)
without becoming firehose unstable, which again prevents large
deviations in our model between the anisotropic and isotropic cases except for
the weakest shocks with
M<Misotr(r=1). The low-Mach-number
shocks are weakly entropy increasing in the ideal gas model and should,
therefore, be studied more carefully using kinetic analysis. In conclusion, the
results of our study point out the importance of kinetic analysis of up- and
downstream plasma to fully understand the physics of shock acceleration.
Acknowledgements
R. V. acknowledges the financial support of the Academy of Finland (project # 46331) and the PLATON Network (EC contract # HPRN-CT-2000-00153).