A&A 378, L1-L4 (2001)
DOI: 10.1051/0004-6361:20011061

Rotational splitting of helioseismic modes influenced by a magnetic atmosphere

B. Pintér1 - R. New1 - R. Erdélyi2


1 - School of Science and Mathematics, Sheffield Hallam University, Howard Street, Sheffield, S1 1WB, UK
2 - Space & Atmosphere Research Center, Dept. of Applied Mathematics, University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK

Received 18 July 2001 / Accepted 25 July 2001

Abstract
In the present paper the splitting of sectoral ($m=\pm l$) helioseismic eigenmodes (f- and p-modes) is studied in the presence of a magnetic atmosphere. The solar interior is in a steady state, with sub-photospheric plasma flow along the equator representing solar rotation. The Cartesian geometry employed restricts the present study to sectoral modes, $m=\pm l$. We work with $l \ge 50$, which guarantees that the modes do not deeply penetrate into the solar interior and therefore experience an approximately uniform rotation. Potentially observable effects are predicted and developments of the model to aid detections are discussed.

Key words: Sun: helioseismology - Sun: oscillations - Sun: interior - Sun: atmosphere - Sun: magnetic fields - Sun: rotation


  
1 Introduction

The Sun's acoustic vibrations (p-modes) are sensitive to the rotation of the solar interior. Crudely speaking, eigenmodes set up by waves propagating in the same sense as the solar rotation have a somewhat greater wavelength than those set up by counter propagating waves. This leads to a splitting between the frequencies of modes of the same angular degree, l, but different azimuthal order, m, which would be degenerate in a non-rotating Sun. The sidereal rotation frequency of the equatorial solar surface is approximately 460 nHz, and the individual m-components of a given l-multiplet are separated by roughly this frequency (although only l+m= even are detectable given observational geometries). As the Sun does not rotate as a solid sphere, the precise values of the splittings, $\Delta\nu_{nlm}$, are determined by weighted averages of rotation over the depths (determined by l and the radial order, n) and the latitudes (determined by l and m) sensed by given modes.

Variations over the solar cycle in the values of $\Delta\nu_{nlm}$ are expected and have been observed. There are two broad categories of effect. Firstly, the frequencies of individual modes are known to vary in ways that correlate strongly with solar magnetic activity indicators (Libbrecht & Woodard 1990; Howe et al. 1999; Elsworth et al. 1990; Jiménez Reyes et al. 1998; Chaplin et al. 2001), although the precise mechanisms responsible for these shifts have not been unambiguously identified (Roberts & Campbell 1986; Campbell & Roberts 1989; Evans & Roberts 1992; Erdélyi & Taroyan 1999; Taroyan & Erdélyi 2000; Erdélyi & Taroyan 2001). Since the magnetic field varies both in magnitude and in distribution over latitude during the solar cycle, individual components of a multiplet sensing different latitudes are expected to undergo different shifts (Dziembowski & Goode 1997). Such latitude dependence was established for intermediate ( 5 < l < 100) modes by Libbrecht & Woodard (1990) and is a subject of detailed study in the more extensive data sets available for the current activity cycle (for example, Howe et al. 2001). Secondly, the details of solar rotation itself have been observed to vary with the solar cycle. For example, torsional oscillations (bands in the rotation profile which alternate faster and slower than average) have been observed to migrate towards the equator during the rising phase of the current activity cycle (Howe et al. 2000a; Toomre et al. 2000). In addition to effects clearly linked to the solar cycle, intriguing oscillatory behaviour has been observed in the rotation profile just above and below the bottom of the convection zone (Howe et al. 2000b).

This paper evaluates one potential contribution to changes in $\Delta\nu_{nlm}$ which arises from interactions between the p-modes and the solar atmospheric magnetic field with a steady solar interior.

The geometry of the model is immediately relevant to sectoral ($m=\pm l$) modes of sufficiently high l to penetrate only a short distance into the convection zone. The model is an extended version of the work by Campbell & Roberts (1989).

  
2 Equilibrium model


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{DG183_f1.eps}\end{figure} Figure 1: The atmospheric magnetic induction, B, and plasma density, $\rho $, as function of height, z, for $B_{\rm c} \equiv B_0(z=-L)$ = 0, 10, 50, 100, 120 and 145 G. The magnetic field strength increases from zero to its maximum, $B_{\rm c}$, in a characteristic transitional layer (0 $\leq z\leq - L$, L=2 Mm). The equilibrium density at and beneath the photosphere, $\rho _0(z \geq 0)$, does not vary with $B_{\rm c}$. The solar interior is steady, field-free and polytropic.
Open with DEXTER

To model $\Delta\nu_{nl\pm l}$ as a function of magnetic field, we build on the work of Pintér et al. (2001a,b). In this description the Sun is modeled with a three-layer structure, representing the solar interior, chromosphere and corona in Cartesian geometry (see Fig. 1). For the solar interior we consider an adiabatic temperature profile, where the temperature increases linearly with depth with a gradient of $(\gamma - 1)g$. The solar interior is in a steady state, i.e. there is a homogeneous constant equilibrium flow, ${\vec v}_0(z) = (v_0(z), 0, 0)$ in the horizontal direction (x-axis), where

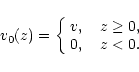
\begin{displaymath}v_0(z)=\left\{\begin{array}{ll} v, \ \ \ z \geq 0,\\ 0, \ \ \ z<0. \end{array}\right. \end{displaymath}

In this work $v=\pm 2$ km s $^{\mbox-1}$ to approximately represent the equatorial rotation speed for co- and counter-propagating modes in surface regions. We restrict our analysis to modes of l = 50, 75 and 100, which do not penetrate deeply into the Sun, so that the surface velocity can be used as an approximate estimate of the velocity encountered by the mode (Christensen-Dalsgaard 1994).

The solar chromosphere and corona are embedded in a unidirectional horizontal magnetic field ${\vec B}_0(z) = (B_0(z)$,0,0). The atmospheric magnetic field lines are parallel or antiparallel to the sub-photospheric velocity. We only consider parallel propagations, i.e. ${\vec k} \times {\vec B}_0 = $ 0. The chromosphere is a transitional layer, where the strength of the magnetic field increases continuously from zero to its coronal maximum value. In the corona the magnetic field strength decreases exponentially (e-fold > 20Mm) with height resulting in a constant coronal Alfvén speed in this model. The continuous spatial variation of the magnetic field, B0(z), is displayed in Fig. 1 for different strengths of the atmospheric magnetic field together with the plasma density.

We consider eigen-oscillations of which the kinetic and magnetic energy is confined to a finite region both below and above the photosphere ( $E_{\rm kin}\rightarrow 0$ and $E_{\rm mag}\rightarrow 0$ as $\vert z\vert\rightarrow \infty$).

In the Sun sectoral helioseismic oscillation modes, with m = l and m = - l, propagate simultaneously to and fro along the solar equator - thus, with and against rotational flow, v0, and horizontal atmospheric magnetic field, B0. An approximately equivalent situation can be modelled in our system by considering modes of fixed kx but with v0 and B0 which reverse direction. In fact it is only necessary to reverse v0, as all contributions to physical effects caused by magnetic field are proportional to B02. The approximation arises from the fact that our model incorporates a constant v0; by working with relatively high l values, we achieve this to an acceptable extent.

In conclusion, we evaluate the rotational splitting of sectoral modes, $\Delta\nu_{nl\pm l}(B_{\rm c})\ \equiv \nu_{nl\mbox-l}(B_{\rm c};\ v) - \nu_{nll}(B_{\rm c};\ v)$by calculating the frequency difference for reversed flow velocities, $\nu_{nll}(B_{\rm c};\ -v) - \nu_{nll}(B_{\rm c};\ v)$.

  
3 Results and discussions


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{DG183_f2.eps}\end{figure} Figure 2: Frequency spectrum of the f- and the first ten p-modes as a function of $B_{\rm c}$ for v = 0 and for the two sectoral modes with l = 100 for velocity v = 2 km s $^{\mbox-1}$.
Open with DEXTER

The frequency spectrum of the oscillation modes as a function of $B_{\rm c}$ can be seen in Fig. 2. $B_{\rm c}$ is the magnetic field strength taken at the top of the transitional layer, at z = - L, where L = 2 Mm throughout the present paper. The angular degree of eigen-oscillations is fixed at l = 100. Eigenmodes can oscillate with global frequencies between the lower and upper magneto-acoustic cut-off frequencies, $\nu_{\rm I}$ and $\nu_{\rm II}$, respectively, and below the characteristic slow frequency, $\nu_{\rm c}\equiv\nu_{\rm c}(z= - L$). The region below $\nu_{\rm c}$ is called the slow continuum. Global p-modes with frequencies in the slow continuum region couple resonantly to a local slow magneto-hydrodynamic oscillation at a certain height in the transitional layer, where the local frequency of the slow mode matches the global frequency of the f- or p-mode. This resonant coupling makes dissipation important resulting in complex eigen-frequencies (see Pintér 1999; Pintér et al. 2001a,b). It can be shown that the imaginary part of the global frequency measures the contribution of the resonant effect to the spectral line-width of the f- and p-modes, namely $\Gamma\sim - 2$ Im($\nu$). Oscillations with frequencies above $\nu_{\rm II}$ and between $\nu_{\rm I}$ and $\nu_{\rm c}$ are not trapped modes. They show a "leaky" character which is out of the scope of the present paper. The f-, p1- and p2-modes have a gap in an interval of $B_{\rm c}$, while p-modes with n > 2 exist only for strong enough magnetic fields. Mode frequencies for v = 0 are plotted with solid lines. In Cartesian geometry modes of different m cannot be represented. Global p-modes which propagate parallel and antiparallel to the bulk motion are equivalent to m = l and m = - l sectoral modes, respectively. As expected, Fig. 2 shows that the presence of a plasma flow decreases the frequencies of oscillations that propagate along the flow, while frequencies of modes propagating into the opposite direction are increased by the flow by about 50 $\mu$Hz (for l = 100).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{DG183_f3.eps}\end{figure} Figure 3: Frequency shifts, $\Delta \nu \equiv \nu (B_{\rm c}=0)-\nu (B_{\rm c})$, of the f- and the first ten p-modes as a function of $B_{\rm c}$.
Open with DEXTER

The influence of an atmospheric magnetic field on mode frequencies, $\nu_{nl}$, is too small to observe in Fig. 2, as the effect is of the order of a few $\mu$Hz. The frequency shifts of the f- and ten p-modes due to a change of the magnetic field strength, $\Delta \nu _{nl}(B_{\rm c}) \equiv \nu _{nl}(B_{\rm c}) - \nu _{nl}(B_{\rm c} = 0)$, are better emphasized in Fig. 3. In order to avoid crowding of graphs in the figure, only the case v = 0 is displayed. A stronger magnetic field increases the mode frequencies, except that of the third p-mode, which is close to $\nu_{\rm I}$ and $\nu_{\rm c}$ (see Fig. 2) for l = 100. The higher the radial mode number the stronger the magnetic effect on the frequency. The frequency of p10-mode at around 3.9 mHz varies more than 4 $\mu$Hz as $B_{\rm c}$ varies between zero and 150 G.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{DG183_f4.eps}\end{figure} Figure 4: Frequency splitting of the f- and the first ten p-modes as a function of $B_{\rm c}$ for flow velocity v=2  km s $^{\mbox-1}$ for l=100.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{DG183_f5.eps}\end{figure} Figure 5: Frequency splitting of the f- and the first nine p-modes as a function of $B_{\rm c}$ for flow velocity v=2 km s $^{\mbox-1}$ for l=75.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{DG183_f6.eps}\end{figure} Figure 6: Frequency splitting of the f- and the first eight p-modes as a function of $B_{\rm c}$ for flow velocity v=2 km s $^{\mbox-1}$ for l=50.
Open with DEXTER

When we look at the frequency spectrum against $B_{\rm c}$ in detail we find that the slope of graphs of $\nu_{nl}$ versus $B_{\rm c}$ are different for v and -v. Hence, $\Delta\nu_{nl\pm l}(B_{\rm c})$ varies with $B_{\rm c})$, because - as we argued above - rotational splitting is equivalent to the frequency difference for positive and negative v.

We show $\Delta\nu_{nl\pm l}(B_{\rm c})$ in Figs. 4 to 6 for three different values of the angular degree for v=2 km s $^{\mbox-1}$. The splittings are around 91, 68.5 and 46 $\mu$Hz for l = 100, 75 and 50, respectively and they can be increased by the atmospheric magnetic field by some hundreds of nHz. $\Delta\nu_{nl\pm l}$ for the p3-, p2- and p1-modes for l=100, 75 and 50, respectively, show different behaviour compared to modes of different n. They vary more rapidly with $B_{\rm c})$ than those of the other modes, because the frequencies are near the top of the slow continuum, $\nu_{\rm c}$ (e.g. see Fig. 2).

The mean increase of $\Delta\nu_{nl\pm l}$ with B for ten p-modes for l = 100 is around 370 nHz, which is a 0.41% relative increase. For GONG and MDI data, the observational error of measuring $\Delta\nu_{n 100\pm 100}$ due to rotational splitting is better than 0.25% (private communication with R. Howe). Hence, the effect obtained in the present model is on the verge of detectability, and ought to be detectable by combining a number of modes. On the other hand there are other competing effects - such as those due to zonal flows, referred to in the introduction - which are of about the same order. One possible way of helping to differentiate between the several competing shifts would be to evaluate the present effect for all m. This requires a move to spherical geometry, which is in progress.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{DG183_f7.eps}\end{figure} Figure 7: Line-width, $\Delta \Gamma \equiv \Gamma _{B_{\rm c}=0}-\Gamma _{B_{\rm c}}$, of the f- p1- and p2-modes as a function of $B_{\rm c}$.
Open with DEXTER

The contribution to the line-width of f- and p-modes that are resonantly coupled to local slow oscillations are presented in Fig. 7 for v = 0 and for the two sectoral modes for v=2 km s $^{\mbox-1}$. The lines are wider for antiparallel and narrower for parallel propagation. The flow effect on the damping rate is a secondary (consequently a very small) effect. The origin of the effect of a sub-photospheric plasma flow on the line-width of global oscillations is that the resonant position, i.e. the height where the mode interacts resonantly with a local slow mode in the atmosphere, is shifted by the Doppler effect caused by the sub-photospheric horizontal plasma motion. It should be noted that the shifts predicted in Figs. 4 to 6 also may contribute to observed widths of modes within a multiplet, since B-field variations over time and sampling volume will "smear out" the precise frequency of a given mode.

Acknowledgements
The authors thank R. Howe, B. Roberts and Y. Taroyan for discussions and comments. R.E. acknowledges M. Kéray for patient encouragement. B.P. is grateful to PPARC for financial support. B.P. & R.E. also acknowledge the financial support obtained from the NSF, Hungary (OTKA, Ref. No. TO32462).

References

 
Copyright ESO 2001