A&A 378, 180-191 (2001)
DOI: 10.1051/0004-6361:20011183
Diversity of planetary systems from evolution of solids in protoplanetary disks
K. Kornet1 - T. F. Stepinski2 - M. Rózyczka1
1 - Nicolaus Copernicus Astronomical Center , Bartycka 18 , Warsaw, 00-716, Poland
2 -
Lunar and Planetary Institute, 3600 Bay Area Blvd., Houston, TX
77058, USA
Received 1 June 2001 / Accepted 6 August 2001
Abstract
We have developed and applied a model designed to track
simultaneously the evolution of gas and solids in protoplanetary disks
from an early stage, when all solids are in the dust form, to the
stage when most solids are in the form of a planetesimal swarm. The
model is computationally efficient and allows for a global,
comprehensive approach to the evolution of solid particles due to
gas-solid coupling, coagulation, sedimentation, and
evaporation/condensation. The co-evolution of gas and solids is
calculated for 107 yr for several evolution regimes and starting
from a comprehensive domain of initial conditions. The output of a
single evolutionary run is a spatial distribution of mass locked in a
planetesimal swarm. Because swarm's mass distribution is related to the
architecture of a nascent planetary system, diversity of swarms is
taken as a proxy for a diversity of planetary systems. We have found
that disks with low values of specific angular momentum are bled out
of solids and do not form planetary systems. Disks with high and
intermediate values of specific angular momentum form diverse
planetary systems. Solar-like planetary systems form from disks with
initial masses 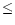 0.02
0.02 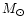 and angular momenta
and angular momenta 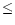
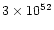 gcm2s-1. Planets more massive than Jupiter can form
at locations as close as 1 AU from the central star according to
our model.
gcm2s-1. Planets more massive than Jupiter can form
at locations as close as 1 AU from the central star according to
our model.
Key words: accretion disks - solar system: formation
The architecture of a planetary system results from a chain of
processes that start at the formation of a protoplanetary disk (PPD)
around a nascent star. A protoplanetary disk is a mixture of gas and
solids and is made up from a material that, during the formation
process, did not become directly part of the star, but, due to its
excess angular momentum, remained in orbit around the newborn
star. Global properties of protoplanetary disks, such as their masses
and sizes are known in abundance from astronomical
observations. Typical disk masses are between 0.001 and 0.1 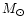 and typical disk sizes are between a few and a few hundred
AU (see Beckwith & Sargent 1993; Beckwith 1994 and references
therein). The ranges of about two orders of magnitude in observed
masses and sizes of protoplanetary disks are partially due to
different stages at which different disks are observed (Stepinski
1998a) and partially due to an intrinsic scatter in initial
conditions. On the other hand, the structure of a planetary system is
known only for a single object - the Solar System. High accuracy
spectroscopy has revealed the existence of over 60 solar-type stars
with unresolved companions that could plausibly be planets (cfa-www.harvard.edu/planets/). If these companions are indeed planets
formed in the same way as planets in the Solar System, a broad
distribution of their orbital parameters suggests a large diversity in
possible configuration of planetary systems. We postulate that indeed
the dispersion in protoplanetary disks initial conditions leads to
architecture diversity among planetary systems.
and typical disk sizes are between a few and a few hundred
AU (see Beckwith & Sargent 1993; Beckwith 1994 and references
therein). The ranges of about two orders of magnitude in observed
masses and sizes of protoplanetary disks are partially due to
different stages at which different disks are observed (Stepinski
1998a) and partially due to an intrinsic scatter in initial
conditions. On the other hand, the structure of a planetary system is
known only for a single object - the Solar System. High accuracy
spectroscopy has revealed the existence of over 60 solar-type stars
with unresolved companions that could plausibly be planets (cfa-www.harvard.edu/planets/). If these companions are indeed planets
formed in the same way as planets in the Solar System, a broad
distribution of their orbital parameters suggests a large diversity in
possible configuration of planetary systems. We postulate that indeed
the dispersion in protoplanetary disks initial conditions leads to
architecture diversity among planetary systems.
A protoplanetary disk is an evolving object; its properties such as
mass and size are functions of time. The evolutions of gaseous and
solids components of a protoplanetary disk accompany each other but
are not identical. One important distinction between the evolution of
the two components is that the gas maintains its form but the solids
do not. Initially the solids are all in the form of a fine dust, but,
given enough time, they convert into roughly 1-10 km sized solid
bodies (planetesimals). It is currently thought (for a review see
Weidenschilling & Cuzzi 1993) that this is achieved via a buildup of
progressively more massive particles by the process of coagulation
culminating in planetesimals. In general, the mass distribution of the
solids evolves due to gas-solid coupling, coagulation, sedimentation,
and evaporation/condensation. Once planetesimals are formed, their
further aggregation leads to planets. This final accumulation stage
received a fair amount of attention (Safronov 1968; Greenberg et al. 1978; Kaula 1979; Wetherill 1980; Nakagawa et al. 1983) because
its physics is fairly well understood, inasmuch as it can be
formulated as the N-body problem with gravitational forces. The
earlier accumulation stages, from dust to planetesimals, are governed
by a complex combination of the processes mentioned above. Although
these processes have been discussed and modeled individually (for a
review see Weidenschilling & Cuzzi 1993), little work has been done to
model the evolution of the solids component of the protoplanetary disk
associated with their collective action.
Cassen (1996) constructed a simple model of disk evolution coupled to an
equally simple prescription for the rate at which condensible material
is decoupled from the gas to become a part of a surviving planetary
system. In his model evaporation/condensation is the only process
affecting the coupling of solids to the gas (coagulation,
sedimentation and aerodynamic drag are not considered). Cassen's model
was designed to reproduce the observed abundances of elements in
chondritic meteorites and not to address the issue of diversity of
planetary systems. Schmitt et al. (1997) constructed a model of a
protoplanetary disk in which dust evolution is directly coupled to the
evolution of the gas. Their model includes all relevant processes
without any further simplification. However it was designed to study
the effects of coagulation on gas opacity, and the computation
followed the dust evolution for only 100 years. Stepinski & Valageas
(1996, 1997) (hereafter referred to as SV96 and SV97) developed a
model capable of simultaneously following the evolution of gas and
solid particles due to gas-solid coupling, coagulation, sedimentation
and evaporation/condensation for up to 107 years. Their model was
designed specifically to obtain the radial distribution of solid
material circumnavigating a star in the form of the planetesimal
swarm. Despite far-reaching simplifications that made those
calculations possible, the model required significant computational
resources and only a handful of evolutionary runs were calculated.
Our current work is based on the ideas developed in SV96 and SV97. Our
first objective is to develop and utilize a computationally efficient
model that tracks the evolution of solids from an early stage, when
they are in the dust form, to the stage when most solids are in the
form of planetesimals. In order to achieve a necessary
computational efficiency, the model developed here introduces further
simplifications on top of those used by SV97. Our second objective is
to use the model to establish the dependence between a distribution of
matter at the early evolutionary stage of a PPD (initial conditions),
and a distribution of matter at the final evolutionary stage (the
planetesimal swarm). Our model is not designed to track the further
evolution of planetesimals into planets, thus, in this paper, the
planetesimal swarm is a surrogate for a planetary system. The
computational efficiency of the model is necessary in order to evolve
an extensive set of initial conditions into an extensive set of
swarms.
Section 2 contains the description of our model. In Sect. 3 we explain the
numerical methods employed to implement the model. The results are presented
in Sect. 4, and the fine details of how exactly gas and solid particles evolve
in a particular disk for 107 yr are discussed in Sect. 5. Finally, in Sect. 6 we present conclusions and discussion.
We model a protoplanetary disk as a two-component turbulent fluid. The
dynamically dominant component is a gaseous protoplanetary disk
(GPD). The collection of all solids in the GPD constitutes the second
component, which we call solid protoplanetary disk
(SPD). SPDs evolves together with, but not identically to
GPDs. The evolution of each component is governed by equations of
continuity and momentum conservation. Both, the GPD and the SPD are
considered to be perfect fluids. The SPD is also a pressureless fluid,
subject to an additional force arising from the friction between solid
particles and the gas. This force is neglected in calculating the
evolution of the GPD. Initial conditions are imposed at the beginning
of what is frequently referred to as a dissipative stage (Cameron
1985) of the protoplanetary disk, when the GPD evolves due to an
anomalous viscosity caused by (unspecified) disk instability. It is
during this stage that the major part of the transition from dust to
planetesimals occurs. The disk is assumed to maintain an axial
symmetry (
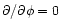 )
and to be geometrically thin
(
)
and to be geometrically thin
(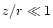 ). We analyze the disk in the cylindrical polar coordinates
). We analyze the disk in the cylindrical polar coordinates
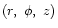 with the star at the origin and the disk's midplane
located in the plane z=0.
with the star at the origin and the disk's midplane
located in the plane z=0.
The gas is explicitly assumed to be turbulent. The precise nature of the turbulence is not identified, but it is expected to be a mechanism intrinsic
to the GPD such as shear-induced instability (Dubrulle 1993), magnetorotational instability (Blaes & Balbus 1994) or thermal convection (Lin & Papaloizou 1980), and not a process induced by the presence of solid particles (Weidenschilling 1980). Thus, in our model, the evolution of the GPD is not influenced by the presence of the SPD.
The average velocity field
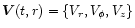 and the average surface density,
and the average surface density, 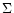 of the GPD can be calculated under a particular model of velocity correlations (Reynolds stress). The details of Reynolds averaging in this context are given in SV97, here it is sufficient to
note that the turbulent viscosity is modeled by
of the GPD can be calculated under a particular model of velocity correlations (Reynolds stress). The details of Reynolds averaging in this context are given in SV97, here it is sufficient to
note that the turbulent viscosity is modeled by
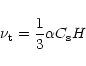 |
(1) |
where  is a free parameter introduced by Shakura and Sunyaev
(1978),
is a free parameter introduced by Shakura and Sunyaev
(1978), 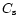 is the speed of sound, and H is disk's
half-thickness. For a given disk model
is the speed of sound, and H is disk's
half-thickness. For a given disk model 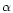 is assumed to be
constant and uniform.
is assumed to be
constant and uniform.
The average surface density of the GPD, 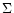 ,
is given by the following evolution equation,
,
is given by the following evolution equation,
![\begin{displaymath}\frac{\partial \Sigma}{\partial t} - \frac{3}{r} \frac{\parti...
...c{\partial}{\partial r} (r^{1/2} \nu_{\rm t} \Sigma)\right]=0.
\end{displaymath}](/articles/aa/full/2001/40/aa1537/img18.gif) |
(2) |
It can be shown (see, for example, Frank et al. 1985) that
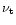 is not an explicit function of time, but instead depends only on the local disk's quantities and can be expressed as
is not an explicit function of time, but instead depends only on the local disk's quantities and can be expressed as
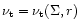 .
The form of this function depends on the opacity law, in our
calculations we used the Rossenland mean opacity given by Ruden & Pollack (1991). Thus, (2) is closed and can be solved given an initial
condition.
.
The form of this function depends on the opacity law, in our
calculations we used the Rossenland mean opacity given by Ruden & Pollack (1991). Thus, (2) is closed and can be solved given an initial
condition.
We obtain solutions to the evolution Eq. (2)
analytically, following the method developed by Stepinski (1998b). In
Stepinski's method initial conditions (the functions
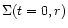 )
are restricted to those having a self-similar form parameterized by
the following three parameters: j0, an angular momentum of the
GPD at t=0 (in units of
)
are restricted to those having a self-similar form parameterized by
the following three parameters: j0, an angular momentum of the
GPD at t=0 (in units of
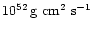 ), m0, the
mass of the GPD at t=0 (in units of
), m0, the
mass of the GPD at t=0 (in units of 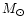 ), and
), and 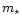 ,
the mass of the central star (in units of
,
the mass of the central star (in units of 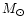 ). It is assumed
that
). It is assumed
that 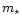 stays constant during the evolution despite the
fact that there is accretion from the disk onto the star. The initial
outer radius of the GPD, r0 (in units of AU) is given by
stays constant during the evolution despite the
fact that there is accretion from the disk onto the star. The initial
outer radius of the GPD, r0 (in units of AU) is given by
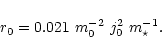 |
(3) |
Thus, if we consider only disks around stars with
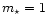 ,
the initial
conditions are parameterized conveniently by only two numbers, j0 and m0.
The analytical method yields an explicit formula
,
the initial
conditions are parameterized conveniently by only two numbers, j0 and m0.
The analytical method yields an explicit formula
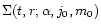 .
Other GPD quantities, including the average velocity field
.
Other GPD quantities, including the average velocity field 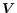 and the midplane temperature T are also given by explicit formulas in the same format.
and the midplane temperature T are also given by explicit formulas in the same format.
In our model the SPD is a collection of solid particles of different
sizes entrained in the GPD. The crucial approximation is that the
size distribution of particles at any given radial location of a disk
is narrowly peaked about a mean value particular for this location and
time instant. Such an approximation was first proposed by Morfill
(1985) who noted that the resulting particle growth rate is not
sensitively dependent on the size distribution. The practical
implementation of this assumption means that a particle size, a, can
be expressed as a single value function of time and position,
a=a(t,r). Collectively, all particles forming the SPD can be
regarded as a turbulent fluid characterized by the average surface
density
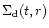 and the average velocity field
and the average velocity field
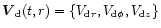 .
The
evolution of the SPD is governed by the set of two equations.
.
The
evolution of the SPD is governed by the set of two equations.
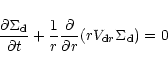 |
(4) |
and
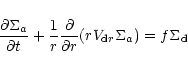 |
(5) |
where
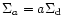 ,
and f is the source
function for particle growth by coagulation (see Sect. 2.4). The first
of these two equations is simply a vertically integrated mass
continuity equation for solid particles. The distribution of mass in
the SPD is driven by the radial component of its average velocity
field that depends on frictional coupling between particles and the
gas. This coupling depends on local particle size and local gas
properties. The particle size changes due to coagulation, whose rate
in turn depends on the density of the SPD. Thus (4) is coupled to both the gas evolution and the
particle size evolution.
,
and f is the source
function for particle growth by coagulation (see Sect. 2.4). The first
of these two equations is simply a vertically integrated mass
continuity equation for solid particles. The distribution of mass in
the SPD is driven by the radial component of its average velocity
field that depends on frictional coupling between particles and the
gas. This coupling depends on local particle size and local gas
properties. The particle size changes due to coagulation, whose rate
in turn depends on the density of the SPD. Thus (4) is coupled to both the gas evolution and the
particle size evolution.
Equation (5) represents the particle size
evolution and encapsulates the coagulation process under assumptions
of our model. It is convenient to convert the usual coagulation
equation
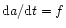 (see Sect. 2.4) into the conservative form (5) that can be viewed as the continuity
equation for "size-weighted'' surface density
(see Sect. 2.4) into the conservative form (5) that can be viewed as the continuity
equation for "size-weighted'' surface density
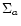 .
The
particle size evolution Eq. (5) is coupled
to the evolution of the gas via
.
The
particle size evolution Eq. (5) is coupled
to the evolution of the gas via
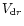 and to the evolution of
the SPD via the source term and the definition of
and to the evolution of
the SPD via the source term and the definition of
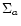 .
.
The evolution of the SPD is determined by solving the set of Eqs. (4)-(5) starting from
prescribed initial conditions. In order to close the set, the
average radial velocity,
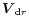 ,
and the source function
for particle coagulation, f, must be expressed in terms of gas
parameters, particle size, and
,
and the source function
for particle coagulation, f, must be expressed in terms of gas
parameters, particle size, and
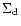 (4)-(5).
(4)-(5).
Because of the coupling to the turbulent GPD, the velocity field of the SPD
consists of average and fluctuating parts. The average velocity field,
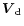 can be calculated under a particular Reynolds stress model for
the SPD. The details of such calculations are given in SV97.
The SV97 method of obtaining the components of
can be calculated under a particular Reynolds stress model for
the SPD. The details of such calculations are given in SV97.
The SV97 method of obtaining the components of
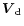 leads to
the system of equations that is nonlinear and not separable,
and thus needs to be solved numerically. Moreover, in general, the system
depends on particle densities, requiring a simultaneous solution of
velocities and particles densities. This high computational load
makes this approach impractical for our current purpose.
Therefore, in this paper we calculate
leads to
the system of equations that is nonlinear and not separable,
and thus needs to be solved numerically. Moreover, in general, the system
depends on particle densities, requiring a simultaneous solution of
velocities and particles densities. This high computational load
makes this approach impractical for our current purpose.
Therefore, in this paper we calculate
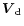 in a simpler, more approximate fashion that leads to an explicit formula for
in a simpler, more approximate fashion that leads to an explicit formula for
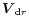 .
For the purpose of calculating
.
For the purpose of calculating
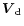 we assume that solid particles are coupled to the average flow of the gas. Under such an assumption and
because of the previous assumption about particle sizes (Sect. 2.2), the velocity field of the SPD is tantamount to velocities of specified individual particles. The radial component of
we assume that solid particles are coupled to the average flow of the gas. Under such an assumption and
because of the previous assumption about particle sizes (Sect. 2.2), the velocity field of the SPD is tantamount to velocities of specified individual particles. The radial component of
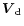 can be expressed as
can be expressed as
![\begin{displaymath}V_{{\rm d}r}= V_{\rm k} { {\left [\Delta \Lambda + {V_r\over V_{\rm k}}\right ]}\over {1+\Lambda^2} }\cdot
\end{displaymath}](/articles/aa/full/2001/40/aa1537/img38.gif) |
(6) |
In (6)
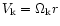 is the Keplerian velocity,
is the Keplerian velocity,
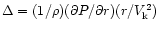 is the ratio of the
residual gravity to the central gravity, and
is the ratio of the
residual gravity to the central gravity, and
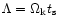 ,
where
,
where 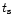 is the so-called stopping time. The residual gravity is
the name given to the support against the central gravity provided by
the pressure gradient in the gaseous disk. The stopping time is a
convenient measure of the strength of the frictional force. The value
of
is the so-called stopping time. The residual gravity is
the name given to the support against the central gravity provided by
the pressure gradient in the gaseous disk. The stopping time is a
convenient measure of the strength of the frictional force. The value
of 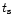 depends on particle size, the density of the gas and the
speed of the particle relative to the gas, v. The
dimensionless quantity
depends on particle size, the density of the gas and the
speed of the particle relative to the gas, v. The
dimensionless quantity 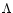 determines efficiency of gas-solids
coupling. If
determines efficiency of gas-solids
coupling. If
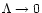 ,
the stopping time is small
compared to the orbital period, and solids are strongly coupled to the
gas. If
,
the stopping time is small
compared to the orbital period, and solids are strongly coupled to the
gas. If
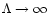 ,
the stopping time is very long
compared to the orbital period and solids are decoupled
from the gas.
,
the stopping time is very long
compared to the orbital period and solids are decoupled
from the gas.
Although (6) is written in the format suggesting that
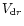 is given explicitly, this is not necessarily the case because
the quantity
is given explicitly, this is not necessarily the case because
the quantity 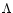 depends, in general, on the relative velocity v and
thus on
depends, in general, on the relative velocity v and
thus on
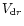 .
Recall that the stopping time is defined as
.
Recall that the stopping time is defined as
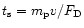 ,
where
,
where 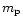 is a mass of a solid particle and
is a mass of a solid particle and 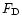 is the drag force. The drag law takes different forms in different physical regimes. SV96 gives a complete description of
is the drag force. The drag law takes different forms in different physical regimes. SV96 gives a complete description of 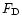 in all regimes. Here it is sufficient to note that when the mean free path of gas
molecules is larger than the size of the particle,
in all regimes. Here it is sufficient to note that when the mean free path of gas
molecules is larger than the size of the particle, 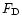 is given by the
Epstein law, otherwise it is given by the Stokes law. Furthermore, the Stokes law takes three different forms depending on the value of the Reynolds number. Taking these laws into consideration we find out that
is given by the
Epstein law, otherwise it is given by the Stokes law. Furthermore, the Stokes law takes three different forms depending on the value of the Reynolds number. Taking these laws into consideration we find out that 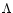 does
not depend on v in the Epstein regime and in the first Stokes regime.
In the second Stokes regime
does
not depend on v in the Epstein regime and in the first Stokes regime.
In the second Stokes regime
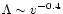 ,
and in the third Stokes
regime
,
and in the third Stokes
regime
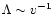 .
These two regimes apply when solids are large.
Relative velocity between a large solid and the gas is dominated by its
transverse component which is of the order of
.
These two regimes apply when solids are large.
Relative velocity between a large solid and the gas is dominated by its
transverse component which is of the order of
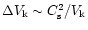 .
For the sake of simplicity we assume that in these regimes
.
For the sake of simplicity we assume that in these regimes
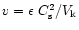 ,
where
,
where 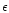 is a free constant parameter (
is a free constant parameter (
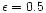 is
used in our calculations). With such an approximation the formula (6) becomes indeed explicit and the radial velocity of a solid particle and thus the radial component of
is
used in our calculations). With such an approximation the formula (6) becomes indeed explicit and the radial velocity of a solid particle and thus the radial component of
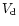 is given in terms of particle size and the gas properties.
is given in terms of particle size and the gas properties.
The presence of two terms in the numerator of (6)
reflects the existence of two mechanisms driving the radial motion of
solid particles. The term
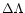 corresponds to engendering
radial motion of particles by virtue of the difference between
tangential velocities of the gas and the particles and its magnitude
is of the order of
corresponds to engendering
radial motion of particles by virtue of the difference between
tangential velocities of the gas and the particles and its magnitude
is of the order of
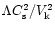 .
The term
.
The term
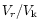 corresponds to radial motion of particles induced by the radial
flow of the gas, and its magnitude is of the order of
corresponds to radial motion of particles induced by the radial
flow of the gas, and its magnitude is of the order of
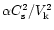 .
The relative importance of these two terms is
.
The relative importance of these two terms is
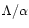 .
Thus, only small particles (those that are strongly
coupled to the gas) are carried radially by the gas accretion flow, whereas
larger particles moves radially because their transverse (orbital)
velocities are decreased by an aerodynamic drag.
.
Thus, only small particles (those that are strongly
coupled to the gas) are carried radially by the gas accretion flow, whereas
larger particles moves radially because their transverse (orbital)
velocities are decreased by an aerodynamic drag.
The most important feature of the radial velocity field of the
SPD is its dependence on 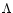 .
Within our approximations,
(6) is an explicit formula, and the character of
the function
.
Within our approximations,
(6) is an explicit formula, and the character of
the function
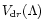 can easily be deduced. The
can easily be deduced. The
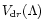 has a maximum at
has a maximum at
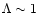 .
Thus,
particles with
.
Thus,
particles with
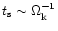 acquire the highest inward
velocity,
acquire the highest inward
velocity,
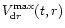 .
Because the stopping time
depends on both particle size and gas properties, that
velocity is not reached by particles of only one, well defined size.
Instead, particles of different sizes reach
.
Because the stopping time
depends on both particle size and gas properties, that
velocity is not reached by particles of only one, well defined size.
Instead, particles of different sizes reach
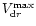 depending on location in the disk and the time. From
(6) it is clear that very small particles, those
with
depending on location in the disk and the time. From
(6) it is clear that very small particles, those
with
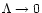 ,
move radially with
,
move radially with
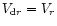 ,
and very large particles, those with
,
and very large particles, those with
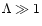 ,
have
,
have
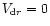 .
.
We assume that solid particles are spheres with bulk density
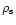 and mass
and mass 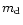 each, where
each, where
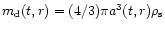 .
Because of our assumption about the size
distribution of particles (Sect. 2.2) only particles of the same size
are present at a particular location, at any given time. The density
of matter concentrated into solid particles is
.
Because of our assumption about the size
distribution of particles (Sect. 2.2) only particles of the same size
are present at a particular location, at any given time. The density
of matter concentrated into solid particles is
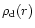 and
the particles' number density is
and
the particles' number density is
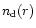 .
The geometrical
cross section for collision between two such particles is
.
The geometrical
cross section for collision between two such particles is
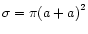 and the mean time between collisions is
and the mean time between collisions is
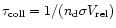 where
where
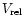 is the
mean relative speed between particles. Assuming that particles always
stick to each other upon collision, the growth of particle mass
is the
mean relative speed between particles. Assuming that particles always
stick to each other upon collision, the growth of particle mass
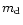 in unit time can be expressed as follow
in unit time can be expressed as follow
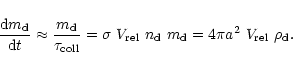 |
(7) |
The magnitude of
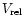 has been derived in SV97 to be
has been derived in SV97 to be
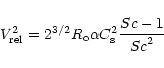 |
(8) |
where 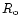 is the Rossby number for turbulent motion and Sc denotes
the Schmidt number. In the present calculations we assume
is the Rossby number for turbulent motion and Sc denotes
the Schmidt number. In the present calculations we assume
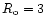 and
and
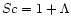 .
Substituting (8) into (7) we obtain the size evolution equation
.
Substituting (8) into (7) we obtain the size evolution equation
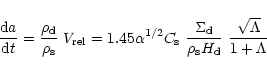 |
(9) |
where we used the relation
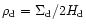 .
An approximate formula for the half-thickness of the SPD,
.
An approximate formula for the half-thickness of the SPD, 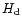 ,
has
been derived by SV97 and can be expressed as
,
has
been derived by SV97 and can be expressed as
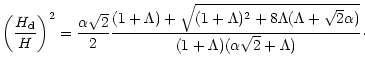 |
|
|
(10) |
The right hand side of (9) is the source function for particle growth by coagulation, f, present in Eq. (5). From (9), (10), and the fact that 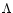 is given in terms of a particle size and the gas
properties it is clear that f is given in terms of only a,
is given in terms of a particle size and the gas
properties it is clear that f is given in terms of only a,
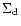 and the gas properties. Thus substituting f and
and the gas properties. Thus substituting f and
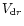 into the
the system of Eqs. (4)-(5) yields
the closed system with two unknowns,
into the
the system of Eqs. (4)-(5) yields
the closed system with two unknowns,
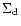 and
and
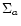 .
.
The midplane temperature, T, of the gas in the disk is calculated
from our GPD model (Sect. 2.1). For any particular time the
temperature decreases with distance from the star. The particle
traveling inward will evaporate when it finds itself at the location
where the ambient gas is sufficiently hot. Such a location defines an
evaporation radius,
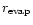 ,
that depends on the composition of
the particle. The evaporation radius decreases with time, as the
entire disk cools down during its evolution. We consider, in separate
calculations, three distinct, idealized forms of solid particles,
water ice, low-temperature silicates, and high-temperature silicates
to account for solids species with different evaporation temperatures
and bulk densities. The corresponding evaporation temperatures,
,
that depends on the composition of
the particle. The evaporation radius decreases with time, as the
entire disk cools down during its evolution. We consider, in separate
calculations, three distinct, idealized forms of solid particles,
water ice, low-temperature silicates, and high-temperature silicates
to account for solids species with different evaporation temperatures
and bulk densities. The corresponding evaporation temperatures,
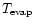 ,
are 150 K, 400 K and 1350 K, and the corresponding bulk
densities,
,
are 150 K, 400 K and 1350 K, and the corresponding bulk
densities,
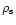 ,
are 1, 2.6 and 3.3 gcm-3. In our
calculations we treat vapor as particles with
,
are 1, 2.6 and 3.3 gcm-3. In our
calculations we treat vapor as particles with
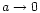 that
are completely coupled to the gas. The model permits the outward
movement of vapor particles into the
that
are completely coupled to the gas. The model permits the outward
movement of vapor particles into the
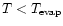 environment
where they condense. However, in our calculations, the radial velocity
of solids at the location of the evaporation radius was always
directed inward and such condensation has not occurred.
environment
where they condense. However, in our calculations, the radial velocity
of solids at the location of the evaporation radius was always
directed inward and such condensation has not occurred.
Equations (4) and (5) are solved
numerically to obtain spatio-temporal distributions of mass in the
SPD. The SPD expands and/or shrinks during its evolution, and its
maximum extent is a priori unknown. Because of this feature we solve
our equations on a moving grid, whose outer boundary follows the
motion of the outer edge of the SPD. We define a new independent
variable,
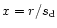 where
where
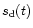 is the instantaneous
outer radius of the SPD. In order to preserve the forms of Eqs. (4) and (5) we also introduce new
dependent variables
is the instantaneous
outer radius of the SPD. In order to preserve the forms of Eqs. (4) and (5) we also introduce new
dependent variables
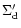 and
and
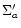 and
rescale the SPD's radial velocity
and
rescale the SPD's radial velocity
The outer edge of the disk is now always at
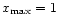 ,
whereas the inner edge has to be arbitrarily assigned a
small number
,
whereas the inner edge has to be arbitrarily assigned a
small number
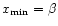 .
The value of
.
The value of
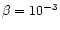 was
used in our calculations. We use a grid of 50 points equidistant in
was
used in our calculations. We use a grid of 50 points equidistant in
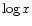 ,
and distributed between
,
and distributed between
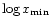 and
and
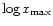 .
The transformed equations are solved using standard methods of numerical
hydrodynamics. We employ a second-order code originally described by
Rózyczka (1985), and based on the same philosophy as the
popular ZEUS code (Stone & Norman 1992). However, we use a
monotonization procedure proposed by van Albada et al. (1982), instead
of the standard monotonization method (van Leer 1977) used in
Rózyczka's code. Because
.
The transformed equations are solved using standard methods of numerical
hydrodynamics. We employ a second-order code originally described by
Rózyczka (1985), and based on the same philosophy as the
popular ZEUS code (Stone & Norman 1992). However, we use a
monotonization procedure proposed by van Albada et al. (1982), instead
of the standard monotonization method (van Leer 1977) used in
Rózyczka's code. Because
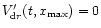 no
boundary condition at
no
boundary condition at
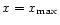 is required. The value of
is required. The value of
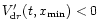 because the inner edge is always in
the accretion zone of the disk. Therefore a free outflow boundary
conditions is applied at
because the inner edge is always in
the accretion zone of the disk. Therefore a free outflow boundary
conditions is applied at
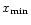 .
.
Several tests of the code were performed (analytical solutions of
simple evolutionary cases were recovered, and in a few more
complicated cases full agreement was reached with numerical solutions
of the original set of equations). We also checked that the results
were not sensitive to the choice of 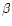 (provided its value was
not too large).
(provided its value was
not too large).
We have performed a large suite of calculations to answer the
following question: What is the dependence of the global properties of
the nascent planetary system (represented here by the swarm of
planetesimals at t=107 yr) on initial conditions of the GPD? Each
individual calculation tracks the evolution of the GPD and the SPD
from a particular initial condition (at the time arbitrarily set to
t=0) to a configuration reached t=107 years later when all
solids are either in the form of planetesimals or have been accreted
onto the star or evaporated. Each evolutionary run is labeled by
values of four parameters
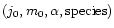 .
The
first two labels, total angular momentum and total mass of the GPD at
t=0, characterize the initial conditions (see Sect. 2.1). To
cover the range of masses and angular momenta indicated by
observations, we use 14 values of j0 between 0.5 and 50 and 11 values
of m0 between 0.02 and 0.2 (i.e. we consider 154 different
initial conditions). The initial radial distribution of solids is
.
The
first two labels, total angular momentum and total mass of the GPD at
t=0, characterize the initial conditions (see Sect. 2.1). To
cover the range of masses and angular momenta indicated by
observations, we use 14 values of j0 between 0.5 and 50 and 11 values
of m0 between 0.02 and 0.2 (i.e. we consider 154 different
initial conditions). The initial radial distribution of solids is
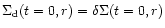 ,
where
,
where
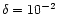 for ice and
for ice and
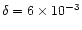 for silicates to account for
cosmic abundance. The third label, the Shakura-Sunayev parameter
for silicates to account for
cosmic abundance. The third label, the Shakura-Sunayev parameter 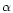 ,
characterizes the turbulence in the GPD and influences the
rate of the disk's evolution. We use four values of
,
characterizes the turbulence in the GPD and influences the
rate of the disk's evolution. We use four values of 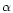 ,
10-4, 10-3, 10-2 and 10-1. Finally, the fourth label
describes the composition of solids, their evaporation temperature and
the bulk density. We consider three different species of solids (see
Sect. 2.5). Altogether 1848 evolutionary runs were calculated.
,
10-4, 10-3, 10-2 and 10-1. Finally, the fourth label
describes the composition of solids, their evaporation temperature and
the bulk density. We consider three different species of solids (see
Sect. 2.5). Altogether 1848 evolutionary runs were calculated.
The global properties of the swarm of planetesimals are
represented by two numbers, the total mass of the SPD at t=107 yr, 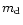 ,
and the radius of the SPD at t=107 yr,
,
and the radius of the SPD at t=107 yr, 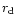 .
Thus, we use
the results of our calculations to construct a transformation
.
Thus, we use
the results of our calculations to construct a transformation
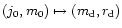 .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{KSM1537f1.eps}
\end{figure}](/articles/aa/full/2001/40/aa1537/Timg115.gif) |
Figure 1:
The radius (the bottom face of each cube)
and the total mass (the top face of each cube) of icy planetesimal swarm at t=107 years as functions of initial conditions. The functions are shown in the form of contour plots. The contours' labels for  are in units of AU and the contours' labels for
are in units of AU and the contours' labels for 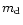 are in units of
are in units of
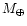 .
Cubes are marked by corresponding values of .
Cubes are marked by corresponding values of 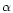 . . |
| Open with DEXTER |
Figure 1 shows the results of our calculations for solids
composed of water ice. The figure has four panels, each for a
different value of 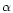 .
For a particular value of
.
For a particular value of 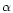 the
plot shows a "cube'' with
the
plot shows a "cube'' with
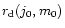 displayed on the bottom
face and
displayed on the bottom
face and
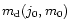 displayed on the top face. These two
functions are represented as contour plots. Each labelled curve on the
bottom face of the cube represents a set of initial conditions that
result in a planetesimal swarm with the radius indicated by the
label. Similarly, each labelled curve on the top face of the cube
represents a set of initial conditions that results in a planetesimal
swarm with the total mass indicated by the label. The functions
displayed on the top face. These two
functions are represented as contour plots. Each labelled curve on the
bottom face of the cube represents a set of initial conditions that
result in a planetesimal swarm with the radius indicated by the
label. Similarly, each labelled curve on the top face of the cube
represents a set of initial conditions that results in a planetesimal
swarm with the total mass indicated by the label. The functions
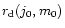 and
and
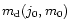 are obtained via
interpolation from the 154 values actually calculated. A wavy
character of some contours lines is due to limited coverage of
calculated values and would disappear for a dense enough grid of
(j0, m0). The cube is constructed from the two contour plots in
order to better illustrate the full transformation
are obtained via
interpolation from the 154 values actually calculated. A wavy
character of some contours lines is due to limited coverage of
calculated values and would disappear for a dense enough grid of
(j0, m0). The cube is constructed from the two contour plots in
order to better illustrate the full transformation
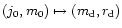 .
One can choose a particular initial
condition,
(j0, m0), on, say the bottom face of the cube, find a
corresponding value of
.
One can choose a particular initial
condition,
(j0, m0), on, say the bottom face of the cube, find a
corresponding value of 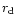 and then move straight up to the
top face of the cube to find a corresponding value of
and then move straight up to the
top face of the cube to find a corresponding value of 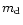 .
.
Analyzing Fig. 1 we find that the domain of initial
conditions
(j0, m0) can be divided into two portions by contours
labeled "0''. These contours, that coincide on the bottom and the top
face of each cube (less than perfect coincidence is due to
imperfections of interpolation), are the demarcation lines between
initial conditions that lead to formation of a planetesimal swarm and
those that do not. Disks evolving from initial conditions located
below a 0-labeled contour are, over time, bled from all solids leaving
no material behind to form planetesimals. Note that such, no-swarm,
initial conditions are those that correspond to the GPD that is
initially heavy and small (small values of j0 correspond to small
values of r0) and thus hot. The no-swarm initial conditions are,
in the first approximation, those for which
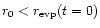 .
In
such a disk all solids are initially in the vapor form. As the GPD
evolves it expands and cools, its radius increases
and the value of
.
In
such a disk all solids are initially in the vapor form. As the GPD
evolves it expands and cools, its radius increases
and the value of
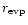 decreases, leading, eventually, to the
emergence of the region of the disk where solids may exist. However,
in the process of disk expansion the major portion of gas and
vapor moves inward and is accreted onto the star. Only a small
portion of gas and vapor moves outward, increasing the size of
the disk. This small amount of the vapor condenses into small solids
right outside
decreases, leading, eventually, to the
emergence of the region of the disk where solids may exist. However,
in the process of disk expansion the major portion of gas and
vapor moves inward and is accreted onto the star. Only a small
portion of gas and vapor moves outward, increasing the size of
the disk. This small amount of the vapor condenses into small solids
right outside
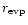 .
On a relatively short timescale these
solid particles coagulate, gain inward radial velocities and move back
to the location
.
On a relatively short timescale these
solid particles coagulate, gain inward radial velocities and move back
to the location
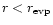 where they evaporate again. Eventually,
all vapor is accreted onto the star and the disk is bled from the
solid component. The region of no-swarm initial conditions is the
largest for
where they evaporate again. Eventually,
all vapor is accreted onto the star and the disk is bled from the
solid component. The region of no-swarm initial conditions is the
largest for
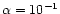 because, everything else being equal,
disks with higher values of
because, everything else being equal,
disks with higher values of 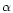 are hotter. Decreasing
are hotter. Decreasing 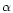 results in progressively smaller set of no-swarm initial
conditions. Finally, for
results in progressively smaller set of no-swarm initial
conditions. Finally, for
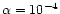 all initial
conditions considered here lead to the formation of a swarm.
all initial
conditions considered here lead to the formation of a swarm.
It is interesting to understand how the size and the mass of the swarm
depend on initial conditions. Consider a family of initial conditions defined
by
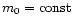 line on any frame in Fig. 1.
Such a family can be sorted by an increasing value of j0 starting from
line on any frame in Fig. 1.
Such a family can be sorted by an increasing value of j0 starting from
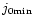 that corresponds to an initial condition located just on the
0-labeled contour. The masses of swarms formed in disks evolving from
succeeding initial conditions increase quickly at first, but then stay constant after reaching a certain "saturation'' mass. The radii of swarms increase
without saturation, but at a decreasing rate. This pattern is independent of
the values of m0 and/or
that corresponds to an initial condition located just on the
0-labeled contour. The masses of swarms formed in disks evolving from
succeeding initial conditions increase quickly at first, but then stay constant after reaching a certain "saturation'' mass. The radii of swarms increase
without saturation, but at a decreasing rate. This pattern is independent of
the values of m0 and/or 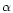 ,
although the value of the saturation
mass depends on these parameters.
,
although the value of the saturation
mass depends on these parameters.
These results can be explained as follows. As discussed above, disks
with
 ,
accrete all solids onto the
star. For disks with j0 just larger than
,
accrete all solids onto the
star. For disks with j0 just larger than
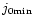 ,
a small
outer portion of the disk has a temperature smaller than
,
a small
outer portion of the disk has a temperature smaller than
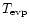 and small solid particles exist there at t=0. They coagulate on a
relatively short timescale to achieve the maximum-speed size. At that
stage
and small solid particles exist there at t=0. They coagulate on a
relatively short timescale to achieve the maximum-speed size. At that
stage
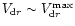 and most of particles
are lost to the evaporation zone. Some particles survive because they
manage to grow to sizes bigger than the maximum-speed size and slow
down before falling into the evaporation zone (see Sect. 2.3).
These particles form a residual swarm, whose mass is much smaller than
the original mass of the SPD. The larger the value of j0, the
larger is the initial disk, the more particles avoid falling into the
evaporation zone, and the more massive swarm is formed. For large
enough values of j0, the great majority of particles have enough
time to grow to large sizes that prevent them from migration
into the evaporation zone. The mass of the resulting swarm is
about equal to the initial mass of the SPD. In such cases the
solid material is reshuffled within the disk, but its total mass is
basically preserved.
and most of particles
are lost to the evaporation zone. Some particles survive because they
manage to grow to sizes bigger than the maximum-speed size and slow
down before falling into the evaporation zone (see Sect. 2.3).
These particles form a residual swarm, whose mass is much smaller than
the original mass of the SPD. The larger the value of j0, the
larger is the initial disk, the more particles avoid falling into the
evaporation zone, and the more massive swarm is formed. For large
enough values of j0, the great majority of particles have enough
time to grow to large sizes that prevent them from migration
into the evaporation zone. The mass of the resulting swarm is
about equal to the initial mass of the SPD. In such cases the
solid material is reshuffled within the disk, but its total mass is
basically preserved.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{KSM1537f2.eps}
\end{figure}](/articles/aa/full/2001/40/aa1537/Timg127.gif) |
Figure 2:
The radius (the bottom face of each cube)
and the total mass (the top face of each cube) of high-temperature silicates planetesimal swarm at t=107 years as functions of initial conditions. The functions are shown in the form of contour plots. The contours' labels for 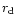 are in units of AU and the contours' labels for
are in units of AU and the contours' labels for 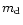 are in units of
are in units of
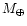 .
Cubes are marked by corresponding values of .
Cubes are marked by corresponding values of 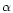 . . |
| Open with DEXTER |
Figure 2 shows the results of our calculations for solids
composed of high-temperature silicates. The transformation
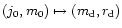 for the SPD consisting of silicates is
qualitatively similar to the transformation for the SPD consisting of
ice. This is to be expected considering that mechanism of such a
transformation depends on particle material via just one parameter
(
for the SPD consisting of silicates is
qualitatively similar to the transformation for the SPD consisting of
ice. This is to be expected considering that mechanism of such a
transformation depends on particle material via just one parameter
(
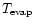 ). The key differences between silicates and the ice are
as follows. The no-swarm portion of the
(j0, m0) plane is
slightly smaller for silicates than it is for the ice because
). The key differences between silicates and the ice are
as follows. The no-swarm portion of the
(j0, m0) plane is
slightly smaller for silicates than it is for the ice because
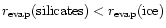 so, other things being
equal,
so, other things being
equal,
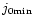 is smaller for the silicates. For the same,
swarm-forming initial conditions, the size of the ice swarm is larger
than the size of the silicate swarm, mostly because the inner radius
of the silicate swarm is smaller than the inner radius of the ice
swarm. Note that, although the original protoplanetary disk contains
much more ices than silicates, the final silicates swarm is not
necessarily less massive than the final ice swarm. Results for
low-temperature silicates (not shown here) fall between those for ice
and high-temperature silicates.
is smaller for the silicates. For the same,
swarm-forming initial conditions, the size of the ice swarm is larger
than the size of the silicate swarm, mostly because the inner radius
of the silicate swarm is smaller than the inner radius of the ice
swarm. Note that, although the original protoplanetary disk contains
much more ices than silicates, the final silicates swarm is not
necessarily less massive than the final ice swarm. Results for
low-temperature silicates (not shown here) fall between those for ice
and high-temperature silicates.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{KSM1537f3.eps}
\end{figure}](/articles/aa/full/2001/40/aa1537/Timg129.gif) |
Figure 3:
Summary of the evolution of protoplanetary disk with
j0=10.4, m0=0.182 and
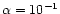 .
The bottom face of each
cube is a contour plot depicting the surface density as function of t and r. The contours' labels are in units of g/cm2. The top
face of a gas cube shows T(t,r), contours' labels are in K. The
top faces of solids cubes show a(t,s), contours' labels are in
cm. Note that cubes have different radial ranges. .
The bottom face of each
cube is a contour plot depicting the surface density as function of t and r. The contours' labels are in units of g/cm2. The top
face of a gas cube shows T(t,r), contours' labels are in K. The
top faces of solids cubes show a(t,s), contours' labels are in
cm. Note that cubes have different radial ranges. |
| Open with DEXTER |
Although the focus of this paper is on the
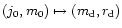 transformation (see Sect. 4), it is also interesting
to track the evolution of an example protoplanetary disk
in detail. In this section we present results of
our calculations pertaining to the evolution of a disk characterized
by
transformation (see Sect. 4), it is also interesting
to track the evolution of an example protoplanetary disk
in detail. In this section we present results of
our calculations pertaining to the evolution of a disk characterized
by
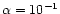 and starting from initial conditions parameterized
by j0=10.4 and m0=0.182. We have chosen this particular case
because it provides an example of rather dramatic evolutionary changes
of gas and solids components, and it illustrates all relevant
physical processes. In other, possibly more realistic, scenarios not
all evolutionary features may be observed in a single run.
and starting from initial conditions parameterized
by j0=10.4 and m0=0.182. We have chosen this particular case
because it provides an example of rather dramatic evolutionary changes
of gas and solids components, and it illustrates all relevant
physical processes. In other, possibly more realistic, scenarios not
all evolutionary features may be observed in a single run.
At t=0 the GPD extends to 68 AU. Ice SPD, low-temperature silicates
SPD and high-temperature silicates SPD extend from 12.2 AU to 68 AU,
3.4 AU to 68 AU and 1.1 AU to 68 AU, respectively. Their masses are,
respectively, equal to 606, 364, 364
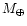 .
The mass of the
SPD is entirely in the form of small particles (assumed size is
10-3 cm). At t=107 yr the GPD has lost most of its mass, but
it extends to a very large radius (7300 AU). The ice SPD extends from
0.64 AU to 11.6 AU and has a mass of 56
.
The mass of the
SPD is entirely in the form of small particles (assumed size is
10-3 cm). At t=107 yr the GPD has lost most of its mass, but
it extends to a very large radius (7300 AU). The ice SPD extends from
0.64 AU to 11.6 AU and has a mass of 56
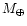 .
The
low-temperature silicates SPD extends from 0.17 AU to 5.4 AU and has a
mass of 38
.
The
low-temperature silicates SPD extends from 0.17 AU to 5.4 AU and has a
mass of 38
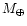 .
The high-temperature silicates SPD extends
from 0.08 AU to 5.5 AU and its mass is 84
.
The high-temperature silicates SPD extends
from 0.08 AU to 5.5 AU and its mass is 84
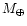 .
Thus, during
the 107 yr of evolution the disk lost more than 90% of ice and
low-temperature silicates and about 80% of high-temperature
silicates. All solids have been redistributed, their final
distributions bearing no resemblance to the original ones. Most mass
of the final SPD is locked in planetesimals with a > 104 cm. Note
that the sizes of swarms given above are rather formal values, as the
bulk of the mass resides in a much narrower ring (see below).
.
Thus, during
the 107 yr of evolution the disk lost more than 90% of ice and
low-temperature silicates and about 80% of high-temperature
silicates. All solids have been redistributed, their final
distributions bearing no resemblance to the original ones. Most mass
of the final SPD is locked in planetesimals with a > 104 cm. Note
that the sizes of swarms given above are rather formal values, as the
bulk of the mass resides in a much narrower ring (see below).
Figure 3 shows the summary of the disk evolution. The figure
has four panels, one for the gas, and the rest for the three species
of solids. Each panel is in the form of a "cube'', in the same sense
as in Figs. 1-2, to represent a pair of functions of
two independent variables, t and r. For GPD, these functions
are T(t,r) (shown on the top face of the cube), and
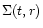 (shown on the bottom face of the cube). For SPD the functions are
a(t,r) (shown on the top face of the cube), and
(shown on the bottom face of the cube). For SPD the functions are
a(t,r) (shown on the top face of the cube), and
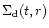 (shown on the bottom face of the cube). All functions are
represented as contour plots obtained
via interpolation from a finite number of values that actually were
computed. Note that the computed values are not given on a regular
grid of (t,r), and a triangular interpolation has to be used.
(shown on the bottom face of the cube). All functions are
represented as contour plots obtained
via interpolation from a finite number of values that actually were
computed. Note that the computed values are not given on a regular
grid of (t,r), and a triangular interpolation has to be used.
Functions T(t,r) and
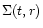 describe the evolution of the
GPD. There are six constant temperature contours, three of them chosen
to coincide with
describe the evolution of the
GPD. There are six constant temperature contours, three of them chosen
to coincide with
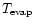 for the three species of solids. The
curvatures of the temperature contours point to the overall cooling of
the disk. In particular the evaporation radii for all species of
solids decrease with time. There are 10 constant surface density
contours to illustrate the evolution of the gaseous component. These contours
show that the mass of the GPD decreases rapidly. They also illustrate the
spreading of the GPD (note that contours corresponding to
for the three species of solids. The
curvatures of the temperature contours point to the overall cooling of
the disk. In particular the evaporation radii for all species of
solids decrease with time. There are 10 constant surface density
contours to illustrate the evolution of the gaseous component. These contours
show that the mass of the GPD decreases rapidly. They also illustrate the
spreading of the GPD (note that contours corresponding to
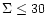 gcm-2 start at progressively later times).
gcm-2 start at progressively later times).
Functions a(t,r) and
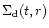 indicate the evolution of
the SPD. The evolution of all solids species are qualitatively
similar. For t > 10 yr the contour a=10-2 cm coincides with the
indicate the evolution of
the SPD. The evolution of all solids species are qualitatively
similar. For t > 10 yr the contour a=10-2 cm coincides with the
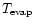 contour and demarcates disk locations where only vapor
exists from locations where solid bodies may exist. The "mohawk-like''
pattern formed by the collection of constant a contours sheds light
on how the evolution of solids proceeds. A t=t0 line on the contour
plot depicting the function a(t,r) gives the radial distribution of
particle size at t0, whereas the r=r0 line gives the history of
particle sizes at r0. The inward migration of the outer edge of the
SPD can be deduced from the fact that contours corresponding to
progressively larger sizes end at progressively smaller radii. At
earlier times the contours of constant a are almost parallel to the
r axis, indicating small variability of particle sizes along the
radius of the disk. For later times the bending of the contours
increases indicating more particle size variability.
contour and demarcates disk locations where only vapor
exists from locations where solid bodies may exist. The "mohawk-like''
pattern formed by the collection of constant a contours sheds light
on how the evolution of solids proceeds. A t=t0 line on the contour
plot depicting the function a(t,r) gives the radial distribution of
particle size at t0, whereas the r=r0 line gives the history of
particle sizes at r0. The inward migration of the outer edge of the
SPD can be deduced from the fact that contours corresponding to
progressively larger sizes end at progressively smaller radii. At
earlier times the contours of constant a are almost parallel to the
r axis, indicating small variability of particle sizes along the
radius of the disk. For later times the bending of the contours
increases indicating more particle size variability.
To fully understand the evolution of the SPD, we need to inspect the
function
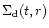 in addition to the function
a(t,r). The most important, additional information from studying
in addition to the function
a(t,r). The most important, additional information from studying
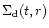 is that it falls off rapidly at a certain
radius that is almost time-independent and is close to
is that it falls off rapidly at a certain
radius that is almost time-independent and is close to
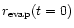 .
Thus, although some solids exist between
.
Thus, although some solids exist between
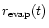 and
and
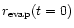 (as shown by
the particle size plot), their surface density there is negligible
and we can take
(as shown by
the particle size plot), their surface density there is negligible
and we can take
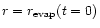 as an effective inner radius of
the SPD. The explanation of this phenomenon is as follows. The
viscous timescale of this model is long, and up to t=104 yr the location
of
as an effective inner radius of
the SPD. The explanation of this phenomenon is as follows. The
viscous timescale of this model is long, and up to t=104 yr the location
of
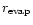 does not change much. However, the coagulation timescale
is shorter, and by that time solids, initially in the form of small
particles, have coagulated into relatively large bodies. From t=104 yr to
t=107 yr
does not change much. However, the coagulation timescale
is shorter, and by that time solids, initially in the form of small
particles, have coagulated into relatively large bodies. From t=104 yr to
t=107 yr
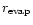 decreases steadily and the solids are free,
in principle, to migrate inward. However, again the coagulation
timescale is faster than the viscous timescale and few solid bodies
actually migrate inward, whereas the majority manage to stop their migration by
increasing their size. This phenomenon was already seen in SV97
calculations and its detailed explanation is given there.
decreases steadily and the solids are free,
in principle, to migrate inward. However, again the coagulation
timescale is faster than the viscous timescale and few solid bodies
actually migrate inward, whereas the majority manage to stop their migration by
increasing their size. This phenomenon was already seen in SV97
calculations and its detailed explanation is given there.
Figure 4 shows, on the linear scale, functions
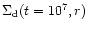 for all species of solids. This figure carries the same
information, albeit in a more readable form, as the information along
t=107 yr lines on contour plots of Fig. 3. In our
calculations we consider the swarm to be fully assembled at t=107yr, and thus Fig. 4 illustrates the final distribution
of mass locked in planetesimals. In this particular swarm the high
and low temperature silicates coexist between 2 AU and 5.5 AU, but
only high-temperature silicates are found between 1 AU and 2 AU. The
amount of solids at radii smaller than 1 AU is
negligible. Icy planetesimals do exist in a significant amount between
6 AU and 11.6 AU, i.e. they are completely separated from
silicates. Most of the ice resides at about 10.
There is enough material in the swarm to form a planetary system composed
of an icy planet (or planets) with the total mass of
for all species of solids. This figure carries the same
information, albeit in a more readable form, as the information along
t=107 yr lines on contour plots of Fig. 3. In our
calculations we consider the swarm to be fully assembled at t=107yr, and thus Fig. 4 illustrates the final distribution
of mass locked in planetesimals. In this particular swarm the high
and low temperature silicates coexist between 2 AU and 5.5 AU, but
only high-temperature silicates are found between 1 AU and 2 AU. The
amount of solids at radii smaller than 1 AU is
negligible. Icy planetesimals do exist in a significant amount between
6 AU and 11.6 AU, i.e. they are completely separated from
silicates. Most of the ice resides at about 10.
There is enough material in the swarm to form a planetary system composed
of an icy planet (or planets) with the total mass of
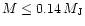 located
at about 10 AU and a silicate planet (or planets) with the total mass of
located
at about 10 AU and a silicate planet (or planets) with the total mass of
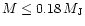 located between 1 AU and 5 AU.
located between 1 AU and 5 AU.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{KSM1537f4.eps}
\end{figure}](/articles/aa/full/2001/40/aa1537/Timg138.gif) |
Figure 4:
Radial distribution of the surface density of solids in a disk characterized by
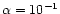 ,
j0=10.4 and m0=0.182 at t=107 yr.
The values of ,
j0=10.4 and m0=0.182 at t=107 yr.
The values of
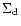 were computed at finite number of locations
indicated by circles. Light gray circles are for the ice, dark gray circles are
for the low-temperature silicates and black circles are for high-temperature
silicates. The size of the circle is proportional (nonlinearly) to the logarithm of the solids size. The dashed line indicates the surface density of the gas.
were computed at finite number of locations
indicated by circles. Light gray circles are for the ice, dark gray circles are
for the low-temperature silicates and black circles are for high-temperature
silicates. The size of the circle is proportional (nonlinearly) to the logarithm of the solids size. The dashed line indicates the surface density of the gas. |
| Open with DEXTER |
We have developed a formalism that allows us to calculate globally the
evolution of solids in a protoplanetary disk. The formalism is
based on the method developed by SV97, but it relies on two additional
approximations. First, we use an analytical model of GPD in
place of the numerical model used in SV97. Second, for gas-solids
interactions we assume a coupling between solid particles and
average flow of the gas instead of a coupling between particles and
instantaneous, turbulent flow as considered in SV97. Because of these
changes the computational efficiency of our new formalism is
significantly higher. Both formalisms produce qualitatively similar
results, as can be assessed by comparing details of disk evolution
(Sect. 5) with analogous results in Sects. 4 and 5 of SV97. Thus, as far
as the evolution of a particular disk is considered, we confirm the
earlier results discussed in detail in Sect. 6 of SV97.
The efficiency of the new formalism allows for a broad search
through plausible initial conditions in order to establish the
relation between those conditions and the properties of emerging
planetesimal swarms. To investigate the diversity of the swarms, we
performed a systematic search through initial conditions by
sampling a 2-D parameter space confined by the minimum and maximum
values of j0 and m0 as indicated by observations.
Our calculations produce planetesimal swarms,
which are taken here as surrogates for planetary systems. In reality,
further redistribution of mass may occur during the planetesimals to
planets accumulation, as well as during subsequent gravitational
interactions between just formed planets and a residual swarm (Del
Popolo et al. 2001) or a gaseous disk (Ward 1997). These processes
introduce further diversity of planetary systems that is not addressed
by our calculations. It should be also mentioned that a profound
redistribution of various PPD components, accompanied by a significant
mass loss from the disk, may result from eruptive events observed in
those objects (e.q. FU Ori outbursts). Such events, likely to occur
prior to a dissipative stage of the disk, are beyond the scope of the
present paper.
Our most important finding is that the diversity of planetary
systems emerges naturally from the process of the
evolution of solids in protoplanetary disks of diverse initial
configurations. In other words, if protoplanetary disks form in
variety of masses and sizes, this variation alone leads to formation
of extremely different planetary systems. In particular, we have found that for
certain initial configurations of protoplanetary disks, a planetesimal
swarm, and thus the planetary system, does not form at all. These
configurations are characterized, in general, by small
specific angular momentum (small initial sizes relative to their
initial masses). In these disks solids migrate into the evaporation
zone where they are destroyed and accreted onto the star before they
have time to grow and stop their inward motion. The size of the
no-swarm domain of initial conditions depends on the species of solids
and on the timescale of disk evolution (related to the viscosity parameter 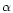 ). Configurations with large values of specific angular
momentum (large initial sizes with respect to their masses) tend to
redistribute solids during their evolution without losing them to the
star. The residual swarms have relatively large masses. Finally,
configurations with intermediate values of specific angular momentum
lose a fraction of solids during their evolutions, producing less
massive swarms. Statistical analysis of astronomical observations may,
in principle, establish relative frequencies of different types of
initial conditions. Such analysis, which is beyond the scope of this
paper, coupled to our model may predict relative frequencies of
different sorts of potential planetary systems.
). Configurations with large values of specific angular
momentum (large initial sizes with respect to their masses) tend to
redistribute solids during their evolution without losing them to the
star. The residual swarms have relatively large masses. Finally,
configurations with intermediate values of specific angular momentum
lose a fraction of solids during their evolutions, producing less
massive swarms. Statistical analysis of astronomical observations may,
in principle, establish relative frequencies of different types of
initial conditions. Such analysis, which is beyond the scope of this
paper, coupled to our model may predict relative frequencies of
different sorts of potential planetary systems.
It is interesting to see which initial conditions lead to a
planetary system that resembles our Solar System. We can approximate
the size of the planetesimal swarm from which the Solar System formed
by the current radius of the Kuiper Belt (30-50 AU). For the mass of
the swarm we can take the mass of solids in the present Solar System,
<100
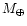 .
Figure 1 shows that regardless of the
value of
.
Figure 1 shows that regardless of the
value of 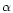 ,
swarms with such properties can originate only from
a protoplanetary disks with
,
swarms with such properties can originate only from
a protoplanetary disks with
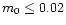 and
and 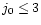 .
Specifically, assuming
.
Specifically, assuming
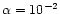 ,
only two models among
those actually calculated fulfill roughly the above conditions. The
first model, with j0=3 and m0=0.02, originally extends to 440 AU
and has the mass of 67
,
only two models among
those actually calculated fulfill roughly the above conditions. The
first model, with j0=3 and m0=0.02, originally extends to 440 AU
and has the mass of 67
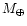 in icy particles and 40
in icy particles and 40
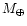 in high-temperature silicates. The final icy swarm
extends from 1 AU to 54 AU and has the mass of 66
in high-temperature silicates. The final icy swarm
extends from 1 AU to 54 AU and has the mass of 66
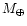 ,
while
the final silicates swarm extends from 0.3 AU to 37 AU and has the
mass of 39
,
while
the final silicates swarm extends from 0.3 AU to 37 AU and has the
mass of 39
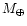 .
The second model, with j0=1 and
m0=0.02, originally extends to 50 AU and has the mass of 67
.
The second model, with j0=1 and
m0=0.02, originally extends to 50 AU and has the mass of 67
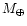 in icy particles and 40
in icy particles and 40
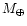 in high-temperature
particles. The final icy swarm extends from 2.25 AU to 18 AU and has
the mass of 64
in high-temperature
particles. The final icy swarm extends from 2.25 AU to 18 AU and has
the mass of 64
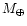 ,
while the final silicates swarm extends
from 0.2 AU to 12 AU and has the mass of 39
,
while the final silicates swarm extends
from 0.2 AU to 12 AU and has the mass of 39
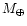 .
.
Neither of these two models fits perfectly with the Solar System. The
j0=3 model leaves too much ice in terrestrial planets zone, while
the j0=1 model produces a swarm that is smaller than the present-day
Solar System. Nevertheless, both models produce swarms that, at least
in the global, qualitative sense, can lead to the formation of the
planetary system somewhat similar to our own. Interestingly, disks
that produce solar-like planetary systems have initial global
properties similar to that postulated in the so-called "minimum-mass''
solar nebula model (Weidenschilling 1977). This similarity is
coincidental inasmuch as in our model there is no a priori
requirement of preserving the total mass of the solids. In other
words, the fact that disks leading to the solar-like planetary system
preserve the original mass of the solid component is a result
(and perhaps an unexpected one) from our model, and not a build-in
property.
More massive swarms are possible if initial disks are more massive and
have enough angular momentum. The amount of gas left in the disk after
107 years depends on the value of 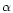 (the smaller the
(the smaller the 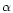 ,
the more gas is left). Portions of this gas can be
incorporated into planetary masses, while the remaining gas interacts
with newly formed planets, causing further changes to the
configuration of a system. Within the limits of the approximations
adopted here, the in situ formation of massive planets at 1-5 AU from
a star can be explained in terms of SPD evolution alone (i.e. without
planetary migration). However, in situ formation of such planets at
0.1 AU (the so-called "hot Jupiters'', of which the companion to 51 Peg
is a primary example) is rather unlikely, as reasonable initial
conditions do not produce swarms with adequate surface density
distributions.
,
the more gas is left). Portions of this gas can be
incorporated into planetary masses, while the remaining gas interacts
with newly formed planets, causing further changes to the
configuration of a system. Within the limits of the approximations
adopted here, the in situ formation of massive planets at 1-5 AU from
a star can be explained in terms of SPD evolution alone (i.e. without
planetary migration). However, in situ formation of such planets at
0.1 AU (the so-called "hot Jupiters'', of which the companion to 51 Peg
is a primary example) is rather unlikely, as reasonable initial
conditions do not produce swarms with adequate surface density
distributions.
Finally, it is important to remember that our model is built on the
premise that transformation of solids from dust to planetesimals occurs
through the process of hierarchical coagulation. If coagulation is
not the major factor in such transformation, our
model is invalid. One cannot definitively exclude a possibility that a
collective process, such as, for example, the gravitational instability
of a dust layer (Goldreich & Ward 1973) transforms small particles
rapidly into planetesimals. However, the formation of a midplane layer
of dust, thin enough to be susceptible to the gravitational
instability is unlikely in a turbulent disk. It has been
proposed (Barge & Sommeria 1995; Tanga et al. 1996) that the
gravitational instability may work for the solids component in vortices
appearing in the disk, but neither the existence of such vortices nor
their ability to form planetesimals was demonstrated. Thus, coagulation
remains the most likely mechanism of a planetesimal formation. The
"single-size'' approximation used here for the description of
coagulation is obviously rather crude. However, we
believe that, despite its limitations, our model captures the essence
of processes leading to formation of a planetesimal swarm, and it provides a
good qualitative illustration of the evolution of solids in a
protoplanetary disk.
Acknowledgements
This research was conducted at the Lunar and Planetary Institute,
which is operated by the Universities Space Research Association under
contract No. NASW-4574 with the National Aeronautics and Space
Administration, and at the Nicolaus Copernicus Astronomical Center.
This is Lunar and Planetary Institute Contribution No. 1096.
K. K. and M. R. acknowledge support from the Committee for Scientific
Research through the grant 2P03D01419.
The authors thank the referee, Dr. J. Lunine, for constructive comments.
-
Beckwith, S. V. W., & Sargent, A. I. 1993, in Protostars & Planets III, ed. E.H. Levy, & J.I. Lunine (Univ. Arizona Press, Tucson), 521
In the text
-
Beckwith, S. V. W. 1994, in Theory of Accretion Disks - 2, ed. W. J. Duschl, J. Frank, F. Meyer, E. Meyer-Hofmeister, & W. M. Tscharnuter, NATO Advanced Science Institutes (ASI) Series C, 417, 1
In the text
-
Blaes, O. M., & Balbus, S. A. 1994, ApJ, 421, 163
In the text
NASA ADS
-
Cameron, A. G. W. 1985, in Protostars & planets II, ed. D.C. Black, & M. S. Matthews (Univ. Arizona Press, Tucson), 1073
In the text
-
Cassen, P. M. 1996, Meteorit. Planet. Sci., 31, 793
In the text
-
Del Popolo, A., Gambera, M., & Bihal Ercan, E. 2001, MNRAS (submitted)
In the text
-
Dubrulle, B. 1993, Icarus, 106, 59
NASA ADS
-
Frank, J. F., King, A. R., & Raine, D. J. 1985, in Accretion Power in Astrophysics (Cambridge Univ. Press), 77
-
Goldreich, P., & Ward, W. R. 1973, ApJ, 183, 1051
In the text
NASA ADS
-
Greenberg, R., Wacker, J. F., Hartmann, J. F., & Chapman, C. R. 1978,
Icarus, 35, 1
In the text
NASA ADS
-
Kaula, W. M. 1979, Icarus, 40, 262
In the text
NASA ADS
-
Lin, D. N. C., & Papaloizou, J. C. B. 1980, MNRAS, 191, 37
In the text
NASA ADS
-
Morfill, G. E. 1985, in Birth and Infancy of Stars, ed. R. Lucas, A. Omont,
& R. Stora (Elsevier Science Publishers), 693
In the text
-
Nakagawa, Y., Hayashi, C., & Nakazawa, K. 1983, Icarus, 54, 361
In the text
NASA ADS
-
Rozyczka, M. 1985, A&A, 143, 59
NASA ADS
-
Ruden, S. P., & Pollack, J. B. 1991, ApJ, 375, 740
In the text
NASA ADS
-
Safranov, V. S. 1968, in Evolution of the Protoplanetary Cloud and
the Formation of the Earth and Planets (Nauka Press, Moscow)
-
Schmitt, W., Henning, T., & Mucha, R. 1997, A&A, 325, 569
In the text
NASA ADS
-
Shakura, N. J., Sunyaev, R. A., & Zilitinkevich, S. S. 1978, A&A, 62, 179
In the text
NASA ADS
-
Stepinski, T. F., & Valageas, P. 1996, A&A, 309, 301
In the text
NASA ADS
-
Stepinski, T. F., & Valageas, P. 1997, A&A, 319, 1007
In the text
NASA ADS
-
Stepinski, T. F. 1998a, ApJ, 507, 361
In the text
NASA ADS
-
Stepinski, T. F. 1998b, Icarus, 132, 100
In the text
NASA ADS
-
Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753
In the text
NASA ADS
-
van Albada, G. D., van Leer, B., & Roberts, W. W. 1982, A&A 108, 76
In the text
NASA ADS
-
van Leer, B. 1977, J. Comp. Phys., 23, 276
In the text
NASA ADS
-
Ward, W. R. 1997, Icarus, 126, 261
In the text
NASA ADS
-
Weidenschilling, S. J. 1977, Ap&SS, 51, 153
In the text
NASA ADS
-
Weidenschilling, S. J. 1980, Icarus, 44, 172
In the text
NASA ADS
-
Weidenschilling, S. J., & Cuzzi, J. N. 1993, in Protostars &
Planets III, ed. E. H. Levy, & J. I. Lunine (Univ. of Arizona
Press, Tucson), 1031
In the text
-
Wetherill, G. W. 1980, ARA&A, 18, 77
In the text
NASA ADS
Copyright ESO 2001
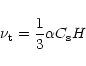
![\begin{displaymath}\frac{\partial \Sigma}{\partial t} - \frac{3}{r} \frac{\parti...
...c{\partial}{\partial r} (r^{1/2} \nu_{\rm t} \Sigma)\right]=0.
\end{displaymath}](/articles/aa/full/2001/40/aa1537/img18.gif)
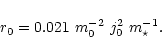
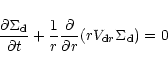
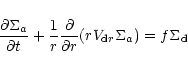
![\begin{displaymath}V_{{\rm d}r}= V_{\rm k} { {\left [\Delta \Lambda + {V_r\over V_{\rm k}}\right ]}\over {1+\Lambda^2} }\cdot
\end{displaymath}](/articles/aa/full/2001/40/aa1537/img38.gif)
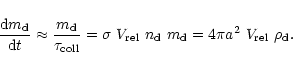
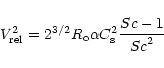
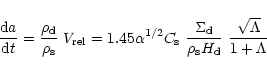
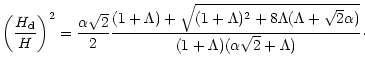
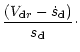
![\begin{figure}
\par\includegraphics[width=14cm,clip]{KSM1537f1.eps}
\end{figure}](/articles/aa/full/2001/40/aa1537/Timg115.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{KSM1537f2.eps}
\end{figure}](/articles/aa/full/2001/40/aa1537/Timg127.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{KSM1537f3.eps}
\end{figure}](/articles/aa/full/2001/40/aa1537/Timg129.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{KSM1537f4.eps}
\end{figure}](/articles/aa/full/2001/40/aa1537/Timg138.gif)