1 - Astronomical Observatory, Jagiellonian University, Kraków, Poland
2 - Max-Planck-Institut für Radioastronomie, Bonn, Germany
3 - Observatoire de Paris, DAEC and UMR 8631, CNRS and Université Paris 7, Meudon, France

Abstract
By observing the interacting galaxy NGC 3627 in radio polarization we try to answer the question; to which degree does the magnetic field follow the galactic gas flow. We obtained total power and polarized intensity maps at 8.46 GHz and 4.85 GHz using the VLA in its compact D-configuration. In order to overcome the zero-spacing problems, the interferometric data were combined with single-dish measurements obtained with the Effelsberg 100-m radio telescope. The observed magnetic field structure in NGC 3627 suggests that two field components are superposed. One component smoothly fills the interarm space and shows up also in the outermost disk regions, the other component follows a symmetric S-shaped structure. In the western disk the latter component is well aligned with an optical dust lane, following a bend which is possibly caused by external interactions. However, in the SE disk the magnetic field crosses a heavy dust lane segment, apparently being insensitive to strong density-wave effects. We suggest that the magnetic field is decoupled from the gas by high turbulent diffusion, in agreement with the large H I line width in this region. We discuss in detail the possible influence of compression effects and non-axisymmetric gas flows on the general magnetic field asymmetries in NGC 3627. On the basis of the Faraday rotation distribution we also suggest the existence of a large ionized halo around this galaxy.

Key words: galaxies: magnetic fields - galaxies: interacting - galaxies: individual: NGC 3627 - radio continuum: galaxies

A crucial question in the physics of galactic magnetic fields is whether the field only passively follows the gas flows or whether it can develop its own structures driven by small-scale turbulent processes (e.g. Donner & Brandenburg 1990; Beck et al. 1996; Moss 2000). The first possibility implies that the magnetic diffusion is very low and the magnetic field remains perfectly frozen into the gas, following precisely its motions. In the second case, substantial turbulent diffusion (several orders of magnitude higher than the Ohmic diffusion) must exist, allowing large-scale field structures to be built from small-scale perturbations caused by turbulent gas motions. Observations of normal spirals do not provide a clear discrimination between these two possibilities. Most of the spiral galaxies show regular magnetic fields with a strong radial component (Beck et al. 1996) resisting the differential rotation shear, which indicates a loose connection of the magnetic field to the gas. In this case the radial field component would be produced by the dynamo mechanism (Beck et al. 1996), without any need of density wave flows (see Knapik et al. 2000). On the other hand, Neininger & Horellou (1996) identified in M 51 a magnetic field component clearly associated with local compression effects (traced by heavy dust lanes) as expected for a frozen-in magnetic field. Even more pronounced association of magnetic fields with large-scale gas flows was found by Beck et al. (1999) in the strongly barred galaxy NGC 1097, in which the orientation of the magnetic field shows rapid changes, as expected for a large-scale bar-induced shock. However, the fact that the field lines are bending some 1 kpc upstream of the suspected location of the shock in the bar remains inexplicable in terms of classical MHD models.

In normal, symmetric spirals the dynamo process produces a spiral-like magnetic field with a pitch angle similar to that of the spiral arms, thus almost parallel to the density wave shocks making their effects upon the field structure very difficult to observe. For this reason we performed a two-frequency high-resolution study of NGC 3627, an Sb galaxy with a peculiar, asymmetric spiral structure, interacting tidally within the Leo Triplet group and suspected to have also a perturbed velocity field (see e.g. Haynes et al. 1979). The galaxy is described in more detail in our earlier low-resolution study of this object (Soida et al. 1999). It shows a bar and two asymmetric spiral arms with strong density wave effects. While the western arm is accompanied by weak traces of star formation, the eastern arm contains a straight actively star-forming segment in its inner part (see Fig. 3). NGC 3627 possesses X-ray properties of a galaxy with a recent starburst (Dahlem et al. 1996), but its far-infrared emission (more sensitive to the actual content of young stars) is similar to that of normal spirals (Hughes et al. 1991). Our previous study clearly revealed the existence of a widespread interarm regular field in addition to possible field compression effects. Here we discuss in detail the magnetic field structure in NGC 3627 with a beam size six times smaller than in our previous work. The use of two frequencies enables to determine the Faraday rotation distribution from which the global magnetic field structure may be derived.

2 Observations and data reduction

The observations of total power and linearly polarized radio emission from NGC 3627 were performed in November 1997 at 8.46 GHz and 4.85 GHz using the Very Large Array (VLA) of the National Radio Astronomy Observatory (NRAO). The most compact D-array configuration was used. The total observation time (including calibration) was 14 hours at 8.46 GHz and 10 hours at 4.85 GHz.

The intensity scale was calibrated by observing 3C 286, adopting the flux densities of Baars et al. (1977). The position angle of the linearly polarized emission was calibrated using the same source with an assumed position angle of 33 $\hbox{$^\circ$ }$ . The phase calibrator 1117+146 was used to determine the telescope phases and the instrumental polarization. To check these calibration procedures 3C 138 was observed once each day.

The data reduction has been performed using the AIPS data reduction package. The edited and calibrated visibility data were Fourier transformed to obtain the maps of Stokes parameters I, Qand U at both frequencies. The maps, uniformly weighted (with $\rm ROBUST=0$ ) to obtain the best resolution and sensitivity compromise, have a synthesized beam with half-power width (HPBW) of 11 $\hbox {$^{\prime \prime }$ }$ and 13 $\hbox{$.\!\!^{\prime\prime}$ }$ 5 at 8.46 GHz and 4.85 GHz, respectively. Naturally weighted maps at 8.46 GHz with a resolution (after a slight convolution) identical to that at 4.85 GHz (13 $\hbox{$.\!\!^{\prime\prime}$ }$ 5) were also obtained. The Q and U maps were combined to get distributions of the linearly polarized emission (corrected for the positive zero level offset) and of the position angle of the magnetic vectors ( $\vec{B}$ -vectors).

To increase the sensitivity to extended structures we combined the data at 8.46 GHz with our earlier observations at 10.55 GHz made with the 100 m Effelsberg radio telescope (Soida et al. 1999). The brightness values at 10.55 GHz were rescaled to 8.46 GHz assuming a spectral index of 0.64. At 4.85 GHz we performed new observations with the Effelsberg telescope. We obtained 11 azimuth-elevation maps of NGC 3627, then combined into the distributions of Stokes parameters I, U and Q. They were merged with our VLA maps. At both frequencies we recovered about 10% of the total power flux and about 5% polarized flux lost due to the missing zero-spacing effect.

Faraday rotation measures in NGC 3627 scarcely exceed 150 rad/m² (see Fig. 8) which corresponds to a polarization angle offset of $4\hbox{$^\circ$ }$ between 10.55 GHz and 8.46 GHz. The highest RM values coincide with localized peaks of polarized intensity where the combination of Effelsberg and VLA data adds little extended emission. Moreover, adding the single dish data increased the integrated polarized flux only by some 5%. For these reasons the Faraday rotation between the discussed frequencies has no effect upon the process of combining VLA and Effelsberg polarization maps.

3 Results

3.1 Total power emission

The total power map at 8.46 GHz at the resolution of 11 $^{\prime \prime }$ clearly shows two emission components: an S-shaped ridge associated with spiral arms and the bar as well as more diffuse interarm emission (Fig. 1). In both halves (NW and SE) of the bar the inner bright ridge is displaced towards the leading edges with respect to rotation. On the eastern disk side the total power ridge runs parallel to the heavy dust lane and to the star-forming, H $\alpha$ -bright chain (Figs. 2 and 3), visible also in the distribution of CO and dust (Reuter et al. 1996; Sievers et al. 1994). The total power ridge running along the western arm coincides with both the chain of H II regions (Fig. 3) and the dust lane (Fig. 2). Its localized maxima only partly correspond to individual H $\alpha$ peaks. Bright total power peaks also coincide with the galaxy centre, the bar ends, with a large H II complex in the southern disk at RA $_{2000}=11^{\rm h} 20^{\rm m} 16^{\rm s}$ Dec $_{2000}=+12\hbox{$^\circ$ }57\hbox{$^\prime$ }45\hbox{$^{\prime\prime}$ }$ and with another star-forming clump at the southern tip of the western arm. A very steep brightness gradient occurs at both frequencies along the NW disk boundary, despite the high sensitivity of the map at 4.86 GHz, showing well the diffuse emission in the eastern disk outskirts, including extensions to the north and NE.

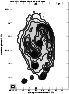$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F01.eps}}\end{figure}$	Figure 1: The combined VLA and Effelsberg total power map of NGC 3627 at 8.46 GHz with uniform weighting providing the highest resolution of 11 $\hbox {$^{\prime \prime }$ }$ (contours and greyscale). The contour levels are (3, 5, 10, 15, 20, 30, 70, 100, 150 200)*27 $\mu$ Jy/b.a.
Open with DEXTER

$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F02.eps}}\end{figure}$	Figure 2: The combined VLA and Effelsberg total power map of NGC 3627 at 8.46 GHz with a natural weighting (resolution 13 $\hbox{$.\!\!^{\prime\prime}$ }$ 5) superimposed on the optical image from Arp (1966). The contour levels are (3, 5, 10, 15, 20, 30, 50, 70, 100, 150, 200, 350, 600, 900)*12 $\mu$ Jy/b.a. The map resolution is $13\hbox{$.\!\!^{\prime\prime}$ }$ 5.
Open with DEXTER

$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F03.eps}}\end{figure}$	Figure 3: The combined VLA and Effelsberg total power map of NGC 3627 at 4.85 GHz superimposed upon the H $\alpha$ image from Smith et al. (1994). The contour levels are: (3, 5, 10, 15, 20, 30, 50, 70, 100, 150, 200, 350, 600, 900)*20 $\mu$ Jy/b.a. The resolution is 13 $\hbox{$.\!\!^{\prime\prime}$ }$ 5.
Open with DEXTER

The spectral index distribution over the disk of NGC 3627 is shown in Fig. 4. Apart from some strong variations close to the disk edges, caused partly by a still remaining slight zero-spacing problem, the spectral index $\alpha$ flattens to some 0.5-0.6 ( $S \propto \nu^{-\alpha}$ ) in star-forming regions at the bar ends and in the star-forming chain in the eastern disk. A particular flattening to 0.3-0.4 is observed at the position of the southern star-forming complex at RA $_{2000}=11^{\rm h} 20^{\rm m} 16^{\rm s}$ Dec $_{2000}=+12\hbox{$^\circ$ }57\hbox{$^\prime$ }45\hbox{$^{\prime\prime}$ }$ and at the southern end of the western arm. The spectral index in the inner disk is about 0.7-0.8 and the same values are found along the western total power ridge with only slight flattening (to some 0.68) at the positions of H II regions. A significant steepening to about 1.0-1.1 occurs in the interarm region SW of the centre.

$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F04.eps}}\end{figure}$	Figure 4: The distribution of spectral index between 8.46 GHz and 4.85 GHz in the disk of NGC 3627 at a resolution of 13 $\hbox{$.\!\!^{\prime\prime}$ }$ 5. The contour levels are (1, 2, 3, 4...)*0.1. Numbers inside the Figure show the values of spectral index in selected regions of spectral flattening.
Open with DEXTER

3.2 Polarization

The brightest polarized features at 8.46 GHz (Fig. 5) are found in the western disk and northeast of the nucleus. A very bright polarized peak is located in the middle portion of the western dust lane. The polarized intensity makes an S-shaped ridge with $\vec{B}$ -vectors aligned along it. In the western disk the polarized ridge crosses the mentioned bright peak of polarized intensity and extends further southwards along the western dust lane. In addition, broad polarized features fill the interarm space in the NE and SW disk (as suggested by Soida et al. 1999). The polarization in the SW interarm region is contaminated by extensions from the discussed bright polarized peak in the western spiral arm.

$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F05.eps}}\end{figure}$

Figure 5: The contours and greyscale of polarized intensity of NGC 3627 at 8.46 GHz with $\vec{B}$ -vectors of length proportional to the polarization degree at the resolution of $11\hbox {$^{\prime \prime }$ }$ . The contour levels are (3, 5, 8, 13, 21)*8 $\mu$ Jy/b.a. Apparent $\vec{B}$ -vectors without correction for Faraday rotation are plotted. A polarization vector equal to $1\hbox {$^\prime $ }$ length corresponds to a polarization degree of 60%. A white cross denotes the optical disk centre.

Open with DEXTER

In the western disk the $\vec{B}$ -vectors at 8.46 GHz run parallel to the dust lane (Fig. 6), but in the interarm region they make a smooth transition to the eastern arm. However, in the vicinity of RA $_{2000}=11^{\rm h} 20^{\rm m} 13\hbox{$.\!\!^{\rm s}$ }2$ Dec $_{2000}=+13\hbox{$^\circ$ } 00\hbox{$^\prime$ }$ the $\vec{B}$ -vectors in the S-shaped feature (above this position) and in the interarm region (below this position) have orientations differing by about $90\hbox{$^\circ$ }$ . This occurs some $11\hbox {$^{\prime \prime }$ }$ (a full beam size) south of the dust lane and cannot result from pure resolution effects. It also gives rise to beam depolarization causing the unpolarized "hole'' at the indicated position. The difference in position angles between the interarm region and the S-shaped feature becomes even more impressive after deprojection to the face-on view (Fig. 10). In the eastern disk, the S-shaped ridge and the $\vec{B}$ -vector orientations run across the optical arm and a heavy dust lane at a high angle. This is rarely observed in normal galaxies until now. The $\vec{B}$ -vectors in this "magnetic arm'' also meet at right angles with the interarm vectors, which corresponds to a depolarized region observed at low resolution by Soida et al. (1999).

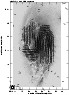$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F06.eps}}\end{figure}$	Figure 6: The $\vec{B}$ -vectors of length proportional to polarized intensity of NGC 3627 at 8.46 GHz superimposed onto the optical image by Arp (1966). A vector length of 10 $^{\prime \prime }$ corresponds to a polarized intensity of 50 $\mu$ Jy/b.a. The orientations of vectors have been corrected for Faraday rotation effects. The map resolution is $11\hbox {$^{\prime \prime }$ }$ .
Open with DEXTER

$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F07.eps}}\end{figure}$

Figure 7: The contours and greyplot of the polarized emission from NGC 3627 at 4.86 GHz (resolution of $13\hbox{$.\!\!^{\prime\prime}$ }$ 5) with superimposed vectors of polarization degree. The combined VLA and Effelsberg map is used. The contour levels are (3, 5, 8, 13, 21)*10 $\mu$ Jy/b.a. A polarization vector equal to $1\hbox {$^\prime $ }$ length corresponds to the polarization degree of 60%.

Open with DEXTER

The more sensitive polarization map at 4.85 GHz (Fig. 7) reveals a regular spiral structure in the outer disk of NGC 3627. This is visible along both the western (north and south of RA $_{2000}=11^{\rm h} 20^{\rm m} 11^{\rm s}$ Dec $_{2000}=+12\hbox{$^\circ$ }59\hbox{$^\prime$ }$ ) and eastern (around RA $_{2000}=11^{\rm h} 20^{\rm m} 20^{\rm s}$ Dec $_{2000}=+13\hbox{$^\circ$ } 00\hbox{$^\prime$ }$ ) disk boundary where the $\vec{B}$ -vectors form a regular spiral structure considerably inclined with respect to adjacent dust lanes. The polarized region in the SE disk (RA $_{2000}=11^{\rm h} 20^{\rm m} 20^{\rm s}$ Dec $_{2000}=+12\hbox{$^\circ$ }57\hbox{$^\prime$ }45\hbox{$^{\prime\prime}$ }$ ) with magnetic vectors bent outwards was found to extend beyond the optical image (compare Figs. 7 and 6). It is particularly well visible when single-dish Effelsberg data are added.

3.3 Faraday rotation

$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F08.eps}}\end{figure}$	Figure 8: The distribution of Faraday rotation between 8.46 GHz and 4.85 GHz in the disk of NGC 3627 presented in the form of symbols with sizes corresponding to particular RM ranges (see the Figure legend). At both frequencies maps with a resolution of 13 $\hbox{$.\!\!^{\prime\prime}$ }$ 5 were used. The greyscale plot shows the RM errors due to noise.
Open with DEXTER

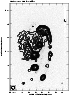$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1357F09.eps}}\end{figure}$	Figure 9: The overlay of the map of thermal flux at 8.46 GHz obtained under the assumption of a constant nonthermal spectral index of 0.9, onto the H $\alpha$ image from Smith et al. (1994). The contour levels are (2, 5, 8, 12, 20, 30, 50, 100)*20 $\mu$ Jy/b.a.
Open with DEXTER

The map of Faraday rotation measures (RM) between 8.46 GHz and 4.85 GHz is shown in Fig. 8. A foreground Faraday rotation correction of 50 rad/m² has been applied as a best guess between values for that region given by Simard-Normandin & Kronberg (1980) and the mean RM for the whole disk of NGC 3627. Regions of large positive RM (>150 rad/m²) were found close to the star-forming region in the northern bar portion and in the interarm region in the SW disk. Large negative RMs (absolute values in excess of 150 rad/m²) extend between the southern bar end and the H II complex at RA $_{2000}=11^{\rm h} 20^{\rm m} 16^{\rm s}$ Dec $_{2000}=+12\hbox{$^\circ$ }57\hbox{$^\prime$ }45\hbox{$^{\prime\prime}$ }$ . They also are present in the SW disk where a sudden change of RM signs takes place. Apart from that the Faraday rotation measures are generally small, scarcely exceeding $\pm 50$ rad/m². They are changing sign along spiral arms over regions several kpc in size, not providing any clear picture of a single global magnetic field symmetry. The "magnetic arm'' crossing the optical dust lane in the eastern disk also shows the reversal of RM sign.

4 Discussion

4.1 Thermal and nonthermal emission

The radio spectrum of a given region of the galactic disk results from a combination of diffuse emission from nonthermal electrons filling the whole disk, nonthermal emission from young supernova remnants (SNR), and free-free emission from the ionized gas, both usually concentrated along the spiral arms. The spectrum of the diffuse component is determined by the balance between the propagation effects and synchrotron losses (Lerche & Schlickeiser 1981), it is usually assumed to vary little across the disk (van der Kruit 1977; Hummel & Gräve 1990; Ehle & Beck 1993). The bright total power peaks correspond well to maxima visible in the H $\alpha$ map (Fig. 3).

According to the above we interpret the spectral flattening in the total power peaks as being due to an increased fraction of thermal emission mixed with contributions from young SNR's, which is usually several times smaller than that from the free-free emission (Urbanik 1987). Assuming a mean nonthermal spectral index of 0.9 (the mean value in the NE disk, away from star-forming complexes) and neglecting the SNR contribution, the thermal fraction $f_{\rm th}$ at 8.46 GHz is about 40% in the bar ends and $\simeq$ 60% in the southern star-forming complex mentioned in Sect. 3.1. There is a very good correspondence between the thermal brightness derived from the spectrum and the distribution of H $\alpha$ emission (Fig. 9).

The knowledge of nonthermal intensity enables us to estimate the magnetic field strength in specific regions of NGC 3627. We assumed a nonthermal spectral index of 0.9, a face-on nonthermal disk thickness of 2 kpc, a lower electron energy cutoff at 300 MeV and a proton-to-electron ratio of 100. The errors of the field strength include the uncertainty in the last three quantities of a factor of 2. We computed pressure-balance magnetic field strengths constituting the minimum field strength below which the mixture of cosmic rays and magnetic field becomes unstable. For the mean magnetic field inside the contour level of $90\mu$ Jy/b.a. (1% of the maximum brightness) we obtained $11\pm 2~\mu$ G for the total field. From the polarized intensity in this area we found $4\pm 1~\mu$ G for the regular magnetic field. For the interarm regions we obtained: $10\pm 3~\mu$ G for the NE and $10\pm 2~\mu$ G for the SW interarm regions. We also computed the mean pressure-balance magnetic field strengths averaged along the spiral arms. Along the western arm we obtained $11\pm 3~\mu$ G and along the eastern arm $12\pm 3~\mu$ G, again with no significant difference. For the regular fields we obtained $5\pm 1~\mu$ G for the western arm and $4\pm 1~\mu$ G for the eastern one thus a marginally stronger pressure balance regular field in the western arm. We note, however, that these values represent the minimum field strength ensuring its stable configuration for a given synchrotron brightness. While this is probably valid on average in the disk, the magnetic field may be stronger in specific regions than expected from pressure balance, without causing a stability problem.

We verified our estimates by predicting a Faraday rotation in the region around RA $_{2000}=11^{\rm h} 20^{\rm m} 12\hbox{$.\!\!^{\rm s}$ }6$ Dec $_{2000}=+13\hbox{$^\circ$ }00\hbox{$^\prime$ }16\hbox{$^{\prime\prime}$ }$ , where the regular field runs along the minor axis, mostly parallel to the line of sight. The measured RM in this area is measured $130\pm 16$ rad/m² while its thermal brightness is 0.48 mJy/b.a. To reproduce consistently these values we assumed that 20% of thermal emission originates in the diffuse gas responsible for Faraday effects (Walterbos & Braun 1994) which has a face-on full thickness of 1400 pc (Fletcher et al. in prep.). We obtained a filling factor of the diffuse gas of 0.025, thus similar to the value suggested for the Milky Way by Fletcher et al. (in prep.), implying a peak electron density $n_0\approx 1.1$ cm^-3corresponding to a mean electron density along the line of sight of 0.03 cm^-3. This is comparable to the value usually adopted for our Galaxy.

4.2 Compression effects of the gas and magnetic field

The western total power ridge has a typical nonthermal spectrum. Under the above assumption the mean thermal fraction at 8.46 GHz and its rms variation along the ridge is $9\pm 5\%$ . It also has a counterpart in the polarized emission and we can largely attribute it to effects of magnetic field enhancement in the dust lane. The same is true for the total power bridge crossing the centre of NGC 3627, whose distortion toward the leading bar edges is suggestive for compression effects on the front side of the bar (e.g. Patsis & Athanassoula 2000). We also see some polarized emission extending beyond the northern bar end, to the side opposite of the arm, resembling the "T-regions'' discussed by Patsis & Athanassoula (2000).

The western disk boundary shows some signs of gas and magnetic field compression by external influences. We note a steep total power gradient and a bright polarized peak in the western disk. There is another (weaker) polarization peak just adjacent to the nucleus (Fig. 5), it is probably associated with compression by shocks occurring in the central part of the bar. This has been observed in barred spirals (Beck et al. 1999) while a very bright, elongated polarized area on one side of the galaxy is rather uncommon. It is coincident with a "pushed inwards'' segment of the dust lane at an azimuth angle of 280 $^\circ$ , $\ln(r)\approx 0.4$ (Fig. 11), followed by a similar deviation of magnetic pitch angles, it is also accompanied by a steep H I density gradient along the western disk side discussed by Haynes et al. (1979).

We note that the SW disk region (west and south of the nucleus) has a mean nonthermal brightness by about 10% higher than the NE disk while its mean star formation level (as measured by a thermal flux) is about 3 times lower. The western disk portion may thus have the magnetic field relative to its star formation level considerably stronger than the eastern one. This is suggestive for some external field enhancement (e.g. by compression).

All these phenomena occurring together may constitute a signature of compression effects, possibly caused by the encounter with the gas tidally stripped during interactions with NGC 3628 (see e.g. numerical models by Rots 1978). However, a simple picture of gas and magnetic field compression does not explain large magnetic pitch angles observed westwards of the western dust lane (upstream of a possible flow, north and south of RA $_{2000}=10^{\rm h} 22^{\rm m} 10^{\rm s}$ Dec $_{2000}=+12\hbox{$^\circ$ }59\hbox{$^\prime$ }$ , see Fig. 7). The magnetic pitch angles are considerably greater than those of the adjacent dust lane. A better explanation may involve the magnetic field connected to dense gas in the western dust lane detected in CO by Reuter et al. (1996). In the warmer medium outside the lane the pitch angle could be determined by the dynamo process while the dust lane formation (distorted by the gas infall) locally aligns the magnetic field with the lane. A detailed test will be possible once the kinematical properties of various gas phases with a few arcsec resolution are known.

$\begin{figure} \par\resizebox{12cm}{!}{\includegraphics{MS1357F10.eps}}\parbox[b]{55mm}{ } \end{figure}$	Figure 10: The orientation of $\vec{B}$ -vectors of polarized intensity at 8.46 GHz compared to the optical image of Arp (1966), rectified to the face-on position (resolution of $11\hbox {$^{\prime \prime }$ }$ ).
Open with DEXTER

4.3 Two magnetic field components in NGC 3627?

The polarized component associated with the bar and spiral arm forms an S-shaped polarized ridge which is quite symmetric in the inner part (Figs. 10 and 11). At larger radii its western part follows the "pushed-in'' western arm and its sharply bending outer segment. The eastern portion preserves a constant large pitch angle, remaining insensitive to any effects of the gas compression. The latter property is uncommon among normal spirals in which the magnetic field is usually parallel to the dust lanes. Another known example of a magnetic arm crossing the optical one is NGC 2997 (Han et al. 1999). Apparently, the gas flow in the bar generates its own magnetic field component, which reacts in a different way to the compression effects in the NW and in SE spiral arm segments. Zhang et al. (1993) observing the H I motions at the resolution of $19\hbox{$^{\prime\prime}$ }$ noted a kinematical difference between these regions. While the region of the northern bar end and the NE arm segment shows a rather regular velocity field, strong gas motion perturbations occur in the SE disk which are also visible in the CO map by Reuter et al. 1996. We note the counter-rotating plume found there by Haynes et al. (1979) east of RA $_{2000}=11^{\rm h} 20^{\rm m} 20^{\rm s}$ Dec $_{2000}=+12\hbox{$^\circ$ }59\hbox{$^\prime$ }$ . The H I line observed by Zhang et al. (1993) is considerably broader there as well. We may speculate that an increased turbulent activity (due e.g. to violent, interaction-induced shearing gas motions) gives rise to much larger turbulent diffusion and much weaker coupling of magnetic field to the gas than in the more quiet NW arm segment. Such a "decoupling'' has also been obtained by Elstner et al. (2000) in the MHD model with an increased turbulent diffusion in spiral arms. This effect may also occur in case of cold, dense gas. Even in case of a low ionization level the magnetic field may still be tied to the molecular matter due to efficient collisions between ions and neutral atoms, still yielding a low diffusion coefficient. In the SE region of NGC 3627 an increased turbulent diffusion may liberate the magnetic field from the cold gas which forms the prominent dust lane segment. An alternative possibility that the magnetic field remains tied to the gas but the peculiar SE part of the S-shaped structure is strongly bent away from the plane of NGC 3627, running high above the dust lane has to be considered, too.

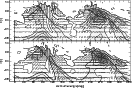$\begin{figure} \par\resizebox{11.5cm}{!}{\includegraphics{MS1357F11.eps}} { } \end{figure}$

Figure 11: The distribution of polarized intensity and $\vec{B}$ -vector orientations at 4.85 GHz (upper panel) and at 8.46 GHz (lower panel) in the frame of azimuthal angle in the disk and $\ln(r)$ . The azimuthal angle runs anticlockwise from the southern major axis end. The maps at the resolution of $13\hbox{$.\!\!^{\prime\prime}$ }$ 5 were used. Thick lines denote the optically visible dust lanes.

Open with DEXTER

There are arguments in support of both possibilities. Assuming that the peculiar arm is in the plane would imply a high Faraday rotation, as the magnetic field would be mostly parallel to the line of sight while the underlying star-forming region supplies enough ionized gas. The problem would disappear if the magnetic arm were bent strongly out of plane making the regular field almost perpendicular to the line of sight. One of most recent determinations of the distance to NGC 3627 is 11.9 kpc (Ryan & Visvanathan 1989). If the polarized arm were inclined to the plane only by $30\hbox{$^\circ$ }$ , its eastern part would deviate by more than 2.5 kpc from the disk plane. Additionally the gas density (hence Faraday rotation) would be small there. On the other hand, its polarized synchrotron brightness is the same as that of its NW counterpart (Fig. 5) which raises some problems with supplying cosmic ray electrons to such a height above the disk. In NGC 5775, showing cosmic ray streaming along regular fields highly inclined to the plane (Tüllmann et al. 2000) the polarized brightness at 4.86 GHz fades by a factor of 2.5-3 over the distance of 1.5 kpc from the plane. In NGC 3627 it decreases only by a factor of 0.7 over the length of the whole polarized arm, though we still cannot reject some ultra-fast cosmic-ray electron propagation along this feature. We note also that, if we assume the magnetic field strongly coupled to the gas, we need also to explain a complete lack of regular magnetic fields in a very strong SE dust lane segment. Projected to the sky plane at almost a right angle to the polarized arm it would strongly depolarize its middle portion, which is not the case (Fig. 5). Finally, we note that out to the radius of $1\hbox{$.\mkern-4mu^\prime$ }5$ the NW and SE parts of the S-shaped feature look very symmetric, both in the distribution of polarized intensity and in the orientation of polarization $\vec{B}$ -vectors (Fig. 11), which would need a very special geometry of an asymmetric structure, three-dimensionally bent out of the plane. A detailed discussion of the nature of this polarized arm requires data on gas kinematics of this region with arcsecond resolution.

The interarm magnetic field SW and NE of the centre (around RA $_{2000}=11^{\rm h} 20^{\rm m} 14\hbox{$.\!\!^{\rm s}$ }0$ Dec $_{2000}=+12\hbox{$^\circ$ }59\hbox{$^\prime$ }$ and RA $_{2000}=11^{\rm h} 20^{\rm m} 18\hbox{$.\!\!^{\rm s}$ }0$ Dec $_{2000}=+13\hbox{$^\circ$ } 00\hbox{$^\prime$ }$ ) apparently behaves in a way different from that associated with spiral arms. In the inner disk $(\ln(r)<0.4)$ the interarm field has an average pitch angle of $27\pm 2\hbox{$^\circ$ }$ in the eastern disk and $16 \pm 2\hbox{$^\circ$ }$ in the western interarm region. This is smaller than the pitch angle of $\approx$ 50 $\hbox{$^\circ$ }$ - $60\hbox{$^\circ$ }$ in the S-shaped component within the same galactocentric distance (Figs. 10 and 11). A strong difference in magnetic pitch angles between the bar/spiral and interarm fields is visible both in the NW and the SE disk at azimuthal angles of about $100\hbox{$^\circ$ }$ and 300 $^\circ$ . In the SE disk the region along which the $\vec{B}$ -vectors differ by $90\hbox{$^\circ$ }$ shows no association with the heavy dust lane. In the NW region the turning of $\vec{B}$ -vectors occurs some 1 kpc upstream of the lane. Some departures from the general rotation of the CO-emitting gas were found close to the eastern jump in the magnetic field direction (Reuter et al. 1996). However, because of limited resolution these residuals may be due to generally complex gas kinematics in this region (Zhang et al. 1993). No velocity perturbations are seen close to the NW magnetic field jump. There is no evidence for associations of sudden turns with any shock-like phenomena which would suggest that the S-shaped feature and the interarm field constitute the same magnetic field strongly distorted by density wave flows (e.g. Otmianowska-Mazur & Chiba (1995). We may speculate that rapid turns in the field direction may constitute intrinsic magnetic features at the interface of two physically distinct magnetic field components. One of them is associated with the bar and spiral arms while the second component is generated by the turbulent dynamo process acting in the interarm space, unperturbed by the density waves. Both SW and NE interarm regions contain some weak dust filaments too. However, in large regions around RA $_{2000}=11^{\rm h} 20^{\rm m} 14\hbox{$.\!\!^{\rm s}$ }0$ Dec $_{2000} = +12\hbox{$^\circ$ }58\hbox{$^\prime$ }30\hbox{$^{\prime\prime}$ }$ and RA $_{2000} = 11^{\rm h} 20^{\rm m} 17\hbox{$.\!\!^{\rm s}$ }0$ Dec $_{2000} = +13\hbox{$^\circ$ }00\hbox{$^\prime$ }45\hbox{$^{\prime\prime}$ }$ the $\vec{B}$ -vectors deviate by more than $30\hbox{$^\circ$ }$ from underlying dust structures. It is thus unlikely that the magnetic pitch angle in the interarm region is determined by local compression effects traced by the dust filaments.

We also note that the interarm magnetic pitch angles are somewhat greater in the eastern, uncompressed region (possibly containing a pulled-out gas, Haynes et al. 1979). This bears resemblance to some wind-swept galaxies like NGC 2276 (Hummel & Beck 1995) or NGC 4254 (Soida et al. 1996). Such a picture is suggestive for some global non-circular component of the gas motion in NGC 3627 oriented generally from the NW-W-SW directions towards the east, as indeed expected from the kinematic picture discussed by Haynes et al. (1979).

5 Summary and conclusions

We observed the Leo Triplet spiral NGC 3627 with the VLA D-array at 8.46 GHz and 4.85 GHz. The data were combined with the Effelsberg single-dish observations at 10.55 GHz and at 4.85 GHz to increase the sensitivity to extended structures. The following results were obtained:

Unusual magnetic fields in the interacting spiral NGC 3627

1 Introduction

2 Observations and data reduction

3 Results

3.1 Total power emission

3.2 Polarization

3.3 Faraday rotation

4 Discussion

4.1 Thermal and nonthermal emission

4.2 Compression effects of the gas and magnetic field

4.3 Two magnetic field components in NGC 3627?

5 Summary and conclusions

References