A&A 377, 955-963 (2001)
DOI: 10.1051/0004-6361:20011129
B. Deufel - C. P. Dullemond - H. C. Spruit
Max-Planck-Institut für Astrophysik, Karl-Schwarzschildstr. 1, 85740 Garching, Germany
Received 21 June 2001 / Accepted 8 August 2001
Abstract
We consider the interaction of a slowly rotating
unmagnetized neutron star with a hot (ion supported, ADAF) accretion
flow. The virialized protons of the ADAF penetrate into the neutron
star atmosphere, heating a surface layer. Detailed calculations are
presented of the equilibrium between heating by the protons,
electron thermal conduction, bremsstrahlung and multiple Compton
scattering in this layer. Its temperature is of the order 40-70 keV.
Its optical depth increases with the incident proton energy flux,
and is of the order unity for accretion at 10-2-10-1 of
the Eddington rate. At these rates, the X-ray spectrum produced by
the layer has a hard tail extending to 100 keV, and is similar to
the observed spectra of accreting neutron stars in their hard
states. The steep gradient at the base of the heated layer gives
rise to an excess of photons at the soft end of the spectrum
(compared to a blackbody) through an "inverse photosphere effect''.
The differences with respect to previous studies of similar problems
are discussed, they are due mostly to a more accurate treatment of
the proton penetration process and the vertical structure of the
heated layer.
Key words: accretion, accretion disks - radiative transfer - stars: neutron - X-rays: stars
The spherical accretion of matter onto the surface of an unmagnetized neutron star (NS) has attracted much attention since Zel'dovich & Shakura (1969) [henceforce ZS69] first addressed this problem more than thirty years ago. As a model for the then newly discovered X-ray stars, these authors considered a neutron star whose surface was heated by radially infalling gas, and modeled this gas as consisting of freely falling ions. A hot X-ray emitting layer is formed, the temperature of which depends on the penetration depth of the protons into the atmosphere of the star. The model could reproduce the observed hard X-rays, but was eclipsed by accretion disk models once it was realized that accretion is not radial because of the angular momentum constraint. The disk model, however, only explains the sub-keV part of NS spectra, somewhat in contradiction with observed spectra. In addition to the optically thick disk, an additional source of hot gas thus had to be found to produce the hard X-rays. This was proposed in the form of the so-called two-temperature accretion flows (Shapiro et al. 1976; Ichimaru 1977; Rees et al. 1982; Narayan & Yi 1994, 1995). In this form of accretion, now called ADAF, the flow is geometrically thick, supported by virialized protons, while the electrons stay at a lower temperature around 100 keV due to their high radiative energy losses and the low rate at which Coulomb interactions transfer accretion energy from the ions to the electrons. While it is not entirely clear at the moment how such a flow would originate from the cool disk present at larger distances from the star's surface, the observed hard X-ray component is often taken as an indication of its existence. If accretion near the star takes indeed place in the form of such a two-temperature plasma, the star's surface is exposed to protons with energies around 50 MeV, and the physics is very much like the model proposed by ZS69. It is therefore interesting to pick up this line of theory and revisit proton-injection models in context of NS-ADAF accretion.
In ZS69 the importance of the penetration depth of the accreted protons for the outcoming spectrum was recognized. The penetration length in terms of the amount of material required to stop the protons was estimated and used as a model parameter. The injected energy of the infalling protons per unit time and mass in the neutron star atmosphere was then uniformly distributed in this stopping layer. A second parameter of their model was the accretion rate (or luminosity). Their computed spectra essentially show a blackbody spectrum with a high-energy tail due to Comptonization in the heated atmosphere.
A more detailed numerical approach was presented by Alme & Wilson (1973). They introduced more physics into their model and also realized that the proton deceleration depends on the atmospheric temperature. They solved the atmospheric structure and the beam deceleration simultaneously in a time dependent evolution of the model. But they did not account for the strong dependence of proton deceleration on the local proton velocity and used an estimate only for the amount of material needed to stop the infalling protons. Their resulting spectra again show a blackbody plus an additional high energy tail.
Bildsten et al. (1992) were interested in the fate of the accreted CNO elements in the neutron star atmosphere. They assumed an isothermal atmosphere at a temperature defined by the accretion rate and the proton stopping depth. Again a similar estimate for the penetration depth of the ions was used.
The model of spherical accretion onto a neutron star was revisited by Turolla et al. (1994). They confirmed the existence of the formerly known "cold'' solutions (as in Alme & Wilson 1973). In addition to this, they also found "hot'' solutions for the same luminosities. But their work was limited by the fact that the spectrum was just described in terms of a mean photon energy.
Zane et al. (1998) confirmed the existence of the hot solutions with a much
more accurate treatment of the radiative processes including pair
processes. The emergent spectra of the hot solution should be
characterized by hard spectra peaking at ![]() 100 keV. Both
models use the stopping depth as a free input parameter.
The effect of thermal conduction was not included in these calculations.
100 keV. Both
models use the stopping depth as a free input parameter.
The effect of thermal conduction was not included in these calculations.
In continuation of this series of papers Zampieri et al. (1995)
presented solutions for neutron stars accreting at low rates,
i.e. with luminosities
![]() -
-
![]() . They showed that the deviations from a blackbody spectrum
with the effective temperature of the neutron star increase with
decreasing accretion luminosities.
. They showed that the deviations from a blackbody spectrum
with the effective temperature of the neutron star increase with
decreasing accretion luminosities.
Proton illumination is not only restricted to the accretion of matter onto the surface of a neutron star. Spruit (1997), Spruit & Haardt (2000) and Deufel & Spruit (2000) have shown that this process might also be of importance for accretion disks embedded in a hot corona. With an improved version of the code used in Deufel & Spruit (2000) we reconsider the accretion of matter onto the surface of a neutron star (i.e. ion illumination of a neutron star surface). The code now includes a better treatment of the radiative processes by including thermal emission due to bremsstrahlung. We also allow for energy redistribution due to electron thermal conduction within the atmosphere. The interaction between the accreted protons and the neutron star atmosphere and the radiative processes are computed time dependently in a one-dimensional, plane-parallel approximation. The density distribution through the atmosphere is found from hydrostatic equilibrium including the pressure from the penetrating ions.
In the following we give a complete description of our model. First the heating of the electrons via Coulomb interactions is presented. We show that the use of a stopping depth treated as a free parameter is not sufficiently accurate for the calculation of the proton stopping. The radiative processes are treated by solving the radiative transfer equation instead of the Monte Carlo method used before. This has advantages in terms of computation speed and the ability to treat layers of arbitrary absorption optical depth.
We consider protons in the vicinity of a neutron star of mass
![]() and radius
and radius ![]() .
In ADAF accretion the typical
energy of such protons at the surface of a neutron star is the virial
temperature,
.
In ADAF accretion the typical
energy of such protons at the surface of a neutron star is the virial
temperature,
If protons with such energies encounter a much a cooler and dense
medium, they will be stopped very efficiently by Coulomb interactions
with the cold electrons inside their Debye sphere. The stopping of a
fast particle in an ionized plasma was quantitatively discussed by
Spitzer (1962). In a time ![]() ,
such a proton with energy
,
such a proton with energy
![]() will loose an amount of energy
will loose an amount of energy ![]() ,
,
Now we can express the energy loss of a proton moving at an angle
![]() with respect to the vertical coordinate z, per unit of
vertical Thomson depth,
with respect to the vertical coordinate z, per unit of
vertical Thomson depth,
![]() ,
by
,
by
As mentioned in Sect. 1 the penetration depth
significantly influences the outcoming spectrum of the proton
illumination model. Usually a global estimate is used to calculate the
stopping depth of the protons in an atmosphere. The estimate for the
stopping length
![]() is obtained following
Spitzer (1962),
is obtained following
Spitzer (1962),
| Temperature |
||||||
|
|
1 | 10 | 100 | |||
| num | est | num | est | num | est | |
| 23 | 0.2 | 0.8 | 0.4 | 0.8 | 6.8 | 7.8 |
| 46 | 0.8 | 3.1 | 0.9 | 2.4 | 10.2 | 12.4 |
| 92 | 3.1 | 12.4 | 2.6 | 8.9 | 15.9 | 21.6 |
Table 1 gives some values for the estimated stopping depth [from Eq. (6)] and the calculated stopping depth [according to Eq. (4)] by following a penetrating proton through an isothermal electron layer until it has lost all of its energy in excess with respect to the ambient electrons. The estimated stopping depth is generally higher than the numerical result due to the reasons mentioned above. For low electron temperatures these discrepancies are quite conspicuous.
The stopped protons accumulate at their stopping depth in the neutron star atmosphere. To maintain charge neutrality, an equal number of electrons has to move to the same location. The ADAF electrons entering the disk are stopped over a much short distance, compared with the protons. To make them move to the location where the protons come to rest in the disk, an electric field has to develop in the neutron star atmosphere, such that the resulting electron current has just this property. We assume that such an equilibrium actually develops, on the grounds that any charge imbalance will quickly lead to the buildup of a strong restoring electric field.
Equation (4) is only valid for non-relativistic conditions,
whose validity needs to be checked for the high proton temperatures in
an ADAF. Analytic expressions for relativistic temperatures exist only
in special cases. Stepney (1983) has derived such an expression for
the rate of transfer of energy between populations with relativistic
Maxwellian distributions in terms of an integral over the scattering
cross-section. In the case of hot protons heating cooler electrons
the Rutherford cross-section is the relevant cross-section. An
expression in closed form for the heating rate (in ergs cm-3s-1) is given by Stepney & Guilbert (1983),
![\begin{displaymath}\times \left[{\displaystyle\frac{2(\theta_{\rm e}+\theta_{\rm...
...theta_{\rm p}}
{\theta_{\rm e}\theta_{\rm p}}}\right)\right],
\end{displaymath}](/articles/aa/full/2001/39/aah2960/img46.gif) |
(7) |
The proton-electron heating rate according to the stopping formula
derived from Spitzer's theory is given by
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2960_f1.ps}\end{figure}](/articles/aa/full/2001/39/aah2960/Timg50.gif) |
Figure 1: Energy loss rates of a hot thermal distribution of protons in a cooler ionized hydrogen plasma (with temperature indicated along the curves). Solid line: fully relativistic expression of Stepney & Guilbert (1983), dash-dotted line: the non relativistic expression from Spitzer's (1962) theory. Dashed line: Spitzer's formula, but averaged over a relativistic instead of a classical Maxwellian. Spitzer's treatment is accurate to better than 5% for proton temperatures <100 MeV. |
| Open with DEXTER | |
We compute the density distribution through our plane-parallel one dimensional model atmosphere from the equation of hydrostatic equilibrium,
We solve our pressure profile by starting with ![]() at the top
of our atmosphere and integrate Eq. (10) to the maximum
optical depth of our model atmosphere
at the top
of our atmosphere and integrate Eq. (10) to the maximum
optical depth of our model atmosphere
![]() .
We usually set
.
We usually set
![]() .
At this optical depth the energy flux of the
protons is already negligible.
.
At this optical depth the energy flux of the
protons is already negligible.
The protons from the ADAF have a temperature of the order of the
virial temperature [Eq. (1)]. As mentioned above we use a
Maxwell distribution for the proton velocities. Additionally, the
ADAF has a rotation rate, which is somewhat smaller than the Keplerian
rate
![]() (e.g. Narayan & Yi 1995). When computing the
penetration of the protons we take the Maxwellian velocity component
of the protons. Further we take into account the component
of velocity tangential to the neutron star surface due to the ADAF
rotation. Instead of using a detailed model of an ADAF in which these
velocity components can in principle be determined quantitatively, we
model it with a temperature
(e.g. Narayan & Yi 1995). When computing the
penetration of the protons we take the Maxwellian velocity component
of the protons. Further we take into account the component
of velocity tangential to the neutron star surface due to the ADAF
rotation. Instead of using a detailed model of an ADAF in which these
velocity components can in principle be determined quantitatively, we
model it with a temperature
![]() and tangential
velocity
and tangential
velocity
![]() ,
i.e. we use the parameters
,
i.e. we use the parameters ![]() and
and ![]() to scale these quantities. Both the tangential and vertical
velocity components add to the energy deposited, but are not
equivalent since the thickness of the heated layer is smaller the more
the protons enter tangentially.
to scale these quantities. Both the tangential and vertical
velocity components add to the energy deposited, but are not
equivalent since the thickness of the heated layer is smaller the more
the protons enter tangentially.
The radiative transfer equation appropriate for our model is
The bremsstrahlung absorption coefficient
![]() is
given by
is
given by
The bremsstrahlung emission
![]() is given by
is given by
Whenever the temperatures of our solutions are low enough,
![]() ,
we can simplify the Compton emissivity
Eq. (15) without compromising accuracy. We
introduce the angle-averaged Compton cross section
,
we can simplify the Compton emissivity
Eq. (15) without compromising accuracy. We
introduce the angle-averaged Compton cross section
![]() defined as
defined as
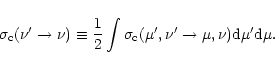 |
(16) |
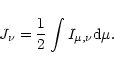 |
(17) |
Equations (11)-(15), (18) constitute the complete set of equations for the radiative transfer. Since Eq. (11) and Eqs. (15), (18) are mutually dependent, the solution cannot be found by direct evaluation. To solve the system, we use a standard Lambda Iteration scheme [see e.g. Rutten 1999 and references therein; see also Zane et al. 1996; Poutanen & Svensson 1996].
We discretize frequency ![]() with equal spacing in
with equal spacing in ![]() ,
and
photon angle
,
and
photon angle
![]() according to the roots of the Legendre
polynomials of order n. At the start of the procedure we choose
according to the roots of the Legendre
polynomials of order n. At the start of the procedure we choose
![]() ,
or any other initial guess that might be
appropriate. For each
,
or any other initial guess that might be
appropriate. For each ![]() and
and ![]() we now integrate the
transfer equation (Eq. (11)) from z=0 to
we now integrate the
transfer equation (Eq. (11)) from z=0 to
![]() for
for ![]() ,
or from
,
or from
![]() to
z=0 for
to
z=0 for ![]() .
At z=0 we impose zero inward flux as boundary
condition, while at
.
At z=0 we impose zero inward flux as boundary
condition, while at
![]() we choose a Planck function
at temperature
we choose a Planck function
at temperature
![]() as the starting value for the
integration. The temperature
as the starting value for the
integration. The temperature
![]() of this Planck function
is chosen such that:
of this Planck function
is chosen such that:
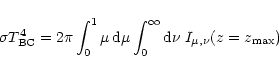 |
(19) |
After performing this operation for every ![]() and
and ![]() ,
we can
evaluate the new
,
we can
evaluate the new
![]() by employing
Eqs. (15), (18). This
new
by employing
Eqs. (15), (18). This
new
![]() is inserted into Eq. (11) and
the integration of Eq. (11) is repeated along the
lines sketched above. After each iteration the relative difference of
the solution with the previous iteration step is computed. If this
relative difference drops below 10-3, we assume that the solution
has converged. Since in our solutions the scattering optical depths
remains always of the order of a few, we need not worry about the
well-known convergence problems of the lambda iteration procedure
sketched above.
is inserted into Eq. (11) and
the integration of Eq. (11) is repeated along the
lines sketched above. After each iteration the relative difference of
the solution with the previous iteration step is computed. If this
relative difference drops below 10-3, we assume that the solution
has converged. Since in our solutions the scattering optical depths
remains always of the order of a few, we need not worry about the
well-known convergence problems of the lambda iteration procedure
sketched above.
Once the radiative transfer solution is obtained, the radiative
heating and cooling rates can be evaluated by flux differences. The
flux at each position x is defined as
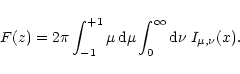 |
(20) |
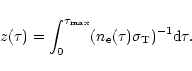 |
(22) |
We also checked our solution for the importance of pair processes,
calculating the pair number densities according to 1998. We
find that in our model the electron temperatures are too low and the
electron densities too high for pair production to become important.
![\begin{figure}
\par\includegraphics[width=12cm]{h2960_f2.eps} \end{figure}](/articles/aa/full/2001/39/aah2960/Timg107.gif) |
Figure 2:
Upper left: emergent spectrum (solid line), thermalized downward
directed spectrum (dashed line) and blackbody input spectrum at
the base (dotted - dashed line); upper right panel: combined
heating rates from proton heating and electron thermal
conductivity (solid line) and radiative cooling rates due to
Comptonization and bremsstrahlung (squares) - the dotted line
shows the rates from electron conductivity alone; lower panels
show from left to right and from top to bottom the electron
temperature |
| Open with DEXTER | |
| |
Figure 3:
Emergent model spectra and temperature profiles at a fixed
proton energy flux
|
| Open with DEXTER | |
| |
Figure 4:
Emergent spectra and temperature profiles for various values
of the proton energy flux (in ergcm-2 s-1, denoted by the
numbers of the lines) at constant proton temperature, |
| Open with DEXTER | |
| |
Figure 5:
Emergent spectra and temperature profiles at
low proton energy flux (in ergcm-2 s-1, denoted by the
numbers of the lines) and constant proton temperature, |
| Open with DEXTER | |
We start our calculations with an isothermal atmosphere in hydrostatic
equilibrium according to Sect. 2.2. For the initial
electron temperature we set ![]() = 1 keV throughout the layer. After each
time step we obtain the heating rates
= 1 keV throughout the layer. After each
time step we obtain the heating rates
![]() from the
Coulomb interactions and the cooling rates
from the
Coulomb interactions and the cooling rates
![]() due to
the radiative processes bremsstrahlung and multiple Compton
scattering as a function of optical depth.
The time step of every cycle in our simulation is adjusted to the
shortest energy exchange time scale occurring in the calculation.
due to
the radiative processes bremsstrahlung and multiple Compton
scattering as a function of optical depth.
The time step of every cycle in our simulation is adjusted to the
shortest energy exchange time scale occurring in the calculation.
Additionally we include the energy redistribution due to electron thermal conductivity. Generally the flow of heat per unit area, Q, in the presence of a temperature gradient, is given by (see e.g. Spitzer 1962)
Now we can calculate the total change of enthalpy per time step,
For our model calculations we use fixed values for the mass
![]() and the radius
and the radius
![]() cm for the neutron star.
For the rotational angular velocity of the accreting material we use
cm for the neutron star.
For the rotational angular velocity of the accreting material we use
![]() .
The results depend on the proton energy flux per unit
area of the neutron star surface. In order to make the results
interpretable in terms of a total luminosity, we assume that 60% of
the neutron star surface is involved in the accretion process. This
takes into account the approximate vertical extent of an ADAF
(Popham & Sunyaev 2001).
.
The results depend on the proton energy flux per unit
area of the neutron star surface. In order to make the results
interpretable in terms of a total luminosity, we assume that 60% of
the neutron star surface is involved in the accretion process. This
takes into account the approximate vertical extent of an ADAF
(Popham & Sunyaev 2001).
Figure 2 shows an equilibrium solution for a proton energy flux
![]() ergcm-2s-1,
ergcm-2s-1,
![]() ,
yielding a luminosity of
,
yielding a luminosity of
![]() .
The neutron star atmosphere is clearly divided into two
parts. A hot surface layer is separated by a sharp temperature
front from the much cooler bottom part. The maximum temperature in the hot
part of the atmosphere is
.
The neutron star atmosphere is clearly divided into two
parts. A hot surface layer is separated by a sharp temperature
front from the much cooler bottom part. The maximum temperature in the hot
part of the atmosphere is
![]() keV. This is
considerably hotter than previous calculations showed
(e.g. Alme & Wilson 1973; Turolla et al. 1994) but also significantly cooler
than the "hot'' solutions from Turolla et al. (1994) and Zane et al. (1998). We
did not find any comparable hot solutions.
keV. This is
considerably hotter than previous calculations showed
(e.g. Alme & Wilson 1973; Turolla et al. 1994) but also significantly cooler
than the "hot'' solutions from Turolla et al. (1994) and Zane et al. (1998). We
did not find any comparable hot solutions.
Figure 2 also shows that energy redistribution through electron
conductivity gets important at the transition zone from the hot to the
cool part. The emergent model spectrum in Fig. 2 illustrates
that the hot part acts as an effective Comptonization layer with an
optical thickness of order unity. The downward directed photons are
almost completely thermalized in the cold part. This justifies our
assumption of Sect. 2.4 that the downward flux of photons
is converted into a black body flux of upward soft photons of
temperature
![]() at the base of our model since almost all the
thermalization has already taken place.
at the base of our model since almost all the
thermalization has already taken place.
Figure 3 shows the emergent spectra and temperature profiles
through the atmosphere at a fixed proton energy flux level
![]() ergcm-2 for various proton temperatures,
ergcm-2 for various proton temperatures,
![]() .
The higher the initial proton temperature the lower is the
electron temperature in the hot part of the atmosphere and vice versa
for the cold part. The optical depth of the hot part is of order
unity in every case. As a consequence harder spectra are produced
with lower initial proton temperatures. This can be explained with the
decreasing penetration depth of the protons at smaller velocities: the
heating rates in the upper part of the atmosphere are increased and
thus the temperature is higher there.
.
The higher the initial proton temperature the lower is the
electron temperature in the hot part of the atmosphere and vice versa
for the cold part. The optical depth of the hot part is of order
unity in every case. As a consequence harder spectra are produced
with lower initial proton temperatures. This can be explained with the
decreasing penetration depth of the protons at smaller velocities: the
heating rates in the upper part of the atmosphere are increased and
thus the temperature is higher there.
Figures 4 and 5 show the dependence of the
solution on the proton energy flux at constant proton temperature,
![]() .
At low proton energy flux (Fig. 5) the optical
depth of the hot part is small (
.
At low proton energy flux (Fig. 5) the optical
depth of the hot part is small (
![]() ).
The solutions for these cases are comparable to those found by
Zampieri et al. (1995). But the temperature of the hot part in our solutions
turns out to be much higher than in their solutions. This hot part
causes an (energetically unimportant) bump in the emergent spectra at
high frequencies due to optically thin bremsstrahlung emission in this
layer. As in Zampieri et al. (1995) the emergent spectra are significantly
harder than the blackbody at the layer effective temperature,
).
The solutions for these cases are comparable to those found by
Zampieri et al. (1995). But the temperature of the hot part in our solutions
turns out to be much higher than in their solutions. This hot part
causes an (energetically unimportant) bump in the emergent spectra at
high frequencies due to optically thin bremsstrahlung emission in this
layer. As in Zampieri et al. (1995) the emergent spectra are significantly
harder than the blackbody at the layer effective temperature,
![]() .
We also see a harder spectrum
with respect to the blackbody of the layer effective temperature at
the lowest luminosity.
.
We also see a harder spectrum
with respect to the blackbody of the layer effective temperature at
the lowest luminosity.
By further increasing the proton energy flux
the temperature jump moves inward to greater optical depth reaching
order unity at the highest flux levels. Thereby the temperature in the
hot part is roughly kept at a constant value in contrast to the
temperature of the cold part, which increases continously. At
![]() ergcm-2 s-1 the hot part
acts as an effective Comptonization layer for the cool thermal photons
from the interior. In addition the electron thermal conduction
smoothes the temperature profile and the shock is not as sharp as in the
low energy flux cases.
ergcm-2 s-1 the hot part
acts as an effective Comptonization layer for the cool thermal photons
from the interior. In addition the electron thermal conduction
smoothes the temperature profile and the shock is not as sharp as in the
low energy flux cases.
Evident in our model spectra is an excess of soft photons (see e.g.
Figs. 2, 3, 5) with respect to a
blackbody with the effective temperature of the corresponding energy
flux. Though energetically unimportant it is an interesting feature of
our model spectra. This soft photon excess is caused by the reverse
temperature profile of the atmosphere, i.e. the high temperatures are
above the cooler parts (in contrast to e.g. the solar photosphere).
Figure 6 shows the absorption optical depth as a function of
the photon energy and electron temperature for an equilibrium solution
with ![]() and
and ![]() .
The line for
.
The line for
![]() is
emphasized. For low photon energies
is
emphasized. For low photon energies
![]() is found high
in the neutron star atmosphere, where the temperature is high.
For high frequency photons the atmosphere gets more and more
transparent and
is found high
in the neutron star atmosphere, where the temperature is high.
For high frequency photons the atmosphere gets more and more
transparent and
![]() occurs at lower temperatures.
Thus the high frequency photons decouple at lower temperatures and
propagate outwards. As a result there is an excess of low energy
photons, which decouple from the atmosphere at higher temperatures.
occurs at lower temperatures.
Thus the high frequency photons decouple at lower temperatures and
propagate outwards. As a result there is an excess of low energy
photons, which decouple from the atmosphere at higher temperatures.
The same arguments explain the harder spectra at low proton energy
fluxes. Here the temperature profile in the atmosphere is dominated by
the increase of temperature with optical depth, as has already been
explained by Zampieri et al. (1995). Thereby the high energy photons decouple
in the deeper, hotter layers and propagate out freely. This
contribution to the high energy part of the spectrum causes the harder
spectrum compared to the blackbody of the layer effective temperature.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2960_f6.ps}\end{figure}](/articles/aa/full/2001/39/aah2960/Timg126.gif) |
Figure 6:
Absorption optical depth as a function of photon energy and
atmospheric temperature for an equilibrium solution with |
| Open with DEXTER | |
The main conclusion from our work is that a neutron star surface embedded in a hot ADAF-type accretion flow does not act like a simple blackbody thermalizer. Instead the interaction with the hot ions produces spectra with pronounced high energy, comptonized tails.
We have considered the accretion of protons onto the surface of a
neutron star for a wide range of proton energy fluxes. In our model
the stopping depth of the protons is obtained self consistently. We
allow for the scaling of the proton temperature
![]() ,
which in our model controls the vertical velocity
component of the protons. Further we consider accretion from an ADAF,
where the protons have a tangential velocity component
,
which in our model controls the vertical velocity
component of the protons. Further we consider accretion from an ADAF,
where the protons have a tangential velocity component
![]() .
By variation of the proton temperature and the proton
energy flux a range of X-ray spectra can be produced. Our
model computations show that the local proton energy flux determines the
optical depth of the hot part whereas the temperatures through the
atmosphere are determined by the initial proton temperatures.
.
By variation of the proton temperature and the proton
energy flux a range of X-ray spectra can be produced. Our
model computations show that the local proton energy flux determines the
optical depth of the hot part whereas the temperatures through the
atmosphere are determined by the initial proton temperatures.
Previous models considered spherical accretion onto the neutron star. The free infall velocity of the protons was used in such models. If accretion takes place from an accretion disk or an ADAF, the vertical velocity component is considerably smaller than than the free infall velocity. This has important consequences on the emergent spectra as our solutions suggest: at the same local energy flux a decrease in the vertical proton velocity increases the temperature of the hot part of the atmosphere, and X-ray spectra similar to those of neutron stars in their hard states can be produced. Figure 7 shows a comparison of a model spectrum with observed spectra of X-ray bursters in their low/hard states (taken from Gilfanov et al. 1998).
A question left unanswered by our studies is how the spectrum from the surface is modified by the overlying accretion flow. E.g. an overlying optically thick boundary layer might significantly thermalize hard photons from the neutron star surface again. But we can conclude that the input spectrum at the bottom of a boundary layer is not Planckian at high proton energy fluxes. If the boundary layer is optically thin the contribution to the observed hard spectral component at high proton energy fluxes might be quite important. A discussion whether there is an optically thin boundary layer can be found in e.g. Barret et al. (2000). For low accretion rates the boundary layer is indeed optically thin (e.g. King & Lasota 1987).
Detailed studies about the accretion disk boundary layer around a NS
have been performed by Popham & Sunyaev (2001). They show that the accretion disk
near the NS is radially and vertically extended and that the angular
velocity ![]() is reduced with respect to the Keplerian value. Such
a boundary layer naturally produces a proton illumination scenario as
described in our model. Their boundary layer is optically thin to
absorption. For high luminosities this region has a radial extent
larger than one stellar radius, i.e. the hard radiation from the NS
surface, produced by proton illumination, can easily propagate
outwards without being thermalized. The boundary layer even further
enhances comptonization as the gas there is hot (
is reduced with respect to the Keplerian value. Such
a boundary layer naturally produces a proton illumination scenario as
described in our model. Their boundary layer is optically thin to
absorption. For high luminosities this region has a radial extent
larger than one stellar radius, i.e. the hard radiation from the NS
surface, produced by proton illumination, can easily propagate
outwards without being thermalized. The boundary layer even further
enhances comptonization as the gas there is hot (![]() 108 K).
108 K).
Our results emphasize the importance of the neutron star surface for
the contribution to the hard spectral component in low mass X-ray
binaries (LMXBs). A prerequisite for the occurrence of a hard spectral
component is a high local proton energy flux. The local proton energy
flux onto the neutron star surface depends on both the mass accretion
rate and the size of the accretion belt on the neutron star. Our model
computations have local validity, i.e. if the involved accretion belt
is small, high proton energy fluxes on the neutron star surface can
even occur at accretion rates well beneath the Eddington limit.
Therefore our model does not exclude the possibility of hard spectral
components from the neutron star surface at low luminosities, as is
observed.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{h2960_f7.ps}\end{figure}](/articles/aa/full/2001/39/aah2960/Timg131.gif) |
Figure 7:
Comparison of an emergent model spectrum with
|
| Open with DEXTER | |
Acknowledgements
We thank Roberto Turolla for the usage of the CSK subroutines. We are grateful to Marat Gilfanov for the neutron star spectra. This research has made use of data obtained through the HEASARC Online Service, provided by the NASA/GSFC. This work was done in the research network "Accretion onto black holes, compact stars and proto stars'' funded by the European Commission under contract number ERBFMRX-CT98-0195.