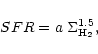A&A 377, 835-844 (2001)
DOI: 10.1051/0004-6361:20011163
Radial B-V/V-K color gradients, extinction-free
QBVK combined color indices, and the history
of star formation of the Cartwheel ring galaxy
E. I. Vorobyov1 - D. Bizyaev2
1 - Institute of Physics, Stachki 194, Rostov-on-Don, Russia
2 -
Sternberg Astronomical Institute, Universitetskiy prospect 13, Moscow, Russia
Received 9 April 2001 / Accepted 20 August 2001
Abstract
In this paper we model and analyse the B-V/V-K radial color gradients observed in the Cartwheel ring galaxy.
Along with the color-color diagrams, we use the QBVK combined color indices, which
minimise the uncertainties in the observed B-V and V-K colors introduced by dust extinction.
To model the optical and near-infrared color properties of the Cartwheel galaxy, we assume that
an intruder galaxy generates an expanding ring density wave in the Cartwheel's disk,
which in its turn triggers massive star formation along the wave's perimeter according to the Schmidt law.
We use the population synthesis to calculate the color properties of stellar populations
formed in the expanding density wave.
The results of color modelling suggest that the pre-collision Cartwheel was a
late-type spiral, embedded
in an extensive gaseous disk of sub-critical surface density. The properties of the old stellar disk
are typical for the late-type Freeman disks, with the central surface brightness in V-band and
the scale length being
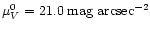 and
R0=2 kpc respectively. The pre-collision gaseous disk has a metallicity gradient
ranging from
and
R0=2 kpc respectively. The pre-collision gaseous disk has a metallicity gradient
ranging from
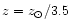 at the outer regions to
at the outer regions to
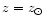 in the central regions.
At present, the wave of star formation has passed the initial extent of the pre-collision,
old stellar disk and is currently moving in the predominantly gaseous,
low-metallicity disk at the radius of 16 kpc.
Neither young stellar populations formed in an expanding density wave,
nor their mixture with the old, pre-collision stellar populations can reproduce the
B-V and V-K colors of the Cartwheel's nucleus+inner ring.
We find that an additional 10-Myr-old burst of star formation in the nuclear regions,
along with the visual extinction of
in the central regions.
At present, the wave of star formation has passed the initial extent of the pre-collision,
old stellar disk and is currently moving in the predominantly gaseous,
low-metallicity disk at the radius of 16 kpc.
Neither young stellar populations formed in an expanding density wave,
nor their mixture with the old, pre-collision stellar populations can reproduce the
B-V and V-K colors of the Cartwheel's nucleus+inner ring.
We find that an additional 10-Myr-old burst of star formation in the nuclear regions,
along with the visual extinction of
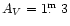 ,
might be responsible for the peculiar colors of the Cartwheel's nucleus.
,
might be responsible for the peculiar colors of the Cartwheel's nucleus.
Key words: galaxies: individual: The Cartwheel - galaxies: stellar content - galaxies: formation
Ring galaxies are believed to be the result of a head-on galaxy-galaxy collision.
Such a near-central collision generates an
expanding ring density wave in the disk of a larger galaxy.
It is likely that star formation will be induced along the wave's perimeter
when the gas density exceeds a threshold (Appleton & Struck-Marcell 1987).
As such a wave of star formation advances radially from the nucleus,
it leaves behind evolved stellar populations, with the youngest stars located at the current position of the wave.
It is expected that this might result in the radial color distribution of stars in the galactic disk, with the
inner regions being redder than the outer parts of the disk.
Indeed, observations of the Cartwheel ring galaxy (Marcum et al. 1992)
reveal the presence of the optical and near-infrared
B-V/V-K radial color gradients in the galactic disk.
Recent observations of a sample of northern ring galaxies by Appleton  Marston (1997) show
that most of them exhibit radial color gradients
similar to the pattern observed in the Cartwheel.
Marston (1997) show
that most of them exhibit radial color gradients
similar to the pattern observed in the Cartwheel.
Numerical modelling of the Cartwheel's radial color gradients
by Korchagin et al. (2001) shows that the young stellar populations formed in the
expanding density wave exhibit regular reddening of colors towards the nucleus only for the sub-solar
metallicities of the star-forming gas (
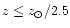 ). Even in the most favorable case of
). Even in the most favorable case of
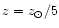 ,
the model colors are much bluer as compared to those observed in the Cartwheel.
Korchagin et al. (2001) argue that the pre-collision disk of old stars is needed to reconcile the
model and the Cartwheel's colors.
However, their conclusions are based on the direct quantitative
comparison of the model and the Cartwheel's B-V and V-K colors,
which is complicated due to uncertainties in the amount of internal extinction in the Cartwheel's disk.
,
the model colors are much bluer as compared to those observed in the Cartwheel.
Korchagin et al. (2001) argue that the pre-collision disk of old stars is needed to reconcile the
model and the Cartwheel's colors.
However, their conclusions are based on the direct quantitative
comparison of the model and the Cartwheel's B-V and V-K colors,
which is complicated due to uncertainties in the amount of internal extinction in the Cartwheel's disk.
In this paper we re-address the question of theoretical modelling of the B-V/V-K
radial color gradients observed in the Cartwheel galaxy.
We attempt to exclude the complicated influence of dust extinction on the theoretical interpretation
of the Cartwheel's B-V/V-K radial color gradients. To do this, we use
insensitive to dust extinction QBVK combined color indices.
Such color indices were successfully applied for structure modelling
of dusty galaxies by Zasov  Moiseev (1998) and Bizyaev et al. (2000, 2001).
Moiseev (1998) and Bizyaev et al. (2000, 2001).
In Sect. 2 we analyse the QBVK radial distribution observed in the Cartwheel's disk and
consider the factors defining the value of QBVK. In Sect. 3 we formulate the adopted
model of star formation in the Cartwheel galaxy. In Sect. 4 we compare
the model B-V/V-K radial color
gradients and QBVK index profiles, obtained in the framework of a first major
episode of star formation in the Cartwheel's disk, with the observed radial profiles.
We consider a possibility that the Cartwheel has an old stellar disk typical for the late-type
spirals. In Sect. 5 we attempt to model the peculiar colors of the Cartwheel's nucleus
and the inner ring. The main results are summarized in Sect. 6.
The B-V/V-K radial color gradients of the Cartwheel galaxy are shown in Fig. 1,
which is a reproduction of Fig. 3 of Marcum et al. (1992).
The annular points are numbered according to radius, beginning with the inner ring (point I)
and ending with the outer ring (points VIII and IX).
These colors have only been corrected for Galactic reddening using
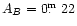 and the standard ISM extinction curve (Marcum et al. 1992).
and the standard ISM extinction curve (Marcum et al. 1992).
Previous modelling of the Cartwheel's radial color gradient was seriously complicated by the
uncertainties in the amount of internal extinction in the galactic disk.
The internal extinction is only measured towards two bright HII regions
in the Cartwheel's outer ring (
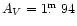 )
and is not applicable to the whole galactic disk. The value of internal extinction interior to the outer ring
of
)
and is not applicable to the whole galactic disk. The value of internal extinction interior to the outer ring
of
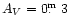 has been estimated from the available
has been estimated from the available
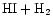 data (Korchagin et al. 2001).
Clearly, correction for the internal extinction would greatly distort the observed Cartwheel's
B-V/V-K radial color pattern,
as shown by correction vectors in Fig. 1, and complicate the task of color interpretation.
data (Korchagin et al. 2001).
Clearly, correction for the internal extinction would greatly distort the observed Cartwheel's
B-V/V-K radial color pattern,
as shown by correction vectors in Fig. 1, and complicate the task of color interpretation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F1.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg20.gif) |
Figure 1:
Radial B-V/V-K color gradients of the Cartwheel galaxy.
This is a reproduction of Fig. 3
of Marcum et al. (1992).
|
| Open with DEXTER |
To avoid the complicated influence of dust on the Cartwheel's radial color gradient, we use insensitive to
dust extinction QBVK combined color index defined as:
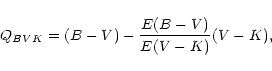 |
(1) |
where (B-V) and (V-K) are colors, and E(B-V) and E(V-K) are color excesses.
For dust properties typical for the Galaxy (RV=3.1) the ratio of color excesses
E(B-V)/E(V-K)
is equal to 0.365 (Cardelli et al. 1989). This value is valid for a "dust shield'' approximation, i.e.
when all dust is located between an observer and a galaxy. For a homogeneous mixture of dust and stars the ratio
of color excesses
E(B-V)/E(V-K)is 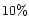 less than for a "dust shield'' approximation (Zasov & Moiseev 1998) and equal to 0.329.
As to the Cartwheel galaxy, the internal extinction dominates at the outer ring
and is comparable to the Galactic reddening in the inner part (Korchagin et al. 2001).
Hence, we choose a "homogeneous mixture'' approximation rather than a "dust shield'' for modelling
the Cartwheel's color properties.
less than for a "dust shield'' approximation (Zasov & Moiseev 1998) and equal to 0.329.
As to the Cartwheel galaxy, the internal extinction dominates at the outer ring
and is comparable to the Galactic reddening in the inner part (Korchagin et al. 2001).
Hence, we choose a "homogeneous mixture'' approximation rather than a "dust shield'' for modelling
the Cartwheel's color properties.
The following factors define the value of QBVK:
a) Contribution of young, blue stars to the integrated flux, i.e. the history of star formation in a certain region of a galaxy.
Figures 2a and 2b show the QBVK combined color indices of a single starburst superimposed
on the old stellar population of 10 Gyr. Calculations are performed using the program of Worthey (1994).
Metallicities of both the young and old stellar populations are equal to
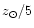 (
(
![$\rm [Fe/H]=-0.7$](/articles/aa/full/2001/39/aah2789/img24.gif) ).
Figure 2a illustrates the influence of different relative contributions of young stars on the QBVKindices for a single 50-Myr-old starburst.
Figure 2b shows the dependence of the QBVK indices on the age of a starburst.
Here, both the young and old stellar populations
contribute equally to the total stellar mass.
As it can be seen, QBVK indices are sensitive to the age of a starburst and
to the relative contribution of young stars.
).
Figure 2a illustrates the influence of different relative contributions of young stars on the QBVKindices for a single 50-Myr-old starburst.
Figure 2b shows the dependence of the QBVK indices on the age of a starburst.
Here, both the young and old stellar populations
contribute equally to the total stellar mass.
As it can be seen, QBVK indices are sensitive to the age of a starburst and
to the relative contribution of young stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F1.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Tfigure2.gif) |
Figure 2:
The QBVK indices of a single starburst superimposed
on the old stellar population of 10 Gyr. a) The influence of different relative contributions of young stars
on the QBVK indices for a single starburst of 50 Myr old.
b) Dependence of the QBVK indices on the age of a starburst.
c) The QBVK indices as a function of metallicities
of old and young stellar populations (equal for both populations).
|
| Open with DEXTER |
Thus, a young burst of star formation should essentially influence the value of QBVK.
Relative increase of young stars
in a certain region of a galaxy makes its colors bluer, thus, lowering the value of QBVK (Fig. 2a).
On the other hand, the red supergiant flash (Charlot & Bruzual 1991) makes the luminosity
of a young stellar cluster in
the K-band to peak at 10 Myr after the burst, which noticeably lowers the value of QBVK (Fig. 2b).
b) Heavy element abundances.
Figure 2c gives QBVK indices as a function of metallicities
of the old and young stellar populations (equal for both populations). The age of a single starburst is equal to 50 Myr.
Metallicity gradient alone can essentially influence the value of QBVK,
while other starburst parameters remain unchanged.
c) Dust properties.
Cardelli et al. (1989) found that for the dust properties different from those of the Galaxy, i.e. for RV other than 3.1, the
ratio of color excesses
E(B-V)/E(V-K) changes. However, the Cartwheel's QBVK distribution remains qualitatively
unchanged for a fairly wide range of RV. Thus, the value of RV=3.1 is adopted for the rest of the paper.
Figure 3 shows the Cartwheel's QBVK distribution as a function of photometric annulus. Combined color indices are calculated
using observational data of Marcum et al. (1992). The numbering of photometric annuli is in accordance with Fig. 3 of Marcum et al. (1992).
The Cartwheel's QBVK radial distribution remarkably separates into three sub-profiles, which
correspond to three structurally different parts of the Cartwheel: annuli 0 and 1 correspond to the nucleus and the inner ring,
annuli 2-7 are the inter-ring region, and annuli 8 and 9 correspond to the outer ring.
Combined color indices are insensitive to dust extinction and
can be directly understood in terms of stellar populations. This natural separation of QBVK indices implies that
the nucleus+inner ring, inter-ring region and the outer ring of the Cartwheel consist of different stellar populations.
Nucleus and the inner ring.
The old stellar content of the nucleus is confirmed by the detection of late-type stellar
absorption spectrum (Fosbury & Hawarden 1977). However, recent mid-infrared
and
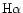 observations indicate that the old stellar populations may not totally
dominate the spectrum. ISOCAM images (Charmandaris et al. 1999) show
significant 7
observations indicate that the old stellar populations may not totally
dominate the spectrum. ISOCAM images (Charmandaris et al. 1999) show
significant 7  m and 15
m and 15  m emission in the nucleus and the inner ring,
which implies a low-level star formation activity. Detection of weak Ha emission from
the nucleus and inner ring also indicates that there might be some low-level star formation in the
Cartwheel's central regions (Amram et al. 1998).
m emission in the nucleus and the inner ring,
which implies a low-level star formation activity. Detection of weak Ha emission from
the nucleus and inner ring also indicates that there might be some low-level star formation in the
Cartwheel's central regions (Amram et al. 1998).
The inter-ring region. As
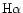 observations indicate, it is almost totally devoid of any star
formation activity (Amram et al. 1998) and is probably populated by density wave born, post-collision stars with an admixture of old,
pre-collision stars as implied by progressively reddened B-V/V-K colors towards the Cartwheel's nucleus.
The possibility that dust extinction is responsible for this
reddening of colors will be tested in numerical simulations in Sect. 4.
observations indicate, it is almost totally devoid of any star
formation activity (Amram et al. 1998) and is probably populated by density wave born, post-collision stars with an admixture of old,
pre-collision stars as implied by progressively reddened B-V/V-K colors towards the Cartwheel's nucleus.
The possibility that dust extinction is responsible for this
reddening of colors will be tested in numerical simulations in Sect. 4.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F3.ps}\end{figure}](/articles/aa/full/2001/39/aah2789/Timg26.gif) |
Figure 3:
The Cartwheel's QBVK distribution as a function of
photometric annulus.
|
| Open with DEXTER |
The outer ring. Models of ring galaxy formation predict that the
Cartwheel's outer ring is the current location of an outwardly propagating star formation wave (Appleton & Struck-Marcell 1987;
Struck-Marcell  Appleton 1987). Hence, a large gradient in the QBVK distribution
seen across the outer ring in Fig. 3 is indicative of rapid changes
in the photometric properties of young stellar populations. Probably, the
outer edge of the ring is so young that it has not yet produced any supergiants,
whereas the inner edge is in the red-supergiant-flash stage (Marcum et al. 1992).
Existence of the red supergiant flash is confirmed in observations
of the young stellar cluster NGC 2004 in the LMC (Bica & Alloin 1987).
Appleton 1987). Hence, a large gradient in the QBVK distribution
seen across the outer ring in Fig. 3 is indicative of rapid changes
in the photometric properties of young stellar populations. Probably, the
outer edge of the ring is so young that it has not yet produced any supergiants,
whereas the inner edge is in the red-supergiant-flash stage (Marcum et al. 1992).
Existence of the red supergiant flash is confirmed in observations
of the young stellar cluster NGC 2004 in the LMC (Bica & Alloin 1987).
To model the optical and near-infrared color properties of the Cartwheel galaxy, we assume that the
head-on galaxy-galaxy collision generates an outwardly propagating ring density wave in the disk of the Cartwheel.
Additionally, we assume that the collision is central or near-central so that we can neglect the azimuthal variations in
the strength of the density wave.
Massive star formation in the Cartwheel galaxy is restricted to the outer ring, which is the current location
of the density wave. Almost no sigh of
star formation activity is found just behind and ahead of the outer ring (Higdon 1995).
To imitate the propagating star formation in the Cartwheel's disk,
we assume that the star formation rate is proportional to a ring density enhancement expanding
radially in a gaseous disk with velocity v. The density enhancement is given by a Gaussian function:
![\begin{displaymath}C(r-vt)=A(r) \; \exp\left[ - {(r-vt)^2 \over L^2}\right],
\end{displaymath}](/articles/aa/full/2001/39/aah2789/img27.gif) |
(2) |
where A(r) is the amplitude of the density enhancement and L is a half-width of the density enhancement.
The balance of surface density of stars (
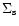 )
at a distance r from the center and time t can be then written as follows
(Korchagin et al. 2001):
)
at a distance r from the center and time t can be then written as follows
(Korchagin et al. 2001):
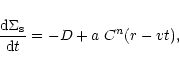 |
(3) |
where the first term in the right-hand side of Eq. (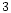 )
is the rate of death of stars:
)
is the rate of death of stars:
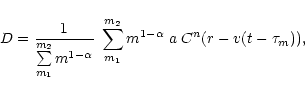 |
(4) |
where 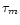 is the life-time of a star of mass m, and
is the life-time of a star of mass m, and 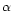 is the slope of the IMF.
is the slope of the IMF.
We consider a circular density
enhancement propagating from the center of a gaseous disk to the present location of the
Cartwheel's outer ring at 16 kpc
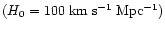 .
The computational area is divided into 10 annuli as in Plate 1 of Marcum et al. (1992).
Annulus 1 is two kiloparsec wide and centered at 3.1 kpc, thus covering the current location of the inner ring. The centroids of annuli
2-9 are separated by 1.25 kpc, with the 2-nd annulus centered at 6.8 kpc.
The 0-th annulus represents the nucleus.
The mass of stars formed in each annulus is distributed into individual stellar masses
using the Salpeter IMF with
.
The computational area is divided into 10 annuli as in Plate 1 of Marcum et al. (1992).
Annulus 1 is two kiloparsec wide and centered at 3.1 kpc, thus covering the current location of the inner ring. The centroids of annuli
2-9 are separated by 1.25 kpc, with the 2-nd annulus centered at 6.8 kpc.
The 0-th annulus represents the nucleus.
The mass of stars formed in each annulus is distributed into individual stellar masses
using the Salpeter IMF with
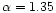 and the stellar mass interval of
and the stellar mass interval of
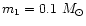 and
and
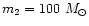 .
The luminosity of each annulus at a given band A after time t can be computed as:
.
The luminosity of each annulus at a given band A after time t can be computed as:
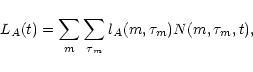 |
(5) |
where
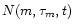 is the number of stars in a given annulus at time t with mass m and age
is the number of stars in a given annulus at time t with mass m and age 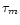 ,
and
,
and
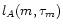 is the luminosity of a star in the band A.
Stellar luminosities
is the luminosity of a star in the band A.
Stellar luminosities
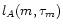 are obtained using stellar evolutionary (Schaller et al. 1992) and atmospheric (Kurucz 1992)
models. The population synthesis code used in this work is explained in
detail in Mayya (1995, 1997).
This code synthesizes a number of observable quantities in the optical and near-infrared
parts of the spectrum, which are suitable for comparison with the observed
properties of giant star-forming complexes. Since the Cartwheel is a recent phenomenon
with high rates of star formation, this code is especially suitable for our purposes.
The results of this code are compared with those of other existing codes by Charlot (1996).
are obtained using stellar evolutionary (Schaller et al. 1992) and atmospheric (Kurucz 1992)
models. The population synthesis code used in this work is explained in
detail in Mayya (1995, 1997).
This code synthesizes a number of observable quantities in the optical and near-infrared
parts of the spectrum, which are suitable for comparison with the observed
properties of giant star-forming complexes. Since the Cartwheel is a recent phenomenon
with high rates of star formation, this code is especially suitable for our purposes.
The results of this code are compared with those of other existing codes by Charlot (1996).
Classic Schmidt law of star formation (n=1.5) is assumed throughout the paper (Kennicutt 1989).
The half-width of a density enhancement L is chosen so as to reproduce the observed
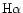 surface brightness profile in the
Cartwheel's outer ring (Higdon 1995). This gives the value of L=1 kpc.
Velocity of a propagating density enhancement
v=55 km s-1 is assumed to coincide
with the expansion velocity of the outer ring
surface brightness profile in the
Cartwheel's outer ring (Higdon 1995). This gives the value of L=1 kpc.
Velocity of a propagating density enhancement
v=55 km s-1 is assumed to coincide
with the expansion velocity of the outer ring
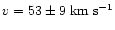 ,
the value derived by Higdon (1996) from HI kinematics of the outer ring.
,
the value derived by Higdon (1996) from HI kinematics of the outer ring.
With the values of L and v being fixed, the coefficient a and the amplitude of density enhancement
A(r) constitute the set of parameters, which determine the number of stars
 formed by a density wave
in each photometric annulus (see Eq. (5)). The birthrate of stars a relates the star formation rate
observed in the Cartwheel galaxy with the assumed Schmidt law of star formation (see Eq. (3)).
We estimate its value for the Cartwheel's outer ring using the measured rate of star formation
67
formed by a density wave
in each photometric annulus (see Eq. (5)). The birthrate of stars a relates the star formation rate
observed in the Cartwheel galaxy with the assumed Schmidt law of star formation (see Eq. (3)).
We estimate its value for the Cartwheel's outer ring using the measured rate of star formation
67
 (Higdon 1995), the
mean surface density of gas
(Higdon 1995), the
mean surface density of gas
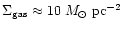 (Higdon 1996)
and the outer ring's area of 250 kpc2.
This gives the dimensionless value of a=0.0025 when masses, time scales, and distance scales are expressed in
units
(Higdon 1996)
and the outer ring's area of 250 kpc2.
This gives the dimensionless value of a=0.0025 when masses, time scales, and distance scales are expressed in
units
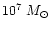 ,
106 yrs, and 1 kpc respectively.
,
106 yrs, and 1 kpc respectively.
We assume that the amplitude of density enhancement A(r) is twice as big as the unperturbed,
pre-collision gas surface density, which is typical for the spirals and is confirmed in
numerical simulations by Appleton  Struck-Marcell (1987).
To constrain the pre-collision radial profile of gas, we fit the model R-band and
Struck-Marcell (1987).
To constrain the pre-collision radial profile of gas, we fit the model R-band and
 surface brightness profiles of stellar populations formed in the expanding density wave
to the profiles observed in the Cartwheel. We do this by
varying the radial profile of gas in the pre-collision galactic disk.
surface brightness profiles of stellar populations formed in the expanding density wave
to the profiles observed in the Cartwheel. We do this by
varying the radial profile of gas in the pre-collision galactic disk.
4 Model B-V/V-K radial color gradients and QBVK indices of the Cartwheel
galaxy
4.1 Density wave in a purely gaseous disk
As mentioned in the introduction, Korchagin et al. (2001) found that the density
wave propagating in a purely gaseous disk of uniform metallicity cannot reproduce
the Cartwheel's B-V/V-K radial color gradient. The model colors are much bluer
as compared to those observed in the Cartwheel. Korchagin et al. (2001) argued
that the pre-collision disk of old stars was needed to reconcile the model and the Cartwheel's colors.
We mainly confirm their conclusion. However, use of the extinction-free QBVK
indices allows us to notice some interesting features that have been missed
by Korchagin et al. (2001).
As in Korchagin et al. (2001), we consider the expanding density wave in a purely gaseous
disk with five different metallicities:
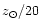 ,
,
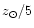 ,
,
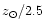 ,
,
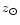 ,
and
,
and
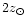 .
Our computations show that the model B-V and
V-K colors are bluer as compared to the Cartwheel's colors for each metallicity
of the star-forming gas.
If dust extinction were solely responsible for this difference between the model and
observed colors, then the model QBVK indices would lie within
the observed limits. Indeed, use of the QBVKindices minimises the uncertainties in observed colors introduced by dust extinction.
However, we find that the model QBVK indices lie beyond the observed limits for most of
the photometric annuli, thus indicating that the reddening of the observed colors with respect to
the model colors of those annuli cannot be attributed to the extinction
gradient in the Cartwheel's disk.
.
Our computations show that the model B-V and
V-K colors are bluer as compared to the Cartwheel's colors for each metallicity
of the star-forming gas.
If dust extinction were solely responsible for this difference between the model and
observed colors, then the model QBVK indices would lie within
the observed limits. Indeed, use of the QBVKindices minimises the uncertainties in observed colors introduced by dust extinction.
However, we find that the model QBVK indices lie beyond the observed limits for most of
the photometric annuli, thus indicating that the reddening of the observed colors with respect to
the model colors of those annuli cannot be attributed to the extinction
gradient in the Cartwheel's disk.
In case of
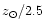 and
and
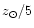 ,
however, the QBVK indices
of the Cartwheel's outer region (annuli VI-IX)
lie within the observed limits, thus indicating that dust extinction could
be responsible for the reddening of the observed colors in this region.
Here, we note that Korchagin et al. (2001)
used a uniform metallicity of
,
however, the QBVK indices
of the Cartwheel's outer region (annuli VI-IX)
lie within the observed limits, thus indicating that dust extinction could
be responsible for the reddening of the observed colors in this region.
Here, we note that Korchagin et al. (2001)
used a uniform metallicity of
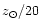 to model the Cartwheel's radial color gradient.
While this choice is certainly justified for the Cartwheel's outer ring (Fosbury & Hawarden 1977),
it is hard to believe that such a low metallicity is present in the Cartwheel's central regions.
Due to very weak line emission, there have been no measurements of heavy element
abundances interior to the outer ring.
However, it is known that most galactic disks have a metallicity gradient, with metallicities in the
nucleus up to
to model the Cartwheel's radial color gradient.
While this choice is certainly justified for the Cartwheel's outer ring (Fosbury & Hawarden 1977),
it is hard to believe that such a low metallicity is present in the Cartwheel's central regions.
Due to very weak line emission, there have been no measurements of heavy element
abundances interior to the outer ring.
However, it is known that most galactic disks have a metallicity gradient, with metallicities in the
nucleus up to 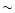 10 times higher than in the outer parts of the disk
(Smartt
10 times higher than in the outer parts of the disk
(Smartt  Rolleston 1997).
In this paper we assume that metallicity gradient is present in the pre-collision gaseous disk of
the Cartwheel galaxy and choose its value so as to provide a better fit
of the model QBVK indices with those observed in the Cartwheel's disk.
The best fit is found for the metallicity gradient
spanning the range from
Rolleston 1997).
In this paper we assume that metallicity gradient is present in the pre-collision gaseous disk of
the Cartwheel galaxy and choose its value so as to provide a better fit
of the model QBVK indices with those observed in the Cartwheel's disk.
The best fit is found for the metallicity gradient
spanning the range from
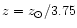 at annuli IX, VIII, and VII,
at annuli IX, VIII, and VII,
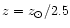 at annuli VI and V, to
at annuli VI and V, to
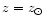 at annuli IV-nucleus.
at annuli IV-nucleus.
The open circles in Fig. 4a show the model B-V/V-K colors of stellar populations formed in the
density wave propagating in a purely gaseous disk with the metallicity gradient given above.
The open circles in Fig. 4b illustrate the corresponding model QBVK indices.
The outer three photometric annuli (9, 8, and 7) and the nucleus are identified both for
the model colors and the colors observed in the Cartwheel galaxy,
the latter being shown by the filled triangles with error bars.
The model B-V/V-K colors do not exhibit a regular reddening towards the nucleus and
are bluer as compared to the Cartwheel's colors.
On the same time, the model and the Cartwheel's QBVK indices
show a good correspondence for the outer ring and two inner annuli adjacent to the outer ring,
implying that the difference of the corresponding B-V/V-Kcolors in Fig. 4a might be related to the internal extinction gradient existing in
the Cartwheel's disk.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F4.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg52.gif) |
Figure 4:
a) The B-V and V-K color-color diagram and b)
the QBVK combined index profiles. The open circles show the model profiles
for the density wave of amplitude
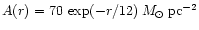 and velocity
and velocity
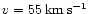 expanding radially in a purely gaseous disk.
The metallicity gradient of the gaseous disk ranges from
expanding radially in a purely gaseous disk.
The metallicity gradient of the gaseous disk ranges from
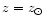 at the
nucleus+annuli I-IV,
at the
nucleus+annuli I-IV,
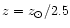 at annuli V-VI, to
at annuli V-VI, to
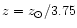 at annuli VII-IX. The filled triangles with error bars show the radial color gradients
and index profiles observed in the Cartwheel galaxy.
at annuli VII-IX. The filled triangles with error bars show the radial color gradients
and index profiles observed in the Cartwheel galaxy.
|
| Open with DEXTER |
Now we consider an extreme case and assume that the difference of the model and observed
B-V/V-K colors in Fig. 4a is solely due to internal extinction gradient in the Cartwheel's disk.
We warn, however, that this assumption is applicable only to those annuli,
which QBVK indices lie within the observed limits,
as in this case their colors are reddened along the correction vector.
The values of color excess E(B-V), implied by this difference, are listed
in Col. 2 of Table 1. The surface densities of gas
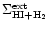 in Col. 3 are obtained from Col. 2 using the standard mass-to-dust ratio and
RV=3.1 (Bohlin et al. 1978). Column 4 in Table 1 gives
the observed surface densities of atomic and molecular hydrogen
in Col. 3 are obtained from Col. 2 using the standard mass-to-dust ratio and
RV=3.1 (Bohlin et al. 1978). Column 4 in Table 1 gives
the observed surface densities of atomic and molecular hydrogen
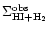 in each annulus
(Higdon 1996; Horellou et al. 1998).
in each annulus
(Higdon 1996; Horellou et al. 1998).
It can be noticed that the extinction-estimated gas densities in Col. 3 are below the detection upper
limit for the outer ring+annulus VII.
Hence, the internal extinction gradient can indeed be responsible for the difference between
the observed and model B-V/V-K colors of this region in Fig. 4a.
Very large values of
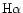 equivalent widths were found by
Higdon (1995) in the Cartwheel's outer ring, especially in the ring's southern quadrant,
which peaks at
equivalent widths were found by
Higdon (1995) in the Cartwheel's outer ring, especially in the ring's southern quadrant,
which peaks at
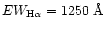 and exceeds
and exceeds
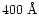 everywhere. The
everywhere. The
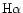 equivalent width
(
equivalent width
(
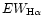 )
is sensitive to the ratio of ionizing,
massive (>
)
is sensitive to the ratio of ionizing,
massive (>
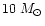 )
stars to lower mass red giant stars and can be used
to measure the relative strengths of these two populations (Kennicutt 1983).
Table 2 presents
)
stars to lower mass red giant stars and can be used
to measure the relative strengths of these two populations (Kennicutt 1983).
Table 2 presents
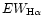 of stellar populations born in the expanding ring
density wave.
of stellar populations born in the expanding ring
density wave.
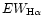 are computed at the time when the wave reaches
the present position of the Cartwheel's outer ring at 16 kpc. All parameters of Fig. 4 are retained.
As it is seen in Table 2, the averaged over
annuli VIII and IX model value of
are computed at the time when the wave reaches
the present position of the Cartwheel's outer ring at 16 kpc. All parameters of Fig. 4 are retained.
As it is seen in Table 2, the averaged over
annuli VIII and IX model value of
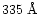 is close to
the azimuthally averaged value of
is close to
the azimuthally averaged value of
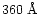 measured
in the Cartwheel's outer ring by Higdon (1995).
The large model and observed
measured
in the Cartwheel's outer ring by Higdon (1995).
The large model and observed
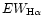 in the outer ring
indicate that the Cartwheel is experiencing the first major episode of star formation at this radius.
in the outer ring
indicate that the Cartwheel is experiencing the first major episode of star formation at this radius.
Table 2:
Model
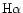 equivalent widths.
equivalent widths.
| annulus |
VI |
VII |
VIII |
IX |
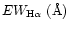 |
0.03 |
0.3 |
53 |
620 |
Korchagin et al. (2001) argued that the colors of the Cartwheel galaxy cannot be reproduced
by a density wave propagating in a purely gaseous disk irrespective of its metallicity.
While this is certainly true for the
Cartwheel's inner region, we find that the observed B-V/V-K colors and QBVK
indices of the outer ring+annulus VII can be well reproduced by a density wave
propagating in a purely gaseous disk of
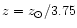 .
.
4.2 The pre-collision old stellar disk
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F5.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg69.gif) |
Figure 5:
The radial surface brightness profiles in a)
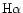 and b)
R-band, c) the B-V/V-K color-color diagram,
and d) the QBVK radial profiles.
The open circles show the model profiles for the density wave of amplitude
and b)
R-band, c) the B-V/V-K color-color diagram,
and d) the QBVK radial profiles.
The open circles show the model profiles for the density wave of amplitude
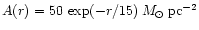 and velocity
and velocity
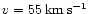 expanding radially in the galactic disk. The central surface brightness
in the V-band of the old stellar component of the galactic disk
is
expanding radially in the galactic disk. The central surface brightness
in the V-band of the old stellar component of the galactic disk
is
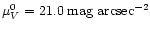 and the scale length is R0=2 kpc.
The gaseous component has the metallicity gradient ranging from
and the scale length is R0=2 kpc.
The gaseous component has the metallicity gradient ranging from
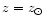 at
the nucleus+annuli I-III to
at
the nucleus+annuli I-III to
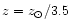 at annuli IV-IX. The filled triangles with error bars
show a), b) the measured radial surface brightness profiles, c) the radial color gradients
and d) index profiles of the Cartwheel galaxy.
at annuli IV-IX. The filled triangles with error bars
show a), b) the measured radial surface brightness profiles, c) the radial color gradients
and d) index profiles of the Cartwheel galaxy. |
| Open with DEXTER |
To reconcile the model and observed B-V/V-K colors and QBVKindices of the Cartwheel's inner region in Fig. 4 (annuli VI-nucleus),
we follow the prescriptions given in Korchagin et al. (2001) and consider
a possibility that the pre-collision Cartwheel had an old stellar disk.
We assume that the properties of the old stellar disk are
typical for the late-type Freeman disks (
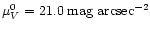 and R0=2 kpc) rather than for low surface
brightness galaxies (
and R0=2 kpc) rather than for low surface
brightness galaxies (
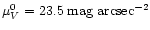 and R0=5 kpc) as adopted by Korchagin et al. (2001).
Metallicity of the pre-collision gaseous disk is assumed to span the range from
and R0=5 kpc) as adopted by Korchagin et al. (2001).
Metallicity of the pre-collision gaseous disk is assumed to span the range from
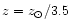 at six outermost annuli to
at six outermost annuli to
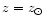 at the inner annuli and the nucleus.
Galactic collision generates an expanding density wave, which adds the newly born
stellar populations to the old stellar populations existed before the collision.
at the inner annuli and the nucleus.
Galactic collision generates an expanding density wave, which adds the newly born
stellar populations to the old stellar populations existed before the collision.
Figures 5a and 5b show the resulting model
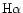 and R-band
surface brightness profiles. Interior to the outer ring, the model R-band profile
shows a good correspondence to the observed profile, as illustrated in Fig. 5b by
the open circles and filled triangles respectively.
Measured by Higdon (1995) R-band surface brightness of the inner ring
is roughly twice the peak value of the outer ring and this feature is well reproduced in Fig. 5b.
and R-band
surface brightness profiles. Interior to the outer ring, the model R-band profile
shows a good correspondence to the observed profile, as illustrated in Fig. 5b by
the open circles and filled triangles respectively.
Measured by Higdon (1995) R-band surface brightness of the inner ring
is roughly twice the peak value of the outer ring and this feature is well reproduced in Fig. 5b.
The model radial B-V/V-K colors, shown by the open circles in Fig. 5c,
exhibit regular reddening towards the nucleus reminiscent of that observed in the Cartwheel's disk.
The sequence of QBVK indices observed in the Cartwheel's outer ring
and the inter-ring region is well reproduced, as shown by the open circles in Fig. 5d.
This implies that the difference of the model and observed colors for each photometric
annulus can be understood in terms of internal extinction.
This is certainly not true
for the Cartwheel's inner ring and the nucleus, as their B-V/V-K colors
are not reddened along the correction vector with respect to the model colors.
This results in a substantial disagreement of the corresponding QBVK indices.
As in Sect. 4.1, we consider an extreme case and assume that the
difference of the model and observed B-V/V-K colors of the outer ring and the inter-ring region
in Fig. 5c is solely due to internal extinction gradient in the Cartwheel's disk.
The values of E(B-V) implied by this difference are listed
in Col. 2 of Table 3.
It can be noticed that the extinction-estimated gas densities in Col. 3 are below the detection upper
limit in Col. 4 for all annuli. Hence, the internal extinction gradient can be responsible for the
difference between the observed and model B-V/V-K colors of the inter-ring region
and the outer ring in Fig. 5c.
Comparison of Figs. 4a and 5c shows that the model B-V/V-K colors of
the outer ring+annulus VII in Fig. 5c
are not affected noticeably by the old stellar populations.
Indeed, Fig. 6 illustrates the ratio of fluxes of the old stellar populations to
the young density-wave-born stellar populations in V-band (
![$F_{V}[\rm o/dw]$](/articles/aa/full/2001/39/aah2789/img74.gif) )
and
K-band (
)
and
K-band (
![$F_{K}[\rm o/dw]$](/articles/aa/full/2001/39/aah2789/img75.gif) )
as a function of galactic radius.
It is seen that the old stellar populations dominate at the smaller radii (
)
as a function of galactic radius.
It is seen that the old stellar populations dominate at the smaller radii (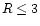 kpc)
in both bands. At the intermediate radii (
kpc)
in both bands. At the intermediate radii (
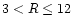 kpc), input from the young
stellar populations to the total flux in V-band is ten times (on average)
the input from the old stellar populations, while both stellar populations contribute
comparable fluxes in K-band. The young stellar populations totally dominate
at the larger radii (R > 12 kpc) in both bands.
This indicates that the colors of the Cartwheel's outer ring are determined by the young
density-wave-born stellar populations and can be reproduced by a density wave
propagating in a purely gaseous disk, as argued in Sect. 4.1.
We note, however, that the interpretation of colors
of the Cartwheel's inner region do require the presence of the old pre-collision stellar disk, which
is in agreement with conclusions of Korchagin et al. (2001).
kpc), input from the young
stellar populations to the total flux in V-band is ten times (on average)
the input from the old stellar populations, while both stellar populations contribute
comparable fluxes in K-band. The young stellar populations totally dominate
at the larger radii (R > 12 kpc) in both bands.
This indicates that the colors of the Cartwheel's outer ring are determined by the young
density-wave-born stellar populations and can be reproduced by a density wave
propagating in a purely gaseous disk, as argued in Sect. 4.1.
We note, however, that the interpretation of colors
of the Cartwheel's inner region do require the presence of the old pre-collision stellar disk, which
is in agreement with conclusions of Korchagin et al. (2001).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F6.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg78.gif) |
Figure 6:
The ratio of fluxes in V-band (the upper frame) and K-band (the lower frame)
of the old, pre-collision stellar populations to the young stellar populations formed
in the density wave. All parameters of
Fig. 5 are retained. The numbering of annuli is in accordance with Fig. 1. |
| Open with DEXTER |
Thus, theoretical modelling of the color gradients observed in the Cartwheel galaxy
suggests that the pre-collision Cartwheel was a late-type spiral (R<12 kpc)
embedded into an extensive HI disk. The subcritical gas disk of
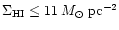 (Higdon 1996)
at larger radii (
(Higdon 1996)
at larger radii (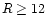 kpc) prevented robust massive star formation (MSF)
and chemical enrichment over the disk's lifetime.
The passage of a companion galaxy initiated an outwardly propagating ring density wave,
which triggered high rates of MSF along it's perimeter.
The density wave has passed the original extend of the pre-collision
stellar disk and is currently moving in the predominantly gaseous,
low-metallicity disk at the radius of the Cartwheel's outer ring (
kpc) prevented robust massive star formation (MSF)
and chemical enrichment over the disk's lifetime.
The passage of a companion galaxy initiated an outwardly propagating ring density wave,
which triggered high rates of MSF along it's perimeter.
The density wave has passed the original extend of the pre-collision
stellar disk and is currently moving in the predominantly gaseous,
low-metallicity disk at the radius of the Cartwheel's outer ring (
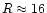 kpc).
kpc).
Another result of color modelling is a possible presence of a
large internal extinction gradient across the outer ring of the Cartwheel (annuli VIII and IX).
Indeed, if the difference between the model and observed B-V/V-K colors of the
Cartwheel's outer ring in Figs. 4a and
5c can be attributed to the internal extinction as shown above, then E(B-V)
in the outer edge of the outer ring (annulus IX)
is about two times
higher as compared to E(B-V) in the inner edge of the outer ring (annulus VIII).
Models of ring galaxies predict that the Cartwheel's outer ring is the current
location of a star formation wave (Appleton  Struck-Marcell 1987;
Struck-Marcell
Struck-Marcell 1987;
Struck-Marcell  Appleton 1987).
The star formation wave is expected to compress the gas ahead by a coherent action
of shock waves, expanding superbubbles, ultraviolet radiation from massive stars, ets.,
thus increasing the value of extinction at the leading edge of the wave.
Observationally proved presence of such an extinction gradient across
the outer ring might be a powerful confirmation of propagating nature of star formation
in ring galaxies. More sophisticated models of star formation in the ring galaxies are
needed to investigate these aspects.
Appleton 1987).
The star formation wave is expected to compress the gas ahead by a coherent action
of shock waves, expanding superbubbles, ultraviolet radiation from massive stars, ets.,
thus increasing the value of extinction at the leading edge of the wave.
Observationally proved presence of such an extinction gradient across
the outer ring might be a powerful confirmation of propagating nature of star formation
in ring galaxies. More sophisticated models of star formation in the ring galaxies are
needed to investigate these aspects.
5 The inner ring and the nucleus
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F7.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg82.gif) |
Figure 7:
a) The B-V/V-K color-color diagram, and b)
the QBVK radial profiles. All parameters are the same as in Fig. 5,
but with an additional 10-Myr-old burst of star formation in the Cartwheel's nuclear region. |
| Open with DEXTER |
In the cloud-fluid models of ring galaxies, Appleton  Struck-Marcell (1987)
predicted that the infall of gas behind the ring should lead to a strong compression of gas in
the central parts. In case of the Cartwheel galaxy, a large-scale radial infall of HI was reported
by Higdon (1996). Recent observation in the mid-infrared
(Charmandaris et al. 1999) and in
Struck-Marcell (1987)
predicted that the infall of gas behind the ring should lead to a strong compression of gas in
the central parts. In case of the Cartwheel galaxy, a large-scale radial infall of HI was reported
by Higdon (1996). Recent observation in the mid-infrared
(Charmandaris et al. 1999) and in
 line
(Amram et al. 1998) have shown that the Cartwheel's inner ring and
the nucleus might have a low level star formation activity.
line
(Amram et al. 1998) have shown that the Cartwheel's inner ring and
the nucleus might have a low level star formation activity.
In this section, we perform numerical modelling of the B-V/V-K colors and
QBVK indices measured in the Cartwheel's inner ring and the nucleus (Marcum et al. 1992).
To do this, we assume that the star formation takes place not only along the perimeter of the expanding
density wave, but also in the central region of the Cartwheel.
We set off an outwardly propagating density enhancement of amplitude
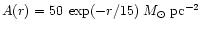 and velocity
and velocity
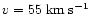 and compute the luminosity of pre-collision and post-collision stars
as in Sect. 4.
Then we add the luminosity of stars born in the central region and use the total luminosity
in each annulus to calculate the resulting surface brightness, color, and index profiles.
and compute the luminosity of pre-collision and post-collision stars
as in Sect. 4.
Then we add the luminosity of stars born in the central region and use the total luminosity
in each annulus to calculate the resulting surface brightness, color, and index profiles.
While the inner ring and the nucleus are currently
HI poor with
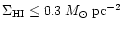 (Higdon 1996),
they have a significant amount of molecular hydrogen as suggested by
recent CO observations of Horellou et al. (1998).
We assume that molecular hydrogen in
the Cartwheel is exponentially distributed in the central 9.5 kpc, with the peak surface density of
35
(Higdon 1996),
they have a significant amount of molecular hydrogen as suggested by
recent CO observations of Horellou et al. (1998).
We assume that molecular hydrogen in
the Cartwheel is exponentially distributed in the central 9.5 kpc, with the peak surface density of
35
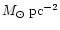 in the nucleus and the scale length of 3 kpc
(radius of the inner ring). The total mass of
in the nucleus and the scale length of 3 kpc
(radius of the inner ring). The total mass of 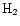 is then close
is then close
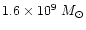 ,
as estimated by Horrelou et al. (1998)
for the solar metallicity. Metallicity in the central part of the Cartwheel is unknown.
We assume that star-forming gas in the central 9.5 kpc is of solar metallicity,
as suggested by numerical modelling in Sect. 4.
The star formation law in the nucleus and the inner ring is assumed to follow
the classic Schmidt behavior:
,
as estimated by Horrelou et al. (1998)
for the solar metallicity. Metallicity in the central part of the Cartwheel is unknown.
We assume that star-forming gas in the central 9.5 kpc is of solar metallicity,
as suggested by numerical modelling in Sect. 4.
The star formation law in the nucleus and the inner ring is assumed to follow
the classic Schmidt behavior:
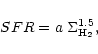 |
(6) |
with the rate of star formation a defined as in Eq. (3).
We use two conventional models for star formation: a constant star formation and a short starburst.
In both models star formation proceeds until
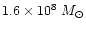 of stars is formed,
which is
of stars is formed,
which is 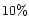 of the initial mass of gas. In the short starburst model we increase
the rate of star formation a to shorten the star formation event.
of the initial mass of gas. In the short starburst model we increase
the rate of star formation a to shorten the star formation event.
Constant star formation in the nuclear region for the last 60 Myr.
Assumption of the constant star formation activity in the Cartwheel's central region allows
us to reach a better agreement between the model and observed
B-V/V-K colors and QBVK indices of the nucleus and the inner ring.
The model QBVK index of the inner ring lies within
the observed limits, which is not the case in Fig. 5d. Now, however, the
inner ring+nucleus and the outer ring have comparable
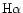 fluxes.
This is problematic since observations indicate that the Cartwheel lacks
strong
fluxes.
This is problematic since observations indicate that the Cartwheel lacks
strong
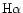 emission from the nucleus and the inner ring,
while it has a large
emission from the nucleus and the inner ring,
while it has a large
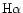 luminosity in the outer ring
(Higdon 1995; Amram et al. 1998).
We assume that the lack of strong
luminosity in the outer ring
(Higdon 1995; Amram et al. 1998).
We assume that the lack of strong
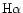 emission from the nucleus and the inner ring is the result of a burst-like nature
of star formation in the nuclear region.
If the active star formation in the nucleus+inner ring had ceased about ten
million years ago, then the observed
emission from the nucleus and the inner ring is the result of a burst-like nature
of star formation in the nuclear region.
If the active star formation in the nucleus+inner ring had ceased about ten
million years ago, then the observed
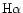 flux would have
fallen considerably at present.
flux would have
fallen considerably at present.
Short starburst in the nuclear region. Infall of gas into central parts of a galaxy is
known to trigger starbursts. We assume that the large-scale radial infall of gas,
reported by Higdon (1996), has triggered a short starburst in the
Cartwheel's nucleus and the inner ring ten million years ago.
The resulting model B-V/V-K radial color gradients and QBVK
radial profiles are illustrated with the open circles in Figs. 7a and 7b respectively,
while the filled triangles with error bars indicate the corresponding radial profiles observed in
the Cartwheel galaxy. The sequence of QBVK indices observed in the galaxy is
well reproduced, as shown by the open circles in Fig. 7b.
Now, the model peak value of
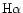 surface brightness at the outer ring
is 60 times larger than the model peak value at the nucleus, which is close to what is
observed in the Cartwheel galaxy (Amram et al. 1998).
surface brightness at the outer ring
is 60 times larger than the model peak value at the nucleus, which is close to what is
observed in the Cartwheel galaxy (Amram et al. 1998).
The difference of the model and Cartwheel's B-V/V-K colors of the inner ring (annulus I)
and the nucleus, which is seen in Fig. 7a, can be
explained in terms of internal extinction using the same approach as in Sect. 4.
Implied by this difference, color excess E(B-V) of the Cartwheel's nucleus
is
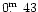 ,
which is equivalent to
,
which is equivalent to
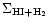 of 19
of 19
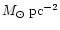 (Bohlin et al. 1978). If molecular hydrogen is exponentially distributed in the central 9.5 kpc,
then this value of
(Bohlin et al. 1978). If molecular hydrogen is exponentially distributed in the central 9.5 kpc,
then this value of
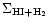 might be below the detection upper limits of molecular hydrogen in the Cartwheel's nucleus.
Hence, the internal extinction can be responsible for the difference between
the model and observed B-V/V-K colors of the nucleus shown in Fig. 7a.
This conclusion is also true for the Cartwheel's inner ring,
where
might be below the detection upper limits of molecular hydrogen in the Cartwheel's nucleus.
Hence, the internal extinction can be responsible for the difference between
the model and observed B-V/V-K colors of the nucleus shown in Fig. 7a.
This conclusion is also true for the Cartwheel's inner ring,
where
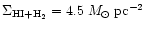 is inferred
using
is inferred
using
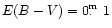 .
Now, the young post-collision stellar populations and the old pre-collision stellar
populations contribute equally to the total flux in the V- and K-bands at the smaller
radii (
.
Now, the young post-collision stellar populations and the old pre-collision stellar
populations contribute equally to the total flux in the V- and K-bands at the smaller
radii (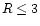 kpc).
kpc).
In this paper we model and analyse the B-V/V-K radial color gradients observed in
the Cartwheel ring galaxy. We use the QBVK combined color indices
to analyse the Cartwheel's B-V/V-K radial color gradients. Use of the QBVKindices minimises the uncertainties in the observed B-V and V-K colors introduced
by dust extinction. We find that the QBVK radial profile observed in
the Cartwheel's disk falls naturally into three sub-profiles, which correspond to
the nucleus+inner ring, the inter-ring region, and the outer ring of the galaxy.
Combined color indices are insensitive to dust extinction and can be directly understood
in terms of stellar populations. This implies that the nucleus+inner ring, inter-ring region,
and the outer ring of the Cartwheel might consist of different stellar populations.
To model the optical and near-infrared color properties of the Cartwheel galaxy, we use a toy model,
which imitates the propagating star formation in the galactic disk. Namely, we assume that the
star formation rate is proportional to a Gaussian density enhancement, expanding
radially in a gaseous disk. We use the population synthesis to calculate the color properties
of stellar populations formed by this density enhancement.
The results of color modelling strongly suggest that the pre-collision Cartwheel was a
late-type spiral. The old stellar disk was embedded
in an extensive gaseous disk of sub-critical surface density.
Existence of the pre-collision stellar disk of low surface brightness
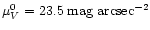 ,
extending out to the current location of
the Cartwheel's outer ring at 16 kpc (R0=5 kpc),
was first reported by Korchagin et al. (2001). However, we find that the
pre-collision stellar disk might be smaller, extending out to
,
extending out to the current location of
the Cartwheel's outer ring at 16 kpc (R0=5 kpc),
was first reported by Korchagin et al. (2001). However, we find that the
pre-collision stellar disk might be smaller, extending out to 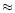 12 kpc.
Properties of the pre-collision stellar disk are typical for the late-type Freeman disks
(
12 kpc.
Properties of the pre-collision stellar disk are typical for the late-type Freeman disks
(
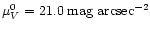 and R0=2 kpc) rather than for low surface
brightness galaxies as found by Korchagin et al. (2001).
The pre-collision gaseous disk had a metallicity gradient ranging from
and R0=2 kpc) rather than for low surface
brightness galaxies as found by Korchagin et al. (2001).
The pre-collision gaseous disk had a metallicity gradient ranging from
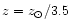 at the outer parts to
at the outer parts to
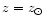 in the central parts.
Approximately 300 Myr ago, the Cartwheel galaxy collided face-on and near-centrally
with a companion galaxy. This collision generated an expanding ring density wave,
which triggered massive star formation along the wave's perimeter.
in the central parts.
Approximately 300 Myr ago, the Cartwheel galaxy collided face-on and near-centrally
with a companion galaxy. This collision generated an expanding ring density wave,
which triggered massive star formation along the wave's perimeter.
The results of our modelling show that the young stellar populations, formed by the density wave,
dominate in the outer ring. Thus, the wave of star formation has passed the extent of
the pre-collision stellar disk and is currently moving in the predominantly gaseous,
low-metallicity disk at the radius of 16 kpc.
In the region between the inner and the outer rings, however,
the young stellar populations and the pre-collision stellar populations
contribute comparable fluxes in K-band. We find that the Cartwheel's B-V/V-K colors
and QBVK indices of this inter-ring region cannot be successfully modelled without
taking into consideration the relative input from the old, pre-collision stellar populations.
The observed colors of the nucleus+inner ring are most difficult to model. Neither
young stellar populations formed in the expanding density wave,
nor their mixture with the old, pre-collision stellar populations can reproduce the
B-V and V-K colors of the Cartwheel's nucleus+inner ring.
We find that an additional 10-Myr-ago burst of star formation in the nuclear regions,
along with the visual extinction of
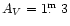 ,
might be responsible for
the peculiar colors of the Cartwheel's nucleus.
This is not totally unexpected, as some observational evidence
points to the existence of a low-level star formation activity in the central regions (Amram et al. 1998;
Charmandaris et al. 1999) and the large-scale radial infall of gas in the Cartwheel,
reported by Higdon (1996), might have triggered bursts of star formation in the past.
,
might be responsible for
the peculiar colors of the Cartwheel's nucleus.
This is not totally unexpected, as some observational evidence
points to the existence of a low-level star formation activity in the central regions (Amram et al. 1998;
Charmandaris et al. 1999) and the large-scale radial infall of gas in the Cartwheel,
reported by Higdon (1996), might have triggered bursts of star formation in the past.
Acknowledgements
The authors thank two anonymous referees for useful comments.
The authors are grateful to Dr. Y. D. Mayya for providing his population synthesis program.
Our special thanks are to Dr. V. Korchagin for continuous encouragement. We also thank Dr. de Jong
for providing his observational data.
-
Amram, O., Mendes de Oliveira, C., Boulesteix, J., & Balkowaki, C.
1998, A&A, 330, 881
In the text
NASA ADS
-
Appleton, P. N., & Marston, A. P. 1997, AJ, 113, 201
In the text
NASA ADS
-
Appleton, P. N., & Struck-Marcell, C. 1987, ApJ, 318, 103
In the text
NASA ADS
-
Bica, E., & Alloin, D. 1987, A&A, 186, 49
In the text
NASA ADS
-
Bizyaev, D., Zasov, A., & Kajsin, S. 2000, Proc. of 33rd ESLAB Symp.,
Star formation from the small to the large scale, ed. F. Favata, A. A. Kaas, & A.
Wilson, ESA SP-445
In the text
-
Bizyaev, D., Zasov, A., & Kaisin, S. 2001, Astron. Lett., 27, 217
In the text
-
Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 225
In the text
-
Cardelli, J. A., Geoffrey, C. C., & Mathis, J. S. 1989, ApJ, 345, 245
In the text
NASA ADS
-
Charlot, S. 1996, in From Stars to Galaxies, ed. C. Leitherer,
U. Fritze-v. Alvensleben, & J. Huchra (San Francisco: ASP), ASP Conf. Ser., 98, 275
In the text
-
Charlot, S., & Bruzual, A. 1991, ApJ, 367, 126
In the text
NASA ADS
-
Charmandaris, V., Laurent, O., Mirabel, et al. 1999, A&A, 341, 69
In the text
NASA ADS
-
de Jong, R. S. 1996, A&A, 313, 377
NASA ADS
-
Fosbury, R. A. E., & Hawarden, T. G. 1977, MNRAS, 178, 473
In the text
NASA ADS
-
Freeman, K. C. 1970, ApJ, 160, 811
NASA ADS
-
Higdon, J. L. 1995, ApJ, 455, 524
In the text
NASA ADS
-
Higdon, J. L. 1996, ApJ, 467, 241
In the text
NASA ADS
-
Horellou, G., Charmandaris, V., Combes, et al. 1998, A&A, 340, L51
In the text
NASA ADS
-
Kennicutt, R. C. 1983, ApJ, 272, 54
In the text
NASA ADS
-
Kennicutt, R. C. 1989, ApJ, 344, 685
In the text
NASA ADS
-
Korchagin, V., Mayya, Y. D., & Vorobyov, E. I. 2001, ApJ, 554, 281
In the text
NASA ADS
-
Kurucz, R. L. 1992, Stellar Populations of Galaxies, ed. B. Barbuy
& A. Renzini (New York: Kluwer), IAU Symp., 149, 225
In the text
-
Marcum, P. M., Appleton, P. N., & Higdon, J. L. 1992,
ApJ, 399, 57
In the text
NASA ADS
-
Mayya, Y. D. 1995, AJ, 109, 2503
In the text
NASA ADS
-
Mayya, Y. D. 1997, ApJ, 482, L149
In the text
NASA ADS
-
Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269
In the text
NASA ADS
-
Smartt, S. L., & Rolleston, W. R. J. 1997, ApJ, 481, L47
In the text
NASA ADS
-
Struck-Marcell, C., & Appleton, P. N. 1987, ApJ, 323, 480
In the text
NASA ADS
-
Zasov, A. V., & Moiseev, A. V. 1998, Astron. Lett., 24, 677
In the text
-
Worthey, G. 1994, ApJS, 95, 107
In the text
NASA ADS
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F1.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg20.gif)
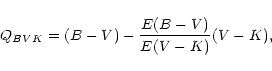
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F1.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Tfigure2.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F3.ps}\end{figure}](/articles/aa/full/2001/39/aah2789/Timg26.gif)
![\begin{displaymath}C(r-vt)=A(r) \; \exp\left[ - {(r-vt)^2 \over L^2}\right],
\end{displaymath}](/articles/aa/full/2001/39/aah2789/img27.gif)
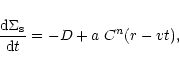
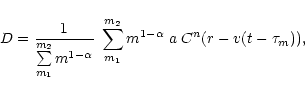
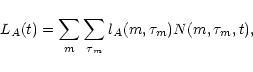
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F4.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg52.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F5.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F6.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg78.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2789F7.ps} \end{figure}](/articles/aa/full/2001/39/aah2789/Timg82.gif)