A&A 377, 898-910 (2001)
DOI: 10.1051/0004-6361:20011092

An analysis of the light curve of the post common envelope binary MT Serpentis

A. Bruch¹ - L. P. R. Vaz² - M. P. Diaz³

1 - Laboratório Nacional de Astrofísica, CP 21, 37500-000 Itajubá - MG, Brazil
2 - Departamento de Física, ICEx-UFMG, CP. 702, 30123-970 Belo Horizonte - MG, Brazil
3 - Instituto Astronômico e Geofísico, USP, CP 9638, 01065-970 São Paulo - SP, Brazil

Received 8 March 2001 / Accepted 26 July 2001

Abstract
Photometric observations of MT Ser, the central star of the planetary nebula Abell 41 are presented. The periodic modulations detected by Grauer & Bond (1983) are confirmed, thus firmly establishing the binary nature of MT Ser. The significantly enlarged time base permits us to derive more accurate ephemeris. The orbital period is either P₁ = 0.113226533 days or twice that value, P₂ = 0.226453066 days. We analyze the light curve (after a careful subtraction of the nebular contribution) with the Wilson-Devinney light curve synthesis routine. Since it is not a priori clear which is the true orbital period of MT Ser, two radically different models, one based on P₁ the other on P₂ are considered: (1) A low temperature component orbiting around a hot sub-dwarf. The variability is then due to a reflection effect together with ellipsoidal variations of one or both components. (2) Two hot sub-dwarfs of similar temperature and luminosity, partially eclipsing each other and exhibiting ellipsoidal variations. In both models, the primary as well as the secondary component are required to almost fill their respective Roche lobes. A contact configuration is possible. Pros and cons can be found for either of the two models. A final decision between them has to await the observations of a radial velocity curve. The orbital period is currently decreasing at a rate of $\dot{P}/P = -1.15 \times 10^{-9}\, {\rm d}^{-1}$. Interpreting this as due to mass loss via a stellar winds permits us to estimate mass loss rates depending on the different model assumptions.

Key words: stars: variables: other - stars: individual: MT Ser

   
1 Introduction

MT Ser is the binary central star of the planetary nebula Abell 41. Its double star nature manifests itself through orbital variations with a period of $2^{\rm h}43^{\rm m}$ discovered by Grauer & Bond (1983) (hereafter referred to as GB83). Green et al. (1984) classified the primary as a sdO star. The secondary is suspected by GB83 to be a late type dwarf star, but - as Green et al. (1984) pointed out - an alternative model is not excluded. GB83 showed that angular momentum loss from the system caused by gravitational radiation can bring the surface of the secondary in touch with its critical Roche surface within the relatively short time of $1.8 \times 10^9$ years within their model. When this happens the sub-dwarf primary will have evolved into a white dwarf and MT Ser is expected to initiate activity as a cataclysmic variable. It should therefore presently be regarded as a pre-cataclysmic binary.

Such systems are thought to be the result of common envelope evolution of an initially much wider binary: On the red giant or asymptotic giant branch the more massive primary expands to an extent that it engulfs the low mass secondary which is still on the main sequence. Frictional angular momentum loss lets the secondary spiral towards the core of the giant. Depending on the initial parameters and the details of the evolution during the common envelope phase, after the ejection of the envelope the core of the giant - now a hot sub-dwarf - and the late type dwarf may reappear as a close binary with an orbital period of the order of hours.

Not many binaries in the phase between the common envelope and the birth as a cataclysmic variable are known. MT Ser as the central star of a planetary nebula has obviously emerged from the common envelope phase only quite recently. Therefore, the system might still exhibit features which can shed some light on the so far largely unknown details of the common envelope evolution. Although this is not the topic of the present work a basic understanding of the structure and the dynamics of MT Ser are an obvious prerequisite for an investigation of such features. Since these fundamental parameters are still unknown or at least quite uncertain, we will try here to improve this situation.

Although the planetary nebula around MT Ser, Abell 41, has been the subject of numerous studies which sometimes included global properties of the central star (Abell 1966; Shaw & Kaler 1989; Tylenda et al. 1989; Tylenda et al. 1991; and Pollacco & Bell 1997; to cite only a few of the more important papers) detailed investigations remain scarce. In their discovery paper of the orbital variations GB83 derive some limits of system parameters but were not able to settle down on definite values. Not even the orbital period is certain: It cannot be excluded that the period is twice as long as the value quoted above, a suspicion which will be substantiated in the present paper. Taking the results of GB83 together with a spectrum in the blue spectral range, which apart from the strong nebular emission lines also reveals some absorptions of the central star, permitting it to be classified as sdO, Green et al. (1984) modified the model for MT Ser somewhat (in particular concerning the temperature of the hot component) but otherwise largely agreed with GB83. However, they also discuss briefly an alternative model consisting of two hot sub-dwarfs. Further detailed observations of MT Ser have not been published.

Here, we report about time resolved photometric observations of the system with the aim to obtain a high quality orbital light curve which enables the determination of reliable system parameters via light curve synthesis using the Wilson-Devinney code (Wilson & Devinney 1971; Wilson 1979).

2 Observations

All observations were obtained at the 0.6-m telescope of the Instituto Astronômico e Geofísico, University of São Paulo, at the Pico dos Dias Observatory of the Laboratório Nacional de Astrofísica, Brazil. Light curves were observed in five nights in August 1997. A Bfilter was used throughout in order to inhibit the contamination of the measurements by the strongest nebular emission lines (in particular H$\alpha$). Moreover this facilitates a comparison with the results of GB83 who have also observed most of their light curves in B. The integration time was $90^{\rm s}$, with a dead time of $8^{\rm s}$ between integrations. A back-illuminated EEV CCD was used as detector. A journal of the observations is given in Table 1.

 

 

Table 1: Journal of observations of MT Ser.

	HJD
Date	(2450000+)	$N^\ast$
1997 Aug. 22	683.403-.589	144
1997 Aug. 23	684.488-.562	65
1997 Aug. 25	686.401-.580	153
1997 Aug. 26	687.400-.575	154
1997 Aug. 27	688.405-.573	148

$\parbox{6.9cm}{$^\ast$\space Number of integrations.}$

   
3 Data reduction

Since the aim of this study is a quantitative light curve analysis, care must be taken to subtract the contribution of the planetary nebulae from underneath the stellar image before measuring its magnitude because any such contribution would dilute the light curve, faking smaller amplitudes. Therefore, standard photometry techniques on CCD images cannot be used.

In order to solve this problem, first a high S/N image of the nebula was constructed: The individual CCD frames of 1997 Aug. 26 (a night with photometric observing conditions) were cross-correlated in x and ydirections to one particular frame which served as template. Gaussian fits to the peak of the cross-correlation function yielded the positional drift between individual frames. After correction for this shift, the frames were co-added. An attempt to subtract (after sky subtraction) scaled versions of the profile of the brightest star in the field of view, located approximately $4^{\prime}_{\raisebox{.6ex}{\hspace{.12em}.}}3$ west and 3' north of MT Ser (henceforth called C₁), always left spurious spikes or dips in the difference image, presumable because of slight dependences of the PSF on the location in the image. Another, less rigorous method met more success: Spline interpolations were calculated for the pixels of each image line and column containing a contribution of the planetary nebula. Those regions which are (according to a visual inspection) noticeably influenced by the PSF of the central star, got zero weight. Thus, the spline was interpolated beneath the stellar profile. The difference between the spline and the original image then contains only the contribution of the central star. It was subtracted from the original, yielding the intrinsic profile of the nebula. Clearly, this procedure is not ideal. The outer (visually not obvious) parts of the stellar PSF may still contribute to the nebular, and in particular the method assumes that the nebula is not strongly structured beneath the stellar profile. However, the star being much brighter than the integrated nebular light beneath the stellar image we are confident that such systematic errors remain small enough to be neglected in view of the other sources of uncertainty in the final results.

Summing up all the counts of the nebula (taking care to avoid some faint stars projected on its outer parts) and comparing them to the counts observed from star C₁, yields a magnitude difference $m_{\rm neb} - m_{C_1} = 3^{\raisebox{.3ex}{\scriptsize m}}_{\raisebox{.6ex}{\hspace{.17em}.}}06$. The systematic errors certainly dominate over the random ones. Therefore, we do not quote statistical errors.

In order finally to perform the photometry of MT Ser, the IRAF script LCURVE was applied which makes use of DAOPHOT/APPHOT routines. In the normal mode this routine defines annuli for the star and the sky around the centre of the stellar image which scale with the width of the PSF in order to account for seeing variations. In this way, instrumental magnitudes for C₁ and several other comparison stars in the field were determined. However, this method cannot be applied to MT Ser because it would inevitably lead to a wrong background subtraction. Therefore, in the next reduction step the extraction aperture was held fixed at a diameter of 4 pixels. The sky radius was defined large enough to ensure that no nebular contribution would be seen and was also fixed. With these parameters, magnitudes were determined for MT Ser and again for the comparison stars. At a FWHM of the stellar profile of 2.0 pixels some light of the star is lost when a 4 pixel aperture is used. This holds for MT Ser as well as for the comparison stars. The difference between the instrumental magnitudes of the latter, determined with the standard procedure and the small aperture, respectively, measures thus the loss of light which occurred when the small aperture was used. It was applied as a correction to the magnitude determined for MT Ser, after the contribution of the nebula to the light in the small aperture - determined from the nebular image constructed above - had been subtracted.

The mean magnitude difference between MT Ser and C₁ is found to be $3^{\raisebox{.3ex}{\scriptsize m}}_{\raisebox{.6ex}{\hspace{.17em}.}}21 \pm 0^{\raisebox{.3ex}{\scriptsize m}}_{\raisebox{.6ex}{\hspace{.17em}.}}11$, where the uncertainty is dominated by the orbital variations of MT Ser. Together with the above derived magnitude difference between C₁ and the nebula, this leads to a flux ratio $F_{\rm MT}/F_{\rm neb}=0.87$ in the B band. This value agrees quite well with the ratio of 0.814 determined by Shaw & Kaler (1989).

   
4 Orbital ephemeris and light curve

According to an estimate of GB83 the time-scale for the decrease of the orbital period of MT Ser due to gravitational radiation is comparatively short. Therefore, they urge other observers to obtain timings. The present light curves permit us to measure the epochs of six minima (a further minimum occurred a few minutes before the end of the observations, making an accurate timing difficult; therefore it is not considered here).

The individual light curves were fitted by a spline which was then evaluated to find the minima. The corresponding timings are listed in Table 2 which also includes the minimum epochs measured by GB83.

 

 

Table 2: Times of minimum for MT Ser.

HJD	E	O-C $_{\rm lin}$	O-C $_{\rm quad}$
2444703.9734	-3347	-0.003785	-0.002478
2444705.9029	-3330	+0.000868	+0.002168
2445082.9480	0	+0.001618	+0.001618
2445084.8715	17	+0.000267	+0.000261
2445087.9277	44	-0.000651	-0.000667
2445115.6691	289	+0.000250	+0.000145
2445115.7829	290	+0.000823	+0.000718
2445117.7061	307	-0.000825	-0.000937
2445117.8197	308	-0.000450	-0.000562
2445118.7249	316	-0.001065	-0.001180
2450683.4683	49463	-0.002120	-0.002217
2450686.4165	49489	+0.002232	+0.002145
2450686.5278	49490	+0.000334	+0.000247
2450687.4341	49498	+0.000772	+0.000688
2450687.5454	49499	-0.001127	-0.001210
2450688.4521	49507	-0.000201	-0.000281

The ephemeris determined by GB83 are accurate enough so that no cycle count ambiguities occur at the epoch of our measurements. The cycle numbers of the minima observed here are also quoted in Table 2. Combining the present minimum timings with those of GB83, the much longer time base permits us to determine a considerably more accurate period for MT Ser. Improved values for the minimum epoch, T₀, and the period, P, were determined by minimizing $\chi^2$ of the O-C values of the minimum times. The revised ephemeris is:

HJD (min)	=	2445082.9461	+	0.113226533	$\times$	E
		$\pm$ 4		$\pm$ 15

The O-C values of the individual minima with respect to this ephemeris are also given in Table 2.

Although according the to model of GB83 a change of the period due to gravitational radiation should only become detectable on time scales of 100 years or more, we also fitted a quadratic ephemeris to the minimum timings:

HJD(min)=	2445082.94638	+	0.11326899	E-	7.36$\times$10-12	E2
	$\pm 37$		$\pm 12$		$\pm 25$

Table 2 contains the O-C values also for this case. As can be seen, the quadratic term is highly significant within the formal error. The issue of the period derivative will be discussed further in Sect. 7.

The combined light curves, folded on the period P₁ = 0.113226533 days (linear ephemeris), are shown in the upper panel of Fig. 1. Since it cannot be excluded that the true period is twice as long, the light curves were also folded on $2 \times P_1 \equiv P_2$, as shown in the upper panel of Fig. 2. In the P₂ curve the minimum at phase 0.5 appears to be slightly less deep than the one at phase 0. Moreover, there is no indication of flat topped maxima as were seen by GB83 and taken by them as an argument against an ellipticity effect and thus against the longer period. Therefore, the present results appear to be slightly in favor of a true period twice as long as originally assumed. In this case the variations are expected to be due to an elliptical shape of the hotter star (which we will refer to as the primary regardless of its mass being higher or lower than that of the cooler star) and - as it turns out, see Sect. 5.2 - to eclipses, while in the other case they would be explained as a reflection effect off the illuminated face of the less luminous star. Evidently, this has a tremendous bearing on any model of MT Ser. We will not try to decide the question of the true period based on a visual inspection of the light curves alone. We will rather try to find solutions using light curve synthesis for both cases.

	Figure 1: Top: Light curve of MT Ser folded on the nominal orbital period, P=P1, (dots) and two different model light curves (solid and dashed lines). Centre and bottom: O-C curve between the observations and the model light curves; for details, see text.
Open with DEXTER

   
5 Light curve synthesis

In view of the ambiguity of the true orbital period of MT Ser two radically different models for MT Ser appear to be viable.

Model 1: Assuming the shorter of the two possible periods (P₁) to be correct, a reflection effect dominated model suggests itself, with the system consisting of a hot primary and a cooler secondary. The variations are caused by the phase dependent aspect of that side of the secondary star which is heated by the primary. Such a scenario leads to a single maximum and minimum per orbit. This is the model advocated by GB83.

Model 2: If P₂ is the correct period, two minima and maxima per orbit must be explained. This is best done by a model in which ellipsoidal variations dominate. Again, the system is considered to be composed of two components. However, in this case their relative temperatures or luminosities are not constrained a priori. The size of at least one and possibly both of the components is not small compared to its Roche lobe, leading to ellipsoidal deformations of its shape. The orbital variations are then due to the variable aspect of the deformed component(s), leading to two maxima and minima per orbit.

In the following, model calculations using the Wilson-Devinney code (Wilson & Devinney 1971; Wilson 1979) will be analyzed in an attempt to discriminate between these two models.

	Figure 2: Top: Light curve of MT Ser folded on the alternative orbital period, $2 \times P = P_2$, (dots) and model light curve (solid line). Bottom: O-C curve between the observations and the model light curve; for details, see text.
Open with DEXTER

   
5.1 Reflection dominated model

A model light curve of a pure reflection effect has always an almost sinusoidal shape. Different choices of gravitational or limb darkening coefficients lead only to minute modifications. The deviations from a pure sinusoidal shape increase slightly with increasing orbital inclination in the sense that the maximum becomes narrower.

In contrast, the observed light curve of MT Ser has a maximum which is significantly broader than the minimum (see Fig. 1). Moreover, it has not the flat-topped appearance as the light curves observed by GB83 which they used as an argument against a model dominated by ellipsoidal variations. But even in their observations, the flat top does not appear always [see their Fig. 1 (first maximum) and Fig. 3]. In view of the above remarks on the reflection effect, the broad maximum immediately suggests that a pure reflection effect is not able to explain the variations. Moreover, the light curve exhibits an abrupt change in slope close to phase 0.28, and another less obvious break close to phase 0.8. Thus, apart from the reflection effect, some other cause must contribute to the variations.

A formal two-component sine fit with periods fixed at P₁ and P₁/2 matches the observed light curve approximately. While the phases of minimum of both sine terms agree with phase 0 within their uncertainties, the amplitude of the P₁/2-term is 23% of that of the P₁ term. This suggests that a satisfactory description of the light curve might be achieved by allowing for a (modest) contribution of an ellipsoidal effect along with the reflection effect.

Such a hybrid model requires a trade off between several parameters in order to match the observed light curve: (1) the orbital inclination must be small enough so that no eclipses occur; (2) the secondary must be large enough in order to intercept enough radiation of the primary to be heated sufficiently, (3) The ellipsoidal variations must not become so large compared to the reflection effect as to cause a secondary minimum near phase 0.5 in the light curve; (4) the temperature difference between the components must be large enough to cause a significant temperature difference also between the illuminated and unilluminated hemispheres of the secondary, and thus to enable a reflection effect leading to variations with the observed amplitudes in the light curve; (5) if the ellipsoidal variations are due to the secondary, the primary must not be too luminous since otherwise small ellipsoidal variations would be drowned; this can be achieved by reducing either the temperature or the size of the primary; (6) if the ellipsoidal variations are due to the primary, it must fill a considerable fraction of its Roche lobe.

Having these constraints in mind, mode 2 of the Wilson Devinney code (suitable for detached binaries with no constraints on surface potentials) was used in combination with the SIMPLEX parameter optimization algorithm (Caceci & Cacheris 1984) to find a parameter set which leads to an optimal agreement between model light curve and observations. A circular orbit and, for simplicity, black body radiation characteristics for both stars were assumed. The temperature of the primary, T₁, was fixed at 50000 K, following Green et al. (1984). In order not to rely on the uncertain parameter estimates of GB83 all other parameters which might influence the light curve were left free to vary. These are: the orbital inclination i, the temperature of the secondary T₂, the dimensionless surface potentials $\Omega_1$ and $\Omega_2$ of the components (see Kopal 1959), the mass ratio q = M₂/M₁, and the atmospheric constants (gravity darkening exponents $\beta_1$ and $\beta_2$, limb darkening coefficients $\mu_1$ and $\mu_2$, and albedos A₁ and A₂) of both components. We also permitted a contribution of a constant light source (third light L₃; positive or negative) in order to allow for uncertainties in the subtraction of the nebular contribution to the light curve (see Sect. 3). However, in all calculations the best fit solution yielded L₃=0. Finally, a possible slight phase shift $\Delta \phi$ of the minimum with respect to the epoch given in Sect. 4 was taken into account.

The resulting best fit parameters lead to a configuration in which (only) the primary overfills its Roche-lobe. This is unphysical because in such a situation both (not just one) components should be larger than their respective Roche-lobes. Moreover, it is difficult to see how in the ensuing contact configuration a drastic temperature difference between the components could be maintained. Therefore, we imposed the additional constraint on the optimization algorithm that both components must remain within their Roche-lobes.

The best fit solution resulting under these conditions (Model 1.1) is only slightly different from the original solution. It is shown as a thin solid line in Fig. 1. The best fit parameters are listed in Table 3. Instead of the Roche potentials at the stellar surfaces the more directly interpretable Roche-lobe filling factor ( $FF_{\rm RL}$) - defined as the ratio of the distances from the stellar centre to the surface of the star and to the critical Roche surface, respectively, in the direction facing away from the companion star - is given in the table. The parameter errors were derived using the WD differential corrections routine. They are thus based on formal statistics but can probably only be regarded as lower limits to more realistic errors: while the internal errors represent the uncertainty related to the scattering of the observations and to the formal least squares solution, the possible existence of families of practically undistinguishable solutions may result in uncertainty intervals much larger than the formal ones. Regard, for example, the mass ratio which has a small formal error but is quite different for Models 1.1 and 1.3 (see below), although the resulting light curves are practically identical.

As can be seen from Table 3 the errors of the atmospheric parameters $\beta$, $\mu$ and A are exceedingly large, probably due to parameter correlations. Thus, it does not make much sense to handle them as independent parameters. Therefore, in another model run (Model 1.2) they were fixed to plausible values. For stars with radiative envelopes Rafert & Twigg (1980) found empirically a mean value of $\beta = 0.96$ for the gravity darkening exponent. Within the errors this is identical with the usually adopted theoretical value of $\beta=1$ (Lucy 1967). While the primary of MT Ser certainly has got a radiative envelope, this is less clear for the secondary. However, since the parameter optimization for Model 1.2 led to a somewhat hotter secondary than in the case of Model 1.1 (above the limit of the low $\beta$ stars; see Fig. 1 of Rafert & Twigg 1980), $\beta = 1.0$ was adopted for both stars. Test calculation using $\beta = 0.32$ for the cool component (appropriate for stars with convective atmospheres; Lucy 1967) yield almost indistinguishable light curves. Rafert & Twigg (1980) also determined empirically the albedos of stars in the temperature range of interest here and found a mean value of A=1.02. Since this is not significanly different from A=1 and since albedos larger than unity are difficult to explain, we fix the albedos of both components to A=1.0. The limb darkening coefficients were fixed to $\mu_1 = 0.18$ and $\mu_2 = 0.58$as calculated for stars of the respective temperatures and of intermediate surface accelerations ( $\log g = 4.5$) by Wade & Rucinski (1985). Leaving all other parameters free and imposing again the condition that none of the components overfills its Roche-lobe leads to a best fit model as shown by the thick solid line in Fig. 1. The corresponding parameter values and their errors are included in Table 3.

Figure 1 shows that Model 1.2 predicts grazing eclipses, as evidenced by the V-shape of the calculated light curve at phase 0 and the slight dip around phase 0.5 (see insert in Fig. 1). While this improves the fit to the light curve minimum compared with Model 1.1, there is no trace of a secondary eclipse cutting into the maximum in the observations. Therefore, we calculated a third model (Model 1.3), keeping the atmospheric parameters fixed to those of Model 1.2 and the orbital inclination to the value found for Model 1.1. The resulting light curve is virtually indistinguishable from that of Model 1.1. The corresponding best fit parameter values are also included in Table 3.

 

 

Table 3: Best fit WD model parameters for Model 1.

Parameter	Model 1.1	Model 1.2	Model 1.3
i [$^\circ$]	42.52 $\pm$1.73	52.42 $\pm$0.87	42.52$^\ast$
T2 [K]	7517 $\pm$2065	7942 $\pm$260	8866 $\pm$85
$(FF_{\rm RL})_1$	0.995 $\pm$0.051	0.951 $\pm$0.006	0.999 $\pm$0.007
$(FF_{\rm RL})_2$	0.973 $\pm$0.056	0.882 $\pm$0.008	0.971 $\pm$0.012
q = M2/M1	0.916 $\pm$0.014	1.143 $\pm$0.009	1.415 $\pm$0.008
$\beta_1$	0.97 $\pm$2.38	1.0$^\ast$	1.0$^\ast$
$\beta_2$	0.32 $\pm$81.49	1.0$^\ast$	1.0$^\ast$
$\mu_1$	0.15 $\pm$0.27	0.18$^\ast$	0.18$^\ast$
$\mu_2$	0.16 $\pm$0.49	0.58$^\ast$	0.58$^\ast$
A1	1.00 $\pm$39.70	1.0$^\ast$	1.0$^\ast$
A2	2.42 $\pm$8.65	1.0$^\ast$	1.0$^\ast$
$\Delta \phi$	-0.0006 $\pm$0.0006	-0.0002 $\pm$0.0006	-0.0013 $\pm$0.0007

$\parbox{15cm}{ $^\ast$\space Fixed parameter.}$

   
5.2 Ellipsoidal variations dominated model

The light curve folded on Period P₂ (Fig. 2) displays two almost equally deep minima, both of which are quite symmetrical. Above a certain minimum level the slope suddenly becomes less steep. This is best seen close to phase 0.1 (or in binned versions of the light curve). The maxima are significantly broader than the minima.

The minima are very reminiscent of eclipses. Their almost equal depth suggests that both component of the binary system should have a very similar temperature. The out-of-eclipse variations (i.e. the maxima) should then be due to ellipsoidal variations of one or both stars.

The temperature of 50000 K of MT Ser measured by Green et al. (1984) is so high that optical observations always sample the Rayleigh-Jeans part of the spectral energy distribution. The temperatures of both components being very similar in the present model, it is then practically impossible to determine the temperatures of both components by WD model calculations. Only the ratio of the primary and secondary star temperature, T₁/T₂, can be derived in this way. Therefore we fixed T₁ to 50000 K. Tests with other values confirmed that the best fit model is independent of T₁ even if T₁ is varied within a wide range, as long as T₂ is permitted to vary accordingly. The ratio T₁/T₂remains constant.

Choosing again mode 2 of the WD code the same parameters as in Model 1 were left free to vary. The SIMPLEX algorithm (Caceci & Cacheris 1984) then converged on a very good solution (Model 2.1). The best fit light curve is shown as a solid line in Fig. 2. The corresponding parameter values together with their formal errors as derived from the WD differential corrections routine are summarized in Table 4.

 

 

Table 4: Best fit WD model parameters for Model 2.1.

Parameter	Best fit		Formal	Confidence range
	value		error
i [$^\circ$]	67.12	$\pm$	0.36	66.19	...	67.95
T2 [K]	45590	$\pm$	1570	42500	...	49000
$(FF_{\rm RL})_1$	0.990	$\pm$	0.010	0.963	...	1
$(FF_{\rm RL})_2$	0.995	$\pm$	0.005	0.976	...	1
q (M2/M1)	1.982	$\pm$	0.008	1.961	...	1.994
$\beta_1$	1.18	$\pm$	1.26	0.17	...	2.27
$\beta_2$	1.13	$\pm$	0.68	0.35	...	2.00
$\mu_1$	0.14	$\pm$	0.40	0	...	0.53
$\mu_2$	0.15	$\pm$	0.24	0	...	0.53
A1	0.75	$\pm$	1.85	0	...	2.70
A2	0.85	$\pm$	0.84	0.06	...	1.80
$\Delta \phi$	0.0011	$\pm$	0.0003	-0.0019	...	0.0045
L3	-0.0004			-0.0033	...	0.0035

As in the case of Model 1 some parameters are not well constrained, reflecting their small influence on the light curve. These are the gravity darkening exponents ($\beta_1$, $\beta_2$), the albedos (A₁, A₂), and the limb darkening coefficients ($\mu_1$, $\mu_2$). Even so it is satisfying, although possibly accidental, that in spite of the large formal errors the best fit values of the former two quantities determined for MT Ser are not very different from the mean values found empirically for comparable stars by Rafert & Twigg (1980). We recalculated the WD model fit with fixed values of $\beta_1$=$\beta_2$=1; A₁=A₂=1 and $\mu_1$=$\mu_2$=0.18 (see Sect. 5.1). As expected, the resulting best fit values for the free parameters deviate only insignificantly (within the formal errors) from those quoted in Table 4.

As can be seen from Table 4 the best fit solution leads to a configuration in which the two components are almost in contact with each other. Within the formal errors (which may well underestimate the true errors as argued above and will further be elaborated upon below) a contact configuration is permitted.

Moreover, the large value of the mass ratio $q \approx 2$ is somewhat disturbing. The physical implications of the currently discussed model are those of a close binary having just emerged from a common envelope phase (as suggested by the presence of the planetary nebula). If both components are not in contact with each other, this configuration and their similar temperature indicate that they should be in a similar evolutionary stage. This makes it difficult to explain a large difference in mass. If they are in physical and thus thermal contact they might have similar temperatures even if the masses were different. But then we would expect the less evolved and thus less massive star to be heated by the more massive component. It can then attain a similar but not a higher temperature than the latter star. This is in contrast to the derived mass ratio which suggests that the hotter component is the less massive one. It is true that a different scenario might be devised in which the more evolved star lost so much mass during the common envelope phase that it emerges as the less massive component. However, while this might lead to a situation with q slightly larger than 1, it appears difficult to achieve $q \approx 2$ in this way. Note that for similar reasons it is difficult to believe in the reality of the mass ratio of q=1.4 ensuing from Model 1.3.

In view of this problem we searched for physically more plausible solutions. Since the components are practically in contact with each other we investigated models adopting WD mode 4 (primary star fills its Roche lobe), mode 5 (secondary star fills its Roche lobe) and mode 6 (both components fill their Roche lobe; contact configuration). The important parameters determining the shape of the light curve are the orbital inclination i, the secondary star temperature T₂, the mass ratio q, and the surface potential $\Omega$ of the secondary (mode 4) or the primary (mode 5) component, respectively. The other components were fixed to the theoretical values discussed above or the best fit values found in the initial model calculations.

It turned out that in all modes good solutions could be achieved within a wide range of mass ratios. They are practically indistinguishable from the solid line in Fig. 2. Thus, q is not well constrained. Therefore, in additional model calculations the mass ratio was fixed to a number of different values, and only the other parameters were permitted to vary. The differences between the individual models were minute: For all values of the mass ratio, i and T₂ varied within a small range. In the case of modes 4 and 5 the component which does not fill its Roche lobe generally attains a filling factor of more than 0.99. For some mass ratios the additional constraint that none of the stars overfills its Roche lobe had to be imposed in order to avoid a formal fit solution with a filling factor >1, indicating that any deviations from a true contact configuration are not significant. In view of the similarity of the results obtained with WD modes 4, 5 and 6 we restrict the subsequent discussion to the calculations in mode 6 (contact configuration) for simplicity (Model 2.2).

Statistically acceptable solutions (as discussed in more detail in Sect. 6.1) were found for values $0.19 \le q \le 5.7$. The best fit solutions for the corresponding values of T₂ and i are plotted as a function of q in Fig. 3.

	Figure 3: Best fit values for the orbital inclination (solid line; left hand scale) and the secondary star temperature (broken line; right hand scale) as a function of the adopted mass ratio q=M2/M1 for Model 2, calculated assuming a contact configuration.
Open with DEXTER

   
6 Implications of the model calculations

In this section we will discuss the implications of the model calculations with the aim to decide between the two competing models. First, the formal acceptability of the fits is evaluated, while a discussion of the astrophysical aspects follows in Sect. 6.2.

   
6.1 Formal aspects of the model calculations

The prime requirement for a good fit is - apart from its astrophysical viability - that the O-C curve, i.e. the difference between the observations and the model light curve, should consist of randomly distributed data. In the lower frames of Figs. 1 and 2 the O-C curves of Models 1.1, 1.2 and 2.1, respectively, are shown.

It is obvious that the O-C curves of Model 1 show considerable structure, indicating a less than ideal model fit. The observed minimum is deeper than the calculated one, yielding positive O-C values. The opposite is true for the maximum; in particular in the case of Model 1.2 which predicts an unobserved shallow secondary minimum. But also at phases intermediate between maximum and minimum correlated residuals are clearly present.

In order to quantify the statistical deviations of the O-C values from a purely random distribution, a formal R-statistics analysis (Bruch 1999) was undertaken. For Model 1.1, R = 0.157 (for 651 data points). The corresponding R-probability (i.e. the statistical probability for completely random data scattered around 0 to have an even smaller value of R, or - somewhat loosely spoken - the probability for correlations to be present in the residuals) is P_R = 0.99998. Model 1.2 yields an R-probability even closer to 1. Thus, the formal analysis confirms the visual impression that from a purely statistical point of view Model 1 does not lead to a good fit to the observations.

This is different for Model 2.1. In this case the O-C curve does not show systematic deviations from a random distribution. The R-probability is P_R = 0.20 which is in excellent agreement with the hypothesis of the absence of correlated residuals. Therefore, statistically, Model 2.1 is completely satisfactory. The same holds true for Model 2.2. The R-probability remains close to P_R=0.20 for $0.19 \le q \le 5.7$. Only very close to the borders of this range P_R starts to increase reaching a value of $P_R \approx 0.9$ at the edges.

These positive results open another way to determine confidence ranges which may be more realistic than the formal errors quoted in Table 4. We modified each parameter (keeping all other parameters fixed) until the R-probability for the residuals reaches P_R = 0.90, indicating a significant correlations between the residuals and thus systematic differences between data and fit. The corresponding "90% confidence ranges'' for the parameters are also quoted in Table 4. In some cases the parameters assumed unphysical values before P_R=0.90 was reached. Then, the physically sensible limit enters the table. This applies in particular to the upper boundary of the Roche-lobe filling factor. Larger values lead to an over-contact configuration (but note that in contrast to Model 1 this is not wholly impossible in the present case because the temperatures of the components are similar!). Although these confidence ranges might be somewhat more realistic than the formal errors they must still be regarded as lower limits because they do not take into account correlations between parameters: The effect of modifying one parameter could be neutralized by corresponding modifications of one or more other parameters, permitting wider parameter ranges.

This last point becomes particularly evident regarding the large range of permitted values for the mass ratio when a contact configuration is adopted. As was argued in Sect. 5.2 not the entire range of statistically acceptable values of q makes sense physically, but only values of . To be definite, we limit the subsequent discussion to two particular values, namley q=1.0 (Model 2.2.1) and q=0.5 (Model 2.2.2). The corresponding confidence ranges for the free parameters in Model 2.2 are listed in Table 5.

 

 

Table 5: Parameter confidence ranges for Model 2.2.

	q = 1.0		q = 0.5		...
inclination i	64.8	...	66.6	66.4	...	68.1
temperature T2	41800	...	48900	41040	...	48350

Finally, we note that the phase shift $\Delta \phi$ for both, Model 1 and Model 2, is well compatible with 0 within the confidence or error range. Therefore, there is no need to revise the zero-point of the ephemeris given in Sect. 4. The contribution of third light - 0 for Model 1, and expressed in Table 4 in fractions of the total system brightness at phase 0.25 for Model 2 - is vanishingly small, suggesting that the subtraction of nebular light was even more successful than could be expected. But since there is always the specter of parameter correlations we tried to find solutions with a larger (positive or negative) contribution of third light. However, these attempts did not meet success.

   
6.2 Astrophysical implications of the models

Perhaps the most significant result of the model calculations is the fact that (for both models) the primary as well as the secondary components of MT Ser are very close to filling their respective Roche lobes.

In the subsequent discussion we will compare model predictions - considering Models 1.1, 2.2.1 and 2.2.2 - concerning the system luminosity and the distance to MT Ser to corresponding literature results, mainly based on studies of the planetary nebula. To do so, however, assumptions concerning the component masses are required. For all models, three mass values are considered: Two values which generously embrace the possible mass range which might be realized in MT Ser, and a plausible intermediate one. They will be referred to as the high (H) and low (L) mass limit, and the intermediate (I) mass, respectively. The adopted mass values are listed in Table 6.

In Model 1 we expect the primary component to be a hot sub-dwarf. It will probably evolve into a white dwarf without substantial further mass loss. Therefore, it must not have more than the Chandrasekhar mass (1.43 $M_\odot$), while the lower mass limit is given by the low mass cut-off of the white dwarf mass distribution which we place at 0.2 $M_\odot$ to be on the safe side. As intermediate mass a value of 0.6 $M_\odot$ is adopted, close to the peak of the white dwarf mass distribution. Together with the mass ratio of 0.92 (see Table 3) the component masses as listed in Table 6 result.

 

 

Table 6: Stellar parameters derived from model calculations.

	Model 1.1			Model 2.2.1			Model 2.2.2
	H	I	L	H	I	L	H	I	L
primary star mass ($M_\odot$)	1.43	0.6	0.2	1.43	0.6	0.2	1.43	0.6	0.4
secondary star mass ($M_\odot$)	1.31	0.55	0.18	1.43	0.6	0.2	0.72	0.30	0.2
component separation ($R_\odot$)	1.38	1.03	0.71	2.22	1.66	1.15	2.02	1.51	1.32
primary star radius ($R_\odot$)	0.62	0.46	0.32	1.00	0.75	0.52	1.05	0.78	0.68
secondary star radius ($R_\odot$)	0.58	0.44	0.30	1.00	0.75	0.52	0.78	0.58	0.51
$\log g\, \rm {(cm\, s^{-2})}$ (primary star)	5.01	4.89	4.73	4.59	4.46	4.31	4.55	4.43	4.37
$\log g\, \rm {(cm\, s^{-2})}$ (secondary star)	5.02	4.90	4.73	4.59	4.46	4.31	4.51	4.38	4.32
system luminosity ( $10^3\,L_\odot$) ( $T_1=50\,000$ K)	2.14	1.20	0.57	9.42	5.28	2.51	8.37	4.68	3.58
system luminosity ( $10^3\,L_\odot$) ( $T_1=35\,000$ K)	0.44	0.25	0.12	2.24	1.31	0.61	2.00	1.13	0.86
MB ( $T_1=50\,000$ K)	0.34	0.97	1.77	-1.38	-0.75	0.06	-1.22	-0.60	-0.30
MB ( $T_1=35\,000$ K)	1.06	1.68	2.48	-0.80	-0.22	0.61	-0.66	-0.03	0.26
distance (kpc) ( $T_1=50\,000$ K; AB=2.28)	5.9	4.9	3.0	13.0	9.7	6.7	12.0	9.0	7.8
distance (kpc) ( $T_1=50\,000$ K; AB=1.09)	10.1	7.6	5.2	22.4	16.8	11.6	20.9	15.7	13.6
distance (kpc) ( $T_1=35\,000$ K; AB=2.28)	4.2	3.2	2.2	9.9	7.6	5.2	9.3	6.9	6.1
distance (kpc) ( $T_1=35\,000$ K; AB=1.09)	7.3	5.5	3.9	17.2	13.1	9.0	16.0	12.0	10.5

Within Model 2 both components are hot sub-dwarfs which are expected to become white dwarfs. Therefore, for Model 2.2.1 (q=1) the above values of 1.43 $M_\odot$, 0.6 $M_\odot$, and 0.2 $M_\odot$ for the H, I, and L cases, respectively, are adopted for both stars, while for Model 2.2.2 (q=0.5) the additional contraint applies that none of the components may have a mass above or below the permitted range for a white dwarf. As intermediate mass case it is assumed that the primary component has a mass corresponding to the peak of the white dwarf mass distribution (0.6 $M_\odot$,).

   
6.2.1 System luminosity

The radii of the components in units of their separation a can be calculated from the Roche potentials at their surfaces as given by the best fit WD model. Both components are severely distorted by tidal effects. We take the stellar radii to be equal to the mean of the distance from their centres to the surfaces in the direction towards the companion star and in opposite direction. A more sophisticated definition of the mean radius is not warranted. Together with the known period, Kepler's third law furnishes the component separation a and then R₁ and R₂ in absolute units. The corresponding numbers are listed in Table 6. Finally, the radii and the temperatures - black body characteristics are assumed - of the two components yield the total luminosity of the system, also listed in Table 6.

The luminosities, based on T₁=50000 K, are in contradiction to values derived in the literature from observation of the planetary nebula. The Zanstra luminosity was determined by Shaw & Kaler (1989) to be <400$L_\odot$, while Tylenda et al. (1991) gave a value of $\log\,L$=2.79 (L=617$L_\odot$), only marginally consistent with the lower luminosity limit for Model 1.1. This discrepancy can be resolved to a large degree if our adopted temperatures are too high. In fact, the Zanstra temperature as measured by Shaw & Kaler (1989) is 35000 K, whereas Tylenda et al. (1991) found $\log T=4.51$ (T=32360K).

In order to investigate the effect of a lower temperature, a new WD solution for Model 1 was determined with T₁ fixed at 35000 K, leaving the more important parameters i, T₂, $\Omega_1$, $\Omega_2$ and q free to vary, while keeping the atmospheric parameters fixed at their previously determined values. The WD fit converged on a solution (the statistical quality of which is as bad as that found in the high temperature case) with a somewhat higher secondary star temperature of 7940 K. Using the fitted values of q to calculate M₂ from the adopted value of M₁ for the H, I and L cases, and the surface potential to obtain the stellar radii, the system luminosity was recalculated as listed in Table 6 ( $T_1=35\,000$ K case). Within Model 2 the secondary star temperature scales linearly with T₁ (see Sect. 5.2). Therefore, the luminosities for the $T_1=35\,000$ K case were simply recalculated using the previously derived stellar radii and the lower temperature values.

It can be seen that in general the luminosities based on Model 1.1 are now even lower than quoted in the literature. Thus, allowing for the uncertainty of the primary star temperature (possibly somewhere between 50000 K and 35000 K) Model 1.1 is not in contradiction with independent measurements of the system luminosity. Concerning Model 2, the calculated luminosities are still too high. Only in the low mass case of Model 2.2.1 it is just within the range of the literature values.

   
6.2.2 The distance to MT Ser

In order to obtain a photometric parallax for MT Ser, the ratio of the total energy emitted per surface unit of black bodies with temperatures such as those of the MT Ser components to the energy emitted per wavelength unit at the central wavelength of the B band (4400 Å) was first calculated. The luminosities of the individual components were divided by this ratio and then the resulting values of the two stars were summed, yielding the energy emitted by the system per wavelength unit at 4400 Å. Together with the calibration constant of Bessel (1979) for the B band this yields the absolute B magnitudes as listed in Table 6 for the two cases $T_1=50\,000$ K and $T_1=35\,000$ K.

This energy corresponds to the mean apparent B magnitude of MT Ser which can be estimated from Figs. 1 and 2 of GB83. However, the light level is different at the two observations, B=15.63 on 1982, May 28, and B=15.77 during 1982, April. GB83 attribute this difference to different filter sets and diaphragm sizes used at the two occasions, and in consequence to different contributions from the surrounding planetary nebula. At a diameter of $18^{\prime\prime}_{\raisebox{.6ex}{\hspace{.12em}.}}4$ (Acker et al. 1992) the latter has a size typical for apertures used in photoelectric photometry. Therefore we assume that those observations yielding the brighter mean magnitude for MT Ser contains most of the planetary nebula. The flux ratio between the nebula and the central star derived in Sect. 3 translates into a magnitude difference of $0^{\raisebox{.3ex}{\scriptsize m}}_{\raisebox{.6ex}{\hspace{.17em}.}}83$. Thus, the B magnitude of the central star alone is $16^{\raisebox{.3ex}{\scriptsize m}}_{\raisebox{.6ex}{\hspace{.17em}.}}46$. This is in good agreement with Shaw & Kaler (1989) who found B=16.45$\pm$0.11.

The last ingredient needed to determine a photometric parallax is the interstellar extinction. Shaw & Kaler (1989) derived the reddening constant c (the logarithmic extinction at H$\beta$) from the H$\alpha$-to-H$\beta$ ratio of the planetary nebula as c=0.85. Interpolating between their values of the conversion factor between c and E(B-V), which is itself a function of c (see also Kaler & Lutz 1985), we get E(B-V)=0.56. Assuming the ratio between total to selective absorption to be R=3.1 and using the interstellar extinction curve of Cardelli et al. (1989) this yields an absorption in the B band of $A_B = 2^{\raisebox{.3ex}{\scriptsize m}}_{\raisebox{.6ex}{\hspace{.17em}.}}28$. A value of c discrepant from that of Shaw & Kaler (1989) has been derived by Tylenda et al. (1991). They give three values (two based on the H$\alpha$-to-H$\beta$ ratio and the other one on the radio-to-H$\beta$ ratio) with a mean of c=0.38 which translates into A_B=1.09. An independent estimate of the extinction by Green et al. (1984) is based on the comparison of the expected colours of a pure Rayleigh-Jeans spectrum and the observed colours of MT Ser. They find A_V=1.5, corresponding to A_B=2.0, close to the higher of the two values derived from nebular physics.

The resulting distances for the high and low temperature cases and the two absorption values are listed in Table 6. In the literature statistical distances for the planetary nebula are cited as 4.3 kpc (Abell 1966), 4.51 kpc (Cahn & Kaler 1971), 5.4 kpc (Maciel 1984), <3.76 kpc (Shaw & Kaler 1989), and 4.60 kpc (Cahn et al. 1992). This is consistent with the range of photometric parallaxes predicted from Model 1 in the high absorption case. In constrast, the parallaxes derived from Model 2 are only marginally consistent with the literature values in the low mass, low temperature, high aborption case.

These results are certainly a strong argument in favour of Model 1. However, it would be premature to rule out Model 2 based on the only marginal consistency of the predicted distance with measurements for the planetary nebula. It is well known that such measurements are notoriously difficult and unreliable as discussed e.g. by Cahn et al. (1992), resulting in significant systematic errors.

   
6.2.3 The surface gravity of the components

Green et al. (1984) estimated the surface gravity of MT Ser comparing the mean of their two spectra with synthetic spectra for hot high-gravity stars of Wesemael et al. (1984). They get $\log g = 6 \pm 1$. With the component radii as given in Table 6 and the assumed masses surface gravities can be calculated for the various models. They are also quoted in Table 6. In the case of Model 1 the secondary can be disregarded in this context because its contribution to the total light is very small; therefore the observed surface gravity is only due to the primary.

The calculated values for $\log g$ are only marginally consistent with the observations, and more so for Model 1 than for Model 2. Several factors may contribute to this discrepancy:

(1) Green et al. (1984) based their estimate of $\log g$ on LTE model atmosphere calculations. They point out that such models overestimate gravities by factors of 2-4 as compared to more realistic NLTE models.

(2) The surface gravity is a sensitive function of the absorption line width. Larger widths lead to higher gravities. In a close binary system such as MT Ser a bound rotation of the components can be expected. Considering the orbital inclination, the period, and the stellar radii, projected rotational velocities of 97-187 kms^-1 (Model 1) and 105-205 kms^-1 (Model 2) are calculated for the different model assumptions.

(3) The surface gravity quoted by Green et al. (1984) is based on the sum of two spectra. Possible line shifts due to orbital motion which may mimick a broader line are not considered. In the different cases of Model 1 the orbital inclination, the component separation, the period and the mass ratio yield a projected radial velocity amplitude of the primary star (the contribution of the secondary to the optical light is negligible) in the range 109-210 kms^-1. Within Model 2 both components have comparable luminosities [ $L_1/L_2 = (R_1^2/R_2^2) \times (T_1^4/T_2^4) \approx 0.69$ in the most favourable case]. Therefore, the observed spectrum will be a superposition of the spectra of both components. Hence even in a single spectrum the lines are broadened by orbital motion. Here, the expected radial velocity difference of the components is up to 237-452 kms^-1 in the different model cases.

(4) At least within Model 1 a significant reflection effect is present which will tend to reduce the depth of the absorption lines.

In order to investigate if the effects of rotation and orbital motion are able to broaden the observed spectral lines sufficiently to mimick the high surface gravity observed by Green et al. (1984) we calculated line profiles for H$\beta$, assuming LTE and hydrostatic equilibrium (and neglecting radiation pressure) for a temperature of 40000 K (note that in this case the line depth is somewhat deeper than for higher temperatures but the shape of the lines is not much affected). Three profiles were calculated assuming $\log g$=6; $V \sin i$=0 (profile h), $\log g$=5; $V \sin i$=0 (profile l1) and $\log g$=5; $V \sin i$=200kms^-1 (profile l2).

As expected, profile h is significantly broader than profiles l1 and l2. The difference between the latter is basically confined to the line centres. The rotation decreases the line depth, but the flancs are hardly affected. Thus, a rotation of the star up to the maximum velocity expected in the case of MT Ser does not significantly broaden the line. Therefore, this effect is not likely to explain the discrepancy between observed and predicted surface gravities.

This is different when orbital motion is considered. We shifted profile l2 by $\pm2.7$ Å ( $166\, {\rm km\,s}^{-1}$) and added the results in order to simulate the combined profile due to two stars in orbital revolution. The results (as well as profile h) were convolved with a Gaussian in order to mimick the resolution of the MT Ser spectrum of Green et al. (1984). The final line shapes of the simulated binary line and the high gravity line differ in detail, but - disregarding the shallow outer parts of the line flancs and the depth relative to the continuum - are not so different as to be easily distinguished in a spectrum with a S/N ratio as low as observed by Green et al. (1984). This, together with the fact that the value of $\log g$ quoted by Green et al. (1984) may in reality be an upper limit, lets us conclude that the apparent disparity between the observed and the calculated surface gravity of MT Ser is not a matter of concern.

Although best fit values of the only model parameters which are directly a function of the surface gravity, namely the limb darkening coefficients, are well consistent with high gravity hot stars (Wade & Rucinski 1985), their confidence ranges are large enough so that no contradictions arise even if considerably lower gravities are assumed. This holds true also if the component temperatures are as low as those proposed by Tylenda et al. (1991).

   
6.2.4 The geometry of the system

From the shape of the planetary nebula in a high-resolution CCD-image Pollaco & Bell (1997) deduce an orbital inclination of 66$^\circ$ for the central binary system. This holds true under the assumption that an elliptical structure seen close to the centre of the nebula is in fact circular and inclined to the line of sight, and if it has been ejected in the orbital plane. Comparing this to the results or our model calculations we find disagreement with Model 1 ( $i=42^\circ_{\raisebox{.6ex}{\hspace{.05em}.}}5$ for Model 1.1 and $i=48^\circ_{\raisebox{.6ex}{\hspace{.05em}.}}8$ for Model 1.2), whereas the agreement with Model 2 (Model 2.1: $i=67^\circ_{\raisebox{.6ex}{\hspace{.05em}.}}1$; Model 2.2.1: $i=65^\circ_{\raisebox{.6ex}{\hspace{.05em}.}}7$; Model 2.2.2: $i=67^\circ_{\raisebox{.6ex}{\hspace{.05em}.}}2$) is almost perfect.

   
7 The derivative of the orbital period and the mass loss rate

In Sect. 4 it was found that the orbital ephemeris has a significant negative quadratic term, indicating a decreasing period. The derivative of the period is given by $\dot{P} \equiv {\rm d}P/{\rm d}t = 2b/P$, where b is the coefficient of E²of the quadratic ephemeris. Thus, $\dot{P} = -(1.30 \pm 0.04)\times 10^{-10}$if P=P₁ and $\dot{P} = -(2.60 \pm 0.09)\times 10^{-10}$if P=P₂ [note that $b(P_2) = 4\times b(P_1)$]. The relative period decrease is then $\dot{P}/P = - (1.15 \pm 0.04) \times 10^{-9}\, {\rm d}^{-1}$.

The period derivative is three orders of magnitudes larger than predicted by GB83 who assumed gravitational radiation to be the sole agent for angular momentum (AM) loss. Qualitatively, this difference is readily explained if the mass loss which gave origin to the formation of the planetary nebula is still ongoing.

In order to quantify this idea we assume that one or both binary components lose mass via a stellar wind. The ejected mass takes away rotational AM of the stars. In a close binary system such as MT Ser bound rotation may be assumed. Thus, rotational AM loss will result in a decrease of the binary orbit. In order to derive constraints on the mass loss from the system, me may therefore, in a reasonable approximation, equate the orbital angular momentum loss as indicated by the negative period derivative to the rotational AM loss of the component stars due to a stellar wind. This is an approximate approach because regarding the AM balance both, orbital and rotational contributions have to be considered, whereas equating the above mentioned quantities only the orbital angular momentum is regarded. While the orbital motion is certainly responsible for the major part of the total AM of the system, in view of the relative sizes of the components as derived in Sect. 5, and depending on their internal structure, the rotational angular momentum may not be negligible altogether. However, for an approximate determination of the mass loss from the system it will suffice to regard only the orbital AM loss here.

In a strongly idealized scenario we assume an isotropic wind to emanate from the stellar surface and to take away an amount of angular momentum corresponding to the AM of the wind mass due to the stellar rotation at the location where it left the star. The quantification of this concept for the individual stellar surface elements and the integration over the entire surface yields a rate of angular momentum loss of

$$\dot{J}_{\rm rot} = \frac{\pi}{3}\, \frac{\dot{M}}{P} \, R_{\rm eff}^2$$

where $\dot{M}$ is the entire mass loss rate from the star, $R_{\rm eff}$ is the effective stellar radius (assuming a spherical star) which - for the time being, but see below - is taken to be the geometrical radius, and P is the rotational period which is considered here as identical to the orbital period.

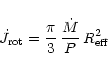
In an inertial reference frame the orbital AM, $J_{\rm orb}$, (assuming a circular orbit) can be expressed as a function of the period, P, the masses, M₁ and M₂, of the components (assumed to be point-like) and the orbital radius, a₁, of the primary star. The temporal derivative of the orbital AM, $\dot{J}_{\rm orb}$, is then the sum of the partial derivatives with respect to P, M₁, M₂and a₁. Of course, in a Keplerian orbit these are not independent. Since the derivative of the orbital period, $\dot{P}$, is a measured quantity, and because we are interested in the mass loss rates (i.e. $\dot{M}_1$ and $\dot{M}_2$) we use Kepler's third law to express a₁in terms of P, M₁ and M₂. This yields $\dot{a}_1$ in terms of $\dot{P}$, $\dot{M}_1$ and $\dot{M}_2$. Using the corresponding expression to eleminate $\dot{a}_1$ from the equation for $\dot{J}_{\rm orb}$, we finally get a (somewhat lengthy) expression for the derivative of the orbital angular momentum which depends on P, M₁, M₂, a₁, $\dot{P}$, $\dot{M}_1$ and $\dot{M}_2$. Except for the latter two quantities all are known either from direct observations or were derived within a specific model (see Table 6). Thus, choosing values for $\dot{M}_2$and $\dot{M}_2$ such that $\dot{J}_{{\rm rot},1} + \dot{J}_{{\rm rot},2} = \dot{J}_{\rm orb}$ gives us an estimate (within the numerous approximations involved) for the mass loss of the system.

For Model 1 we assume that only the primary (evolved) star loses mass. Then, $\dot{M}_{\rm tot} \equiv \dot{M}_1 + \dot{M}_2 = \dot{M}_1$. For Model 2 we investigate the cases $\dot{M}_{\rm tot} = \dot{M}_1$, $\dot{M}_{\rm tot} = \dot{M}_2$ and $\dot{M}_1 = \dot{M}_2 = 0.5 \, \dot{M}_{\rm tot}$. Within Model 1 agreement between $\dot{J}_{\rm rot}$ and $\dot{J}_{\rm orb}$is achieved for mass loss rates of $1.8\times 10^{-7}~M_\odot~{\rm yr}^{-1}$, $7.3\times 10^{-8}~M_\odot~{\rm yr}^{-1}$ and $2.4\times 10^{-8}~M_\odot~{\rm yr}^{-1}$ in the H, I and L cases, respectively.

In contrast, no solution exists for Model 2. For all mass loss rates the rotational angular momentum loss is less than the predicted orbital angular momentum loss. This is only different, if an "efficiency factor'' f for the rotational AM loss is introduced, assuming that $R_{\rm eff} = fR$, where R is the true geometrical radius of the star. This may be thought of as roughly simulating a magnetically coupled wind which dynamically decouples from the stellar rotation only at the radius $R_{\rm eff}$. It is then found that solutions for $\dot{M}$ such that $\dot{J}_{\rm rot} = \dot{J}_{\rm orb}$ exist for efficiency factors for Model 2.2.1, and - in the case of Model 2.2.2 - for ( $\dot{M}_{\rm tot} = \dot{M}_1$), ( $\dot{M}_1 = \dot{M}_2$) and ( $\dot{M}_{\rm tot} = \dot{M}_2$). The functional dependence between the efficiency factor and the total mass loss rate is shown in Fig. 4 for Model 1.1 (upper frame), Model 2.2.1 (case $\dot{M}_1 = \dot{M}_2$; middle frame) and Model 2.2.2 (case $\dot{M}_1 = \dot{M}_2$; lower frame).

Figure 4: Total mass loss rate from the stellar components of MT Ser necessary to explain the observed period derivative as a function of the efficiency factor for removal of rotational angular momentum by a stellar wind for Models 1.1 (assuming $\dot{M}_{\rm tot} = \dot{M}_1$) ( top), Model 2.2.1 ( $\dot{M}_1 = \dot{M}_2$) ( middle) and Model 2.2.2 ( $\dot{M}_1 = \dot{M}_2$) ( bottom). For details, see text.

Open with DEXTER

   
8 Conclusions

We have analyzed the light curve of MT Ser, the binary central star of the planetary nebula Abell 41, within the framework of two quite different models. An unambiguous decision between the two models appears impossible in view of the current knowledge about the system.

Model 1 consists of a hot sub-dwarf and a cool companion leading to brightness variations dominated by the combined effect of reflection of the light of the hot component off the illuminated surface of the cooler star and of ellipsoidal variations of one or both components. It suffers from an unsatisfactory match between the observed and the best fit WD model light curve. Moreover, the orbital inclination would be much lower than suggested by the morphology of the planetary nebula. Points in favour of Model 1 are the agreement of the predicted system luminosity with that of the central star of the planetary nebula and of the predicted distance with the one derived from nebular physics. These quantities, however, may not be very reliable as pointed out in the literature.

Model 2 explains the observed light curve as being due to the combined effect of partial eclipses and ellipsoidal variations in a system consisting of two hot sub-dwarfs with almost equal temperatures. The points in favour of Model 1 (predicted system luminosity and distance) are just those points where Model 2 has difficulties: Both, luminosity and distance are too high (at least if extreme model parameters are avoided). As if to make up for this deficiency the best fit WD light curve for Model 2 is in excellent agreement with the observations. The O-C curve is indistinguishable from a random distribution of data points. Moreover, the orbital inclination is almost hauntingly close to that derived from the structure of the nebula surrounding MT Ser.

Thus, both models have pros and cons. A final decision may have to be postponed until a radial velocity curve is available which will permit to definitely exclude either the longer or the shorter of the possible values of the orbital period. Such observations are complicated by the strong Balmer emission lines of the planetary nebula superposed upon the stellar absorptions, making the use of the fainter helium lines indispensable for radial velocity measurements. Moreover, in the case of Model 2, blending of the lines of both stellar components will be an additional serious complication.

If the model of two hot sub-dwarfs similar in size and almost in contact with each other in a $5^{\rm h}26^{\rm m}$ orbit is realized MT Ser loses its status as the pre-cataclysmic binary with the shortest orbital period. In fact, it should not be regarded as a pre-cataclysmic binary at all since it will not evolve into a cataclysmic variable; at least not into a classical one. Instead, both components will turn into white dwarfs. Their current separation is such that angular momentum loss due to gravitational radiation (assuming that the currently elevated level of angular momentum loss indicated by the high value of $\dot{P}$ is due to ongoing mass loss of the planetary nebula phase and will not persist for a long time) makes their orbit decay on time scales of $0.6 \times 10^9$ years or $16 \times 10^9$ years in the high and low mass limits, respectively. The system may then turn into a double degenerate cataclysmic variable of the AM CVn type.

Acknowledgements

This work was partially supported by grants of the Conselho Nacional de Pesquisa (CNPq; grant No. 301029), the Fundação Amparo a Pesquisa de Minas Gerais (FAPEMIG; grant No. 205096).

References

 
• Abell, G. O. 1966, ApJ, 144, 259 In the text NASA ADS  
• Acker, A., Ochsenbein, F., Stenholm, B., et al. 1992, Strasbourg-ESO catalogue of galactic planetary nebulae (ESO, Garching) In the text  
• Bessell, M. S. 1979, PASP, 91, 589 In the text NASA ADS  
• Bruch, A. 1999, AJ, 117, 3031 In the text NASA ADS  
• Caceci, M. S., & Cacheris, W. P. 1984, Byte, May 1984, 340 In the text  
• Cahn, J. H., & Kaler, J. B. 1971, ApJS, 22, 319 In the text NASA ADS  
• Cahn, J. H., Kaler, J. B., & Stanghellini, L. 1992, A&AS, 94, 399 In the text NASA ADS  
• Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 247 In the text  
• Grauer, A. D., & Bond, H. E. 1983, ApJ, 271, 259 (GB83) In the text NASA ADS  
• Green, R. F., Liebert, J., & Wesemael, F. 1984, ApJ, 280, 177 In the text NASA ADS  
• Kaler, J. B., & Lutz, J. H. 1985, PASP, 97, 700 In the text NASA ADS  
• Kopal, Z. 1959, Close Binary Systems (Chapman and Hall, London) In the text  
• Lucy, L. B. 1967, Z. Astrophys., 65, 89 In the text  
• Maciel, W. J. 1984, A&AS, 55, 253 In the text NASA ADS  
• Pollacco, D. L., & Bell, S. A. 1997, MNRAS, 284, 32 In the text NASA ADS  
• Rafert, J. B., & Twigg, L. W. 1980, MNRAS, 193, 76 In the text  
• Shaw, A. R., & Kaler, J. B. 1989, ApJS, 69, 495 In the text NASA ADS  
• Tylenda, R., Acker, A., Gleizes, F., & Stenholm, B. 1989, A&AS, 77, 39 In the text NASA ADS  
• Tylenda, R., Stasinska, G., Acker, A., & Stenholm, B. 1991, A&A, 246, 221 In the text NASA ADS  
• Wade, R. A., & Rucinski, S. M. 1985, A&AS, 60, 471 In the text NASA ADS  
• Wesemael, F., Green, R. F., & Liebert, J. 1984, ApJS, 58, 379 In the text NASA ADS  
• Wilson, R. E. 1979, ApJ, 234, 1054 In the text NASA ADS  
• Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 In the text NASA ADS