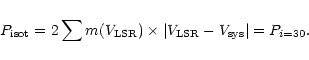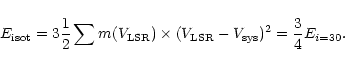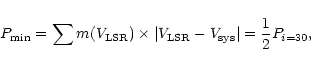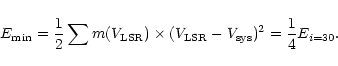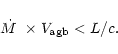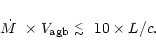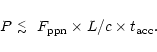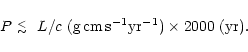A&A 377, 868-897 (2001)
DOI: 10.1051/0004-6361:20011090
Mass, linear momentum and kinetic energy of bipolar flows
in
protoplanetary nebulae
V. Bujarrabal
1
-
A. Castro-Carrizo
1 -
J. Alcolea
1 -
C. Sánchez Contreras
1,2
1 -
Observatorio Astronómico Nacional, Apartado 1143,
28800 Alcalá de Henares, Spain
2 -
Jet Propulsion Laboratory, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
Received 16 February 2001 / Accepted 26 July 2001
Abstract
We have studied the CO emission from protoplanetary nebulae (PPNe).
Our sample is composed of 37 objects and includes, we think, all well
identified PPNe detected in CO, together with the two yellow hypergiants
emitting in CO and one young PN. We present a summary of the existing CO
data, including accurate new observations of the 12CO and 13CO J=1-0
and J=2-1 lines in 16 objects.
We identify in the nebulae a slowly expanding shell (represented
in the spectra by a central core) and a fast outflow (corresponding to the
line wings), that in the well studied PPNe is known to be bipolar.
Excluding poor data, we end up with a sample of 32 sources
(including the 16 observed by us); fast flows are detected in 28 of these
nebulae, being absent in only 4. We present a method to estimate from these
data the mass, "scalar'' momentum and kinetic energy of the different
components of the molecular outflows.
We argue that the uncertainties of our method can hardly lead to
significant overestimates of these parameters, although
underestimates may be present in not well studied objects.
The total nebular mass is often as high as  1
1  ,
and the mass-loss
rate, that (presumably during the last stages of the AGB phase) originated
the nebula, had typical values
,
and the mass-loss
rate, that (presumably during the last stages of the AGB phase) originated
the nebula, had typical values  10-4
10-4  yr-1.
The momentum corresponding to this mass ejection process in most studied
nebulae is accurately coincident with the maximum momentum that radiation
pressure, acting through absorption by dust grains, is able to supply
(under expected conditions). We estimate that this high-efficiency process
lasts about 1000-10000 yr, after which the star has
ejected a good fraction of its mass and the AGB phase ends. On the other
hand, the fast molecular outflows, that have probably been accelerated by
shock interaction with axial post-AGB jets, carry a significant fraction of
the nebular mass, with a very high momentum (in most cases between
1037 and 1040 gcms-1) and very high kinetic energy
(usually between 1044 and 1047 erg).
In general, yellow hypergiants and post-AGB objects with low initial mass
show nebular masses and momenta that are, respectively, higher and lower
than these values.
We compare the momenta of the fast outflows with those that can be supplied
by radiation pressure, taking into account the expected short acceleration
times and some effects that can increase the momentum transfer.
We find that in about 80% of PPNe, the fast molecular flows have
too high momenta to be powered by radiation pressure.
In some cases the momentum of the outflow is
yr-1.
The momentum corresponding to this mass ejection process in most studied
nebulae is accurately coincident with the maximum momentum that radiation
pressure, acting through absorption by dust grains, is able to supply
(under expected conditions). We estimate that this high-efficiency process
lasts about 1000-10000 yr, after which the star has
ejected a good fraction of its mass and the AGB phase ends. On the other
hand, the fast molecular outflows, that have probably been accelerated by
shock interaction with axial post-AGB jets, carry a significant fraction of
the nebular mass, with a very high momentum (in most cases between
1037 and 1040 gcms-1) and very high kinetic energy
(usually between 1044 and 1047 erg).
In general, yellow hypergiants and post-AGB objects with low initial mass
show nebular masses and momenta that are, respectively, higher and lower
than these values.
We compare the momenta of the fast outflows with those that can be supplied
by radiation pressure, taking into account the expected short acceleration
times and some effects that can increase the momentum transfer.
We find that in about 80% of PPNe, the fast molecular flows have
too high momenta to be powered by radiation pressure.
In some cases the momentum of the outflow is  1000 larger than
that carried by radiation pressure; such high factors are difficult to
explain even under exceptional conditions.
Wind interaction is the basic phenomenon in the PN shaping from the
former AGB envelopes; we conclude that this interaction systematically
takes place along a dominant direction and that this process is not powered
by radiation pressure.
Due to the lack of theoretical studies, the possible momentum source
remains a matter of speculation.
1000 larger than
that carried by radiation pressure; such high factors are difficult to
explain even under exceptional conditions.
Wind interaction is the basic phenomenon in the PN shaping from the
former AGB envelopes; we conclude that this interaction systematically
takes place along a dominant direction and that this process is not powered
by radiation pressure.
Due to the lack of theoretical studies, the possible momentum source
remains a matter of speculation.
Key words: stars: AGB and post-AGB - stars: circumstellar matter -
radio-lines: stars - planetary nebulae
Recent observations of molecular lines in the protoplanetary nebulae (PPNe)
OH231.8+4.2 (Sánchez Contreras et al. 1997; Alcolea et al.
2001), M1-92 (Bujarrabal et al. 1998a) and HD101584 (Olofsson & Nyman 1999)
have pointed out the presence of very massive and fast bipolar outflows.
The dynamics of these well studied
objects is dominated by a fast flow in the direction of the symmetry
axis of the nebula, with velocities  100 km s-1. Values of the total
nebular mass close to 1
100 km s-1. Values of the total
nebular mass close to 1  are found. A significant fraction of the mass
belongs to the fast component, that therefore carries very high kinetic
momentum and energy,
are found. A significant fraction of the mass
belongs to the fast component, that therefore carries very high kinetic
momentum and energy, 
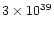 g cm s-1 and 1046 erg,
respectively. (A first measurement of the high mass and
momentum in OH231.8+4.2 is due to Knapp 1986, who also compared the
momenta carried by the nebular mass and the stellar light.)
Typically, the gas in these outflows shows a very low temperature,
g cm s-1 and 1046 erg,
respectively. (A first measurement of the high mass and
momentum in OH231.8+4.2 is due to Knapp 1986, who also compared the
momenta carried by the nebular mass and the stellar light.)
Typically, the gas in these outflows shows a very low temperature,
 10-20 K, this is the reason why they are mainly detected by means of
observations of molecular lines (hot nebular gas is also detected, from
optical and NIR lines for instance, but its mass is much smaller).
It is thought that these axial flows are the result of the acceleration of
the previous AGB wind, that is massive but slow, by shock interaction with
the post-AGB ejections, that would be much faster and run along the axial
direction.
Observations of dust emission and scattered light also allow the detection
of the massive component of the nebula, confirming the mass and density
values found from molecular lines, but do not provide information on the
kinematics, see e.g. Bujarrabal et al. (1997, 1998b), Sahai et al.
(1999b).
10-20 K, this is the reason why they are mainly detected by means of
observations of molecular lines (hot nebular gas is also detected, from
optical and NIR lines for instance, but its mass is much smaller).
It is thought that these axial flows are the result of the acceleration of
the previous AGB wind, that is massive but slow, by shock interaction with
the post-AGB ejections, that would be much faster and run along the axial
direction.
Observations of dust emission and scattered light also allow the detection
of the massive component of the nebula, confirming the mass and density
values found from molecular lines, but do not provide information on the
kinematics, see e.g. Bujarrabal et al. (1997, 1998b), Sahai et al.
(1999b).
Even if the studied objects in those papers are quite luminous (typically,
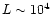
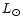 ), the linear momentum associated to the fast
molecular flow is too high (by orders of magnitude) to be supplied
by radiation pressure, given the relatively short times
during which the wind-interaction phenomenon probably took place, 100-200
yr. In this case, we will say that the mass outflow is "overluminous''.
For example, in M1-92, the momentum carried by the
molecular outflow is
), the linear momentum associated to the fast
molecular flow is too high (by orders of magnitude) to be supplied
by radiation pressure, given the relatively short times
during which the wind-interaction phenomenon probably took place, 100-200
yr. In this case, we will say that the mass outflow is "overluminous''.
For example, in M1-92, the momentum carried by the
molecular outflow is 
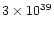 g cm s-1; the star emits about
g cm s-1; the star emits about
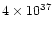 erg s-1, equivalent in momentum to
erg s-1, equivalent in momentum to
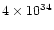 g cm s-1
per year, so the star would need about 105 yr to release
such a high linear momentum, but the wind interaction lasted just
g cm s-1
per year, so the star would need about 105 yr to release
such a high linear momentum, but the wind interaction lasted just  100
yr (with an upper limit of 900 yr, the total post-AGB life of the
object; see more details in Bujarrabal et al. 1998a).
100
yr (with an upper limit of 900 yr, the total post-AGB life of the
object; see more details in Bujarrabal et al. 1998a).
The measured kinetic energies and momenta are so high that it is difficult
to find other mechanisms that could power these very energetic ejections
satisfying the principles of conservation. (Similar
"overluminous'' flows are well known to occur in star-forming regions, for
which the accretion of material from the protostellar cloud is invoked to
power the bipolar jets.)
If such a property is found to be typical in PPNe, we would have to
conclude that, from the point of view of the dynamics involved, presently
we have no explanation for the shaping of planetary nebulae from the
previous AGB envelopes. However, only a few nebulae have been properly
studied at this respect.
In this paper we present a systematic study of the molecular outflows in
PPNe. We have cataloged all well identified PPNe showing CO
emission and have performed accurate new observations in a sizable number
of objects. From the CO data, we have calculated the nebular mass and the
linear momentum and kinetic energy of the flows. Our results are
compared with the momentum and kinetic energy that can be provided by the
stellar radiation pressure.
Table 2:
Sample of PPNe observed in CO in other papers.
| name |
coordinates |
 |
 LSR
LSR |
spectral |
i |
D |
L |
comments |
| |
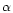 (2000)
(2000) |
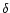 (2000)
(2000) |
|
(km s-1) |
type |
( ) ) |
(kpc) |
(103 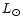 ) ) |
|
| |
|
|
|
|
|
|
|
|
|
| Red Rectangle |
06 19 58.2 |
-10 38 15 |
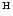 |
01 |
A12,3 |
154,5 |
0.38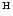 |
16 |
low-mass star |
| IRAS06176-1036 |
|
|
|
|
|
|
|
|
| IRAS07134+1005 |
07 16 10.3 |
09 59 48 |
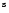 |
727 |
F58 |
509,10 |
3
7,9,10,11 |
13.510 |
|
| HD56126 |
|
|
|
|
|
|
|
|
| OH231.8+4.2 |
07 42 16.9 |
-14 42 50 |
12 |
3313 |
M9III13 |
4013 |
1.513 |
1013 |
well studied |
| IRAS07399-1435 |
|
|
|
|
|
|
|
|
| Hen3-401 |
10 19 32.5 |
-60 13 29 |
14 |
-3015 |
B115,16 |
15?14 |
315 |
3.614 |
|
| IRAS10178-5958 |
|
|
|
|
|
|
|
|
| Roberts22 |
10 21 33.8 |
-58 05 48 |
17 |
015 |
A2Iab18 |
1517 |
217 |
3017 |
|
| IRAS10197-5750 |
|
|
|
|
|
|
|
|
| HD101584 |
11 40 58.8 |
-55 34 26 |
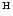 |
4119 |
F0Iape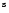 |
? |
120 |
320 |
well studied |
| IRAS11385-5517 |
|
|
|
|
|
|
|
|
| Boomerang Nebula |
12 44 45.5 |
-54 31 12 |
21 |
-415 |
G0III15 |
? |
1.521 |
0.321 |
well studied |
| IRAS12419-5414 |
|
|
|
|
|
|
|
|
| He2-113 |
14 59 53.5 |
-54 18 08 |
22 |
-5623 |
WC1024 |
? |
1.224 |
524 |
|
| IRAS14562-5406 |
|
|
|
|
|
|
|
|
| Mz-3 |
16 17 13.6 |
-51 59 06 |
25 |
-1715 |
B026 |
2027 |
1.815,28 |
5.725,26 |
|
| IRAS16133-5151 |
|
|
|
|
|
|
|
|
| M2-9 |
17 05 37.9 |
10 08 32 |
29 |
8029 |
Be30 |
1729 |
0.6431 |
0.5531 |
low-mass star |
| IRAS17028-1004 |
|
|
|
|
|
|
|
|
| CPD-568032 |
17 09 00.9 |
-56 54 48 |
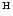 |
-6032,23 |
WC1024 |
? |
1.524 |
5.224 |
|
| IRAS17047-5650 |
|
|
|
|
|
|
|
|
| IRAS17150-3224 |
17 18 19.7 |
-32 27 21 |
33 |
1434 |
G2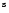 |
? |
2.4235 |
1135,36 |
|
| AFGL6815 |
|
|
|
|
|
|
| OH17.7-2.0 |
18 30 30.7 |
-14 28 57 |
37 |
6138 |
F039,40 |
? |
2
38 |
2.938 |
|
| IRAS18276-1431 |
|
|
|
|
|
|
|
|
| RSct |
18 47 29.0 |
-05 42 19 |
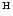 |
5641 |
G0-K232 |
? |
0.46 |
46 |
low-mass star |
| IRAS18448-0545 |
|
|
|
|
|
|
|
|
| M1-92 |
19 36 18.9 |
29 32 50 |
43 |
-143 |
B0.5IV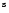 |
3543 |
2.543 |
1043 |
well studied |
| IRAS19343+2926 |
|
|
|
|
|
|
|
|
| IRAS19475+3119 |
19 49 29.6 |
31 27 16 |
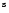 |
1844 |
F3Ia44 |
? |
645 |
12.60,45 |
|
| HD331319 |
|
|
|
|
|
|
|
|
| IRAS20000+3239 |
20 01 59.4 |
32 47 32 |
40 |
13.544 |
G8Ia8 |
? |
? |
0.55
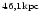 |
|
| |
|
|
|
|
|
|
|
|
| IRAS20028+3910 |
20 04 35.9 |
39 18 45 |
47 |
5.944 |
? |
? |
2.5
11,44,48 |
6.6
11,35,44,48 |
|
| |
|
|
|
|
|
|
|
|
| IRAS21282+5050 |
21 29 58.5 |
51 04 01 |
49 |
1850 |
O9.5,WC1151 |
909 |
39 |
5.39 |
|
| |
|
|
|
|
|
|
|
|
| IRAS22223+4327 |
22 24 31.0 |
43 43 09 |
40 |
-3048 |
G0Ia8 |
? |
? |
0.36
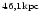 |
|
| |
|
|
|
|
|
|
|
|
| IRAS22574+6609 |
22 59 18.3 |
66 25 47 |
33 |
-6444 |
? |
? |
? |
0.15
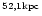 |
|

The goal of this work is to estimate the mass of the bipolar outflows in
PPNe, as well as the momentum and energy carried by them. We used for that
purpose CO emission, since, as far as we know, it is the best tracer of
the total nebular mass. We have chosen a sample of PPNe
emitting in CO; we think that our sample includes all well identified PPNe
that have been detected in CO emission (up to December 2000). We also
included three related objects (see below).
The basic criterion for the classification of a nebula as protoplanetary is
the presence of a cool and thick circumstellar envelope and a bimodal
spectral energy distribution (SED), showing that the envelope is well
detached from the central star and that the stellar temperature is between
 3000 and
3000 and  30000 K (in general corresponding to intermediate
spectral types: WC10-11, B, A, F, G, or K; in many cases, independent
studies have confirmed the stellar type).
Therefore, the selected objects lost large amounts of mass in the past,
when the central stars were probably cooler. These central stars seem
to be now evolving toward very hot objects, and will soon illuminate and
ionize the nebula.
Objects associated to interstellar clouds are rejected. Standard PNe
showing strong CO emission, and sometimes wide line wings (as for instance
M1-16), were not considered in our study. For further discussion on
these criteria, see e.g. Kwok (1993).
30000 K (in general corresponding to intermediate
spectral types: WC10-11, B, A, F, G, or K; in many cases, independent
studies have confirmed the stellar type).
Therefore, the selected objects lost large amounts of mass in the past,
when the central stars were probably cooler. These central stars seem
to be now evolving toward very hot objects, and will soon illuminate and
ionize the nebula.
Objects associated to interstellar clouds are rejected. Standard PNe
showing strong CO emission, and sometimes wide line wings (as for instance
M1-16), were not considered in our study. For further discussion on
these criteria, see e.g. Kwok (1993).
We did not include nebulae of uncertain classification. Accordingly, we
have not studied objects like AFGL190 (IRAS01144+6658),
IRAS19454+2920 and IRAS19480+2504, that show a heavy envelope (detected
by means IRAS photometry and CO line emission), because the temperature of
their central stars is not known (see Volk & Kwok 1989; Likkel et al.
1991; Volk et al. 1993; Groenewegen et al. 1998).
However, we have included in our sample IRAS23321+6545, IRAS20028+3910,
and IRAS22574+6609, even if the spectral types of the stars are unknown,
because they show a clearly bimodal SED, indicating the emissions of a cool
and massive envelope and probably of a relatively hot stellar component, as
well as a bipolar image in HST high-resolution observations (Ueta et al. 2000). IRAS22574+6609, moreover, shows FIR
dust features usually associated to PPNe (Hrivnak & Kwok 1991).
OH231.8+4.2 is assumed to be a PPN, in spite of the late (and peculiar)
spectrum of its central star, because it presents a massive envelope with
well developed shocks, a property characteristic of post-AGB objects and
very rare in AGB stars.
CRL2477 is assumed to be a PPN because of its bimodal SED (Groenewegen et al. 1996),
but the nature of the central star is controversial and it is
possible that two evolved objects are coincident in the line of sight.
NGC7027 is not a PPNe but a young PN; it is included in our list,
in spite of its very hot central star, because its envelope has
a short kinematical age ( 1000 yr, Graham et al. 1993) and a
massive molecular component, similarly to PPNe.
Finally, we have included in our list two objects that show heavy envelopes
and are thought to be hypergiants, IRC+10420 and AFGL2343 (the only two
hypergiants surrounded by massive nebulae, see e.g. de Jager 1998 and
discussion in 5.1.7).
The evolution of such objects is uncertain, but it seems that they were
cooler in the past, when they ejected most of the circumstellar shell, and
that they are becoming hotter rapidly. So these hypergiants are very
probably following an evolutionary path similar to that of PPNe. In
general, these objects are included in our list to allow a comparison of
the properties of PPNe and of related objects.
1000 yr, Graham et al. 1993) and a
massive molecular component, similarly to PPNe.
Finally, we have included in our list two objects that show heavy envelopes
and are thought to be hypergiants, IRC+10420 and AFGL2343 (the only two
hypergiants surrounded by massive nebulae, see e.g. de Jager 1998 and
discussion in 5.1.7).
The evolution of such objects is uncertain, but it seems that they were
cooler in the past, when they ejected most of the circumstellar shell, and
that they are becoming hotter rapidly. So these hypergiants are very
probably following an evolutionary path similar to that of PPNe. In
general, these objects are included in our list to allow a comparison of
the properties of PPNe and of related objects.
In our sample we include the PPNe with low initial mass in which CO has
been certainly detected: 89 Her, the Red Rectangle, M2-9 and R Sct (see
Alcolea & Bujarrabal 1991; R Sct is a peculiar RV Tau variable). We note
that PPNe with low initial mass show an anomalously low CO emission;
in particular, CO is not detected in other RV Tau variables and in M1-91.
We recall that the post-red-giant evolution of these low-mass stars may be
very slow and that they will perhaps not become standard PNe, due to the
extreme dilution of the expanding shell.
We have performed high-sensitivity observations (Sect. 3) of some PPNe
showing CO line emission, including in particular a well studied PPN that
seems to have no wings in the CO lines, IRAS22272+5435. In general, we
selected for observation objects for which useful 13CO J=1-0 data were
expected, also trying to sample the variety of sources described above.
For the objects not observed by us, we have taken data from the literature.
The final sample is defined in Tables 1 and 2, respectively for the
sources for which the relevant CO data have been and have not been obtained
in this work.
In these tables we include the most usual source name and the IRAS catalog
name, the coordinates, the adopted systemic velocity (
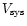 ), the
spectral type of the central star, the inclination of the nebula axis with
respect to the plane of the sky (i), the distance (D) and the total
luminosity calculated for this distance. Relevant references used to
calculate the above parameters are given by the superindexes.
), the
spectral type of the central star, the inclination of the nebula axis with
respect to the plane of the sky (i), the distance (D) and the total
luminosity calculated for this distance. Relevant references used to
calculate the above parameters are given by the superindexes.
The coordinates given in Table 1 are those observed by us, in Table 2
we show the best coordinates we have found in the literature. The
systemic velocity is deduced from the CO profiles. When the profiles are
composite, with a central intense component and wide wings, we chose the
centroid of the central component, since in well studied objects it seems
to correspond to the part of the envelope not affected by the post-AGB wind
interaction (e.g. Bujarrabal et al. 1998a, Sect. 8.1). When such a
structure is not clear, we take for
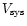 the line centroid. The values
for i and D are taken from specific studies on each nebula. When the
inclination is not known, we will adopt the intermediate value i =
30
the line centroid. The values
for i and D are taken from specific studies on each nebula. When the
inclination is not known, we will adopt the intermediate value i =
30 (see discussion in Sect. 4).
Note that the distance is sometimes poorly known in PPNe.
Some comments on the sources, mostly related to their evolutionary status,
are also given.
(see discussion in Sect. 4).
Note that the distance is sometimes poorly known in PPNe.
Some comments on the sources, mostly related to their evolutionary status,
are also given.
We have performed observations of the J=1-0 and J=2-1 transitions of 12CO
and 13CO in a sample of 16 protoplanetary nebulae (PPNe) and related
objects, using the IRAM 30 m radiotelescope, at Pico de Veleta (Granada,
Spain). Two observing runs were necessary, in August and November 1998.
SIS receivers working in the 3 and 1 mm bands were used, often
simultaneously. The receivers were tuned always in SSB mode, with
typical system temperatures of  1000 K, at
1000 K, at
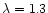 mm,
and 500 K, at
mm,
and 500 K, at
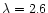 mm (in units of
mm (in units of
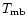 ,
see below).
Spectral resolutions between 0.3 and 2.6 km s-1 were used.
,
see below).
Spectral resolutions between 0.3 and 2.6 km s-1 were used.
Weather conditions were good for most observations, with zenith opacities
at 230 GHz ranging from about 0.3 to 0.8. The pointing of the telescope
was verified every about two hours or every time we moved into a new
target, by observing continuum sources close in the sky to it. The spatial
resolution is of 12-13'' at 1.3 mm and of about 22'' at 2.6 mm.
The data presented here are calibrated in units of Main Beam
Rayleigh-Jeans-equivalent Antenna Temperature,
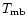 ,
using the
chopper-wheel method by observing hot (ambient) and cold loads (liquid
nitrogen). In addition, observations of well known intense sources were
used to check the calibration. In particular we took as standard the AGB
star IRC+10216, for which we used the following intensities at the central
velocity:
,
using the
chopper-wheel method by observing hot (ambient) and cold loads (liquid
nitrogen). In addition, observations of well known intense sources were
used to check the calibration. In particular we took as standard the AGB
star IRC+10216, for which we used the following intensities at the central
velocity:
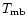 (12CO, J=1-0) = 23 K,
(12CO, J=1-0) = 23 K,
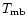 (12CO, J=2-1) = 63 K,
(12CO, J=2-1) = 63 K,
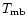 (13CO, J=1-0) = 1 K,
(13CO, J=1-0) = 1 K,
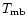 (13CO, J=2-1) = 4.3 K.
We note that due to recent improvements in the beam shape, the main-beam
temperatures of 1mm lines appear now somewhat higher than in older
observations (by factors 1.3-1.5).
(13CO, J=2-1) = 4.3 K.
We note that due to recent improvements in the beam shape, the main-beam
temperatures of 1mm lines appear now somewhat higher than in older
observations (by factors 1.3-1.5).
The observed spectra are shown in Figs. 1 to 16.
As baseline, only straight lines were subtracted.
Usually, PPNe are angularly compact objects, compared with the resolution
of the telescope, and observations of a single point are enough to measure
the total emission. However, the angular extent of some of
the observed objects is known to be comparable to the 12-13'' beam of the
30 m telescope at 230 GHz. We have performed small maps of a few objects
but, due to their small size, the information on the nebula shape is poor
and the main result from our maps is simply its image extent at half
maximum; see Sect. 5.
We will calculate the mass emitting in a spectral range within a CO
rotational line from the discussion on the CO excitation and emissivity by
Bujarrabal et al. (1997) and the properties of the CO emission from well
studied nebulae (Sect. 1). The possible associated errors are discussed
in that paper and Sect. 4.2.
Note that, when the source is significantly extended compared with the
telescope resolution, a correction to the central brightness temperature
proportional to the area of the beam-convolved image is necessary.
The emissivity is parametrized by the value of a (constant) rotational
temperature,
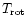 .
In previous papers, see Bujarrabal et al.
(1997, 1998a) and Sánchez Contreras et al. (1997), we have shown that
the characteristic rotational temperature of the CO emission in the best
studied nebulae is low, between 10 and 30 K, and remains significantly
constant across most of the source. In those objects in which good 12CO
and 13CO data exist, we will estimate the values of this parameter
from the observed J=2-1/J=1-0 line ratio; this is equivalent to
take the value of
.
In previous papers, see Bujarrabal et al.
(1997, 1998a) and Sánchez Contreras et al. (1997), we have shown that
the characteristic rotational temperature of the CO emission in the best
studied nebulae is low, between 10 and 30 K, and remains significantly
constant across most of the source. In those objects in which good 12CO
and 13CO data exist, we will estimate the values of this parameter
from the observed J=2-1/J=1-0 line ratio; this is equivalent to
take the value of
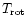 that leads to the same value of the total mass
from the data of both lines (of both 12CO and 13CO), see Sect. 5.1.
As we will see, we systematically obtain values of
that leads to the same value of the total mass
from the data of both lines (of both 12CO and 13CO), see Sect. 5.1.
As we will see, we systematically obtain values of
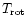 compatible
with the above range. For objects in which such an estimate is not
possible, we will assume
compatible
with the above range. For objects in which such an estimate is not
possible, we will assume
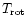
 15 K. The emissivities for a
given
15 K. The emissivities for a
given
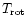 and so the conversion from
and so the conversion from
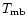 to emitting mass are
calculated assuming optically thin emission.
At least for 13CO J=1-0, the optical depth is
found to be lower than one in the well studied objects (see also 4.2); for
that reason (and the larger telescope beam), this line will be preferably used.
to emitting mass are
calculated assuming optically thin emission.
At least for 13CO J=1-0, the optical depth is
found to be lower than one in the well studied objects (see also 4.2); for
that reason (and the larger telescope beam), this line will be preferably used.
We will adopt the relative CO abundances X(12CO) =
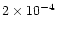 and
X(13CO) =
and
X(13CO) =
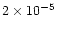 .
These relatively high values are characteristic of AGB envelopes and PPNe
with strong CO emission (Bujarrabal et al. 1997, 1998a, Alcolea et al.
2001, etc.), and therefore can be safely applied to not very evolved PPNe,
in which photodissociation by the stellar UV is not important yet.
.
These relatively high values are characteristic of AGB envelopes and PPNe
with strong CO emission (Bujarrabal et al. 1997, 1998a, Alcolea et al.
2001, etc.), and therefore can be safely applied to not very evolved PPNe,
in which photodissociation by the stellar UV is not important yet.
The spectral sampling used in our calculations are defined in terms of
LSR velocity,
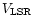 .
We will assume that the CO emission in the line wings comes from more or
less elongated structures in which the velocity is
mainly axial, as found for M1-92, OH231.8+4.2, etc. Then,
.
We will assume that the CO emission in the line wings comes from more or
less elongated structures in which the velocity is
mainly axial, as found for M1-92, OH231.8+4.2, etc. Then,
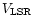 can be converted into actual flow velocity of the emitting gas,
V; provided that we know the inclination of the
axis with respect to the plane of the sky, i, and that we can deduce a
systemic LSR velocity,
can be converted into actual flow velocity of the emitting gas,
V; provided that we know the inclination of the
axis with respect to the plane of the sky, i, and that we can deduce a
systemic LSR velocity,
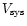 ,
from the CO profiles. Note that
,
from the CO profiles. Note that
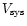 is expected to give the movement of the center of gravity,
defining the rest frame for which those parameters are calculated.
Then,
is expected to give the movement of the center of gravity,
defining the rest frame for which those parameters are calculated.
Then,
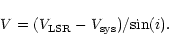 |
(1) |
Once we know the mass emitting in a spectral range, m, and the expansion
velocity corresponding to it, V, we can calculate the total mass, linear
"momentum'', P, and kinetic energy, E, by summing over the whole spectra
the values of m and of the products m|V| and
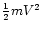 .
So, we
calculate
.
So, we
calculate
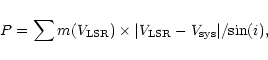 |
(2) |
and
![\begin{displaymath}E = \frac{1}{2} \sum m(V_{\rm LSR}) \times
[(V_{\rm LSR} - V_{\rm sys})/{\rm sin}(i)]^2.
\end{displaymath}](/articles/aa/full/2001/39/aah2711/img53.gif) |
(3) |
Note that we are not exactly calculating a linear momentum, since the sum
is not performed vectorially. When the flow is exactly bipolar, our method
gives the sum of the moduli of the momenta in the two opposite directions.
In general, we calculate sums of momentum moduli for different directions.
The calculated parameter (the total "scalar momentum'') is however relevant
for our purposes, since it can be compared with the "momentum'' carried by
radiation pressure per unit time, calculated as L/c, which has the same
meaning.
When the inclination of the nebula axis is not known, we will use i =
30 ,
as we have mentioned. This assumption is intermediate between
the extreme cases, perpendicular or parallel to the plane of the sky.
Note, moreover, that if we
calculate the sum of the momentum moduli from observations of a spherically
symmetric envelope, with constant radial velocity, we find exactly the same
formula as for a bipolar flow with i = 30
,
as we have mentioned. This assumption is intermediate between
the extreme cases, perpendicular or parallel to the plane of the sky.
Note, moreover, that if we
calculate the sum of the momentum moduli from observations of a spherically
symmetric envelope, with constant radial velocity, we find exactly the same
formula as for a bipolar flow with i = 30 ,
i.e.:
,
i.e.:
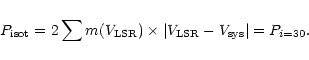 |
(4) |
In this isotropical case,
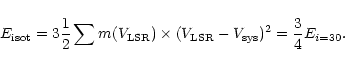 |
(5) |
Note that the total mass calculation only depends on the velocity
integrated intensity, it is therefore independent of the assumed source
geometry.
For all possible density and velocity distributions (keeping the value of
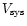 as that of the reference frame), there is a lower limit for the
momentum and energy: those calculated assuming bipolar ejections with
as that of the reference frame), there is a lower limit for the
momentum and energy: those calculated assuming bipolar ejections with
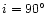 ,
i.e. in the line of sight:
,
i.e. in the line of sight:
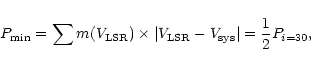 |
(6) |
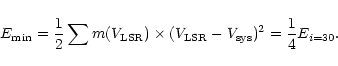 |
(7) |
The minimum momentum is just one half of that given by our previous
isotropic and
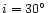 approximations.
approximations.
There are other possible models for the mass and velocity distributions, but
in general all them give similar results for the momentum and energy to
those presented here.
We can see more detailed source descriptions and the derived results in
e.g. Bujarrabal et al. (1998a) and Alcolea et al. (2001), based on
their high-quality CO maps.
We also mention the disk model used in Sahai et al. (2000) for the PPN
Frosty Leo. In this model the gas flows in a plane perpendicular to the
nebula symmetry axis at constant velocity; the axis inclination is again
the basic geometric parameter. The expansion
velocity is given in this model by the
maximum of the relative observed velocity,
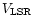 -
-
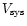 ,
divided
by cos(i). The resulting momentum and energy expression are slightly more
complex than in the axial-flow case, but the results do not differ from
those of the other simple models (see Sect. 4.2 and Sahai et al.).
,
divided
by cos(i). The resulting momentum and energy expression are slightly more
complex than in the axial-flow case, but the results do not differ from
those of the other simple models (see Sect. 4.2 and Sahai et al.).
Only when the gas velocity is assumed to be closely parallel to the plane
of the sky (for instance in a bipolar flow with i  0
0 or in
a disk with the axis close to the line of sight), the corrections needed to
convert the observational parameters to momentum and energy are very high.
In the objects treated here we never assumed values of i smaller than
15
or in
a disk with the axis close to the line of sight), the corrections needed to
convert the observational parameters to momentum and energy are very high.
In the objects treated here we never assumed values of i smaller than
15 (Tables 1, 2).
(Tables 1, 2).
As we have mentioned, PPNe often show different kinematical
components. In several sources, there is clearly a central low-velocity
feature in the CO profiles. In the well studied cases
(see Sect. 8.1),
this central spectral component is known to come from a spherical slowly
expanding envelope or from a disk/torus perpendicular to the nebula axis.
In these sources, the line core is thought to represent the
part of the AGB envelope that has not been affected by the wind interaction
characteristic of the protoplanetary evolution.
Therefore we must treat separately the line wings and the line core.
For the line wings, the most interesting spectral feature for us,
we will in general assume the bipolar flow model, as discussed
above. Except for some well studied cases mentioned in Sect. 5, for the
line core we will assume isotropic expansion and spherical symmetry, since
these values will be in that way more directly comparable to those usually
found for AGB envelopes.
The assumptions listed in Sect. 4.1 could lead, if they are not
satisfied, to errors. In a previous work (Bujarrabal et al. 1997), we
have already discussed these error sources. In this paper we will adapt
this discussion, without repeating all details, to the models used here.
1.
We are assuming optically thin emission, at least in the 13CO
J=1-0 transition. The main reason to believe that this hypothesis is
reasonable is that the 13CO lines are in all cases significantly weaker
than the 12CO lines, in spite of the similar excitation properties of
both molecules and the similar extents found from both theoretical
reasoning (i.e. from photodissociation theory, Mamon et al. 1988) and
observational results (see maps by Bujarrabal et al. 1998a; Sánchez
Contreras et al. 1997). Under these conditions, 13CO/12CO line
ratios much lower than 1 can only be explained if at least the
13CO lines are optically thin. Nevertheless, if these lines were opaque,
our calculations of mass, momentum and energy would lead to
underestimates of the true values (but never overestimates); in any
case the above discussion strongly suggests that the possible
underestimate is moderate, mainly in the relatively weak line wings and
well studied objects.
2.
We also assume a relatively low rotational
temperature ( 15 K), that is used to parametrize the CO line
excitation. As we have discussed in Sect. 4.1, such low values are found
in the PPNe in which the CO line emission has been well observed.
Note that rotational temperatures larger than 30 K (if the emission is not
resolved by the telescope and optically thin) would lead to values of the
brightness temperature ratio 13CO J=2-1/J=1-0
15 K), that is used to parametrize the CO line
excitation. As we have discussed in Sect. 4.1, such low values are found
in the PPNe in which the CO line emission has been well observed.
Note that rotational temperatures larger than 30 K (if the emission is not
resolved by the telescope and optically thin) would lead to values of the
brightness temperature ratio 13CO J=2-1/J=1-0
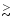 12, which is
certainly not observed. As we have discussed in Bujarrabal
et al. (1997), the emissivity in the observed lines for this low
12, which is
certainly not observed. As we have discussed in Bujarrabal
et al. (1997), the emissivity in the observed lines for this low
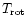 is close to the absolute maximum. Only overestimates by less
than a factor 2 in the mass, momentum and energy are then expected due to
errors in the excitation treatment. Of course, significant underestimates
are possible if
is close to the absolute maximum. Only overestimates by less
than a factor 2 in the mass, momentum and energy are then expected due to
errors in the excitation treatment. Of course, significant underestimates
are possible if
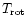 is in fact very large; the underestimate for
is in fact very large; the underestimate for
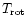 = 40 K is by about a factor 3.
We have mentioned that the mass of the hot gas is small (Sect. 1); if a
massive warm componet exist, we would again underestimate the total mass
and momentum.
= 40 K is by about a factor 3.
We have mentioned that the mass of the hot gas is small (Sect. 1); if a
massive warm componet exist, we would again underestimate the total mass
and momentum.
Bujarrabal et al. (1997) calculated the effects of departures from
thermalization in the CO level population. For the high number densities
calculated in well observed nebulae,
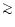 104 cm-3 (Bujarrabal et al. 1998a;
Alcolea et al. 2001), the relevant lines are almost
thermalized and only small corrections to the emissivity are expected. In
any case, even for extreme departures the possible overestimates would
not exceed a factor 1.5.
104 cm-3 (Bujarrabal et al. 1998a;
Alcolea et al. 2001), the relevant lines are almost
thermalized and only small corrections to the emissivity are expected. In
any case, even for extreme departures the possible overestimates would
not exceed a factor 1.5.
The case of the PPN IRAS22272+5435 illustrates the moderate uncertainties
that one can expect in our calculations due to the excitation assumptions.
In Sect. 5.1.12 and Table 3, we present results of the molecular mass of
this source, for which some indication exists that the observed lines come
from an envelope similar to that of an AGB star. We calculate the molecular
mass and the dynamical parameters assuming three models for the CO
excitation: our standard model for spherical-isotropic expansion (with
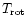 = 15 K), our model
for spherical-isotropic expansion and assuming
= 15 K), our model
for spherical-isotropic expansion and assuming
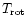 = 25 K (a value
that, as we will see, may be present in some PPNe), and assuming that the
lines come from an envelope similar in density, abundance and temperature
distribution to those of AGB stars.
As we see in Table 3, the results are comparable for the different models.
(It is well known that CO data analysis provides robust ways to determine
the mass in the CO-rich envelopes, due to the low dependence of the results
on the excitation conditions and general assumptions, see e.g.
Bujarrabal 1999.)
= 25 K (a value
that, as we will see, may be present in some PPNe), and assuming that the
lines come from an envelope similar in density, abundance and temperature
distribution to those of AGB stars.
As we see in Table 3, the results are comparable for the different models.
(It is well known that CO data analysis provides robust ways to determine
the mass in the CO-rich envelopes, due to the low dependence of the results
on the excitation conditions and general assumptions, see e.g.
Bujarrabal 1999.)
3.
We are taking a relatively high value of the 13CO relative
abundance, X(13CO) =
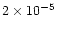 ,
as usually found in molecule-rich PPNe
and AGB envelopes (Kahane et al. 1992; Bujarrabal et al. 1994). Such a
value of X(13CO) almost corresponds to the maximum number of 13CO
molecules that can be formed for the expected 13C abundance.
As discussed by Bujarrabal et al. (1997), some PPNe are known
to show relatively low molecular abundances, probably due to
photodissociation by the UV photons emitted by the (already) warm central
star. Therefore, again we can hardly expect strongly overestimated values
of the derived parameters from the possible errors in the assumed X(13CO)
value.
However, if in some source the molecular photodissociation is very
efficient we would severely underestimate the mass, as well as the other
dynamical parameters.
It is difficult to limit such an effect. We hope that the fact
that our sample mostly includes intense sources in molecular emission
implies that their molecular component includes most of the nebular mass;
this is known to be case in well studied nebulae like CRL2688, CRL618,
M1-92, OH231.8+4.2, etc. In any case, we must keep in mind that the
parameters derived here always refer to the (cool) molecular component of
PPNe.
,
as usually found in molecule-rich PPNe
and AGB envelopes (Kahane et al. 1992; Bujarrabal et al. 1994). Such a
value of X(13CO) almost corresponds to the maximum number of 13CO
molecules that can be formed for the expected 13C abundance.
As discussed by Bujarrabal et al. (1997), some PPNe are known
to show relatively low molecular abundances, probably due to
photodissociation by the UV photons emitted by the (already) warm central
star. Therefore, again we can hardly expect strongly overestimated values
of the derived parameters from the possible errors in the assumed X(13CO)
value.
However, if in some source the molecular photodissociation is very
efficient we would severely underestimate the mass, as well as the other
dynamical parameters.
It is difficult to limit such an effect. We hope that the fact
that our sample mostly includes intense sources in molecular emission
implies that their molecular component includes most of the nebular mass;
this is known to be case in well studied nebulae like CRL2688, CRL618,
M1-92, OH231.8+4.2, etc. In any case, we must keep in mind that the
parameters derived here always refer to the (cool) molecular component of
PPNe.
4.
We have also mentioned in Sect. 4.1 that the uncertainty in the
nebula structure and kinematics affects the determination of the momentum
and energy (not of the total mass). When we use a bipolar jet model with
inclination i (values listed in Tables 1, 2), the maximum possible
overestimate of the momentum due to errors in the inclinations is by a
factor 1/sin(i). For the discussed sources, for which we always take i
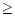 15
15 ,
this factor does not exceed 3.9. The energy measurement
is more uncertain, it can be overestimated by a factor 1/sin2(i). When
the model source is spherical with isotropic flow, the maximum
overestimate of P is by a factor 2 (3 for the energy). For most sources,
the inclination of the axis is relatively well known, so significantly
smaller errors are expected. For the others we adopt
,
this factor does not exceed 3.9. The energy measurement
is more uncertain, it can be overestimated by a factor 1/sin2(i). When
the model source is spherical with isotropic flow, the maximum
overestimate of P is by a factor 2 (3 for the energy). For most sources,
the inclination of the axis is relatively well known, so significantly
smaller errors are expected. For the others we adopt
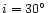 ,
the
maximum overestimate of P is then by a factor 2.
On the other hand, if the true inclination of the mass flow with respect to
the plane of the sky is close to 0
,
the
maximum overestimate of P is then by a factor 2.
On the other hand, if the true inclination of the mass flow with respect to
the plane of the sky is close to 0 ,
we may strongly underestimate
P and E. The probability that i is smaller than
15
,
we may strongly underestimate
P and E. The probability that i is smaller than
15 ,
assuming a random distribution of the nebula axes, is 0.26.
Therefore, for
,
assuming a random distribution of the nebula axes, is 0.26.
Therefore, for  75% of the sources with uncertain inclination, the
underestimate of the momentum is smaller than a factor
75% of the sources with uncertain inclination, the
underestimate of the momentum is smaller than a factor  2. It is
possible that in some object the momentum underestimate is significantly
stronger.
2. It is
possible that in some object the momentum underestimate is significantly
stronger.
Note that this discussion holds almost exactly if the velocity/mass
distributions are more complex than assumed.
In Sect. 4.1 we discuss calculations for one object, Frosty Leo,
assuming very different geometries, namely: our standard bipolar flow, a
spherical-isotropic expansion, and a disk-like distribution (see results in
Table 3). We discuss the case of this source because its well known image
in the optical could suggest very different configurations for the CO
cloud, see 5.1.3. As we see, the differences between the results for such
different geometries are small, provided that the inclination of the flow
with respect to the plane of the sky is not very small.
As we have mentioned, the distance to some sources is quite uncertain. But
we note that the parameters derived from the molecular observations (mass,
linear momentum and kinetic energy of the flows) depend on D2, in the
same way as the stellar total luminosity and the momentum carried by it.
Therefore, our main result, the comparison between the gas outflow momentum
(energy) and the momentum (energy) carried by the stellar radiation,
is not directly affected by the errors in the distance.
The mass, linear momentum and kinetic energy of the different nebular
components calculated in the objects observed by us, following the methods
described in Sect. 4, are summarized in Table 3.
In this section, we discuss the parameters used for each nebula.
The adopted values for the axis
inclination i and the distance D are listed in Table 1 (Sect. 2).
We will also discuss (mainly for the first sources) the
errors and limits due to the CO data uncertainties, as well as to the
excitation and source models. In Sect. 5.2 we discuss the calculations
for sources observed in CO by other authors; the difference of the
treatment is due to the different quality of the data, the results, as
we will see, are very similar for both groups.
Our spectra (Fig. 1, Sect. 3) show a central component and
weak wings, that are not seen in the 13CO J=1-0 line. We deduced from
inspection of the 12CO J=2-1 line that the slow component is
characterized by a systemic velocity
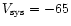 km s-1 (LSR) and a
velocity range equal to
km s-1 (LSR) and a
velocity range equal to
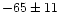 km s-1. The very compact
HST image (2-3'' wide, Sahai et al. 2000) suggests that the nebula
is much smaller than the resolution of our telescope, as recently confirmed
by unpublished CO maps of this source.
The CO line intensity ratios are compatible with the
range of low rotational temperatures assumed in our standard model (10-20 K). We will accordingly apply our standard procedure to the calculation
of the mass, momentum and kinetic energy in this source, using the 12CO
J=1-0 line and a bipolar outflow model (with i = 25
km s-1. The very compact
HST image (2-3'' wide, Sahai et al. 2000) suggests that the nebula
is much smaller than the resolution of our telescope, as recently confirmed
by unpublished CO maps of this source.
The CO line intensity ratios are compatible with the
range of low rotational temperatures assumed in our standard model (10-20 K). We will accordingly apply our standard procedure to the calculation
of the mass, momentum and kinetic energy in this source, using the 12CO
J=1-0 line and a bipolar outflow model (with i = 25 )
for the weak
line wings, and using the 13CO J=1-0 line and a spherical model for the
line core.
We have checked that, at least for the line core, both 12CO and 13CO
J=1-0 lines would produce very similar results, which is a consistency
proof of the assumed excitation, abundances and low opacities. The results
obtained for the fast component are in any case uncertain, due to its weak
emission. The distance to this source, see Table 1, is poorly known, but
this should not affect our main results (Sect. 4.2).
)
for the weak
line wings, and using the 13CO J=1-0 line and a spherical model for the
line core.
We have checked that, at least for the line core, both 12CO and 13CO
J=1-0 lines would produce very similar results, which is a consistency
proof of the assumed excitation, abundances and low opacities. The results
obtained for the fast component are in any case uncertain, due to its weak
emission. The distance to this source, see Table 1, is poorly known, but
this should not affect our main results (Sect. 4.2).
The results of the calculations with this model are given in Table 3. Since
the fast outflow is assumed to have i = 25 ,
the lower limit to
its momentum (for an unrealistic flow in the direction of the line of sight,
see Sect. 4.2) would be 2.4 times smaller than the value in the table.
Calculations with a spherical-isotropic model for the fast gas would yield
a momentum about 1.2 times smaller that the adopted result.
,
the lower limit to
its momentum (for an unrealistic flow in the direction of the line of sight,
see Sect. 4.2) would be 2.4 times smaller than the value in the table.
Calculations with a spherical-isotropic model for the fast gas would yield
a momentum about 1.2 times smaller that the adopted result.
As we see in Fig. 2, the CO lines of CRL618 show a
clearly composite structure, with a central strong core and wide wings.
From existent mapping observations of the central component (e.g.
Bujarrabal et al. 1988), it is known that this spectral feature comes
from a quasi-spherical structure extended about 15 arcsec. The wide
line wings, on the other hand, are known to come from a bipolar inner flow
(Neri et al. 1992) extended less than 5''.
Therefore, the spatial resolution of our CO J=1-0 single-dish observations,
 22'', is wide enough to collect all its flux.
We deduced from our spectra a
systemic velocity
22'', is wide enough to collect all its flux.
We deduced from our spectra a
systemic velocity
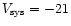 km s-1 and an expansion velocity for the
central component equal to 17.5 km s-1. In this case it is therefore fully
justified to use a spherical model for the line core and a bipolar fast
flow (with
km s-1 and an expansion velocity for the
central component equal to 17.5 km s-1. In this case it is therefore fully
justified to use a spherical model for the line core and a bipolar fast
flow (with
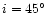 )
for the line wings (Sect. 4).
The wings are very weak in the 13CO lines; therefore, we calculated
the parameters for them from the 12CO lines (mainly J=1-0).
For a spherical-isotropic model, the momentum calculated for the fast
outflow would be 1.4 times larger than
the value for our standard bipolar model; the minimum momentum (if the
material flows in the direction of the line of sight) would be
1.4 times smaller.
)
for the line wings (Sect. 4).
The wings are very weak in the 13CO lines; therefore, we calculated
the parameters for them from the 12CO lines (mainly J=1-0).
For a spherical-isotropic model, the momentum calculated for the fast
outflow would be 1.4 times larger than
the value for our standard bipolar model; the minimum momentum (if the
material flows in the direction of the line of sight) would be
1.4 times smaller.
Some authors (see Bujarrabal et al. 1988 and references therein) have
proposed somewhat larger rotational temperatures in this source than those
found in other PPNe.
For the line core, the rotational temperature derived from the 13CO
J=2-1/J=1-0 brightness ratio is  25 K,
the correction factor with respect to our standard estimate (for
25 K,
the correction factor with respect to our standard estimate (for
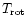 = 15 K) is only
= 15 K) is only  1.4. The (12CO) line wings suggest a low
excitation temperature and the correction factor is still smaller.
Therefore, we will only apply the above correction to the central spectral
component.
1.4. The (12CO) line wings suggest a low
excitation temperature and the correction factor is still smaller.
Therefore, we will only apply the above correction to the central spectral
component.
Table 3:
Calculations of the mass, momentum and kinetic energy for the
sources observed in CO by us.
| source |
mass |
momentum |
kinetic energy |
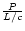 |
comments |
| |
M( ) ) |
P(gcms-1) |
E(erg) |
(yr) |
|
| |
|
|
|
|
|
| IRAS04296+3429 |
|
|
|
|
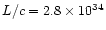 gcms-1yr-1
gcms-1yr-1 |
| slow component |
0.13 |
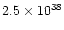 |
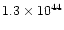 |
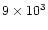 |
|
| fast outflow |
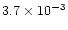 ? ? |
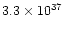 ? ? |
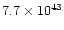 ? ? |
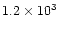 ? ? |
from 12CO J=1-0, uncertain analysis |
| CRL618 |
|
|
|
|
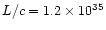 gcms-1yr-1
gcms-1yr-1 |
| slow component |
0.65 |
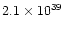 |
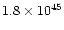 |
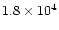 |
assuming
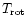 = 25 K
= 25 K |
| fast outflow |
0.045 |
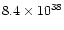 |
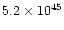 |
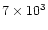 |
from 12CO J=1-0 |
| Frosty Leo |
|
|
|
|
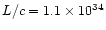 gcms-1yr-1
gcms-1yr-1 |
| slow component |
0.36 |
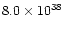 |
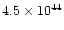 |
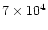 |
|
| fast outflow |
0.56 |
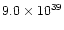 |
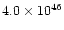 |
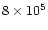 |
bipolar model |
| fast outflow |
0.60 |
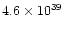 |
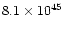 |
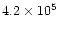 |
spherical-isotropic model |
| fast outflow |
0.56 |
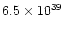 |
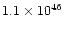 |
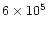 |
disk, constant radial velocity |
| IRAS17436+5003 |
|
|
|
|
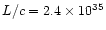 gcms-1yr-1
gcms-1yr-1 |
| slow component |
0.57 |
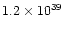 |
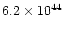 |
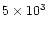 |
|
| fast outflow |
0.11 |
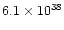 |
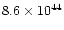 |
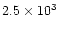 |
weak wings |
| He3-1475 |
|
|
|
|
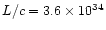 gcms-1yr-1
gcms-1yr-1 |
| slow component |
0.16 |
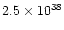 |
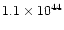 |
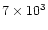 |
|
| fast outflow |
0.47 |
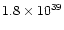 |
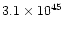 |
 |
|
| 89 Her |
|
|
|
|
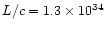 gcms-1yr-1
gcms-1yr-1 |
| slow component |
 |
 |
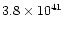 |
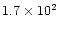 |
|
| fast outflow |
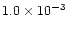 |
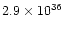 |
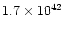 |
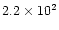 |
|
| AFGL2343 |
|
|
|
|
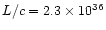 gcms-1yr-1
gcms-1yr-1 |
| unique, fast component |
4.8 |
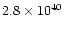 |
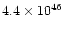 |
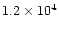 |
spherical envelope |
| IRC+10420 |
|
|
|
|
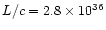 gcms-1yr-1
gcms-1yr-1 |
| unique,fast component |
2.1 |
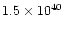 |
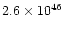 |
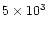 |
spherical envelope; extended |
| IRAS19500-1709 |
|
|
|
|
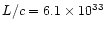 gcms-1yr-1
gcms-1yr-1 |
| slow component |
0.026 |
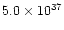 |
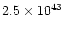 |
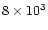 |
|
| fast outflow |
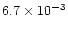 |
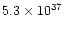 |
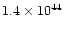 |
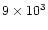 |
|
| CRL2477 |
|
|
|
|
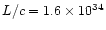 gcms-1yr-1
gcms-1yr-1 |
| unique, fast component |
0.11 |
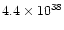 |
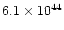 |
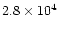 |
bipolar outflow (?) |
| CRL2688 |
|
|
|
|
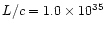 gcms-1yr-1
gcms-1yr-1 |
| slow component |
0.69 |
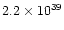 |
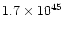 |
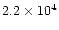 |
|
| fast outflow |
0.062 |
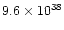 |
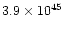 |
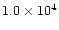 |
bipolar model;
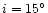 |
| fast outflow |
0.062 |
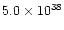 |
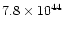 |
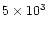 |
spherical model |
| NGC7027 |
|
|
|
|
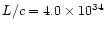 gcms-1yr-1
gcms-1yr-1 |
| main component |
0.60 |
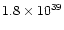 |
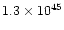 |
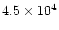 |
from 12CO J=1-0; extended |
| main component |
0.17 |
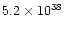 |
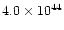 |
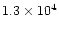 |
from 13CO J=1-0 |
| very fast outflow |
0.033 |
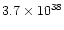 |
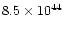 |
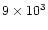 |
from 12CO J=1-0; spherical model |
| IRAS22272+5435 |
|
|
|
|
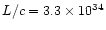 gcms-1yr-1
gcms-1yr-1 |
| unique, slow component |
0.14 |
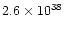 |
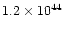 |
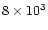 |
spherical envelope; extended |
| unique, slow component |
0.20 |
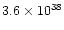 |
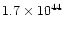 |
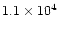 |
spherical envelope;
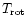 = 25 K
= 25 K |
| unique, slow component |
0.18 |
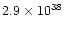 |
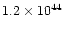 |
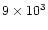 |
AGB envelope model |
| no fast outflow detected |
<
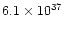 |
|
<
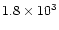 |
|
| IRAS23304+6147 |
|
|
|
|
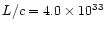 gcms-1yr-1
gcms-1yr-1 |
| slow component |
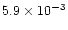 |
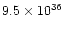 |
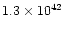 |
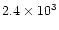 |
from 12CO J=2-1, underestimate? |
| fast component |
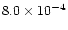 |
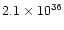 |
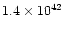 |
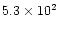 |
from 12CO J=2-1, underestimate? |
| IRAS23321+6545 |
|
|
|
|
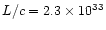 gcms-1yr-1
gcms-1yr-1 |
| unique, fast component |
0.014 |
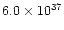 |
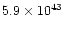 |
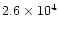 |
bipolar (?);
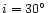 ,
D = 1 kpc (?) ,
D = 1 kpc (?) |
| M2-56 |
|
|
|
|
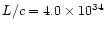 gcms-1yr-1
gcms-1yr-1 |
| slow component |
0.046 |
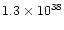 |
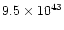 |
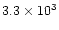 |
from 12CO J=1-0 |
| fast component |
0.059 |
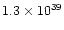 |
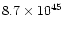 |
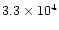 |
from 12CO J=1-0 |
The CO spectra of Frosty Leo show a central intense feature that will be
taken as the slow component, with
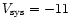 km s-1 and an expansion
velocity of 10 km s-1. The line wings in this source are very conspicuous at
all wavelengths, but being much weaker in 13CO, which suggests optically
thin emission at least in the 13CO lines.
We performed small maps that show that the source is not resolved in
CO emission, with an extent
km s-1 and an expansion
velocity of 10 km s-1. The line wings in this source are very conspicuous at
all wavelengths, but being much weaker in 13CO, which suggests optically
thin emission at least in the 13CO lines.
We performed small maps that show that the source is not resolved in
CO emission, with an extent
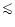 5''. The 13CO J=2-1/J=1-0 line ratio
indicates a rotational temperature compatible with our range of low
temperatures (Sect. 4). The HST image (Sahai et al. 2000)
suggests that the compact CO emission comes from the bright equatorial
regions of the nebula.
Therefore, in this source it is justified to calculate mass, momentum and
energy for the fast component using the disk model described in Sect. 4.1
(with
5''. The 13CO J=2-1/J=1-0 line ratio
indicates a rotational temperature compatible with our range of low
temperatures (Sect. 4). The HST image (Sahai et al. 2000)
suggests that the compact CO emission comes from the bright equatorial
regions of the nebula.
Therefore, in this source it is justified to calculate mass, momentum and
energy for the fast component using the disk model described in Sect. 4.1
(with
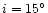 ), together with the standard bipolar and spherical
models. As we can see in Table 3, the results do not strongly depend on the
used geometrical model.
Note the particularly high ratio between the gas and radiation momenta.
), together with the standard bipolar and spherical
models. As we can see in Table 3, the results do not strongly depend on the
used geometrical model.
Note the particularly high ratio between the gas and radiation momenta.
Finally we note that this source is one of those characterized by a
particularly low 12CO/13CO line ratio. Even for the
line wings and the J=1-0 transition, the line ratio is <3. Similar
results (e.g. Bujarrabal et al. 1990) have been interpreted as showing
the presence of a very low 12C/13C abundance ratio in some
evolved nebulae. See Sahai et al. (2000) for more details.
This source shows line wings that are weak, but can be identified even in
13CO J=1-0; in any case we have checked that the parameters obtained from
12CO and 13CO J=1-0 are quite similar. No extent in the CO lines was
detected by Bujarrabal et al. (1992), using the 30-m telescope. The
13CO J=2-1/J=1-0 line ratio indicates a rotational temperature compatible
with our general assumptions. We will accordingly use the 13CO J=1-0
transition with our standard procedure; an expansion velocity of 11 km s-1
for the slow component is used.
Note that the inclination is not known, so we take a bipolar outflow with
i = 30 .
The lower limit to the momentum due to this assumption is just a factor 2
lower than the values given in Table 3.
.
The lower limit to the momentum due to this assumption is just a factor 2
lower than the values given in Table 3.
He3-1475 shows wide CO profiles, from which we deduce
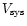 = 50
km s-1 LSR.
We have chosen a composite model with a slow component, corresponding
to the line core and an expansion velocity
= 50
km s-1 LSR.
We have chosen a composite model with a slow component, corresponding
to the line core and an expansion velocity  7 km s-1, and a fast
outflow, that is assumed to be bipolar in view of the spectacular elongated
structure of the nebula (Borkowski et al. 1997). The identification of the
line core in this source is not straightforward, but we note that
variations of its expansion velocity affect only slightly the momentum and
energy calculations of the fast outflow, due to the very large velocity and
strong CO emission of the later. The wings are detected in all lines;
note some galactic contamination in 12CO J=1-0.
We performed small maps that indicate a negligible CO extent,
compared with the telescope resolution. The rotational temperature
suggested by the line ratios is compatible with our general assumptions.
Therefore, we apply to this source our standard procedure, for both the
line core and the wings.
7 km s-1, and a fast
outflow, that is assumed to be bipolar in view of the spectacular elongated
structure of the nebula (Borkowski et al. 1997). The identification of the
line core in this source is not straightforward, but we note that
variations of its expansion velocity affect only slightly the momentum and
energy calculations of the fast outflow, due to the very large velocity and
strong CO emission of the later. The wings are detected in all lines;
note some galactic contamination in 12CO J=1-0.
We performed small maps that indicate a negligible CO extent,
compared with the telescope resolution. The rotational temperature
suggested by the line ratios is compatible with our general assumptions.
Therefore, we apply to this source our standard procedure, for both the
line core and the wings.
This source shows a very low 12CO/13CO line ratio; even in the
relatively weak line wings and the J=1-0 transition, the line ratio is
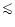 3, see Sect. 5.1.3. If we recalculate the mass, momentum and
energy from the 12CO J=1-0 (assuming an abundance X(12CO) =
3, see Sect. 5.1.3. If we recalculate the mass, momentum and
energy from the 12CO J=1-0 (assuming an abundance X(12CO) =
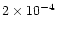 )
we find for all three parameters values about three times smaller than
those given in Table 3.
)
we find for all three parameters values about three times smaller than
those given in Table 3.
The difference between line core and wings in the CO lines from 89Her is
not clear. We adopt, somewhat arbitrarily, a slow component velocity  3 km s-1 (note that the line is anomalously narrow, as always found in
low-mass PPNe, see Sect. 8.2). The systemic velocity is -8 km s-1. The
analysis is simplified by the fact that no sign of departure from spherical
symmetry and radial expansion is found from the CO mapping of this source
(Alcolea & Bujarrabal 1995), so the model would be the same for the line
core and wings. These authors also confirm the small extent of the source.
The line ratios are consistent with the low rotational temperatures adopted
in our standard procedure.
3 km s-1 (note that the line is anomalously narrow, as always found in
low-mass PPNe, see Sect. 8.2). The systemic velocity is -8 km s-1. The
analysis is simplified by the fact that no sign of departure from spherical
symmetry and radial expansion is found from the CO mapping of this source
(Alcolea & Bujarrabal 1995), so the model would be the same for the line
core and wings. These authors also confirm the small extent of the source.
The line ratios are consistent with the low rotational temperatures adopted
in our standard procedure.
AFGL2343 and IRC+10420 are yellow hypergiant stars surrounded by a
very thick circumstellar envelope (see de Jager 1998 and Sect. 2).
We have included these two stars in our sample because its evolution may be
similar to that of PPNe (Sect. 2), but we must keep in mind that they are
relatively different objects than the rest of the sample.
Both stars show probably spherical envelopes with radial expansion. This is
deduced for IRC+10420 from observations in OH maser and CO and SiO
thermal emissions (Nedoluha & Bowers 1992; Neri et al. 1998;
Castro-Carrizo et al. 2001). For AFGL2343, there are
high-resolution CO data (Neri et al., in preparation) and accurate NIR
mapping (Hawkins et al. 1995). Our CO spectra are consistent with this
interpretation, they show very wide profiles with no clear core+wing
structure; the total widths suggest high expansion velocities of 33
km s-1 and 35 km s-1 respectively for AFGL2343 and IRC+10420. We adopted
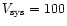 · km s-1, for AFGL2343, and
· km s-1, for AFGL2343, and
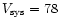 km s-1, for
IRC+10420. Note the variations in the profile from line to line,
suggesting opacity effects in, certainly, the 12CO J=2-1 transition and
also, probably, in the J=1-0 one. Data from Neri et al. suggest a CO
source size much smaller than our J=1-0 beam; only for IRC+10420 the
convolved size could be slightly larger than the telescope beam, for this
source we introduced a correction of a factor 1.3 to the deduced values to
take into account the extent. The line ratios
are consistent with the low
km s-1, for
IRC+10420. Note the variations in the profile from line to line,
suggesting opacity effects in, certainly, the 12CO J=2-1 transition and
also, probably, in the J=1-0 one. Data from Neri et al. suggest a CO
source size much smaller than our J=1-0 beam; only for IRC+10420 the
convolved size could be slightly larger than the telescope beam, for this
source we introduced a correction of a factor 1.3 to the deduced values to
take into account the extent. The line ratios
are consistent with the low
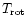 adopted here.
adopted here.
We accordingly apply our standard procedure to
AFGL2343 and IRC+10420, assuming spherical
symmetry and radial expansion for the whole CO emission.
Note the very high mass of these
envelopes, already suggested from previous data.
For AFGL2343 we adopted the distance deduced from the Hipparcos paralax,
which is uncertain but compatible with the high luminosity of hypergiants.
Recently, Josselin & Lèbre (2001) have argued that this object could be
a "normal'' PPN, at a much shorter distance and with a much lower
luminosity. If this is the case, the values of the mass and momentum we
derive will be also smaller (proportionally to D2), but the ratio
between the gas and luminosity momenta will remain the same as that given
in Table 3, indeed comparable to those found in most PPNe.
This source shows a clear separation between slow and fast outflow
components. The small CO extent (Bujarrabal et al. 1992) and the line
intensity ratios confirm the assumptions in our standard model. The
systemic velocity is deduced from the spectra to be 25 km s-1, and the
expansion velocity of the slow component is taken to be 10 km s-1. Since the
inclination is not known, we will use i = 30 ,
so the lower limit
to the momentum (energy) is 2 (4) times smaller than the value in the
table.
We have checked that the 12CO line gives similar values for the dynamical
parameters.
,
so the lower limit
to the momentum (energy) is 2 (4) times smaller than the value in the
table.
We have checked that the 12CO line gives similar values for the dynamical
parameters.
We recall the uncertain post-AGB nature of this source (Sect. 2).
We also note the galactic contamination close to
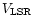 =
0 km s-1, we have restored the profiles by interpolating adjacent channels.
Due to this contamination and to the unknown inclination of the source, we
have assumed a unique bipolar component with i = 30
=
0 km s-1, we have restored the profiles by interpolating adjacent channels.
Due to this contamination and to the unknown inclination of the source, we
have assumed a unique bipolar component with i = 30 ;
remember that
in this case the lower limit to the momentum is 2 times smaller than the
calculated value. The adopted systemic velocity is 4 km s-1.
Neri et al. (1998) deduced a very small size for the CO cloud and the very
low J=2-1/J=1-0 intensity ratio confirms the usually assumed low
;
remember that
in this case the lower limit to the momentum is 2 times smaller than the
calculated value. The adopted systemic velocity is 4 km s-1.
Neri et al. (1998) deduced a very small size for the CO cloud and the very
low J=2-1/J=1-0 intensity ratio confirms the usually assumed low
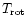 .
.
This well studied source shows profiles clearly composed of a core plus
wide wings. The extent of the line core CO emission (at half maximum) is
 10'' (Yamamura et al. 1996; Cox et al. 2000), which is taken
into account in our calculations.
Multiple jets are found in this nebula, but the overall inclination is
relatively well known, see Sahai et al. (1998).
From the maps by Cox et al., it can be seen that most of the line-wing
emission comes from an axial flow. Some high-velocity CO emission also
comes from a peculiar extension in the equatorial plane. We estimate from
those maps that the bipolar approximation may be wrong for just
10'' (Yamamura et al. 1996; Cox et al. 2000), which is taken
into account in our calculations.
Multiple jets are found in this nebula, but the overall inclination is
relatively well known, see Sahai et al. (1998).
From the maps by Cox et al., it can be seen that most of the line-wing
emission comes from an axial flow. Some high-velocity CO emission also
comes from a peculiar extension in the equatorial plane. We estimate from
those maps that the bipolar approximation may be wrong for just  1/4
of the wing integrated intensity; the possible correction is in any case
small, compared to uncertainties due to other reasons.
We also note that, given the small inclination angle, the effects
on the calculated values of the geometry are particularly important in this
source. In order to get an idea of the uncertainties due to the complex
geometry, we are also giving in Table 3 calculations following the
spherical-isotropic approximation for the fast outflow, although our
discussion will be based on the results obtained following our bipolar
model.
1/4
of the wing integrated intensity; the possible correction is in any case
small, compared to uncertainties due to other reasons.
We also note that, given the small inclination angle, the effects
on the calculated values of the geometry are particularly important in this
source. In order to get an idea of the uncertainties due to the complex
geometry, we are also giving in Table 3 calculations following the
spherical-isotropic approximation for the fast outflow, although our
discussion will be based on the results obtained following our bipolar
model.
We have adopted, from the shape of the line core,
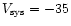 km s-1 and
an expansion velocity for the slow component equal to 15 km s-1.
We have checked that the 13CO line ratio is compatible with the assumed
low temperatures and that both 12CO and 13CO J=1-0 lines give similar
results (within a factor 2, being the mass from the 12CO data somewhat
smaller, as expected if some opacity effect is present).
km s-1 and
an expansion velocity for the slow component equal to 15 km s-1.
We have checked that the 13CO line ratio is compatible with the assumed
low temperatures and that both 12CO and 13CO J=1-0 lines give similar
results (within a factor 2, being the mass from the 12CO data somewhat
smaller, as expected if some opacity effect is present).
NGC7027 is a young PN, with a hot central star that shows particularly
intense and well studied CO emission (contrarily to other PNe). The
analysis of our data on NGC7027 is particularly difficult because of the
extent of the CO emission, that is known to arise from a structure about
20-25'' wide (Bieging et al. 1991; Graham et al. 1993). Our maps are
not good enough as to allow an accurate spatial integration of the
brightness, so we must assume an intrinsic source size and multiply by the
brightness observed in the central position. We deduce that the
area of the convolved profile is twice that of our J=1-0 beam. Due to
the uncertainty of this correction, it is difficult to check that the line
ratios are compatible with the assumed rotational temperatures. We will use
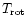 = 15 K, but we mention that if we instead take 30 K, as proposed
by Jaminet et al. (1991) from multiline CO observations, the correction
to our values of the mass, momentum and energy would just be of a factor
1.6.
= 15 K, but we mention that if we instead take 30 K, as proposed
by Jaminet et al. (1991) from multiline CO observations, the correction
to our values of the mass, momentum and energy would just be of a factor
1.6.
The accurate mapping by Bieging et al. and Graham et al. suggests that
the CO emission mainly comes from a radially expanding shell. We therefore
apply a spherical-isotropic model, considering separately an inner spectral
region defined by the velocity range 5-51 km s-1 (we have assumed
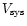 = 26 km s-1) and the rest of the profile: the weak and very wide
wings, see Fig. 12. These remarkable very wide wings have been detected
for the first and its origin is unknown, the asymmetry in the profiles may
be due to observational effects.
= 26 km s-1) and the rest of the profile: the weak and very wide
wings, see Fig. 12. These remarkable very wide wings have been detected
for the first and its origin is unknown, the asymmetry in the profiles may
be due to observational effects.
The 12CO/13CO line intensity ratio in NGC7027 shows the opposite
phenomenon than for other PPNe mentioned above. The line ratio is very
high, compared with the usual observations in evolved objects. This result
may be due to the presence of selective photodissociation by UV photons
from the inner hot star (see Fong et al. 2001, where it is
discussed the case of this and other PNe that have developed a massive PDR
and also show very faint 13CO lines).
Under this interpretation, 12CO would
survive in a relatively thick layer, much thicker than that in which 13CO
is abundant. In view of this phenomenon, we think that it is more
meaningful to use for our purposes the 12CO J=1-0 observations.
Therefore, the values of the calculated parameters may be underestimated
for this source due to opacity effects, but this underestimate is
probably minor for the high-velocity component, in view of their very low
brightness and the large extent of the source. For the sake of comparison,
we also show the mass, momentum and energy derived from 13CO J=1-0 for
the inner intense spectral feature (assuming our standard 13CO
abundance). These figures then represent the dynamical parameters for the
layer that is rich in 13CO, probably much thinner than the 12CO-rich
shell.
IRAS22272+5435 is one of the few PPNe emitting in CO that show no sign of
high-velocity line-wings down to a good limit, compared to the intensity of
the main component, that appears very similar to the profiles observed from
shells around AGB envelopes. We use
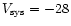 km s-1. The image in
12CO J=1-0 is practically circular and extending 21'' (Neri et al.
1998), i.e. comparable to our beam.
Assuming that the brightness distribution is the same for 12CO
and 13CO J=1-0, we derive that a correction of a factor 1.9 must be
applied in our analysis to account for the extent. The 13CO line ratio
suggests a low rotational temperature. So, our standard method is applied
to a unique spherical component.
km s-1. The image in
12CO J=1-0 is practically circular and extending 21'' (Neri et al.
1998), i.e. comparable to our beam.
Assuming that the brightness distribution is the same for 12CO
and 13CO J=1-0, we derive that a correction of a factor 1.9 must be
applied in our analysis to account for the extent. The 13CO line ratio
suggests a low rotational temperature. So, our standard method is applied
to a unique spherical component.
Since the CO emission is very similar to that of AGB envelopes, we apply
the usual methods to calculate mass loss rates and
circumstellar molecular mass in such objects. We will follow the method
described by Loup et al. (1993), that takes into account the CO
excitation and opacity (from model grids) and the theoretical
photodissociation radius. We use an expansion velocity of 8 km s-1, a
fractional 12CO abundance X(12CO) =
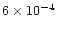 (typical of C-rich AGB
envelopes), and D = 1.7 kpc (Table 1). (Note that in this source the
12CO/13CO J=1-0 line ratio is larger than 20, in spite of the signs of
opacity effects in 12CO J=1-0, suggesting that in this source
X(12CO)/X(13CO) must be larger than the values we have adopted up to
now.) The results are
(typical of C-rich AGB
envelopes), and D = 1.7 kpc (Table 1). (Note that in this source the
12CO/13CO J=1-0 line ratio is larger than 20, in spite of the signs of
opacity effects in 12CO J=1-0, suggesting that in this source
X(12CO)/X(13CO) must be larger than the values we have adopted up to
now.) The results are  =
=
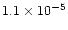
 yr-1 and a photodissociation radius
yr-1 and a photodissociation radius
 cm,
with an envelope formation time
cm,
with an envelope formation time 
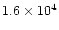 yr.
For the used expansion velocity,
these figures give a total mass in the CO-rich envelope
yr.
For the used expansion velocity,
these figures give a total mass in the CO-rich envelope  0.18
0.18  ,
very similar to that deduced from 13CO J=1-0 and our standard
method (0.14
,
very similar to that deduced from 13CO J=1-0 and our standard
method (0.14  ). Both results as well as the deduced values for the other
parameters are given in Table 3.
). Both results as well as the deduced values for the other
parameters are given in Table 3.
Following the method depicted in Sect. 5.2, we have (crudely) estimated
an upper limit for the momentum carried by the bipolar outflow (if it
exists). We used our 13CO J=1-0 spectrum, assuming that the wings are
not detected down to a level  5% of the peak intensity and adopting
that the typical width for the detected line is 20 km s-1. See results in
Table 3.
5% of the peak intensity and adopting
that the typical width for the detected line is 20 km s-1. See results in
Table 3.
The existing information on these two sources is poor. They have been
observed in the optical by Hrivnak et al. (1999) and Ueta et al.
(2000), showing a subarcsec image. IRAS23321+6545 has been mapped in CO
by Neri et al., its image being also very small. We have only observed them
in 12CO J=2-1 and 13CO J=1-0 being the 13CO emission very weak,
undetected in IRAS23304+6147. In view of the lack of data on them, we
will apply our standard procedure.
For IRAS23304+6147 we will use the 12CO line, so we must keep in mind
that opacity effects may be present (see discussion in Sect. 5.2).
However, the intensity contrast between the 12CO J=2-1 and the 13CO
J=1-0 is very strong, larger than  80 (the theoretical intensity
ratio derived for optically thin emission and the other assumptions used
here). Therefore, we believe that such opacity effects are not very
important in this source and that the derived values from 12CO J=2-1 are
not strong underestimates. The systemic velocity is -16 km s-1. For the
central part of the line we use a spherical-isotropic model with expansion
velocity equal to 9 km s-1. For the line wings, we use our bipolar model with
i = 90
80 (the theoretical intensity
ratio derived for optically thin emission and the other assumptions used
here). Therefore, we believe that such opacity effects are not very
important in this source and that the derived values from 12CO J=2-1 are
not strong underestimates. The systemic velocity is -16 km s-1. For the
central part of the line we use a spherical-isotropic model with expansion
velocity equal to 9 km s-1. For the line wings, we use our bipolar model with
i = 90 ,
so the momentum and energy results are directly the
minimum values (if only geometry effects are considered).
,
so the momentum and energy results are directly the
minimum values (if only geometry effects are considered).
For IRAS23321+6545 we will use the 13CO J=1-0 line, with the systemic
velocity and velocity range deduced from the 12CO line,
respectively
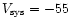 km s-1 and
km s-1 and
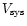
 20 km s-1. Note the
galactic contamination, that does not affect the 13CO nebular line. We
suppose a unique component in the bipolar approximation with i =
30
20 km s-1. Note the
galactic contamination, that does not affect the 13CO nebular line. We
suppose a unique component in the bipolar approximation with i =
30 .
The bipolarity of the outflow is in this case also suggested by the HST
images (Ueta et al. 2000). For this source the distance is not known, we
will adopt D = 1 kpc; this value could be a lower limit in view of the
low values found for the distance-dependent parameters (M, P, L,
etc.), which could be underestimated (but not the comparison of M, P
and E with the stellar luminosity).
.
The bipolarity of the outflow is in this case also suggested by the HST
images (Ueta et al. 2000). For this source the distance is not known, we
will adopt D = 1 kpc; this value could be a lower limit in view of the
low values found for the distance-dependent parameters (M, P, L,
etc.), which could be underestimated (but not the comparison of M, P
and E with the stellar luminosity).
This source has been recently mapped with the Plateau de Bure
interferometer (paper in preparation), confirming the presence of a
high-velocity outflow and an hourglass-like structure. Model fitting of the
maps per velocity indicates an inclination with respect to the plane of the
sky i  15
15 .
Only a small fraction of the source (a couple of
extreme axial knots) is found to be placed in the limit of the J=1-0 beam
of the 30 m telescope. In order to estimate the effect of the source extent,
we performed a small map, the resulting correction for the wing emission
shown in Fig. 16 is not very large,
.
Only a small fraction of the source (a couple of
extreme axial knots) is found to be placed in the limit of the J=1-0 beam
of the 30 m telescope. In order to estimate the effect of the source extent,
we performed a small map, the resulting correction for the wing emission
shown in Fig. 16 is not very large,  40%.
The low value of i suggests that the dynamical parameters in this source
can be overestimated in the central hourglass-like region, since the
projection correction may be too large if a component of the expansion is
perpendicular to the axis. We recall that the overestimate of the
momentum from our model with respect to an isotropical expansion is of a
factor 2.
40%.
The low value of i suggests that the dynamical parameters in this source
can be overestimated in the central hourglass-like region, since the
projection correction may be too large if a component of the expansion is
perpendicular to the axis. We recall that the overestimate of the
momentum from our model with respect to an isotropical expansion is of a
factor 2.
The wings are very weak in 13CO J=1-0, so we used in our calculations the
12CO J=1-0 line.
We have checked that the calculated mass values for the line core are not
smaller when using the 12CO line instead of the 13CO line, so opacity
effects are negligible even for the central velocities. We assumed a
systemic velocity of -27 km s-1 (LSR) and an expansion velocity for the
slow component equal to 14 km s-1.
For the PPNe detected in CO by other authors, we
have chosen the best published spectra, i.e. those with the highest
S/N ratio, preferably 13CO and J=1-0 lines, and with information
as complete as possible on the observation conditions. The lines are
analyzed as explained before, taking into account the effects
due to the different beam sizes and efficiencies.
When possible, i.e. for a few well studied nebulae, we
will directly use the published results on mass and kinematics. See
parameters of these nebulae in Table 2 and the results of our calculations
in Table 4.
Note that our results for this group of sources, including the absence of
line wings, are often very uncertain because of the scarce data on CO and
on other needed parameters. The 12CO J=2-1 line, used
when it is the only available spectrum with high S/N ratio, probably leads
to an important underestimate of the derived mass, momentum and energy,
because of probable high opacity and possible resolution of the
spatial source extent. See the case of Roberts22 in Sect. 5.2.5. When
other lines are used, our method gives mass values comparable to
other estimates, see general discussion in Sects. 4 and 5.1.12, 5.2.3, 5.2.15.
For these CO lines taken from the literature, we will mainly analyze the
line wings and the associated
fast outflows. Often the quality of the observations is not good enough to
allow a study of the slow component, since the definition of the different
spectral features needs high-quality profiles and since the opacity effects
for the line core are expected to be particularly important.
We also tried to estimate limits in the cases in which the line wings are
not detected. The treatment of limits in our case is very difficult, since
when the line wings are not detected we lack also for information on the
velocity. All we can do, under these conditions, is to perform crude
estimates, based on the "reasonable'' assumption that the extent of each
line wing should be comparable to the width of the detected profile.
The typical LSR velocity of the wing would then be equal to the systemic
velocity 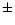 this width. Given the uncertainties of the analysis, we will
only estimate limits to the scalar momentum.
We did not consider the nondetections when only the 12CO J=2-1 line is
available, since then the accumulation of uncertainties yields useless data.
These limits are given in Table 4 for the four sources for which the
method can be applied.
this width. Given the uncertainties of the analysis, we will
only estimate limits to the scalar momentum.
We did not consider the nondetections when only the 12CO J=2-1 line is
available, since then the accumulation of uncertainties yields useless data.
These limits are given in Table 4 for the four sources for which the
method can be applied.
Now we discuss the details of the analysis source per source.
This source shows narrow lines with wings, that will be analyzed as
coming from a bipolar outflow. But we must keep in mind that the kinematics
of the Red Rectangle may be different from that usual in PPNe (Jura et al. 1995).
We will use the 12CO J=2-1 line by Jura et al.,
the best CO spectrum published for this source. We derive
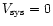 km s-1, and that the line wings extend between -7.4 and -2 km s-1 and between
2 and 7.3 km s-1 LSR. The
source is assumed to be small compared to the beam of the telescope (IRAM
30 m), since mapping with this instrument scarcely detected any extent
(unpublished observations). Other parameters used are in Table 2.
km s-1, and that the line wings extend between -7.4 and -2 km s-1 and between
2 and 7.3 km s-1 LSR. The
source is assumed to be small compared to the beam of the telescope (IRAM
30 m), since mapping with this instrument scarcely detected any extent
(unpublished observations). Other parameters used are in Table 2.
This source shows no wings in the CO lines (Bujarrabal et al. 1992; Knapp
et al. 1998), down to a limit of about 1/10 of the peak for the 12CO
lines. We estimated a limit to the momentum using the 12CO J=1-0 line by
Bujarrabal et al., and the prescriptions explained in Sect. 5.2; we adopted a
typical width for the detected spectrum  20 km s-1. The CO source is
not significantly extended, so no correction for this is done. The rest of
the parameters used in the analysis (Table 2) are relatively well known for
this source.
20 km s-1. The CO source is
not significantly extended, so no correction for this is done. The rest of
the parameters used in the analysis (Table 2) are relatively well known for
this source.
Table 4:
Calculations of the mass, momentum and kinetic energy for the
sources observed in CO by other authors.
| source |
mass |
momentum |
kinetic energy |
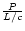 |
comments |
| |
M( ) ) |
P(gcms-1) |
E(erg) |
(yr) |
|
| |
|
|
|
|
|
| Red Rectangle |
|
|
|
|
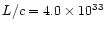 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
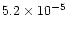 |
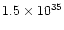 |
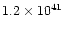 |
38 |
peculiar dynamics, underestimate? |
| IRAS07134+1005 |
|
|
|
|
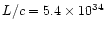 gcms-1yr-1
gcms-1yr-1 |
| no fast outflow detected |
<
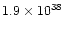 |
|
<
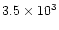 |
|
| OH231.8+4.2 |
|
|
|
|
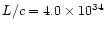 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
0.22 |
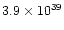 |
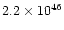 |
105 |
well studied, conspicuous bipolar flow |
| Hen3-401 |
|
|
|
|
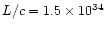 gcms-1yr-1
gcms-1yr-1 |
| fast outflow? |
>0.01? |
>
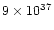 ?
? |
>
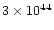 ? ? |
>
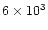 ? ? |
poor data, uncertain analysis |
| Roberts22 |
|
|
|
|
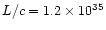 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
>0.018 |
>
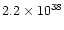 |
>
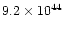 |
>
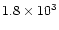 |
probable underestimate, unique component |
| HD101584 |
|
|
|
|
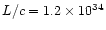 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
0.1 |
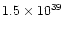 |
1046 |
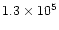 |
well studied, conspicuous bipolar flow |
| Boomerang Nebula |
|
|
|
|
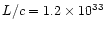 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
1.9 |
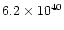 |
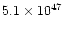 |
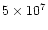 |
outer shell, spherical? |
| fast outflow |
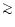 0.07 0.07 |
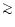
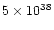 |
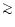
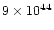 |
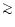
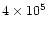 |
inner shell, spherical? |
| He2-113 |
|
|
|
|
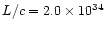 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
>
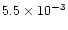 |
>
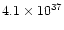 |
>
 |
>
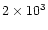 |
probable underestimate, uncertain analysis |
| Mz-3 |
|
|
|
|
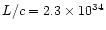 gcms-1yr-1
gcms-1yr-1 |
| no fast outflow detected |
|
|
|
poor limit, only 12CO J=2-1 |
| M2-9 |
|
|
|
|
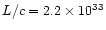 gcms-1yr-1
gcms-1yr-1 |
| no fast outflow detected |
<
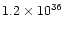 |
|
<
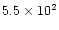 |
|
| CPD-568032 |
|
|
|
|
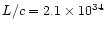 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
0.043 |
 |
 |
 |
|
| IRAS17150-3224 |
|
|
|
|
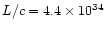 gcms-1yr-1
gcms-1yr-1 |
| no fast outflow detected |
|
|
|
poor limit, only 12CO J=2-1 |
| OH17.7-2.0 |
|
|
|
|
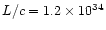 gcms-1yr-1
gcms-1yr-1 |
| no fast outflow detected |
|
|
|
poor limit, only 12CO J=2-1 |
| RSct |
|
|
|
|
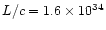 gcms-1yr-1
gcms-1yr-1 |
| no fast outflow detected |
<
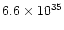 |
|
<41 |
|
| M1-92 |
|
|
|
|
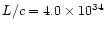 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
0.7 |
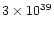 |
 |
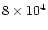 |
well studied, conspicuous bipolar flow |
| IRAS19475+3119 |
|
|
|
|
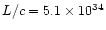 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
>0.026 |
>
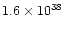 |
>
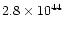 |
>
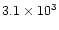 |
probable underestimate |
| IRAS20000+3239 |
|
|
|
|
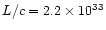 gcms-1yr-1
gcms-1yr-1 |
| no fast outflow detected |
|
|
|
poor limit, only 12CO J=2-1 |
| IRAS20028+3910 |
|
|
|
|
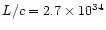 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
>
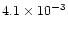 |
>
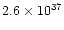 |
>
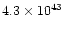 |
>103 |
probable underestimate |
| IRAS21282+5050 |
|
|
|
|
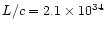 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
0.2 |
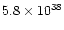 |
 |
 |
|
| IRAS22223+4327 |
|
|
|
|
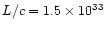 gcms-1yr-1
gcms-1yr-1 |
| fast outflow |
>
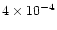 |
>
 |
>
 |
>
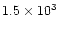 |
probable underestimate, uncertain analysis |
| IRAS22574+6609 |
|
|
|
|
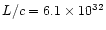 gcms-1yr-1
gcms-1yr-1 |
| no fast outflow detected |
<
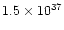 |
|
<
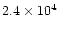 |
poor limit |
This nebula has been studied by Sánchez Contreras et al. (1997) using a
method almost identical to ours and accurate mapping. We will adopt the
results given in that paper without any change. As discussed by Sánchez
Contreras et al. (1997) and Alcolea et al. (2001), the nebular mass
obtained in this way is compatible with the values got from other
molecular lines and FIR data.
The CO spectra published by Bujarrabal & Bachiller (1991) show a
profile about 30-40 km s-1 wide with some indication of fast outflow
emission. The analysis of these data is very uncertain due to the poor
profiles. In particular, only the 12CO J=2-1 line shows some indication
of its shape, so an underestimate of the derived parameters is expected
(see Sect. 5.2). We will assume, perhaps arbitrarily, that the line core
extends about 22 km s-1 around the systemic velocity,
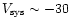 km s-1 LSR. Following Bujarrabal and Bachiller, we will assume that the
extent of the source is significantly smaller than the telescope resolution.
km s-1 LSR. Following Bujarrabal and Bachiller, we will assume that the
extent of the source is significantly smaller than the telescope resolution.
Observations of 12CO J=2-1 by Bujarrabal & Bachiller (1991) show a very
broad profile, about 100 km s-1 wide. As for other sources with similar
characteristics (Sect. 5.1), we take the whole spectra in our analysis,
and note that very similar results are obtained if a slow component with
expansion velocities of about 10 km s-1 is considered. Bujarrabal and
Bachiller note that the source does not seem to be extended.
The values obtained for the total mass (Table 4) are lower by about a
factor 10 than the results by Bujarrabal and Bachiller, from fitting of the
CO line by a model of AGB envelope emission, and by Sahai et al. (1999b),
from analysis of the circumstellar dust scattering.
Probably the use of the usually opaque 12CO J=2-1 line in our analysis,
that assumes optically thin emission, has led to a severe underestimate
of the molecular mass and, therefore, of the outflow momentum and energy.
We will use the accurate observations by Olofsson & Nyman (1999). These
authors calculate mass and scalar momentum from their 13CO and 12CO
spectra. We will adopt their values, correcting for an inclination i =
30 ,
as used here when the inclination is uncertain, and a
13CO relative abundance equal to
,
as used here when the inclination is uncertain, and a
13CO relative abundance equal to
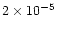 ,
in order to be coherent
with the rest of our paper. We also calculate the kinetic energy from their
spectrum, using the above prescriptions.
,
in order to be coherent
with the rest of our paper. We also calculate the kinetic energy from their
spectrum, using the above prescriptions.
The Boomerang Nebula was observed in 12CO J=1-0 and J=2-1 and 13CO
J=1-0 by Sahai & Nyman (1997). These authors found complex, very wide
spectra that were interpreted as due to an outer very cold shell plus an
inner less cold envelope. They fitted the data using detailed model
calculations and assuming spherical shells with radial expansion at
constant velocity. Even if this model is not similar to the bipolar
outflows found in other PPNe, we will take the mass of both components from
that paper and calculate momentum and energy from the masses and velocities
given there (Table 4). We note that, as we have discussed several times in
this paper, the calculation of mass and momentum from the results by Sahai
and Nyman probably depends only slightly on the assumed geometry and would
be approximate in the case that one or both components are bipolar. Note
that for the inner shell Sahai and Nyman only give a lower limit for the
mass.
We have used the 12CO J=2-1 profile published by Knapp et al. (1990),
which shows wide line wings, although the profile structure is poorly
defined. From discussion in Knapp et al. (1989), we infer that the units
in Knapp et al. (1990) are equivalent to
 .
The CO extent is unknown, but optical and radiocontinuum images are very
small, 1-2'', see de Marco et al. (1997) and Bedding & Zijlstra
(1994), so we will assume that the CO shell is also much smaller than the
telescope resolution in those observations (32''). Since
the inclination of the (putative) bipolar outflow is unknown, we will use
.
The CO extent is unknown, but optical and radiocontinuum images are very
small, 1-2'', see de Marco et al. (1997) and Bedding & Zijlstra
(1994), so we will assume that the CO shell is also much smaller than the
telescope resolution in those observations (32''). Since
the inclination of the (putative) bipolar outflow is unknown, we will use
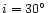 .
Other parameters used in our analysis are
.
Other parameters used in our analysis are
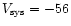 km s-1 (LSR) and CO line wings extending from -90 to -67 km s-1 and
from -48 to -30 km s-1.
In general, this object has not been well studied (not only in CO), so
the derived parameters remain quite uncertain.
km s-1 (LSR) and CO line wings extending from -90 to -67 km s-1 and
from -48 to -30 km s-1.
In general, this object has not been well studied (not only in CO), so
the derived parameters remain quite uncertain.
The 12CO J=2-1 observations by Bujarrabal & Bachiller (1991) show a
relatively narrow profile ( 20 km s-1 wide) with no sign of wings.
However the observational data are poor and the limit to the wing emission
is just about 1/3 of the line peak.
No attempt to estimate limits is done for this source (see discussion in
Sect. 5.2).
20 km s-1 wide) with no sign of wings.
However the observational data are poor and the limit to the wing emission
is just about 1/3 of the line peak.
No attempt to estimate limits is done for this source (see discussion in
Sect. 5.2).
M2-9 has been observed in 12CO J=1-0 and J=2-1 by Bachiller et al.
(1988, 1990), with the 30 m IRAM telescope,
and by Zweigle et al. (1997), who performed high-resolution
mapping in 12CO J=1-0. Zweigle et al. found a small extent for the CO
cloud,
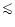 10'', as well as the absence of line wings down to a level
of about 1/10 of the peak, i.e.
10'', as well as the absence of line wings down to a level
of about 1/10 of the peak, i.e.
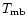 (12CO J=1-0)
(12CO J=1-0)
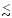 0.015 K
(30 m-telescope scale; see also Bachiller et al. 1988). The velocity
width of the lines in this source is very low, indicating an expansion
velocity
0.015 K
(30 m-telescope scale; see also Bachiller et al. 1988). The velocity
width of the lines in this source is very low, indicating an expansion
velocity  7 km s-1. We will use these figures to crudely estimate a
limit for the momentum in the fast outflow, if it exists, following the
method in Sect. 5.2; no correction for the spatial extent was done.
7 km s-1. We will use these figures to crudely estimate a
limit for the momentum in the fast outflow, if it exists, following the
method in Sect. 5.2; no correction for the spatial extent was done.
Exceptionally, we will estimate the mass in the slow envelope in this
source, since it is well mapped in CO and this value will be useful later
(Sect. 8).
Using our standard method and the above values, we get that the molecular
mass in M2-9 is
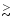
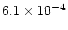
 ;
the upper limit is taken
following the discussion by Zweigle et al., who argue that the CO
abundance in this source may be 10 times lower than the one adopted here.
Indeed, the mass deduced from the fitting of the IR emission by Alcolea &
Bujarrabal (1991) is higher than 0.1
;
the upper limit is taken
following the discussion by Zweigle et al., who argue that the CO
abundance in this source may be 10 times lower than the one adopted here.
Indeed, the mass deduced from the fitting of the IR emission by Alcolea &
Bujarrabal (1991) is higher than 0.1  ,
and the extent of the beautiful
nebula imaged in the optical is much larger than the CO ring; probably, CO
has been strongly photodissociated in this source and its emission just
probes a small fraction of the nebular material.
Note that, corrected the abundance difference, the molecular mass value
obtained here is in good agreement with that given by Zweigle et al.
,
and the extent of the beautiful
nebula imaged in the optical is much larger than the CO ring; probably, CO
has been strongly photodissociated in this source and its emission just
probes a small fraction of the nebular material.
Note that, corrected the abundance difference, the molecular mass value
obtained here is in good agreement with that given by Zweigle et al.
The most useful CO data for this source is the 12CO J=1-0 spectrum by
Nyman et al. (1992), see also Knapp et al. (1990). The profiles are
clearly composite, with well defined line wings probably associated to a
bipolar outflow.
The CO extent is unknown but the optical image is very small, 1-2'' (de
Marco et al. 1997), so no correction for spatial extent is applied.
The inclination of the source axis is unknown, therefore we take
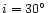 .
The derived velocities from the spectrum are
.
The derived velocities from the spectrum are
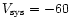 km s-1
LSR and wings spanning from -130 to -73 km s-1 and from -42 to 20 km s-1.
km s-1
LSR and wings spanning from -130 to -73 km s-1 and from -42 to 20 km s-1.
The best CO data are from Hu et al. (1993), who published a 12CO J=2-1
spectrum. The line is not well measured, showing a narrow profile (about 20
km s-1) and no sign of wings up to a limit of 1/5 of the peak.
No attempt to estimate limits to the outflow mass and momentum is done (see
Sect. 5.2).
This source is difficult to observe in CO due to strong galactic
contamination. The best published spectrum is that of 12CO J=2-1 by Heske
et al. (1990), in which no line wing is detected, but to a poor limit
(partially due to the galactic contamination).
No attempt to estimate limits is done for this source (see discussion in
Sect. 5.2).
R Sct is a (peculiar) RV Tauri variable, then probably a post-red-giant
object with low initial mass (e.g. Alcolea & Bujarrabal 1991). R Sct is
the only RV Tau star showing well detected CO emission.
12CO J=2-1 and J=1-0 and 13CO J=2-1 spectra of R Sct were published by
Alcolea & Bujarrabal (1991) and Bujarrabal et al. (1990). The lines are
narrow ( 10 km s-1) with no wings down to a limit of about 1/10 of the
peak. We used their 12CO J=1-0 line to estimate a limit to the fast
outflow momentum (Sect. 5.2); note the low value obtained (Table 4).
10 km s-1) with no wings down to a limit of about 1/10 of the
peak. We used their 12CO J=1-0 line to estimate a limit to the fast
outflow momentum (Sect. 5.2); note the low value obtained (Table 4).
Also in this case, we will estimate the mass of the slow component from the
12CO J=1-0 data in Bujarrabal et al. (1990) and using our standard
formulae. We obtain for the unique detected component a mass of about
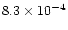
 .
This value is in good agreement with that derived by
Alcolea & Bujarrabal (1991) by fitting the photometric data on the SED of
this source.
.
This value is in good agreement with that derived by
Alcolea & Bujarrabal (1991) by fitting the photometric data on the SED of
this source.
M1-92, Minkowski's Footprint, is probably the best studied PPN in CO
emission. We published accurate 13CO J=2-1 maps (Bujarrabal 1998a), that
were modeled using parameters (distance, inclination, 13CO abundance,
etc.) compatible with those given here. We therefore reproduce in Table 4
the results obtained in that paper for the well defined and studied bipolar
outflow. We can see in Bujarrabal et al. (1998a,b) that the mass
distribution obtained from this method is compatible with the data of the
different CO lines and the results from observations of dust emission and
scattering.
We take the 12CO J=2-1 spectrum by Likkel et al. (1991), since their
J=1-0 data are poor. For these old data from the 30 m IRAM telescope, we
will assume that the beam resolution is  14''. We take i =
30
14''. We take i =
30 ,
in view of the absence of information on this parameter.
We derive from the spectrum
,
in view of the absence of information on this parameter.
We derive from the spectrum
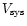 = 18 km s-1 LSR and the presence of
wings from -10 to 8 and from 27 to 47 km s-1. The
luminosity given in Table 2 was calculated by us, for the distance by Likkel
et al. (1987), after integrating the IRAS fluxes, NIR fluxes from Hrivnak
et al. (1994), and V and B magnitudes from the Simbad database.
= 18 km s-1 LSR and the presence of
wings from -10 to 8 and from 27 to 47 km s-1. The
luminosity given in Table 2 was calculated by us, for the distance by Likkel
et al. (1987), after integrating the IRAS fluxes, NIR fluxes from Hrivnak
et al. (1994), and V and B magnitudes from the Simbad database.
12CO J=2-1 and J=1-0 were observed by Likkel et al. (1991), the J=1-0
line being only tentatively detected.
Line widths  20-30 km s-1 were found. The profiles are apparently
complex but do not show wings, with a limit to their intensity of
about 1/5 of the line peak. We could
not find any indication on the distance to this source, so we assumed it to
be 1 kpc (probably an underestimate, see Sect. 5.1.13).
No attempt to estimate limits is done for this source (see discussion in
Sect. 5.2).
20-30 km s-1 were found. The profiles are apparently
complex but do not show wings, with a limit to their intensity of
about 1/5 of the line peak. We could
not find any indication on the distance to this source, so we assumed it to
be 1 kpc (probably an underestimate, see Sect. 5.1.13).
No attempt to estimate limits is done for this source (see discussion in
Sect. 5.2).
The 12CO J=2-1 profile by Likkel et al. (1991) shows a hint of line
wings. We take
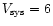 km s-1 and wings between -17 and -5 km s-1 and
between 17 and 32 km s-1 (LSR). As in Sect. 5.2.16, we assume that the
resolution of the 30 m IRAM's telescope in these observations was
km s-1 and wings between -17 and -5 km s-1 and
between 17 and 32 km s-1 (LSR). As in Sect. 5.2.16, we assume that the
resolution of the 30 m IRAM's telescope in these observations was  14''. The CO extent was tentatively detected by Neri et al. (1998), who
give an ucertain value of the extent of
14''. The CO extent was tentatively detected by Neri et al. (1998), who
give an ucertain value of the extent of  11'' for 12CO J=1-0.
HST images in the optical are about 2'' wide (Hrivnak et al. 1999), and in the IR the source extent is about 1'' (Meixner et al. 1999). We accordingly do not correct for the source extent in our
calculations. The axis inclination is not known, so we take
11'' for 12CO J=1-0.
HST images in the optical are about 2'' wide (Hrivnak et al. 1999), and in the IR the source extent is about 1'' (Meixner et al. 1999). We accordingly do not correct for the source extent in our
calculations. The axis inclination is not known, so we take
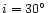 .
.
This source has been relatively well studied in CO emission. Meixner et al. (1998) performed interferometric maps and found that CO is abundant
in a (hollow) shell about 10'' wide. However, line wings are detected
only in the single-dish 12CO data by Likkel et al. (1988). We will
use their J=1-0 profile; no correction for the source extent is done here.
We take
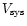 = 18 km s-1 LSR and wings in the ranges
= 18 km s-1 LSR and wings in the ranges
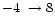 · km s-1 and
· km s-1 and
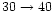 km s-1.
km s-1.
The best CO measurement in this source is the 12CO J=2-1 spectrum by
Omont et al. (1993), see also Likkel et al. (1991). We assume in
this case that the telescope beam is 14'' wide at half maximum (Sect. 5.2.16).
The CO extent is unknown in this source, but its IR image is very compact
(1-2'', Meixner et al. 1999), and we assume the CO source to be much
smaller than the beam. We find from Omont et al's data,
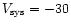 km s-1 and wings between -52 and -41 km s-1and between -18 and -8 km s-1.
Due to the lack of data on this source, we assume i = 30
km s-1 and wings between -52 and -41 km s-1and between -18 and -8 km s-1.
Due to the lack of data on this source, we assume i = 30 and
D = 1 kpc (this value probably being a lower limit, see Sect. 5.1.13).
and
D = 1 kpc (this value probably being a lower limit, see Sect. 5.1.13).
The best CO profiles of this source (12CO J=2-1 and J=1-0, by Likkel et al. 1991) are
 40 km s-1 wide and show no clear
wings. The S/N ratio and the profile shape in these observations are not
good enough to allow a limit for the line wing emission better than about
1/10 of the peak. In the J=1-0 line one tentatively sees wings that are not
confirmed in the J=2-1 profile. In any case, we used the J=1-0 line by
Likkel et al. to crudely estimate a momentum limit for the fast outflow,
with the method and limitations explained in Sect. 5.2. We assumed a
typical width
40 km s-1 wide and show no clear
wings. The S/N ratio and the profile shape in these observations are not
good enough to allow a limit for the line wing emission better than about
1/10 of the peak. In the J=1-0 line one tentatively sees wings that are not
confirmed in the J=2-1 profile. In any case, we used the J=1-0 line by
Likkel et al. to crudely estimate a momentum limit for the fast outflow,
with the method and limitations explained in Sect. 5.2. We assumed a
typical width  20 km s-1 for the line core. Note that in this source
the limit to the momentum is moreover uncertain due to the unknown
distance, but that this does not affect the value of
20 km s-1 for the line core. Note that in this source
the limit to the momentum is moreover uncertain due to the unknown
distance, but that this does not affect the value of
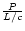 ,
also
quoted in Table 4.
,
also
quoted in Table 4.
As we will see in the next sections, we are interested in estimating, from
the existing data, the time spent by the sources studied here as post-AGB
stars (
 )
and the time during which the high-velocity CO outflows
were accelerated (
)
and the time during which the high-velocity CO outflows
were accelerated (
 ).
).
An approximate upper limit to the value of
 in individual sources
is given by the typical value of the
total post-AGB lifetime,
in individual sources
is given by the typical value of the
total post-AGB lifetime,  1000 yr. Such a value of the "transit'' time
from the AGB to the PN phase can be derived following several methods and
agrees with theoretical estimates (see e.g. Bujarrabal et al. 1988).
1000 yr. Such a value of the "transit'' time
from the AGB to the PN phase can be derived following several methods and
agrees with theoretical estimates (see e.g. Bujarrabal et al. 1988).
When possible,
 is calculated for individual sources from data on
the CO outflow, i.e. dividing the characteristic length by the velocity,
taking into account the inclination of the jets with respect to the plane
of the sky (Table 1). When accurate CO data are not available, but the
circumstellar shell is known to be detached and there are measurements of
its inner radius (
is calculated for individual sources from data on
the CO outflow, i.e. dividing the characteristic length by the velocity,
taking into account the inclination of the jets with respect to the plane
of the sky (Table 1). When accurate CO data are not available, but the
circumstellar shell is known to be detached and there are measurements of
its inner radius (
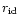 ), we assume that
), we assume that


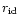 /
/
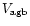 ,
where
,
where
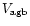 is the expansion
velocity of the AGB
wind measured as the half-width of the CO line-core (see Sects. 4.1 and 8.1). A relatively uncertain estimate of
is the expansion
velocity of the AGB
wind measured as the half-width of the CO line-core (see Sects. 4.1 and 8.1). A relatively uncertain estimate of
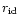 can be made from
fitting the source's SED (spectral energy distribution) by means of dust
absorption-emission models. In some cases, this estimate of
can be made from
fitting the source's SED (spectral energy distribution) by means of dust
absorption-emission models. In some cases, this estimate of
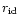 is
compatible with IR mapping (Meixner et al. 1997), but in general the
results from pure SED fitting are uncertain (compare the measured values
of
is
compatible with IR mapping (Meixner et al. 1997), but in general the
results from pure SED fitting are uncertain (compare the measured values
of
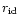 in Table 5 for AFGL2343, IRAS22272+5435 and
IRAS07134+1005 with those estimated from the SED by Kwok et al. 1989;
Hrivnak et al. 1989) and must be used with caution.
In IRAS21282+5050 the inner radii
determined from CO and IR mapping are significantly different; we suggest
that this can be due to CO photodissociation by the stellar UV radiation,
since this source is known to present a well developed central PDR with a
mass
in Table 5 for AFGL2343, IRAS22272+5435 and
IRAS07134+1005 with those estimated from the SED by Kwok et al. 1989;
Hrivnak et al. 1989) and must be used with caution.
In IRAS21282+5050 the inner radii
determined from CO and IR mapping are significantly different; we suggest
that this can be due to CO photodissociation by the stellar UV radiation,
since this source is known to present a well developed central PDR with a
mass  0.1
0.1  (Fong et al. 2001).
We will accordingly prefer the IR data in this
case, but keeping in mind the uncertainty of the result. We will not use in
our estimates the values of shell radii and velocities obtained from the
HH-like objects emitting in atomic lines (like those observed in
He3-1475, Riera et al. 1995), since the interpretation in terms of
(Fong et al. 2001).
We will accordingly prefer the IR data in this
case, but keeping in mind the uncertainty of the result. We will not use in
our estimates the values of shell radii and velocities obtained from the
HH-like objects emitting in atomic lines (like those observed in
He3-1475, Riera et al. 1995), since the interpretation in terms of
 of the kinematics of this gas (probably ejected in the post-AGB
phase and excited by counter-shocks) is not obvious.
However, we will use the radii of the
(empty) shells found by de Marco et al. (1997) from high-resolution
mapping of H
of the kinematics of this gas (probably ejected in the post-AGB
phase and excited by counter-shocks) is not obvious.
However, we will use the radii of the
(empty) shells found by de Marco et al. (1997) from high-resolution
mapping of H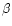 emission, since those structures, when detected, are
often comparable in size to the inner layers of the dense shells.
The values we obtain for
emission, since those structures, when detected, are
often comparable in size to the inner layers of the dense shells.
The values we obtain for
 are given in Table 5. See velocities
from the CO profiles in Sect. 5; some references on bipolar jets'
structure are detailed in this section and those on the detached shell size
are also given in Table 5.
Other parameters needed in the calculation, like the distance and
inclination, are taken from Table 1.
are given in Table 5. See velocities
from the CO profiles in Sect. 5; some references on bipolar jets'
structure are detailed in this section and those on the detached shell size
are also given in Table 5.
Other parameters needed in the calculation, like the distance and
inclination, are taken from Table 1.
Table 5:
Characteristic time spent by the studied sources as PPNe,
 ,
and time needed to accelerate the observed molecular outflows,
,
and time needed to accelerate the observed molecular outflows,
 .
.
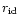 is the inner radius of the detached shell, when it can
be estimated.
is the inner radius of the detached shell, when it can
be estimated.
| name |
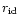 |
 |
 |
refs. |
comments |
| |
(cm) |
(yr) |
(yr) |
|
|
| |
|
|
|
|
|
| IRAS04296+3429 |
1016 |
370 |
<370 |
1, 2 |
|
| CRL618 |
|
110 |
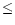 110 110 |
0, 3 |
complex law for V(r), well studied |
| Frosty Leo |
|
300-900 |
 500 500 |
0, 4 |
|
| IRAS17436+5003 |

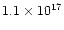 |
 2400 2400 |
|
5 |
uncertain
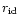 |
| He3-1475 |
? |
? |
|
|
|
| 89 Her |
? |
? |
|
|
|
| AFGL2343 |
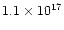 |
1100 |
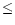 1100 ? 1100 ? |
6 |
yellow hypergiant |
| IRC+10420 |
1017 |
900 |
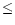 900 ? 900 ? |
7 |
yellow hypergiant |
| IRAS19500-1709 |
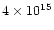 |
120 |
<120 |
5, 2 |
|
| CRL2477 |
? |
? |
|
|
|
| CRL2688 |
|
200 |
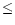 200 200 |
0, 8 |
complex law for V(r), well studied |
| NGC7027 |
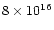 |
1300 |
<1300 |
9 |
young PN, very fast outflow not considered |
| IRAS22272+5435 |
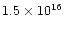 |
480 |
|
1, 2 |
no fast outflow detected |
| IRAS23304+6147 |

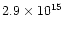 |
 100 100 |
|
1 |
uncertain
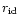 |
| IRAS23321+6545 |
? |
? |
|
|
|
M2-56 |
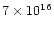 |
1500 |
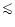 300 300 |
0 |
well studied |
| Red Rectangle |

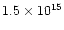 |
 120 120 |
|
10 |
uncertain
 |
| IRAS07134+1005 |
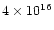 |
1300 |
|
2, 5 |
no fast outflow detected |
| OH231.8+4.2 |
|
800 |
 160 160 |
0, 11 |
well studied |
| Roberts22 |
? |
 440 440 |
<440 |
12 |
combining CO spectra and
optical imaging |
| HD101584 |
|
150 |
 30 30 |
0, 13 |
well studied |
| He2-113 |
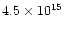 |
140 |
<140 |
14 |
|
| M2-9 |
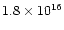 |
830 |
|
15 |
no fast outflow detected |
| CPD-568032 |
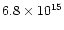 |
140 |
<140 |
14 |
|
| OH17.7-2.0 |

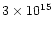 |
 80 80 |
|
16 |
uncertain
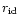 ,
no fast outflow detected ,
no fast outflow detected |
| RSct |

 |
 1900 1900 |
|
10 |
uncertain
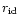 ,
no fast outflow detected ,
no fast outflow detected |
| M1-92 |
|
900 |
 100 100 |
0, 17 |
well studied |
IRAS21282+5050 |
5-
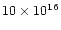 |
1400 ? |
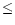 1400 ? 1400 ? |
18 |
|

A first estimate of the typical value of the time
needed to form the high-velocity flows (the acceleration time,
 )
is given by statistical studies (Bujarrabal et al. 1992; Trammell et al. 1994), that show that bipolar ejections appear and are already
massive in PPNe that are thought to be relatively young. Therefore,
the strong gas acceleration took place at the beginning of its evolution
and was very short, much shorter than the characteristic PPN lifetime. So,
)
is given by statistical studies (Bujarrabal et al. 1992; Trammell et al. 1994), that show that bipolar ejections appear and are already
massive in PPNe that are thought to be relatively young. Therefore,
the strong gas acceleration took place at the beginning of its evolution
and was very short, much shorter than the characteristic PPN lifetime. So,
 <
<
 ,
for individual sources,
,
for individual sources,

 1000 yr, in general.
1000 yr, in general.
A better estimate of
 can be reached in some cases, in which a
clearly linear dependence of the velocity of the fast molecular gas on the
distance to the central star has been found; such a result is sometimes
called the "Hubble law'' of the PPN kinematics. It has been argued (e.g.
Alcolea et al. 2001 and references therein) that this law strongly
suggests that the acceleration of the massive nebular flow was produced in
a very short time, compared to the total lifetime of the nebula, since free
movement is the easiest explanation of the Hubble law.
The duration of such a process can readily be estimated from the dispersion
of the empirical dependence of the velocity with the distance. The
characteristic acceleration time (
can be reached in some cases, in which a
clearly linear dependence of the velocity of the fast molecular gas on the
distance to the central star has been found; such a result is sometimes
called the "Hubble law'' of the PPN kinematics. It has been argued (e.g.
Alcolea et al. 2001 and references therein) that this law strongly
suggests that the acceleration of the massive nebular flow was produced in
a very short time, compared to the total lifetime of the nebula, since free
movement is the easiest explanation of the Hubble law.
The duration of such a process can readily be estimated from the dispersion
of the empirical dependence of the velocity with the distance. The
characteristic acceleration time (
 )
should be given by the
characteristic PPN time (that can be derived with the same result for all
points in which the law is satisfied), multiplied by a factor equal to the
relative dispersion of the observational points in the velocity vs.
distance diagram (
)
should be given by the
characteristic PPN time (that can be derived with the same result for all
points in which the law is satisfied), multiplied by a factor equal to the
relative dispersion of the observational points in the velocity vs.
distance diagram (
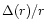 ).
We must keep in mind that, since some part of this dispersion can be due to
inhomogeneities in the density distribution or observational noise, the
values so obtained could be overestimates of the actual
).
We must keep in mind that, since some part of this dispersion can be due to
inhomogeneities in the density distribution or observational noise, the
values so obtained could be overestimates of the actual
 .
So, for these sources we will adopt
.
So, for these sources we will adopt

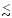
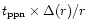 .
.
The typical acceleration times so calculated are astonishingly short.
Mainly for the well studied cases, for which the above overestimate is
not important. In OH231.8+4.2 (Alcolea et al. 2001), the "Hubble law''
applies along a very elongated structure with a dispersion,
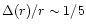 ;
the kinematical PPN age of this nebula is
;
the kinematical PPN age of this nebula is
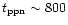 yr, so the acceleration time,
yr, so the acceleration time,
 ,
is
,
is
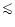 160 yr. For
M1-92 the velocity as a function of the distance was modelized by
Bujarrabal et al. (1998a). From the comparison of the model predictions
with the observations, we estimate that in this source
160 yr. For
M1-92 the velocity as a function of the distance was modelized by
Bujarrabal et al. (1998a). From the comparison of the model predictions
with the observations, we estimate that in this source
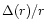
 1/8-1/10; the PPN time
1/8-1/10; the PPN time  900 yr, so
900 yr, so

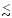 100 yr. The
molecular outflow in HD101584 also shows a clear distance dependence
(Olofsson & Nyman 1999), with a dispersion
100 yr. The
molecular outflow in HD101584 also shows a clear distance dependence
(Olofsson & Nyman 1999), with a dispersion
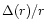
 1/5 and
1/5 and

 150 yr; so, for HD101584 we obtain
150 yr; so, for HD101584 we obtain

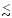 30
yr. Note that we assumed in this calculation a standard value of the
inclination of the flow axis with respect to the plane of the sky (i =
30
30
yr. Note that we assumed in this calculation a standard value of the
inclination of the flow axis with respect to the plane of the sky (i =
30 see Sect. 5.2.6), Olofsson and Nyman favor smaller values of
this parameter, which would lead to even smaller acceleration times.
Recent, unpublished CO observations of M2-56 have also shown a linear
distance dependence of the outflow velocity, with
see Sect. 5.2.6), Olofsson and Nyman favor smaller values of
this parameter, which would lead to even smaller acceleration times.
Recent, unpublished CO observations of M2-56 have also shown a linear
distance dependence of the outflow velocity, with
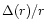
 1/5,
and
1/5,
and
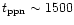 yr. These maps also show the presence of a
central ring with an inner radius of about 1-2'', equivalent to
yr. These maps also show the presence of a
central ring with an inner radius of about 1-2'', equivalent to
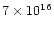 cm; for an expansion velocity of the slow component of 14 km s-1,
the obtained kinematical post-AGB time is again
cm; for an expansion velocity of the slow component of 14 km s-1,
the obtained kinematical post-AGB time is again  1500 yr. Therefore,
for M2-56 we find
1500 yr. Therefore,
for M2-56 we find
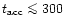 yr.
yr.
In other less well studied cases, we only can assume that

 .
Sometimes, the absence of shocks at present is complete,
with no trace of even weak shocks, strongly suggesting that the interaction
took place in a time much shorter than
.
Sometimes, the absence of shocks at present is complete,
with no trace of even weak shocks, strongly suggesting that the interaction
took place in a time much shorter than
 .
This is the case of
Frosty Leo (Sahai et al. 2000), in which the extent of the CO emitting
region is
.
This is the case of
Frosty Leo (Sahai et al. 2000), in which the extent of the CO emitting
region is  5'' and the velocity dispersion observed is
5'' and the velocity dispersion observed is  80
km s-1. The kinematical age
80
km s-1. The kinematical age
 ranges between
ranges between  900 yr,
calculated assuming isotropic expansion in the central region, and 300 yr
assuming bipolar ejections with an inclination with respect to the plane of
the sky i = 15
900 yr,
calculated assuming isotropic expansion in the central region, and 300 yr
assuming bipolar ejections with an inclination with respect to the plane of
the sky i = 15 (Sect. 5.1.3). A different case is that of the
fast outflow of CRL618, which is small in the sky plane (
(Sect. 5.1.3). A different case is that of the
fast outflow of CRL618, which is small in the sky plane ( 2'', see
Neri et al. 1992) and show velocities projected in the line of sight
2'', see
Neri et al. 1992) and show velocities projected in the line of sight
 70-80 km s-1. In this source, the velocity/distance relation seems
more complex than the linear dependence above discussed, and it is possible
that some significant acceleration of the outflow is still taking place.
For the inclination and distance values in Table 1, we calculate
an age for the nebulae
70-80 km s-1. In this source, the velocity/distance relation seems
more complex than the linear dependence above discussed, and it is possible
that some significant acceleration of the outflow is still taking place.
For the inclination and distance values in Table 1, we calculate
an age for the nebulae

 110 yr. So the high momentum
carried by the flow was adquired in a time
110 yr. So the high momentum
carried by the flow was adquired in a time
 comparable or smaller
than this value.
A similar calculation can be done for CRL2688, from the maps by Cox et al. (2000), in which no "Hubble law'' is found. Cox et al. calculated,
using similar parameters than in our work and from the movements of the
axial flow, values of
comparable or smaller
than this value.
A similar calculation can be done for CRL2688, from the maps by Cox et al. (2000), in which no "Hubble law'' is found. Cox et al. calculated,
using similar parameters than in our work and from the movements of the
axial flow, values of
 ranging between 250 and 125 yr, for all
clumps except for the outermost northern component, for which
ranging between 250 and 125 yr, for all
clumps except for the outermost northern component, for which

 1200 yr. Since this outer clump just represents a very small part of
the nebula, possibly decelerated by interaction with the slow wind,
we can conclude that for CRL2688
1200 yr. Since this outer clump just represents a very small part of
the nebula, possibly decelerated by interaction with the slow wind,
we can conclude that for CRL2688


 200 yr.
200 yr.
For the other sources of our sample, the poor maps or the lack of further
information on the acceleration time lead to less meaningful limits,
usually
 < 1000 yr.
< 1000 yr.
Our best estimates (often limits) to the typical acceleration times of the
fast outflows (
 )
in individual objects are given in Table 5,
together with our estimates of
)
in individual objects are given in Table 5,
together with our estimates of
 and some comments on how they are
determined. As we see, the
typical values for
and some comments on how they are
determined. As we see, the
typical values for
 in protoplanetary nebulae are very low,
particularly for the well studied sources. Although these estimates are
crude, the results for the different sources are quite compatible, so they
probably have, at least, a statistical meaning and can be used to derive a
typical value
in protoplanetary nebulae are very low,
particularly for the well studied sources. Although these estimates are
crude, the results for the different sources are quite compatible, so they
probably have, at least, a statistical meaning and can be used to derive a
typical value
 = 100-200 yr for PPNe.
= 100-200 yr for PPNe.
For the studied hypergiants, AFGL2343 and IRC+10420,

 1000 yr; these objects show clearly detached shells and
1000 yr; these objects show clearly detached shells and
 in them
can be understood as the time elapsed since the end of the copious
mass-loss process.
in them
can be understood as the time elapsed since the end of the copious
mass-loss process.
 may be an upper limit to the acceleration time
also in hypergiants, if in these objects the high-mass shell was
significantly accelerated after its ejection (as we are
assuming for standard post-AGB objects). But the evolution of yellow
hypergiants and the dynamics of their circumstellar shells are poorly known
and we are not sure on the meaning of
may be an upper limit to the acceleration time
also in hypergiants, if in these objects the high-mass shell was
significantly accelerated after its ejection (as we are
assuming for standard post-AGB objects). But the evolution of yellow
hypergiants and the dynamics of their circumstellar shells are poorly known
and we are not sure on the meaning of
 in this case (see
discussion in Sect. 5.1.7, particularly for AFGL2343).
in this case (see
discussion in Sect. 5.1.7, particularly for AFGL2343).
It is well known that the radiation pressure of the stellar light, acting
primarily onto dust grains, can accelerate the circumstellar envelopes
around AGB stars, explaining its expansion velocity (
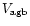 )
and, in
fact, its formation (e.g. Kwok 1975; Ivezic & Elitzur 1995). In a
first approximation, there is a limit for the momentum won by the outflow:
)
and, in
fact, its formation (e.g. Kwok 1975; Ivezic & Elitzur 1995). In a
first approximation, there is a limit for the momentum won by the outflow:
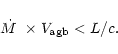 |
(8) |
However, this is not exactly the momentum conservation law (that must be
satisfied in any case), since we are dealing with "scalar momenta'', i.e.
with the momentum moduli integrated over a shell. When the dust opacity is
very high, we must take into account the so called "multiple scattering'':
the fact that a stellar photon can be scattered, or absorbed and reemitted,
several times before leaving the envelope. Under such a situation, the
conservation law imposes (e.g. Knapp 1986; Ivezic & Elitzur 1995):
 |
(9) |
Where
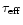 is the efficient opacity governing the multiple photon
absorption. When the nebula is very opaque, which is our case,
is the efficient opacity governing the multiple photon
absorption. When the nebula is very opaque, which is our case,
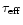 is the opacity at the wavelength at which the maximum emission of the
nebula takes place, 5-20
is the opacity at the wavelength at which the maximum emission of the
nebula takes place, 5-20 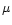 m, characteristic of the relatively cold
dust grains. This is due to that once a photon is
absorbed by the dust it is reemitted as radiation at the characteristic
dust emission wavelengths, and continues being absorbed and emitted at these
long waves.
m, characteristic of the relatively cold
dust grains. This is due to that once a photon is
absorbed by the dust it is reemitted as radiation at the characteristic
dust emission wavelengths, and continues being absorbed and emitted at these
long waves.
The studies of the dust emission and absorption in AGB envelopes reveal
that the most opaque shells (like that of IRC+10216, with 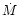
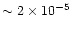
 yr-1) have opacities in the optical and UV of about 10-20
(e.g. Rowan-Robinson & Harris 1983; Rowan-Robinson 1980). We can
assume, lacking for a better information, that when the late AGB star ejects
its heavy envelope, with
yr-1) have opacities in the optical and UV of about 10-20
(e.g. Rowan-Robinson & Harris 1983; Rowan-Robinson 1980). We can
assume, lacking for a better information, that when the late AGB star ejects
its heavy envelope, with 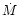
 1-
1-
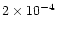
 yr-1 (see Sect. 8.1), this dust opacity scales with the mass loss rate, reaching values
yr-1 (see Sect. 8.1), this dust opacity scales with the mass loss rate, reaching values
 100. In the IR, where
100. In the IR, where
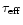 must be evaluated, we expect an
opacity about 10 times smaller (for the usual dust extinction laws, see the
above references), so for PPNe we can expect typical values
must be evaluated, we expect an
opacity about 10 times smaller (for the usual dust extinction laws, see the
above references), so for PPNe we can expect typical values
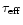
 10. Therefore, the ejection of this superwind must satisfy
10. Therefore, the ejection of this superwind must satisfy
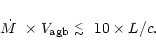 |
(10) |
Note that this formula gives a maximum momentum under the expected
conditions, not an absolute maximum, since
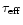 is just a
characteristic opacity.
is just a
characteristic opacity.
Let us first introduce a general factor,
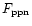 ,
for estimating the
maximum momentum won in this post-AGB acceleration during a characteristic
time
,
for estimating the
maximum momentum won in this post-AGB acceleration during a characteristic
time
 :
:
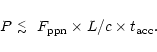 |
(11) |
If we try to explain by radiation pressure the axial acceleration of the
molecular nebula during the PPN phase, we must take into account that only
about one half of the radiation momentum can be used to produce expansion
along an axis.
So, we conclude from the above discussion that
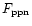 is typically
is typically
 5-10, when radiation pressure directly acts onto grains in the
molecular flow.
Of course, if we try to apply such a limit to the momenta obtained in
Sect. 5, we must conclude that this process cannot explain at all
the acceleration of the observed bipolar outflows.
5-10, when radiation pressure directly acts onto grains in the
molecular flow.
Of course, if we try to apply such a limit to the momenta obtained in
Sect. 5, we must conclude that this process cannot explain at all
the acceleration of the observed bipolar outflows.
Another argument against this simple mechanism has been found by Alcolea
et al. (2001), based on that the very high drift velocity between the
dust grains and the gas. Alcolea et al. argue that, if the outflow in the
well studied PPN OH231.8+4.2 is powered by radiation pressure acting
primarily onto grains, one expects that the dust must flow at a velocity
higher than that of the gas by  100 km s-1. This would produce
structures in the images of dust scattered light and gas emission separated
by a distance comparable to the size of the nebula itself. However, the
observations indicate that both gas and dust features are exactly
coincident, within the observational uncertainties: better than
typically 5% of the distance to the center.
100 km s-1. This would produce
structures in the images of dust scattered light and gas emission separated
by a distance comparable to the size of the nebula itself. However, the
observations indicate that both gas and dust features are exactly
coincident, within the observational uncertainties: better than
typically 5% of the distance to the center.
On the other hand, we have mentioned in Sect. 1 that there are good
reasons to think that the momentum of the dense bipolar outflows is
transferred to them from very fast and collimated post-AGB jets by shocks.
Such jets (often observed to be expelled by the post-AGB stars, e.g. Kwok
2000) will be assumed to be completely different from the molecular flows
(probed by CO lines), whose material was probably ejected by the AGB star.
So the problem of the momentum in the PPN bipolar flows would be to
explain the momentum of the post-AGB jets,
particularly if we assume that they are powered by radiation pressure.
But in this case we must recalculate the correction factor in Eq. (11).
When the radiation pressure is transferred to the
nebula by the intermediate of a shock front, a fraction of the energy of
the impinging jet can be converted into
scalar momentum. This holds when the shock is "energy driven'', i.e.
when the shock is adiabatic and the radiated energy is negligible. In this
case, the temperature increases by a large factor in the shocked region
where a kind of explosion is produced (in all directions).
Since the ratio between the energy and momentum of the fast post-AGB jets
(i.e. its velocity) is much higher than for the dense molecular outflow,
this conversion can significantly increase the "scalar momentum'' won by the
latter. This situation would not happen in the opposite case, when the shock
is radiative (isothermal or momentum-driven shock), in which no significant
correction factor appears.
The idea of that the shocks that accelerated the bipolar molecular outflow
(observed in CO emission) could be strongly adiabatic is surprising.
In many well studied cases, the properties of the accelerated material
suggest the opposite. For instance, the temperatures of this accelerated
gas are systematically found to be very low (10-20 K, see Sect. 4),
indicating a very fast cooling after the passage of such an energetic
shock. The very collimated molecular outflow found in
OH231.8+4.2 suggests the presence of a "snow-plug'' effect in the shock,
which is characteristic of momentum-driven shocks and very different from
the roughly isotropic inflation expected in adiabatic shocks. Sánchez
Contreras et al. (2000) argue that, in view of the high densities
calculated for this nebula (as for others), theoretical cooling models
predict isothermal shocks in the inner parts of the nebulae, where the
acceleration took place, and that adiabatic shocks would only appear in the
very outer regions. The narrow walls of the fast-flowing cavities observed
in several PPNe (M1-92, Bujarrabal et al. 1998; Roberts 22, Sahai et al. 1999c;
Frosty Leo, Sahai et al. 2000;
etc.) also suggest a strong compression of the accelerated material, as
expected in isothermal shocks. The case of Hen3-401 is similar (Sahai
et al. 1999b), in this nebula the very extended lobes show straight and
narrow walls that had been predicted for momentum-driven shocks. However,
the PPN Mz-3 and some PNe (e.g. Balick 2000), show inflated lobes
that could be explained as the result of an adiabatic shock.
Therefore, we cannot exclude the presence of adiabatic shocks in the early
evolution of PPNe, but they are probably not a systematic phenomenon.
The increase of the momentum transferred to the dense shell due to the
presence of adiabatic shocks is approximately limited by the ratio between
the velocity of the fast post-AGB jets and the resulting velocity for the
accelerated dense shell (neglecting the increase in internal energy). The
velocity of the fast post-AGB jets responsible
for the acceleration of the molecular flows is not known; hot, ionized gas
is observed in PNe and PPNe with velocities as high as 1000-2000 km s-1
(e.g. Kwok 2000). Since the velocities of the molecular outflow usually
range between 50 and 100 km s-1, we can give an estimate for the
velocity ratio of approximately a factor 20. This factor does not give the
increase of the momentum in the axial direction due to adiabatic shocks,
since in first approximation only the outwards axial movements would become
the observed molecular outflows, a factor 1/4 must then apply. Even if the
collimation process is very efficient, it is difficult to accept that
expansion in all direction becomes an outward, axial flow. Since we are
looking for upper limits to the momentum transfer factor, we will assume
that the resulting correction
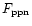 ,
to be included in Eq. (11), is
then of about 10-20.
We are aware that this estimate is uncertain, but our present
knowledge does not allow us to think that
,
to be included in Eq. (11), is
then of about 10-20.
We are aware that this estimate is uncertain, but our present
knowledge does not allow us to think that
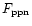 can be larger than this
factor.
can be larger than this
factor.
Note that if momentum is transferred to the fast molecular outflow by means
of post-AGB jets, which are themselves accelerated by radiation pressure
acting onto grains, we cannot assume that multiple scattering is
significant. The reason is the very high velocity of the post-AGB jets,
since the opacity in a flow varies inversely with the velocity for a given
mass loss rate.
In summary, if radiation pressure acting onto grains
is the final source of the momentum,
we find that the maximum momentum won by the bipolar flows in PPNe must
satisfy:
If radiation pressure acts directly on the shell that will be accelerated,
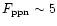 -10.
If radiation pressure acts by the intermediate of some very fast (and
collimated) post-AGB wind, we get
-10.
If radiation pressure acts by the intermediate of some very fast (and
collimated) post-AGB wind, we get
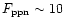 -20.
Since typically
-20.
Since typically
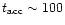 -200 yr (Sect. 6), the limit to
P is:
-200 yr (Sect. 6), the limit to
P is:
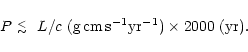 |
(12) |
The above limit is of course only approximate. We note that it has been
derived assuming that the acceleration and properties of the late-AGB and
post-AGB jets are similar to those presently observed in AGB stars. In
particular, we have assumed that radiation pressure acts firstly onto
grains. This is to be expected, since we have found that the acceleration
is produced in the very first post-AGB phases, in which the star is still
cool; see discussion on other scenarios in Sect. 9.
We will assume that the slow component often observed in PPNe is the
fraction of the fossil AGB envelope that has not been accelerated by the
post-AGB wind interaction (see also Sect. 4.1). Firstly, its velocity is
comparable to that commonly observed in AGB envelopes. Moreover, in
several well mapped sources,
the shape of this component is spherical and extended, as for AGB
envelopes, suggesting that in them the axial disruption by wind interaction
characteristic of PPNe has not reached the full extent of the AGB envelope.
This is the case of CRL618 (Yamamura et al. 1994), CRL2688 (Yamamura
et al. 1996) and IRAS21282+5050 (Meixner et al. 1998). In the other
well studied cases, this component is toroidal and perpendicular to the
nebular symmetry axis, as expected if it is the residual of an extended
axial acceleration; these are M2-56, OH231.8+4.2 (Alcolea et al.
2001), M2-9 (Zweigle et al. 1997) and M1-92 (Bujarrabal et al.
1998).
Table 6:
Characteristic radius and formation time of the slow outflows in
the PPNe that have been well observed in CO. We also quote the total
nebular mass and the average mass rate at which the nebula was ejected
during the late AGB phases.
| name |
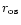 |
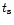 |
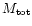 |
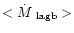 |
refs. |
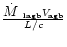 |
comments |
| |
(cm) |
(yr) |
( ) ) |
( yr-1) yr-1) |
|
|
|
| |
|
|
|
|
|
|
|
| IRAS04296+3429 |

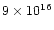 |
 3000 3000 |
0.13 |

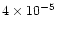 |
0, 1 |
3.1 |
size from optical image |
| CRL618 |
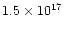 |
2700 |
0.7 |
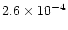 |
0, 2 |
7.6 |
size from CO maps |
| Frosty Leo |

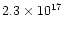 |
7300 |
0.9 |

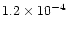 |
0, 3 |
22. |
size from optical and CO images |
| IRAS17436+5003 |
<
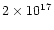 |
<5000 |
0.7 |
>
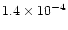 |
0 |
>1 |
assumed radius: <3'', from CO data |
| He3-1475 |

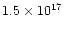 |
 7000 7000 |
0.63 |

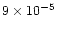 |
0, 4 |
 3.5 3.5 |
size from optical image |
| 89 Her |
1016 |
1000 |
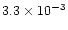 |
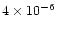 |
0, 5 |
0.19 |
size from CO mapping |
| AFGL2343 |
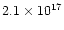 |
1000 |
4.8 |
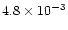 |
0, 6 |
14. |
CO+IR size, unique velocity component |
| IRC+10420 |
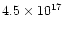 |
4000 |
2.1 |
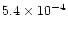 |
0, 7 |
1.4 |
CO size, unique velocity component |
| IRAS19500-1709 |
<
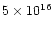 |
<1600 |
0.033 |
>
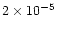 |
0 |
>6.6 |
assumed radius: <3'', from CO data |
| CRL2477 |
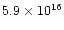 |
? |
? |
? |
0, 7 |
? |
size from CO, unidentified slow flow |
| CRL2688 |
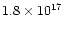 |
3800 |
0.75 |
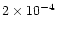 |
0, 8 |
6. |
size from CO mapping |
| NGC7027 |
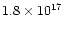 |
>1500 |
0.6 |
<
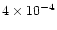 |
0, 9 |
<43 |
size from CO mapping |
| IRAS22272+5435 |
 |
10000 |
0.2 |
 |
0, 7 |
1. |
size from CO mapping |
| IRAS23304+6147 |
 ? ? |
210? |
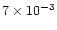 |
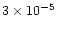 ? ? |
0, 10 |
14? |
poor information on extent |
| IRAS23321+6545 |
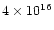 |
? |
? |
? |
0, 7 |
? |
size from CO,
unidentified slow flow |
M2-56 |
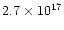 |
4500 |
0.11 |
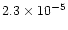 |
0 |
1.6 |
size from CO mapping |
| OH231.8+4.2 |
1017 |
4000 |
0.9 |
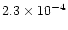 |
11 |
9. |
size from optical and CO images |
| M2-9 |
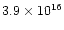 |
960 |
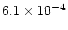 |
 6.4
10-7
6.4
10-7 |
0, 12 |
 0.41 0.41 |
from CO mapping |
| RSct |
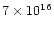 |
2500 |
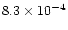 |
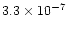 |
0, 13 |
0.02 |
from CO mapping |
| M1-92 |
1017 |
4000 |
0.9 |
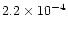 |
14 |
9. |
from CO mapping |

In order to estimate the mass loss rate responsible for the observed
nebulae (that supposedly took place during the last phases of the AGB, and
that was the responsible for its end), we have first estimated the outer
radius of this slow remnant,
 .
We recall that, in the well studied
cases mentioned above, the extent of this CO shell
is much smaller than that expected from photodissociation due to the
interstellar UV field (see calculations by Mamon et al. 1988).
So, the slow component is spatially bounded mainly by a sudden density
decrease and not by molecule dissociation, and, therefore, its measured
extent probably corresponds to the actual size of the shell formed under
this regime of high mass ejection.
.
We recall that, in the well studied
cases mentioned above, the extent of this CO shell
is much smaller than that expected from photodissociation due to the
interstellar UV field (see calculations by Mamon et al. 1988).
So, the slow component is spatially bounded mainly by a sudden density
decrease and not by molecule dissociation, and, therefore, its measured
extent probably corresponds to the actual size of the shell formed under
this regime of high mass ejection.
From
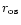 and the slow component velocities,
and the slow component velocities,
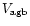 (see Sects. 5,
6), we can calculate the time needed to eject the whole nebula by the
former AGB star,
(see Sects. 5,
6), we can calculate the time needed to eject the whole nebula by the
former AGB star,
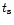 .
In this calculation, the inner radius
.
In this calculation, the inner radius
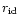 is
assumed to be very small, except for the hypergiant AFGL2343, the young
PN NGC7027, M2-56, M2-9 and R Sct, for which we took values from
Table 5 (Sect. 6). See values of
is
assumed to be very small, except for the hypergiant AFGL2343, the young
PN NGC7027, M2-56, M2-9 and R Sct, for which we took values from
Table 5 (Sect. 6). See values of
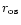 and
and
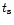 in Table 6.
in Table 6.
We can also estimate the total mass of the nebula,
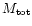 ,
from the
masses of both (slow and fast) components detected in CO, see values in
Table 6. From
,
from the
masses of both (slow and fast) components detected in CO, see values in
Table 6. From
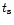 and
and
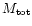 ,
we estimate average mass loss rates
during the late AGB phases.
Only average rates are obtained, but since these values are probably the
maximum allowed mass-loss rates (see below) it is possible that they were
kept more or less constant during the relevant phase. The obtained values
are listed in Table 6 (
,
we estimate average mass loss rates
during the late AGB phases.
Only average rates are obtained, but since these values are probably the
maximum allowed mass-loss rates (see below) it is possible that they were
kept more or less constant during the relevant phase. The obtained values
are listed in Table 6 (
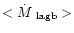 ), for the objects in which the
existing data allow a reasonable estimate.
), for the objects in which the
existing data allow a reasonable estimate.
As we see in Table 6, the yellow hypergiants (AFGL2343 and IRC+10420,
see Sect. 2) show very massive molecular envelopes and very high
mass-loss rates, between
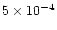 and
and
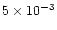
 yr-1. On the other
hand, the PPNe with low initial mass (89 Her, M2-9 and
R Sct; no estimate was done for the Red Rectangle) show very low-mass
molecular nebulae, as it was already known (e.g. Alcolea & Bujarrabal
1991). Our analysis also gives a very high mass-loss rate (during its past
AGB phase) for the young PN NGC7027. This value is probably an
upper limit, since the high velocity and the thin shell found in this
source suggest that the bulk of the gas has been already compressed and
accelerated by the passage of shocks and, therefore, our value
yr-1. On the other
hand, the PPNe with low initial mass (89 Her, M2-9 and
R Sct; no estimate was done for the Red Rectangle) show very low-mass
molecular nebulae, as it was already known (e.g. Alcolea & Bujarrabal
1991). Our analysis also gives a very high mass-loss rate (during its past
AGB phase) for the young PN NGC7027. This value is probably an
upper limit, since the high velocity and the thin shell found in this
source suggest that the bulk of the gas has been already compressed and
accelerated by the passage of shocks and, therefore, our value
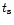 is
probably an underestimate. The other, "normal'' PPNe have total masses
ranging in general between 0.1 and 1
is
probably an underestimate. The other, "normal'' PPNe have total masses
ranging in general between 0.1 and 1  .
The only exceptions are
IRAS19500-1709 and IRAS23304+6147; these also have very low luminosity,
both low nebular mass and luminosity could be due either to that they are
low-mass objects or (more probably) to an underestimate of the distance.
The (late AGB) mass-loss rates that gave rise to these heavy envelopes
range between
.
The only exceptions are
IRAS19500-1709 and IRAS23304+6147; these also have very low luminosity,
both low nebular mass and luminosity could be due either to that they are
low-mass objects or (more probably) to an underestimate of the distance.
The (late AGB) mass-loss rates that gave rise to these heavy envelopes
range between
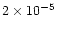 and
and
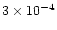
 yr-1 for PPNe, with an average
around 10-4
yr-1 for PPNe, with an average
around 10-4  yr-1.
We note that such large ejection rates are not observed in stars that are
presently in the AGB, in which we
hardly find rates larger than
yr-1.
We note that such large ejection rates are not observed in stars that are
presently in the AGB, in which we
hardly find rates larger than
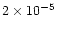
 ,
the mass-loss rate of the
famous, dense envelope of IRC+10216 (see e.g. Loup et al. 1993;
Bujarrabal 1999; note that the total mass in the envelope around
IRC+10216 is
,
the mass-loss rate of the
famous, dense envelope of IRC+10216 (see e.g. Loup et al. 1993;
Bujarrabal 1999; note that the total mass in the envelope around
IRC+10216 is  0.2
0.2  ).
).
Finally, we calculate the "scalar'' momentum carried by this component
per unit time when it was ejected, i.e. before the post-AGB wind
interaction,
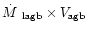 .
(We recall that the scalar
momentum is calculated by integrating the moduli of the momentum to the
whole source, disregarding the vectorial nature of this parameter.) Its
values are compared with the momentum carried by the stellar radiation,
L/c. The resulting ratios are listed in Table 6; note that this
parameter is distance independent.
We find a very high momentum in the young PN NGC7027; as we mentioned
above, the whole nebula has probably won significant amounts of momentum in
the post-AGB phase. The low-mass objects give relatively low values of the
momentum. The rest of the nebulae, the standard PPNe and the hypergiants,
give values of the ratio
.
(We recall that the scalar
momentum is calculated by integrating the moduli of the momentum to the
whole source, disregarding the vectorial nature of this parameter.) Its
values are compared with the momentum carried by the stellar radiation,
L/c. The resulting ratios are listed in Table 6; note that this
parameter is distance independent.
We find a very high momentum in the young PN NGC7027; as we mentioned
above, the whole nebula has probably won significant amounts of momentum in
the post-AGB phase. The low-mass objects give relatively low values of the
momentum. The rest of the nebulae, the standard PPNe and the hypergiants,
give values of the ratio
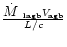 between 1 and 22, with most objects
presenting a value
between 1 and 22, with most objects
presenting a value  5-10. These figures are coincident with the
expected maximum efficiency of momentum transfer for the stellar radiation
pressure to gaseous shells, via photon absorption by dust grains (see
Sect. 7).
5-10. These figures are coincident with the
expected maximum efficiency of momentum transfer for the stellar radiation
pressure to gaseous shells, via photon absorption by dust grains (see
Sect. 7).
The values of the mass-loss rate and the
ejected mass during the last AGB phases are so large, compared to those
commonly found in AGB stars, that the ejection of the planetary nebula and
the end of the AGB phase should be interpreted as due to a discrete,
quasi-explosive phenomenon of mass ejection, rather than to a smooth
process lasting the whole AGB phase.
Only 4 sources in our sample (IRAS22272+5435, IRAS07134+1005, M2-9
and R Sct), out of 32 for which reasonably good CO data exist, show no line
wings down to a low level, i.e. less that 1/10 of the peak.
Of these sources, IRAS22272+5435 was accurately observed by us and shows
no wings to less that 1/50 of the peak in 12CO J=2-1.
Five sources show no line wings, but the existing information is poor and
the limits are not significant (Mz3, IRAS17150-3224, OH17.7-2.0,
IRAS20000+3239 and IRAS22574+6609).
As we have mentioned, the mass and momentum carried by the fast molecular
flows in PPNe is very high. At least 9 PPNe in our sample have fast
outflows with mass
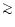 0.1
0.1  .
As we argue in Sect. 7.1, the flow momentum (P)
cannot in principle be explained by radiation pressure when
.
As we argue in Sect. 7.1, the flow momentum (P)
cannot in principle be explained by radiation pressure when
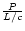 is larger than about 2000 yr.
See values of P and
is larger than about 2000 yr.
See values of P and
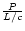 in Tables 3, 4.
For our statistical study of the outflow momenta,
we will not take into account the five objects in which the upper limits
to the line-wing emission are not significant, one object in which the
lower limit is too low to be useful (IRAS20028+3910,
in Tables 3, 4.
For our statistical study of the outflow momenta,
we will not take into account the five objects in which the upper limits
to the line-wing emission are not significant, one object in which the
lower limit is too low to be useful (IRAS20028+3910,
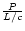 >
1000 yr), two objects in which the comparison with radiation pressure momentum
is not conclusive (IRAS04296+3429: uncertain ratio
>
1000 yr), two objects in which the comparison with radiation pressure momentum
is not conclusive (IRAS04296+3429: uncertain ratio
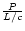
 1200 yr; IRAS07134+1005:
1200 yr; IRAS07134+1005:
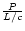 < 3500 yr), as well as the
hypergiants (for which the typical times of the wind interaction are not
well known). We are left with 27 objects that show reasonably useful
CO data. Of them, only 6 nebulae (namely
IRAS22272+5435, IRAS23304+6147, 89 Her, the Red Rectangle, M2-9 and
R Sct), i.e. 22%, show values of
< 3500 yr), as well as the
hypergiants (for which the typical times of the wind interaction are not
well known). We are left with 27 objects that show reasonably useful
CO data. Of them, only 6 nebulae (namely
IRAS22272+5435, IRAS23304+6147, 89 Her, the Red Rectangle, M2-9 and
R Sct), i.e. 22%, show values of
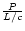 smaller than 2000 yr.
Four of them are the four low-mass objects in our list (see further
discussion below).
For this 22% of the nebulae, the usual assumption that the stellar
radiation pressure powers the bipolar protoplanetary flows is not
incompatible with the observations.
For the rest of the objects (21, 78%), the momentum carried by the bipolar
flows is too large to be explained, under standard conditions, by
radiation pressure. Such a percentage is in any case a lower limit, since
our calculation procedure can lead to underestimates of the mass and
momentum in not well studied objects (Sect. 4.2), due to errors in the
geometrical and CO emission models (significant overestimates are not
expected). In particular, CO photodissociation by interstellar or stellar
UV radiation could yield very low CO emission, despite a high actual mass
of the envelope.
smaller than 2000 yr.
Four of them are the four low-mass objects in our list (see further
discussion below).
For this 22% of the nebulae, the usual assumption that the stellar
radiation pressure powers the bipolar protoplanetary flows is not
incompatible with the observations.
For the rest of the objects (21, 78%), the momentum carried by the bipolar
flows is too large to be explained, under standard conditions, by
radiation pressure. Such a percentage is in any case a lower limit, since
our calculation procedure can lead to underestimates of the mass and
momentum in not well studied objects (Sect. 4.2), due to errors in the
geometrical and CO emission models (significant overestimates are not
expected). In particular, CO photodissociation by interstellar or stellar
UV radiation could yield very low CO emission, despite a high actual mass
of the envelope.
We could imagine that the correction factor
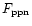 applied in Eq. (11)
(Sect. 7) can be increased by some extra factor (of unknown origin). But
there are PPNe in our sample with
applied in Eq. (11)
(Sect. 7) can be increased by some extra factor (of unknown origin). But
there are PPNe in our sample with
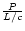
 105 yr. These
objects include precisely some of the best studied nebulae, for which the
possible underestimate of the molecular masses inherent to our
calculation method (Sect. 4.2) is expected to be less important: Frosty Leo,
He3-1475, OH231.8+4.2, HD101584, the Boomerang Nebula and M1-92.
A correction factor (Eq. (11))
105 yr. These
objects include precisely some of the best studied nebulae, for which the
possible underestimate of the molecular masses inherent to our
calculation method (Sect. 4.2) is expected to be less important: Frosty Leo,
He3-1475, OH231.8+4.2, HD101584, the Boomerang Nebula and M1-92.
A correction factor (Eq. (11))
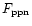
 500-1000 would be
necessary.
An inspection of the arguments in Sects. 7 and 9.1 shows that such high
values of
500-1000 would be
necessary.
An inspection of the arguments in Sects. 7 and 9.1 shows that such high
values of
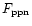 seems difficult to justify.
seems difficult to justify.
The case of the objects with low initial mass is remarkable: we have seen
that the four studied nebulae (89 Her, the Red Rectangle, M2-9 and R
Sct; see Alcolea & Bujarrabal 1991) are among the six sources showing
comparatively low flow momentum. Only in the first two ones a relatively
fast CO component is detected and with a mass not higher than 10-3
 .
It was known that these PPNe with low initial mass often show very
weak and narrow CO lines. This may be due to a small CO abundance and/or
extent in the nebula, probably because of photodissociation; this is
particularly the case of M2-9 and of the Red Rectangle (Sect. 5.2.10,
Alcolea & Bujarrabal 1991).
It is also possible that in low-mass objects the post-AGB evolution
starts when only a small fraction of the stellar mass has been ejected, and
so the momentum of the nebulae never reaches a high value. This
could be the case of 89 Her and R Sct, where the mass derived from the FIR
spectrum is low and comparable to that derived from CO. But we note that
the detection of the coldest grains from FIR dust emission is difficult,
which would also yield an underestimate of the total nebular mass.
.
It was known that these PPNe with low initial mass often show very
weak and narrow CO lines. This may be due to a small CO abundance and/or
extent in the nebula, probably because of photodissociation; this is
particularly the case of M2-9 and of the Red Rectangle (Sect. 5.2.10,
Alcolea & Bujarrabal 1991).
It is also possible that in low-mass objects the post-AGB evolution
starts when only a small fraction of the stellar mass has been ejected, and
so the momentum of the nebulae never reaches a high value. This
could be the case of 89 Her and R Sct, where the mass derived from the FIR
spectrum is low and comparable to that derived from CO. But we note that
the detection of the coldest grains from FIR dust emission is difficult,
which would also yield an underestimate of the total nebular mass.
The hypergiants in our sample show very high nebular mass,
 2
2  ,
and momenta, with and
,
and momenta, with and
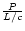 equal to
equal to
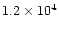 (AFGL2343)
and
(AFGL2343)
and
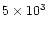 yr (IRC+10420). Note also their high expansion velocities,
higher than 30 km s-1.
Since the acceleration times in them may be as high as 1000 yr (Sect. 2),
we cannot exclude that the observed fast shells have been accelerated by
radiation pressure with
yr (IRC+10420). Note also their high expansion velocities,
higher than 30 km s-1.
Since the acceleration times in them may be as high as 1000 yr (Sect. 2),
we cannot exclude that the observed fast shells have been accelerated by
radiation pressure with
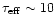 ;
high values of this
parameter can be expected in envelopes in which the mass-loss rate is as
high as 10-3
;
high values of this
parameter can be expected in envelopes in which the mass-loss rate is as
high as 10-3  yr-1. (It has been claimed that perhaps AFGL2343 is not
a hypergiant but a normal PPN, see Sect. 5.1.7, in this case this object
would also have an overluminous fast outflow.)
yr-1. (It has been claimed that perhaps AFGL2343 is not
a hypergiant but a normal PPN, see Sect. 5.1.7, in this case this object
would also have an overluminous fast outflow.)
The young PN NGC7027 shows a main component with high velocity (larger
than 20 km s-1) and mass ( 0.5
0.5  ), that probably corresponds to most
of the AGB envelope accelerated by post-AGB wind interaction.
), that probably corresponds to most
of the AGB envelope accelerated by post-AGB wind interaction.
We have also calculated the kinetic energy carried by the fast
molecular outflows in PPNe (Tables 3, 4). Most of the standard PPNe show
values of the kinetic energy in the range 1044-1046 erg.
Again low-mass post-AGB stars and hypergiants show values respectively
under and over this range. We also note the very high energy carried by the
Boomerang Nebula (
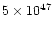 erg), a peculiar PPN showing a very
massive, fast and cold envelope (Sahai & Nyman 1997). Note that the
energy radiated by a post-AGB star in 100-200 yr is of the order of 1-
erg), a peculiar PPN showing a very
massive, fast and cold envelope (Sahai & Nyman 1997). Note that the
energy radiated by a post-AGB star in 100-200 yr is of the order of 1-
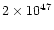 erg; so, from the point of view of the energy conservation,
radiation pressure could explain the observed flows in PPNe with efficiency
factors of a few per cent.
erg; so, from the point of view of the energy conservation,
radiation pressure could explain the observed flows in PPNe with efficiency
factors of a few per cent.
As we have seen (Sect. 8.2), radiation pressure under standard conditions
(acting primarily onto grains) can explain the high mass-loss rates that,
during the AGB phase, gave rise to the observed massive PPNe. However, this
process seems unable to explain the great amounts of momentum won by a part
of this envelope during the post-AGB phase, even if radiation pressure acts
via post-AGB jets.
As we have mentioned in Sect. 8.2, the star radiates energy enough to
explain the kinetic energies observed in the bipolar flows.
The problem is the relatively low amount of radiated momentum.
But the ill definition of our "scalar momentum'' leads to some correction
factors to the conservation law that are not easy to calculate.
We have argued that the presently observed post-AGB jets carry a relatively
small mass and therefore the opacity of the dust in them should not be high
(Sect. 7).
We cannot discard however some unexpected
situation in which the relevant opacity is not that of dust in the IR, like
in the case of a transitional increase of the photospheric temperature
allowing important absorption by lines or Ly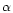 continuum, in which
the efficient opacity could be much larger.
We recall that this is not expected from what we know on this subject,
since the bipolar flow acceleration seems to take place in the very first
phases of the post-AGB evolution, when the star is still cool. For
instance, only
continuum, in which
the efficient opacity could be much larger.
We recall that this is not expected from what we know on this subject,
since the bipolar flow acceleration seems to take place in the very first
phases of the post-AGB evolution, when the star is still cool. For
instance, only  10-9 of the total radiation of a 5600 K black
body (corresponding to a G0-type star) takes place in the Ly
10-9 of the total radiation of a 5600 K black
body (corresponding to a G0-type star) takes place in the Ly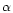 continuum. For these very low amounts of energy, what is relevant is not
the momentum- but the energy-conservation law, that would avoid the
acceleration of the flows by radiation pressure. In general we recall that
stars with
continuum. For these very low amounts of energy, what is relevant is not
the momentum- but the energy-conservation law, that would avoid the
acceleration of the flows by radiation pressure. In general we recall that
stars with
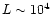
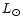 can typically radiate
can typically radiate
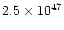 erg in 200 yr, though the energies of the flows are often
erg in 200 yr, though the energies of the flows are often
 1046 erg.
Perhaps a sudden reaccretion of previously ejected material could yield
some kind of nova-like phenomenon in the stellar surface, leading to an
important increase of the photospheric temperature (independently of an
eventual increase of the luminosity). Perhaps a strong dependence of
atmosphere's opacity on the stellar latitude would allow the presence of
regions in which the radiation from the stellar very hot core can reach the
surface (the poles?, due to centrifulgal distortion or non radial
pulsations?), though the rest of the stellar surface still remains cool.
1046 erg.
Perhaps a sudden reaccretion of previously ejected material could yield
some kind of nova-like phenomenon in the stellar surface, leading to an
important increase of the photospheric temperature (independently of an
eventual increase of the luminosity). Perhaps a strong dependence of
atmosphere's opacity on the stellar latitude would allow the presence of
regions in which the radiation from the stellar very hot core can reach the
surface (the poles?, due to centrifulgal distortion or non radial
pulsations?), though the rest of the stellar surface still remains cool.
We could also imagine that the post-AGB jets are not produced under the
form of a steady mass loss (as usually assumed in wind interaction models),
but under the form of a sudden ejection of a large fraction of the stellar
mass, in which a massive formation of dust occurs yielding a very large
opacity. For instance, the sudden ejection of 0.1  ,
forming grains at
about
,
forming grains at
about
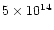 cm, could attain opacities
cm, could attain opacities  1000 in the IR. But when
this shell is accelerated, its opacity rapidly decreases and
1000 in the IR. But when
this shell is accelerated, its opacity rapidly decreases and
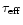
 1 after only
1 after only  30 yr expanding at 200 km s-1; so in this case the
acceleration time is extremely short.
30 yr expanding at 200 km s-1; so in this case the
acceleration time is extremely short.
We can still speculate on a different scenario, in which an exceptionally
fast jet, with velocities  1000 km s-1, shocks with the AGB envelope at
two points in the axis, producing a very hot adiabatic shock.
By some mechanism, the resulting
expansion would have been strongly collimated to yield the present axial
flows. It is not clear how radiation pressure can yield so high velocities,
since existing models predict moderate kinematics (Kwok 1975; Ivezic &
Elitzur 1995; etc.). (Note that, since these jets are produced in the very
first post-AGB phases, the stellar properties are thought to be similar to
those of AGB stars, for which those models are developed.) A theory
explaining such a strong acceleration of the post-AGB jets by radiation
pressure and the subsequent very energetic shocks, in particular why the
dense accelerated gas does not radiate the internal energy (Sect. 7.1),
is obviously missing.
1000 km s-1, shocks with the AGB envelope at
two points in the axis, producing a very hot adiabatic shock.
By some mechanism, the resulting
expansion would have been strongly collimated to yield the present axial
flows. It is not clear how radiation pressure can yield so high velocities,
since existing models predict moderate kinematics (Kwok 1975; Ivezic &
Elitzur 1995; etc.). (Note that, since these jets are produced in the very
first post-AGB phases, the stellar properties are thought to be similar to
those of AGB stars, for which those models are developed.) A theory
explaining such a strong acceleration of the post-AGB jets by radiation
pressure and the subsequent very energetic shocks, in particular why the
dense accelerated gas does not radiate the internal energy (Sect. 7.1),
is obviously missing.
When trying to find other sources of energy that could explain the observed
outflows, the conservation of energy becomes the relevant constraint.
We can imagine that the energy needed could come from the ejection of the
pulsating stellar layers after an ultimate pulse. However, the kinetic
energy of 0.2  pulsating at 20 km s-1 (a typical pulsation velocity) is
just
pulsating at 20 km s-1 (a typical pulsation velocity) is
just 
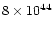 erg. Also we note that we do not expect this
pulsation to occur in only one direction.
erg. Also we note that we do not expect this
pulsation to occur in only one direction.
Accretion onto the stellar surface may provide the energy required: 0.2  falling
in a star with a mass equal to 1
falling
in a star with a mass equal to 1  and a radius equal to
1013 cm releases a gravitational energy
and a radius equal to
1013 cm releases a gravitational energy 
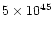 erg,
compatible with the observed ones in most cases. This energy could be
converted into kinetic energy in the axial direction by a process similar
to that at work in forming stars and in active galactic nuclei, that
involves the presence of magnetic fields and also explains the collimation
of the axial jets.
Theoretical studies for the specific case of PPNe would also be needed.
The release of gravitational energy could be due to the approximation of
a stellar companion, but then both stars would practically get in contact
(with other cataclysmic consequences not observed).
Moreover, it is difficult to understand why this approximation takes place,
for almost all possible star pairs, exactly at the end of the AGB phase of
the primary. Finally we note that the presence of a stellar companyon
should help to produce accretion of circumstellar material. However, we
still lack for a study quantitatively comparing the apparent ubiquity of
the overluminous outflows in PPNe with the expected number of post-AGB
stars belonging to the appropiate multiple systems; it should be also
understood why, under the binary star assumption, such
jets only appear in the AGB phase for a few well known symbiotic stars.
erg,
compatible with the observed ones in most cases. This energy could be
converted into kinetic energy in the axial direction by a process similar
to that at work in forming stars and in active galactic nuclei, that
involves the presence of magnetic fields and also explains the collimation
of the axial jets.
Theoretical studies for the specific case of PPNe would also be needed.
The release of gravitational energy could be due to the approximation of
a stellar companion, but then both stars would practically get in contact
(with other cataclysmic consequences not observed).
Moreover, it is difficult to understand why this approximation takes place,
for almost all possible star pairs, exactly at the end of the AGB phase of
the primary. Finally we note that the presence of a stellar companyon
should help to produce accretion of circumstellar material. However, we
still lack for a study quantitatively comparing the apparent ubiquity of
the overluminous outflows in PPNe with the expected number of post-AGB
stars belonging to the appropiate multiple systems; it should be also
understood why, under the binary star assumption, such
jets only appear in the AGB phase for a few well known symbiotic stars.
1:
We present and analyze CO data on 37 objects, most of them protoplanetary
nebulae (PPNe), including also the two hypergiants surrounded by heavy
circumstellar envelopes, AFGL2343 and IRC+10420 (that are probably
following an evolution similar to that of PPNe), and the young
planetary nebula NGC7027 (that shows a some nebular properties similar to
those of PPNe). We think that our sample includes all well identified PPNe
that have been detected in CO. We have performed new very sensitive
observations in 16 of these sources of 12CO and 13CO lines (both J=1-0
and J=2-1 transitions in most sources). For the others, we take CO data
from the literature; in some of these sources, the published observations
are found to be of poor quality for our purposes.
2:
In the CO spectra, it is often possible to identify the different
components characteristic of the CO emission from PPNe, namely the central
core, corresponding to slow ejections (probably a remnant of the previous
AGB wind), and the line wings, corresponding to bipolar fast flows
(probably the result of the acceleration of a part of the AGB envelope by
interaction with post-AGB fast, axial jets). The main goal of our study is
the calculation of the mass, the linear momentum and the kinetic energy of
these components from the CO spectra.
3:
The method followed to calculate those parameters and the meaning and
uncertainties of the derived results are discussed in detail. It is
concluded that the errors are small (less than about a factor 2 in the
developed examples), and that only significant underestimates of the mass
and dynamical parameters can be expected. Errors are particularly small in
well studied objects, in which the shell extent and the CO excitation and
opacity can be determined.
4:
The mass of the whole nebula is calculated, together with the associated
mass-loss rates at which the total envelope was
expelled during the late AGB phases (see Sect. 8.1, Table 6). The mass of
most PPNe is larger than 0.1  ,
being often
,
being often  1
1  .
The
corresponding mass-loss rates range between
.
The
corresponding mass-loss rates range between
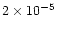 and
and
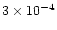
 yr-1, with typical values
yr-1, with typical values  10-4
10-4  yr-1. The exceptions are the
objects with low initial mass (89 Her, M2-9 and R Sct) and the yellow
hypergiants (AFGL2343 and IRC+10420), for which the the calculated
masses and mass-loss rates are significantly lower and higher, respectively.
yr-1. The exceptions are the
objects with low initial mass (89 Her, M2-9 and R Sct) and the yellow
hypergiants (AFGL2343 and IRC+10420), for which the the calculated
masses and mass-loss rates are significantly lower and higher, respectively.
5:
We also estimated the values of the "scalar'' momentum (integration to the
whole nebula of the momentum modulus) that was carried by this late AGB
wind. After taking into account the effects of multiple scattering, we find
the momentum of such a wind to be very close to the maximum momentum
that can be supplied by radiation pressure. The duration of this high
efficiency process is of a few thousand years, after which the star has
lost a good fraction of its mass, its surface temperature starts increasing
and the AGB phase ends.
6:
We have studied the properties of the high-velocity molecular outflows by
means of the line wings (often) detected in CO spectra. Only four objects
(IRAS22272+5435, IRAS07134+1005, M2-9 and R Sct) out of the 37
nebulae in our sample show no line wings to a low level (weaker
than  1/10 of the line maximum). Five others show no wings, but the
existing observations are poor and do not allow meaningful conclusions.
1/10 of the line maximum). Five others show no wings, but the
existing observations are poor and do not allow meaningful conclusions.
7:
Calculations of the momentum carried by the fast CO outflows yield very
high values, between 1038 and
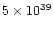 g cm s-1 in most PPNe.
Their kinetic energy is also very high, often between 1045 and
1047 erg. The formation of these flows is the dominant phenomenon in
the post-AGB dynamics.
These values are compared with the momentum that can be provided by the
stellar luminosity. We have taken into account the expected acceleration
times, estimated for some sources, as well as correction factors due to
eventual multiple scattering and conversion of energy into scalar
momentum in adiabatic shocks (under the expected conditions).
Of the 27 objects in which the observational data are good enough, only in
6 of them (IRAS22272+5435, IRAS23304+6147, 89 Her, the Red Rectangle,
M2-9 and R Sct), 22% of our sample,
the measured momentum could be explained by
radiation pressure. In the rest of the nebulae (21 objects, 78%), the
stellar radiation is unable to explain the acceleration of the observed
fast molecular flows. This percentage is probably a lower limit because, as
we have mentioned, the calculated masses and momenta could be
underestimates in not well studied sources.
g cm s-1 in most PPNe.
Their kinetic energy is also very high, often between 1045 and
1047 erg. The formation of these flows is the dominant phenomenon in
the post-AGB dynamics.
These values are compared with the momentum that can be provided by the
stellar luminosity. We have taken into account the expected acceleration
times, estimated for some sources, as well as correction factors due to
eventual multiple scattering and conversion of energy into scalar
momentum in adiabatic shocks (under the expected conditions).
Of the 27 objects in which the observational data are good enough, only in
6 of them (IRAS22272+5435, IRAS23304+6147, 89 Her, the Red Rectangle,
M2-9 and R Sct), 22% of our sample,
the measured momentum could be explained by
radiation pressure. In the rest of the nebulae (21 objects, 78%), the
stellar radiation is unable to explain the acceleration of the observed
fast molecular flows. This percentage is probably a lower limit because, as
we have mentioned, the calculated masses and momenta could be
underestimates in not well studied sources.
8:
In some cases, including most of the well studied objects, we find a ratio
between the outflow momentum and the radiation momentum
 500-1000. The correction factor, due to the effects mentioned above, can just
reach a value
500-1000. The correction factor, due to the effects mentioned above, can just
reach a value  10-20; values
10-20; values
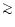 500-1000 are completely
unexpected for the standard conditions under which radiation pressure acts.
500-1000 are completely
unexpected for the standard conditions under which radiation pressure acts.
9:
Among the six objects showing relatively low outflow momenta,
we can find the four PPNe with low initial mass
included in our sample (89 Her, the Red Rectangle, M2-9 and R Sct).
The weak CO emission from this kind of sources was already noticed. We
discuss on the origin of this anomaly, that could be due to a low CO
abundance or extent.
10:
Excluding the four low-mass objects, in more than 90% of PPNe (21/23) the
fast bipolar flows would not be explained by radiation pressure.
We conclude that the mechanism that powers the very energetic bipolar
flows, and is finally reponsible for the PN shaping, is unknown,
deserving theoretical developments.
11:
We discuss different processes that could substitute the standard effect of
radiation pressure.
The most promising could be radiation pressure if unexpected opacity
effects are present and conversion into bipolar jet momentum of
gravitational energy of reaccreted material. Due to the lack of
theoretical developments, this topic remains a matter of speculation.
Note added in proof: A very recent work, Zijlstra et al. (2001, MNRAS, 322, 280), has confirmed from OH maser data on several PPNe the general structure and velocity field used here, including the Hubble-like velocity law, which were deduced by us from CO observations.
Acknowledgements
This work has been financially supported by the Spanish DGES, under
project PB96-0104. We are grateful to Noam Soker for fruitful discussions
on the ejection mechanisms. We made use of the Simbad database, operated at
CDS, Strasbourg, France.
-
Alcolea, J., & Bujarrabal, V. 1991, A&A, 245, 499
In the text
NASA ADS
-
Alcolea, J., & Bujarrabal, V. 1995, A&A, 303, L21
In the text
NASA ADS
-
Alcolea, J., Bujarrabal, V., Sánchez Contreras, C., Neri, R., & Zweigle, J.
2001, A&A, 373, 932
In the text
NASA ADS
-
Allen, D. A. 1978, MNRAS, 184, 601
NASA ADS
-
Allen, D. A., Hyland, A. R., & Caswell, J. L. 1980, MNRAS, 192, 505
NASA ADS
-
Andrei, A. H., Assafin, M., Puliaev, S. P., et al.
1999, AJ, 117, 483
NASA ADS
-
Assafin, M., Andrei, A. H., Puliaev, S. P., et al.
1996, A&AS, 117, 335
NASA ADS
-
Bachiller, R., Gómez-González, J., Bujarrabal, V., & Martín-Pintado, J.
1988, A&A, 196, L5
In the text
NASA ADS
-
Bachiller, R., Martín-Pintado, J., & Bujarrabal, V. 1999, A&A, 227, 188
-
Balick, B. 2000, in Asymmetrical Planetary Nebulae II: From Origins to Microestructures, ed. J. H. Kastner, N. Soker, & S. A. Rappaport,
ASP Conf. Ser., 199, 41
In the text
-
Bedding, T. R., & Zijlstra, A. A. 1994, A&A, 283, 955
In the text
NASA ADS
-
Bieging, J. H., Wilner, D., & Thronson, H. A. Jr. 1991, ApJ, 379, 271
In the text
NASA ADS
-
Borkowski, K. J., Blondin, J. M., & Harrington, J. P. 1997, ApJ, 482, L97
In the text
NASA ADS
-
Bowers, P. F., Johnston, K. J., & Spencer, J. H. 1983, ApJ, 274, 733
NASA ADS
-
Bujarrabal, V., Gómez-González, J., Bachiller, R., & Martín-Pintado, J.
1988, A&A, 204, 242
In the text
NASA ADS
-
Bujarrabal, V., Alcolea, J., & Bachiller, R. 1990, A&A, 234, 355
In the text
NASA ADS
-
Bujarrabal, V., & Bachiller, R. 1991, A&A, 242, 247
In the text
NASA ADS
-
Bujarrabal, V., Alcolea, J., & Planesas, P. 1992, A&A, 257, 701
In the text
NASA ADS
-
Bujarrabal, V., Fuente, A., & Omont, A. 1994, A&A, 285, 247
In the text
NASA ADS
-
Bujarrabal, V., Alcolea, J., Neri, R., & Grewing, M. 1997, A&A, 320,
540
In the text
NASA ADS
-
Bujarrabal, V., Alcolea, J., & Neri, R. 1998a, ApJ, 504, 915
In the text
NASA ADS
-
Bujarrabal, V., Alcolea, J., Sahai, R., Zamorano, J., & Zijlstra, A. A. 1998b,
A&A, 331, 361
In the text
NASA ADS
-
Bujarrabal, V. 1999, in Asymptotic Giant Branch Starts, IAU Symp. 191, ed. T. Le Bertre, A. Lébre, & C. Waelkens, ASP, 363
In the text
-
Calvet, N., & Cohen, M. 1978, MNRAS, 182, 687
NASA ADS
-
Castro-Carrizo, A., Lucas, R., Bujarrabal, V., Colomer, F., & Alcolea, J. 2001, A&A, 368, L34
In the text
NASA ADS
-
Cohen, M., Kunkel, W.,
Lasker, B. M., Osmer, P. S., & Fitzgerald, M. P. 1978, ApJ, 221, 151
NASA ADS
-
Cox, P., Lucas, R., Huggins, P. J., et al. 2000, A&A, 353, L25
In the text
NASA ADS
-
Crowther, P. A., de Marco, O., & Barlow, M. J. 1998, MNRAS, 296, 367
NASA ADS
-
Dayal, A., Hoffman, W. F., Bieging, J. H., et al.
1998, ApJ, 492, 603
NASA ADS
-
Decin, L., van Winckel, H., Waelkens, C., & Bakker, E. J. 1998, A&A, 332, 928
NASA ADS
-
de Jager, C. 1998, A&AR, 8, 145
In the text
-
de Marco, O., Barlow, M. J., & Storey, P. J. 1997, MNRAS, 292, 86
In the text
NASA ADS
-
de Marco, O., & Crowther, P. A. 1998, MNRAS, 296, 419
NASA ADS
-
Fong, D., Meixner, M., Castro-Carrizo, A., et al. 2001, A&A, 367, 652
In the text
NASA ADS
-
Forveille, T., Morris, M., Omont, A., & Likkel, L. 1987, A&A, 176, L13
NASA ADS
-
Goodrich, R. W. 1991, ApJ, 376, 654
NASA ADS
-
Graham, J. R., Serabyn, E., Herbst, T. M., et al. 1993, AJ, 105, 250
In the text
NASA ADS
-
Groenewegen, M. A. T., Oudmaijer, R. D., Goudfrooij, P., van den Hoek, L. B., & van
Kerkwijk, M. H. 1996, A&A, 305, 475
In the text
NASA ADS
-
Groenewegen, M. A. T., Whitelock, P. A., Smith, C. H., & Kerschbaum, F. 1998, MNRAS,
293, 18
In the text
NASA ADS
-
Hawkins, G. W., Skinner, C. J., Meixner, M., et al. 1995, ApJ, 452, 314
In the text
NASA ADS
-
Heske, A., Habing, H. J., Forveille, T., Omont, A., & van der Veen, W. E. C. J. 1990,
A&A, 239, 173
In the text
NASA ADS
-
Hrivnak, B. J., Kwok, S., & Volk, K. M. 1989, ApJ, 346, 265
In the text
NASA ADS
-
Hrivnak, B. J., & Kwok, S. 1991, ApJ, 368, 564
In the text
NASA ADS
-
Hrivnak, B. J., Kwok, S., & Geballe, T. R. 1994, ApJ, 420, 786
In the text
-
Hrivnak, B. J. 1995, ApJ, 438, 341
NASA ADS
-
Hrivnak, B. J., Langill, P. P., Su, K. Y. L., & Kwok, S. 1999, ApJ, 513, 421
In the text
NASA ADS
-
Hu, J. Y., Slijkhuis, S., Nguyen-Q-Rieu, & de Jong, T. 1993, A&A, 273, 185
In the text
NASA ADS
-
Ivezic, Z., & Elitzur, M. 1995, ApJ, 445, 415
In the text
NASA ADS
-
Jaminet, P. A., Danchi, W. C., Sutton, E. C., et al. 1991, ApJ, 380, 461
In the text
NASA ADS
-
Jones, T. J., Humphreys, R. M., Gehrz, R. D., et al. 1993, ApJ, 411, 323
NASA ADS
-
Josselin, E., & Lèbre, A. 2001, A&A, 367, 826
In the text
NASA ADS
-
Jourdain de Muizon, M., Cox, P., & Lequeux, J. 1990, A&AS, 83, 337
NASA ADS
-
Jura, M., Balm, S. P., & Kahane, C. 1995, ApJ, 453, 721
In the text
NASA ADS
-
Kahane, C., Cernicharo, J., Gómez-González, J., & Guélin, M. 1992, A&A,
256, 235
In the text
NASA ADS
-
Kastner, J. H., Weintraub, D. A., Zuckerman, B., et al. 1992, ApJ, 398, 552
NASA ADS
-
Kelly, D. M., & Latter, W. B. 1995, AJ, 109, 1320
NASA ADS
-
Klochkova, V. G., Szczerba, R., Panchuk, V. E., & Volk, K. 1999, A&A, 345, 905
NASA ADS
-
Knapp, G. R. 1986, ApJ, 311, 731
In the text
NASA ADS
-
Knapp, G. R., Sutin, B. M., Phillips, T. G., et al. 1989, ApJ, 336, 822
In the text
NASA ADS
-
Knapp, G. R., Young, K., Lee, E., & Jorissen, A. 1998, ApJS, 117, 209
In the text
NASA ADS
-
Knapp, G. R., Gammie, C. F., Young, K., & Phillips, T. G. 1990, in Submillimeter Astronomy, ed. G. Watt, & A. Webster (Kluwer, Dordrecht), 33
In the text
-
Knapp, G. R., Bowers, P. F., Young, K., & Phillips, T. G. 1995, ApJ,
455, 293
NASA ADS
-
Kwok, S. 1975, ApJ, 198, 583
In the text
NASA ADS
-
Kwok, S., Volk, K., & Hrivnak, B. J. 1989, ApJ, 345, L51
In the text
NASA ADS
-
Kwok, S. 1993, ARA&A, 31, 63
In the text
NASA ADS
-
Kwok, S., Hrivnak, B. J., & Geballe, T. R. 1995, ApJ, 454, 394
NASA ADS
-
Kwok, S., Hrivnak, B. J., Zhang, C. Y., & Langill, P. L. 1996, ApJ,
472, 287
NASA ADS
-
Kwok, S. 2000, The Origin and Evolution of Planetary Nebulae
(Cambridge Univ. Press, Cambridge)
In the text
-
Le Bertre, T., Heydari-Malayeri, M., Epchtein, N., Gouiffes, C., & Perrier, C.
1989, A&A, 225, 417
NASA ADS
-
Likkel, L., Morris, M., Omont, A., & Forveille, T. 1987, A&A, 173, L11
In the text
NASA ADS
-
Likkel, L., Morris, M., Forveille, T., & Omont, A. 1988, A&A, 198, L1
In the text
NASA ADS
-
Likkel, L., Forveille, T., Omont, A., & Morris, M. 1991, A&A, 246, 153
In the text
NASA ADS
-
Lopez, B., Mekarnia, D., & Lefevre, J. 1995, A&A, 296, 752
NASA ADS
-
Loup, C., Forveille, T., Omont, A., & Paul, J. F. 1993, A&AS, 99, 291
In the text
-
Mamon, G. A., Glassgold, A. E., & Huggins, P. J. 1988, ApJ, 328, 797
In the text
NASA ADS
-
Mauron, N., Le Borgne, J.-F., & Picquette, M. 1989, A&A, 218, 213
NASA ADS
-
Meaburn, J., & Walsh, J. R. 1985, MNRAS, 215, 761
NASA ADS
-
Meixner, M., Skinner, C. J., Graham, J. R., et al.
1997, ApJ, 482, 897
In the text
NASA ADS
-
Meixner, M., Campbell, M. T., Welch, W. J., & Likkel, L. 1998, ApJ,
509, 392
In the text
NASA ADS
-
Meixner, M., Ueta, T., Dayal, A., et al. 1999, ApJS, 122, 221
In the text
NASA ADS
-
Nedoluha, G. E., & Bowers, P. F. 1992, ApJ, 392, 249
In the text
NASA ADS
-
Neri, R., García-Burillo, S., Guélin, M., et al. 1992, A&A, 262, 544
In the text
NASA ADS
-
Neri, R., Kahane, C., Lucas, R., Bujarrabal, V., & Loup, C. 1998, A&AS, 130, 1
In the text
NASA ADS
-
Nyman, L.-Å., Booth, R. S., Carlström, U., et al. 1992, A&AS, 93, 121
In the text
NASA ADS
-
Olofsson, H., & Nyman, L.-Å. 1999, A&A, 347, 194
In the text
NASA ADS
-
Omont, A., Loup, C., Forveille, T., et al. 1993, A&A, 267, 515
In the text
NASA ADS
-
Quinn, D. E., Moore, T. J. T., Smith, R. G., Smith, C. H., & Fujiyoshi, T. 1996,
MNRAS, 283, 1379
NASA ADS
-
Reddy, B. E., & Hrivnak, B. J. 1999, AJ, 117, 1834
NASA ADS
-
Redman, M. P., O'Connor, J. A., Holloway, A. J., Bryce, M., & Meaburn, J. 2000,
MNRAS, 312, L23
NASA ADS
-
Riera, A., García-Lario, P., Manchado, A., Pottasch, S. R., & Raga, A. C.
1995, A&A, 302, 137
In the text
NASA ADS
-
Roddier, F., Roddier, C., Graves, J. E., & Northcott, M. J. 1995, ApJ, 443, 249
NASA ADS
-
Rowan-Robinson, M. 1980, ApJS, 44, 403
In the text
NASA ADS
-
Rowan-Robinson, M., & Harris, S. 1983, MNRAS, 202, 797
In the text
NASA ADS
-
Sahai, R., & Nyman, L.-Å. 1997, ApJ, 487, L155
In the text
NASA ADS
-
Sahai, R., Trauger, J. T., Watson, A. M., et al. 1998, ApJ, 493, 301
In the text
NASA ADS
-
Sahai, R. 1999, ApJ, 524, L125
In the text
NASA ADS
-
Sahai, R., Bujarrabal, V., Castro-Carrizo, A., & Zijlstra, A. A. 2000, A&A, 360, L9
In the text
-
Sahai, R., Bujarrabal, V., & Zijlstra, A. 1999a, ApJ, 518, L115
NASA ADS
-
Sahai, R., Zijlstra, A., Bujarrabal, V., & te Lintel Hekkert, P. 1999b, AJ,
117, 1408
In the text
NASA ADS
-
Sánchez Contreras, C., Bujarrabal, V., & Alcolea, J. 1997, A&A, 327, 689
In the text
NASA ADS
-
Sánchez Contreras, C., Bujarrabal, V., Neri, R., & Alcolea, J. 2000, A&A,
357, 651
In the text
NASA ADS
-
Schwartz, H. E., Aspin, C., Corradi, R. L. M., & Reipurth, B. 1997, A&A, 319, 267
NASA ADS
-
Shenton, M., Monier, R., Evans, A., et al. 1994, A&A, 287, 866
NASA ADS
-
Skinner, C. J., Meixner, M., Barlow, M. J., et al. 1997, A&A, 328, 290
NASA ADS
-
Szczerba, R., Omont, A., Volk, K., Cox, P., & Kwok, S. 1997, A&A, 317, 859
NASA ADS
-
Swings, J. P., & Andrillat, Y. 1979, A&A, 74, 85
NASA ADS
-
Trammell, S. R., Dinnerstein, H. L., & Goodrich, R. W. 1994, AJ, 108, 984
In the text
NASA ADS
-
Trams, N. R., Lamers, H. J. G. L. M., van der Veen, W. E. C. J., Waelkens, C., & Waters,
L. B. F. M. 1990, A&A, 233, 153
NASA ADS
-
Ueta, T., Meixner, M., & Bobrowsky, M. 2000, ApJ, 528, 861
In the text
NASA ADS
-
van der Veen, W. E. C. J., Habing, H.J., & Geballe, T. R. 1989, A&A, 226, 108 NASA ADS
-
van der Veen, W. E. C. J., Omont, A., Habing, H. J., & Matthews, H. E. 1995, A&A,
295, 445
NASA ADS
-
Volk, K., & Kwok, S. 1989, ApJ, 342, 345
In the text
NASA ADS
-
Volk, K., Kwok, S., & Woodsworth, A. W. 1993, ApJ, 402, 292
In the text
NASA ADS
-
Woodsworth, A. W., Kwok, S., & Chan, S. J. 1990, A&A, 228, 503
NASA ADS
-
Yamamura, I., Shibata, K. M., Kasuga, T., & Deguchi, S. 1994, ApJ, 427, 406
In the text
NASA ADS
-
Yamamura, I., Onaka, T., Kamijo, F., Deguchi, S., & Ukita, N. 1996, ApJ, 465,
926
In the text
NASA ADS
-
Yuasa, M., Unno, W., & Magono, S. 1999, PASJ, 51, 197
NASA ADS
-
Zweigle, J., Neri, R., Bachiller, R., Bujarrabal, V., & Grewing, M. 1997, A&A,
324, 624
In the text
NASA ADS
Copyright ESO 2001


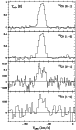

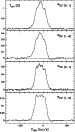

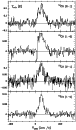
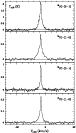
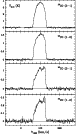
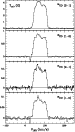
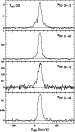

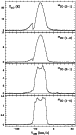
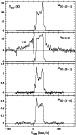

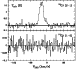
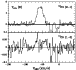
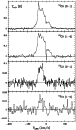
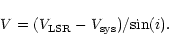
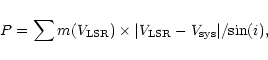
![\begin{displaymath}E = \frac{1}{2} \sum m(V_{\rm LSR}) \times
[(V_{\rm LSR} - V_{\rm sys})/{\rm sin}(i)]^2.
\end{displaymath}](/articles/aa/full/2001/39/aah2711/img53.gif)