A&A 377, L27-L30 (2001)
DOI: 10.1051/0004-6361:20011211
The interpretation of MnII emission from late-type B stars
T. A. A. Sigut
Department of Physics and Astronomy, The University of Western Ontario,
London, Ontario, Canada N6A 3K7
Received 12 March 2001 / Accepted 29 August 2001
Abstract
The photospheric Mn II emission lines Wahlgren & Hubrig (2000) detect
in the spectra of several late-type B and HgMn stars and
attribute to fluorescent excitation are more naturally explained by
interlocked non-LTE effects acting in a photosphere in which the manganese abundance is
stratified with depth. The case is particularly strong for HD 186122 (46 Aql) and
HD 179761 both of which require the manganese overabundance to be concentrated
to column masses of 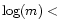
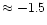 .
.
Key words: line: formation - radiative transfer - stars: chemically peculiar,
emission-line, Be
Stellar emission lines are usually interpreted as evidence for a chromospheric temperature rise, mass outflow, or the presence of circumstellar material. However, emission lines from
"classical" stellar photospheres, in which none of the previous mechanisms operate,
cannot be ruled out a priori as the specific intensity in a transition is determined by a source function which may respond in a complex way to the presence of non-local sources and sinks of line photons. Examples of this caveat are the photospheric emission lines of Mn II multiplet 13 (
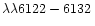 Å,
Å,
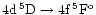 )
recently detected in the spectra of the 3He star 3 Cen A (HD 120709, B5III-IVp) and the hot, mild, HgMn star 46 Aql (HD 186122, B9 III) by Sigut et al. (2000). Sigut (2001) has demonstrated that these emission lines can arise via inter-locked non-LTE effects which decouple the line source function from the local Planck function
and result in a line source function which rises with photospheric height. It was also argued that an essential ingredient in reproducing the strength of the observed manganese emission within the non-LTE framework is a stratification of the manganese abundance profile in the photosphere, concentrating the manganese in a layer at small column mass.
)
recently detected in the spectra of the 3He star 3 Cen A (HD 120709, B5III-IVp) and the hot, mild, HgMn star 46 Aql (HD 186122, B9 III) by Sigut et al. (2000). Sigut (2001) has demonstrated that these emission lines can arise via inter-locked non-LTE effects which decouple the line source function from the local Planck function
and result in a line source function which rises with photospheric height. It was also argued that an essential ingredient in reproducing the strength of the observed manganese emission within the non-LTE framework is a stratification of the manganese abundance profile in the photosphere, concentrating the manganese in a layer at small column mass.
Recently, Wahlgren & Hubrig (2000, W&H hereafter) have also detected weak emission
from Mn II multiplet 13, as well as from additional transitions of Cr II and Ti II, in the red spectra of several late-type B and HgMn stars.
W&H postulate selective excitation via Ly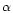 fluorescence as the emission mechanism.
In this letter, it is demonstrated that the Mn II emission detected by W&H is
consistent with the non-LTE excitation mechanism of Sigut (2001).
Specific stratification models for each star are proposed as constrained by the available observations. The possible role of Ly
fluorescence as the emission mechanism.
In this letter, it is demonstrated that the Mn II emission detected by W&H is
consistent with the non-LTE excitation mechanism of Sigut (2001).
Specific stratification models for each star are proposed as constrained by the available observations. The possible role of Ly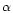 fluorescent excitation is also discussed.
fluorescent excitation is also discussed.
The coupled equations of radiative transfer and statistical equilibrium for
Mn II were solved with the MULTI code, v2.0, of Carlsson (1992). Solutions were obtained in model photospheres appropriate for the seven late-B and HgMn stars for which W&H list Mn II multiplet 13 (
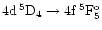 ,
,
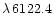 Å) equivalent widths (see Table 1).
For each star, the
Å) equivalent widths (see Table 1).
For each star, the
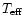 and
and 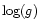 adopted by W&H were used,
and each model photosphere
was represented by an Kurucz LTE model atmosphere.
Direct comparison to non-LTE model atmospheres (Grigsby 1991;
Grigsby et al. 1992) and to observed UV-to-optical spectral
energy distributions (Fitzpatrick & Massa 1999) demonstrates that the
approximation of LTE model atmospheres is a reasonable one for this range of stellar parameters.
adopted by W&H were used,
and each model photosphere
was represented by an Kurucz LTE model atmosphere.
Direct comparison to non-LTE model atmospheres (Grigsby 1991;
Grigsby et al. 1992) and to observed UV-to-optical spectral
energy distributions (Fitzpatrick & Massa 1999) demonstrates that the
approximation of LTE model atmospheres is a reasonable one for this range of stellar parameters.
The Mn II model atom consisted of 84 total 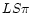 multiplet levels
from the quintet and septet symmetries. The atomic data used was the same as that described in
Sigut (2001). To obtain a realistic
assessment of the uncertainties in the non-LTE predictions due to the large uncertainties
in the basic atomic data, Monte Carlo simulations were performed. Generous errors were assigned
to all of the atomic data (see Sigut 2001), and
15 sets of Mn II atomic data were realized and used in the non-LTE calculations.
This gave, for each model photosphere and stratification model, 15 estimates of the equivalent width
of each Mn II transition, and the standard deviation in
these values was taken as an estimate of the uncertainty.
The use of Monte Carlo simulation to estimate the errors in non-LTE calculations is
discussed by Sigut (1996).
multiplet levels
from the quintet and septet symmetries. The atomic data used was the same as that described in
Sigut (2001). To obtain a realistic
assessment of the uncertainties in the non-LTE predictions due to the large uncertainties
in the basic atomic data, Monte Carlo simulations were performed. Generous errors were assigned
to all of the atomic data (see Sigut 2001), and
15 sets of Mn II atomic data were realized and used in the non-LTE calculations.
This gave, for each model photosphere and stratification model, 15 estimates of the equivalent width
of each Mn II transition, and the standard deviation in
these values was taken as an estimate of the uncertainty.
The use of Monte Carlo simulation to estimate the errors in non-LTE calculations is
discussed by Sigut (1996).
Stratification of the manganese abundance profile with photospheric depth was represented by
a simple two-zone model depending on four parameters: the manganese abundance in the lower
zone (
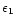 ), the manganese abundance in the upper zone (
), the manganese abundance in the upper zone (
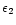 ), the location in
column mass of the transition between the two zones (B), and a parameter setting the sharpness of
the transition between the zones (A). In terms of these parameters, the
particle conservation equation at each depth was written as
), the location in
column mass of the transition between the two zones (B), and a parameter setting the sharpness of
the transition between the zones (A). In terms of these parameters, the
particle conservation equation at each depth was written as
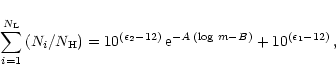 |
(1) |
for
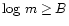 ,
and
,
and
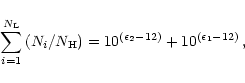 |
(2) |
for
 .
Here
.
Here  is the hydrogen number density,
is the hydrogen number density,  the number of
Mn II/Mn III levels included in the non-LTE solution (namely 85),
and m is the photospheric column mass.
Figure 1 illustrates this simple, two-zone model for some
representative choices of the parameters.
the number of
Mn II/Mn III levels included in the non-LTE solution (namely 85),
and m is the photospheric column mass.
Figure 1 illustrates this simple, two-zone model for some
representative choices of the parameters.
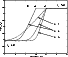 |
Figure 1:
The two-zone stratification model for the manganese abundance
for several choices of the model parameters. |
| Open with DEXTER |
The calculated non-LTE Mn II equivalent widths for various stratification models were
compared to the late B-star observations of W&H. The zone abundances,
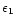 and
and
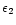 ,
were independently varied from 2.92 to 7.92 in steps of 0.5 dex
,
were independently varied from 2.92 to 7.92 in steps of 0.5 dex![[*]](/icons/foot_motif.gif) .
Only models with an overabundance in the upper zone (
.
Only models with an overabundance in the upper zone (
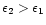 )
were considered, aside from a reference grid of unstratified models covering the same abundance range. Parameter B, which determines the location of the transition between the zones, was assumed to have values of -1.0, -1.5, or -2.0. Models with B>-1 gave predictions which differed little from unstratified models of abundance
)
were considered, aside from a reference grid of unstratified models covering the same abundance range. Parameter B, which determines the location of the transition between the zones, was assumed to have values of -1.0, -1.5, or -2.0. Models with B>-1 gave predictions which differed little from unstratified models of abundance
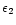 because the zone boundary is near or below the depth of formation of multiplet 13. Parameter A, governing the sharpness of the transition between the two zones, was assumed to have values of 2, 4, or 6. As can be seen from Fig. 1, larger values for parameter A give a sharper transition between the two abundance zones.
because the zone boundary is near or below the depth of formation of multiplet 13. Parameter A, governing the sharpness of the transition between the two zones, was assumed to have values of 2, 4, or 6. As can be seen from Fig. 1, larger values for parameter A give a sharper transition between the two abundance zones.
Given these parameters, acceptable stratification models for each star were chosen to
reproduce two observations: (1) the strength of Mn II multiplet 13,
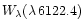 ,
and (2) the photospheric manganese abundance determined by previous workers,
,
and (2) the photospheric manganese abundance determined by previous workers,
![$\mbox{\rm [Mn/H]}$](/articles/aa/full/2001/39/aadc121/img23.gif) .
The form of the second constraint stems from the fact that
none of the available abundance studies for the stars of Table 1
provide equivalent widths for manganese. Therefore, the manganese abundances derived by these
studies were assumed to parameterize the strengths of the weak, optical, Mn II transitions used. To implement the constraint
.
The form of the second constraint stems from the fact that
none of the available abundance studies for the stars of Table 1
provide equivalent widths for manganese. Therefore, the manganese abundances derived by these
studies were assumed to parameterize the strengths of the weak, optical, Mn II transitions used. To implement the constraint
![$\mbox{\rm [Mn/H]}$](/articles/aa/full/2001/39/aadc121/img23.gif) ,
an LTE abundance analysis was performed
on the predicted non-LTE equivalent width of
,
an LTE abundance analysis was performed
on the predicted non-LTE equivalent width of
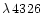 (Mn II
(Mn II
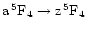 )
in each stratification model. This generally weak, visible line is typical of those used in the abundance analysis of manganese. The hyperfine structure of
)
in each stratification model. This generally weak, visible line is typical of those used in the abundance analysis of manganese. The hyperfine structure of
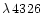 was explicitly included in both the LTE and non-LTE calculations
using the experimental measurements of Holt et al. (1999). A probable error of
was explicitly included in both the LTE and non-LTE calculations
using the experimental measurements of Holt et al. (1999). A probable error of 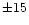 % was assigned to the
% was assigned to the
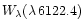 data of W&H, and
data of W&H, and 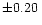 dex to the various LTE manganese abundance determinations. As noted by Sigut et al. (2000),
the oscillator strength of
dex to the various LTE manganese abundance determinations. As noted by Sigut et al. (2000),
the oscillator strength of
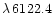 is unlikely to be in error by a large amount.
is unlikely to be in error by a large amount.
Table 1 summarizes an analysis of the W&H stars using models with
a uniform manganese abundance as a function of photospheric depth.
For the four stars with available [Mn/H], Table 1 gives the (unstratified)
manganese abundance range (under column "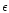 Range") for which the LTE abundance required to match the computed non-LTE equivalent width of
Range") for which the LTE abundance required to match the computed non-LTE equivalent width of
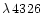 matches the literature value within
matches the literature value within 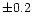 dex. The next column,
dex. The next column,
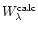 ,
gives the predicted non-LTE
equivalent width of
,
gives the predicted non-LTE
equivalent width of
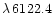 ,
along with its
,
along with its 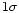 error, for a manganese abundance at the midpoint of this range. In all cases, the unstratified models which match the LTE manganese abundance fail by large amounts to explain the strength of the
error, for a manganese abundance at the midpoint of this range. In all cases, the unstratified models which match the LTE manganese abundance fail by large amounts to explain the strength of the
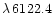 emission.
The closest match is for HD 196426 where the calculated
emission.
The closest match is for HD 196426 where the calculated
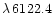 strength differs from the observed value by over 5 standard deviations. The remaining stars all differ by more than 10 standard deviations. Thus unstratified models are unable to simultaneously match both constraints,
prompting stratified models to be considered in the next section.
strength differs from the observed value by over 5 standard deviations. The remaining stars all differ by more than 10 standard deviations. Thus unstratified models are unable to simultaneously match both constraints,
prompting stratified models to be considered in the next section.
For the three remaining stars, the constraint of [Mn/H] is unavailable, and it is not possible to
rule out unstratified models. In this case, the column "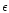 Range" reports the range of
manganese abundances for which the predicted equivalent width of
Range" reports the range of
manganese abundances for which the predicted equivalent width of
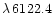 matches the observed value within the combined observational and theoretical errors. The range of abundances found are generally solar to sub-solar.
matches the observed value within the combined observational and theoretical errors. The range of abundances found are generally solar to sub-solar.
One possible strategy to salvage unstratified models is to assume that the
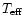 and
and 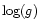 values for the stars are in error by large amounts. For the two stars with large manganese
overabundances relative to the sun, HD 186122 (46 Aql) and HD 179761, it was not possible to find unstratified models matching both constraints within
values for the stars are in error by large amounts. For the two stars with large manganese
overabundances relative to the sun, HD 186122 (46 Aql) and HD 179761, it was not possible to find unstratified models matching both constraints within 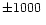 K in
K in
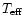 and
and
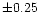 dex in
dex in 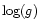 .
However, for the two remaining stars with only modest manganese overabundances, matching unstratified models could be found. A model with
.
However, for the two remaining stars with only modest manganese overabundances, matching unstratified models could be found. A model with
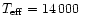 K and
K and
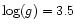 can reproduce the HD 196426 observations for the narrow abundance range of
can reproduce the HD 196426 observations for the narrow abundance range of
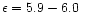 dex. For HD 209459, a model with
dex. For HD 209459, a model with
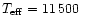 K and
K and
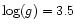 can reproduce the observations for the abundance range of
can reproduce the observations for the abundance range of
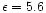 -5.7 dex.
However, the errors in
-5.7 dex.
However, the errors in
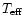 implied in both cases are
implied in both cases are 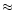 1000 K
and are at the outer limit of plausibility (Adelman & Rayle 2000).
For this reason, stratified models for these two stars have also been investigated.
1000 K
and are at the outer limit of plausibility (Adelman & Rayle 2000).
For this reason, stratified models for these two stars have also been investigated.
 |
Figure 2:
Stratified models for HD 186122 (46 Aql).
The ( A, B) parameters of Eqs. (1) and (2) are indicated in each panel.
As described in the text, viable stratified models only occur in the overlap region
of the circles and filled squares. All models in the (
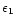 , ,
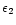 )
plane were considered except those below and to the right of the solid line. )
plane were considered except those below and to the right of the solid line. |
| Open with DEXTER |
Given the failure of unstratified models to reproduce the observations, particularly for
HD 186122 (46 Aql) and HD 179761, stratified models were considered. Figure 2 presents the results for 46 Aql. Each panel in the figure represents a single choice of the parameters B (location of the zone transition) and A (sharpness of the zone transition). Given the (B, A) values, a square is plotted in the (
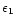 ,
,
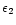 )
plane if that stratified model can reproduce the [Mn/H] abundance within
)
plane if that stratified model can reproduce the [Mn/H] abundance within 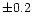 dex, and an open circle is plotted if that stratified model can reproduce the strength of
dex, and an open circle is plotted if that stratified model can reproduce the strength of
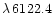 within the combined theoretical and experimental errors. Thus a consistent stratified model is represented by a circle containing a filled square. For 46 Aql, only models with B=-1.5 and A=6 or
B=-2.0 and
within the combined theoretical and experimental errors. Thus a consistent stratified model is represented by a circle containing a filled square. For 46 Aql, only models with B=-1.5 and A=6 or
B=-2.0 and 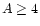 give consistent results. This occurs for an upper zone abundance
in the range of
give consistent results. This occurs for an upper zone abundance
in the range of
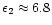 -7.5 although the exact value depends on the chosen (B, A) parameters. The lower zone abundance is less well defined with matching models generally occurring for
-7.5 although the exact value depends on the chosen (B, A) parameters. The lower zone abundance is less well defined with matching models generally occurring for
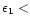
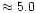 .
.
Figure 3 summaries the matching stratification models for the three remaining stars with both multiplet 13 equivalent widths and [Mn/H] abundances. In this figure, a symbol is plotted in the (
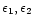 )
plane only if that model matches both constraints,
unlike Fig. 2. For HD 179761, which like 46 Aql has a large [Mn/H] enhancement, matching models are only found for
)
plane only if that model matches both constraints,
unlike Fig. 2. For HD 179761, which like 46 Aql has a large [Mn/H] enhancement, matching models are only found for 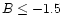 and
and 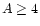 with
with
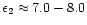 and
and
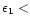
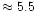 .
However, for the two remaining stars with only moderate manganese overabundances, a wide variety of stratification models can match the observations.
.
However, for the two remaining stars with only moderate manganese overabundances, a wide variety of stratification models can match the observations.
W&H suggest an alternative origin for the Mn II emission lines, namely Ly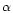 fluorescent excitation with the Mn II emission formed by population cascade as in a photoionized nebula. W&H note close wavelength co-incidences between transitions in the Mn II term system and Ly
fluorescent excitation with the Mn II emission formed by population cascade as in a photoionized nebula. W&H note close wavelength co-incidences between transitions in the Mn II term system and Ly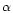 ,
most notably those connecting the ground state with the lower level of multiplet 13,
,
most notably those connecting the ground state with the lower level of multiplet 13,
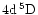 ,
and those connecting the low-lying meta-stable
state
,
and those connecting the low-lying meta-stable
state 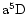 with the upper level of multiplet 13,
with the upper level of multiplet 13,
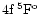 .
Seductive as these close overlaps may be, wavelength coincidence alone is not sufficient for fluorescent excitation. Consider a weak, Mn II transition with line profile
.
Seductive as these close overlaps may be, wavelength coincidence alone is not sufficient for fluorescent excitation. Consider a weak, Mn II transition with line profile
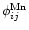 within
within 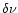 of Ly
of Ly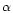 .
The net excitation rate in this transition due to Ly
.
The net excitation rate in this transition due to Ly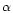 is
is
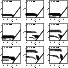 |
Figure 3:
Matching stratification models for HD 209459 (squares), HD 196426 (circles),
and HD 179761 (crosses). Unlike Fig. 2, each symbol represents a viable
stratification model. |
| Open with DEXTER |
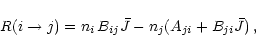 |
(3) |
where
![\begin{displaymath}%
\bar{J}=\int\,\phi_{ij}^{\rm Mn}\,J_{\nu}\,{\rm d}\nu\, = \Lambda[S^{\rm Ly\alpha}] \,.
\end{displaymath}](/articles/aa/full/2001/39/aadc121/img72.gif) |
(4) |
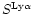 is the Ly
is the Ly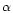 source function, and
source function, and 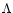 is the
is the 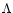 -operator representing, in integral-operator form, the formal solution to the transfer equation.
The second step in Eq. (3) assumes that Ly
-operator representing, in integral-operator form, the formal solution to the transfer equation.
The second step in Eq. (3) assumes that Ly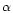 will dominate the radiation field at this frequency and that
will dominate the radiation field at this frequency and that 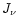 is sensibly constant over the narrow range of
is sensibly constant over the narrow range of 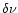 .
At the depth of formation of weak Mn II transitions, the optical depth at this frequency will be large, and
.
At the depth of formation of weak Mn II transitions, the optical depth at this frequency will be large, and 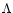 is essentially the unit operator.
The net rate is therefore
is essentially the unit operator.
The net rate is therefore
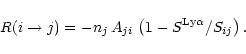 |
(5) |
Here the definition of the line source function for the Mn II transition,
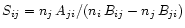 ,
has been used. Direct calculation in this work suggests that in an unstratified photosphere, Mn II
,
has been used. Direct calculation in this work suggests that in an unstratified photosphere, Mn II
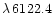 forms near
forms near
 to -1, depending on the abundance. At these photospheric depths,
the Mn II departure co-efficients are nearly equal due to strong collisional coupling, and this thermalizes the line source functions to the local Planck function (i.e.
to -1, depending on the abundance. At these photospheric depths,
the Mn II departure co-efficients are nearly equal due to strong collisional coupling, and this thermalizes the line source functions to the local Planck function (i.e.
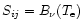 ). Thus, Ly
). Thus, Ly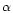 fluorescent excitation requires that the Ly
fluorescent excitation requires that the Ly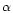 source function exceed the local Planck function. If Ly
source function exceed the local Planck function. If Ly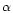 is thermalized with
is thermalized with
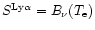 ,
the net pumping rate is zero regardless of the number of close wavelength co-incidences with Ly
,
the net pumping rate is zero regardless of the number of close wavelength co-incidences with Ly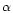 .
.
At the depth of formation of multiplet 13, the mean optical depth in Ly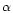 is
is
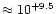 .
Using the results of Gayley (1992a, 1992b) to estimate the thermalization length of Ly
.
Using the results of Gayley (1992a, 1992b) to estimate the thermalization length of Ly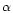 in typical late-B photospheres, one finds that Ly
in typical late-B photospheres, one finds that Ly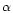 is effectively thermalized with its source function equal to the Planck function at
the local kinetic temperature. Thus, the net pumping rate due to Ly
is effectively thermalized with its source function equal to the Planck function at
the local kinetic temperature. Thus, the net pumping rate due to Ly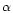 fluorescence is zero. The thermalized radiation field in Ly
fluorescence is zero. The thermalized radiation field in Ly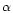 will also act maintain the LTE population ratio between the first two hydrogen levels; any postulated interlocked effects (for example, photon loses in H
will also act maintain the LTE population ratio between the first two hydrogen levels; any postulated interlocked effects (for example, photon loses in H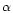 ,
which might be invoked to provide additional population to n=2) will not disturb the thermalization of the Ly
,
which might be invoked to provide additional population to n=2) will not disturb the thermalization of the Ly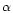 source function in these deep photospheric layers.
source function in these deep photospheric layers.
All of the stars found by W&H to have emission in Mn II multiplet 13 can be interpreted
in terms of standard, non-LTE line formation acting in the photosphere.
In addition, evidence for the stratification of the manganese abundance profile is
particularly strong for HD 186122 (46 Aql) and HD 179761 both of which require manganese to be confined to column masses above
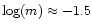 to be consistent with the available observations.
to be consistent with the available observations.
Modeling of a wider wavelength range of the Mn II spectrum should provide much tighter constraints on the possible stratification models for HgMn and related stars. In addition,
it is important to demonstrate that the weak emission lines of Ti II and Cr II also noted by W&H can be interpreted within the non-LTE framework presented in this letter.
Acknowledgements
I would like to thank J. D. Landstreet for many helpful discussions, and the referees, Glenn Wahlgren and Mike Dworetsky, for their comments. This work is supported by the
Natural Sciences and Engineering Research Council of Canada.
-
Adelman, S. J., & Rayle, K. E. 2000, MNRAS, 355, 308
In the text
NASA ADS
-
Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197
NASA ADS
-
Carlsson, M. 1992, in Cool Stars, Stellar Systems, and the Sun, ed. M. S. Giampap,
& J. A. Bookbinder, ASP Conf. Ser. 26, 499
In the text
-
Fitzpatrick, E. L., & Massa, D. 1999, ApJ, 525, 1011
In the text
NASA ADS
-
Gayley K. G. 1992a, ApJS, 78, 549
In the text
NASA ADS
-
Gayley K. G. 1992b, ApJ, 390, 573
In the text
NASA ADS
-
Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, ed. N. Prantzos, E. Vangioni, & M. Cassé (Cambridge University Press), 15
-
Grigsby, J. A. 1991, ApJ, 380, 606
In the text
NASA ADS
-
Grigsby, J. A., Morrison, N. D., & Anderson, L. A. 1992, ApJS, 78, 205
In the text
NASA ADS
-
Holt, R. A., Scholl, T. J., & Rosner, S. D. 1999, MNRAS, 306, 107
In the text
NASA ADS
-
Sigut, T. A. A. 2001, ApJ, 546, L118
In the text
NASA ADS
-
Sigut, T. A. A. 1996, ApJ, 473, 452
In the text
NASA ADS
-
Sigut, T. A. A., Landstreet, J. D., & Shorlin, S. L. S. 2000,
ApJ, 530, L89
In the text
NASA ADS
-
Wahlgren, G. M., & Hubrig, S. 2000, A&A, 2000, 362, L13
In the text
NASA ADS
Copyright ESO 2001
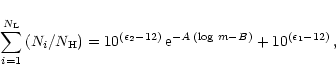
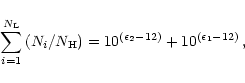




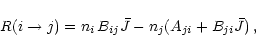
![\begin{displaymath}%
\bar{J}=\int\,\phi_{ij}^{\rm Mn}\,J_{\nu}\,{\rm d}\nu\, = \Lambda[S^{\rm Ly\alpha}] \,.
\end{displaymath}](/articles/aa/full/2001/39/aadc121/img72.gif)