A&A 377, 522-537 (2001)
DOI: 10.1051/0004-6361:20011115
S. Liberatore1 - J.-P. J. Lafon1 - N. Berruyer2
1 - Observatoire de Paris-Meudon, DASGAL/UMR 8633, 92195 Meudon, France
2 -
Observatoire de la Côte d'Azur, Laboratoire G. D. Cassini/UMR 6529, 06304 Nice, France
Received 12 May 2000 / Accepted 3 August 2001
Abstract
Models of stationary dust-driven winds of late-type stars are investigated.
The flow is described successively using three models which couple, in
spherical symmetry, the grain-gas dynamics
in a self-consistent way with radiative transfer.
Complete radiative transfer including multiple scattering,
absorption and thermal emission
is taken into account to determine the temperature of dust grains
which in turn governs their thermal emission.
The medium is not necessarily optically thin.
The first model is used
to check one classical hypothesis, that where the gas and the grains
expand at the same velocity, the
flow is described by a one-fluid model.
This model is then improved in a second model, to include complete momentum coupling
between gas and grains by friction.
Finally, a third model
includes grains and gas coupled
by friction as well as the effects of inertial force on grains.
By means of a numerical iteration, dynamics and radiative transfer are coupled in order
to achieve a self-consistent solution in all cases.
Even for fairly low non-zero optical depths, coupling of radiation with dynamics
is found to be important for wind models which are all
highly sensitive to input data. In conclusion, approximations
(position and momentum coupling) for the dynamics should be relaxed.
Key words: stars: mass loss - circumstellar matter - hydrodynamics - radiative transfer
The existence of circumstellar dust grains and mass loss in cool stars is by now well established (Cassinelli 1979; Zuckerman 1980). A wealth of papers have been devoted to the investigation of the hydrodynamical and thermodynamical role of dust in the circumstellar environment (see for instance Winters et al. 2000 and the reviews of Lafon & Berruyer 1991 and Sedlmayr & Dominik 1995, and references therein).
Whatever the mechanisms causing the wind, the mass loss is controlled by the radiative pressure on dust grains. Photons emitted by the star are absorbed by grains and partially scattered in a more or less isotropic way. A part of the momentum carried by the absorbed photons is transferred to the grains. Friction between grains and atoms or molecules then transmits part of the grain's momentum to the gas.
Much effort was devoted to the study of grain formation and growth (Salpeter 1974a; Draine 1979; Deguchi 1980; Lafon 1991; Patzer et al. 1998), and the construction of mass outflow models (Salpeter 1974b; Kwok 1975; Lucy 1976; Menietti & Fix 1978; Phillips 1979; Deguchi 1980; Winters et al. 2000).
Many models assume (following Gilman 1972) that the whole momentum transferred to the dust grains from the stellar radiation is transferred to the gas by collisions. This "momentum coupling assumption'' provides a highly simplified method of calculating grain and gas velocities, but its influence on the overall structure of the wind models has never really been quantitatively checked.
Krüger et al. (1994) and Krüger & Sedlmayr (1997) built a two-fluid model for stationary dust-driven winds where the dust and the gas components are coupled through the condensation of dust from the gas phase and grain-gas collisions. The radiative transfer on dust is derived from a semi-analytical method developed by Lucy (1971). Moreover, the medium used in the model is optically thin, and the radiative transfer is not self-consistent with the dynamics.
Another work that is close to our purpose has been carried out by Simis et al. (2001). They have combined time-dependent hydrodynamics with a two-fluid model for dust-driven AGB winds. However, they estimate the gas-grain momentum transfer from each time step to the next before which the terminal velocity is assumed to be reached (as a function of some mean free path typical for this process). They also assumed a grey dust opacity.
Tielens (1983) or Netzer & Elitzur (1993) do not explicitly solve the equation of motion for the dust component. The dust is assumed to move with its equilibrium drift velocity relative to the gas.
In order to remove highly inaccurate approximations of dynamics and radiative transfer, we choose hereafter to limit the number of mechanisms to the minimum necessary. Radiative transfer is treated for all frequencies, self-consistently. Simplifying assumptions such as grey opacity, isotropic scattering or the Eddington approximation are relaxed. The question of dynamics is treated for three types of models based respectively on the position cloupling assumption, the momentum coupling assumption and finally on the full problem where the inertial force on grains is taken into account.
The equations for the three dynamical models and for radiative transfer are displayed in Sect. 2. Solutions of dynamical equations (in the three cases), radiative transfer and the coupling between the two problems are explained in Sect. 3. In Sect. 4 we discuss and compare self-consistent models of dust driven wind (Position Coupling, Momentum Coupling and Full Problem). The main conclusions are given in Sect. 5. They will be developed more extensively in future papers.
The following simplifying assumptions are used:
the flow is stationary, spherically symmetric and grains exist above some
reference level r0, which we refer to as "the base of the wind''.
The central star is a blackbody at a given temperature ![]() .
The wind is neutral and isothermal. In fact, the scale height of the gas temperature
is very much larger than any other scales in the considered envelope (Berruyer 1991).
The balance between radiation absorbed and emitted by the grains determines
the equilibrium grain temperature.
.
The wind is neutral and isothermal. In fact, the scale height of the gas temperature
is very much larger than any other scales in the considered envelope (Berruyer 1991).
The balance between radiation absorbed and emitted by the grains determines
the equilibrium grain temperature.
There is an energy equation for the dust alone. To determine the gas temperature profile, it would be necessary to solve the radiative transfer in the gas, which is in fact never optically thick enough to require this. The gas and dust temperatures are consistent in all processes. Variations in gas temperature, however, can induce variations of the nucleation and growth rates, and subsequently their optical properties. Finally, this creates feedback effects on radiative transfer and consistent dynamics. The variations in gas temperature in the considered range of radial distances are very small and hereafter all the effects will be ignored.
Berruyer (1991) studied, for a set of assumed kinetic temperature profiles, the stability of a static model of envelope in the presence of dust grains. Conditions under which the presence of dust grains may generate an instability in a static envelope and drive the motion of the gas component were determined: convectively unstable configurations exist, in spite of the mechanical equilibrium. Furthermore, Berruyer (1991) showed that for envelopes where temperature decreases less steeply than 1/r, the hydrostatic equilibrium is impossible in the outer layers, and the dust-driving is an extra mechanism which essentially modifies the velocity profile and the mass loss rate. Nevertheless, stricto sensu, the dust grains do not "create'' the wind.
Both time-dependent effects and thermal coupling between gas and grains will be neglected. The dust grains are spherical in shape and uniform in density. They scatter almost isotropically, i.e., only first order effects in anisotropic scattering are taken into account.
We can neglect electrostatic drag, which is about a factor 104 smaller than the collisional drag for a cool star (Tabak et al. 1975). We have neglected the fragmentation and coalescence effects (Scalo 1977; Simpson et al. 1980; Biermann & Harwitt 1980) and have ignored grain pressure. Indeed, if the grains were treated as a perfect gas, with a kinetic temperature similar to the gas kinetic temperature, grain pressure for any reasonable wind model would be smaller than gas pressure by about a factor of 10-14 and would therefore have no great effect.
In this paper, three models corresponding to three descriptions of the dynamics problem are presented (PC, MC and FP), and in each case dynamics are fully coupled with radiative transfer (described bellow). The results are compared in Sect. 2.3.
The motion of the grains is submitted to the equations of mass conservation:
![]() is the radiative force on each grain.
is the radiative force on each grain.
![]() is the frictional force which couples the gas
to each grain.
is the frictional force which couples the gas
to each grain.
![]() is the gravitational acceleration.
is the gravitational acceleration.
The mass density of the grains
![]() is defined by:
is defined by:
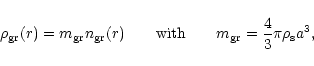 |
(6) |
The fact that the size of the grains is much smaller than the mean free-path of the gas particles implies that the classical Stoke's law from Batchelor (1967) does not apply. The collisional drag for circumstellar grains has been carefully calculated by Baines et al. (1965). The transfer of momentum assuming specular reflexion of the gas particles on the grains ensures the maximum transfer.
The expression of the frictional force is:
For our forthcoming models, it is convenient to write the frictional force solely in terms of
velocities in order to limit the number of independent variables in the momentum conservation equations.
With Eq. (1) we have thus:
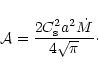 |
(12) |
For cool stars, grains are presumably generated inside the flow. Our model starts at the moment the grains formed. It therefore appears reasonable to assume that at the base of the flow the gas and the grains have the same velocity. This will be our second boundary condition.
A discussion about the behaviour of the flow when grains appear is given by Berruyer & Frisch (1983). Two different dynamical regimes exist, a boundary layer regime where the grains are submitted to a very strong acceleration (the gas keeping an almost constant velocity), and an outer regime where the two fluids are strongly coupled. Our numerical results scrutinize the velocity of grains just outside the boundary layer because this boundary layer is very thin and cannot be computed.
This approximation corresponds to a strongly
local coupling where there are enough collisions between gas and grains
for the two phases to move together.
The grains are thus "frozen'' in the gas;
there is only one fluid velocity:
Addition of Eqs. (5) and (2)
of momentum conservation,
using Eq. (13) leads to:
Gas and grains are coupled by friction. Under this approximation,
the whole momentum given to grains by
the radiative force is transferred to the gas by grain-gas collisions. In other words,
the radiative force is set equal to the frictional force (the grain mass
is taken to be equal to zero):
One can also use another approximation in which the gravity of grains is taken into account.
we shall call it the "Partial Momentum Coupling''
because only part of the momentum given to the
grains by radiative pressure is released to the gas by collisions. The other part
counter-balance the gravitationnal force and:
Comparing the results obtained using these approximations allows us to study the effect of gravity on the grains.
Boundary conditions are the same as in full problem except for those concerning initial velocities. In all cases except in the full problem, initial grain and gas velocities are not equal because the boundary layer is removed by degeneracy of the differential equation for the grains.
The time-independent equation of radiative transfer for
anisotropic scattering and isotropic source can be written as:
| = | 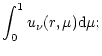 |
(22) | |
| = | 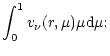 |
(23) | |
| = | 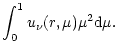 |
(24) |
The discussion on anisotropic scattering can be found in Leung's (1975) paper. According to
Leung (1975), and using the first order
asymmetry parameter ![]() (computed using the Mie scattering theory)
which is equal to zero for isotropic
scattering, to 1 for forward scattering and to -1 for backward scattering,
the zero and first order moments of Eq. (19) with respect to
(computed using the Mie scattering theory)
which is equal to zero for isotropic
scattering, to 1 for forward scattering and to -1 for backward scattering,
the zero and first order moments of Eq. (19) with respect to ![]() are:
are:
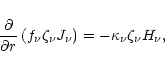 |
(29) |
| = | (31) | ||
| = | (32) | ||
| = | (33) |
| z | = | (34) | |
| = | (r2 - z2)1/2. | (35) |
According to Leung (1975), with these coordinates
we obtain two coupled first-order differential equations:
![$\displaystyle S_{\nu}(\mu) = \frac{1}{(\sigma^a_{\nu} + \sigma^d_{\nu})} \left[...
...1} I_{\nu}(\mu')p_{\nu}(\mu, \mu'){\rm d}\mu' + \sigma^a_{\nu} B_{\nu} \right].$](/articles/aa/full/2001/38/aa9916/img113.gif) |
(39) |
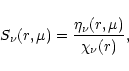 |
(40) |
| (41) |
| (42) |
The evaluation of ![]() and
and
![]() follows from Eqs. (27) and (28).
The equation of radiative equilibrium which specifies the temperature
follows from Eqs. (27) and (28).
The equation of radiative equilibrium which specifies the temperature
![]() ,
is given
by (radiative equilibrium):
,
is given
by (radiative equilibrium):
![\begin{displaymath}\int_0^{\infty}\left[ \epsilon_{\nu}^{\ast}(r)-\kappa_{\nu}^{\ast}(r)J_{\nu}(r)\right]{\rm d}\nu
= 0.
\end{displaymath}](/articles/aa/full/2001/38/aa9916/img119.gif) |
(43) |
The radiation coming from the interstellar medium was taken zero:
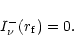 |
(44) |
![]() For moment equations.
For moment equations.
The following quantities are defined at each boundary
![]() :
:
Downward flux:
![$\displaystyle \frac{1}{2}
\frac{\displaystyle \int_0^1 \left[ I_{\nu}(r_{\rm B}...
..._{\nu}(r_{\rm B}, -\mu\right]
\mu{\rm d}\mu }{\displaystyle J_{\nu}(r_{\rm B})}$](/articles/aa/full/2001/38/aa9916/img127.gif) |
(47) | ||
| = | 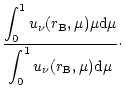 |
(48) |
Usually ![]() is known at the outer boundary
is known at the outer boundary ![]() while
while ![]() is partialy
known at the inner boundary r0.
The net flux at each boundary is noted
is partialy
known at the inner boundary r0.
The net flux at each boundary is noted
![]() .
It can be expressed in terms of the above
quantities:
.
It can be expressed in terms of the above
quantities:
At the outer boundary,
![]() ,
Eq. (26) together with Eqs. (27) and (28) yields:
,
Eq. (26) together with Eqs. (27) and (28) yields:
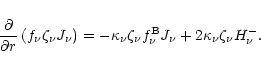 |
(50) |
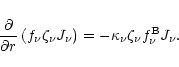 |
(51) |
At the inner boundary r=r0,
in the same way the boundary condition can be expressed as:
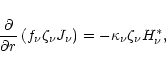 |
(52) |
There are various contributions to
![]() :
:
- The flux
![]() ,
where
,
where
![]() is the flux of photons from the
star, assumed to be that of a Planck function
is the flux of photons from the
star, assumed to be that of a Planck function
![]() (blackbody of temperature
(blackbody of temperature ![]() )
with a dilution
factor of
)
with a dilution
factor of
![]() ,
where
,
where ![]() is the stellar
radius.
is the stellar
radius.
![]() corresponds to the re-emitted and scattered photons
from the dust shell which cross
the inner cavity (
corresponds to the re-emitted and scattered photons
from the dust shell which cross
the inner cavity (
![]() )
and re-enter the dust shell.
The contribution of
)
and re-enter the dust shell.
The contribution of
![]() is taken into account by Leung (1976) in the radiative transfer calculation.
is taken into account by Leung (1976) in the radiative transfer calculation.
- The flux
![]() correspond to the re-emitted and scattered photons
from the dust shell which cross the inner
boundary in the reverse direction.
correspond to the re-emitted and scattered photons
from the dust shell which cross the inner
boundary in the reverse direction.
![]() For ray equations.
For ray equations.
The boundary conditions associated with Eq. (38) are:
At the surface
![]() ,
,
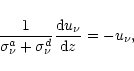 |
(53) |
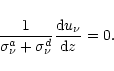 |
(54) |
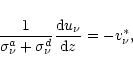 |
(55) |
At each step of the iteration scheme concerning the radiative transfer,
![]() is determined as:
is determined as:
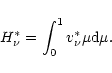 |
(56) |
We solve the radiative transfer problem as a two-point boundary value problem.
Using two auxiliary functions - the Eddington factor ![]() and the sphericity function
and the sphericity function
![]() ,
which respectively characterize the
anisotropy of the radiation field,
the geometry of the problem (and depend on
,
which respectively characterize the
anisotropy of the radiation field,
the geometry of the problem (and depend on ![]() )
- we transform the equation of radiation transport
into a quasi-diffusion equation. The "Quasi-Diffusion Method'' essentially consists in two parts:
assuming the radiation field
isotropic, i.e., setting
)
- we transform the equation of radiation transport
into a quasi-diffusion equation. The "Quasi-Diffusion Method'' essentially consists in two parts:
assuming the radiation field
isotropic, i.e., setting ![]() ,
,
![]() and
and
![]() ,
we solve a set of moment and energy-balance
equations to determine
,
we solve a set of moment and energy-balance
equations to determine ![]() ,
,
![]() and then the source function.
We then find the angular
distribution of the radiation field using a ray-tracing method and hence update
and then the source function.
We then find the angular
distribution of the radiation field using a ray-tracing method and hence update
![]() ,
,
![]() and
and
![]() .
Even anisotropic scattering can easily be taken into account.
.
Even anisotropic scattering can easily be taken into account.
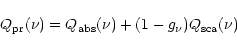 |
(57) |
In the case of an optically thin medium,
the Eddington flux H is that of a blackbody:
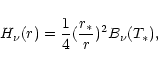 |
(59) |
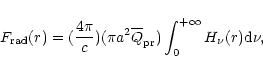 |
(60) |
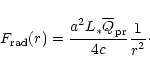 |
(63) |
Since attention is drawn mainly to dynamics we arbitrarily take ![]() m
which is a likely grain size. The values of
m
which is a likely grain size. The values of
![]() ,
,
![]() and
and ![]() are those for graphite grains
from Draine (1985).
With these values at
are those for graphite grains
from Draine (1985).
With these values at
![]() ,
,
![]() .
.
For optically thin media, iterations start with this expression of the radiative force. It will also be useful to compare the model based on this force profile to the full solution.
In these cases we compute the optical depth at some frequency of
reference
![]() .
This frequency has been choosen in the spectral range where the radiative force
is most efficient (
.
This frequency has been choosen in the spectral range where the radiative force
is most efficient (
![]() ), that is to say in a spectral zone where
), that is to say in a spectral zone where
![]() is maximum.
Hence, we will denote the optical depth at the
frequency reference by
is maximum.
Hence, we will denote the optical depth at the
frequency reference by
![]() .
.
Due to the coupling of dynamics with radiative transfer, the numerical solution
in any of the three considered dynamical regimes requires iterations.
After assuming a radiative pressure profile we first look for the velocity profile,
then determine the radiative pressure profile from the radiative transfer in a given velocity/density
field. The process is then repeated.
At each step of iterations (indexed by some integer n), dynamics is governed by
an equation with a critical point at
![]() ,
but at various radial
distances
,
but at various radial
distances
![]() .
The solution of the problem
will be found if convergence of the iterative scheme is obtained.
In this case,
.
The solution of the problem
will be found if convergence of the iterative scheme is obtained.
In this case,
![]() tends to a limit say
tends to a limit say ![]() (where the velocity is equal
to the sound velocity).
(where the velocity is equal
to the sound velocity).
Using Eq. (16) with Eqs. (1) and (3)
we obtain a wind equation of the form:
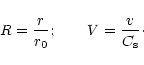 |
(66) |
This is a wind equation similar to that of Parker (1958,1960a,b)
for solar wind with a critical point at
V=1,
![]() which is a saddle point.
The only solution with pressure reaching zero at infinity
is the transsonic critical solution
that crosses the sonic point
(V=1) with an outwardly increasing velocity.
Velocity is subsonic at the base of the wind
and the gas pressure falls to zero at infinity (Mihalas 1978).
which is a saddle point.
The only solution with pressure reaching zero at infinity
is the transsonic critical solution
that crosses the sonic point
(V=1) with an outwardly increasing velocity.
Velocity is subsonic at the base of the wind
and the gas pressure falls to zero at infinity (Mihalas 1978).
At each step of iteration the wind has the same topological structure as a coronal wind. The topology of the solutions ensures numerical stability, provided the integration is started slightly from the right and left of the critical point.
The critical (sonic) radius ![]() ,
where
,
where
![]() ,
is the solution of the equation:
,
is the solution of the equation:
In comparison with the isothermal model of solar wind studied by Parker (1958,1960a,b), we can write Eq. (68) as:
It is obvious that under the position coupling approximation,
the critical distance ![]() is smaller than
is smaller than
![]() ,
which,
due to the difference of temperatures (absence of corona),
does not actually implies that
,
which,
due to the difference of temperatures (absence of corona),
does not actually implies that ![]() is smaller in the
case of an evolved star, than for the solar wind.
is smaller in the
case of an evolved star, than for the solar wind.
If the medium is considered as optically thin, the radiative
force varies as R-2, and the position of the sonic point is:
![]() .
Using a radiative pressure derived from a radiative transfer code, we solve Eq. (69) using a classical numerical method.
If Eq. (69) has no solution, it is impossible to find a sonic point in the circumstellar envelope. If there is more than
one solution, there is a sonic point which exists as a critical point and also a point for which the gradient of the velocity is
zero and beyond which the velocity begins to decrease before once again increasing. This case will be investigated in more detail
in a forthcoming paper.
.
Using a radiative pressure derived from a radiative transfer code, we solve Eq. (69) using a classical numerical method.
If Eq. (69) has no solution, it is impossible to find a sonic point in the circumstellar envelope. If there is more than
one solution, there is a sonic point which exists as a critical point and also a point for which the gradient of the velocity is
zero and beyond which the velocity begins to decrease before once again increasing. This case will be investigated in more detail
in a forthcoming paper.
Now, we want to study only models with one solution for Eq. (69).
The velocity gradient at the sonic point is given by the l'Hospital's rule:
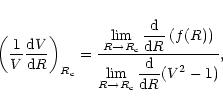 |
(70) |
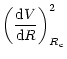 |
= | 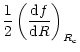 |
|
| = | 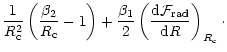 |
(71) |
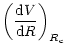 |
= | 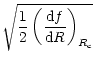 |
(72) |
| = | 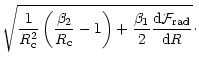 |
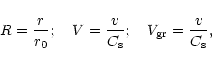 |
(74) |
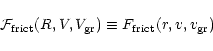 |
(76) |
 |
(77) |
To find ![]() ,
where
,
where
![]() ,
we need to solve the non-linear equation:
,
we need to solve the non-linear equation:
Then we can distinguish two cases.
![]() Momentum coupling.
Momentum coupling.
Here we analyse the case of momentum coupling using Eq. (17). A priori it would be more fitting to use Eq. (18) which includes gravity. In fact all calculations performed in this case reveal that the difference between the relevant results is very small whereas the equations and computation are much less lengthy. For this reason, we analyse only the case where grain mass is neglected.
Using Eq. (11), with dimensionless variables,
the degenerated form of Eq. (17) for grains becomes:
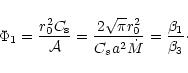 |
(83) |
![$\displaystyle B(R_{\rm c}, V_{\rm gr_c}) = - \frac{\beta_3}{2}\frac{1}{R_{\rm c...
...r_c}}\right)\left( 1 + \frac{F_{\rm c}}{H_{\rm c}}\right)
- H_{\rm c} \right] ,$](/articles/aa/full/2001/38/aa9916/img229.gif) |
(88) |
![$\displaystyle D(R_{\rm c},V_{\rm gr_c}) = -\frac{1}{R_{\rm c}^2}\left( \frac{\b...
...\rm d}g(R)}{{\rm d}R}\right)_{R_{\rm c}} -\frac{2F_{\rm c}}{R_{\rm c}}\right]
,$](/articles/aa/full/2001/38/aa9916/img230.gif) |
(89) |
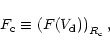 |
(90) |
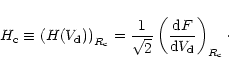 |
(91) |
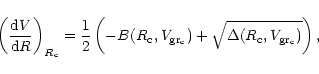 |
(92) |
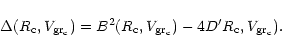 |
(93) |
Numerical integration can be performed in the case of Position Coupling.
A test on the gradient velocity at each point
is made to ascertain whether it is positive or negative. In the cases where this quantity is negative,
an instability, characterised by an inverse gradient pressure, arises and develops
at each iteration step leading to a divergence.
![]() Full problem.
Full problem.
When the momentum coupling approximation is relaxed,
the problem described by Eq. (78)
and Eq. (5) reads:
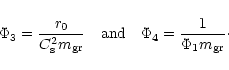 |
(95) |
The model now becomes much more complicated. We have now two independent variables V and
![]() .
In the three dimensional space
.
In the three dimensional space
![]() ,
there is a line of points solutions of
Eq. (81) located in the plane V=1. On part of this line the critical points are
saddle points. The solution to our problem will be sought among the critical wind-type solutions
which pass through these saddle points. The boundary condition at the base of the wind (
,
there is a line of points solutions of
Eq. (81) located in the plane V=1. On part of this line the critical points are
saddle points. The solution to our problem will be sought among the critical wind-type solutions
which pass through these saddle points. The boundary condition at the base of the wind (
![]() )
will allow us to make a unique determination.
)
will allow us to make a unique determination.
Using Eq. (92), Eq. (81) may be written as:
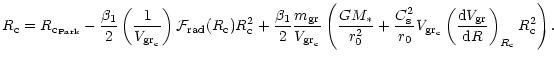 |
(96) |
A numerical solution can be found using a shooting-splitting method described by Berruyer & Frisch (1983). We used this method in the case of optically thick media.
Two gradients (grains and gas velocities) are required.
The gradient of the grains velocity in ![]() can be deduced from Eq. (92):
can be deduced from Eq. (92):
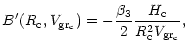 |
(99) |
![$\displaystyle D'(R_{\rm c}, V_{\rm gr_c}) = -\frac{1}{R_{\rm c}^2}\left( \frac{...
...}V_{\rm gr}}{{\rm d}R}\right)_{R_{\rm c}}
-\frac{2F_{\rm c}}{R_{\rm c}}\right].$](/articles/aa/full/2001/38/aa9916/img244.gif) |
(100) |
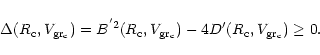 |
(102) |
At first, we look for that part of the critical line where
![]() .
For each
.
For each ![]() in this
line, we derive
in this
line, we derive
![]() from Eq. (81),
from Eq. (81),
![]() from Eq. (95) and
from Eq. (95) and
![]() from Eq. (98).
It is possible to perform integration inwards.
The method of shooting-splitting
enables us to find out the transsonic solution among these curves,
for each possible choice of
from Eq. (98).
It is possible to perform integration inwards.
The method of shooting-splitting
enables us to find out the transsonic solution among these curves,
for each possible choice of ![]() .
.
The shooting-splitting method is carried out until the relation (82) between the gas and
the grain velocities is satisfied, with an accuracy roughly equal to that of the
shooting-splitting method. Henceforth, we shall refer to the point where this limit is reached as ![]() .
.
When dynamics is coupled with the radiative transfer, the main difficulty encountered is the uncertainty of the existence of a critical point and a transsonic solution at each iteration. It is possible, for instance, to find a critical point which has a saddle configuration, but a negative gradient velocity for grains or gas in the subsonic part of the wind.
The Momentum Coupling Hypothesis can be used to determine an initial profile for the full problem and allow a preliminary research of models with solutions.
Details of the numerical procedure used to solve the radiative transfer equations developed in sect. 3.1.1 are described by Leung (1976). The special form of the linearized equations allows us to use an efficient algorithm devised by Rybicki (1971). Explanations on the radiative transport code can be found in Spagna & Leung (1983) and Egan et al. (1988).
Let us summarize the main steps of the solution. The differential equations described in Sect. 3.1.1 are solved numerically using the finite differences method. In particular, since the moment and energy balance equations are nonlinear, they are solved using an iterative scheme similar to the Newton-Raphson method, which includes the following steps:
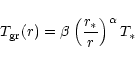 |
(103) |
An improvement is obtained by starting with
the profile of
![]() in an optically thin circumstellar envelope.
For subsequent more opaque models, we simply use the temperature distribution calculated in the previous model
as the starting solution.
This provides an extremely smooth and efficient scheme.
in an optically thin circumstellar envelope.
For subsequent more opaque models, we simply use the temperature distribution calculated in the previous model
as the starting solution.
This provides an extremely smooth and efficient scheme.
Coupling grain-gas dynamics with radiative transfer is difficult because of the different natures of the two physical problems. More specifically, dynamics is a local problem whereas radiative transfer is a global one. Thus, the solution of the radiative transfer uses an iterative scheme with an imposed radial grid, while the solution of dynamics requires the generation of a variable grid (with variable steps) together with the integration. A code was built in order to couple dynamics with radiative transfer through an iterative scheme. This not only allowed dynamical results to be used as an input in the transfer, but also, conversely, transfer results to be used as an input for dynamics. An initial radiative pressure profile is given to the dynamical code which provides a velocity profile, and then from this a number density profile of dust grains as an input of the radiative transfer code. Then we calculate opacities necessary to deduce a new radiative pressure profile, and so on, until convergence of the global iterative scheme is obtained.
This scheme is sketched in Fig. 1 which shows that,
in order to couple
the two codes, we calculate the density profile
![]() ,
obtained in the radial grid of the dynamics by interpolation, into the radial grid of the transfer.
We also want to obtain the profile of radiative force
,
obtained in the radial grid of the dynamics by interpolation, into the radial grid of the transfer.
We also want to obtain the profile of radiative force
![]() at each new step in the grid of dynamics as results from the integration.
at each new step in the grid of dynamics as results from the integration.
For these two calculations, we use the piecewise Cubic Splines numerical method (Mathews 1992). The principle is to construct a cubic function on each interval so that the resulting piecewise curve and its first and second derivatives are all continuous on the larger interval which includes the dimension of the circumstellar envelope. This method is used to "piece together'' the graphs of lower-degree polynomials. This allows for good accuracy in our calculations, with a no wiggling graph. Another advantage is to have one Spline function on each interval, and the values of the radiative force at each point of the envelope without having to define the radial grid of dynamics before the integration. The calculus of the coefficients S(i,j) (indicated in Fig. 1) of these cubic polynomes can be found in Mathews (1992).
Another numerical difficulty is encountered in the generation of the radiative transfer's fixed radial grid.
Indeed, with most finite-difference methods, the succes of the transfer code's iterative scheme
depends on the proper choice of spatial grid. As we are solving
a boundary value problem, the boundary conditions must be satisfied accurately. In order that
information be transmitted correctly at the interior points, it is necessary that near
the boundaries,
![]() ,
the optical depth in a layer of the dimension of the considered
step be markedly less than one for the most opaque part of the spectrum.
Away from the boundaries, no such
constraint exists and larger
,
the optical depth in a layer of the dimension of the considered
step be markedly less than one for the most opaque part of the spectrum.
Away from the boundaries, no such
constraint exists and larger
![]() can be used. It is also essential
that the radial increment
can be used. It is also essential
that the radial increment ![]() be small enough to ensure uniform
accuracy of the results. In regions where the source function varies rapidly, the number of radial steps
must also be increased (Leung 1976).
be small enough to ensure uniform
accuracy of the results. In regions where the source function varies rapidly, the number of radial steps
must also be increased (Leung 1976).
Thus, at each iteration of the iterative system coupling dynamics with transfer, we must conduct numerical tests to check whether our previous choice of spatial grid was suitable for the new iteration.
| |
Figure 1: General numerical scheme concerning our three models (position coupling, momentum coupling and full problem) coupled with the transfer. |
| Open with DEXTER | |
Table 1 indicates the input parameters for two models, the
Position Coupling Hypothesis (PCH) and Momentum Coupling Hypothesis (MCH),
for which only the mass loss rate (
![]() )
of the dust grains is different.
The inner and the outer radii are expressed in units of the
stellar radius. This radius is deduced
from the stellar luminosity
)
of the dust grains is different.
The inner and the outer radii are expressed in units of the
stellar radius. This radius is deduced
from the stellar luminosity ![]() and the stellar effective temperature
and the stellar effective temperature ![]() with the expression
with the expression
![]() where
where ![]() is the
Stefan-Boltzmann constant.
We use the stellar radius for the purpose of the discussion, but in order to improve numerical stability
the numerical calculations for the dynamics use the inner radius R0 as a unit.
Table 2 lists some output physical quantities for both models (PCH and MCH).
is the
Stefan-Boltzmann constant.
We use the stellar radius for the purpose of the discussion, but in order to improve numerical stability
the numerical calculations for the dynamics use the inner radius R0 as a unit.
Table 2 lists some output physical quantities for both models (PCH and MCH).
With the same
![]() for PCH and MCH, it is impossible in both cases to find
a solution where the limit
for PCH and MCH, it is impossible in both cases to find
a solution where the limit ![]() of the critical point
of the critical point
![]() ,
if this limit exists, remains greater than r0. This is a very good first example of the much marked
differences between PCH and MCH.
,
if this limit exists, remains greater than r0. This is a very good first example of the much marked
differences between PCH and MCH.
| INPUT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| PCH: |
|
|
|
|
| MCH: |
|
|
|
|
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[]{CourbePSTPAPIER2.eps}}\end{figure}](/articles/aa/full/2001/38/aa9916/Timg282.gif) |
Figure 2:
Velocity profiles for the grains (
|
| Open with DEXTER | |
| OUTPUT | PCH | MCH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.75 |
|
|
|
3.21 | 5.93 |
|
|
0.75 | 5.60 |
|
|
3.21 | 57.02 |
|
|
1.00 | 22.00 |
|
|
7.00 | 7.00 |
|
|
0.090 | 0.107 |
First, let us note that in order to find the same limit ![]() in both cases,
the mass loss rate of dust grains (
in both cases,
the mass loss rate of dust grains (
![]() )
in PCH must be taken very
low compared to the mass loss rate of the gas (
)
in PCH must be taken very
low compared to the mass loss rate of the gas (![]() ); indeed, the mass loss rate
ratio
); indeed, the mass loss rate
ratio
![]() is very high
(whereas one would expect a few 102).
Furthermore, to estimate the minimum of this ratio in PCH (such
that
is very high
(whereas one would expect a few 102).
Furthermore, to estimate the minimum of this ratio in PCH (such
that
![]() ), we use
the R-2 law (64) for
radiative force in an optically thin medium.
For carbon grains, all the numerical computations show that the solution
), we use
the R-2 law (64) for
radiative force in an optically thin medium.
For carbon grains, all the numerical computations show that the solution
![]() ,
for each R.
Since
,
for each R.
Since
![]() ,
for
,
for
![]() ,
the critical radius Eq. (69) is:
,
the critical radius Eq. (69) is:
The model using MCH enables us to explain this undersized value of
![]() when we use PCH.
To do this, we solve the self-consitent problem with the two assumptions MCH and PCH in such a way that the
solutions give rise to the same sonic point (cf. Fig. 2).
To obtain this result, we use
the same set of input parameters (cf. Table 1),
except
when we use PCH.
To do this, we solve the self-consitent problem with the two assumptions MCH and PCH in such a way that the
solutions give rise to the same sonic point (cf. Fig. 2).
To obtain this result, we use
the same set of input parameters (cf. Table 1),
except
![]() .
.
![]() is found equal to
is found equal to
![]() with MCH,
which correspond to a mass loss rate ratio of
with MCH,
which correspond to a mass loss rate ratio of
![]() (cf. Table 1). This
mass loss rate ratio is much more realistic, emphasizing that the drift
velocity between the grains and the gas must be taken into account when
dynamics is coupled with radiative transfer.
(cf. Table 1). This
mass loss rate ratio is much more realistic, emphasizing that the drift
velocity between the grains and the gas must be taken into account when
dynamics is coupled with radiative transfer.
The difference between the two models (PCH and MCH) is obvious
when comparing the sonic point Eq. (69) with Eqs. (84) and (86). Since, with our choice of parameters, both solutions are optically thin,
the two radiative force profiles are very similar
to the R-2 law. In this case, the only difference between the two equations comes
from the ratio of densities
![]() ,
which
corresponds exactly to
,
which
corresponds exactly to
![]() for PCH and to
for PCH and to
![]() for MCH.
Since we have the same critical point, the ratio of densities is also
the same at
for MCH.
Since we have the same critical point, the ratio of densities is also
the same at
![]() ,
which implies different mass loss rate ratios.
With the value of
,
which implies different mass loss rate ratios.
With the value of
![]() of table 2,
of table 2,
![]() ,
which is the value of
the mass loss rate of the grains in PCH.
,
which is the value of
the mass loss rate of the grains in PCH.
Furthermore, if the two ratios of densities are identical at
![]() ,
they can not be
equal at another point in the circumstellar envelope due to the increase of the drift velocity with R (see Fig. 2 where velocities of gas and grains are plotted). For the PCH
model, this ratio is constant. This indicates that the density of grains relative to that of the gas
varies with the radial distance, which suggests that drift velocity changes not only
the results for velocity profiles but also all the physical conditions in the whole envelope. This has
substantial consequences for thermodynamical conditions for instance, but also in the study of nucleation
and growth of dust grains, or the propagation of shock waves.
,
they can not be
equal at another point in the circumstellar envelope due to the increase of the drift velocity with R (see Fig. 2 where velocities of gas and grains are plotted). For the PCH
model, this ratio is constant. This indicates that the density of grains relative to that of the gas
varies with the radial distance, which suggests that drift velocity changes not only
the results for velocity profiles but also all the physical conditions in the whole envelope. This has
substantial consequences for thermodynamical conditions for instance, but also in the study of nucleation
and growth of dust grains, or the propagation of shock waves.
At the outer limit of the envelope, the ratio of the terminal
velocities of grains (noted
![]() in Table 2) for MCH and PCH
is comparable to the ratio of the mass
loss rates of dust grains. This indicates that the number
densities of grains in the two models become closer when the radial distance increases,
contrarily to those of the gas, since the terminal velocity of the gas (
in Table 2) for MCH and PCH
is comparable to the ratio of the mass
loss rates of dust grains. This indicates that the number
densities of grains in the two models become closer when the radial distance increases,
contrarily to those of the gas, since the terminal velocity of the gas (![]() )
under MCH is lower than that of grains by a factor ten.
)
under MCH is lower than that of grains by a factor ten.
It is also interesting to make a further comparison. In Table 4, we replace
the mass loss rate for dust under MCH
(
![]() yr) with that previously chosen under PCH
(
yr) with that previously chosen under PCH
(
![]() yr). In this
case, convergence is impossible because as early as at the first step
in the MCH model, the optical
depth is very high and unrealistic (about 5000). The critical point is close to that
of the thermal wind model. In fact, if this model could converge, the position of the critical point
would be farther than in PCH because of the decrease in radiative force for a thick medium.
This confirms the large difference between the two approximations.
With MCH, the medium will be more opaque.
yr). In this
case, convergence is impossible because as early as at the first step
in the MCH model, the optical
depth is very high and unrealistic (about 5000). The critical point is close to that
of the thermal wind model. In fact, if this model could converge, the position of the critical point
would be farther than in PCH because of the decrease in radiative force for a thick medium.
This confirms the large difference between the two approximations.
With MCH, the medium will be more opaque.
It is, nevertheless, much easier with PCH than with MCH to explore coupling between dynamics and radiative transfer. With this assumption we can determine many fields of investigation and speculate about effects of dust grains on radiative transfer and mass loss. This interesting study will be the subject of our next paper. It will allow us to improve significantly the exploration of self-consistent models that take into account drift velocity.
| INPUT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| OUTPUT | thin | thick |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44.30 | 35.54 |
|
|
2.62 | 2.37 |
|
|
72.77 | 55.54 |
|
|
35 | 43 |
|
|
0.40 | 1.25 |
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[]{CourbeMCHPAPIER2.eps}}\end{figure}](/articles/aa/full/2001/38/aa9916/Timg342.gif) |
Figure 3:
Solutions of the MCH model. We note A the optically thin
solutions, i.e. obtained with the R-2 for the radiative force.
Solutions B are obtained with the self-consistent calculation.
The radial distance is expressed in units of the stellar radius (
|
| Open with DEXTER | |
Let us now continue looking at self-consistent models using MCH for which the solution is optically thick.
In Table 3 physical input parameters are listed for a new self-consistent model
that will be compared to the model which ignores radiative transfer
(where
![]() ). This model corresponds
to the first step of iterations. Hereafter we shall call it the "R-2 model''.
). This model corresponds
to the first step of iterations. Hereafter we shall call it the "R-2 model''.
Table 4 gives a few output physical quantities:
the column "thin'' (respectively "thick'') displays results of the R-2
model (respectively the self-consistent one).
It is worth noting that the R-2 model suggests that the medium may be optically thin since the optical
depth
![]() ,
but that after this first step
the final solution of the self-consistent model is
,
but that after this first step
the final solution of the self-consistent model is
![]() .
The circumstellar envelope is in fact optically thick.
The R-2 model, therefore, does not accurately approximate the self-consistent model.
The differences between
the two approaches are highly significant. Most of the results in Table 4 confirm this.
.
The circumstellar envelope is in fact optically thick.
The R-2 model, therefore, does not accurately approximate the self-consistent model.
The differences between
the two approaches are highly significant. Most of the results in Table 4 confirm this.
In Fig. 3 we compare the self-consistent optically thick solution (indexed by B) with the R-2
model (indexed by A).
Profiles of grain velocity
![]() ,
gas velocity V, dust number density
,
gas velocity V, dust number density
![]() and radiative force
and radiative force
![]() are sketched.
are sketched.
![]() and
and
![]() are drawn
solely in the subsonic part of the wind to highlight the zone where differences between models A and B
for these two quantities are greater.
are drawn
solely in the subsonic part of the wind to highlight the zone where differences between models A and B
for these two quantities are greater.
We see that the relative diminution of
![]() in model B compared to model A
is amplified with increasing R in the innermost part of the envelope. In this region,
in model B compared to model A
is amplified with increasing R in the innermost part of the envelope. In this region,
![]() of
model B is higher than
of
model B is higher than
![]() of model A,
especially at the inner boundary where, after coupling with radiative transfer,
the density is multiplied by a factor of about 3. The density in the inner part of the wind is very sensitive to the variations in radiative force. The effect of dust grains on radiative pressure
is an attenuation by absorption and scattering of the radiation. Thermal emission by the grains is not
efficient because the maximum emission is in the infra-red spectral region, where the undimensioned
cross section of radiative pressure
of model A,
especially at the inner boundary where, after coupling with radiative transfer,
the density is multiplied by a factor of about 3. The density in the inner part of the wind is very sensitive to the variations in radiative force. The effect of dust grains on radiative pressure
is an attenuation by absorption and scattering of the radiation. Thermal emission by the grains is not
efficient because the maximum emission is in the infra-red spectral region, where the undimensioned
cross section of radiative pressure
![]() is low and also because the field is very isotropic.
On the other hand, multiple scattering may be able to
increase the radiative force, but our results show that absorption does inhibit such an effect.
is low and also because the field is very isotropic.
On the other hand, multiple scattering may be able to
increase the radiative force, but our results show that absorption does inhibit such an effect.
Furthermore, at R=R0,
![]() is attenuated by the radiation
coming from the inner layers of the dust envelope. In our model, we make
a sharp separation between the thick medium, where dust grains exist, and the thin medium where we have just
gas between the star and the circumstellar envelope. The radiation coming from the envelope at
R=R0, therefore, is no more isotropic and can play a significant role when cumulated with the effect of all grains in a sphere
of radius larger than R0 by about the mean free path.
We may be inclined to expect that for an optically thicker medium this mean
free path would be small and that the net Eddington flux at R=R0 would decrease,
but the number density of grains is actually greater
and allows this increase of the radiative flux. In fact, the amount of inward flux close to R0 depends
on the number of grains rather than the size of the region emitting photons, all the more so as when R increases,
temperature and thermal emission of the dust grains decrease.
is attenuated by the radiation
coming from the inner layers of the dust envelope. In our model, we make
a sharp separation between the thick medium, where dust grains exist, and the thin medium where we have just
gas between the star and the circumstellar envelope. The radiation coming from the envelope at
R=R0, therefore, is no more isotropic and can play a significant role when cumulated with the effect of all grains in a sphere
of radius larger than R0 by about the mean free path.
We may be inclined to expect that for an optically thicker medium this mean
free path would be small and that the net Eddington flux at R=R0 would decrease,
but the number density of grains is actually greater
and allows this increase of the radiative flux. In fact, the amount of inward flux close to R0 depends
on the number of grains rather than the size of the region emitting photons, all the more so as when R increases,
temperature and thermal emission of the dust grains decrease.
Furthermore, beyond a few stellar radii in the envelope, and after a strong decrease,
the number densities of both models are very close, but the influence
of the inner part of the wind (in a zone lower than the subsonic region) remains
effective over the whole envelope (cf. the velocities profiles).
Indeed, grain and gas velocities are lower for solution B:
the dust velocity profile is roughly about 1/3 below the solution A. Precisely
the terminal velocities
![]() for solution A and
for solution A and
![]() for solution B.
for solution B.
Grains increase the wind velocity, driving the gas by friction, but they also attenuate the effect of radiative force through the effects of radiative transfer. This highlights two antagonistic mechanisms involving the dust grains.
Another effect on the wind structure appears in the self-consistent problem. The decrease
in grain velocity between models A and B is greater than that of the gas, as is shown by
the terminal velocities values for the two components (cf. Table 4).
Let us remember that MCH consists of identifying
radiative force and frictional force,
so that frictional force decreases as soon as radiative force does so.
Frictional force is proportional to the gas density and a function that increases with
drift velocity. Because of the simultaneous
decrease in gas velocity when the radiative force decreases,
the density of the gas increases for a given position. Thus the drift velocity ![]() must also decrease in a self-consistent model.
must also decrease in a self-consistent model.
So when the medium becomes more opaque, not only do
![]() and V decrease but also
and V decrease but also ![]() .
This is why the
effect of radiative transfer on dynamics is higher for the grain velocity than for that of the gas. This
shows that values of the terminal velocities of gas in models A and B are very close.
.
This is why the
effect of radiative transfer on dynamics is higher for the grain velocity than for that of the gas. This
shows that values of the terminal velocities of gas in models A and B are very close.
| OUTPUT | thin | thick |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43.58 | 32.78 |
|
|
2.59 | 2.29 |
|
|
69.28 | 49.11 |
|
|
35.79 | 45.55 |
|
|
17.58 | 20.45 |
|
|
0.42 | 1.69 |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[]{Courbe2PAPIER2.eps}}\par\end{figure}](/articles/aa/full/2001/38/aa9916/Timg362.gif) |
Figure 4:
Velocity profiles of dust grain (
|
| Open with DEXTER | |
Table 5 is as Table 4, but for
the full problem (FPB).
We can note that
![]() .
In fact, the initial values of
.
In fact, the initial values of
![]() and V are the same, but they rapidly differ through a boundary layer (see the paper
by Berruyer & Frisch 1983). Since the radial dimension
and V are the same, but they rapidly differ through a boundary layer (see the paper
by Berruyer & Frisch 1983). Since the radial dimension ![]() of this boundary layer is
very small, r0 and
of this boundary layer is
very small, r0 and
![]() are practically identical, when compared with other useful scales.
Differences between the thin model and the thick model are amplified. The shift in the
sonic points is larger in the full problem than in the case of MCH and
the increase in the optical depth is greater still.
The first conclusion we can draw, therefore, is that with a self-consistent treatment,
dynamics requires the solution of the full problem.
are practically identical, when compared with other useful scales.
Differences between the thin model and the thick model are amplified. The shift in the
sonic points is larger in the full problem than in the case of MCH and
the increase in the optical depth is greater still.
The first conclusion we can draw, therefore, is that with a self-consistent treatment,
dynamics requires the solution of the full problem.
In Fig. 4 this conclusion is still more obvious. When we compare thin models (MCH and FPB) with thick models, we see that the differences between velocities increase. When the medium is more opaque, the effects of the inertial force become marked compared with other terms of the momentum transfer for dust grains.
Furthermore, the radius ![]() increases but
the dimension
increases but
the dimension
![]() of that region where
the equation is not degenerated is greater and
the inertial force is efficient over a greater part of the subsonic zone of the wind.
The zone where MCH can be used also increases in size.
of that region where
the equation is not degenerated is greater and
the inertial force is efficient over a greater part of the subsonic zone of the wind.
The zone where MCH can be used also increases in size.
We can highlight the greater difference between the two models when the medium is more opaque by considering the double effects of the inertial force. At first, this force decreases the dust grains and gas velocity. Moreover, according to Eq. (4) (mass conservation for dust grains), when dust grains velocity decreases, their density increases. An increased density in radiative transfer leads to a lower radiative force and then to a still lower velocity. In the self-consistent model, both mechanisms due to the inertial force work to reduce the velocity.
Finally, the effect of radiative transfer on the drift velocity described for MCH is amplified under FPB conditions. A part of the momentum given to the grains by the radiative force is transferred to the gas while another part is used to overcome inertia and gravitationnal forces. For a given radiative force, we have a lower frictional force, and, since radiative force is also lower, velocity is lower, density is greater, and drift velocity is lower at each point of the envelope. Furthermore, since when MCH is relaxed both the gas and the grains have smaller velocities, and the sonic point is located further away from the star, FPB amplifies the faster diminution of grain velocity compared with gas velocity with MCH.
Whatever the choice for the treatment of dynamics, there are cases where the coupling with radiative transfer can produce fairly strong effects. The presented two-fluid, self-consitent models for dust driven winds show that the optical depth of the circumstellar envelope, even if very small, plays a highly significant role in dynamics. Depending on whether the medium is optically thick or not, solutions with different features are obtained. The roles of the drift velocity and the inertial force appear emphasized. In particular, the inclusion of drift velocities changes the mass ratio of dust grains to gas with the radial distance. Nonetheless, models using position coupling are very useful as tools for numerical experiments.
Wind structure, especially at the base of the envelope, is very sensitive to change in the radiative force profile, in particular through the number density of dust grains which determines the radiative force and the optical depth. When the medium becomes more opaque, the outwards flux is weakened and so the radiative force is weakened.
Grains accelerate the wind by friction with the gas but they can also weaken the radiative force, so that the presence of dust grains has two antagonistic effects on the wind structure.
The grain velocity is more sensitive than that of gas to the coupling with the radiative transfer. This effect is amplified under conditions of the full problem.
Including inertial force into the models decreases velocities and increases densities essentially in the inner part of the envelope. Those effects are amplified with the self-consistent model.
Acknowledgements
Part of this work has been performed using the computing facilities provided by the program "Simulations Interactives et Visualisation en Astronomie et Mécanique (SIVAM)''.At each step of iterations, we determined the radiative force profile from the solution of the radiative transfer obtained using the code of Leung (1976) who can be thanked for leaving this code for public use.
The authors would like also to thank Dr. Rubens Freire for several helpful discussions.