4 Statistical analysis

Figure 10: DCF autocorrelations for the optical and UMRAO radio fluxes shown in Fig. 8; the data have been binned over 2 days, while the DCF was obtained with a bin size of 25 days.

In this section we apply the Discrete Correlation Function (DCF) analysis to the data shown in Fig. 8 in order to investigate the existence of characteristic time scales of variability and of optical-radio correlations.

The DCF is a method specifically designed for unevenly sampled datasets (Edelson & Krolik 1988; Hufnagel & Bregman 1992), which also allows an estimate of the accuracy of its results.

Given two datasets a_i and b_j, one has first to combine all pairs, calculating the unbinned discrete correlations:

$${\rm UDCF}_{ij}={{(a_i- \overline a)(b_j- \overline b)} \over {\sigma_a \sigma_b}},$$

where $\overline a$, $\overline b$ are the average values of the two datasets, and $\sigma_a$, $\sigma_b$ their standard deviations. The DCF is obtained by binning the ${\rm UDCF}_{ij}$ in time for each time lag $\tau$:

$${\rm DCF} (\tau)= {1 \over M} \sum {\rm UDCF}_{ij}(\tau),$$

where M is the number of pairs a_i, b_j whose time lag $\Delta_{ij}=t_j - t_i$ is inside the $\tau$ bin. Spurious correlations can be found, of the order of $\pm M^{-1/2}$. The standard error for each bin is:

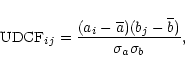
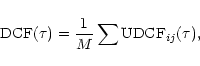
$$\sigma_{\rm DCF} (\tau) = {1 \over {M-1}} \left\{ \sum \left[ {\rm UDCF}_{ij} - {\rm DCF}(\tau) \right] ^2 \right\} ^{1/2}.$$

A positive peak of the DCF means correlation, which is stronger as the value of the peak approaches and exceeds one. A negative peak implies anticorrelation. Moreover, the width of the peak must be comparable to those of the autocorrelation functions, obtained by applying the DCF to each dataset coupled with itself.

A preliminary binning of data in time before calculating the DCF usually leads to better results, smoothing out flickering. The size of this binning is crucial especially in the optical, where short-term variations are frequent, since it can remove important information. Furthermore, an increase of the data binning interval implies an increase of the spurious correlations, while an increase of the DCF bin size has the opposite effect. Also the choice of the DCF binning is a delicate point, determining the balance between resolution and noise. In general, a similar value of M for each DCF bin and a limit of $10\%$ to the appearance of spurious correlations must be assured in order to get reliable results.

Another method frequently used for searching characteristic time scales of variability is the Discrete Fourier Transform (DFT) spectral analysis for unevenly sampled data. We have adopted the implementation of the Lomb normalized periodogram method (Lomb 1976) discussed by Press et al. (1992). The presence of a sinusoidal component of frequency $\omega_0=2 \pi \nu$ in the dataset is revealed by a large value of the periodogram $P(\omega)$ at $\omega = \omega_0$. The significance of the peaks is estimated by the false alarm probability, i.e. the probability that a peak is of height z or higher if the data are pure noise. It is given by $F=1-(1-{\rm e}^{-z})^M$, where M is the number of independent frequencies. Since we have scanned frequencies up to the Nyquist frequency $\nu_{\rm c}=N/(2T)$ that the N data would have were they evenly spaced over the period T, we have set M=N. For very clumpy datasets as we have when considering the optical light curve, the value of M (and hence the false alarm probability) may be overestimated, and the significance of the peaks is consequently underestimated (see also Horne & Baliunas 1986).

4.1 Search for characteristic time scales of variability

The optical DCF autocorrelation is plotted in Fig. 10 (top panel):

Figure 11: The light curve of AO 0235+16 at $8.0\rm ~GHz$ folded assuming a period of 2069 days.

as expected, it is dominated by flicker noise and reveals an important double-peaked signal at $\tau \sim 4100$-4200 days (11.2-11.5 years), and not negligible ones at $\tau \sim 1200$ and $\sim$2100 days ($\sim$3.28 and $\sim$5.75 years). These can thus be regarded as characteristic time scales of optical variability for AO 0235+16. A visual inspection of the optical light curve in Fig. 8 confirms these features.

The peak at $\tau \sim 5000$ days in the optical autocorrelation is just one point affected by a large error, deriving from the correlation between the 1979 and 1992 outbursts.

The fact that the maxima at about $\pm 4200$ days exceed 1 is due to the choice of a 2 day binning on the original dataset; a larger time interval for data binning (e.g. 20 days) would reduce the importance of these features with respect to the central maximum, but would force the choice of a much larger DCF bin ($\sim$100 days) in order to avoid important spurious correlations. This in turn would imply missing important details.

Figure 10 also presents the DCF autocorrelation for UMRAO radio fluxes. The peaks are wider than in the optical case, reflecting the broader outbursts of the radio light curves when compared with the optical ones. An important double-peaked maximum appears at 3900-4200days (10.7-11.5 years) at all three frequencies, whose similarity with the optical one suggests radio-optical correlation. Other noticeable peaks are seen at 5300-5400 and 6100-6200 days (14.5-14.8, 16.7-17.0 years) in the DCF autocorrelation function for the $8.0\rm ~GHz$ band. At $14.5\rm ~GHz$ the former appears reduced, while the latter, deriving mainly from the coupling of the 1975 and 1992 outbursts, is enhanced. At $4.8\rm ~GHz$ both disappear, but in this case the light curve is less extended in time; in particular, the 1975 outburst is totally missing.

As for the Metsähovi radio light curves at 22 and $37\rm ~GHz$, their less dense sampling and more limited time extension lead to higher spurious effects, especially for large values of $\tau$. However, their autocorrelation functions confirm the signal centred at $\tau \sim 4000$ days, and present noticeable peaks at about 2000 days, that is the time separation between the outbursts detected in 1987, 1992, and 1998.

The most interesting point emerging from the above discussion is the $\sim$11.2 year characteristic time scale of variability, which is common to the optical and radio fluxes. By looking at the light curves in Fig. 8, one can understand this result by noticing that at a distance of about 4100 days the 1975 peak correlates with the 1987 one, and this latter with the 1998 flare, while the 1982 outburst correlates with the 1992 one. This means that there seems to be a $\sim$4100 day characteristic variability time scale intersecting another $\sim$4100 day time scale, which on one side is somehow surprising. On the other side, both the optical and the Metsähovi radio autocorrelations suggest that there may be a "periodicity" of about half the above time scale. Indeed, the 25 year time extension of the AO 0235+16 light curves would allow to interpret this halved time scale in terms of periodicity. The point is to understand why UMRAO radio autocorrelation functions do not show a strong signal at $\tau \sim 2050$ days. The reason is that this signal is damped by the delay of the 1982 outburst. Indeed, by looking at the $8.0\rm ~GHz$light curve (Fig. 8), the best sampled one, one can recognize five large-amplitude outbursts peaking at ${\rm JD}-2442000=723.60$, 3031.44, 4901.27, 6908.74, and 9000.00, spaced by 2308, 1870, 2007, and 2091 days, respectively. The average period would thus be $2069\,\pm\, 184$ days, i.e. $5.67\,\pm\, 0.50$ years. The $8.0\rm ~GHz$ light curve folded assuming a period of 2069 days is presented in Fig. 11:

Figure 12: The light curve of AO 0235+16 in the R band folded assuming a period of 2069 days.

the delay of the 1982 outburst is clearly visible.

Notice that a weak signal at about 2000 days is actually present in the $14.5\rm ~GHz$ autocorrelation function because at this frequency the 1982 outburst was preceded by a kind of pre-outburst that made the flux reach a high level earlier than the $8.0\rm ~GHz$ one.

We have checked the reliability of the results obtained by the autocorrelation analysis by means of the Discrete Fourier Transform (DFT) technique for unevenly sampled data implemented by Press et al. (1992). In both the radio and the optical cases we obtained many signals with significance levels F better than 0.001. In particular, the 2069 day periodicity previously inferred is confirmed by the DFT analysis on UMRAO data. At $8.0\rm ~GHz$, a clear maximum ($P\sim 79$) is found at frequencies $\nu \sim 4.8$- $4.9\times 10^{-4} \rm ~ day^{-1}$, corresponding to periods of $\sim$2050-2080 days. Other strong signals in the $8.0\rm ~GHz$ data are found at 3.7, 2.8, and 1.8 years ($P \sim 88$, 46, 45, respectively). At $14.5\rm ~GHz$ the strongest maximum of the Lomb periodogram ($P \sim 81$) is right at $\nu~\sim~\mbox{4.8$-$ 4.9}~\times~10^{-4} \rm ~ day^{-1}$, followed by the maxima ($P \sim 68$, 49, 48) corresponding to 2.8, 1.8, and 3.7 year periods, confirming the results obtained for the $8.0\rm ~GHz$ data. Similar results are also found for the $4.8\rm ~GHz$ dataset.

The DFT technique applied to the optical fluxes gives much more signals, making the spectral analysis rather complex. Surprisingly, the $\sim$2100 day time scale discovered in the optical autocorrelation function and obtained by the DFT analysis of UMRAO data gives only a weak signal (significance level better than $3\%$ only). To better visualize the matter, Fig. 12 shows the optical light curve in the R band folded assuming a 2069 day period. Notice that such a period would not explain some important outbursts, in particular the major outburst observed in 1979. Other signals obtained by the DFT analysis at 2.8 and 1.6-1.9 years confirm the time scales found for the radio fluxes, while there is not a strong optical signal corresponding to the 3.7 years in the radio. The strongest DFT signal corresponds to a $\sim$200 day time scale, which is the time separation between the two peaks observed in the 1997-1998 outburst.

4.2 Optical-radio cross-correlation

The results of the DCF cross-correlation between data in the R band and the $8.0\rm ~GHz$ ones are shown in Fig. 13 (bottom panel): the well-defined positive peak at $\tau \sim 0$-60 days suggests optical-radio correlation, with optical variations that can be both simultaneous and leading the radio ones by a couple of months. The DCF applied to the optical and $14.5\rm ~GHz$ datasets leads to a similar result (see Fig. 13, top panel): the radio variations appear correlated and delayed of 0-50 days with respect to the optical ones. These results are in agreement with what was derived by Clements et al. (1995).

As for the radio-radio correlations, Clements et al. (1995) found no time delay between the 14.5 and $8.0\rm ~GHz$ datasets and between the 8.0 and $4.8\rm ~GHz$ ones. However, as previously discussed, at least during the 1992-1993 and 1998 outbursts, the radio light curves seem to indicate that the flux variation at the higher frequencies may have led that observed at the lower ones. Figure 14 shows the results of the DCF cross-correlation between the 22 and $8.0\rm ~GHz$ fluxes: in the top panel, where all data have been considered, the peak is not exactly centred at $\tau=0$. This might suggest that the $22\rm ~GHz$ fluxes can lead the $8.0\rm ~GHz$ ones by several days. In the bottom panel of Fig. 14 only data after ${\rm JD}=2450300$ were taken into account, so that only the 1998 outburst is considered: the delay effect in this case is enhanced. This is in agreement with what was observed by O'Dell et al. (1988) when analyzing the variability of AO 0235+16 at eight radio frequencies, from $318\rm ~MHz$ to $14.5\rm ~GHz$. They found that flux-density variations are clearly correlated, and events occur first at the higher frequencies and propagate to lower frequencies with decreasing amplitude.