A&A 377, 396-412 (2001)
DOI: 10.1051/0004-6361:20011112

Optical and radio variability of the BL Lacertae object AO 0235+16: A possible 5-6 year periodicity

C. M. Raiteri ¹ - M. Villata ¹ - H. D. Aller ² - M. F. Aller ² - J. Heidt ³ - O. M. Kurtanidze ^4,5 - L. Lanteri ¹ - M. Maesano ⁶ - E. Massaro ⁶ - F. Montagni ⁶ - R. Nesci ⁶ - K. Nilsson ⁷ - M. G. Nikolashvili ⁴ - P. Nurmi ⁷ - L. Ostorero ⁸ - T. Pursimo ⁷ - R. Rekola ⁷ - A. Sillanpää ⁷ - L. O. Takalo ⁷ - H. Teräsranta ⁹ - G. Tosti ¹⁰ - T. J. Balonek ¹¹ - M. Feldt ¹² - A. Heines ³ - C. Heisler ^13, - J. Hu ¹⁴ - M. Kidger ¹⁵ - J. R. Mattox ¹⁶ - E. J. McGrath ¹¹ - A. Pati ¹⁷ - R. Robb ¹⁸ - A. C. Sadun ¹⁹ - P. Shastri ¹⁷ - S. J. Wagner ³ - J. Wei ¹⁴ - X. Wu ¹⁴

1 - Osservatorio Astronomico di Torino, Via Osservatorio 20, 10025 Pino Torinese, Italy
2 - Dept. of Astronomy, Dennison Bldg., U. Michigan, Ann Arbor, MI 48109, USA
3 - Landessternwarte Königstuhl, W-6900 Heidelberg 1, Germany
4 - Abastumani Astrophysical Observatory, Georgia
5 - Astrophysikalisches Institute Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
6 - Dipartimento di Fisica, Università La Sapienza, Roma, P.le A. Moro 2, 00185 Roma, Italy
7 - Tuorla Observatory, 21500 Piikkiö, Finland
8 - Dipartimento di Fisica Generale, Università di Torino, Via P. Giuria 1, 10125 Torino, Italy
9 - Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
10 - Cattedra di Astrofisica, Università di Perugia, Via B. Bonfigli, 06126 Perugia, Italy
11 - Foggy Bottom Observatory, Colgate University, Hamilton, NY, USA
12 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
13 - Mount Stromlo and Siding Spring Observatories, Canberra, Australia
14 - Beijing Astronomical Observatory, Beijing, China
15 - Teide Observatory, Tenerife, Spain
16 - Dept. of Chemistry, Physics, & Astronomy, Francis Marion University, PO Box 100547, Florence, SC 29501-0547, USA
17 - Vainu Bappu Observatory, Indian Institute of Astrophysics, Dept. of Science & Technology, Kavalur, India
18 - Dept. of Physics and Astronomy, University of Victoria, British Columbia, Canada
19 - Dept. of Physics, University of Colorado at Denver, PO Box 173364, Denver, CO 80217-3364, USA

Received 19 June 2001 / Accepted 7 August 2001

Abstract
The BL Lacertae object AO 0235+16 is well known for its extreme optical and radio variability. New optical and radio data have been collected in the last four years by a wide international collaboration, which confirm the intense activity of this source: on the long term, overall variations of $5\rm ~mag$ in the R band and up to a factor 18 in the radio fluxes were detected, while short-term variability up to $0.5\rm ~mag$ in a few hours and $1.3\rm ~mag$ in one day was observed in the optical band. The optical data also include the results of the Whole Earth Blazar Telescope (WEBT) first-light campaign organized in November 1997, involving a dozen optical observatories. The optical spectrum is observed to basically steepen when the source gets fainter. We have investigated the existence of typical variability time scales and of possible correlations between the optical and radio emissions by means of visual inspection and Discrete Correlation Function (DCF) analysis. On the long term, the autocorrelation function of the optical data shows a double-peaked maximum at 4100-4200 days (11.2-11.5 years), while a double-peaked maximum at 3900-4200 days (10.7-11.5 years) is visible in the radio autocorrelation functions. The existence of this similar characteristic time scale of variability in the two bands is by itself an indication of optical-radio correlation. A further analysis by means of Discrete Fourier Transform (DFT) technique and folded light curves reveals that the major radio outbursts repeat quasi-regularly with a periodicity of $\sim$5.7 years, i.e. half the above time scale. This period is also in agreement with the occurrence of some of the major optical outbursts, but not all of them. Visual inspection and DCF analysis of the optical and radio light curves then reveal that in some cases optical outbursts seem to be simultaneous with radio ones, but in other cases they lead the radio events. Moreover, a deep inspection of the radio light curves suggests that in at least two occasions (the 1992-1993 and 1998 outbursts) flux variations at the higher frequencies may have led those at the lower ones.

Key words: galaxies: active - BL Lacertae objects: general - BL Lacertae objects: individual: AO 0235+16

1 Introduction

BL Lacertae objects, together with quasars with flat radio spectrum, belong to the class of active galactic nuclei called blazars. These are objects characterized by extreme emission variability at all wavelengths, noticeable emission at the $\gamma$-ray energies, important polarization, superluminal motion, brightness temperatures by far exceeding the Compton limit (see e.g. Urry 1999 for a review).

The general scenario for the blazar emissivity has long been set: it foresees a plasma jet coming out from a supermassive, rotating black hole surrounded by an accretion disk. In the jet, which is closely aligned with our line of sight, relativistic electrons produce soft photons (from radio to the UV-X-rays) through synchrotron emission, and high-energy photons (up to the TeV energies) via inverse Compton scattering. However, theoretical models differ in the jet structure and physics, and in the origin of the seed photons that are energized to the $\gamma$-ray energies. Constraints on the theoretical models can come from dense optical and radio monitoring, and simultaneous observations throughout all the electromagnetic spectrum, from the radio to the $\gamma$-ray band. Indeed, multiwavelength variability studies (see Ulrich et al. 1997 for a review) can give information on the compactness of the emitting regions, and verify the existence of correlations and time delays among the emissions in different bands. This in turn can shed light on the location of the emitting regions in the jet and on the nature of the seed photons that are comptonized. International collaborations among optical astronomers such as the OJ-94 Project and the Whole Earth Blazar Telescope (WEBT) were born in the last years to make the observational effort more efficient.

In this paper we present the results of a wide collaboration aimed to study the optical and radio variability of the BL Lac object AO 0235+16. Partial and very preliminary results were presented in Villata et al. (1999), where the light curve in the R band from January 1993 to January 1999 was shown and radio-optical correlations during that period analyzed by means of the Discrete Correlation Function (DCF).

The source AO 0235+16 is a well known blazar at z=0.94 that exhibits spectacular emission variations on both short ($\sim$day) and long (months, years) time scales.

It was classified as a BL Lac object by Spinrad & Smith (1975), who observed a $\sim$2 mag variation. Noticeable optical outbursts were described by Rieke et al. (1976), Pica et al. (1980), Webb et al. (1988), Webb & Smith (1989), Webb et al. (2000). From the data reported in the literature, an overall brightness variation of more than $5\rm ~mag$ can be seen, which makes AO 0235+16 one of the most interesting sources for variability studies.

As for the short-term optical behaviour, intraday variability was observed in a number of occasions (Heidt & Wagner 1996; Noble & Miller 1996; Romero et al. 2000). In particular, changes of $0.5\rm ~mag$ were measured by Romero et al. (2000) within a single night, and variations of more than $1\rm ~mag$ in about 24 hours.

Many optical data were taken in the period 1993-1996 by the astronomers participating in the international collaboration called OJ-94 Project, who observed AO 0235+16 as a "complementary" object, in addition to OJ 287 and 3C 66A. The results of their monitoring were published in Takalo et al. (1998). Some of the groups belonging to the OJ-94 Project have then continued to observe AO 0235+16.

A huge monitoring effort has been pursued in the radio band by the University of Michigan Radio Observatory (UMRAO), in the USA, and by the Metsähovi Radio Observatory, in Finland. Indeed, this object is of extreme interest also in the radio band. Long-term radio light curves at frequencies above $1\rm ~GHz$ have shown that it exhibits frequent, relatively well-resolved, high-amplitude events (O'Dell et al. 1988; Clements et al. 1995). This makes AO 0235+16 particularly suitable for studies of correlated activity. Moreover, several recent papers have argued that unusually high Doppler factors/large Lorentz factors may be present: Jorstad et al. (2001) infer a Lorentz factor greater than 45 based on $43\rm ~GHz$ proper motions, using VLBA observations during 1995 and 1996; a Doppler factor for the bulk flow of order 100 was inferred from radio short-term variability in an earlier paper by Kraus et al. (1999). Doppler factors larger than 80 (and Lorentz factors $\Gamma > 60$) were found by Fujisawa et al. (1999) by applying the inverse-Compton effect and equipartition models to VLBI observations at $22\rm ~GHz$. Recent VSOP observations of AO 0235+16 by Frey et al. (2000) have led to an estimate of $T_{\rm b} > 5.8 \times 10^{13} \rm ~ K$ for the rest-frame brightness temperature of the core, which is the highest value measured with VSOP to date and implies a Doppler factor of $\sim$100.

Optical and radio data on AO 0235+16 taken in the last four years (1996-2000) by a wide international collaboration are presented in Sect. 2, and inserted in the source long-term light curves, dating back from the mid seventies. The results of the Whole Earth Blazar Telescope (WEBT) first-light campaign on AO 0235+16 in autumn 1997 are also included. Optical spectra are derived and spectral changes discussed in the same section. Radio light curves are shown in Sect. 3, where the behaviour of the radio flux is analyzed side by side with the optical one. Statistical analysis is presented in Sect. 4: autocorrelation function and Discrete Fourier Transform (DFT) methods are applied to search for characteristic time scales of variability in both the radio and optical domains; DCF analysis is then performed to check the existence of radio-optical correlations. A final discussion is contained in Sect. 5.

2 Optical behaviour of AO 0235+16

The long-term monitoring optical light curves of AO 0235+16 in the Johnson's UBV and Cousins' RI bands are shown in Fig. 1.

Figure 1: Long-term monitoring light curves of AO 0235+16 in UBVRI; data are from Kinman & Rieke (1975), Rieke et al. (1976), O'Dell et al. (1978a,b), Pica et al. (1980), Impey et al. (1982), Barbieri et al. (1982), Moles et al. (1985), Smith et al. (1987), Sillanpää et al. (1988a), Webb & Smith (1989), Mead et al. (1990), Sitko & Sitko (1991), Sillanpää et al. (1991), Takalo et al. (1992), Xie et al. (1992), Rabbette et al. (1996), Webb et al. (1997), Takalo et al. (1998), Xie et al. (1999), and Ghosh et al. (2000); data plotted after the vertical line are from the present work.

Open with DEXTER

	Figure 2: Light curves of AO 0235+16 in BVRI bands in the years 1996-2000; all data are from the present work.
Open with DEXTER

As generally happens, the best sampled band in the past is the B one, while the use of CCD cameras has led people to observe chiefly in the R band. The data plotted before the vertical line at ${\rm JD}=2450300$ were derived from the literature (see references in the caption); those after are new observations presented in this paper. Thirteen optical observatories all over the world were involved in this project; their names, nationality, position (longitude and latitude), diameter of the telescope and filters used are indicated in Table 1.

 

 

Table 1: List of participating observatories by longitude.

Observatory	Nation	Long. (deg)	Lat. (deg)	Tel. diam. (m)	Filters	Symbola
MSSSO	Australia	+149.066	-31.277	1.0	R	filled triangles
Xinglong	China	+117.575	+40.393	0.6	R	filled squares
Vainu Bappu	India	+78.83	+12.57	2.0	R	asterisks
Abastumani	Georgia	+42.80	+41.80	0.7	R	open circles
Tuorla	Finland	+22.17	+60.27	1.03	V
Roma	Italy	+12.70	+41.80	0.5, 0.7	BVRI	open triangles
Perugia	Italy	+12.372	+43.112	0.4	VRI	open diamonds
Torino	Italy	+7.775	+45.038	1.05	BVRI	open squares
Calar Alto	Spain	-2.546	+37.224	2.2	R	filled circles
Teide	Spain	-16.5	+28.16	0.82	BVRI	crosses
NOT	Spain	-17.88	+28.75	2.56	BVRI	asterisks
Foggy Bottom	USA	-74.25	+43.24	0.4	R	filled stars
Climenhaga	Canada	-123.22	+48.25	0.5	R	filled diamonds

^a The symbols are used to distinguish the R band data plotted in Figs. 3-7.

Seven of them (MSSSO, Xinglong, Vainu Bappu, Calar Alto, Teide, Foggy Bottom, Climenhanga) participated only during the WEBT campaign in November 1997 (see Sect. 2.1) or around that period, while the others provided the long-term optical monitoring. All observers took frames by means of CCD cameras and performed data reduction using standard procedures; the source magnitude was obtained by differential photometry, adopting the reference stars calibrated by Smith et al. (1985) and Fiorucci et al. (1998).

Although the intense source variability makes a comparison among the different datasets difficult to perform, a general agreement was found where the data overlap in time. Many large-amplitude outbursts are visible from Fig. 1; in the B band the minimum and maximum magnitudes observed were $15.09\pm 0.18$ ( ${\rm JD}=2443907$) and $20.5\pm 0.05$ ( ${\rm JD}=2449692$), respectively. In the R band the range of magnitudes spanned is from $14.03 \pm 0.08$ ( ${\rm JD}=2450811$) to $19.47 \pm 0.06$ ( ${\rm JD}=2450278$).

An enlargement of the BVRI light curves in the period 1996-2000 is shown in Fig. 2; an inspection of the R-band curve, the best sampled one, reveals three major peaks, one for each of the last three observing seasons.

Details of the 1997-1998 season are visible in Fig. 3,

	Figure 3: Light curve of AO 0235+16 in the Cousins' R band from August 1997 to March 1998; data are from Vainu Bappu (asterisks), Abastumani (open circles), Roma (triangles), Perugia (diamonds), Torino (squares), and Teide (crosses); data from the WEBT campaign occurred from November 1 to 11, 1997 ( ${\rm JD}=2450754$-2450764) are plotted as dark dots.
Open with DEXTER

where different symbols refer to different observatories (see caption to the figure), with the exception of dark dots, which indicate data collected during the WEBT campaign.

The peak at ${\rm JD}=2450811$ was observed by both the Perugia and the Roma Observatories, and corresponding peaks were seen also in the BVI bands (see Figs. 1 and 2). What is quite impressive is the extreme sharpness of the flare: a brightness increase of $1\rm ~mag$ in 4 days (inside a $2.8\rm ~mag$ rise in 27days) was followed by a $1.3\rm ~mag$ decrease in only one day, leading to a $2.0\rm ~mag$ fall in 13 days.

A smoother behaviour characterizes the 1998-1999 observational season (see Fig. 4):

	Figure 4: Light curve of AO 0235+16 in the Cousins' R band from July 1998 to January 1999; data are from Abastumani (circles), Roma (triangles), Perugia (diamonds), Torino (squares), Teide (crosses), and NOT (asterisks).
Open with DEXTER

the source was found to be very bright at the beginning of the season, skimming R=14, and then a continuous decrease, interrupted by a couple of flares, led to $R\sim 19$, with a jump of $5\rm ~mag$.

In the last observing season the temporal coverage was definitely worse than in the previous two seasons (see Fig. 2); however, a quite interesting feature is the fall of $1.6\rm ~mag$ in 48 hours occurred in the R band at the beginning of September 1999 ( ${\rm JD}=2451425.657$- 2451427.657).

2.1 The November 1997 WEBT campaign

The WEBT is an international collaboration among astronomers from all the world with the aim of organizing optical campaigns on blazars of specific interest (Mattox 1999a,b; Villata et al. 2000). These campaigns, lasting from a few days to several weeks, are generally undertaken in concert with observations at other wavelengths, and can be triggered by the discovery of a flaring state of an object, usually in the optical band.

This was indeed the case for the first-light WEBT campaign: the November 1997 observations of AO 0235+16 were started after the detection of a considerable brightness increase (about $1\rm ~mag$ in a week) at the end of October 1997 (Webb et al. 1997). An EGRET target of opportunity observation occurred between November 3 and 11, 1997, but only an upper limit of $16 \times 10^{-8} ~ \rm photons \, cm^{-2} \, s^{-1}$ above $100\rm ~MeV$ could be inferred (Hartman, private communication). Observations by RXTE did not find a high X-ray flux (Webb et al. 2000).

The light curve obtained in the first 11 days of November 1997 is plotted in Fig. 5.

	Figure 5: Light curve of AO 0235+16 in the Cousins' R band during the first-light WEBT campaign of November 1997; for the explanation of symbols see Table 1.
Open with DEXTER

Data from each observatory are indicated with a different symbol, according to Table 1 (Col. 7). Weather was rather bad in those days in most of western Europe and North America, so that the temporal density of the curve is far from ideal, and far even from the density reached in more recent WEBT campaigns (see Villata et al. 2000, 2001); however, the common observational effort of many observatories around the world led to a satisfactory time coverage.

In order to avoid spurious variations due to possible systematic effects among data from different observatories, in the following only flux changes observed by the same telescope will be considered. A brightness increase of $1.25\rm ~mag$ in two days was detected at the beginning of the campaign and noticeable flux oscillations were observed all the time. Variations of 0.2- $0.4\rm ~mag$ in 5-7 hours were found in a number of cases; very impressive is the dimming of half a magnitude in about 5 hours detected in the night between November 3 and 4. Similar very fast variations have recently been observed by Romero et al. (2000).

	Figure 6: A selection of optical spectra from Roma (triangles), Torino (squares), and Teide (crosses); Julian Dates (-2442000) are indicated on the right; straight lines are drawn only to guide the eye through points of the same spectrum; no vertical shift is applied.
Open with DEXTER

2.2 Spectral behaviour in the optical band

	Figure 7: The spectral index $\alpha$ as a function of the R flux for the 40 optical spectra from Roma (triangles), Torino (squares), and Teide (crosses).
Open with DEXTER

One item that is interesting to investigate when studying the optical variability of blazars is whether the flux variations are accompanied by spectral changes. In the new data presented in this paper we identified 47 optical spectra collecting data in at least three filters taken by the same telescope, with the requirement that the delay from the first frame to the last one is not greater than 50 min. We discarded 7 spectra which contained large errors and analyzed the remaining 40. A selection of these "well behaved" spectra is presented in Fig. 6 in the $\log \nu$ - $\log (\nu F_{\nu})$ plane, using different symbols for data taken at different telescopes. When taking into account that some discrepancies in the spectral shape can arise from not completely equal photometric systems used in the various observatories, no significant variations can be recognized when the flux changes. However, a deeper inspection reveals that the spread corresponding to the B band is larger than that relative to the I one. This would suggest that the flux variations are of larger amplitude at the higher frequencies, as already observed in other blazars. All 40 "well behaved" optical spectra were then fitted by a classical power law: $F_{\nu} \propto \nu^{\alpha}$ with a $\chi^2$ minimizing procedure. The results are shown in Fig. 7, where the spectral index $\alpha$ is plotted as a function of the flux in the R band and $\alpha$ values with errors greater than 0.25 have been eliminated. One can notice that for high flux levels $\alpha$ presents an almost constant value of -2.8--2.7, while it tends to decrease with decreasing flux, although there is a not negligible spread. This means that the spectrum basically steepens when the source gets fainter, a behaviour that is common to blazars.

3 Radio and optical fluxes: Visual correlation analysis

Radio light curves of AO 0235+16 are shown in Fig. 8: data at 22 and $37\rm ~GHz$ are from the Metsähovi Radio Observatory, those at 4.8, 8.0, and $14.5\rm ~GHz$ are from the University of Michigan Radio Astronomy Observatory (UMRAO). The observations at the Metsähovi Radio Observatory were made with the $13.7\rm ~m$antenna using standard ON/ON techniques with DR 21 used as a calibration source. Details on the observing procedure and data reduction can be found in Teräsranta et al. (1992, 1998). The data from UMRAO were taken with the $26\rm ~m$ paraboloid of the University of Michigan. A description of the observing and data reduction procedures is included in Aller et al. (1985, 1999).

As in the optical band, also in the radio AO 0235+16 presents intense activity at all wavelengths, with pronounced outbursts lasting from several months to a few years. The overall flux variations (maximum value over minimum one) detected in the various bands are: 18, 22, 32, 28, and 31 at 37, 22, 14.5, 8.0, and $4.8\rm ~GHz$, respectively. In particular, in the last four years ( ${\rm JD} > 2450300$) variations up to a factor 18 were observed.

In Fig. 8 radio fluxes (in Jy) are compared to the optical ones (in mJy), obtained in the following way: all magnitudes in the B band before ${\rm JD}=2449000$ have been transformed into R ones adopting the mean colour index $<B-R>\ =1.65 \pm 0.16$ (which was derived by considering all the B-R pairs from a same observatory separated by no more than half an hour); these data plus the real R magnitudes after ${\rm JD}=2449000$ have been converted into fluxes by adopting Rieke & Lebovski (1985) and the law by Cardelli et al. (1989), and using a Galactic extinction $A_B=0.341 ~ \rm mag$ (from NED).

The existence of radio-optical correlations for AO 0235+16 was investigated in a number of previous works; evidence for a simultaneous radio and optical variability was found in correspondence to the optical flares of 1975 and 1979 (MacLeod et al. 1976; Ledden et al. 1976; Rieke et al. 1976; Balonek & Dent 1980) and, more recently, to that which occurred in 1997 (Webb et al. 2000).

Clements et al. (1995) analyzed optical data taken in the period 1977-1991 and radio data at $8.0\rm ~GHz$ from UMRAO with the Discrete Correlation Function (DCF), and found that: "Overall, radio events lag optical events with lag times varying from 0 to 2 months". Takalo et al. (1998) visually compared optical data from 1980 to 1996 with combined 22 and $37\rm ~GHz$ data from the Metsähovi Radio Observatory and noticed that some of the optical spikes appear to be coincident with radio flares, while others have no counterparts. Moreover, the general trend looked very similar in both frequency regimes, suggesting some kind of correlation.

	Figure 8: Optical (mJy) and radio (Jy) light curves of AO 0235+16; radio data at 22 and $37\rm ~GHz$ are from the Metsähovi Radio Observatory, those at 14.5, 8.0, and $4.8\rm ~GHz$ are from UMRAO.
Open with DEXTER

A visual inspection of Fig. 8 shows that the big optical outburst of 1975 has a big radio counterpart at 14.5 and $8.0\rm ~GHz$, while in 1979 a noticeable optical peak corresponds to a modest radio peak. Prominent radio outbursts at 22, 14.5, 8.0, and $4.8\rm ~GHz$ were observed in 1982, towards the end of the optical season, so that a possible optical peak might have been missed. A strong brightness increase was detected in 1987 in both optical and radio bands, but in this case the double-peaked optical flare seems to preceed the radio ones. The behaviour of the long radio outburst of 1990-1991 appears more complex; during the radio outburst a sharper optical flare was detected but not followed in details. The radio outburst in 1992-1993 was double-peaked; just before the first radio peak, an optical flare was detected; no other optical data were taken at the time when the radio fluxes reached their maxima. One interesting feature, however, is that if one looks at the better-sampled UMRAO data, the first radio peak seems delayed when proceeding from the higher to the lower radio frequencies. Indeed, the maximum value was reached on October 4, 1992 at $14.5\rm ~GHz$, on October 13 at $8.0\rm ~GHz$, and on November 3 at $4.8\rm ~GHz$. A radio flux increase in 1994 was practically not followed in the optical band.

From these considerations it is clear that the main difficulty in performing a meaningful study on possible radio-optical correlations is the paucity of optical data.

The situation has been noticeably improved in the last years, because of the intense observational effort of the monitoring groups involved in the present work. Indeed, the big outbursts occurred at the end of 1997 and in 1998 were accurately followed in all the radio bands and in the optical one (Fig. 9).

	Figure 9: Optical (mJy) and radio (Jy) light curves of AO 0235+16 in the last years; radio data at 22 and $37\rm ~GHz$ are from the Metsähovi Radio Observatory, those at 14.5, 8.0, and $4.8\rm ~GHz$ are from UMRAO.
Open with DEXTER

A preliminary discussion on the radio-optical correlations in this period was presented by Villata et al. (1999). On December 28, 1997 ( ${\rm JD}=2450811.33$), the R-band flux reached $9.19 \pm 0.68 ~ \rm mJy$ (R=14.03); four days before it was $3.90 \pm 0.11 ~ \rm mJy$ and 24 hours after the peak the flux had dropped to $2.85 \pm 0.13 ~ \rm mJy$. This very sharp peak was observed by two different groups (Perugia and Roma) and also in different bands (see Figs. 1 and 2). At the time of this optical flare, the radio fluxes were in a rising phase: they reached their maximum values later, likely first the shorter (observed by Metsähovi) and then the longer (UMRAO) wavelengths. The peaks at 37 and $22\rm ~GHz$ were detected on March 3 and 2, 1998, respectively, although a gap in the radio datasets does not allow to establish whether the peak of the outburst had already occurred. The maximum value of the $14.5\rm ~GHz$flux was seen on April 14, 1998 ( ${\rm JD}=2450918$), and that at $8.0\rm ~GHz$ on April 5, 1998, but in this case the peak probably occurred later. This peak-delay effect has already been quoted above for the 1992-1993 outburst. The radio outburst at 22 and $14.5\rm ~GHz$ is clearly double-peaked; this feature is recognizable also in the $8.0\rm ~GHz$ data. It is noticeable that the second radio peak could reasonably be contemporaneous at 22, 14.5, and $8.0\rm ~GHz$, the best sampled bands, and corresponds to a second optical flare detected at the beginning of the observing season, in July-August 1998. The solar conjunction period prevented to follow the rising phase of the optical outburst, so that the possibility that the optical peak also in this case preceded the radio ones remains open. A second brighter optical peak detected on August 7, 1998 ( ${\rm JD}=2451032.63$, R flux of $8.94 \pm 0.16 ~ \rm mJy$) occurred when the radio flux was in a decreasing stage. Another important, sharp optical flare was finally detected on September 4, 1999 ( ${\rm JD}=2451425.66$), which again has a radio counterpart, whose peak shows several weeks of delay.

The above discussion demonstrates that, notwithstanding the great observational effort of the last years, we are still far from having the sufficient sampling to derive firm conclusions on the radio-optical correlations. We can only notice that, in general, when the observational coverage is sufficiently good, a long time scale radio flux increase corresponds to a short time scale optical brightness increase, whose peak may precede the radio one. Moreover, there are at least two cases (the 1992-1993 and 1998 double-peaked outbursts) where a progressive time delay in reaching the maximum value is observed when passing from the higher to the lower frequency radio fluxes.

4 Statistical analysis

	Figure 10: DCF autocorrelations for the optical and UMRAO radio fluxes shown in Fig. 8; the data have been binned over 2 days, while the DCF was obtained with a bin size of 25 days.
Open with DEXTER

In this section we apply the Discrete Correlation Function (DCF) analysis to the data shown in Fig. 8 in order to investigate the existence of characteristic time scales of variability and of optical-radio correlations.

The DCF is a method specifically designed for unevenly sampled datasets (Edelson & Krolik 1988; Hufnagel & Bregman 1992), which also allows an estimate of the accuracy of its results.

Given two datasets a_i and b_j, one has first to combine all pairs, calculating the unbinned discrete correlations:

$${\rm UDCF}_{ij}={{(a_i- \overline a)(b_j- \overline b)} \over {\sigma_a \sigma_b}},$$

where $\overline a$, $\overline b$ are the average values of the two datasets, and $\sigma_a$, $\sigma_b$ their standard deviations. The DCF is obtained by binning the ${\rm UDCF}_{ij}$ in time for each time lag $\tau$:

$${\rm DCF} (\tau)= {1 \over M} \sum {\rm UDCF}_{ij}(\tau),$$

where M is the number of pairs a_i, b_j whose time lag $\Delta_{ij}=t_j - t_i$ is inside the $\tau$ bin. Spurious correlations can be found, of the order of $\pm M^{-1/2}$. The standard error for each bin is:

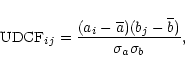
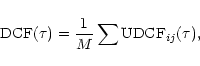
$$\sigma_{\rm DCF} (\tau) = {1 \over {M-1}} \left\{ \sum \left[ {\rm UDCF}_{ij} - {\rm DCF}(\tau) \right] ^2 \right\} ^{1/2}.$$

A positive peak of the DCF means correlation, which is stronger as the value of the peak approaches and exceeds one. A negative peak implies anticorrelation. Moreover, the width of the peak must be comparable to those of the autocorrelation functions, obtained by applying the DCF to each dataset coupled with itself.

A preliminary binning of data in time before calculating the DCF usually leads to better results, smoothing out flickering. The size of this binning is crucial especially in the optical, where short-term variations are frequent, since it can remove important information. Furthermore, an increase of the data binning interval implies an increase of the spurious correlations, while an increase of the DCF bin size has the opposite effect. Also the choice of the DCF binning is a delicate point, determining the balance between resolution and noise. In general, a similar value of M for each DCF bin and a limit of $10\%$ to the appearance of spurious correlations must be assured in order to get reliable results.

Another method frequently used for searching characteristic time scales of variability is the Discrete Fourier Transform (DFT) spectral analysis for unevenly sampled data. We have adopted the implementation of the Lomb normalized periodogram method (Lomb 1976) discussed by Press et al. (1992). The presence of a sinusoidal component of frequency $\omega_0=2 \pi \nu$ in the dataset is revealed by a large value of the periodogram $P(\omega)$ at $\omega = \omega_0$. The significance of the peaks is estimated by the false alarm probability, i.e. the probability that a peak is of height z or higher if the data are pure noise. It is given by $F=1-(1-{\rm e}^{-z})^M$, where M is the number of independent frequencies. Since we have scanned frequencies up to the Nyquist frequency $\nu_{\rm c}=N/(2T)$ that the N data would have were they evenly spaced over the period T, we have set M=N. For very clumpy datasets as we have when considering the optical light curve, the value of M (and hence the false alarm probability) may be overestimated, and the significance of the peaks is consequently underestimated (see also Horne & Baliunas 1986).

4.1 Search for characteristic time scales of variability

The optical DCF autocorrelation is plotted in Fig. 10 (top panel):

	Figure 11: The light curve of AO 0235+16 at $8.0\rm ~GHz$ folded assuming a period of 2069 days.
Open with DEXTER

as expected, it is dominated by flicker noise and reveals an important double-peaked signal at $\tau \sim 4100$-4200 days (11.2-11.5 years), and not negligible ones at $\tau \sim 1200$ and $\sim$2100 days ($\sim$3.28 and $\sim$5.75 years). These can thus be regarded as characteristic time scales of optical variability for AO 0235+16. A visual inspection of the optical light curve in Fig. 8 confirms these features.

The peak at $\tau \sim 5000$ days in the optical autocorrelation is just one point affected by a large error, deriving from the correlation between the 1979 and 1992 outbursts.

The fact that the maxima at about $\pm 4200$ days exceed 1 is due to the choice of a 2 day binning on the original dataset; a larger time interval for data binning (e.g. 20 days) would reduce the importance of these features with respect to the central maximum, but would force the choice of a much larger DCF bin ($\sim$100 days) in order to avoid important spurious correlations. This in turn would imply missing important details.

Figure 10 also presents the DCF autocorrelation for UMRAO radio fluxes. The peaks are wider than in the optical case, reflecting the broader outbursts of the radio light curves when compared with the optical ones. An important double-peaked maximum appears at 3900-4200days (10.7-11.5 years) at all three frequencies, whose similarity with the optical one suggests radio-optical correlation. Other noticeable peaks are seen at 5300-5400 and 6100-6200 days (14.5-14.8, 16.7-17.0 years) in the DCF autocorrelation function for the $8.0\rm ~GHz$ band. At $14.5\rm ~GHz$ the former appears reduced, while the latter, deriving mainly from the coupling of the 1975 and 1992 outbursts, is enhanced. At $4.8\rm ~GHz$ both disappear, but in this case the light curve is less extended in time; in particular, the 1975 outburst is totally missing.

As for the Metsähovi radio light curves at 22 and $37\rm ~GHz$, their less dense sampling and more limited time extension lead to higher spurious effects, especially for large values of $\tau$. However, their autocorrelation functions confirm the signal centred at $\tau \sim 4000$ days, and present noticeable peaks at about 2000 days, that is the time separation between the outbursts detected in 1987, 1992, and 1998.

The most interesting point emerging from the above discussion is the $\sim$11.2 year characteristic time scale of variability, which is common to the optical and radio fluxes. By looking at the light curves in Fig. 8, one can understand this result by noticing that at a distance of about 4100 days the 1975 peak correlates with the 1987 one, and this latter with the 1998 flare, while the 1982 outburst correlates with the 1992 one. This means that there seems to be a $\sim$4100 day characteristic variability time scale intersecting another $\sim$4100 day time scale, which on one side is somehow surprising. On the other side, both the optical and the Metsähovi radio autocorrelations suggest that there may be a "periodicity" of about half the above time scale. Indeed, the 25 year time extension of the AO 0235+16 light curves would allow to interpret this halved time scale in terms of periodicity. The point is to understand why UMRAO radio autocorrelation functions do not show a strong signal at $\tau \sim 2050$ days. The reason is that this signal is damped by the delay of the 1982 outburst. Indeed, by looking at the $8.0\rm ~GHz$light curve (Fig. 8), the best sampled one, one can recognize five large-amplitude outbursts peaking at ${\rm JD}-2442000=723.60$, 3031.44, 4901.27, 6908.74, and 9000.00, spaced by 2308, 1870, 2007, and 2091 days, respectively. The average period would thus be $2069\,\pm\, 184$ days, i.e. $5.67\,\pm\, 0.50$ years. The $8.0\rm ~GHz$ light curve folded assuming a period of 2069 days is presented in Fig. 11:

	Figure 12: The light curve of AO 0235+16 in the R band folded assuming a period of 2069 days.
Open with DEXTER

the delay of the 1982 outburst is clearly visible.

Notice that a weak signal at about 2000 days is actually present in the $14.5\rm ~GHz$ autocorrelation function because at this frequency the 1982 outburst was preceded by a kind of pre-outburst that made the flux reach a high level earlier than the $8.0\rm ~GHz$ one.

We have checked the reliability of the results obtained by the autocorrelation analysis by means of the Discrete Fourier Transform (DFT) technique for unevenly sampled data implemented by Press et al. (1992). In both the radio and the optical cases we obtained many signals with significance levels F better than 0.001. In particular, the 2069 day periodicity previously inferred is confirmed by the DFT analysis on UMRAO data. At $8.0\rm ~GHz$, a clear maximum ($P\sim 79$) is found at frequencies $\nu \sim 4.8$- $4.9\times 10^{-4} \rm ~ day^{-1}$, corresponding to periods of $\sim$2050-2080 days. Other strong signals in the $8.0\rm ~GHz$ data are found at 3.7, 2.8, and 1.8 years ($P \sim 88$, 46, 45, respectively). At $14.5\rm ~GHz$ the strongest maximum of the Lomb periodogram ($P \sim 81$) is right at $\nu~\sim~\mbox{4.8$-$ 4.9}~\times~10^{-4} \rm ~ day^{-1}$, followed by the maxima ($P \sim 68$, 49, 48) corresponding to 2.8, 1.8, and 3.7 year periods, confirming the results obtained for the $8.0\rm ~GHz$ data. Similar results are also found for the $4.8\rm ~GHz$ dataset.

The DFT technique applied to the optical fluxes gives much more signals, making the spectral analysis rather complex. Surprisingly, the $\sim$2100 day time scale discovered in the optical autocorrelation function and obtained by the DFT analysis of UMRAO data gives only a weak signal (significance level better than $3\%$ only). To better visualize the matter, Fig. 12 shows the optical light curve in the R band folded assuming a 2069 day period. Notice that such a period would not explain some important outbursts, in particular the major outburst observed in 1979. Other signals obtained by the DFT analysis at 2.8 and 1.6-1.9 years confirm the time scales found for the radio fluxes, while there is not a strong optical signal corresponding to the 3.7 years in the radio. The strongest DFT signal corresponds to a $\sim$200 day time scale, which is the time separation between the two peaks observed in the 1997-1998 outburst.

4.2 Optical-radio cross-correlation

The results of the DCF cross-correlation between data in the R band and the $8.0\rm ~GHz$ ones are shown in Fig. 13 (bottom panel): the well-defined positive peak at $\tau \sim 0$-60 days suggests optical-radio correlation, with optical variations that can be both simultaneous and leading the radio ones by a couple of months. The DCF applied to the optical and $14.5\rm ~GHz$ datasets leads to a similar result (see Fig. 13, top panel): the radio variations appear correlated and delayed of 0-50 days with respect to the optical ones. These results are in agreement with what was derived by Clements et al. (1995).

As for the radio-radio correlations, Clements et al. (1995) found no time delay between the 14.5 and $8.0\rm ~GHz$ datasets and between the 8.0 and $4.8\rm ~GHz$ ones. However, as previously discussed, at least during the 1992-1993 and 1998 outbursts, the radio light curves seem to indicate that the flux variation at the higher frequencies may have led that observed at the lower ones. Figure 14 shows the results of the DCF cross-correlation between the 22 and $8.0\rm ~GHz$ fluxes: in the top panel, where all data have been considered, the peak is not exactly centred at $\tau=0$. This might suggest that the $22\rm ~GHz$ fluxes can lead the $8.0\rm ~GHz$ ones by several days. In the bottom panel of Fig. 14 only data after ${\rm JD}=2450300$ were taken into account, so that only the 1998 outburst is considered: the delay effect in this case is enhanced. This is in agreement with what was observed by O'Dell et al. (1988) when analyzing the variability of AO 0235+16 at eight radio frequencies, from $318\rm ~MHz$ to $14.5\rm ~GHz$. They found that flux-density variations are clearly correlated, and events occur first at the higher frequencies and propagate to lower frequencies with decreasing amplitude.

5 Discussion and conclusions

Four years of optical and radio monitoring of the BL Lac object AO 0235+16 have confirmed the extreme variability for which this source is well known: a range of more than $5\rm ~mag$ was spanned in the optical band and a total variation of up to a factor 18 was registered in the radio fluxes.

Optical spectral changes are not very evident, but our data suggest a spectrum steepening when the source gets fainter, a feature that has already been recognized for other blazars. This behaviour can be interpreted in terms of radiative losses in the electron population of the emitting jet: when the source is bright, cooling can be balanced or overcome by acceleration processes and the resulting spectrum is flatter; when the flux is low, radiative losses dominate and cause a spectral steepening, since the higher-energy ultra-relativistic electrons emitting synchrotron radiation cool faster than the lower-energy ones. However, also a geometrical interpretation of the kind of that presented in Villata & Raiteri (1999; see also Villata et al. 2000) is possible: if a faint state of the source in a given band occurs when the portion of the curved jet emitting in that band becomes less aligned to the line of sight, then a spectral steepening is expected since the higher-frequency emitting portion of the jet departed first from the line of sight.

	Figure 13: Discrete Correlation Function (DCF) between the R data and $14.5\rm ~GHz$ (top) or $8.0\rm ~GHz$ (bottom) data of AO 0235+16; all datasets have been binned over 2 days, while the DCF bin size is 20 days.
Open with DEXTER

	Figure 14: Discrete Correlation Function (DCF) between the 22 and $8.0\rm ~GHz$ data of AO 0235+16; in the bottom panel only data after ${\rm JD}=2450300$ have been considered; both datasets have been binned over 2 days, while the DCF bin size is 20 days.
Open with DEXTER

Discrete autocorrelation function analysis of the optical and radio light curves points out a characteristic time scale for the flux variability of AO 0235+16 of about 11.2 years. However, a deeper insight into the optical and radio light curves aided by DFT analysis and folded light curves reveals that major outbursts occur at roughly half the above time scale, even if one of the events (the 1982 one) appears noticeably delayed.

Indeed, in the best sampled $8.0\rm ~GHz$ light curve, there are five large-amplitude outbursts whose peaks are separated by 2308, 1870, 2007, and 2091 days, giving an average "period" of 2069$\,\pm\,$184 days, i.e. 5.7$\pm$0.5 years. Taking into account that the AO 0235+16 redshift is z=0.94, the relation $P=P_{\rm obs}/(1+z)$ implies that the period in the source rest frame is around 2.8 years. Other characteristic frequencies resulting from the DFT analysis of the radio light curves correspond to periods of 1.8, 2.8, and 3.7years. In the optical, the sparse sampling makes the analysis of variability time scales rather difficult. However, discrete autocorrelation function, DFT, and folded light curves are compatible with a $\sim$2069 day periodicity. Such periodicity would not account for the observed big 1979 optical outburst, whose radio counterpart was a rather modest flux increase. The optical autocorrelation analysis puts in evidence also another characteristic time scale of variability of about 1200 days (3.3 years), which corresponds to the time separation between the 1975 and 1979 outbursts, while the DFT of the optical data confirm the 1.8 and 2.8 year periods found in the radio data.

A few previous studies investigated the existence of periodicities in AO 0235+16: Webb et al. (1988) analyzed the optical light curve with the Deeming DFT (Deeming 1975), and derived periods of 2.79, 1.53, and 1.29 years. More recently, Webb et al. (2000) used unequal-interval Fourier transform and CLEAN techniques and obtained periods of 2.7 and 1.2 years for the optical variations. The time scales of long-term optical base-level fluctuations have been studied by Smith & Nair (1995) for three classes of AGNs; they found a best fit period of 2.9 years for AO 0235+16, attributing a moderate confidence to the estimate. The Jurkevic technique and the autocorrelation function were adopted by Fan (2001) for the analysis of the optical light curves, inferring periods of 1.56, $2.95\pm0.25$, and $5.87\pm 1.3$ years. This last period is highly compatible with what is derived in the present paper. Roy et al. (2000) made a cross-correlation analysis between optical and UMRAO radio data and applied Lomb-Scargle periodograms to the 14.5 and $8.0\rm ~GHz$ light curves to infer a $\sim$5.8 year periodicity. Their results are in agreement with what we find in the present paper.

If the major outbursts in AO 0235+16 really occur every $5.7 \pm 0.5$ years, the next one should peak around February-March 2004, and a great observational effort should be undertaken since at least summer 2003 to get more information on the details of the flux behaviour in various bands. Unfortunately, the source is not visible from ground-based optical observatories during springtime because of solar conjunction.

On the other hand, another great effort should be addressed to the theoretical interpretation of such recurrent events, in particular to envisage possible mechanisms that can "disturb" the period. Many models have been proposed to explain the $\sim$12 year period inferred from the optical light curve of another well-known BL Lac object, i.e. OJ 287; most of them foresee the existence of a binary black hole system (Sillanpää et al. 1988b; Lehto & Valtonen 1996; Villata et al. 1998; Valtaoja et al. 2000; Abraham 2000). It would be interesting to see whether those models can be adapted to explain the quasi-periodic variability observed in AO 0235+16.

As for the cross-correlation between the optical and radio data, the analysis of the light curves is constrained by the sometimes very sparse optical sampling. However, in general we can say that a radio flux increase always corresponds to each major optical flare; the vice versa is likely true. Such correlation would suggest that the same mechanism is responsible for the optical and radio variations. However, two different behaviours seem to be present: optical and radio fluxes are seen sometimes to reach their maximum values at the same time, while in some cases the higher frequencies lead the lower ones. This would mean that two different mechanisms are presumably at work in the long-term variability. Outbursts occurring simultaneously in all bands may suggest that the synchrotron emission from the radio to the optical band is produced by the same population of relativistic electrons in the same region. But they may also favour the microlensing scenario, which was already suggested for explaining the variability of AO 0235+16 (Stickel et al. 1988; Takalo et al. 1998; Webb et al. 2000; but see Kayser 1988 for a critical discussion). The presence of several foreground objects in the field of the source supports this scenario. One item against this hypothesis is that during the strong flux increase detected in both the optical and radio bands in 1997, the X-ray and $\gamma$-ray fluxes were not seen in a high state.

On the other hand, the fact that in the radio and optical domains the variations observed at the higher frequencies lead those at the lower ones makes one think to an inhomogeneous jet, where a disturbance travelling downstream enhances first the emission at the higher frequencies and then the emission at the lower ones. An alternative view is given by geometrical models such as the previously mentioned helical model by Villata & Raiteri (1999), if we imagine that the portion of the jet emitting the higher-energy radiation gets closer to the line of sight before that producing the lower-energy flux, as already noted for the spectral changes.

A different interpretation is required to explain the noticeable intraday variability shown by AO 0235+16 in both the optical and radio bands. Indeed, on short time scales, the flux behaviour can be very different with respect to that exhibited on long time scales. Kraus et al. (1999) observed an "unusual" radio event in October 1992, in which the $20\rm ~cm$ maximum preceded the maxima at 3.6 and $6\rm ~cm$, and the variation amplitude was larger at the lower frequencies. They applied a number of models, both of intrinsic and of extrinsic nature, and concluded that, in any case, the size of the emitting region must be very small, implying a Doppler factor of order 100. Such a high value was subsequently confirmed by Frey et al. (2000) by analyzing VSOP observations of AO 0235+16.

We found several episodes of very fast intraday variability in the radio light curves; in some cases we are in the presence of single points that appear to deviate from the longer trends shown by the data, but there are cases in which the variation is confirmed by more than one point. Calculation of the brightness temperature for the fastest variability events ( $\Delta F / \Delta t > 0.3 ~ \rm Jy\,day^{-1}$) in the $14.5\rm ~GHz$ light curve (containing data generally of higher signal-to-noise ratio with respect to the lower frequencies ones) led to values by far exceeding the Compton limit, implying Doppler factors in the range 30-70. Indeed, such results must be taken with caution, since a much better sampling is needed in order to derive reliable Doppler factors from the radio intraday variability.

In conclusion, all the items pointed out by the present work (such as the 5.7 year periodicity, delayed flux variations at lower frequencies, high Doppler factors) would need a further observational effort in the next years, in order to fix them to more precise results.

Acknowledgements

We gratefully acknowledge useful suggestions by the referee, Dr. K. Ghosh. We thank R. C. Hartman for communicating us the result of the EGRET VP 6311 on AO 0235+16. This research has made use of:

• the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration;
• data from the University of Michigan Radio Astronomy Observatory, which is supported by the National Science Foundation and by funds from the University of Michigan.

References

 
• Abraham, Z. 2000, A&A, 355, 915 In the text NASA ADS  
• Aller, H. D., Aller, M. F., Latimer, G. E., & Hodge, P. E. 1985, ApJS, 59, 513 In the text NASA ADS  
• Aller, M. F., Aller, H. D., Hughes, P. A., & Latimer, G. E. 1999, ApJ, 512, 601 In the text NASA ADS  
• Balonek, T. J., & Dent, W. A. 1980, ApJ, 240, L3 In the text NASA ADS  
• Barbieri, C., Cristiani, S., & Romano, G. 1982, AJ, 87, 616 In the text NASA ADS  
• Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 In the text NASA ADS  
• Clements, S. D., Smith, A. G., Aller, H. D., & Aller, M. F. 1995, AJ, 110, 529 In the text NASA ADS  
• Cohen, R. D., Smith, H. E., Junkkarinen, V. T., & Burbidge, E. M. 1987, ApJ, 318, 577 NASA ADS  
• Cruz-Gonzales, I., & Hucra, J. P. 1984, AJ, 89, 441 NASA ADS  
• Deeming, T. J. 1975, Ap&SS, 36, 137 In the text NASA ADS  
• Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 In the text NASA ADS  
• Fan, J. H. 2001, Progress in Astronomy, in press In the text  
• Fiorucci, M., Tosti, G., & Rizzi, N. 1998, PASP, 110, 105 In the text NASA ADS  
• Frey, S., Gurvits, L. I., Altschuler, D. R., et al. 2000, PASJ, 52, 975 In the text NASA ADS  
• Fujisawa, K., Kobayashi, H., Wajima, K., et al. 1999, PASJ, 51, 537 In the text NASA ADS  
• Ghosh, K. K., Ramsey, B. D., Sadun, A. C., & Soundararajaperumal, S. 2000, ApJS, 127, 11 In the text NASA ADS  
• Heidt, J., & Wagner, S. J. 1996, A&A, 305, 42 In the text NASA ADS  
• Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 In the text NASA ADS  
• Hufnagel, B. R., & Bregman, J. N. 1992, ApJ, 386, 473 In the text NASA ADS  
• Impey, C. D., Brand, P. W. J. L., & Tapia, S. 1982, MNRAS, 198, 1 In the text NASA ADS  
• Jorstad, S. G., Marscher, A. P., Mattox, J. R., et al. 2001, ApJS, 134, 181 In the text NASA ADS  
• Kayser, R. 1988, A&A, 206, L8 In the text NASA ADS  
• Kinman, T. D., & Rieke, G. H. 1975, IAU Circ., 2868 In the text  
• Kraus, A., Quirrenbach, A., Lobanov, A. P., et al. 1999, A&A, 344, 807 In the text NASA ADS  
• Ledden, J. E., Aller, H. D., & Dent, W. A. 1976, Nature, 260, 752 In the text NASA ADS  
• Lehto, H. J., & Valtonen, M. J. 1996, ApJ, 460, 207 In the text NASA ADS  
• Lomb, N. R. 1976, Ap&SS, 39, 447 In the text NASA ADS  
• MacLeod, J. M., Andrew, B. H., & Harvey, G. A. 1976, Nature, 260, 751 In the text NASA ADS  
• Mattox, J. R. 1999a, in Proc. OJ-94 Annual Meeting 1999, ed. C. M. Raiteri, M. Villata, & L. O. Takalo, Blazar Monitoring towards the Third Millennium (Osservatorio Astronomico di Torino, Pino Torinese), 44 In the text  
• Mattox, J. R. 1999b, PASPC, 189, 95  
• Mead, A. R. G., Ballard, A. R., Brand, P. W. J. L., et al. 1990, A&AS, 83, 183 In the text NASA ADS  
• Moles, M., Garcia-Pelayo, J., Masegosa, J., & Aparicio, A. 1985, ApJS, 58, 255 In the text NASA ADS  
• Noble, J. C., & Miller, H. R. 1996, PASPC, 110, 30 In the text  
• O'Dell, S. L., Puschell, J. J., & Stein, W. A. 1977, ApJ, 213, 351 NASA ADS  
• O'Dell, S. L., Puschell, J. J., Stein, W. A., et al. 1978a, ApJ, 224, 22 In the text NASA ADS  
• O'Dell, S. L., Puschell, J. J., Stein, W. A., & Warnier, J. W. 1978b, ApJS, 38, 267 NASA ADS  
• O'Dell, S. L., Dennison, B., Broderick, J. J., et al. 1988, ApJ, 326, 668 In the text NASA ADS  
• Pica, A. J., Smith, A. G., & Pollock, J. T. 1980, ApJ, 236, 84 In the text NASA ADS  
• Pollock, J. T., Pica, A. J., Smith, A. G., et al. 1979, AJ, 84, 1658 NASA ADS  
• Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran - The Art of Scientific Computing (Cambridge University Press) In the text  
• Rabbette, M., McBreen, B., Steel, S., & Smith, N. 1996, A&A, 310, 1 In the text NASA ADS  
• Raiteri, C. M., Villata, M., Sobrito, G., et al. 1999, PASPC, 159, 135  
• Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 In the text NASA ADS  
• Rieke, G. H., Grasdalen, G. L., Kinman, T. D., et al. 1976, Nature, 260, 754 In the text NASA ADS  
• Romero, G. E., Cellone, S. A., & Combi, J. A. 2000, A&A, 360, L47 In the text NASA ADS  
• Roy, M., Papadakis, I. E., Ramos-Colón, E., et al. 2000, ApJ, 545, 758 In the text NASA ADS  
• Sillanpää, A., Haarala, S., & Korhonen, T. 1988a, A&AS, 72, 347 In the text NASA ADS  
• Sillanpää, A., Haarala, S., Valtonen, M. J., Sundelius, B., & Byrd, G. G. 1988b, ApJ, 325, 628 In the text NASA ADS  
• Sillanpää, A., Mikkola, S., & Valtaoja, L. 1991, A&AS, 88, 225 In the text NASA ADS  
• Sitko, M. L., & Sitko, A. K. 1991, PASP, 103, 160 In the text NASA ADS  
• Smith, A. G., & Nair, A. D. 1995, PASPC, 107, 863 In the text  
• Smith, P. S., Balonek, T. J., Heckert, P. A., Elston, R., & Schmidt, G. D. 1985, AJ, 90, 1184 In the text NASA ADS  
• Smith, P. S., Balonek, T. J., Elston, R., & Heckert, P. A. 1987, ApJS, 64, 459 In the text NASA ADS  
• Spinrad, H., & Smith, H. E. 1975, ApJ, 201, 275 In the text NASA ADS  
• Stickel, M., Fried, J. W., & Kühr, H. 1988, A&A, 198, L13 In the text NASA ADS  
• Takalo, L. O., Sillanpää, A., Nilsson, K., et al. 1992, A&AS, 94, 37 In the text NASA ADS  
• Takalo, L. O., Sillanpää, A., Valtaoja, E., et al. 1998, A&AS, 129, 577 In the text NASA ADS  
• Teräsranta, H., Tornikoski, M., Valtaoja, E., et al. 1992, A&AS, 94, 121 In the text NASA ADS  
• Teräsranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 In the text NASA ADS  
• Ulrich, M.-H., Maraschi, L., & Urry, C. M. 1997, ARA&A, 35, 445 In the text NASA ADS  
• Urry, C. M. 1999, PASPC, 159, 3 In the text  
• Valtaoja, E., Teräsranta, H., Tornikoski, M., et al. 2000, ApJ, 531, 744 In the text NASA ADS  
• Villata, M., & Raiteri, C. M. 1999, A&A, 347, 30 In the text NASA ADS  
• Villata, M., Raiteri, C. M., Sillanpää, A., & Takalo, L. O. 1998, MNRAS, 293, L13 In the text NASA ADS  
• Villata, M., Raiteri, C. M., Tosti, G., et al. 1999, in Proc. OJ-94 Annual Meeting 1999, ed. C. M. Raiteri, M. Villata, & L. O. Takalo, Blazar Monitoring towards the Third Millennium (Osservatorio Astronomico di Torino, Pino Torinese), 73 In the text  
• Villata, M., Mattox, J. R., Massaro, E., et al. 2000, A&A, 363, 108 In the text NASA ADS  
• Villata, M., et al. 2001, A&A, in preparation In the text  
• Webb, J. R., & Smith, A. G. 1989, A&A, 220, 65 In the text NASA ADS  
• Webb, J. R., Smith, A. G., Leacock, R. J., et al. 1988, AJ, 95, 374 In the text NASA ADS  
• Webb, J. R., Howard, E., & Balonek, T. 1997, IAU Circ., 6766 In the text  
• Webb, J. R., Howard, E., Benítez, E., et al. 2000, AJ, 120, 41 In the text NASA ADS  
• Xie, G. Z., Li, K. H., Liu, F. K., et al. 1992, ApJS, 80, 683 In the text NASA ADS  
• Xie, G. Z., Li, K. H., Zhang, X., Bai, J. M., & Liu, W. W. 1999, ApJ, 522, 846 In the text NASA ADS