A&A 377, 672-676 (2001)
DOI: 10.1051/0004-6361:20011113

A model for the strings of ${\eta}$ Carinae

N. Soker

Department of Physics, University of Haifa at Oranim, Tivon 36006, Israel

Received 11 June 2001 / Accepted 8 August 2001

Abstract
We propose a model based on ionization shadows to explain the formation of the long and narrow strings of ${\eta}$ Carinae. Five strings are known, all located along the symmetry axis outside the Homunculus. The model assumes that each string is formed in a shadow behind a dense clump near the symmetry axis. The surrounding gas is ionized first, becomes much hotter, and compresses the gas in the shadow. This leads to the formation of a radial, dense, long, and narrow region, i.e., a string. Later the neutral material in the strings is ionized, and becomes brighter. Still later it re-expands, and we predict that in $\sim$ $100{-}200 ~\rm {yrs}$ the strings will fade. The condition for the model to work is that the ionization front, due to the diffuse ionizing recombination radiation of the surrounding gas, proceeds into the shadow at a velocity slower than the compression speed, which is about the sound speed. From that we get a condition on the mass loss rate of the mass loss episode that formed the strings, which reads $\dot M_{\rm s} \mathrel{<\kern-1.0em\lower0.9ex\hbox{$\sim$ }}10^{-4}~M_\odot\,\rm {yr}^{-1}$. The model can also explain the strings in the planetary nebula NGC 6543.

Key words: stars: early-type - stars: mass loss - stars: individual: ${\eta}$ Carinae - ISM: planetary nebulae: individual: NGC 6543 - ISM: reflection nebulae


1 Introduction

There are several open questions regarding the formation of the nebulosity around the massive star ${\eta}$ Carinae (Davidson & Humphreys 1997; hereafter DH97). Some of the questions concern the nature and formation process of the strings (Weis et al. 1999, hereafter WDC; Weis 2001). WDC identified 5 strings, which are long, $\sim$0.1, and narrow, width of $\sim$0.002, almost straight filaments, denser than their environment, and located close to the symmetry (major) axis of the Homunculus, but outside the Homunculus. They expand radially, following a Hubble-type law, with velocity increasing from $\sim$450 kms-1 in the parts closest to the central star, to $\sim$900 kms-1 at their ends away from the central star (WDC; Weis 2001). From their kinematics it seems that the material in the strings was expelled during the Great Eruption of 1850, or just prior or after the eruption. Interestingly, the planetary nebula (PN) NGC 6543 has filaments similar in many properties to those of ${\eta}$ Car (WDC); they have the same general shape, same relative location, i.e., outside the main nebula near the symmetry (major) axis, and they are also much fainter than the main shell. Kinematically, they expand at much lower velocities $\sim$50 kms-1 (Balick & Preston 1987), as expected in PNe, and their distance to the central star of NGC 6543 is about half the distance of the filaments of ${\eta}$ Car to the center. As discussed later, the proposed model can also explain the formation of the filaments in the PN NGC 6543.

In the present paper we propose a model for the formation of the strings. The explanation for the Hubble-type expansion law of the strings is beyond its scope. We only propose a model for the formation of the long and narrow radial strings, assuming they are formed from material that is already expanding by a Hubble-type law. We propose that each string was formed by the compression of neutral cool gas in an ionization shadow. The surrounding gas was ionized first, and its temperature and pressure became larger by a factor of $\sim$10 than the still cool gas in the shadow. Hence the surrounding gas compresses the gas in the shadow, forming a radially long and narrow tail in the shadow, a string. Garcia-Segura et al. (1999) include photoionization in their gasdynamical numerical simulations of PNe evolution, and convincingly show that ionization shadow is capable of forming dense, radial, straight, and narrow filaments. Nor do we deal with the origin of the material, which could have been expelled by ${\eta}$ Car itself, or was first accreted by a companion and then expelled by the companion (Soker 2001). The proposed model is outlined in Sect. 2. In Sect. 3 we show that it is quite possible that the companion (if it exists) also played a role in the ionization process. The conditions for the formation of the strings from ionization shadows are derived in Sect. 4. A summary of main results is in Sect. 5.

2 The proposed model

The proposed model for the formation of the strings is that of an ionization shadow behind a dense clump. The ionization front proceeds much slower inside the dense clump, hence the clump shades the region behind it from the ionizing radiation, at least during part of the time until it is completely evaporated (e.g., Lopez-Martin et al. 2001). The shadow stays cool, at $T < 10^3 ~\rm {K}$, while its surroundings are ionized and heated, hence it is compressed to a higher density (Cantó et al. 1998; Pavlakis et al.2001). An ionization shadow model for the formation of radially aligned narrow structures was discussed in the context of PNe (Soker 1998, 2000). The strings of ${\eta}$ Car are different in several respects from the situations studied by Soker (1998, 2000). First, the strings in ${\eta}$ Car are very narrow, hence a steady-state neutral tail behind a dense clump cannot be reached (Cantó et al. 1998, Fig. 4; Pavlakis et al. 2001). Second, the structures studied by Soker were located in a dense region in the PN shell, unlike the strings of ${\eta}$ Car, which are located in relatively low density regions outside the main shell of the nebula. The very narrow strings of the PN NGC 6543 (WDC) are also located in a (relatively) low density region outside the dense shell of NGC 6543. Third, the material in ${\eta}$ Car expands with velocities of $\mathrel{>\kern-1.0em\lower0.9ex\hbox{$\sim$ }}$ $400~\rm {km}\,\rm {s}^{-1}$, much faster than the sound speed, unlike in PNe, where the two speeds are comparable.

Because of these differences, the proposed model does not deal with a steady-state model, where a neutral shadow exists until the shadowing clump is ionized; instead it is a dynamic model, where the strings exist for a relatively short time. Before describing the model, we emphasize that the relevant mass loss rates are those along the polar directions (mass loss rate per unit solid angle) were the strings are found, and not the average or equatorial mass loss rates. The scenario has four main phases.
Phase 1 (20 years): during the 20 years of the Great Eruption of 1850 the star lost $\sim$ $2.5~M_\odot$ (DH97). Because of the large optical depth during the eruption, the gas in the wind recombined and cools, down to $T < 10^3 ~\rm {K}$, after leaving the star and expanding. From the shape of the nebula, it seems that the mass loss rate along the polar directions was lower than average, allowing earlier ionization along these directions at later times.
Phase 2 ($\sim$50 years): after the eruption, the average mass loss rate probably dropped to something like its present value of $\dot M \sim 10^{-4}~M_\odot \,\rm {yr}^{-1}$ (DH97; Corcoran et al. 2001b). The mass loss rate increased for a short period of time during the lesser eruption of 1890, but we ignore this mass loss episode (we have no data on the polar mass loss rate, which is relevant for us). As the dense material from the great eruption expanded, the ionization front moved outward. With ionization of fresh neutral material being disregarded, the ionization front $r_{\rm i}$ is given by the equality of the photon luminosity $\dot S_1$ to the total recombination rate

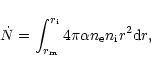\begin{displaymath}\dot N = \int_{r_{\rm m}}^{r_{\rm i}} 4 \pi \alpha n_{\rm e} n_{\rm i} r^2 {\rm d}r, \end{displaymath} (1)

where $r_{\rm m}$ is the minimum radius outer to which recombination occurs, $\alpha$ is the recombination coefficient, and $n_{\rm e}$ and $n_{\rm i}$ are the electron and ion density, respectively (for the purpose of the present paper we can take $n_{\rm i}=n_{\rm p}$, where $n_{\rm p}$ is the proton number density). The wind's density is $\rho = \dot M_{\rm GE} / (4 \pi r^2 v)$, where  $\dot M_{\rm GE}$ is the mass loss rate along the polar directions during the great eruption and v the expansion velocity. We first neglect recombination by the lower density wind blown during the second phase (see next section), and consider the dense material from the Great Eruption, with its inner boundary expanding at $v \sim 650 ~\rm {km}\,\rm {s}^{-1}$, and its outer boundary ejected 20 years earlier (the duration of the Great Eruption). Substituting typical values, taking the mass loss rate along the polar direction to be half the average value, and integrating Eq. (1), we obtain the time when the the entire nebula along the polar direction was ionized.
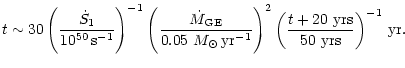$\displaystyle t\sim 30 \left( {{\dot S_1}\over{10^{50} \,\rm {s}^{-1}}} \right)... ...ht)^2 \left( {{t + 20 ~\rm {yrs}}\over{50 ~\rm {yrs}}} \right)^{-1} \,\rm {yr}.$     (2)

We note that a small drop in the mass loss rate along the polar directions can shorten this phase. On the other hand, including ionization of the wind blown by the central star during this phase will give a longer time. Hence we estimate this phase to last $\sim$50 $~\rm {yrs}$. The possibility that the companion plays a role in the ionization process is examined in the next section.
Phase 3 ($\sim$100-200 years): the models assumes that very dense clumps exist along and near the polar directions. These can be formed from in situ instabilities, or from inhomogeneous mass loss process. Hillier et al. (2001) argue that the wind from ${\eta}$ Car is clumpy indeed. Their formation process is beyond the scope of the present paper. The dense clumps form a shadow behind them, so that while the surroundings of the shadow are ionized by stellar radiation, the shadow is ionized by the diffuse recombination radiation. If the ionization, and heating, of the shadow proceeds at a time scale longer than the sound crossing time of the shadow, the hot surrounding gas compresses the cooler gas in the shadow to a higher density, forming a long straight string. The conditions for this to occur are derived in Sect. 4. A typical string width is $d_{\rm s}=0.002 \pc$ (Weis 2001). The compression proceeds at a velocity of the order of the sound speed of the surroundings, $\sim$ $15 ~\rm {km}\,\rm {s}^{-1}$, so that the sound crossing time of a half width (since the compression proceeds from all directions) is

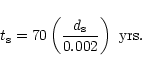\begin{displaymath}t_{\rm s} = 70 \left( {{d_{\rm s}}\over{0.002 \pc}} \right) ~\rm {yrs}. \end{displaymath} (3)

The initial width of the shadowing clump is larger, but after compression (see Sect. 4) the density increases by a factor of $\sim$10 (assuming a pressure equilibrium between the two regions) and the width of the compressed region decreases by a factor of up to $\sim$3. This means that the sound crossing time can be longer, and so can the ionization time by the diffuse radiation. Hence this phase may last $\sim$ $150{-}200 \,\rm {yr}$. If the shadowing clump is ionized in the mean time, then this phase will be shorter. Over all, we take this phase to last $100{-}200 \,\rm {yr}$. Straight, radial, and dense filaments formed by ionization shadow can be clearly seen in the numercial simulations of PNe evolution performed by Garcia-Segura et al. (1999; e.g., their Fig. 2 model G). They also show that ionization front can form the required instabilities to form dense clumps.
Phase 4 ( $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...200-300 years): eventually the shadow is ionized by the diffuse radiation, grows hotter, and reexpands at a time scale of $\sim$100 years. If the shadowing clump still exists, it may stay somewhat cooler and denser than its surroundings, by a factor of $\sim$2 (Cantó et al. 1998), until the entire clump is evaporated and the stellar radiation reaches the shadow. In any case, a steady-state shadow cannot exist in most cases in PNe (Pavlakis et al. 2001), as well as in ${\eta}$ Car. It is very likely that the reexpansion phase has started already. We therefore predict that in $\sim$100 years the strings will fade substantially, and may even disappear.

3 Primary versus secondary ionization

The proposed model involves ionization by the central source along and near the polar directions, as discussed in the previous section. This section examines the possibility that the companion (if it exists) plays a role, even a dominant one, in the ionization process. Let the mass loss rate from the primary star (${\eta}$ Car itself) and the expansion velocity during the relevant ionization epoch be $\dot M_{\rm i}$, and $v_{\rm i}$, respectively, so that the wind's density in a spherical geometry is $\rho = \dot M_{\rm i} / (4 \pi r^2 v_{\rm i})$. Neglecting ionization of new material, assuming spherical symmetry, and neglecting material from the Great Eruption, we find that the ionization front $r_{\rm i}$ is given by the equality of the photon luminosity $\dot S_1$ with the total recombination rate. The recombination rate is given by Eq. (1), with the mass loss rate and velocity being  $\dot M_{\rm i}$ and $v_{\rm i}$, respectively, and $r_{\rm m}$ is the stellar radius, $r_{\rm m}=R_1=0.4$ AU (DH97). Substituting other typical values we obtain the condition for ionization of the entire nebula

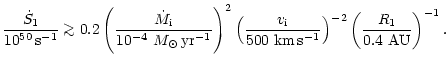$\displaystyle {{\dot S_1}\over{10^{50} \,\rm {s}^{-1}}} \mathrel{\mathchoice {\... ...\,\rm {s}^{-1}}} \right)^{-2} \left( {{R_1}\over {0.4 ~\rm {AU}}} \right)^{-1}.$     (4)

We now consider the ionizing radiation from the secondary, assuming that during the relevant ionization phase (see next section) the secondary does not blow a dense neutral wind along the polar directions, i.e., $\dot M_2 \mathrel{<\kern-1.0em\lower0.9ex\hbox{$\sim$ }}10^{-5}~M_\odot \,\rm {yr}^{-1}$. We also assume that there is no dense accretion flow along the polar directions near the companion. For the companion and orbital parameters we take values which were used in recent years (e.g., Ishibashi et al. 1999; Damineli et al. 2000; Corcoran et al. 2001a, 2001b): mass $M_2=30~M_\odot$, semimajor axis $a=15 ~\rm {AU}$ and eccentricity e=0.8. Let the momentary distance between the two stars be D, and let h be the length along a line perpendicular to the orbital plane and crossing the momentary position of the secondary. The density of the wind blown by the primary as a function of h is $\rho(h)= \dot M_{\rm i} / [4 \pi (D^2 + h^2) v_{\rm i}]$. The total recombination rate per unit solid angle along the direction h is given by

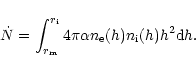\begin{displaymath}\dot N = \int_{r_{\rm m}}^{r_{\rm i}} 4 \pi \alpha n_{\rm e}(h) n_{\rm i}(h) h^2 {\rm d}h. \end{displaymath} (5)

The integral can be solved analytically. Taking $r_{\rm i} \gg r_{\rm m}=0$, i.e., the entire nebula is ionized, we find

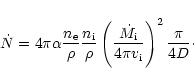\begin{displaymath}\dot N = 4 \pi \alpha {{n_{\rm e}}\over{\rho}} {{n_{\rm i}}\o... ...m i}}\over{4 \pi v_{\rm i}}} \right)^2 {{\pi}\over{4 D}}\cdot \end{displaymath} (6)

Note that along a line from the primary the last term reads 1/R1 instead of $\pi/4 D$. Substituting typical values for the companion: $\dot S_2$, which is the ionizing photon luminosity for a main sequence star of $M_2 \simeq 30~M_\odot$, for a semimajor axis of $15 ~\rm {AU}$ the orbital separation will be >15 $~\rm {AU}$ during most of the orbital period, so that we scale D with  $20 ~\rm {AU}$. The condition for ionizing the entire material along the polar directions by the companion reads
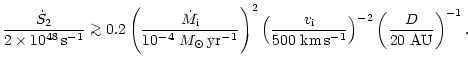$\displaystyle {{\dot S_2}\over{2 \times 10^{48} \,\rm {s}^{-1}}} \mathrel{\math... ...km}\,\rm {s}^{-1}}} \right)^{-2} \left( {{D}\over {20 ~\rm {AU}}} \right)^{-1}.$     (7)

By comparing the conditions for full ionization along the polar directions, Eq. (4) for the primary and Eq. (7) for the secondary, we see that in principle both can be the ionization source, during the phases when the mass loss rate is $\dot M_{\rm i} \mathrel{<\kern-1.0em\lower0.9ex\hbox{$\sim$ }}10^{-4}~M_\odot \,\rm {yr}^{-1}$, the third and fourth phases in the scenario plotted in the previous section. Which of the two ionizing source dominates depends on details such as the departure of mass loss from sphericity and the properties of the wind blown by the companion. In any case, the proposed model for the strings can hold for the cases where no binary companion exists. Two phenomena suggest that the companion indeed plays a role. (1) All the presently known strings are located to the same side of the long axis of the ${\eta}$ Car nebula (WDC). This departure from axisymmetry hints at a role played by a companion in their formation (Soker 2001). (2) The ionization structure near the central source changes on a time scale of 5.5 years (e.g., Smith et al. 2000), which is taken to be the orbital period of the binary system (Damineli 1996; Damineli et al. 2000).

4 Ionization shadow

The proposed model for the formation of the strings is described in Sect. 2. We now derive the conditions for the model to work. Most of the basic physics used below can be found, e.g., in Cantó et al. (1998). Let the proton and electron number densities in the strings' surroundings be $n{\rm _p}$ and $n_{\rm e}$, respectively, and let $n_{\rm H}$be neutral hydrogen number density in the neutral shadow. At phase 3 of the model (see Sect. 2), the surrounding gas is fully ionized and optically thin to ionzing photons. The recombination of the surrounding gas yields a diffuse ionizing flux of $F_{\rm d}=n_{\rm e} n_{\rm p} \alpha_1 l_{\rm r}/4$, where $l_{\rm r}$ is the size of the recombining region, which we take to be of the order of the radius r, and $\alpha_1$ is the recombination coefficient to the ground state of hydrogen. The ionization front proceeds into the neutral shadow at a speed of $c_{\rm i} \simeq F_{\rm d}/n_{\rm H} \simeq F_{\rm d}/n_{\rm p}$. For the shadow to be compressed we require $c_{\rm i}<c_{\rm s}$, where $c_{\rm s} \simeq 15 ~\rm {km}\,\rm {s}^{-1}$ is the sound speed of the ionized surrounding gas. Therefore, our condition for the compression of a long dense tail in the shadow reads $15 {~\rm {km}\,\rm {s}^{-1}} > n_{\rm e} \alpha_1 r /4$, or

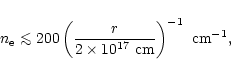\begin{displaymath}n_{\rm e} \mathrel{\mathchoice {\vcenter{\offinterlineskip\ha... ...ver{ 2 \times 10^{17} ~\rm {cm}}} \right)^{-1} ~\rm {cm}^{-1}, \end{displaymath} (8)

where for the distance we took the distance of the parts of the strings closest to the central star 75 years ago, $r \simeq 2 \times 10^{17} ~\rm {cm}$ (considering the inclination of the strings; see WDC). The electron density is a function of the mass loss rate, velocity, and distance to the central star, hence the condition above can be written as

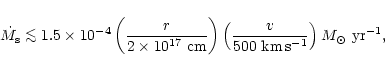\begin{displaymath}\dot M_{\rm s}\mathrel{\mathchoice {\vcenter{\offinterlineski... ...00 ~\rm {km}\,\rm {s}^{-1}}} \right) M_\odot\,\,\rm {yr}^{-1}, \end{displaymath} (9)

where $\dot M_{\rm s}/4\pi$ is the mass loss rate per unit solid angle of the mass loss episode that formed the strings.

The condition on the mass loss rate may seem very stringent, since the average mass loss rate during the great eruption was much higher, $\dot M_{\rm GE} \sim 0.1~M_\odot \,\rm {yr}^{-1}$. But noting the following we argue that this requirement is quite reasonable. First, the strings are located near the long axis of the nebula - the polar directions - and outside the dense part of the nebula. In the main nebula the mass loss rate per unit solid angle along the polar directions is lower than near the equatorial plane, and the mass loss rate which formed the regions outside the main nebula - the Homunculus - were much lower. Therefore, it is likely that the mass loss rate that formed the strings was relatively low. Indeed, from Chandra X-ray observations Seward et al. (2001) deduce a density of $n_H \simeq 50 ~\rm {cm}^{-3}$ in the outskirts of ${\eta}$ Car. Second, WDC show that the PN NGC 6543 contains strings which are similar, in their shape, location, and relative brightness, to those in ${\eta}$ Car. The maximum mass loss rates from asymptotic giant branch progenitors of PNe are $\dot M_{\rm max} \sim 10^{-4}~M_\odot \,\rm {yr}^{-1}$. NGC 6543 does not contain a dense equatorial flow, and the mass loss rate of its progenitor was probably lower, say < $3 \times 10^{-5}~M_\odot \,\rm {yr}^{-1}$. The strings of NGC 6543, which are much fainter than the shell, were formed from a much lower mass loss rate, $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ... $ 3 \times 10^{-6}~M_\odot \,\rm {yr}^{-1}$. We conclude that condition (9) for the formation of the strings of ${\eta}$ Car by ionization shadow is reasonable.

The immediately surrounding gas enters the shadow while compressing the material in the shadow. The recombining time of this material is $\tau_{\rm rec} \simeq 10^3 (n_{\rm e}/100 ~\rm {cm}^{-3})^{-1} \,\rm {yr}$, which is longer than any other relevant time scale. However, the neutral material in the shadow is compressed to an order of magnitude of larger densities, and after being ionized, and before re-expanding, the recombination time is comparable to the re-expansion time $\sim$ $100 \,\rm {yr}$. The recombination of the dense material of the strings makes their formation process more efficient, since their ionization time by the diffuse ionizing radiation takes somewhat longer.

The typical width of the filaments is $\sim$$0.002 \pc$(Weis 2001). If the material was compressed to a density $\sim$10 times higher, the initial width of the material in the long strings was $\sim$3 times larger, i.e. $\sim$$0.006 \pc$. As discussed above, the closest to the central star parts of the strings were at $r \simeq 0.06 \pc$ when the ionization of their surroundings started according to the proposed model. This means that the typical size (diameter if spherical) of the shadowing clumps was $D_{\rm clump} \sim 0.1 r \sim 2 \times 10^{16} ~\rm {cm}$. This is a reasonable size for clumps formed by instabilities, e.g., from winds collision (Dwarkadas & Balick 1998). Narrower filaments, if formed, are short lived. First, the shadowing clump is small and it will evaporate in a short time (assuming it is more or less spherical). Second, even if a compressed tail is formed, it will be ionized and re-expand in a short time. Wider strings can in principle be formed. The question is whether dense clumps of such larger sizes exist. Since the formation process of the dense clumps is beyond the scope of the present paper, we will not comment on this further (see Garcia-Segura et al. 1999).

5 Summary

We proposed a model to explain the formation of the long and narrow strings of ${\eta}$ Car, which are located along the symmetry axis outside the Homunculus. Five such strings were identified by WDC in ${\eta}$ Carinae, and similar strings exist in the PN NGC 6543 (WDC). The Hubble-type expansion law of the strings was beyond the scope of the present paper, and we assumed that the material in the strings had the Hubble-type expansion law before it was compressed. The model assumes that dense clumps near the symmetry axis form an ionization shadow behind them. The surrounding gas is ionized first, becomes much hotter, and compresses the gas in the shadow. This leads to the formation of a radial, dense, long, and narrow region, i.e., a string (Garcia-Segura 1999). Later the neutral material in the strings is ionized, and becomes brighter. Still later it re-expands, and we predicted that in $\sim$ $100{-}200 ~\rm {yrs}$ the string would fade.

We also showed that the companion, if it exists, may play a significant role in the ionization of the strings' surroundings. The condition for the model to work is that the ionization front, due to the diffuse ionizing recombination radiation of the surrounding gas, proceeds into the shadow at a velocity slower than the compression speed, which is about the sound speed. From this we obtain a condition on the density of the strings' surroundings (electron density in Eq. (8)), or on the mass loss rate of the mass loss episode that formed the strings (Eq. (9)). The mass loss rate is much below the average mass loss rate during the Great Eruption of 1850, but we argue that is is quite reasonable along and near the major axis and for material outside the Homunculus.

Acknowledgements
I thank the referee, A. Raga, for his helpful comments. This research was supported in part by grants from the US-Israel Binational Science Foundation.

References

 
Copyright ESO 2001