A&A 377, 473-484 (2001)
DOI: 10.1051/0004-6361:20011135

Statistics and supermetallicity: The metallicity of NGC 6791

B. J. Taylor

Department of Physics and Astronomy, N283 ESC, Brigham Young University, Provo, UT 84602-4360, USA

Received 9 February 2001 / Accepted 9 August 2001

Abstract
For the old galactic cluster NGC 6791, Peterson & Green (1998a) and Chaboyer et al. (1999) have found that [Fe/H] $\sim +0.4$ dex. A second look at that conclusion is taken in this paper. Zero-point problems are reviewed for a high-dispersion analysis done by Peterson & Green, and it is found that accidental errors have not been determined rigorously for the results of that analysis. It is also noted that in a color-magnitude analysis performed by Chaboyer et al., the important metallicity range between 0.0 and +0.3 dex is not explored and hence is not ruled out. Moreover, that analysis does not yield statistically rigorous results, and it appears that such results may not be produced in color-magnitude analysis of clusters in general. Results in the two cited papers and elsewhere are re-evaluated statistically, with an allowance being made for uncertainty in the cluster reddening. Apparently the best that can be said at present is that the cluster metallicity lies in the range from +0.16 to +0.44 dex. This conclusion is stressed by reviewing the immaturity of the underlying data base. The premature conclusion for a high metallicity turns out to be due largely to neglect of accidental errors, though a tendency to ascribe too much weight to high derived metallicities may also play a role.

Key words: stars: abundances - open clusters and associations: individual: NGC 6791


1 Introduction

For the "super-metal-rich'' star $\mu$ Leo, Taylor (1999c) has noted a tendency to adopt high metallicities and describe them in striking language. A lower metallicity is found if the results available for $\mu$ Leo are assessed statistically. It is natural to ask whether a similar problem can be found elsewhere. To answer this question, one would look for a star or cluster with a) a history of non-statistical analysis and b) a high derived metallicity. On both counts, the old galactic cluster NGC 6791 is a promising candidate. In two conspicuous papers, the value of [Fe/H] for this cluster is quoted as $+0.4 \pm 0.1$ dex (Peterson & Green 1998b; Chaboyer et al. 1999). No statistical analysis appears in these papers, and little or no such analysis can be found in other papers on the cluster metallicity.

In this paper, the metallicity of NGC 6791 is reappraised statistically. Accidental errors and their implications receive special attention. In Sect. 2, literature conventions for depicting and using accidental errors are reviewed. The papers of Peterson & Green and Chaboyer et al. are considered in Sects. 3 and 4, respectively. Pertinent results in additional papers are discussed in Sects. 5 through 7. A survey of the collected metallicity determinations is given in Sect. 8. In Sect. 9, a concluding summary is given.

2 The use and meaning of accidental errors

Accidental errors (whether stated or not) have played a pivotal role in interpreting derived metallicities for NGC 6791. To prepare for a discussion of that role, the proper use of accidental errors will be reviewed here. The conventions for depicting such errors in the literature will also be discussed.

It is useful to base a review like this one on a specific (if hypothetical) numerical example. The example chosen here is the following data vector:

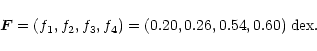\begin{displaymath}{\vec F} = (f_1, f_2, f_3, f_4 ) = (0.20, 0.26, 0.54, 0.60) \mkern6mu {\rm dex}. \end{displaymath} (1)

To define two kinds of rms error to be considered below, let N = 4,

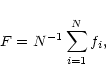\begin{displaymath}F = N^{-1} \sum_{i=1}^N f_i, \end{displaymath} (2)


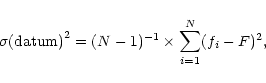\begin{displaymath}\sigma{\rm (datum)}^2 = (N-1)^{-1} \times \sum_{i=1}^N (f_i - F)^2, \end{displaymath} (3)

and

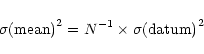\begin{displaymath}\sigma{\rm (mean)}^2 = N^{-1} \times \sigma{\rm (datum)}^2 \end{displaymath} (4)

(see Eqs. (4.5), (4.9), and (4.14) of Taylor 1982, respectively). The quantities $\sigma$(datum) and $\sigma$(mean) are the "rms error per datum'' and the "rms error of the mean'', respectively.

By applying Eqs. (1)-(4), one finds that the mean value of F is

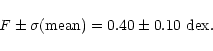\begin{displaymath}{\it F} \pm \sigma{\rm (mean)} = 0.40 \pm 0.10 \mkern6mu {\rm dex}. \end{displaymath} (5)

Equation (5) establishes a so-called "confidence interval''. In general, there is a probability $P \leq 0.683$ that the unknown true average falls within the interval ${\it F} \pm \sigma$(mean)[*]. Moreover, F and $\sigma$(mean) are available for use in statistical tests.

Suppose now that in three published papers, the mean of F is quoted in the following three ways:

1.
$0.40 \pm 0.30$ dex,
2.
$0.40 \pm \sigma{\rm (datum)} = 0.40 \pm 0.20$ dex, and
3.
0.40 dex.
The error bar in the first of these alternatives may include a contribution for estimated systematic effects. In any event, such an error bar is neither $\sigma$(mean) nor $\sigma$(datum). Almost always, these three alternatives are not given with auxiliary information. Note that in all of them, both advantages of rigorous statement like that in Eq. (5) are lost. None of the three examples depict rigorous confidence intervals, so speaking strictly, one does not know what any of the examples mean. Moreover, F and $\sigma$(mean) are not available for statistical testing. In these edited forms, the potential usefulness of the mean datum is seriously limited.

Despite such problems, literature convention in stellar astronomy permits all three of these alternatives. For example, Montgomery et al. (1994) quote a mixed accidental and systematic error in their Sect. 3.1. Cayrel et al. (1985) quote their principal result with two error bars, and while one of them is a pure accidental error, the second (and preferred) error bar includes an allowance for systematic effects. Since the publication of Cayrel et al., their result has sometimes been quoted without any error bar (see, for example, Carney et al. 1987; Griffin & Holweger 1989). Ka\luzny & Udalski (1992; see their Table 1 data and Sect. 2.1) quote $\sigma$(datum) instead of $\sigma$(mean). Two further examples of alternative (2) are given in Sect. 6.1[*].

3 The case for [Fe/H] $\mathsf{= +0.4}$ dex: Peterson & Green (1998b)

3.1 An assessment of systematic effects

In support of a high metallicity for NGC 6791, Peterson & Green (1998b) perform a high-dispersion analysis. Those authors derive the following values of [Fe/H] for a star in NGC 6791:

The star in question is called 2-17 and has a spectral type near F0. "PDOK'' and "K+95'' refer to Peterson et al. (1993) and Kraft et al. (1995), respectively[*]. The third quoted value appears to be an average of the first two, with numbers rounded down to one decimal place. That result will be referred to below as the "PG mean.''

A possible systematic uncertainty in these results may be produced by line-strength contrasts between 2-17 and the Sun. According to Peterson & Green, they limit the effects of such contrasts by analyzing a star which is hotter than the Sun as well as being more metal-rich (see their Sect. 1). However, they do not note that the equivalent widths of the four weakest lines they measure are still about 0.5 dex lower in 2-17 than they are in the Sun (compare Kurucz et al. 1984 and Table 1 of Peterson & Green). Because of that contrast, Peterson & Green point out later in their paper (see their Sect. 2) that a differential comparison of 2-17 to the Sun would not be straightforward. They note that for all but the weakest lines in their list, such an analysis could be hampered by the different amounts of damping in 2-17 and the Sun.

Instead of using differential analysis, Peterson & Green base their results on "external zeroing''. In this method, a value of the solar metallicity is subtracted from a stellar metallicity. The difference between the "PDOK'' and "K+95'' results is largely due to a difference between two adopted solar metallicities (see Peterson & Green, Table 2 and Sect. 2). To gauge the effects of that difference, both results will be retained here.

Another potential problem may be caused by use of a relatively small number of lines. For line numbers $N_{\rm L} < 10$, a set of Arcturus analyses which are closely comparable to each other yields values of [Fe/H] that scatter over more than 0.3 dex (Taylor 1998b, Table 3, entries 3 through 5). The possible scope of this problem might be reduced for the Peterson-Green analysis, for which $N_{\rm L} = 19$. However, the problem may nonetheless exist. If it does, there is no guarantee that either of the zero points adopted by Peterson & Green is correct. Moreover, there is no guarantee that the correct zero point lies between the two they adopt.

3.2 An assessment of accidental error

A second question of interest is the [Fe/H] error bar quoted above. To calculate it, Peterson & Green use a specific version of a procedure which is quite common in high-dispersion spectroscopy. They determine the changes in their derived value of [Fe/H] if a) effective temperature $T_{\rm c}$ is increased by $\delta T_{\rm c} = 80$ K or b) microturbulent velocity $v_{\rm t}$ is lowered by $\delta v_{\rm t} = 0.5$ kms-1. Upon finding that [Fe/H] changes by 0.06 dex in each case, they add these changes together to obtain their final error estimate of 0.12 dex. To determine a counterpart error estimate for log g, Peterson & Green proceed in much the same way. However, they combine two changes of 0.15 dex in an unstated way to yield a net log g uncertainty of 0.2 dex.

To determine a rigorous error bar from the Peterson-Green equivalent widths, one could use a maximum-likelihood analysis or the $\chi ^2$ statistic. The results would be stated as regions in parameter space where the unknown true solution may be found at a stated confidence level P. The adopted value of P might be 68% or 95%, since one or both of these choices are often used. Maximum-likelihood and $\chi ^2$ techniques are described by Lampton et al. (1976, Sect. III) and appear to have been used in X-ray astronomy for some decades.

The procedure adopted instead by Peterson & Green is fallacious. There are five reasons: 1) the authors do not explain their choices of  $\delta T_{\rm c}$ and  $\delta v_{\rm t}$, 2) they appear to combine the effects of $T_{\rm c}$ and $v_{\rm t}$ changes in one way for [Fe/H] and in another way for log g, 3) they do not show that either of those ways yields a rigorously meaningful confidence interval, 4) they do not state a value of P for that confidence interval, and 5) no allowance seems to be made for covariance between derived values of [Fe/H] and $v_{\rm t}$ (see Eq. (10.12) of Kendall & Stuart 1977). Though one might respond to these uncertainties by simply setting the interval aside, it can instead be adopted with a guess about its real meaning. This is the procedure that will be followed here.

A problem which affects procedures like that of Peterson & Green is the tendency for inspection to overrate the significance of discrepancies. Even if their intended value of P was 100%, their actual value of P could be near 68%. The assumption made here is that the Peterson-Green confidence interval yields a 68% confidence estimate for [Fe/H]. The resulting value of $\sigma$(mean) is 0.12 dex[*]. While the actual value of this error could be somewhat larger or smaller, it is reassuring to find that its estimated value resembles an rms error derived from data scatter by Taylor (1994a; see Sect. 3.8 of that paper).

To clarify the nature of this error bar, a non-standard depiction of the Peterson-Green metallicity will be adopted. Lampton et al. point out that if one wishes to express a confidence interval, there are a large number of alternatives to using a centered confidence interval of width 2$\sigma$(mean). The alternative chosen here is to quote a lower limit L(95) in addition to F and $\sigma$(mean). By definition, the unknown true value of [Fe/H] exceeds L(95) at a confidence level of 95%.

Calculations of L(95) are given in Table 1. Note that for the "PDOK'' datum, L(95) is no larger than +0.16 dex (see the boldface entry in Table 1). This limit is achieved without any allowance for the NL effect described in Sect. 3.1.


   
Table 1: 2-17: lower 95% confidence limits for Peterson-Green results${\rm ^a}$.

Quantity		 Entry

Number of contributing lines		 19
Number of parameters determined${\rm ^b}$ 3
Degrees of freedom ($\nu$) 16
$\sigma$ of mean 0.12
$t({\nu},C=0.95){\rm ^c}$ 1.746
[Fe/H](PDOK)${\rm ^d}$ 0.37
$L(95) = {\rm [Fe/H]}-{\sigma}t$ ${\bf0.16}$
[Fe/H](K+95)${\rm ^e}$ 0.48
$L(95) = {\rm [Fe/H]}-{\sigma}t$ 0.27
$^{{\rm a}}$  All entries for L(95), [Fe/H], and $\sigma$ are in dex.
$^{{\rm b}}$  [Fe/H], $\log g$, and microturbulent velocity v are determined.
$^{{\rm c}}$  This is the one-tail value. It applies for the two-tail case if the confidence level C is 0.9.
$^{{\rm d}}$  Based on the log gf system of Peterson et al. (1993).
$^{{\rm e}}$  Based on the log gf system of Kraft et al. (1995).

4 The case for [Fe/H] $\mathsf{= +0.4}$ dex: Chaboyer et al. (1999)

4.1 Analyzing color-magnitude diagrams: A contemporary appraisal

Chaboyer et al. (1999, hereafter CGL) derive conspicuous support for a high cluster metallicity by analyzing color-magnitude (C-M) diagrams. Before the CGL results are assessed, the procedures which are generally applied in C-M analysis of clusters will be reviewed from a statistician's viewpoint.

Like model-atmosphere analyses, C-M analyses are multi-parameter fits. To obtain solutions, selections of the following parameters are varied:

Other parameters that might also be adjusted include a) [element/Fe] ratios and b) the lower threshold p(thres) for the probability that a star is a cluster member, as derived from proper motions. So far, however, values of these latter parameters have been assumed instead of being derived from analyses.

To approach C-M analysis statistically, one might use methods such as those developed by Dolphin (1997) and Hernandez et al. (1999). It is instructive to contrast those procedures with the one which is actually employed. For NGC 6791 and (apparently) in general, C-M cluster fits are derived by using graphs alone. Moreover, results are usually stated without uncertainty ranges. In some papers, an uncertainty range is derived for a given parameter by comparing results from two trial solutions (see, for example, Ka\luzny 1990). However, the values of P for such ranges are not stated.

If analyses based on the prevailing procedure were critiqued by statistical standards, none of them would be acceptable for publication. Results stated without uncertainty ranges would be rejected as useless "bare averages'' with P=0%. Results with confidence ranges would be rejected because those ranges are formally meaningless, and it would be noted that their values of P have been concealed specifically by their non-rigorous derivation.

For NGC 6791 specifically, concern with statistical rigor is underscored by the fact that C-M diagrams are cluttered by binaries and (almost certainly) nonmembers. Values of p(thres) as low as 0.5 (Tripicco et al. 1995) or 0.4 (CGL) are sometimes adopted, thus seemingly guaranteeing that the clutter will not be negligible. To deal with that clutter, principal sequences in the C-M diagram are sometimes picked out by eye (see, for example, Carraro et al. 1994). In the process, a fairly large number of data may be set aside as wild points. It is not obvious that the results of such a procedure would be reproduced by statistical analysis.

4.2 The $\mathsfsl{B-V}$ ambiguity and the CGL C-M analysis

The issue of statistical versus non-statistical analysis is one of two fundamental issues at the foundation of the CGL analysis. The other issue is a tradeoff which may be called the "B-V ambiguity''. Suppose a horizontal shift $\Delta (B-V)$ exists between an isochrone and the principal sequences of NGC 6791. Potentially, this shift has two components:

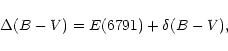\begin{displaymath}\Delta (B-V) = E(6791) + \delta (B-V), \end{displaymath} (6)

with E(6791) and $\delta (B-V)$ being a reddening term and a metallicity term, respectively (see Sect. 3.2 of Tripicco et al. 1995). The problem at hand is to determine either E(6791), $\delta (B-V)$, or both.

For some time, three different ways have been used to resolve the B-V ambiguity. One way is to assume a value of [Fe/H] and so effectively specify a value of $\delta (B-V)$ (see, for example, Demarque et al. 1992). A second way is to include independent information about E(6791) or [Fe/H] (see Ka\luzny & Rucinski 1995 and Tripicco et al. 1995, respectively). The third way is to replace B-V with $(V-I)_{\rm C}$ (Garnavich et al. 1994). A potential advantage of this third approach is the reduced metallicity sensitivity of $(V-I)_{\rm C}$ (see Table 1 of Buser & Kurucz 1992).

CGL adopt a fourth approach. They analyze two data sets, with each set yielding one C-M diagram based on BV photometry and another based on $VI_{\rm C}$ photometry. For each data set, CGL adopt the following vector of trial values of [Fe/H]: (0.0, +0.3, +0.4, +0.5) dex. Their C-M analysis yields a corresponding vector of values of E(6791). Taken together, these two vectors define a metallicity-reddening locus in parameter space. (For plotted examples of such loci, see the dashed lines in Fig. 9 of Tripicco et al. 1995). Ultimately, CGL adopt a range of metallicities and reddenings along their derived locus. That range is chosen to include the C-M fits that CGL deem to be best.

CGL analyze $VI_{\rm C}$ data from Montgomery et al. (1994). In addition, they analyze counterpart M 67 photometry from Montgomery et al. (1993). CGL find that the two clusters yield similar discrepancies at the turnoff point and along the main sequence. In addition, CGL note that some Montgomery et al. observing runs yielded data for both clusters. It would therefore seem feasible to derive corrections from the M 67 photometry, apply them to the photometry for NGC 6791, and then analyze the corrected photometry. However, CGL do not do this. Instead, they accept the fitting problems with the Montgomery et al. (1994) photometry throughout their analyses of NCG 6791.

The problem with the $VI_{\rm C}$ photometry is one of four tactical issues raised by the CGL analysis. CGL do not follow Garnavich et al. (1994) by using radial velocities to define a giant branch for NGC 6791. In addition, CGL use p(thres) = 0.4 for NGC 6791, as noted above. For these reasons and because of the effects of binaries, the color-magnitude diagrams analyzed by CGL are quite cluttered. Finally, CGL go on to solve for all five parameters in the list given in Sect. 4.1. The problem with this approach is that confidence intervals increase in size with the number of parameters solved for, so GGL might fail to detect a condition in which their results are not meaningful because their confidence intervals are too large. All told, it seems fair to question the feasibility of the CGL analysis.

4.3 The CGL C-M analysis: An appraisal of confidence intervals

Suppose it is granted that CGL do not deduce rigorous results. Do their [Fe/H] and reddening limits have at least some tentative meaning? One can answer this question by reviewing CGL's discussion. CGL argue that [Fe/H] is not as low as 0.0 dex, and (with a caveat to be stated below) their Fig. 8 appears to support this conclusion. For values of [Fe/H] between +0.3 and +0.5 dex, however, affairs are more ambiguous.

Suppose that one reads the CGL paper without consulting their C-M diagrams. One finds that in their Sect. 2, CGL consider a metallicity of +0.22 dex derived by Garnavich et al. CGL argue that this metallicity is too low, so they assume tacitly that their C-M analysis rules out such low metallicities. Later, in their Sect. 4, CGL conclude that +0.4 dex is a somewhat better choice for [Fe/H] than +0.3 or +0.5 dex. If this is so, presumably +0.22 dex is even less acceptable than +0.3 dex. CGL's rejection of +0.22 dex is then understandable as long as they tacitly assign a small or zero accidental error to that number[*].

In Sect. 6 of CGL, however, a second picture emerges. There, CGL quote their deduced value of [Fe/H] as $0.4 \pm 0.1$ dex. Assume that +0.3 dex is in fact part of the CGL confidence interval. Since CGL do not test metallicities between +0.3 and 0.0 dex, it is fair to ask whether their confidence interval actually ends somewhere between those two quantities. If it does, not even a tentative argument against results like those of Garnavich et al. may be possible. Much - perhaps all - of the point of the CGL analysis is then lost.

Suppose that these possibilities are now assessed by inspecting pertinent CGL diagrams (see Figs. 2, 5, and 7 of CGL). Before dong this, a statistician might remember that "inspection overrates discrepancies'' - that is, that statistical testing often fails to sustain first impressions that data discrepancies are significant[*]. However, when one looks at the CGL diagrams, no salient discrepancies are found to begin with. The first impression that emerges instead is that there is little to choose between the fits for +0.3, +0.4, and +0.5 dex.

The assessment of these diagrams given by CGL appears in Sect. 4 of their paper. There, they express their preference for the fit for +0.4 dex in a brief discussion which offers little guidance to the reader. One concludes that the CGL analysis does not offer even tentative arguments against a fairly wide range of metallicities. In the data review to be discussed in Sect. 8, the CGL metallicity-reddening locus over the range from about +0.15 to +0.45 dex will be adopted.

5 NGC 6791 and $\mathsf{\mu}$ Leo: Peterson & Green (1998a)

It is now convenient to consider in detail two additional constraints on the metallicity of NGC 6791. One is from Peterson & Green (1998a), who have secured a combined spectrum for a "mean RHB star'' on the red horizontal branch of NGC 6791. They find that that spectrum is very similar to the spectrum of $\mu$ Leo, suggesting that $\mu$ Leo and NGC 6791 have very similar metallicities. Peterson & Green point out that if E(6791) falls between 0.11 and 0.17 mag, $\mu$ Leo falls among the cluster RHB stars in the (MV, B-V) diagram.

To interpret the results of this comparison, one must first find out how it constrains parameters of interest. Some insight into this question may be gained from the Buser-Kurucz (1992) tables. The number of available free variables may be limited by assuming that mass and luminosity are fixed while [M/H] and $T_{\rm c}$ are varied. Changes in log g are then constrained by the fixed mass and the varying value of $T_{\rm c}$. To convert the Buser-Kurucz values of [M/H] to [Fe/H], a scaling factor from the last line of Taylor's (1999b) Table 3 is employed.

The Buser-Kurucz tables imply that if [Fe/H] is decreased (increased) by 0.17 dex while $T_{\rm c}$ is decreased (increased) by 50 K, the value of B-V for a giant resembling $\mu$ Leo remains unchanged. If $\mu$ Leo and the mean RHB star differ in either of these senses, the Peterson-Green estimate of E(6791) is correct, but $\mu$ Leo and NGC 6791 have noticeably different metallicities. Peterson & Green do not say whether they could detect the results of such compensating parameter changes.

Despite this problem, suppose for the sake of argument that $T_{\rm c}$ (and hence [Fe/H]) are actually the same for $\mu$ Leo and the mean RHB star. Starting with this assumption, Peterson & Green consider published metallicities for NGC 6791 and $\mu$ Leo. For NGC 6791, they quote the PG mean (recall Sect. 3.1 of this paper). For $\mu$ Leo, they appear to refer to a result by Peterson (1992) which is 0.2 dex lower than the PG mean. One way to explain this difference is to appeal to systematic errors. Peterson & Green discuss the hypothesis that such errors are to be found in a number of published high-dispersion metallicities for $\mu$ Leo.

Peterson & Green adopt a tacit assumption that accidental errors cannot explain the 0.2-dex difference. In the alternative approach adopted here, the coherence of published metallicities will not be assessed until a set of accidental errors can be employed (see Sect. 8). Meanwhile, the metallicity of $\mu$ Leo will be used to estimate the metallicity of NGC 6791. The adopted $\mu$ Leo metallicity is $+0.231 \pm 0.025$ dex (see Sect. 2 of Taylor 2001). The corresponding metallicity inferred here for NGC 6791 is $+0.23 \pm \sigma$ dex, with 0.04 dex $\leq \sigma \leq 0.14$ dex. The revised error bar is an approximate allowance for the problem of compensating [Fe/H] and $T_{\rm c}$ variations. (An explanation for the adopted error range will be given in Sect. 8.)

6 The metallicities of Friel & Janes (1993)

6.1 Literature treatment

Before Peterson & Green (1998b) published their analysis, the most often-quoted metallicity for NGC 6791 was a low-resolution value of [Fe/H] from Friel & Janes (1993). Those authors measured Mg, Fe-peak blends, and (often) CN for a total of 24 clusters. For NGC 6791, they give a mean metallicity based on Mg, a second mean metallicity based on Fe-peak blends, and individual Fe-peak data for a total of nine stars. It is the Fe-peak data which have commonly been considered, and those data will be assessed here.

The Friel-Janes averaging procedure departs from rigorous statistical practice in three ways. For each program star, Friel & Janes average results from all indices measured for that star. They then report a mean metallicity and an rms error. Apparently those errors are values of $\sigma$(datum) instead of $\sigma$(mean). This conclusion is supported by an analysis of Friel-Janes data for clusters other than NGC 6791 (see Appendix A).

A second problem is that Friel & Janes use no weights when they average data for cluster stars. For full rigor, inverse-variance weighting is required to allow for star-to-star precision differences. A third problem resembles the first. For each of their program clusters, Friel & Janes report an overall metallicity with an rms error, and those errors are again values of $\sigma$(datum) instead of $\sigma$(mean). The existence of these two latter problems is established by calculating unweighted averages of the Friel-Janes data.

CGL have discussed the Friel-Janes data for NGC 6791. Using a plot of those data against dereddened values of B-V, CGL deduce that four cooler stars in the sample have smaller formal metallicities than five hotter stars (compare the first five and last four entries in Table 2). This deduction could not have been made from statistical testing: if an unequal-variance t test is applied to the data in the form plotted by CGL, one finds that the mean hot-star and cool-star metallicities do not differ at 95% confidence (see Appendix A)[*].


   
Table 2: Friel & Janes (1993): NGC 6791 data.
  (B-V)0 [Fe/H] $\sigma$ $\sigma$
Star $\phantom{{\rm ^a}}$(mag)${\rm ^a}$ (dex) $\phantom{{\rm ^b}}$(dex)${\rm ^b}$ $\phantom{{\rm ^c}}$(dex)${\rm ^c}$

3019		 1.22 +0.39 0.15 0.06
NE 18 1.22 +0.26 0.27 0.11
SE 49 1.23 +0.41 0.21 0.09
3009 1.28 +0.23 0.33 0.13
2014 1.29 +0.32 0.28 0.11
3010 1.48 +0.12 0.13 0.05
2038 1.52 +0.20 0.12 0.05
3036 1.55 -0.02 0.26 0.11
2008 1.56 -0.17 0.32 0.13
$^{{\rm a}}$  Assumed E(B-V) = 0.12 mag. Data are as quoted by Friel & Janes (see their Table 3a
for sources), and are not based on post-1991 sources.
$^{{\rm b}}$  Values of $\sigma$(datum) quoted by Friel & Janes.
$^{{\rm c}}$  Values of $\sigma$(mean) derived by using numbers of contributing data quoted by Friel & Janes.

Having deduced that an offset between hot and cool stars exists, CGL postulate that it varies continuously with color. However, by deleting the data for the four cooler stars, they tacitly assume instead that those data are affected by a step function. For the five remaining stars, CGL quote a final mean metallicity of $0.35 \pm 0.22$ dex. They assert that this is a weighted mean, but their error bar cannot be recovered by using inverse-variance weights based on the Friel-Janes values of $\sigma$(datum). In fact, that error bar cannot readily be recovered in any other way.

6.2 Establishing reliable rms errors

It is clear that before the Friel-Janes data can be used, they require a rigorous statistical analysis. First, however, a potential pitfall must be confronted. One might calculate $\sigma$(mean) for each cluster by averaging data for cluster stars and using Eq. (4). The resulting values of $\sigma$(mean) are agreeably small, so this procedure is tempting. However, it neglects the possibility that clusters have low-resolution features which are systematically strong or weak for their metallicities. Such offsets are not eliminated by averaging, so they can bias the resulting mean values (see Table 7 of Taylor 2000). An algorithm is required which incorporates possible offsets of this sort into meaningful values of $\sigma$(mean).

To derive such an algorithm, consider a hypothetical population containing N stars from a single cluster and M field stars. Let a high-dispersion calibration of a low-resolution index be based on this population. Suppose that all cluster stars are allowed to contribute equally to the calibration, and that the index for the cluster is too strong or too weak for its metallicity. In this case, the calibration will be biased (this is easiest to see if $N \gg M$). On the other hand, if the cluster is replaced by a single fictitious mean star, the cluster will contribute neither more nor less to the calibration than any of the genuine field stars. As long as the calibration sample is large enough so that the index is too strong for some of its stars and too weak for others, the calibration will be unbiased. Moreover, the scatter around the calibration can be used to derive an unbiased estimate of $\sigma$(datum) for metallicities inferred from the calibration. This estimate will apply impartially to the genuine field stars and the fictitious mean cluster star.

Ideally, one would simply adopt $\sigma$(datum) as the rms error for the cluster metallicity. Suppose, however, that the calibration data are available graphically but not numerically, as appears to be the case for the Friel-Janes data (see their Fig. 1a). Can one find an accessible population whose scatter yields $\sigma$(datum)? Pending publication of the calibration data, it will be assumed here that $\sigma$(datum) can also be obtained from the scatter of metallicities for stars in a given cluster. For calibrations derived by Taylor (1999b), variance-ratio tests suggest that this assumption is adequate.

Now consider the fictitious mean cluster star again. Suppose that the Friel-Janes data are homoscedastic within clusters-that is, that $\sigma$(datum) is identical for all stars in a given cluster (though it may vary from cluster to cluster). In this case, one could average the data without using weights to derive a mean value for the fictitious star. Next, the scatter around that mean value could be used to obtain the rms error for a single star [which is to say, $\sigma$(datum)]. However, there is another complication: the Friel-Janes data are actually heteroscedastic within clusters. To deal with this problem, one can use inverse-variance weighting to obtain a value of $\sigma$(mean) from data for N cluster stars. Next, one can treat this value of $\sigma$(mean) as if it had been obtained from N homoscedastic data. The required value of $\sigma$(datum) is then simply $[N^{0.5}] \times [\sigma$(mean)] (recall Eq. (3)).

6.3 Testing and reaveraging the Friel-Janes data

Before averaging the data, of course, one must test rigorously for systematic errors of the sort postulated by CGL. A simple way to do this is to calculate regressions of the Friel-Janes metallicities against values of (B-V)0, the zero-reddening B-V color index. Before this is done, the values of $\sigma$(datum) given by Friel & Janes for each cluster star are converted to values of $\sigma$(mean). This is done by using Eq. (4), with N being the number of indices measured by Friel & Janes. Inverse squared values of $\sigma$(mean) are then used as weights. (Note that because the Friel-Janes data are tested in this improved way, this test supersedes the one described in Sect. 6.1.)

For NGC 6791, the slope S obtained in this way is as follows:

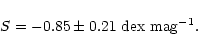\begin{displaymath}S = -0.85 \pm 0.21 \mkern6mu {\rm dex} \mkern6mu {\rm mag}^{-1}. \end{displaymath} (7)

A t test shows that this value of S differs from zero at $C = 99.6\%$ confidence. However, one must evaluate this deduction with some caution. For one thing, Friel & Janes consider data for 26 clusters. For a group this large, there is a substantial probability of a false positive result. Using an algorithm which allows for this problem, one finds that if the null hypothesis (S = 0) is to be rejected at an overall confidence interval exceeding 95%, C should exceed 99.8% (see Appendix A of Taylor 1996). Then, too, Friel & Janes published their paper before the B-V data bases of Montgomery et al. (1994) and Ka\luzny & Rucinski (1995) appeared. Pending use of that photometry to rederive the Friel-Janes metallicity, Eq. (7) should be regarded as tentative, though it will be adopted below.

The value of S in Eq. (7) suggests that data for other clusters should be tested for non-zero slopes. Using data for 11 such clusters with appreciable color ranges among their stars, one finds that

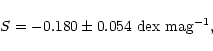\begin{displaymath}S = -0.180 \pm 0.054 \mkern6mu {\rm dex} \mkern6mu {\rm mag}^{-1}, \end{displaymath} (8)

with S differing from zero at 99.8% confidence. In response to Eqs. (7) and (8), the Friel-Janes data are averaged only after correction to a given temperature. The temperature adopted here corresponds to

\begin{displaymath}(B-V)_0 = 1.20 + 0.12{\rm [Fe/H]}, \end{displaymath} (9)

with the stated metallicity term being derived from the Buser-Kurucz tables. The temperature of a relatively hot star is chosen in the hope of minimizing blanketing interference with the Friel-Janes indices. The hottest stars in NGC 6791 that were measured by Friel & Janes have roughly the adopted temperature. Friel & Janes give results at the adopted color index for most of their other clusters as well.

The results of this procedure are given in Table 3. The averages listed there are based on the same weighting procedure that was used to obtain values of S. To test the adopted zero point, the Friel-Janes metallicity for NGC 2682 (M 67) has been compared to a mean high-dispersion metallicity for that cluster. The two metallicities do not quite differ at 95% confidence (see Appendix B), so the Table 3 averages are stated without a zero-point adjustment.


   
Table 3: Revised Friel-Janes metallicities${\rm ^a}$.

Cluster		 E(B-V) [Fe/H] $\phantom{^{\rm c}}\nu^{\rm c}$ Cluster E(B-V) [Fe/H] $\phantom{^{\rm c}}\nu^{\rm c}$

Be 21		 0.70 $-0.90 \pm 0.21$ 6.3 N2477 $\phantom{^{\rm d}}0.30^{\rm d}$ $-0.07 \pm 0.07$ 237
Be 39 0.12 $-0.31 \pm 0.07$ 237 N2506 0.05 $-0.55 \pm 0.07$ 237
IC 166 0.80 $-0.26 \pm 0.13$ 13.2 N2682$^{{\rm e}}$ 0.05 $-0.11 \pm 0.05$ 51
King 8 0.68 $-0.47 \pm 0.14$ 9.0 N2682$^{\rm f}$ 0.05 $-0.021 \pm 0.014$ 22.2
Mel 66 0.14 $-0.51 \pm 0.07$ 237 N3680 0.05 $-0.19 \pm 0.07$ 237
N752 0.04 $-0.21 \pm 0.04$ 34.6 N3960 0.29 $-0.37 \pm 0.07$ 237
N1193 0.12 $-0.59 \pm 0.09$ 15.6 N5822 0.15 $-0.25 \pm 0.07$ 237
N1817 0.28 $-0.42 \pm 0.07$ 237 N6791 0.12 $+0.37 \pm 0.09$ 15.2
N2112 0.60 $-0.50 \pm 0.07$ 237 N6819 0.28 $+0.02 \pm 0.10$ 29.3
N2141 0.30 $-0.37 \pm 0.08$ 23.4 N7142 0.41 $-0.01 \pm 0.05$ 31.3
N2243 0.04 $-0.58 \pm 0.17$ 5 N7789$^{\rm g}$ 0.24 $-0.25 \pm 0.05$ 47.5
N2360 0.09 $-0.32 \pm 0.07$ 237 To 2 0.20 $-0.54 \pm 0.12$ 7.9
N2420 0.02 $-0.41 \pm 0.04$ 30.3        
$^{{\rm a}}$  Units are magnitudes for E(B-V) and dex for [Fe/H] and $\sigma$(mean). Cluster numbers beginning with "N'' are NGC numbers.
$^{{\rm b}}$  The abbreviations included the following: "Be'' for "Berkeley,'' "Mel'' for "Melotte,'' "N'' for "NGC'', and "To'' for "Tombaugh.''
$^{{\rm c}}$  This is the number of degrees of freedom.
$^{{\rm d}}$  In Table 1 of Friel & Janes, a "v'' (presumably "variable'') is attached to this entry.
$^{{\rm e}}$  This entry is from the Friel-Janes data.
$^{\rm f}$  This entry is based solely on high-dispersion data (see Appendix B).
$^{\rm g}$  The datum for star 501 is excluded because its value of $\sigma$(datum) is anomalously low (0.01 dex) and may be a misprint.

It should be emphasized that the Table 3 entry for NGC 6791 is not as well-founded as the entries for other clusters. The need for updated values of B-V has already been mentioned. In addition, the average of the Friel-Janes metallicities for cluster stars should be given with a fully-specified reddening-correction algorithm. At present, only a partial algorithm has been published (see Friel & Janes, Sect. 4.2). When definitive proper motions are available for NGC 6791, it may be necessary to edit the Friel-Janes list of measured cluster members. Finally, the conversion of the Friel-Janes indices to metallicities for NGC 6791 should be rediscussed. Before concluding that those metallicities are unaffected by the relatively high blanketing for NGC 6791, it would seem prudent to make sure that S is effectively zero. Pending decisive solutions of these problems, a tentative Friel-Janes metallicity for NGC 6791 will be adopted below.

7 Other published metallicities

Two other published metallicities for NGC 6791 require comment. One has been derived by Janes (1984) from DDO measurements. That metallicity has been updated by using a calibration given by Taylor (1999b, Table 3, line 3). Values of B-V required for this calculation are from Ka\luzny & Udalski (1992), and have been corrected to the mean zero point of the Ka\luzny-Rucinski and Montgomery et al. B-V data. As in the case of the Friel-Janes results, the value of $\sigma$(mean) for a single star has been adopted (see again line 3, Table 3, of Taylor 1999b).

The other metallicity considered here is part of a set derived from scanner measurements. In that set, $[{\rm M/H}] = +0.75 \pm 0.2$ dex for NGC 6791 and +0.45dex for M 67 (see Spinrad & Taylor 1971; Spinrad & Taylor 1969, respectively). Taylor & Johnson (1987, Table 4) have since used the Spinrad-Taylor data to derive values of an index called G for M 67. The G index is based on values of $(R-I)_{\rm C}$, whose blanketing sensitivity is less than that of the Spinrad-Taylor temperature index (see Table III of Taylor et al. 1987). A metallicity calibration of G has been given by Taylor (1999b). When that calibration is applied to the values of G for M 67, the resulting value of [M/H] is $0.00 \pm 0.04$ dex. This result agrees well with a high-dispersion mean (again see Appendix B). One therefore concludes that the Spinrad-Taylor metallicities for M 67 and (possibly) NGC 6791 should be lowered by about 0.45 dex. Pending measurements of $(R-I)_{\rm C}$ for NGC 6791, the Spinrad-Taylor metallicity for that cluster is therefore set aside.

8 Summary and discussion

8.1 Averaging the published metallicities

It is now possible to estimate the metallicity of NGC 6791. First, however, some allowance must be made for the the uncertainty in the cluster reddening. This is done by deriving metallicities for two illustrative values of E(6791). The adopted values are $E_L = 0.105 \pm 0.018$ mag and $E_U = 0.167 \pm 0.012$ mag (see the second and third results discussed in Appendix C, respectively). These choices are close to the reddening limits estimated by Peterson & Green (1998a) from their spectral comparison.

The CGL analysis is used to convert reddenings to metallicities. To do this, the following estimate of the CGL reddening-metallicity locus is applied:

\begin{displaymath}{\rm [Fe/H]} = 0.83 - 3.77E-1.18E^2, \end{displaymath} (10)

with $E \equiv E(6791)$. This estimate is an average of separate loci for the Ka\luzny-Rucinski (1995) and Montgomery et al. (1994) data bases. The net difference between those loci is 0.06 dex, and is small enough to allow use of a compromise locus in this analysis.

The metallicities collected for this review are listed in Table 4. Comments about results not discussed above are given in footnotes to the table. If possible, the data are corrected for reddening. For all Peterson-Green entries, however, no such corrections are made because there is no obvious way to apply them. Judging from the data for which the corrections are possible, neglect of these corrections has about the same numerical effect as replacing the "PDOK'' entry of Peterson & Green (1998b) with the "K+95'' entry. It will be shown below that the effect of this latter exchange is small.


   
Table 4: Summary of metallicities.
  [Fe/H] [Fe/H]
Source $\phantom{^{\rm a}}(E=0.105)^{\rm a}$ $\phantom{^{\rm b}}(E=0.167)^{\rm b}$

Janes (1984)$^{{\rm c}}$		 $-0.03 \pm 0.12\phantom{-}$ -
Friel & Janes (1993)$^{{\rm d}}$ $0.36 \pm 0.10$ $0.39 \pm 0.10$
Garnavich et al. (1994)$^{{\rm e}}$ 0.13(0.14) 0.20(0.14)
Peterson & Green (1998a)$^{\rm f}$ 0.23(0.14) 0.23(0.14)
Peterson & Green (1998b):    
PDOK $0.37 \pm 0.12$ $0.37 \pm 0.12$
K+95 $0.48 \pm 0.12$ $0.48 \pm 0.12$
CGL$^{\rm g}$ $0.42 \pm 0.07$ $0.17 \pm 0.05$
Average:    
Only PDOK included$^{\rm h}$ $0.35 \pm 0.05$ $0.23 \pm 0.04$
Only K+95 included$^{\rm h}$ $0.36 \pm 0.05$ $0.24 \pm 0.04$
Smallest L(95) 0.25 0.16
Largest $U(95)^{\rm j}$ 0.44 0.31
$^{{\rm a}}$  Units are dex. $E(B-V)=0.105 \pm 0.018$ mag (see Appendix C). Error bars in parentheses are assumed values.
$^{{\rm b}}$  Units are dex. $E(B-V)=0.167 \pm 0.012$ mag (see Appendix C). Error bars in parentheses are assumed values.
$^{{\rm c}}$  For the derivation of this datum, see Sect. 7.
$^{{\rm d}}$  The assumed value of d[Fe/H]/dE(B-V) is 1.2 dex mag-1. This derivative is adopted here despite the fact that it applies only if
   all Friel-Janes indices have been measured (see Sect. 4.2 of Friel & Janes 1993). Allowance has also been made for the
   non-zero slope depicted in Eq. (7).
$^{{\rm e}}$  These data are from measurements of the Ca II lines. The value of d[Fe/H]/dE(B-V) is assumed to be 1 dexmag-1.
   The quoted value of $\sigma$(mean) is an upper limit. Values ranging from 0.14 dex down to 0.04 dex are considered.
$^{\rm f}$  The quoted value of $\sigma$(mean) is an upper limit. Values ranging from 0.14 dex down to 0.04 dex are considered.
$^{\rm g}$  For each column, the quoted metallicity is derived by substituting the reddening adopted for that column into Eq. (10).
$^{\rm h}$  The Janes (1984) metallicity is excluded (see Sect. 8.1). For the Peterson-Green (1998a) and Garnavich et al. (1994) entries,
    the value of $\sigma$(mean) adopted to calculate these means is 0.14 dex.
$^{{\rm j}}$  U(95) is the mirror image of L(95), which was discussed in Sect. 3.2.

Note that if a value of $\sigma$(mean) is not known for a given entry, an "adjustable value'' is adopted (see the entries in parentheses in Table 4). The adjustable value ranges from 0.04 to 0.14 dex. This is the known range of $\sigma$(mean) for low-resolution metallicities in general (Taylor 1994a, Sect. 3.8; Taylor 1999a, Table 2; Taylor 1999b, Table 3). While use of the adjustable value is clearly a stopgap procedure, it is still deemed to be superior to a tacit assumption that accidental errors are small or zero. CGL and Peterson & Green (1998a) both make such an assumption.

As the data are averaged, special attention is paid to the Janes (1984) metallicity. From the Janes DDO data which yield that metallicity, one finds that $E(6791) = 0.054 \pm 0.018$ mag (see Appendix C). Because this result differs from EU at the $5.2\sigma$ level, the Janes metallicity is included only in averaging for EL. At $C \sim 97\%$ confidence or better, the averaging process shows that the entries for EL have too much scatter to be explained by their rms errors. This deduction is quite insensitive to the choice of adjustable value. On the other hand, if the Janes datum is omitted and if the adjustable value is $\geq$0.08 dex, then $C < 95\%$. The Janes datum is therefore excluded from subsequent averaging.

The scatter in the contributing data is also evaluated for EU. No adjustable value in the permitted range is found for which excessive scatter exists at 95% confidence or better. The overall conclusion that applies to the scatter is that it may very well be caused by accidental error alone. This conclusion contrasts with conclusions drawn by CGL and by Peterson & Green (1998a). (For further information about the scatter tests, see Appendix A.)

Using adjustable values of 0.14 dex, mean metallicities are derived for each test reddening. These means are quoted in Table 4. Two means are quoted for each test reddening, with one being based on the "PDOK'' results of Peterson & Green (1998b) and the other being based on their "K+95'' results (recall Sect. 3.1). As implied above, the results of exchanging one result for the other are small. However, caution argues against a permanent conclusion that the zero-point problem is unimportant. The exact uncertainty of the zero point is unknown (recall Sect. 3.2). Moreover, if the rms error of the Peterson-Green datum has been underestimated here, the weight of that datum should be increased in future averaging. This would increase the importance of the zero-point uncertainty.

In the last two lines of Table 4, values of L(95) and U(95) are given. U(95) is a mirror image of L(95) (recall Sect. 3.2). The numbers in the table are the most extreme that are allowed by the adopted range of the adjustable parameter. If one uses those numbers to define cautious limits for the metallicity of NGC 6791, they are found to be +0.16 and +0.44 dex. In effect, these limits say that the metallicity problem is largely unsolved. Certainly a metallicity of +0.4 dex is not decisively favored.

8.2 The maturity of the metallicity data base

A complementary way to assess the problem is to summarize the judgments that have been made above about the maturity of the NGC 6791 data base.

It may be noted that the first two of these problems could likely be solved by expanding the Peterson-Green (1998b) analysis to include stars in the Coma cluster. The mean metallicity of that cluster is well known (see Taylor 1994b). Use of F4-F6 cluster stars such as T19, T86, and T90 would ameliorate the line-strength contrast problem discussed in Sect. 3.1.

8.3 The key role of accidental errors

Despite its length, the list just given does not completely display the nature of the NGC 6791 problem. Some comments are also required about the way in which that problem has been approached.

1) The most important issue has been neglect and other nonrigorous treatment of accidental errors. Even approximate allowance for such errors yields a rather substantial change in conclusions drawn from the metallicity data.

2) Inadequate treatment of error bars poses both direct and indirect problems. This point is illustrated by a second look at comparisons between $\mu$ Leo and the RHB stars in NGC 6791. Suppose that high-dispersion analyses of those stars were to yield precise temperature differences among them. This prospect is entirely within reach, as Smith & Ruck (2000) show. By using such temperature differences, observed color indices, and corrections obtained from the tables of Buser & Kurucz (1992), one could obtain a value of E(6791). That datum would be as reliable as allowed by the zero points of existing B-V photometry for NGC 6791. In addition, the analyses could be used to derive [Fe/H] differences between $\mu$ Leo and the RHB stars. These differences could be averaged to form a precise mean value. In turn, that mean value could be converted to a value of [Fe/H] by using the precise mean metallicity derived statistically for $\mu$ Leo (see Sect. 2 of Taylor 2001). These reddening and metallicity analyses would both be aided by the spectral similarity of $\mu$ Leo and the RHB stars. Unfortunately, these agreeable prospects are probably out of reach at present because the metallicity of $\mu$ Leo is in dispute (see Taylor 1999c, 2001).

3) As noted in Sect. 1, there has been a tendency to derive questionably high metallicities for $\mu$ Leo by using non-statistical means. It is now clear that there is a counterpart tendency for NGC 6791. Taken together, these examples inspire a conjecture which is based on a rule of economics called Gresham's Law. The colloquial statement of that law is that "bad money drives out good money''. Apparently one can also say that "high derived metallicities drive out all others''. If a strikingly high metallicity is obtained for a star or cluster, it seems that it will afterwards be preferred even if it is not well-founded.

On this interpretation, NGC 6791 is now at about the state of the $\mu$ Leo problem as of 1990. At that time, Gratton & Sneden (1990) published a value of [Fe/H] that formally exceeded +0.3 dex. Given that result and the ground-breaking work of Branch et al. (1978), there were two independent papers in the literature which seemed to confirm that $\mu$ Leo has a very high metallicity. On this interpretation, Peterson & Green (1998a) and CGL now fill the same roles for NGC 6791. If affairs are not to go farther than this and "Gresham's Law of high metallicities'' is not to prevail, accidental errors must play their proper role in the NGC 6791 problem.

A widespread judgment that problems are solved by new data alone should be mentioned at this point. It is clear that new data are indeed required to derive reliable metallicities and other results for NGC 6791. However, such data will be just as subject to misinterpretation as extant data are now unless their accidental errors are accurately stated and applied.

9 Summary

As noted in Sect. 1, a metallicity of $+0.4 \pm 0.1$ dex for NGC 6791 has received conspicuous support. When published results are examined closely, however, this support disappears. Instead, an immature data base is found, with an associated list of problems that have yet to be solved. At present, results from that data base suggest only that the metallicity of NGC 6791 is somewhere between +0.16 and +0.44 dex. The major reason for a premature conclusion to the contrary is inadequate treatment and use of accidental errors. However, a tendency to give credence to high metallicities resembling a similar tendency for $\mu$ Leo may also have played a role.

Acknowledgements
I thank Mike and Lisa Joner for carefully proofreading this paper and an anonymous referee for suggesting that sources such as Dolphin (1997) and Hernandez et al. (1999) be referenced. Page charges for this paper have been generously underwritten by the College of Physical and Mathematical Sciences and the Physics and Astronomy Department of Brigham Young University.

Appendix A: Statistical tests

The first test referred to in Sect. 6.1 is performed as follows. Three clusters (NGC 752, 2420, and 7789) are selected because they have data of relatively high precision. For NGC 7789, only data with quoted rms errors less than 0.18 dex are selected. In addition, only stars with (B-V)0 < 1.25 mag are considered, with (B-V)0 being the reddening-corrected value of B-V. This last criterion is adopted to prevent the color dependence of the Friel-Janes metallicities from inflating estimates of their scatter.

Two scatter estimates are then calculated. Briefly, an "external'' variance is derived from the squares of the rms errors quoted by Friel & Janes. A second "internal'' variance is obtained to reflect the amount of scatter around the mean values of [Fe/H] for the three clusters. The external estimate is then found to exceed the internal estimate at better than 99.9% confidence (see line 1 of Table A.1). This means that the Friel-Janes errors are actually too large to explain the scatter in their data.


   
Table A.1: Variance-ratio tests of the Friel-Janes rms errors.
  External Degrees of Internal Degrees of    
Line $\sigma$ freedom $\sigma$ freedom F C

1		 0.113 125 0.061 22 3.41 >0.999 $\phantom{>}$
2 0.046 125 0.061 22 1.75 0.96


   
Table A.2: $\chi ^2$ tests.
  Janes   Peterson-   Degrees of  
Line 1984? Reddening Green mode $\chi ^2$ freedom C

1		 Yes EL PDOK 13.8 5 0.98
2 Yes EL K+95 15.8 5 0.99
3 No EL PDOK 6.7 4 <0.95 $\phantom{<}\mkern4mu$
4 No EL K+95 8.2 4 <0.95 $\phantom{<}\mkern4mu$
5 No EU PDOK 5.7 4 <0.95 $\phantom{<}\mkern4mu$
6 No EU K+95 8.7 4 <0.95 $\phantom{<}\mkern4mu$

The test is then carried out a second time after the external variance is revised. The revision is performed by applying Eq. (4) in the text to each Friel-Janes rms error, with N in that equation being the number of Friel-Janes indices which contribute to each of their metallicity estimates. Note that if the Friel-Janes errors are actually values of $\sigma$(datum), this is the proper procedure for converting them to values of $\sigma$(mean) (recall Eq. (3) in the text). The revised comparison (see line 2 of Table A.1) shows that the external estimate is now smaller than the internal estimate at 96% confidence. Since the two estimates are now more comparable (though not unequivocally identical), it is concluded that the revised Friel-Janes errors are values of $\sigma$(mean).

To apply the second test referred to in Sect. 6.1, hot-star and cool-star means are formed. Each mean is derived by using inverse-variance weights, with the variances being from the Friel-Janes errors as quoted by Friel & Janes. Next, the means are compared by using an unequal-variance t test (see Table 3 of Taylor 1992 for a description of this test). The resulting value of t is 1.80. If the test is repeated with the datum for star 3036 deleted (see Cudworth 1993), t is found to be 1.65. In either event, the null hypothesis (no difference between the hot and cool stars) is not rejected at 95% confidence.

The tests described in Sect. 8 are based on Eq. (B44) of Taylor (1991). For adjustable values of 0.10 dex, illustrative results of those tests are given in Table A.2.

Appendix B: A preliminary mean high-dispersion value of [Fe/H] for M 67

Because a test of a low-resolution metallicity is desired, the following analysis will be restricted to high-disperson data. In addition, results by Griffin (1975, 1979), Cohen (1980), and Peterson (1981) are set aside. All of these data lie near -0.4 or -0.5 dex. The Griffin results are from differential curve-of-growth analyses, and Griffin's data have since been used in model-atmosphere analyses by Foy & Proust (1981). Cohen's result appears with a counterpart for M 71 which was later found to suffer from continuum-placement effects (Cohen 1983).

Values of [Fe/H] were secured from Foy & Proust, Garcia Lopez et al. (1988), Hobbs & Thorburn (1991), Friel & Boesgaard (1992), and Tautvaisiene et al. (2000). For data requiring reddening corrections, E(B-V) was taken to be 0.05 mag. This compromise value is adopted pending a planned review of the M 67 reddening problem. The adopted value of d[Fe/H]/dE(B-V) is 1.2, and is derived from relations given by Cousins (1978), Taylor et al. (1987), McWilliam (1990), and Taylor (1998a). The [Fe/H] corrections from reddening are $\sim$0.02 dex or less, and so are marginally important in this context.

At 98% confidence, an F test suggests that the Foy-Proust and Garcia Lopez et al. data should receive about 0.3 times weight of the remaining data. This deduction is marginal because multiple statistical tests are made in this paper. As a result, there is an increased chance that the formal significance of one of those tests might reach or exceed 95% confidence despite being caused by a random fluctuation (see Taylor 2000, Appendix A, first paragraph). Nevertheless, the deduction from the F test is accepted here for the sake of conservative data treatment.

A weighted average that allows for the precision contrast yields the following result:

\begin{displaymath}{\rm [Fe/H]} = -0.021 \pm 0.014 \mkern6mu {\rm dex}. \end{displaymath} (B.1)

Since the revised Spinrad-Taylor result for M 67 is $0.00 \pm 0.04$ dex, no t test is required to establish its consistency with Eq. (B1). For the Friel-Janes M 67 (1993) result ( $-0.11 \pm 0.05$ dex; see Table 3), a t test shows that the apparent difference from Eq. (B1) is not quite significant at 95% confidence.

Appendix C: The reddening of NGC 6791

Suppose one sets aside all reddening values derived from the C-M diagram and considers only values of E(6791) that may be blanketing-independent. Data of this sort may someday be used to resolve the B-V ambiguity (recall Sect. 4.2). At the moment, there are three values of E(6791) that should be considered: The first and third of these entries are based on B-V values on the mean zero point for the Ka\luzny-Rucinski (1995) and Montgomery et al. (1994) data bases. The second entry is from stars with V > 15, but differs negligibly from a mean derived using a greater contribution from foreground stars.

References

 

Copyright ESO 2001