A&A 377, 566-580 (2001)
DOI: 10.1051/0004-6361:20011137

Submillimeter lines from circumstellar disks around pre-main sequence stars

G.-J. van Zadelhoff1 - E. F. van Dishoeck1 - W.-F. Thi1 - G. A. Blake2


1 - Leiden Observatory, PO Box 9513, 2300 RA Leiden, The Netherlands
2 - Division of Geological and Planetary Sciences, California Institute of Technology, MS 150-21, Pasadena, CA 91125, USA

Received 13 November 2000 / Accepted 9 August 2001

Erratum

Abstract
Observations of submillimeter lines of CO, HCO+, HCN and their isotopes from circumstellar disks around low mass pre-main sequence stars are presented. CO lines up to $J=6\to5$, and HCO+and HCN lines up to $J=4\to3$, are detected from the disks around LkCa 15 and TW Hya. These lines originate from levels with higher excitation temperatures and critical densities than studied before. Combined with interferometer data on lower excitation lines, the line ratios can be used to constrain the physical structure of the disk. The different line ratios and optical depths indicate that most of the observed line emission arises from an intermediate disk layer with high densities of 106-108 cm-3 and moderately warm temperatures in the outer regions. The data are compared with three different disk models from the literature using a full 2D Monte Carlo radiative transfer code. The abundances of the molecules are constrained from the more optically thin 13C species and indicate depletions of $\approx$1-30 for LkCa 15 and very high depletions of >100 for TW Hya with respect to dark cloud abundances. Evidence for significant freeze-out (factors of 10 or larger) of CO and HCO+onto grain surfaces at temperatures below 22 K is found, but the abundances of these molecules must also be low in the warmer upper layer, most likely as a result of photodissociation. A warm upper layer near the surface of a flaring disk heated by stellar and interstellar radiation is an appropriate description of the observations of TW Hya. LkCa 15 seems to be cooler at the surface, perhaps due to dust settling. The density constraints are also well fitted by the flared disk models.

Key words: stars: circumstellar matter - stars: pre-main sequence - stars: planetary systems: protoplanetary disks - accretion, accretion disks


1 Introduction

Circumstellar disks play an essential role in the understanding of the formation of planetary systems such as our own (see Beckwith 1999; Beckwith & Sargent 1996 for recent reviews). These protoplanetary disks contain a few percent of the mass of the pre-main sequence stars which they surround. One of the key questions concerning circumstellar disks is their evolution toward planetary formation. The different evolution scenarios can be constrained by placing limits on the density and temperature distributions in the disks. The standard method for determining the disk physical structure utilizes fits to the observed spectral energy distributions (SEDs) (Adams et al. 1988). This procedure relies on the changing opacity of the dust at different wavelengths. At long wavelengths (typically $\lambda >1$ mm), the dust emission is optically thin and hence traces the product of mass and mean temperature (Beckwith 1999), whereas at shorter wavelengths the disk becomes optically thick so that only the temperature structure and geometry of the disk surface-layer is probed. The derived temperature and density solution is not unique since different distributions or different dust properties are able to fit the SEDs (Bouvier & Bertout 1992; Thamm et al. 1994). In addition, changing dust properties with position in the disk can affect the analysis, as can the disk size. Nevertheless, one of the more robust results has been the recognition of relatively high temperatures in the surface layers of the disk, implying that they need to be heated more efficiently by stellar radiation compared to the traditional thin (flat) disk model. This led Kenyon & Hartmann (1987) to propose a flared disk geometry in which the outer disk intercepts more radiation than does a flat disk.

Hubble Space Telescope (HST) observations of young low mass stars such as HH 30 and HK Tauri show edge on (silhouette) disks which indeed flare noticeably (Burrows et al. 1996). The radiation from the central star incident on the outer parts of the disk changes the temperature and chemistry in those regions, with the temperature change giving rise to a larger scale height and thereby flaring the disk. Recent models by Chiang & Goldreich (1997, 1999) and D'Alessio et al. (1997, 1998, 1999) include the irradiation of flared disks to derive self-consistent models with a warm outer layer. The models by Bell et al. (1997, 1999) take both the stellar radiation and re-processing of radiation in the disk into account. The latter models have an isothermal temperature in the vertical z-direction due to large flaring in the inner disk region, thereby shielding the the outer disk from stellar light. Comparison with the other models provides a good test case whether a high temperature upper layer is needed to satisfy the observational constraints. All three types of models are used in this work and will be discussed in more detail in Sect. 4.

An alternative method to derive the density and temperature structure in disks is through modeling of molecular line emission. Although the inferred solution from observations of a single line is not unique, data on a sufficiently large number of transitions of various molecules can be used to constrain the temperature and density independently. Moreover, careful analysis of the line profiles can provide positional information, since the center of a line probes a different radial part of the disk compared with the wings, unless the disk is nearly face-on. In addition, observations of various isotopomers can give information on different vertical regions of the disks due to their varying optical depths. To date, most data concern the lowest rotational J=1-0 and 2-1 transitions of 12CO and 13CO, which originate from levels at low energies (<20 K) and which have low critical densities (<5000 cm-3) (e.g., Dutrey et al. 1996). Data on molecules with larger dipole moments such as HCN and HCO+ have been limited to the 1.3 m band (Dutrey et al. 1997), except for the case of TW Hya (Kastner et al. 1997). In this paper, higher rotational lines in the 0.8 and 0.45 m atmospheric windows are presented, obtained with the James Clerk Maxwell Telescope (JCMT) and Caltech Submillimeter Observatory (CSO). These lines probe higher temperatures (up to 100 K) and higher densities (up to 107 cm-3) than do presently available spectra.

The observations are accompanied by a detailed analysis of the excitation and radiative transfer of the lines. In contrast with previous models (e.g. Gómez & D'Alessio 2000), our analysis uses statistical equilibrium (SE) rather than local thermodynamic equilibrium (LTE) since the surface layers of the disk may have densities below the critical density of various transitions. In addition, the two-dimensional (2D) code developed by Hogerheijde & van der Tak (2000) is used to calculate the full radiative transfer in the lines. The data can be used to test the disk models described above that are fit to the SEDs available for most T-Tauri and Herbig Ae stars. In addition to constraining the temperature and density, the observations and models also provide information on the depletion of different species.

The molecular abundances and excitation are studied by comparing different isotopomers of CO, HCO+ and HCN for two sources: TW Hya and LkCa 15. TW Hya is nearby (57 pc, Kastner et al. 1997) and has a disk seen nearly face-on. LkCa 15 is located at the edge of the Taurus cloud at $\sim$140 pc and has an inclination of $\sim$60$^\circ$, where 0$^\circ$ is face-on. Both sources show a wealth of molecular lines and are well-suited for developing the analysis tools needed to investigate disk structure.

The outline of this paper is as follows. In Sect. 2, we present the observational data. In Sect. 3, we perform a simple zeroth-order analysis of the observed line ratios to constrain the excitation parameters. The adopted disk models are introduced in Sect. 4.1, whereas the methods for calculating the level populations are explained in Sects. 4.2-4.5. Finally, the results of the analysis are given in Sect. 5 and summarized in Sect. 6.

   
2 Observations


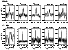  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10460f1.eps}} \end{figure} Figure 1: Top: selected CO, HCO+ and HCN lines toward LkCa 15. The profiles show a double-peaked structure typical for a disk seen at an inclination of about 60$^{\rm o}$. Bottom: selected CO, HCO+ and HCN lines from the face-on disk around TW Hya.
Open with DEXTER

Between September 1998 and December 2000, spectral line observations were obtained for several pre-main sequence low mass stars surrounded by circumstellar disks using the dual polarization B3 receiver at the James Clerk Maxwell Telescope (JCMT[*]) in the 345 GHz (0.8 mm) band. The observations were obtained mostly in single side band (SSB) mode using beam-switching with a typical switch of 180 $^{\prime\prime}$ in azimuth. The spectra were recorded with the Digital Autocorrelation Spectrometer (DAS) at a frequency resolution of $\sim$0.15 MHz ($\sim$0.15 kms-1), and were converted to the main-beam temperature scale using $\eta_{\rm mb}=0.62$. See http://www.jach.hawaii.edu/JACpublic/JCMT/ for details. The calibration was checked regularly at each frequency setting against standard spectra of bright sources obtained by the JCMT staff, and were generally found to agree within 10%. Integration times ranged from 30 min (ON+OFF) for 12CO 3-2 up to 120 min for C18O 3-2, reaching rms noise levels on the $T_{\rm mb}$ scale of about 20 mK after adding the data from the two mixers together and smoothing to 0.3 MHz resolution. A deep integration on the C18O 2-1 line was obtained with receiver A3 for LkCa 15, which has $\eta_{\rm mb}=0.79$.

These data are complemented by observations using the Caltech Submillimeter Observatory (CSO[*]) of the 12CO 6-5 line for the same sources. In addition, the 12CO 2-1 line has been observed with the IRAM 30 m telescope[*] for LkCa 15. For the 12CO 6-5 line, $\eta_{\rm mb}=0.40$, whereas for the IRAM 12CO 2-1 observations the raw data are divided by 0.55 (see http://www.iram.es/).

Interferometer maps of the lowest rotational transitions of several species toward LkCa 15 have been obtained by Qi (2000) using the Owens Valley Millimeter Array (OVRO). Some lines have also been imaged by Simon et al. (2000) and Duvert et al. (2000) with the IRAM Plateau de Bure interferometer. In addition, the Infrared Space Observatory (ISO) has detected the lowest rotational S(0) and S(1) lines of H2, which provide independent constraints on the temperature and mass of warm gas and which are discussed elsewhere (Thi et al. 2001). In this paper only the single dish results on CO, HCO+ and HCN for the sources LkCa 15 and TW Hya are presented.

Figure 1 shows some of the spectra observed toward LkCa 15 and TW Hya. The double peaked profiles for LkCa 15 are consistent with Keplerian rotation of the disk seen at an inclination of $58 \pm 10^{\circ}$ (Qi 2000; Duvert et al. 2000). Since TW Hya is seen face-on, only narrow single-peaked lines are observed from this source. For both stars, the 12CO lines disappear at one beam offset from the source. Table 1 summarizes the measured line parameters and beam sizes at the observed frequencies. The upper-limits for LkCa 15 refer to a 2 $\times$ rms noise level, with the limit on the integrated line strengths obtained by using two separate Gaussians each with a line-width of 1.3 kms-1, as found for 13CO 3-2. For TW Hya, the upper limits assume a Gaussian with a width of 0.76 kms-1, similar to that observed for HCN and H13CO+ 4-3. Note that our HCO+ 4-3 line toward TW Hya is a factor of three weaker than that found by Kastner et al. (1997). We adopt our values in the analysis. The HCN 4-3 integrated intensity is comparable to that found by Kastner et al. (1997) within 10%. There is a hint of a 12CO 6-5 line toward TW Hya, but this is treated as an upper limit.


   
Table 1: Observed line parameters for LkCa 15 and TW Hya.
line $\int$ $T_{\rm mb}$ dv $T_{\rm mb}$ $\Delta V^{a}$ Beam Telescope Date
  K km s-1 K km s-1 $\hbox{$^{\prime\prime}$ }$    
LkCa 15  
CO 6-5 0.53 0.29/0.28 2.0 14.5 CSO Jun. 00
CO 3-2 1.39 0.60/0.56 3.3 13.8 JCMT Nov. 99
CO 3-2 1.17 0.37/0.39 2.2 25.7 CSO Feb. 98
CO 2-1 1.82 0.74/0.76 2.9 10.5 IRAM Dec. 98
13CO 3-2 0.39 0.13/0.15 3.4 14.4 JCMT Sept. 98
13CO 1-0e 7.43     $3.1\times2.6$ OVRO  
C18O 3-2 <0.14b <0.05c   14.5 JCMT Nov. 99
C18O 2-1 <0.20b <0.07c   22.2 JCMT Nov. 98
C18O 1-0e 0.70     $4.3\times 4.0$ OVRO  
HCO+ 4-3 0.26 0.14/0.14 3.3 13.4 JCMT Sept. 98
HCO+ 1-0e 4.19     4.5$\times$3.3 OVRO  
H13CO+ 4-3 <0.13b <0.05c   13.7 JCMT Jan. 00
H13CO+ 1-0e 0.07     $13.0\times10.8$ OVRO  
HCN 4-3 0.25 0.09/0.08 3.3 13.5 JCMT Sept. 98
HCN 1 2-01e 3.04     $4.3\times3.4$ OVRO  
H13CN 3-2e 1.49     $0.9\times 0.6$ OVRO  
H13CN 1 2-01e 1.20     $5.8\times 4.6$ OVRO  
TW Hya  
CO 6-5 <3.22 <1.19 2.46 14.5 CSO Jun. 00
CO 4-3d 5.0     11.0 JCMT  
CO 3-2 1.98 2.94 0.63 13.8 JCMT Nov. 99
CO 3-2 1.00 0.77 1.23 25.7 CSO Jun. 00
CO 2-1d 1.02     20.0 JCMT  
13CO 3-2 0.24 0.29 0.78 14.4 JCMT Feb. 99
13CO 2-1d 0.14     20.0 JCMT  
HCO+ 4-3 0.49 0.72 0.63 13.4 JCMT Nov. 99
H13CO+4-3 0.07 0.08 0.76 13.7 JCMT Dec. 99
HCN 4-3 0.49 0.60 0.76 13.5 JCMT Dec. 00
H13CN 4-3 <0.04f <0.05c 0.76 13.5 JCMT Dec. 00
HCN 3-2d 0.45     20.0 JCMT  
a Width of best single Gaussian fit to total profile.
b Calculated assuming the line is double peaked consisting of two separate Gaussians, each with a width of 1.3 kms-1.
c Listed value is 2$\times$rms.
d Values from Kastner et al. (1997).
e Values from Qi (2000).
f Calculated assuming a line width of 0.76 kms-1.

   
3 Simple one-dimensional analysis

Although the observed line intensities are a complex function of the physical structure of the disk and the line/continuum optical depth, useful insights can be obtained from a simple one dimensional analysis of the line ratios. For constant temperature and density models such as presented by Jansen et al. (1994) and Jansen (1995), the data provide constraints on both parameters. To compare data obtained with different beams the intensities were scaled to the same beam (see Sect. 4.4.2).

Consider first the observed ratios of 12CO and its isotopomers. The 12CO 3-2/13CO 3-2 ratios of 3.3 and 7.6 for LkCa 15 and TW Hya, respectively, indicate that the CO lines are optically thick, assuming a normal isotope ratio of $[^{12}{\rm C}]/[^{13}{\rm C}]=60$ in the solar neighborhood. On the other hand, the 13CO emission has an optical depth of only a few, since the C18O 3-2 emission is not detected. The ratio of peak 3-2 temperatures of >3 (using the 2$\sigma$ limit for C18O) and the observed beam-corrected 1-0 ratio of 5.0 are only marginally smaller than the isotope ratio [13C]/[18O] of 8.3 (Wilson & Rood 1994).

The temperature can be determined from the 13CO 3-2/1-0 ratio of $1.35\,\pm\, 0.4$, which gives temperatures of $\sim$20-40 K in LkCa 15. Care should be taken with the interpretation of this result since the emission of the two lines most likely comes from different regions of the disk due to the difference in optical depth of the two lines (see Sect. 5.1). The beam-corrected ratio for 13CO 3-2/2-1 of 0.9 for TW Hya indicates that the bulk of the gas in this source is colder than 25 K for densities >105 cm-3. The 12CO 6-5 line probes higher temperatures since its upper level lies at an energy of 116 K. The observed ratio $^{12}{\rm CO}~6{-}5/3{-}2=0.42^{+0.21}_{-0.14}$ for LkCa 15 also suggests the presence of gas with a temperature in the range 20-40 K while the upper limit of CO 6-5/3-2 <1.0 for TW Hya gives T<150 K (cf. Fig. 4 of Jansen et al. 1996). The 4-3 (JCMT)/3-2 (CSO) ratio of 0.91 +0.45-0.31 suggests temperatures $\sim$40 K whereas the ratio of both JCMT lines indicates somewhat higher temperatures. The different optical depths of the 3-2 and 6-5 lines imply that they probe different vertical layers of the disk. Such vertical structure may affect these conclusions, though not by large factors (see Sect. 5.1).

probed by molecules with a large dipole moment such as HCO+ and HCN. The measured HCO+/H13CO+ 1-0 ratio of 6.2 for LkCa 15, and the 4-3 ratio of 6.7 for TW Hya and >1.9 for LkCa 15 indicate that the main isotopomeric lines are again optically thick. No limits on HC18O+ exist, but H13CO+may be close to optically thin (see Sect. 5.1). The limit on the H13CO+ 4-3 line toward LkCa 15 together with the 1-0 line detected with OVRO gives a 4-3/1-0 ratio of less than <2.4 and constrains the density to <107 cm-3 in the HCO+ emitting region. The optically thick HCO+ 4-3/1-0 ratio of 0.75 +0.38-0.25 suggests n > 106 cm-3 at T=20-30 K. The HCN 12-01 to H13CN 12-01 ratio of 1.4 indicates that both lines are severely optically thick. The HCN 4-3 line has an even higher critical density than that of HCO+ 4-3. The observed HCN 4-3/1-0 ratio of 1.0 +0.5-0.3 indicates densities $n\approx 10^{7}{-}10^{8}$ cm-3 in the LkCa 15 disk.

For the TW Hya disk, the HCN/H13CN 4-3 ratio has a lower limit of 12.3, indicating that the HCN lines are optically thin or nearly optically thin. The HCN 4-3/3-2 ratio of 0.6 +0.3-0.2constrains its density to lie in the 106 to 108 cm-3 range, and, as the lines are (nearly) optically thin, this should refer to the regions in the disk where HCN is most abundant.

In summary, the simple analysis indicates that the main isotope lines are optically thick, but that the lines of 13C isotopomers of CO and HCO+ have at most moderate optical depths. The bulk of the gas is cold, but the presence of a warm layer is suggested from the CO 4-3 line for TW Hya. The inferred densities in the region where the lines originate are high, at least 106 cm-3, but not sufficient to thermalize all transitions, especially those from high dipole moment species.

   
4 Description of models

4.1 Adopted disk models

In this work, the line emission from three recently published disk models is calculated and compared with observations. Although each of these models has limitations, they are representative of the range of temperatures and densities that may occur in disk models, even if not specifically developed for the large radii probed in this work. The three disk treatments analyzed in detail are:

1.
The model by D'Alessio et al. (1999) (see also D'Alessio et al. 1997; D'Alessio et al. 1998), in which the disks are geometrically thin and in vertical hydrostatic equilibrium. The gas and dust are heated by viscous dissipation, radioactive decay, cosmic rays and stellar irradiation. The gas and dust are coupled and can thus be described by a single temperature. The assumption of a geometrically thin disk implies that the energy balance can be calculated at each radius separately, decoupled from other radii. The temperature and density distribution (Fig. 2, top two figures) have been calculated using this procedure;

2.
The model by Chiang & Goldreich (1997, 1999) represents a passive disk in radiative and hydrostatic balance. The disk structure is bi-layered with a super-heated dust surface layer that is in radiative balance with the light from the central star. This super-heated layer radiates half of its energy toward the midplane, thereby heating the inner regions of the disk. Figure 2 (center two figures) presents the temperature and density distribution from this model;

3.
The model by Bell et al. (1997) and Bell (1999) takes the effect of both stellar irradiation and the reprocessing of radiation into account. This redistribution of energy gives rise to a strong flaring of the disk near the star, but less strongly further away. The assumption of vertical hydrostatic equilibrium is used; however, the flaring of the disk at small radii (the first few AU) may, for high values of the mass accretion rate $\dot{M}$, shield the surface of the disk at larger radii from the radiation. The resulting temperature and density distribution is shown in Fig. 2 (bottom two figures). The shielding of the outer regions results in a cold disk which is approximately isothermal in the vertical direction.

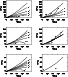  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10460f2.eps}} \end{figure} Figure 2: Comparison of the density in cm-3(left three figures) and the temperature in K (right three figures) for the models of D'Alessio et al. (1999) (top), Chiang & Goldreich (1997) (middle) and Bell (1999) (bottom). All models have a gas+dust mass of 0.024 $M_{\odot }$. Only one quadrant of the 2-D flaring disk is shown.
Open with DEXTER

The published models described above were calculated for different disk masses. Since the results depend sensitively on mass and cannot simply be scaled, this greatly complicates their comparison. To eliminate this uncertainty, the authors have kindly supplied several of their model runs for various masses. The model presented here for LkCa 15 has a mass of 0.024 $M_{\odot }$, close to its observed value (Osterloh & Beckwith 1995). The mass of the TW Hya disk estimated from submillimeter and centimeter continuum observations is $\sim$0.03 $M_{\odot }$, assuming a gas/dust ratio of 100/1 (Holland et al. 2000; Wilner et al. 2000). The disks all have an outer radius of 200 AU, and the precise mass is fixed by dividing the density of an appropriate model by a small factor of less than 3. Figure 3 compares the fraction of mass at a given temperature or density in the three models, whereas the distributions within the disk are shown in Fig. 2. While the density distributions are similar, the temperature distributions between the three models are clearly different. One of the aims of this paper is to investigate whether the molecular line data are consistent with these different types of models.

The adopted models are not tailor-made for the two sources studied here. For example, they do not fit in detail the observed SEDs: the Bell (1999) model is too cold on the outside to reproduce the mid-infrared emission. Chiang et al. (2001) have presented models for LkCa 15 and TW Hya which fit the observed SEDs. However, both models have significant settling of the dust. The gas may still flare out to higher vertical distances, but the SED does not provide observational constraints. For this reason, we adopted the original Chiang & Goldreich (1997) model which has no settling of dust so that the temperature is defined over the entire disk. Other parameters entering the models are the disk accretion rate and the luminosity and effective temperature of the star. For the accretion rate, which enters the D'Alessio et al. models, a value of 10 $^{-8}~M_{\odot}$yr-1 and $\alpha=0.01$ was chosen, which is higher than the observed values of 10-9 and $5\times 10^{-10}~M_{\odot}$yr-1 for LkCa 15 and TW Hya, respectively (Hartman et al. 1998, Muzerolle et al. 2000). However, the observed molecular lines probe the outer region of the disk whereas the accretional heating due to the high values of $\alpha$ and the accretion rate will only affect the inner few AU. The models refer to a 0.5 $M_{\odot }$star with $T_{{\rm eff}}=4000$ K. For comparison, LkCa 15 has a mass of roughly 1 $M_{\odot }$ and an effective temperature of 4400 K (Siess et al. 1999), while TW Hya has a mass of 0.7 $M_{\odot }$ and $T_{{\rm eff}}=4000$ K (Muzerolle et al. 2000).


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10460f3.eps}} \end{figure} Figure 3: Comparison of the fraction of mass in a given temperature and density interval for the models of D'Alessio et al. (1999) (top figures), Chiang & Goldreich (1997) (middle figures) and Bell (1999) (lower figures). The distributions in the disks are plotted in Fig. 2.
Open with DEXTER

4.2 Radiative transfer methods

The radiative transfer in the molecular lines from disks is calculated in two steps. First, the abundances of the molecules in the disk are estimated using a ray-tracing method in the vertical direction through the disk and adopting statistical equilibrium calculations. The ratio of the different modeled lines constrains the range of depletions. This calculation does not take into account the inclination of the source and assumes that the ratio of different lines is less sensitive to inclination than the integrated intensity of a single line.

Once the depletions are constrained, a full 2D radiative transfer calculation is performed using the accelerated Monte Carlo (AMC) code of Hogerheijde & van der Tak (2000), whose results are compared to the observations. The motivation for this elaborate scheme is given in Sect. 4.3 and is driven by the huge computational time involved in the latter calculation. The AMC code has been compared with other radiative line transfer codes in a workshop in Leiden in 1999, where the populations of the levels and convergence have been tested for a set of one-dimensional problems. The comparison of the various codes is described in van Zadelhoff et al. (in preparation)[*].

   
4.3 Level populations and depletions


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10460f4.eps}}\end{figure} Figure 4: The relative populations of levels of the CO molecule (J=3 and J=6) and the HCO+ molecule (J=1 and J=4) for three different calculations (LTE (dotted), SE with no stimulated emission or absorption (dashed) and SE with full 2D radiative transfer (solid)). The levels are calculated for the D'Alessio et al. (1999) model and plotted as a function of height Zat a radius of 175 AU. The assumed abundances are 10-4 for CO and $5\times 10^{-9}$ for HCO+. In the lower plot the HCO+ J=4level population is reduced by a factor of 5 for clarity. It is clearly seen that the populations in the upper layer of the disk are not in LTE.
Open with DEXTER

The level populations xu and xl can be calculated in various ways. The simplest approximation is that of Local Thermodynamic Equilibrium (LTE), which is valid for all levels that are collisionally excited in a gas with densities higher than the critical density for that level. The latter is given by


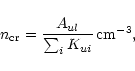\begin{displaymath}n_{\rm cr}=\frac{A_{ul}}{\sum_{i} K_{ui}} \, {\rm cm^{-3}}, \end{displaymath} (1)

where $\sum_{i} K_{ui}$ denotes the sum of all collisional rate coefficients from level u to all other levels i. LTE is usually adopted in the analysis of line emission from disks (e.g., Gómez & D'Alessio 2000; Dutrey et al.1996; Kastner et al. 1997). Although the bulk of the gas is in LTE due to the high densities, the radiation from the central part of the disk can be highly optically thick depending on the molecular abundances and assumed depletions. In that case the outer layers dominate the emission where the densities can fall below the critical densities of the higher frequency lines for high dipole moment molecules. For these regions statistical equilibrium (SE) calculations, also referred to as non-LTE or NLTE, need to be performed.

The populations of the levels are calculated by solving the equation:

 
$\displaystyle \sum_{j>l}[n_{j}A_{jl}+(n_{j}B_{lj}-n_{l}B_{lj})\overline{J}_{jl}... ..._{l}B_{lj}-n_{j}B_{jl})\overline{J}_{lj}] +\sum_{j}[n_{j}C_{jl}-n_{l}C_{lj}]=0,$     (2)

where $\overline{J}_{jl}$ is the integrated mean intensity, Aijand Bij the Einstein coefficients and Cij the collisional rates. The Einstein A coefficients and collisional rate coefficients for CO, HCO+ and HCN are the same as those in Jansen et al. (1994, Table 4). The calculation of the level populations is an iterative process since the integrated mean intensity is directly related to the levels nl, which in turn affects the mean intensity.

Test calculations have been performed for three cases. The first is LTE, where the populations are given by the Boltzmann equation. In this assumption the populations are dominated by collisions and therefore depend only on the local temperature. The second is Statistical Equilibrium without stimulated radiative effects (SE[ $\overline{J}_{\nu}=0$]), in which the populations of the levels are no longer assumed to be dominated by collisions and are calculated explicitly. In this case, Eq. (2) is solved under the assumption that $\overline{J}_{\nu}=0$ for all radiative transitions. The third method is the full Statistical Equilibrium (SE) solution using a Monte Carlo code (Hogerheijde & van der Tak 2000) to calculate the mean intensity $\overline{J}_{\nu}$ for each radiative transition iteratively, taking the line emission and absorption throughout the 2D disk into account.

In Fig. 4, the relative populations for the levels J=3 and 6 of CO and J=1 and 4 of HCO+ are plotted for the LTE, SE( $\overline{J}_{\nu}$ = 0) and SE for the D'Alessio et al. (1999) model. This model is chosen because it has a smooth temperature gradient but does show a temperature inversion in the z-direction. The adopted CO and HCO+ abundances are 10-4 and $5\times 10^{-9}$ respectively, and the turbulent line width is assumed to be 0.2 kms-1. Figure 4 shows that the differences between the three methods are small in the midplane but that they become significant in the lower density upper layers. For the J=1 level of HCO+, the influence of the Cosmic Microwave Background 2.7 K radiation is apparent since its relative population continues to rise toward the outside in the SE calculation compared to the SE( $\overline{J}_{\nu}=0$) calculation. Even though only the full 2D SE calculation describes the populations accurately, its calculation is an enormous computational task due to the large column densities and steep gradients in density and temperature coupled with a narrow velocity profile. In these cases, the convergence criteria of a numerical code become very important. The SE( $\overline{J}_{\nu}=0$) calculation provides better agreement with the SE calculation compared to LTE, especially at larger distances from the star where most of the observed radiation originates. Therefore the SE( $\overline{J}_{\nu}=0$) method is adopted in the ray-tracing calculations.

The abundances and depletion of various molecules are taken into account in two different ways:

1.
A constant model, in which the fractional abundances are the same throughout the disk. In the standard model, abundances close to those found in dark clouds are chosen. These values can be subsequently lowered by a constant factor $D_{\rm C}$ with respect to the standard values. Note that the chemical interpretation of $D_{\rm C}$ may vary: it can be due to freeze-out, photodissociation, different chemistry at high or low densities, or any combination of these. A sketch of the depletion models compared to interstellar abundances is given in Fig. 5;
2.
A jump model, in which the abundances are constant except for regions where the temperature is lower than a critical temperature. Below this temperature the abundance is assumed to drop by a certain factor due to freeze-out of the molecule onto cold dust grains. In this paper, a temperature of 22 K (based on CO freezing onto a CO surface; Sandford & Allamandola 1993) is assumed (see Fig. 5). HCO+ is assumed to follow the CO abundance profile and will thus deplete at the same temperature. For HCN a critical temperature of 80 K is assumed. A more detailed and realistic description of the depletion and abundance variations has been given by Aikawa & Herbst (1999) and Willacy et al. (1998), but these results are too specific for the exploratory purposes of this paper.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10460f5.eps}}\end{figure} Figure 5: The two ways in which the depletion of molecules compared to the interstellar value is taken into account in the computations. On the left a constant depletion $D_{\rm C}$ is shown, whereas on the right a step-function representing the freeze-out of molecules $D_{\rm J}$ below a critical temperature is illustrated.
Open with DEXTER

4.4 Approximate line intensities

   
4.4.1 Vertical radiative transfer
To constrain the depletions and thereby bracket the computational domain of the problem, the intensity of each line is calculated by solving the radiative transfer equation

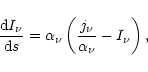\begin{displaymath}\frac{{\rm d}I_{\nu}}{{\rm d}s}=\alpha_{\nu}\left(\frac{j_{\nu}}{\alpha_{\nu}}-I_{\nu}\right), \end{displaymath} (3)

in the vertical direction, where $I_{\nu}$ is the intensity, sthe path length along a ray normal to the disk, $j_{\nu}$ the emission function, and  $\alpha_{\nu}$ the absorption function, which is the inverse of the mean free path. The ratio of the emission and absorption functions is known as the source function. The transfer equation is solved in an iterative ray-tracing procedure using small $\Delta s$ steps from $s_{0} = -\infty$ to $s_{N}= +\infty$ (the observer).

The equation to be solved thus becomes

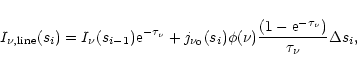\begin{displaymath}I_{\nu ,{\rm line}}(s_{i})=I_{\nu}(s_{i-1}){\rm e}^{-\tau_{\n... ...nu) \frac{(1-{\rm e}^{-\tau_{\nu}})}{\tau_{\nu}} \Delta s_{i}, \end{displaymath} (4)

 where $\phi(\nu)$ is the line emission profile function in frequency space and $I_{\nu}(s_{0})=0$.

The optical depth $\tau_{\nu}$ is the sum of the attenuation by dust and gas along the step-length and is equal to

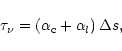\begin{displaymath}\tau_{\nu} = (\alpha_{\rm c}+\alpha_{l}) \, \Delta s, \end{displaymath} (5)

where
$\displaystyle \alpha_{\rm c}$ =$\displaystyle \kappa_{\nu}\frac{m_{\rm gas}}{R_{\rm gd}}\,n_{\rm gas},$ (6)
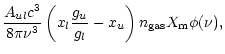$\displaystyle \alpha_{l}$ =$\displaystyle \frac{A_{ul} c^{3}}{8 \pi \nu^{3}} \left(x_{l}\frac{g_{u}}{g_{l}}-x_{u}\right) n_{\rm gas} X_{\rm m} \phi(\nu),$ (7)

and the emission is given by

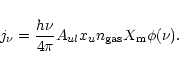\begin{displaymath}j_{\nu} =\frac{h \nu}{4 \pi}A_{ul}x_{u}n_{\rm gas} X_{\rm m}\phi(\nu). \end{displaymath} (8)

In these equations, $m_{\rm gas}$ is the mean molecular weight of a gas particle, $R_{\rm gd}$ the gas to dust ratio, Aul the Einstein coefficient, $\nu$ the frequency of the transition, c the speed of light, $X_{\rm m}$ the abundance of the molecule relative to the gas density  $n_{\rm gas}$, which is taken to be equal to the density of H2, gi the statistical weight of level i and xi the population of level i. A mean molecular weight of 2.2 (proton mass per particle) and $R_{\rm gd}=100$ are adopted. The level populations are solved using SE( $\overline{J}_{\nu}=0$) (Sect. 4.3) for the reasons stated above.

The continuum mass absorption coefficient $\kappa_{\nu}$ is taken from Ossenkopf & Henning (1994) and extended to wavelengths longer than 1.3 mm as

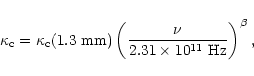\begin{displaymath}\kappa_{\rm c}=\kappa_{\rm c}(1.3~{\rm mm}) \left(\frac{\nu}{2.31 \times 10^{11}\ {\rm Hz}} \right)^\beta, \end{displaymath} (9)

where $\kappa_{\rm c}(1.3~{\rm mm})$depends on the specific coagulation model chosen and $\beta$ is taken to be 1. For this problem the  $\kappa_{\rm c}$values were taken from the model with coagulation at a density of 108 cm-3 covered by a thin ice-layer ( $\kappa_{\rm c}(1.3~{\rm mm})=1.112~{\rm cm}^{2}$g-1). In practice, however, the dust absorption is negligible compared to the line absorption for the molecular transitions in the wavelength range of interest.

   
4.4.2 Calculation of intensity
For comparison with observations and model results, all values are referred to the size of the disk model. The observations are thus scaled as follows:
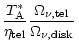$\displaystyle T_{\rm disk, obs}$ = $\displaystyle \frac{T_{\rm A}^{\ast}}{\eta_{{\rm tel}}} \frac{\Omega_{\nu,{\rm tel}}}{\Omega_{\nu,{\rm disk}}}\,$ (10)
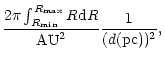$\displaystyle \Omega_{{\rm disk}}$ = $\displaystyle \frac{2 \pi \int_{R_{\rm min}}^{R_{\rm max}} R {\rm d}R}{{\rm AU}^{2}} \frac{1}{({d} ({\rm pc}))^{2}},$ (11)

where the ratio $T_{\rm mb}={T_{\rm A}^{\ast}}/{\eta_{{\rm tel}}}$ is given in Table 1, $\Omega_{\nu,{\rm tel}}$ is the beam size at the frequency of the line in arcsec2, d the distance in parsec, AU the astronomical unit, and $\Omega_{{\rm disk}}$ the size of the disk in arcsec2.

The models are calculated using the ray-tracing Eq. (4) which are weighted according to its emitting surface area

 \begin{displaymath}\overline{I}=\frac{\sum_{i=0}^{Nx} I_{i} \pi (R_{i}^{2}-R_{i-1}^{2})} {2 \pi \int_{R_{\rm min}}^{R_{\rm max}} R {\rm d}R}\cdot \end{displaymath} (12)

Here, $\overline{I}$ is the mean intensity for the entire disk at the surface, with Nx the number of cells in the R-direction. The disk is assumed to be seen face-on. This is a very good approximation for TW Hya, whereas it should still be reasonable for LkCa 15 even though the disk is seen at an inclination of 60$^\circ$. The intensities derived by this method will be used only in the analysis of line ratios, which are less sensitive to inclination effects than absolute values.

The radius of the disk is taken to be 200 AU in all models, or 400 AU diameter. The size of the LkCa 15 disk (d=140 pc) suggested by the OVRO 13CO maps of Qi (2000) is slightly larger (420 AU$\times$530 AU). For TW Hya, no millimeter interferometer observations are available, but mid-infrared and VLA 7 m images suggest a disk size of $\sim$100 AU (Wilner et al. 2000). Scattered light images observed with the Hubble Space Telescope suggest an outer radius of at least 200 AU, however (Weinberger et al. 1999; Krist et al. 2000). We therefore adopt a similar disk size in AU as for LkCa 15, but with d=57 pc.

4.5 Line intensities using full radiative transfer

For the calculation of the populations in SE using full radiative transfer, the Monte Carlo code developed by Hogerheijde & van der Tak (2000) is used. In this code, Eq. (2) is solved in an iterative fashion, where all photons start at the outer boundary with an intensity given by the 2.728 K Cosmic Background radiation. In this calculation, the inferred abundances from the SE( $\overline{J}_{\nu}=0$) method are adopted. The calculated populations at each position in the disk are used to compute the complete line profiles of selected molecules using a program which calculates the sky brightness distribution. The profiles are calculated by constructing a plane through the origin of the disk perpendicular to the line of sight, with a spatial resolution small enough to sample the physical and velocity distributions. Both the spatial resolution and the velocity resolution can be specified. A ray-tracing calculation is performed through this plane from $-\infty$to $+\infty$, keeping track of the intensity in the different velocity bins.

   
5 Results


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10460f6.eps}}\end{figure} Figure 6: The $\tau =1$ surfaces for the observed CO and HCO+ isotopomer lines integrated from the top, overplotted on the temperature (top) and density distribution (bottom) in the model by D'Alessio et al. (1999). The dotted contours are iso-temperature (in K) or iso-density (in cm-3) contour lines. The results are shown for both the standard abundances (left) and depleted by a constant factor $D_{\rm C}=10$(right). The labels indicate: A: 12CO 6-5; B: 12CO 3-2; C: 12CO 2-1; D: 13CO 3-2; E: 13CO 1-0; F: C18O 3-2; G: C18O 2-1; H: HCO+ 4-3; I: HCO+ 1-0; J: H13CO+ 4-3; K: H13CO+ 1-0.
Open with DEXTER

The models are calculated initially using standard dark cloud abundances of CO of $1\times 10^{-4}$, HCO+ of $5\times 10^{-9}$, and HCN of $5\times 10^{-9}$ relative to H2. For the isotope ratios the following values are used throughout: ${^{12}\mbox{C}}/{^{13}\mbox{C}}=60$ and ${^{16}\mbox{O}}/{^{18}\mbox{O}}=500$. These models are referred to as $D_{\rm C}=D_{\rm J}=1$. Subsequently, the values of $D_{\rm C}$ and $D_{\rm J}$ are varied (see Sect. 4.3). The line intensities have been calculated assuming a micro-turbulence of 0.2 kms-1. For TW Hya, this results in calculated line widths of $\sim$0.8 kms-1, in good agreement with observations.

   
5.1 $\tau={\mathit 1}$ surfaces

Significant insight into the observational results can be obtained by investigating the regions of the disk where the different lines become optically thick. At each radius the effective emission region for each line is calculated using the SE( $\overline{J}_{\nu}=0$) method by integrating from the top layer down until $\tau =1$ in line + continuum is reached. Although the $\tau =1$ level is chosen arbitrarily and radiation from deeper in the disk may still escape, it provides a useful measure of the volume of the emitting region for each molecular transition. This calculation is performed only for a face-on disk for simplicity and is thus only applicable for the TW Hya case. It does, however, give an indication of the parts of the disk from which the molecular emission arises in more general cases. For the model by D'Alessio et al. (1999), a contour-plot of the $\tau =1$ surfaces of the observed CO and HCO+ lines is given in Fig. 6, where the former are overplotted on the temperature distribution and the latter on the density distribution. The line emission is dominated by densities and temperatures above the $\tau =1$ contour, which can then be compared to the values derived from the constant temperature and density models given in Sect. 3.

It is seen that, for standard abundances, the 12CO lines become optically thick in the upper, warm layer of the disk where T>40 K. On the other hand, the 13CO lines probe into the colder regions around 20-30 K. Thus, the 12CO excitation temperature should be higher than that of 13CO, which must be taken into account in the analysis of isotopomeric line ratios. Similarly, the higher frequency 3-2 and 6-5 lines generally have higher optical depths than the 1-0 lines, and thus probe better the warmer upper layer. Even C18O is not fully optically thin, but has $\tau\approx 1{-}2$. The low temperature of 20-30 K probed by 13CO is consistent with the simple analysis of the data in Sect. 3.

For the standard HCO+ abundance, the 1-0 to 4-3 lines are optically thick in the outer layers, whereas the H13CO+ lines are close to optically thin throughout the disk. Thus, the HCO+ lines probe densities of order 106-107 cm-3, below the critical density of the 4-3 transition. For H13CO+, the populations will be closer to LTE because its emission arises primarily from regions with densities of 107-108 cm-3. If the HCO+ abundance is depleted by a constant factor $D_{\rm C}=10$, the HCO+ lines become optically thin in the outer regions of the disk and now trace regions with densities of 107-108 cm-3. The HCN 1-0 to 4-3 lines show a similar behavior to HCO+. The densities of 106-108 cm-3 derived from the observed HCO+ and HCN lines in Sect. 3 are consistent with this analysis for modest depletions of both species.

   
5.2 Integrated line ratios: Range of depletions


   
Table 2: Ranges of inferred depletions for the different molecules for the three disk models.
    D'Alessio et al. (1999) Chiang & Goldreich (1997) Bell (1999)
    LkCa 15 TW Hya LkCa 15 TW Hya LkCa 15 TW Hya

CO		 $D_{\rm C}$ [3, 15] >30 [3, 30] >100 [1, 500] [10, 1000]
  $D_{\rm J}$ [3, 30] >1 [1, 15] >1 >1 >1
HCO+ $D_{\rm C}$ [3, 80] >80 [10, 100] >100 [1, 80] [2, 1000]
  $D_{\rm J}$ >1 >1 >10 >1 [1, 100] >1
HCN $D_{\rm C}$ [1, 400] [4, 600] [10, 200] [10, 800] [1, 500] [4, 500]
  $D_{\rm J}$ >1 >1 >1 >1 >1 >1

The numbers in square brackets indicate the range of inferred depletions.

In this section, the relative line intensities obtained in the SE( $\overline{J}_{\nu}=0$) method are used to constrain the abundances of the molecules and the level of depletion. Since lines of different isotopomers arise from different regions, their line ratios will depend on the local depletion values. By calculating models for a range of depletions, the abundances can be derived by varying both the overall depletion $D_{\rm C}$and the jump depletion $D_{\rm J}$ as described in Sect. 4.3. In the comparison of the line ratios, the difference in beam dilution for the two lines must be taken into account (Sect. 4.4.2).

  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10460f7.eps}}\end{figure} Figure 7: The CO/13CO 3-2 (top) and 13CO/C18O 3-2 (bottom) line intensity ratios as functions of the jump depletion $D_{\rm J}$ and the overall depletion $D_{\rm C}$ within the D'Alessio et al. (1999) model. The observed ratios for LkCa 15 CO 3-2/13CO 3-2 (dashed line) and TW Hya (dash-dotted line) are shown in the figures.
Open with DEXTER

Isotope ratios are more sensitive to both $D_{\rm C}$ and $D_{\rm J}$ as compared to ratios of different species. For instance the 12CO emission remains optically thick up to large values of $D_{\rm C}$ and therefore does not probe the region below 22 K, whereas 13CO becomes sensitive to $D_{\rm J}$ for modest values of $D_{\rm C}$. In Fig. 7 the CO/13CO 3-2 and 13CO/C18O 3-2 line intensity ratios are plotted as functions of $D_{\rm J}$ and $D_{\rm C}$. The observed values for LkCa 15 are plotted with dashed lines, and indicate a range $D_{\rm C} \in [3,40]$ when both plots are combined. The ratio for TW Hya (dot-dashed line) indicates a larger depletion with $D_{\rm C} > 100 $ and $D_{\rm J} \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displ... ...\offinterlineskip\halign{\hfil$\scriptscriptstyle .... Combining similar plots for all species and lines, the resulting values of $D_{\rm C}$ and $D_{\rm J}$ are shown in Table 2 for the three models of interest for both sources. The inferred ranges for the disk models are large and it is difficult to give accurate values for molecules for which few lines have been measured. The abundances of all molecules in the TW Hya disk seem to be depleted by a large factor. In general $D_{\rm J} \approx 10$ is taken as a best fit for both sources. In cases where no constraints are available, $D_{\rm J}=10$ has been assumed.


   
Table 3: Integrated intensities for the higher rotational lines for the three disk models.
Model $D_{\rm C}$ $D_{\rm J}$ CO 6-5 CO 3-2 13CO 3-2 C18O 3-2 HCN 4-3 H13CN 4-3 HCO+ 4-3 H13CO+ 4-3
Aa 1 1 0.78 1.15 0.39 0.18 0.39 0.12 0.54 0.15
Bb 1 1 0.076 0.21 0.16 0.11 0.15 0.092 0.17 0.10
Cc 1 1 0.59 0.80 0.42 0.28 0.42 0.20 0.48 0.24
A 5 10 0.61 0.93 0.24 0.074 0.25 0.030 0.37 0.043
B 5 10 0.046 0.16 0.089 0.036 0.096 0.011 0.11 0.018
C 5 10 0.36 0.61 0.23 0.086 0.26 0.049 0.33 0.062
A 10 10 0.44 0.68 0.16 0.044 0.17 0.018 0.26 0.026
B 10 10 0.041 0.15 0.074 0.022 0.081 0.006 0.095 0.009
C 10 10 0.25 0.46 0.16 0.057 0.19 0.031 0.24 0.041
LkCa 15d 0.53 1.39 0.39 <0.14 0.25 $\ldots$ 0.26 <0.13

Model		 $D_{\rm C}$ $D_{\rm J}$ CO 6-5 CO 3-2 13CO 3-2 HCN 4-3 HCN 3-2 H13CN 4-3 HCO+ 4-3 H13CO+ 4-3
A 100 10 0.88 1.84 0.29 0.36 0.22 0.024 0.52 0.038
B 100 10 0.12 1.07 0.14 0.18 0.13 0.004 0.26 7.0E-3
C 100 10 0.60 1.46 0.36 0.46 0.24 0.044 0.58 0.065
A 200 10 0.68 1.81 0.23 0.29 0.17 0.013 0.42 0.021
B 200 10 0.069 0.95 0.083 0.11 0.08 0.002 0.18 3.4E-3
C 200 10 0.57 1.73 0.32 0.43 0.21 0.025 0.55 0.040
B 10 10 0.38 1.41 0.15 0.54 0.48 0.045 0.62 0.06

TW Hyad		 <3.2 1.98 0.24 0.49 0.45 <0.04 0.49 0.07
a D'Alessio et al. (1999) model.
b Bell (1999) model.
c Chiang & Goldreich (1997) model.
d The observed values have an estimated uncertainty of 20%; all values refer to the
original beam size of the observations (see Table 1).


   
Table 4: Integrated intensities for the lower rotational lines for the three disk models.
Model $D_{\rm C}$ $D_{\rm J}$ 13CO 1-0 C18O 1-0 HCN 1-0 H13CN 1-0 HCO+ 1-0 H13CO+ 1-0
Aa 1 1 6.18 1.90 4.47 0.85 4.84 0.20
Bb 1 1 4.04 1.57 2.58 0.76 2.68 0.17
Cc 1 1 8.80 2.88 5.72 0.96 5.94 0.25
A 5 10 3.60 0.53 2.70 0.11 3.11 3.3E-2
B 5 10 2.04 0.32 1.39 5.5E-2 1.56 1.8E-2
C 5 10 3.56 0.62 2.52 0.14 3.06 4.0E-2
A 10 10 2.31 0.31 1.75 6.0E-2 2.11 1.8E-2
B 10 10 1.55 0.18 1.11 2.8E-2 1.31 9.3E-3
C 10 10 2.40 0.38 1.70 7.6E-2 2.10 2.3E-2
LkCa 15a 7.43 0.70 3.04 1.20 4.19 7.E-2
a D'Alessio et al. (1999) model.
b Bell (1999) model.
c Chiang & Goldreich (1997) model.
d The observed values, taken from Qi (2000), have an estimated uncertainty of 20%; all values
refer to the original beam size of the observations (see Table 1).

5.3 Line profiles and intensities

The line profiles are calculated using the full 2D radiative transfer code for the range of depletions derived in Sect. 5.2. The depletions are further constrained by the absolute intensities. Specifically, for LkCa 15 $D_{\rm C}=5$ and 10 with $D_{\rm J}=10$ is taken, and for TW Hya the same $D_{\rm J}=10$ was assumed but with $D_{\rm C}=100$and 200. As a reference, an extra run was performed for LkCa 15 with no depletions. A general turbulent width of 0.2 kms-1 is assumed and the only structured velocity distribution is taken to be the Keplerian rotation of the disk. This velocity component is important for the comparison with observations of sources at non-zero inclination. For these calculations, an inclination of 60$^\circ$ for LkCa 15 and 0$^\circ$ for TW Hya is used. The results are convolved with the appropriate beam as given in Table 1.

A model with no depletion was also run for LkCa 15 with an inclination of 0$^\circ$ to check the effect of inclination. Although the total integrated line intensities changed significantly, their ratios changed only up to 7%. This justifies the approximate radiative transfer approach used in Sect. 5.2 for a first estimate of the depletions.

The resulting integrated intensities are presented in Table 3 for the high-J rotational lines and in Table 4 for the lower-Jtransitions. For six high-J rotational lines, the observed profiles are plotted in Fig. 8 with the three calculated model emission profiles superposed. In the left-hand figures, three lines are shown for LkCa 15 whose clear double peaks are due to the Keplerian rotation in the disk. On the right, the single peaks for a face-on disk such as that around TW Hya are seen. The optically thick lines from the latter source show that the disk can be fitted with a turbulent velocity of 0.2 kms-1.


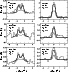  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{ms10460f8.eps}}\end{figure} Figure 8: Observed line profiles for LkCa 15 (left) and TW Hya (right) with the three models superposed (solid: D'Alessio et al.; dashed: Chiang & Goldreich; dash-dotted: Bell). The different transitions are indicated with the adopted depletions compared to standard molecular cloud values.
Open with DEXTER

5.3.1 Depletions

The absolute intensities in Tables 3 and 4 indicate that refinements of the inferred depletions are required, since different molecules favor different amounts of depletion. Note that the intensities computed for the cold Bell model are always smaller compared to the other two models, for both the high and low rotational lines. The reason for this is twofold. First, for a cold isothermal disk structure the level populations of any molecule at densities above the critical density are the same at each position. This means that the optical depth becomes directly proportional to the column of gas. For a model with an increasing temperature, the optical depth will not be directly proportional to the column but smaller. A model with a step function in its temperature will give results in between these two cases. Second, the colder disk will have slightly narrower, more optically thick lines due to the lower thermal motions in the gas, thereby trapping radiation more effectively.

Both effects are visible in the 13CO and CO lines (Fig. 8). The two peaks in the 13CO intensity for the inclined LkCa 15 disk are reduced significantly compared to the emission at line center in the Bell model. In the CO 3-2 line for the face-on TW Hya disk, the emission predicted by the Bell model is extremely optically thick, shown by the flat-topped emission profile. Also, the total linewidth is somewhat smaller compared to the other two disk models due to the low temperatures. Thus, the observed line profiles argue for a rising temperature structure in the vertical direction to prevent the high optical depths found in the cold isothermal model.

To counteract the low intensities found in the Bell model for the TW Hya disk, additional calculations were performed for less severe depletions (Table 3: $D_{\rm J}=10$, $D_{\rm C}=10$). The integrated intensities increase to just above the observed values in this case; however, the lines are extremely optically thick and show nearly square emission profiles, which is not observed for the CO 3-2 and HCO+ 4-3 lines. Thus, the line profiles speak against small depletions. In the two warm disk models, there is no significant difference between the two assumed depletions and only a slight preference can be given to $D_{\rm C}=100$. This is largely based on the HCO+/H13CO+ratio, which is ill fitted by a depletion of 200 and only moderately well for $D_{\rm C}=100$.

For LkCa 15, CO is best fitted with little depletion: all three models indicate $D_{\rm C}$ close to 1 for the lower rotational lines. The upper limit on the C18O 3-2 line and the C18O 1-0 emission would favor some depletion, which, in the case of C18O, can be explained by enhanced photodissociation in the upper layers due to the lack of self shielding. The CO 3-2 intensity is too low in all three models, which may be a sign of extended emission beyond 200 AU since this line is optically thick. The HCO+ and HCN lines are best fitted by a moderate depletion of $D_{\rm C}=5$ and $D_{\rm J}=10$. For HCN, this could again be a sign of a lack of shielding against photodissociation compared to CO. The observed H13CN 1-0 is slightly too high for all three models. Together, the HCN and H13CN data indicate that the HCN abundance needs to be lowered primarily in the surface layer to both bring the main isotope HCN emission down but keep a high H13CN intensity.

5.3.2 Probing the temperature and density structure


   
Table 5: Line ratios obtained for the three disk models.
Line ratio Observed D'Alessio et al. Bell Chiang & Goldreich
  LkCa 15c $D_{\rm C}$, $D_{\rm J}$ Ratio $D_{\rm C}$, $D_{\rm J}$ Ratio $D_{\rm C}$, $D_{\rm J}$ Ratio
               
CO $\frac{6-5}{3-2}$ 0.38 + 0.19- 0.13 5, 10a 0.66 1, 1a 0.36 10, 10 0.55
               
13CO $\frac{3-2}{1-0}$ 0.05 + 0.03- 0.02 1, 1a 0.06 10, 10a 0.05 1, 1a 0.05
               
HCO+ $\frac{4-3}{1-0}$ 0.06 + 0.03- 0.02 1, 1 0.11 1, 1a 0.06 1, 1 0.08
               
H13CO+ $\frac{4-3}{1-0}$ <1.9 10, 10b 1.44 5, 10 1.00 10, 10b 1.78
               
HCN $\frac{4-3}{1-0}$ 0.08 + 0.04- 0.03 5, 10a 0.09 5, 10a 0.07 1, 1a 0.07
  TW Hyac            
CO $\frac{6-5}{3-2}$ <1.62 100, 10 0.48 100/10, 10d 0.12/0.27 100, 10 0.41
CO $\frac{4-3}{3-2}$ 2.53 +1.26-0.84 200, 10 1.28 200/10, 10d 1.01/1.13 100, 10 1.29
HCN $\frac{4-3}{3-2}$ 1.09 +0.54-0.36 100, 10 1.64 100/10, 10d 1.38/1.13 100, 10 1.92
a Ratios for all three combinations of $D_{\rm C}$ and $D_{\rm J}$ fall within the error.
b Ratios for $D_{\rm C}=5, D_{\rm J}=10$ and $D_{\rm C}=10, D_{\rm J}=10$ fall within the error.
c The observed values and all ratios refer to the original beam sizes in which the lines were observed (see Table 1);
  thus, the beam size differs between species and lines. The error bars correspond to a 20% uncertainty.
d Ratios for high and low values of $D_{\rm C}$ are shown.

The calculated line ratios which are sensitive to the temperature and density distribution are summarized in Table 5. The temperature of the upper layer in the LkCa 15 models, as probed by the CO 6-5/3-2 ratio, fits within the errors to all three models, confirming the rather cold upper layer of this disk. However, as explained in the previous section, the absolute intensities are too low in the cold Bell model. To reproduce the observed CO 6-5 intensity, the CO abundance would have to be increased well above the cosmic carbon abundance in the cold isothermal model.

For the TW Hya disk, the modeled CO 4-3/3-2 ratios are on the low side, even in the D'Alessio et al. and Chiang & Goldreich models, indicating that the temperature in the surface layers would need to be higher. However, the calibration uncertainties in the older Kastner et al. (1997) data make this conclusion less firm. Further observations of high-J CO lines are needed to constrain the temperature structure of this disk.

The density is probed by the different HCO+ and HCN ratios. All three models are consistent with the observed 4-3/1-0 ratio for the main isotopes, indicating that the density in the layer above the midplane is in the correct range. The upper limits on the H13CN and H13CO+ prevent any conclusions for the midplane. As Table 5 shows, the models make different predictions for these optically thin species and future observations may be used to distinguish them.

Overall, the absolute line intensities and ratios are consistent with the models of D'Alessio et al. and Chiang & Goldreich for reasonable values of the depletions. The current data cannot distinguish between these two flared disk models. There is some evidence, however, both from the line ratios and from the line profiles that the surface of the disks needs to be warmer than that of a shielded isothermal outer disk such as computed by Bell (1999).

6 Discussion

The high depletions derived for TW Hya are in agreement with the conclusions by Kastner et al. (1997). The depletion can be due to two reasons: the first is a change in the gas- to dust-mass ratio to a value lower than 100 due to removal of gas. The second possibility is a large depletion of CO and other molecules, but not H2. The former possibility could be partly tested by searches for the pure rotational H2 lines (Thi et al. 2001). Regarding the second option, the present analysis indicates that the depletion cannot simply be due to the freezing out of molecules resulting in a large value of $D_{\rm J}$: the molecules also need to be depleted in the warmer upper layers probed by $D_{\rm C}$. This latter conclusion could be consistent with the fact that TW Hya is a very active UV and X-ray producing star (Kastner et al. 1999), capable of destroying CO due to dissociation or ionization. This can be tested by measuring the CO ionization or dissociation products, such as C+, C and CO+. TW Hya seems well described by a flared disk model where the ultraviolet radiation is capable of heating the upper layer (see Sect. 5.3).

The modeling suggests freezing out with a common value of $D_{\rm J}$ of at least 10. The depletion of molecules onto grains can be an important chemical sink in these disks since most of the mass is cold. This makes mass determinations of disks using CO or any of its isotopomers highly uncertain.

New models have recently been fitted to the SEDs of LkCa 15 and TW Hya by Chiang et al. (2001) and Chiang (2000). These models use as one of the main parameters the dust settling toward the midplane. For LkCa 15, the SED modeling indicates that the dust should have settled within the disk scale height H to explain the observations, with a high dust temperature in that region ( $T_{\rm dust}=49$ K at 100 AU). In these high density regions, the gas and dust temperature should be coupled; however at heights above the scale height H the lack of grains will reduce the heating of the gas due to the photo-electric effect, although some small grains may still be present. Together with enhanced cooling due to [O I] and [C II], this may cause a second temperature inversion with a cool upper layer free of dust. The lack of grains in the upper layer would be consistent with the non-detection of LkCa 15 by HST optical images (K. Stapelfeldt, private communication). This suggests a lack of scattering which should have been readily seen for a flared disk at an inclination of 60$^\circ$ with grains well mixed with the gas and an albedo of 0.5. In addition, the models used were calculated for a stellar temperature of 4000 K, whereas LkCa 15 has a higher effective temperature ( $T_{{\rm eff}}=4400$ K) which would result in higher disk dust-temperatures. The relatively low gas temperature in the disk, indicated by the line observations, strengthen the conclusions derived from the scattering and SED observations that dust settling has taken place in LkCa 15. Self-consistent models of the gas temperature and abundances of LkCa 15 are needed, taking dust-settling into account. As noted above, it is not yet possible to distinguish between the D'Alessio et al. (1999) and the Chiang & Goldreich (1997) models with the current observations. The data lack spatial resolution and have insufficient sensitivity to observe the optically thin isotopic lines. In addition to higher spatial resolution and sensitivity, better calibration of the data is needed, all of which will be provided by the Atacama Large Millimeter Array.

7 Conclusions

The main conclusions from this work are:

Acknowledgements
The authors are very grateful to P. D'Alessio, R. Bell and E. Chiang for sending and discussing the models used in the paper. They thank M. Hogerheijde and F. van der Tak for useful discussions and providing their radiative transfer code, and are grateful to the staff of the CSO and JCMT for their support. Astrochemistry in Leiden is supported by a SPINOZA grant from The Netherlands Organization for Scientific Research (NWO). This paper is dedicated to Fred Baas, who died on April 4, 2001. His expert, generous support at the JCMT was essential to make these observations possible.

References

 

Copyright ESO 2001