A&A 377, 428-441 (2001)
DOI: 10.1051/0004-6361:20011134
L. Sodré Jr.1 - D. Proust2 - H. V. Capelato3 - G. B. Lima Neto4 - H. Cuevas5 - H. Quintana6 - P. Fouqué7
1 - Departamento de Astronomia do IAG/USP, Av. Miguel Stefano 4200,
04301-904 São Paulo, Brazil
2 -
Observatoire de Paris - Section de Meudon, DAEC, 92195 Meudon Cedex, France
3 -
Divisão de Astrofísica INPE/MCT, 12225-010 São José dos Campos,
Brazil
4 -
Departamento de Astronomia do IAG/USP, Av. Miguel Stefano 4200,
04301-904 São Paulo, Brazil
5 -
Departamento de Física, Universidad de La Serena, Benavente 980, La Serena,
Chile
6 -
Departamento de Astronomia y Astrofísica, Pontificia Universidad
Católica de Chile, Casilla 104, Santiago 22, Chile
7 -
European Southern Observatory, Casilla 19001, Santiago 19, Chile and
Observatoire de Paris - Section de Meudon, DESPA, 92195 Meudon Cedex, France
Received 13 September 2000 / Accepted 14 June 2001
Abstract
We present a dynamical analysis of the galaxy cluster Abell 970 based
on a new set of radial velocities measured at ESO, Pic du Midi and
Haute-Provence observatories. Our analysis indicates that this cluster
has a substructure and is out of dynamical equilibrium. This conclusion
is also supported by differences in the positions of the peaks of the
surface density distribution and X-ray emission, as well as by the
evidence of a large-scale velocity gradient in the cluster. We also
found a discrepancy between the masses inferred with the virial theorem
and those inferred with the X-ray emission, which
is expected if the galaxies and the
gas inside the cluster are not in hydrostatic equilibrium. Abell 970
has a modest cooling flow, as is expected if it is out of equilibrium.
We propose that cooling flows may have an
intermittent behaviour, with phases of massive cooling flows being
followed by phases without significant cooling flows after the
accretion of a galaxy group massive enough to disrupt the dynamical
equilibrium in the centre of the clusters. A massive cooling flow will
be established again, after a new equilibrium is achieved.
Key words: galaxies: clusters: general - clusters: individual: A970 - distances and redshifts; large-scale structure of Universe; X-ray: general
In the present accepted paradigm of structure formation, small
structures are the first to collapse, then merging hierarchically to
build larger objects. In this framework, clusters of galaxies, the
largest (nearly) virialized structures, may be accreting galaxies
and/or "dark haloes'' even at z=0 (e.g. Lanzoni et al. 2000).
Therefore, the study of galaxy clusters may offer important
informations for observational cosmology, because cluster properties
depend on cosmological parameters and can be used to constrain
cosmological scenarios. For instance, the cluster mass function, which
may be described by the Press-Schechter formalism (Press & Schechter
1974), depends on the density parameter ![]() and on the power
spectrum amplitude and shape parameter (e.g., Lacey & Cole 1994;
Bahcall & Fan 1998). Also, the morphological and dynamical state of
clusters allow us to infer their history and, again, to constrain
cosmological theories of large-scale structure formation (e.g.,
Kauffmann et al. 1999).
and on the power
spectrum amplitude and shape parameter (e.g., Lacey & Cole 1994;
Bahcall & Fan 1998). Also, the morphological and dynamical state of
clusters allow us to infer their history and, again, to constrain
cosmological theories of large-scale structure formation (e.g.,
Kauffmann et al. 1999).
The mass of a cluster may be estimated by several methods: the optical virial mass, from the positions and radial velocities of the cluster galaxies; the X-ray mass, from the X-ray emission of the hot intracluster gas; the gravitational lensing mass, from the distortions produced on background object images by the gravitational field of the cluster. However, a discrepancy between these estimators are often found (e.g., Mushotzky et al. 1995; Girardi et al. 1998; Wu et al. 1998). Virial mass estimates rely on the assumption of dynamical equilibrium. X-ray mass estimates also depend on the dynamical equilibrium hypothesis and on the still not well-constrained intra-cluster gas temperature gradient (Irwing et al. 1999). Finally, mass estimates based on gravitational lensing are considered more reliable than the others (e.g., Mellier 1999) because they are completely independent of the dynamical status of the cluster, and their discrepancies with other methods may be due to non-equilibrium effects in the central region of the clusters (Allen 1998).
An important source of departure from equilibrium (that may affect mass estimates) are the substructures. Their very existence supports the current view that clusters grow hierarchically by accreting nearby groups and galaxies. Note that even the frequency and degree of clumpiness in the central regions of the clusters depends on the cosmology (e.g., Richstone et al. 1992). In many cases, substructures are loosely bound and can survive only a few crossing times in the hostile environment of rich clusters. However, they seem to be very common in present-day clusters. A recent estimate by Kolokotronis et al. (2000) indicates that at least 45% of rich clusters present optical substructures. Substructures are detected in both optical and X-ray images in 23% of the clusters. This last number may then be considered a lower limit on the fraction of real substructures in clusters, and it is large! Indeed, it implies that one in four clusters may be out of equilibrium due to the presence of a substructure. The dynamical status of individual clusters should therefore be examined in detail before being used in other studies.
In this paper we present a study of the dynamical status of the cluster Abell 970, from the analysis of the positions and velocities of cluster galaxies, as well as from the intra-cluster gas X-ray emission. Abell 970 has a richness class R=0 and type B-M III (Abell et al. 1989). Together with a few other clusters (A979, A978 and A993), it is member of the Sextans supercluster (number 88 in the catalogue of Einasto et al. 1997; and number 378 in the catalogue of Kalinkov et al. 1998). It has a moderate cooling flow (White et al. 1997).
A search in the NED database![]() indicates that only 4 radial velocities are
known in the field of the cluster (see Postman et al. 1992) which,
however, have not been published. Here we examine some properties of
the cluster Abell 970, using a set of 69 new radial velocities. The
observations of radial velocities reported here are part of a program
to study the dynamical structure of clusters of galaxies, started some
years ago and with several results already published (see e.g. Proust et al. 1987, 1988, 1992, 1995, 2000; Capelato et al. 1991).
indicates that only 4 radial velocities are
known in the field of the cluster (see Postman et al. 1992) which,
however, have not been published. Here we examine some properties of
the cluster Abell 970, using a set of 69 new radial velocities. The
observations of radial velocities reported here are part of a program
to study the dynamical structure of clusters of galaxies, started some
years ago and with several results already published (see e.g. Proust et al. 1987, 1988, 1992, 1995, 2000; Capelato et al. 1991).
This paper is organized as follows. We present in Sect. 2 the details
of the observations and data reduction. In Sects. 3 and 4 we discuss
the galaxy and the X-ray distributions, respectively. In Sect. 5 we
analyze the velocity distribution of the cluster galaxies. In Sect. 6
we present mass estimates for the central region of the cluster,
derived from the optical and X-ray observations. In Sect. 7 we discuss
the dynamical status of Abell 970. Finally, in Sect. 8 we summarize
our conclusions. We adopt here, whenever necessary,
![]() Mpc-1,
Mpc-1,
![]() and
and
![]() .
.
| GALAXY | R.A | DEC. | TYPE |
|
VELOCITY | R | N |
| (2000) | (2000) |
|
|||||
| 01 | 10 17 25.7 | -10 41 21 | E/D | 16.57 | 17525 52 | 9.72 | e |
| 02 | 10 17 24.6 | -10 41 22 | S0 | 18.00 | 16209 37 | 7.14 | e |
| 03 | 10 17 28.3 | -10 40 59 | S0/S | 18.67 | 18424 74 | 5.48 | e |
| 04 | 10 17 29.7 | -10 40 31 | S0 | 17.62 | 16270 52 | 9.67 | e |
| 05 | 10 17 26.3 | -10 41 34 | S0 | 17.51 | 18357 54 | 6.60 | e |
| 06 | 10 17 23.9 | -10 42 16 | S0/S | 18.41 | 16435 69 | 5.61 | e |
| 07 | 10 17 27.3 | -10 41 51 | E/S0 | 18.36 | 18145 53 | 5.89 | e |
| 08 | 10 17 29.5 | -10 42 17 | S | 18.38 | 17404 71 | 7.42 | e |
| 09 | 10 17 21.7 | -10 42 56 | S | 17.96 | 17631 61 | 6.91 | e |
| 10 | 10 17 24.3 | -10 43 29 | S | 17.95 | 16341 81 | 6.76 | e |
| 11 | 10 17 31.8 | -10 42 59 | S0/S | 18.83 | 17769 81 | 5.79 | e |
| 12 | 10 17 30.0 | -10 43 09 | S0 | 18.45 | 17327 35 | 5.57 | e |
| 13 | 10 17 32.9 | -10 43 52 | S | 18.26 | 16974 36 | 5.14 | e |
| 14 | 10 17 29.4 | -10 44 34 | Sa | 17.69 | 18909 75 | 5.61 | e |
| 15 | 10 17 28.0 | -10 44 18 | S0 | 17.67 | 18030 29 | 8.46 | e |
| 16 | 10 17 20.7 | -10 44 16 | S | 18.56 | 17711 26 | 5.85 | e |
| 17 | 10 17 15.6 | -10 43 28 | Sa | 17.51 | 19503 96 | 2.62 | e |
| 18 | 10 17 12.9 | -10 42 47 | S0 | 17.83 | 19450 51 | 9.10 | e |
| 19 | 10 17 35.6 | -10 39 55 | Sb | 17.15 | 18789 24 | 9.41 | e |
| 20 | 10 17 28.1 | -10 39 27 | Sa | 18.16 | 16842 76 | 4.79 | e |
| 21 | 10 17 27.6 | -10 39 12 | S0 | 18.63 | 16404 92 | 4.48 | e |
| 22 | 10 17 21.0 | -10 40 13 | S0 | 17.18 | 18788 45 | 9.41 | e |
| 23 | 10 17 23.2 | -10 40 18 | E | 18.26 | 19381 40 | 10.12 | e |
| 24 | 10 17 22.0 | -10 39 45 | E | 18.00 | 16847 47 | 6.37 | e |
| 25 | 10 17 22.5 | -10 39 50 | E/S0 | 17.09 | 19483 54 | 9.32 | e |
| 26 | 10 17 25.2 | -10 41 07 | E | 18.87 | 17081 93 | 3.15 | e |
| 27 | 10 17 28.5 | -10 41 13 | E | 17.52 | 33586 98 | 2.84 | e |
| 28 | 10 17 21.9 | -10 43 12 | E/S0 | 18.71 | 17764 64 | 5.17 | e |
| 29 | 10 17 14.4 | -10 39 16 | S | 18.46 | 18415 94 | 3.44 | e |
| 30 | 10 17 12.6 | -10 40 05 | E/S0 | 17.69 | 16533 80 | 5.36 | e |
| 31 | 10 17 33.6 | -10 38 46 | SB | 17.88 | 17779 109 | 4.68 | e |
| 32 | 10 17 44.6 | -10 39 14 | S0/S | 18.09 | 17992 33 | 7.55 | e |
| 33 | 10 17 32.4 | -10 34 27 | S0 | 19.01 | 17606 98 | 2.75 | e |
| 34 | 10 17 30.7 | -10 36 24 | S | 17.43 | 16722 134 | 3.55 | e |
| 35 | 10 17 41.6 | -10 35 46 | S0/S | 17.63 | 21637 37 | 8.62 | e |
| GALAXY | R.A | DEC. | TYPE |
|
VELOCITY | R | N |
| (2000) | (2000) |
|
|||||
| 36 | 10 17 51.1 | -10 35 00 | E | 17.29 | 16661 62 | 4.42 | e |
| 37 | 10 17 36.9 | -10 46 01 | S | 16.8 7 | 11957 79 | 4.97 | e |
| 38 | 10 17 36.8 | -10 46 05 | S0/S | 16.8 7 | 12221 77 | 4.70 | e1 |
| 39 | 10 16 55.8 | -10 38 51 | Sa | 17.83 | 17570 74 | 7.53 | e |
| 40 | 10 16 58.5 | -10 38 07 | S0/S | 16.42 | 17184 44 | 6.33 | e |
| 41 | 10 16 59.7 | -10 37 39 | E | 18.62 | 17873 59 | 6.44 | e |
| 42 | 10 17 00.6 | -10 37 12 | E | 19.16 | 17194 66 | 5.58 | e |
| 43 | 10 17 03.9 | -10 37 38 | E/S0 | 18.11 | 17690 52 | 7.14 | e |
| 44 | 10 17 11.8 | -10 36 07 | E/S0 | 16.43 | 21998 84 | 8.33 | e2 |
| 45 | 10 16 57.5 | -10 40 16 | E | 17.46 | 17903 48 | 9.11 | e |
| 46 | 10 17 02.0 | -10 39 59 | E | 19.10 | 18843 98 | 4.53 | e3 |
| 47 | 10 17 07.6 | -10 45 46 | S0 | 16.89 | 17202 86 | 15.72 | e4 |
| 48 | 10 17 10.2 | -10 46 26 | E/S0 | 17.13 | 17475 46 | 12.24 | e5 |
| 49 | 10 16 49.9 | -10 47 23 | Sb | 16.91 | 17487 64 | 6.73 | e |
| 50 | 10 17 00.5 | -10 47 17 | Sa | 17.38 | 21166 107 | 3.77 | e |
| 51 | 10 16 54.1 | -10 43 10 | S0/S | 18.45 | 17257 85 | 4.71 | e |
| 52 | 10 16 53.2 | -10 43 43 | E | 18.83 | 17351 85 | 6.70 | e |
| 53 | 10 17 47.0 | -10 45 19 | S | 19.14 | 16771 138 | 2.96 | p |
| 54 | 10 18 18.0 | -10 46 48 | E/S0 | 15.95 | 11579 63 | 8.04 | p |
| 55 | 10 18 15.6 | -10 45 03 | S0 | 17.69 | 12056 81 | 3.26 | p |
| 56 | 10 17 51.6 | -10 44 47 | E | 19.44 | 16372 89 | 2.53 | p |
| 57 | 10 17 54.6 | -10 43 47 | S0 | 19.44 | 45962 93 | 2.61 | p |
| 58 | 10 18 06.9 | -10 42 43 | S | 19.13 | 51814 76 | 2.41 | p |
| 59 | 10 18 04.0 | -10 41 44 | SBc | 19.68 | 48068 73 | 3.01 | p |
| 60 | 10 17 57.7 | -10 33 48 | S | 18.52 | 16228 44 | 4.53 | p |
| 61 | 10 18 13.0 | -10 34 42 | S | 18.47 | 11675 69 | 5.34 | o6 |
| 62 | 10 16 55.2 | -10 30 49 | S | 18.16 | 18371 133 | 3.30 | o |
| 63 | 10 16 54.7 | -10 33 22 | S | 17.86 | 17737 75 | 4.47 | o |
| 64 | 10 16 36.9 | -10 32 38 | S0 | 17.58 | 17982 82 | 5.62 | o |
| 65 | 10 16 51.9 | -10 36 15 | S | 17.53 | 18255 84 | 5.39 | o |
| 66 | 10 16 48.8 | -10 39 10 | S0 | 18.67 | 18293 63 | 6.48 | o |
| 67 | 10 17 42.0 | -10 45 49 | E | 18.60 | 12101 114 | 3.22 | o |
| 68 | 10 16 37.3 | -10 32 39 | ? | 18.77 | 17589 136 | 3.04 | o |
| 69 | 10 16 41.3 | -10 52 38 | S | 17.37 | 17649 42 | 8.74 | o |
The new velocities presented in this paper have been obtained with the 1.52 m ESO telescope at La Silla (Chile), the 2.0 m telescope at Pic du Midi (France), and with the 1.93 m telescope at Haute-Provence Observatory (France).
Observations with the 1.52 m ESO telescope were carried out in
February 1996. We used the Boller and Chivens spectrograph at the
Cassegrain focus, equipped with a 600 lines/mm grating blazed at
5000 Å and coupled to an RCA CCD detector (
![]() pixels) with a pixel size of 15
pixels) with a pixel size of 15 ![]() m. The dispersion was 172 Å/mm,
providing spectral coverage from 3750 to 5700 Å. The exposure times
ranged between 30 and 60 min, according to the magnitude of the
object. During the run, calibration exposures were made before and
after each galaxy observation using an He-Ar source.
Observations with the 1.93 m Haute-Provence Observatory telescope were
carried out in November 1997, November 1998 and April 2000. We used the
CARELEC spectrograph at the Cassegrain focus, equipped with a
150 lines/mm grating blazed at 5000 Å and coupled to an EEV CCD
detector (2048
m. The dispersion was 172 Å/mm,
providing spectral coverage from 3750 to 5700 Å. The exposure times
ranged between 30 and 60 min, according to the magnitude of the
object. During the run, calibration exposures were made before and
after each galaxy observation using an He-Ar source.
Observations with the 1.93 m Haute-Provence Observatory telescope were
carried out in November 1997, November 1998 and April 2000. We used the
CARELEC spectrograph at the Cassegrain focus, equipped with a
150 lines/mm grating blazed at 5000 Å and coupled to an EEV CCD
detector (2048![]() 1024 pixels) with a pixel size of 13.5
1024 pixels) with a pixel size of 13.5 ![]() m. The
dispersion of 260 Å/mm allowed a spectral coverage from 3600 to
7300 Å. Wavelength calibration was done using exposures of Hg-Ne
lamps.
m. The
dispersion of 260 Å/mm allowed a spectral coverage from 3600 to
7300 Å. Wavelength calibration was done using exposures of Hg-Ne
lamps.
Part of the velocities were obtained during an observing run at the
2.0 m Bernard Lyot telescope at Pic du Midi Observatory in January 1997.
Despite the declination of Abell 970, we used the ISARD spectrograph in its
long-slit mode with a dispersion of 233 Å/mm with the TEK chip
(1024![]() 1024 pixels) of 25
1024 pixels) of 25 ![]() m, corresponding to 5.8 Å/pixel.
Typically, two exposures of 2700 s each were taken for fields across the
cluster. Wavelength calibration was done using Hg-Ne lamps before and
after each exposure.
m, corresponding to 5.8 Å/pixel.
Typically, two exposures of 2700 s each were taken for fields across the
cluster. Wavelength calibration was done using Hg-Ne lamps before and
after each exposure.
Data reduction was carried out with IRAF![]() using the
longslit package. The spectra were rebinned uniformly in log
wavelength, with a scale of 1 Å/bin. Radial velocities were
determined using the cross-correlation technique (Tonry & Davis 1979)
implemented in the RVSAO package (Kurtz et al. 1991; Mink et al. 1995),
with radial velocity standards obtained from observations of late-type
stars and previously well-studied galaxies.
using the
longslit package. The spectra were rebinned uniformly in log
wavelength, with a scale of 1 Å/bin. Radial velocities were
determined using the cross-correlation technique (Tonry & Davis 1979)
implemented in the RVSAO package (Kurtz et al. 1991; Mink et al. 1995),
with radial velocity standards obtained from observations of late-type
stars and previously well-studied galaxies.
Table 1![]() lists positions and heliocentric velocities for 69 individual
galaxies in the field of the cluster. The entries in the table are:
lists positions and heliocentric velocities for 69 individual
galaxies in the field of the cluster. The entries in the table are:
 |
Figure 1:
Galaxies brighter than
|
| Open with DEXTER | |
We present in Fig. 1 the distribution of galaxies in the
direction of Abell 970, obtained from the COSMOS catalogue, for
galaxies brighter than
![]() (235 objects). The plot
is centered on an E/D galaxy (number 1 in Table 1) and has
(235 objects). The plot
is centered on an E/D galaxy (number 1 in Table 1) and has
![]() (i.e., about
(i.e., about
![]() h50-1 Mpc). It
is interesting to point out that, amongst the galaxies with
known velocities, this is the second brightest cluster galaxy (
h50-1 Mpc). It
is interesting to point out that, amongst the galaxies with
known velocities, this is the second brightest cluster galaxy (
![]() ).
).
The adaptive kernel density map (Silverman 1986) corresponding to this
sample is given in Fig. 2. This figure indicates that the galaxy
distribution in the field of Abell 970 is approximately regular, with
the projected density peaking at the position of the E/D galaxy. There
is a substructure at NW, near galaxy number 40 in Table 1. This is the
brightest cluster galaxy (considering only galaxies with known radial
velocities); it is classified as S0/S and has magnitude
![]() .
This figure also indicates that the cluster radial extension
may attain several Mpc.
.
This figure also indicates that the cluster radial extension
may attain several Mpc.
It is worth noting that all features displayed in this map are significant. The significance regions are obtained through a bootstrap resampling procedure applied to the sample coordinate distribution. This allows the construction of a map of standard deviations of the projected density. By subtracting the projected density map from the standard deviation map (multiplied by a given number, say 3), we define the significance regions of the projected density map as those regions for which the resulting subtracted map is positive.
Abell 970 is an X-ray source, first observed with Einstein IPC in June 1980 (Ulmer et al. 1981). It was also observed during the ROSAT all-sky survey (Voges 1992), in 1990, and is included in the X-ray Brightest Abell type Cluster catalogue (XBACs; Ebeling et al. 1996).
Some properties of the X-ray emission of Abell 970 were derived by
White et al. (1997) from its Einstein IPC image.
They applied a deprojection analysis that, to constrain the cluster
gravitational potential, requires an X-ray temperature (![]() )
and velocity
dispersion (
)
and velocity
dispersion (![]() )
for the cluster. Due to the absence of temperature
measurements for this cluster, these authors estimated
it from a
)
for the cluster. Due to the absence of temperature
measurements for this cluster, these authors estimated
it from a ![]() -
-![]() relation, assuming
relation, assuming
![]() kms-1. The result of the analysis
is
kms-1. The result of the analysis
is
![]() keV. Moreover, White et al. (1997),
using this same data, suggests that Abell 970 has a weak cooling-flow, with
a mass deposition rate
keV. Moreover, White et al. (1997),
using this same data, suggests that Abell 970 has a weak cooling-flow, with
a mass deposition rate
![]() yr-1(see also Loken et al. 1999).
Ebeling et al. (1996)
determined the X-ray flux, luminosity and temperature using an
iterative method running roughly as follows: assuming an initial
X-ray temperature of 5 keV, the bolometric luminosity was computed.
Then, with this luminosity and using the
yr-1(see also Loken et al. 1999).
Ebeling et al. (1996)
determined the X-ray flux, luminosity and temperature using an
iterative method running roughly as follows: assuming an initial
X-ray temperature of 5 keV, the bolometric luminosity was computed.
Then, with this luminosity and using the
![]() relation
from White et al. (1997), a new estimate of the temperature
was made which, in turn, was used to compute a new luminosity and so
on. Thus, with ROSAT data and the above mentioned
relation
from White et al. (1997), a new estimate of the temperature
was made which, in turn, was used to compute a new luminosity and so
on. Thus, with ROSAT data and the above mentioned
![]() relation, Ebeling et al. (1996) quoted a flux equal to
relation, Ebeling et al. (1996) quoted a flux equal to
![]() ergcm-2s-1, luminosity of
ergcm-2s-1, luminosity of
![]() ergs-1 (both in the 0.1-2.4 keV band), and gas
temperature
ergs-1 (both in the 0.1-2.4 keV band), and gas
temperature
![]() keV. By applying this same iterative
method to the Einstein IPC data, Jones & Forman (1999)
derived a X-ray
luminosity of
keV. By applying this same iterative
method to the Einstein IPC data, Jones & Forman (1999)
derived a X-ray
luminosity of
![]() erg s-1 in the [0.5-4.5 keV]
band and a bolometric luminosity equal to
erg s-1 in the [0.5-4.5 keV]
band and a bolometric luminosity equal to
![]() ergs-1, corresponding to a temperature in agreement
with the one given by Ebeling et al. (1996).
ergs-1, corresponding to a temperature in agreement
with the one given by Ebeling et al. (1996).
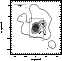 |
Figure 2:
Projected density map of the galaxies brighter than
|
| Open with DEXTER | |
However, since the Einstein IPC detector has some spectroscopic
capability, it is possible to estimate its temperature by a direct
fitting of the available spectra. We have thus obtained both the
"events'' and image (in the 0.2-3.5 keV band, rebinned to 24 arcsec per
pixel) files from the HEASARC Online Service. The spectrum of Abell 970 was
extracted from the events file with XSELECT and analysed with XSPEC
using the PI channels 4-12 (0.5-4.5 keV) within a region of 9.6
arcmin (corresponding to
1 h50-1 Mpc). The X-ray emission was
fitted with a single temperature, absorbed MEKAL model (Kaastra & Mewe
1993; Liedahl et al. 1995). We have also used the recipe given by
Churazov et al. (1996) for computing the weights (available in XSPEC),
based on the smoothed observed spectrum. With these weights, one can
still use the least-square minimisation and the ![]() statistics
to estimate the confidence interval of the fitted parameters.
statistics
to estimate the confidence interval of the fitted parameters.
With only 9 bins covering the 0.5-4.5 keV band, it is impossible to
constrain the metallicity. Therefore we have fixed Z to the
"canonical'' value of ![]()
![]() ,
which is the mean value obtained
for 40 nearby clusters by Fukazawa et al. (1998). Also, with only 3 bins
with energy less than 1 keV, it is difficult to constrain independently
the temperature and the hydrogen column density. This happens because
they are anti-correlated (e.g. Pislar et al. 1997). Therefore, we have also
fixed the hydrogen column density at
,
which is the mean value obtained
for 40 nearby clusters by Fukazawa et al. (1998). Also, with only 3 bins
with energy less than 1 keV, it is difficult to constrain independently
the temperature and the hydrogen column density. This happens because
they are anti-correlated (e.g. Pislar et al. 1997). Therefore, we have also
fixed the hydrogen column density at
![]() cm-2, which is
the galactic value at the Abell 970 position (Dickey &
Lockman 1990). Figure 3 shows the fitting of the
X-ray spectrum using the 9 available energy bins.
The results are summarised in Table 2.
The fitting shown in Fig. 3 presents large residuals at
low energies (
cm-2, which is
the galactic value at the Abell 970 position (Dickey &
Lockman 1990). Figure 3 shows the fitting of the
X-ray spectrum using the 9 available energy bins.
The results are summarised in Table 2.
The fitting shown in Fig. 3 presents large residuals at
low energies (
![]() 1 keV), but beyond
1 keV), but beyond ![]() 2 keV,
which is the region of the spectra
most important for temperature determination, the residuals are acceptable.
Nevertheless, it is worth stressing that the estimated temperature is
strongly dependent on the number of energy bins employed in the analysis.
For instance, keeping only the 8 bins with energy
2 keV,
which is the region of the spectra
most important for temperature determination, the residuals are acceptable.
Nevertheless, it is worth stressing that the estimated temperature is
strongly dependent on the number of energy bins employed in the analysis.
For instance, keeping only the 8 bins with energy
![]() 0.7 keV, the
estimated temperature increases to
4.9-2.1+2.7 kev, with
0.7 keV, the
estimated temperature increases to
4.9-2.1+2.7 kev, with
![]() ,
while with the 7 bins with energy larger than
,
while with the 7 bins with energy larger than
![]() 1 keV the temperature is essentially unconstrained:
1 keV the temperature is essentially unconstrained:
![]() ,
with a
,
with a
![]() .
.
| kT | Z |
|
||
| (keV) | (1020 cm-2) | ( |
(1044 ergs s-1) | |
| 3.3-0.7+1.1 | 5.3 |
0.3 |
1.74-0.10+0.09 | 18.1/7 |
Notes: ![]() Fixed values. Varying the metallicity from 0.1 to 0.5
Fixed values. Varying the metallicity from 0.1 to 0.5 ![]() produces a change in temperature of less than 0.3 keV,
increasing towards
produces a change in temperature of less than 0.3 keV,
increasing towards
![]() .
.
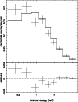 |
Figure 3:
Fit of the Abell 970 IPC X-ray spectrum.
Both the metallicity
and hydrogen column density are fixed (
|
| Open with DEXTER | |
The value of the gas temperature in Table 2,
kT = 3.3 keV, is well below the IPC upper energy cutoff at 4.5 keV.
Although slightly cooler, this value of temperature is
in agreement with those derived by Ebeling et al. (1996) and White et al. (1997), because its error is large (![]() 1 keV
at the 68% confidence level; at the 90% confidence level our
standard solution gives an upper limit for kT of 5.4 keV), due
mainly to the small number of energy bins. We find no evidence from
the data for systematic errors due to unusual background (e.g.,
solar flares).
Using the
1 keV
at the 68% confidence level; at the 90% confidence level our
standard solution gives an upper limit for kT of 5.4 keV), due
mainly to the small number of energy bins. We find no evidence from
the data for systematic errors due to unusual background (e.g.,
solar flares).
Using the
![]() relation given by Wu et al. (1999), the
temperature in Table 2 corresponds to
relation given by Wu et al. (1999), the
temperature in Table 2 corresponds to ![]() in the
range 640-720 kms-1.
in the
range 640-720 kms-1.
In Fig. 4 we display the X-ray isophotes of an
Einstein IPC image in the [0.2-3.5 keV] band. This image has
24 arcsec per pixel. As it can be seen, the X-ray isophotes are also
regular but, interestingly, their peak is not coincident with the peak
of the projected density distribution, being slightly displaced towards
the NW substructure associated to the cluster brightest galaxy (see
Fig. 2).
Figure 4 also suggests that there is no X-ray emission
excess near this substructure. To verify whether this is indeed true,
we have performed a wavelet multi-scale reconstruction on the IPC
image. We have used the package MVM, "Modèle de Vision
Multi-Échelle'', described in detail by Rué & Bijaoui (1997; see
also Slezak et al. 1994 for an application to X-ray cluster images).
With this method, we can remove (spatial) high frequency noise while
retaining small-scale genuine (with ![]() confidence level)
objects. The wavelet image restoration technique is able to locate
structures at various scales simultaneously and superposed objects may
be revealed. The result of this analysis is also shown in
Fig. 4. No emission excess is seen near the substructure.
This is also consistent with the hypothesis that the galaxies in this
substructure are members of a group recently captured by the cluster,
whose X-ray emission is much lower than that of the cluster.
confidence level)
objects. The wavelet image restoration technique is able to locate
structures at various scales simultaneously and superposed objects may
be revealed. The result of this analysis is also shown in
Fig. 4. No emission excess is seen near the substructure.
This is also consistent with the hypothesis that the galaxies in this
substructure are members of a group recently captured by the cluster,
whose X-ray emission is much lower than that of the cluster.
Since the relaxation time of the hot gas is expected to be much lower than that of the galaxies, the non-coincidence between the peak of the galaxy distribution and the X-ray emission may be evidence of a state of non-equilibrium in the galaxy distribution, as expected if the substructure associated with the brightest galaxy has only recently fallen into the cluster. We will explore this point further in next sections.
 |
Figure 4: Left: X-ray isophotes from an Einstein IPC image of Abell 970 (obtained from the HEASARC Online Service) superinposed on a DSS image of the cluster. Upper and left axes give the offset in arcmin from the galaxy number 1 in Table 1. The X-ray levels are linearly spaced. Right: same image but restored with wavelets (see text). |
| Open with DEXTER | |
The X-ray isophotes (even in the restored image) also show a small peak
SE of the cluster centre, at the position of galaxies number 37 and 38 in
Table 1, identified in the COSMOS catalogue as just one galaxy with
magnitude
![]() .
However, an examination of the optical
image of this object using POSS indicates that it indeed corresponds to two
merging galaxies. A butterfly-shape due to the tidal currents induced by
the merger can be noticed in the image and the spectrum of object number 38
has emission lines. It is somewhat surprising that this system is not
catalogued as an IRAS source. The excess of X-ray emission associated with
this galaxy pair may be evidence of an active nucleus excited by the
merger. The magnitudes given in Table 1 were estimated from the COSMOS
magnitude assuming that both galaxies have the same luminosity.
.
However, an examination of the optical
image of this object using POSS indicates that it indeed corresponds to two
merging galaxies. A butterfly-shape due to the tidal currents induced by
the merger can be noticed in the image and the spectrum of object number 38
has emission lines. It is somewhat surprising that this system is not
catalogued as an IRAS source. The excess of X-ray emission associated with
this galaxy pair may be evidence of an active nucleus excited by the
merger. The magnitudes given in Table 1 were estimated from the COSMOS
magnitude assuming that both galaxies have the same luminosity.
Our sample contains 69 velocities in the direction of Abell 970. Figure 5 shows a wedge velocity diagram in the direction of the cluster in right ascension (up) and declination (down), and indicates that most of the velocities are between 15000 and 20000 kms-1. A histogram of the velocity distribution is displayed in Fig. 6. In this section we will discuss the velocity distribution, looking for non-equilibrium effects.
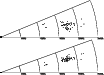 |
Figure 5:
Wedge velocity diagram in right ascension
(up), and declination (down) for the measured galaxies in Abell 970 with
radial velocities smaller than 25000
|
| Open with DEXTER | |
Since the usual recursive ![]() -clipping (Yahil & Vidal 1977) failed to
simultaneously remove the low (
-clipping (Yahil & Vidal 1977) failed to
simultaneously remove the low (
![]() )
and high velocity
(
)
and high velocity
(
![]() )
tails of the distribution, we decided to analyse the
radial velocity distribution of the cluster by constructing four different
data samples to which we applied several statistical tests in order to
assess the normality of their parent distributions. These samples are:
A, comprising all galaxies within
)
tails of the distribution, we decided to analyse the
radial velocity distribution of the cluster by constructing four different
data samples to which we applied several statistical tests in order to
assess the normality of their parent distributions. These samples are:
A, comprising all galaxies within
![]() ;
B, which
is identical to sample A except that the high- and low-velocity tails have
been removed, thus covering the range
;
B, which
is identical to sample A except that the high- and low-velocity tails have
been removed, thus covering the range
![]() ;
C, which is similar to sample B added with the high-velocity tail, that is
;
C, which is similar to sample B added with the high-velocity tail, that is
![]() ;
D, comprising only galaxies in the range
;
D, comprising only galaxies in the range
![]() :
this sample has been considered in view of a
significant gap in the data occurring at
:
this sample has been considered in view of a
significant gap in the data occurring at
![]() (see below).
(see below).
The analysis was made using the ROSTAT statistical package (Beers et al. 1990; Bird & Beers 1993), which proposes various statistical tests based on the empirical distributions of samples. We roughly distinguish 3 categories of normality tests among those included in the ROSTAT package. The first one contains the so-called omnibus tests, which try to quantify the overall deviation of the velocity distribution from a Gaussian, such as the Cramer von-Mises W2 test, the Watson U2 test and the Anderson-Darling A2 test (see Beers et al. 1991, for references). The Kolmogorof-Smirnov (KS) test, which directly calculates the consistency of the observed distribution with a Gaussian, may also be included in this class of tests. The second group of tests are devised to measure the shape of the outskirts of the distribution, such as the kurtosis test (the B2 test) and its robust counterpart, the Tail Index (TI) test (see Bird & Beers 1993, for a discussion), or to test its tail population, such as the a and the W tests, which are most sensitive to the tail of the underlying populations and the u test, which is sensitive to contamination by extreme values (see Yahil & Vidal 1977, for a discussion on these tests). Finally, there are tests which measure the asymmetry of the distribution: the skewness test (B1 test) and its robust version, the Asymmetry Index (AI) test (Bird & Beers 1993). For each of these tests, ROSTAT computes its statistics as well as their associated probabilities p.
The ROSTAT package also provides two statistical tests helping to identify
kinematical substructures in the velocity distributions. These are the gap
analysis (Wainer & Shacht 1978) and the Dip test unimodality (Hartigan &
Hartigan 1985). The Dip test compares the observed distribution against an
uniform one and as so is a conservative test for the unimodality of sample.
The gap analysis estimates the probability that a gap of a given size and
location, between the ordered velocities, may be produced by random sampling
from a Gaussian population. A gap is considered significant if this
probability is less than 0.03. As mentioned above, our radial velocity
sample shows a significant gap at
![]() .
This could be an
indication that the distribution is bimodal. However, the Dip test failed to
reject the unimodality at significance levels better than 10% for any of
the samples.
.
This could be an
indication that the distribution is bimodal. However, the Dip test failed to
reject the unimodality at significance levels better than 10% for any of
the samples.
In Table 3 we list, for each of the samples described above, the values of the statistics and the associated probabilities, p, for the tests discussed above. The B1 and B2 tests were discarded in favour of their robust versions, the AI and the TI tests. Moreover, because the results of the omnibus tests systematically agreed with the KS test, only the results for this last test have been quoted.
| Sample | N | a | p(a) | u | p(u) | W | p(W) |
|
AI |
|
TI |
|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | ||
| A | 65 | 0.639 | 0.01 | 5.005 | 0.838 | 0.01 | 0.01 | 0.069 | 1.292 | 0.05 | ||
| B | 56 | 0.780 | 3.777 | 0.02 | 0.954 | 0.06 | 0.081 | 1.080 | ||||
| C | 59 | 0.711 | 0.01 | 4.730 | 0.881 | 0.01 | 0.01 | 1.057 | 0.04 | 1.273 | 0.05 | |
| D | 48 | 0.829 | 3.403 | 0.01 | 0.940 | 0.02 | -0.514 | 1.015 |
As can be seen from this Table, the normality hypothesis is rejected for
samples A and C at significance levels better than 3% for all the
statistical tests, except the u test. The values of the statistics of
the a and W tests, as well as the TI values, indicate long-tailed
underlying distributions, with sample C being significantly skewed
towards high velocities, a consequence of removing the low-velocity tail
from sample A. Removing both tails of sample A produces sample B,
which seems nearly consistent with normality, as indicated by most of the
tests. Although both the u and the W tests reject normality at high
significance levels for this sample, their results seem contradictory, for
the u statistics suggests a cutoff of the underlying distribution whereas
the W statistics indicates it is long tailed. Notice that both the AI and
TI tests are consistent with a normal underlying distribution for sample B. Very similar results were also obtained for sample D, but now the
distribution seems slightly, but not significantly, skewed towards low
velocities (
![]() ). This is not unexpected for, even if
the marginal indication of bimodality of the distribution given by the gap
analysis were confirmed, there would be no way, at this level of analysis,
to disentangle galaxies belonging to one or to the other underlying
distributions, that is, to B or D. Since the Dip statistics failed to
reject unimodality for any of the samples, we will not consider this
possibility for now, adopting sample B as representative of the radial
velocity distribution of the cluster. We will return to this point at
the end of this section.
). This is not unexpected for, even if
the marginal indication of bimodality of the distribution given by the gap
analysis were confirmed, there would be no way, at this level of analysis,
to disentangle galaxies belonging to one or to the other underlying
distributions, that is, to B or D. Since the Dip statistics failed to
reject unimodality for any of the samples, we will not consider this
possibility for now, adopting sample B as representative of the radial
velocity distribution of the cluster. We will return to this point at
the end of this section.
We will thus assume that the cluster galaxies have radial velocities in the
range between ![]() and
and
![]() .
It is interesting to note that a
low-velocity tail at
.
It is interesting to note that a
low-velocity tail at
![]() ,
similar to the one found here, also
affected the velocity distribution of the cluster Abell 979 (Proust et al.
1995), which is the nearest neighbour cluster of Abell 970 (at about
,
similar to the one found here, also
affected the velocity distribution of the cluster Abell 979 (Proust et al.
1995), which is the nearest neighbour cluster of Abell 970 (at about
![]() NE from its centre), both belonging to the same supercluster. This
suggests the existence of a large foreground structure projected in this
region of the sky.
NE from its centre), both belonging to the same supercluster. This
suggests the existence of a large foreground structure projected in this
region of the sky.
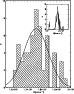 |
Figure 6:
The radial velocity distribution for the
Abell 970 sample of galaxies. The continuous curve shows the Gaussian
distribution corresponding to the mean velocity and velocity dispersion
quoted in the text (normalized to the sample size and range).
The inset displays the velocity distribution between 10000 and 25000
|
| Open with DEXTER | |
Considering only the 56 galaxies within this velocity range, the cluster
mean velocity is
![]() (corresponding to
z =
0.0587)
(corresponding to
z =
0.0587)![]() . For comparison,
the radial velocity of the E/D galaxy located at the centre of main cluster
is
. For comparison,
the radial velocity of the E/D galaxy located at the centre of main cluster
is
![]() ,
near that of the whole cluster, as should be expected
if this is the dominant cluster galaxy. The cluster velocity dispersion,
corrected following Danese et al. (1980) is
,
near that of the whole cluster, as should be expected
if this is the dominant cluster galaxy. The cluster velocity dispersion,
corrected following Danese et al. (1980) is
![]() (at a confidence level of 68%).
Figure 6 presents the radial velocity distribution of the
cluster galaxies, as well as a Gaussian curve with the same mean velocity
and dispersion observed for these galaxies. Note that this value of
(at a confidence level of 68%).
Figure 6 presents the radial velocity distribution of the
cluster galaxies, as well as a Gaussian curve with the same mean velocity
and dispersion observed for these galaxies. Note that this value of
![]() is well above the value favoured by the
is well above the value favoured by the
![]() relation,
relation, ![]()
![]() (cf. Sect. 4).
(cf. Sect. 4).
If we consider the morphological types, the mean velocities and corrected
velocity dispersions are:
![]() and
and
![]() for E + S0 galaxies (35 objects), and
for E + S0 galaxies (35 objects), and
![]() and
and
![]() for S +
I galaxies (19 objects). Hence, contrary to what is observed in most
clusters, where the velocity dispersion of the late type population tends
to be larger than that of the early type population (Sodré et al. 1989;
Stein 1997; Carlberg et al. 1997; Adami et al. 1998), in Abell 970 we do
not see any significant difference between the velocity dispersion of these
two populations. This might be another indication - besides the presence
of a substructure - that Abell 970 is not in overall dynamical
equilibrium.
for S +
I galaxies (19 objects). Hence, contrary to what is observed in most
clusters, where the velocity dispersion of the late type population tends
to be larger than that of the early type population (Sodré et al. 1989;
Stein 1997; Carlberg et al. 1997; Adami et al. 1998), in Abell 970 we do
not see any significant difference between the velocity dispersion of these
two populations. This might be another indication - besides the presence
of a substructure - that Abell 970 is not in overall dynamical
equilibrium.
Let us now consider again the substructure, as well as the peak of the
galaxy distribution (cf. Fig. 2), taking into account the galaxy
velocities. This analysis will be done with galaxies brighter than
![]() ,
the magnitude where the completeness of our
velocity catalogue in the central regions of the cluster is 75%.
,
the magnitude where the completeness of our
velocity catalogue in the central regions of the cluster is 75%.
The substructure NW of the main cluster has, within a 3 arcmin (
274 h50 kpc) circular region centered on the brightest S0/S galaxy, 7
cluster galaxies brighter than
![]() .
Together, these
galaxies have a low velocity dispersion,
.
Together, these
galaxies have a low velocity dispersion,
![]() ,
more typical of that of loose groups. The mean velocity is
,
more typical of that of loose groups. The mean velocity is
![]() ,
significantly higher than the
overall mean velocity of the cluster. Our velocity catalogue contains 2
galaxies fainter that
,
significantly higher than the
overall mean velocity of the cluster. Our velocity catalogue contains 2
galaxies fainter that
![]() inside this region. Their
inclusion does not significantly change the value of the mean velocity,
although it increases the velocity dispersion to
inside this region. Their
inclusion does not significantly change the value of the mean velocity,
although it increases the velocity dispersion to
![]() ,
a value significantly lower than the
cluster overall velocity dispersion. These results are consistent with the
suggestion that this clump of galaxies forms a loose group infalling
towards the cluster main central condensation. Arguing against the reality
of such a group, we notice that its dominant S0/S galaxy is also the lowest
velocity member, with
,
a value significantly lower than the
cluster overall velocity dispersion. These results are consistent with the
suggestion that this clump of galaxies forms a loose group infalling
towards the cluster main central condensation. Arguing against the reality
of such a group, we notice that its dominant S0/S galaxy is also the lowest
velocity member, with
![]() ,
but this is not statistically
significant.
,
but this is not statistically
significant.
The central cluster condensation has a N-S elongation (see
Fig. 2). A closer examination of the galaxy distribution
indicates that this region is dominated by two small clumps of galaxies,
which we will denote by A and B (see also Fig. 7 below).
Considering circular regions of 1 arcmin (![]()
![]() ), the central
clump, A, is tightly concentrated around the E/D galaxy, having 6 galaxies
brighter than
), the central
clump, A, is tightly concentrated around the E/D galaxy, having 6 galaxies
brighter than
![]() with
with
![]() ,
and a
dispersion
,
and a
dispersion
![]() .
The other clump, B, is about 1.5 arcmin NW of
clump A and is more sparse, with only 4 galaxies, of which 3 are tightly
packed in velocity space with velocity dispersion
.
The other clump, B, is about 1.5 arcmin NW of
clump A and is more sparse, with only 4 galaxies, of which 3 are tightly
packed in velocity space with velocity dispersion
![]() and
mean velocity
and
mean velocity
![]() .
The fourth galaxy that is,
apparently, a member of this clump has, however, a very discrepant radial
velocity,
.
The fourth galaxy that is,
apparently, a member of this clump has, however, a very discrepant radial
velocity,
![]() .
Since it is not apparent in Fig. 2, it
is not clear if B is a real substructure or a fortuitous projected group of
cluster galaxies.
.
Since it is not apparent in Fig. 2, it
is not clear if B is a real substructure or a fortuitous projected group of
cluster galaxies.
Figures 7 and 8 display, respectively, the adaptive
kernel maps for the mean velocity and the mean velocity dispersion of the
sample of cluster galaxies with measured radial velocities brighter than
![]() .
These maps were calculated from the local kernel
weighted averages, with initial kernel size usually larger - in our case
by a factor of 3, as a compromise between signal-to-noise and spatial
resolution - than the optimal size prescribed by Silverman (1986), as
suggested by Biviano et al. (1996). Significance regions for each map were
obtained by a bootstrap, in a fashion similar to that applied to the
projected density maps.
.
These maps were calculated from the local kernel
weighted averages, with initial kernel size usually larger - in our case
by a factor of 3, as a compromise between signal-to-noise and spatial
resolution - than the optimal size prescribed by Silverman (1986), as
suggested by Biviano et al. (1996). Significance regions for each map were
obtained by a bootstrap, in a fashion similar to that applied to the
projected density maps.
The mean velocity map of Fig. 7 clearly indicates the
existence of a velocity gradient across the field, roughly in the E-W
direction. This occurs because galaxies with
![]() populate
predominantly the East-side of the field. The mean velocity of the NW group
discussed above is consistent with this gradient. Interestingly, this
gradient is also consistent with the general gradient one would obtain by
considering all galaxies of our catalogue with velocities between
populate
predominantly the East-side of the field. The mean velocity of the NW group
discussed above is consistent with this gradient. Interestingly, this
gradient is also consistent with the general gradient one would obtain by
considering all galaxies of our catalogue with velocities between ![]() and
and
![]() ,
suggesting that the cluster may be part of a larger
structure running more or less in the E-W direction within, at least, this
velocity range. In fact a (smaller) velocity gradient, in this same general
direction, is also depicted by the mean redshifts of the supercluster
members (cf. Einasto et al. 1997).
,
suggesting that the cluster may be part of a larger
structure running more or less in the E-W direction within, at least, this
velocity range. In fact a (smaller) velocity gradient, in this same general
direction, is also depicted by the mean redshifts of the supercluster
members (cf. Einasto et al. 1997).
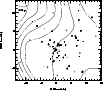 |
Figure 7:
Mean velocity map of the galaxies
kinematically linked to the cluster and brighter than
|
| Open with DEXTER | |
The mean velocity dispersion map displayed in Fig. 8 indicates that there is a radial gradient of the velocity dispersion. This was confirmed by direct calculations of the velocity dispersions within concentric regions centered in the E/D galaxy. Such a gradient is expected if the cluster grows through the capture of low velocity dispersion groups by the central, main galaxy concentration.
The above discussion points to the complexity of the velocity field of
Abell 970. It is possible that the high velocity tail of the cluster velocity
distribution displayed in Fig. 6 may be contaminated by another
component with mean velocity
![]() ,
which
reveals itself trough the peculiarities of its spatial distribution. The
fact that the velocity distribution shows some signs of bimodality, as
pointed out at the beginning of this section, reinforces this suggestion.
If real, this component could be interpreted as a diffuse halo
located at the East-side of the cluster, probably infalling into its dark
matter potential well. If correct, such a scenario may be revealed by
some X-ray emission features typical of gas shocks produced during this
infall.
,
which
reveals itself trough the peculiarities of its spatial distribution. The
fact that the velocity distribution shows some signs of bimodality, as
pointed out at the beginning of this section, reinforces this suggestion.
If real, this component could be interpreted as a diffuse halo
located at the East-side of the cluster, probably infalling into its dark
matter potential well. If correct, such a scenario may be revealed by
some X-ray emission features typical of gas shocks produced during this
infall.
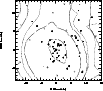 |
Figure 8:
Mean velocity dispersion map of the galaxies
kinematically linked to the cluster and brighter than
|
| Open with DEXTER | |
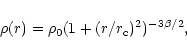 |
(2) |
Furthermore, if we have the density contrast
![]() (where
(where
![]() is the mean density
inside the radius r and
is the mean density
inside the radius r and
![]() is the critical density at the
redshift of the cluster) then we can define
is the critical density at the
redshift of the cluster) then we can define
![]() as
as
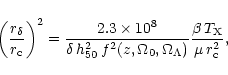 |
(4) |
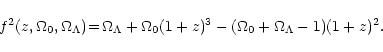 |
(5) |
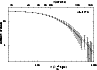 |
Figure 9:
X-ray brightness profile (IPC data with error bars),
obtained with the STSDAS/IRAF task ellipse; the continuous
line is the best-fit |
| Open with DEXTER | |
In Fig. 10 we show the cluster mass profile computed with the
virial mass estimator (VME) which, as discussed by Aceves & Perea (1999),
gives less biased mass estimates when the system is not completely
sampled. These authors also show that the VME overestimates the real mass
by no more than 20% at small radii, being more reliable at larger
apertures. The error bars in Fig. 10 are 1-![]() standard deviations
computed using the bootstrap method. The VME assumes, of course, that the
system is virialized. In general, the presence of substructures or
large-scale flows tend to increase the velocity dispersion of the galaxies,
leading to an overestimation of the mass of the system.
standard deviations
computed using the bootstrap method. The VME assumes, of course, that the
system is virialized. In general, the presence of substructures or
large-scale flows tend to increase the velocity dispersion of the galaxies,
leading to an overestimation of the mass of the system.
The VME of Abell 970, within
1.2 h50-1 Mpc, is
![]() ,
where the error, as before, was computed with
the bootstrap method. Note that, for a virialized cluster, these are lower
limits for the mass, since we have velocities only for the central region
of the system. Indeed, assuming a relation between virial radius and
velocity dispersion similar to that adopted by Girardi et al. (1998), we
estimate that
,
where the error, as before, was computed with
the bootstrap method. Note that, for a virialized cluster, these are lower
limits for the mass, since we have velocities only for the central region
of the system. Indeed, assuming a relation between virial radius and
velocity dispersion similar to that adopted by Girardi et al. (1998), we
estimate that
![]() Mpc, while the velocities have
been measured within a region of radius
Mpc, while the velocities have
been measured within a region of radius ![]() 1.2 h50-1 Mpc.
1.2 h50-1 Mpc.
Figure 10 also displays the run of the total bj luminosity of
the cluster (up to
bj = 19.75). Considering the VME masses, we find that
the mass-luminosity ratio ranges from 1360
![]() at the cluster central region, to
at the cluster central region, to ![]() 450
450
![]() at the largest aperture.
at the largest aperture.
The mass profile derived from the X-ray emission is also presented in
Fig. 10. The VME masses are in excess of the X-ray mass
estimates by large factors, ranging from ![]() 16 for the central
apertures, to about 4 at
16 for the central
apertures, to about 4 at ![]() 1.3
h50-1 Mpc aperture, which
encompasses the whole velocity sample. These factors are well above the
uncertainties discussed above for virialized clusters. In fact, the
dynamical mass determined by the X-ray emission at radius
1.3
h50-1 Mpc aperture, which
encompasses the whole velocity sample. These factors are well above the
uncertainties discussed above for virialized clusters. In fact, the
dynamical mass determined by the X-ray emission at radius
![]() depends essentially on the temperature and the asymptotic slope of the
gas density. Both are poorly determined with the available data; it is then
possible that one of them (or both) are under-estimated, which implies that
we under-estimate the dynamical X-ray mass. For instance, if
depends essentially on the temperature and the asymptotic slope of the
gas density. Both are poorly determined with the available data; it is then
possible that one of them (or both) are under-estimated, which implies that
we under-estimate the dynamical X-ray mass. For instance, if ![]() is as
high as 0.70 and
is as
high as 0.70 and
![]() (cf. the error bars in Table 2), then the
dynamical X-ray mass would be twice the estimated value, i.e.,
M(r=1.2 h50-1 Mpc
(cf. the error bars in Table 2), then the
dynamical X-ray mass would be twice the estimated value, i.e.,
M(r=1.2 h50-1 Mpc
![]() .
On the other hand,
the presence of a substructure associated with the cluster brightest galaxy,
as well as the mean velocity gradient, may be an indication of
non-virialization and, consequently, the VME may be largely overestimated.
.
On the other hand,
the presence of a substructure associated with the cluster brightest galaxy,
as well as the mean velocity gradient, may be an indication of
non-virialization and, consequently, the VME may be largely overestimated.
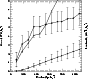 |
Figure 10: Cluster optical masses (circles and dotted lines), X-ray masses (squares and dot-dashed lines) and luminosities (triangles and dashed lines). |
| Open with DEXTER | |
Several lines of evidence indicate that Abell 970 is not in an overall state of virialized equilibrium. Indeed, the presence of a substructure NW of the main galaxy concentration may indicate that the cluster has been capturing groups of galaxies in its neighbourhood. The large-scale gradient in the mean velocity of the galaxies, shown in Fig. 7, is also not expected in virialized systems. Other evidence for non-equilibrium include the discrepancy in the peaks of the X-ray emission and of the galaxy projected density, and the observed differences between optical and X-ray masses.
According to Allen (1998), there is a good agreement between X-ray and
strong gravitational lensing mass measurements only in clusters with strong
cooling flows; in clusters with modest or absent cooling flows, the masses
determined from the X-ray data are 2 to 4 times smaller than those
estimated from strong gravitational lensing. The reason for the mass
discrepancy is the dynamical status of the central regions of the clusters:
those with strong cooling flows are relaxed and virialized, while those
with small cooling flows are out of equilibrium, and the assumption of
hydrostatic equilibrium that underlies the X-ray mass estimates is not
valid. Indeed, the presence or absence of cooling flows can be used as a
diagnostic to verify whether galaxy clusters are in dynamical equilibrium
in their central regions. Abell 970 has at most a weak cooling flow, of
![]() yr-1 (Ebeling et al. 1996), and our
results, indicating that this system is not relaxed, are consistent with
the findings of Allen (1998).
yr-1 (Ebeling et al. 1996), and our
results, indicating that this system is not relaxed, are consistent with
the findings of Allen (1998).
It is interesting to note that the offset between the X-ray and galaxy distribution centres, although significant, is not very large. It is possible that Abell 970 had a much stronger cooling flow until recently, that was interrupted by dynamical perturbations induced by the arrival of a galaxy group (now observed as a substructure) in the central regions of the cluster. Given that in the cluster densest regions the gas relaxes very quickly, compared with the time the galaxy distribution takes to achieve equilibrium, it is natural to think of cooling flows as an intermittent process that is disrupted by dynamical perturbations and that resumes activity after relaxation is achieved. The time scale of intermittence, in this scenario, depends strongly on the accretion rate of groups by the cluster.
In this paper, we have presented an analysis of the galaxy cluster Abell 970, based on a new set of radial velocities and on X-ray observations. The study of the galaxy projected positions reveals a relatively regular distribution, centered on an E/D dominant galaxy. The analysis with the adaptive kernel density map indicates the presence of a statistically significant substructure NW of the cluster main galaxy concentration, centered on a S0/S galaxy that is the brightest cluster member. The X-ray emission distribution does not reveal any emission excess due to that substructure but, interestingly, the peak of the X-ray emission is not coincident with the cluster centre (at the position of the dominant galaxy), being displaced towards the direction of the substructure. These results suggest that this substructure is real and that the cluster may not be in an overall state of dynamical equilibrium.
Further evidence that the cluster is in a state of non-equilibrium comes
from the analysis of the radial velocity distribution. For instance, the
cluster velocity dispersion, 845 kms-1 (increasing to ![]() 1000 kms-1 at the cluster centre), is significantly larger than the value
expected from the
1000 kms-1 at the cluster centre), is significantly larger than the value
expected from the
![]() relation, that is,
relation, that is, ![]() 700 kms-1.
Also, the substructure detected in the galaxy projected distribution has a
much smaller velocity dispersion, 381 kms-1, that is typical of loose
groups. Together, these results suggest that this substructure may be a
group that recently arrived in the central regions of the cluster. The
presence of large scale velocity gradients is further evidence that Abell 970 is out of equilibrium. The virial mass of this cluster is much larger
than the mass inferred from the X-ray emission. This discrepancy is indeed
expected if the underlying hypothesis of these mass estimators, namely that
galaxies and gas inside the cluster are in hydrostatic equilibrium, is not
actually fulfilled.
700 kms-1.
Also, the substructure detected in the galaxy projected distribution has a
much smaller velocity dispersion, 381 kms-1, that is typical of loose
groups. Together, these results suggest that this substructure may be a
group that recently arrived in the central regions of the cluster. The
presence of large scale velocity gradients is further evidence that Abell 970 is out of equilibrium. The virial mass of this cluster is much larger
than the mass inferred from the X-ray emission. This discrepancy is indeed
expected if the underlying hypothesis of these mass estimators, namely that
galaxies and gas inside the cluster are in hydrostatic equilibrium, is not
actually fulfilled.
The fact that Abell 970 has a dim cooling flow also fits nicely in the above scenario if, as suggested by Allen (1998), only clusters in equilibrium exhibit massive cooling flows. Indeed, cooling flows may have an intermittent behaviour: phases of massive cooling flows may be followed by phases without significant cooling flows after the accretion of a galaxy group massive enough to disrupt the dynamical equilibrium in the centre of the clusters. After a new equilibrium is achieved, a massive cooling flow will be established again. Hence, in hierarchical scenarios for structure formation, intermittent cooling-flows should be a common phenomenon.
Acknowledgements
We thank the OHP, Pic du Midi and ESO staff for their assistance during the observations, and especially Gilles Charvin, student at the École Normale Supérieure de Lyon for his valuable scientific collaboration. We also thank Bill Forman and Christine Jones for valuable comments on the spectroscopic capability of the Einstein IPC detector, and Sergio Dos Santos for help with the wavelet package. LSJ, HVC, GBLN and HC thank the financial support provided by FAPESP, CNPq and PRONEX. DP and HQ acknowledge support from ECOS/CONICYT project C96U04. HQ was partly supported by the award of a Presidential Chair in Science (Chile). This research has made use of data obtained through the High Energy Astrophysics Science Archive Research Center Online Service, provided by the NASA/Goddard Space Flight Center, and of the ROE/NRL COSMOS UKST Southern Sky Object Catalog.